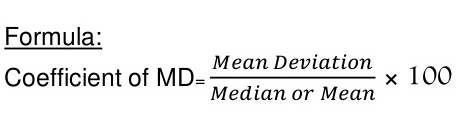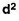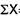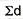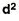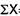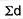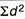UNIT 1
Introduction
The word statistics is derived from the Latin word “Status” that means a group of numbers that represent some information of our human interest. In ancient periods, the use of statistics was made to meet the administrative needs of the state. In modern time, the statistics is not only used for administrative of the state alone, also evaluate all those activities in our lives which can be expressed in quantitative terms.
The term “statistics” is defined in two senses: - in singular and in Plural senses.
Firstly in plural sense, statistics means systematic collection of numerical facts. Secondly in singular sense, the term statistics means the various methods used for collection, analysis and interpretation of numerical facts. It is described as statistical method. In our study we are more concerned with the second meaning of statistics.
Definition:
“Statistics is a body of methods for making wise decisions on the face of uncertainty.” —Wallis and Roberts
“Statistics is a body of methods for obtaining and analyzing numerical data in order to make better decisions in an uncertain world.” —Edward N. Dubois
Statistics are numerical statement of facts in any department of enquiry placed interrelation to each other.- Bouly.
The science of Statistics is essentially a branch of applied mathematics and can be regarded as a mathematics applied to observation data.- R.A fisher.
After analyzing the various definitions of statistics, the most proper definition of statistics are as follows
“Statistics in the plural sense are numerical statements of facts capable of some meaningful analysis and interpretation, and in singular sense, it relates to the collection, classification, presentation and interpretation of numerical data.”
Scope of statistics
Functions of statistics:
2. Presentation of facts – Statistics helps in presenting the complex data in a simple form, so that it becomes easy to understand. Statistical methods present data in the form of graph, diagram, average, coefficient, etc.
3. Comparison – After simplifying the data, it can be correlated and compared. Comparing data relating to fact is one of the functions of statistics as absolute figures convey less meaning.
4. It helps other science- Many laws of economic, law of demand, law of supply have been verified with the help of statistics.
5. Forecasting – Statistics also predicts future course of action. On the basis of estimates with the help of statistics we can make future policies.
6. Policy making – Statistics helps in formulating favorable policies. Based on the forecast the government makes policies.
Uses and importance of statistics:
2. Importance for businessman – statistics helps in providing relevant data. Thus with the help of those data a business man can estimate demand and supply of the commodity.
3. Importance in economics – statistics helps in measuring economics such as gross national output, consumption, saving, investment, expenditures, etc
4. Importance for politician – Politician use statistics in formulating economic, social and educational policies of the country
5. Importance in the field of education – statistics has wide application in education for determining the reliability and viability to a test, factor analysis, etc.
Limitation of statistics:
2. Study of aggregates only – statistics study only aggregates of quantitative facts. It does not study any particular unit. Prof. Horace Sacrist defined statistics, “By statistics we mean aggregates of facts…. and placed in relation to each other”
3. It does not depict the entire story of phenomena – Any phenomena happen, due to many causes. But all the cause is not expressed in numbers. So, correct conclusion cannot be drawn. Analyzing quantitative data and ignoring qualitative data cannot give 100% conclusion.
4. Homogeneity of data – To compare the data, it is essential that whatever statistics are collected, the same must be uniform in quality.
5. It is liable to be miscued – As W.I. King points out, “One of the short-comings of statistics is that do not bear on their face the label of their quality.” Thus the data collected by inexperienced person may be dishonest or biased. So to get correct conclusion data must be used in caution.
6. Too many methods to study a problem –to find a single result many statistical methods are used. All the methods result vary in each case. “It must not be assumed that the statistics is the only method to use in research, neither should this method of considered the best attack for the problem.” —Croxten and Cowden.
Types and method of collection of data
Definition:
Data collection is defined as the procedure of collecting, measuring and analyzing accurate insights for research using standard validated techniques.
Irrespective of the field of research, data collection is the primary and most important step for research. Depending on the required information, the approach of data collection is different for different fields of study.
The objective of data collection is ensuring that rich information and reliable data is collected for statistical analysis so that data-driven decisions can be made for research.
Data collection method:
Data collection methods can be divided into two categories: secondary methods of data collection and primary methods of data collection.
Secondary data - Secondary data is a type of data that has already been published in books, newspapers, magazines, journals, online portals etc. there is lot of information available in these sources. Therefore appropriate secondary data are used in the study plays an important role in terms of increasing the levels of research validity and reliability.
Primary data –
Primary data collection methods can be divided into two groups: quantitative and qualitative.
Quantitative data collection methods are based in mathematical calculations in various formats. Methods of quantitative data collection and analysis include questionnaires with closed-ended questions, methods of correlation and regression, mean, mode and median and others. Quantitative methods are less expensive and they can be applied within shorter duration of time. These methods are easy to make comparison between the findings.
Qualitative research methods, on the other hand, do not involve numbers or mathematical calculations. Qualitative research is closely associated with words, sounds, feeling, emotions, colours and other elements that are non-quantifiable.
Primary and secondary data are discussed more in detail in the below section.
Primary data is the information collected through original or first-hand research. Primary data is more reliable and authenticate as the data is nor changed or altered by any human beings. Also, the data is not published yet. Primary data is gathered by any authorized organization, investigator, and enumerator.
“Data which are gathered originally for a certain purpose are known as primary data.” — Horace Secrist
Sources of primary data
The sources of primary data are as follows –
1. Experiments: In natural sciences, experiments are most reliable source of data collections. Experiments are conducted for medicine, psychological studies, nutrition and other scientific studies. Experiments are conducted in the fields as well as laboratories. The results of experiments are analysed by statistical test and thereafter conclusions are drawn.
2. Survey: surveys are used in social science, management, marketing and psychology to some extent. Surveys are conducted in different methods.
3. Questionnaire: Questionnaires consist of list of question either open ended or close ended for which the participants answer. Questionnaire can be conducted via telephone, mail, institute, fax, etc.
4. Interview: Interviews are expensive method of data collection. The interviewer collects information from each respondent independently. It involves in-depth questioning and follow up question. While taking interview, the interviewer can observe the body language and other reaction to the question.
5. Observation: observation can be conducted with or without knowledge of the participants. Observation can be made either natural or artificially created environment.
Secondary Data:
Secondary data are public information that has been collected by others. The data collected from primary research and used by other is referred as secondary data. The secondary data may be obtained from various sources like industry surveys, database and information system, etc.
“The data which are used in an investigation, but which have been gathered originally by someone else for some other purpose are known as secondary data.” — Blair
Sources of secondary data:
2. Books – books are available on any topic you want to research. Books provide insight on how much information is given for a particular topic and you can prepare your literature review.
3. Journals – journals provide up to date information on the very specific topic on which you want to research. Journal is one of the most important sources for providing the information on data collected.
4. Magazine or newspaper – Newspaper or magazine provide daily information regarding politics, business, sports, fashion, etc which can be used for conducting research.
5. Internet – internet is becoming advance, fast and reachable to the masses and much information is available on internet. Almost all journals, books are available on internet. Some are free and others you have to pay price
6. Company website – company’s website provides lots of information. They have a section called investor relations which contains full of annual reports, regulatory findings and investor presentations that can provide insights into both the individual company’s performance and that of the industry at large.
Key takeaways – data can be collected through primary and secondary data
Preparation of frequency distribution
After data collection, you may face the problem of arranging them into a format from which you will be able to draw some conclusions. The arrangement of these data in different groups on the basis of some similarities is known as classification. According to Tuttle, “ A classification is a scheme for breaking a category into a set of parts, called classes, according to some precisely defined differing characteristics possessed by all the elements of the category” Thus classification, is the process of grouping data into sequences according to their common characteristics, which separate them into different but related parts.
Such classification facilitates analysis of the data and consequently prepares a foundation for absolute interpretation of the obtained scores. The prime objective of the classification of data is concerned with reducing complexities with raw scores by grouping them into some classes. This will provide a comprehensive insight into the data.
The classification procedure in statistics enables the investigators to manage the raw scores in such a way that they can proceed with ease in a systematic and scientific manner.
Key takeaways –
Graphical presentation of data
A graph is a visual form of presentation of statistical data. A graph is more attractive than a table of figure. It helps the common man to understand more efficiently and effectively. It facilitates comparisons between two or more phenomena very easily.
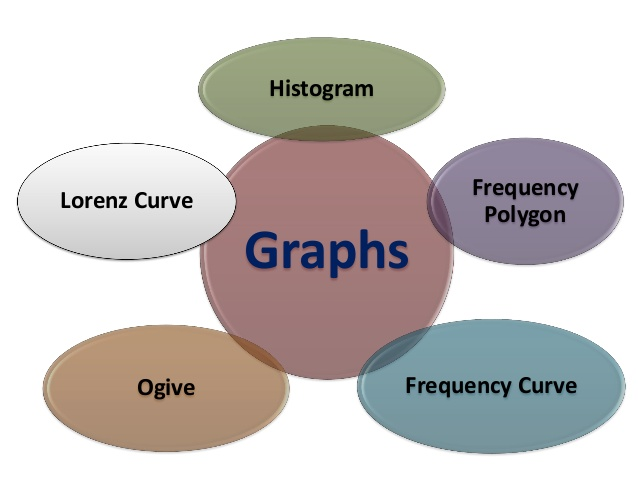
Histogram – histogram is a bar graph representing the frequency of occurrence by classes of data. In histogram data are plotted as a series of rectangle. ‘X axis’ consist of class intervals and ‘Y axis’ shows the frequencies. It is also called stair case or block diagram. Histogram is not suitable for open ended classes.

Frequency polygon –a frequency polygon is a graph where midpoints of each interval are joined by using lines. The heights of the points represent the frequencies. It is usually done by creating a histogram or by calculating the midpoints of each interval from the frequency distribution table.
Frequency curve – a frequency curve is a smooth curve obtained by joining the midpoints of all rectangles forming histogram. It is drawn by using free hand. The curve should begin and end at the base line.
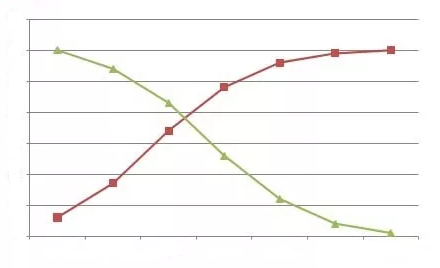
Ogive – An ogive graph shows cumulative frequency in statistics. It estimates the number of observations less than a given value or more than a given value. Cumulative frequency is obtained by adding to the given value
Less than ogive method - The frequencies of all preceding classes are added to the frequency of a class.
More than ogive class - The frequencies of the succeeding classes are added to the frequency of a class
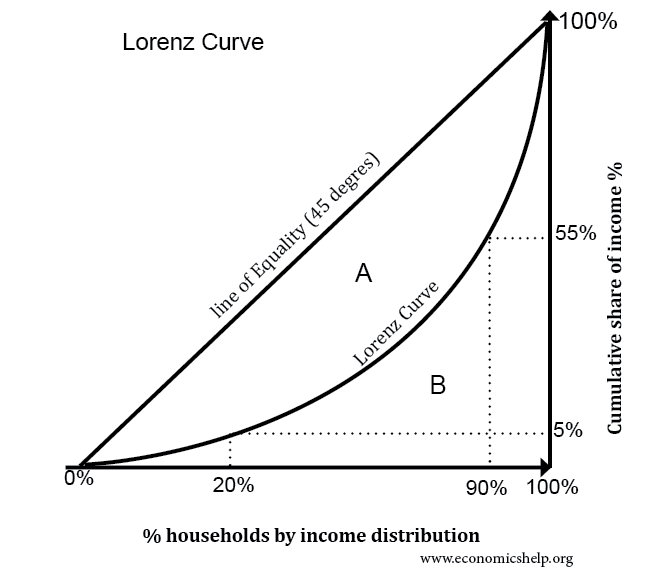
Lorenz curve – It is the graphical representation of income and wealth. It was developed by Max O. Lorenz in 1905. The Lorenz curve shows how wealth, revenue, land, etc are not equally distributed among the people.
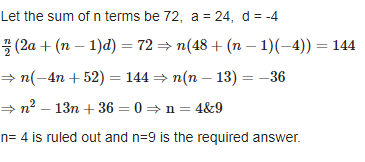
Key takeaways –
Types of series
Arithmetic Progression
Arithmetic Progression Define
An A.P. is referred as a sequence in which terms increase or decrease by a fixed number referred as common difference of the A.P.
AP. Sequence is expressed as a, a + d, a + 2d, …..
a: first term, d: common difference
nth Term formula
an = a + (n-1)d
an: nth term, n: number of terms
Sn Sum of the 1st n terms
Sn = n/2(2a+(n-1)d) = n/2 (a + l)
l= last term
To each term of a given A.P. a fixed number is added or subtracted or multiplied or divided the resulting sequence is an AP with a common difference d.
Consider 2 AP’s a1, a2, a3….. and b1, b2, b3….. with common differences d and d’ respectively then a1+b1, a2+b2, a3+b3…. is also an A.P. with common difference d + d’
General combination of 3 terms in an A.P. a – d, a, a + d.
General combination of 4 terms in an A.P. a – 3d, a – d, a + d, a + 3d.
In case a1, a2, a3,…… an are in A.P. then relation will be a1 + an = a2 + an-1 = a3 + an-2 = ……
If nth term of a sequence is a linear expression in n, the sequence will be an AP; its common difference will be coefficient of n.
In case sum of n terms of a sequence is a quadratic in n, its constant term is zero, the sequence will be an AP, its common difference is twice the coefficient of n2. If constant term is non-zero, it will be an .A.P. from 2nd term onwards.
Example 1
Find the value of n. If a = 10, d = 5, an = 95.
Solution
Given, a = 10, d = 5, an = 95
From the formula of general term, we have:
an = a + (n − 1) × d
95 = 10 + (n − 1) × 5
(n − 1) × 5 = 95 – 10 = 85
(n − 1) = 85/ 5
(n − 1) = 17
n = 17 + 1
n = 18
Example 2
Find the 20th term for the given AP:3, 5, 7, 9, ……
Solution: Given,
3, 5, 7, 9, ……
a = 3, d = 5 – 3 = 2, n = 20
an = a + (n − 1) × d
a20 = 3 + (20 − 1) × 2
a20 = 3 + 38
⇒a20 = 41
Example 3:
Find the sum of first 30 multiples of 4.
Solution: Given, a = 4, n = 30, d = 4
We know,
S = n/2 [2a + (n − 1) × d]
S = 30/2[2 (4) + (30 − 1) × 4]
S = 15[8 + 116]
S = 1860
Example 4 –
How many terms are added in 24+20+16+ ....... 10 make the sum 72.
Solution
We know that sum to first n terms of an A.P. = Sn = n/2 [2a + (n – l) d]
Let the sum of n terms be 72, a = 24, d = -4
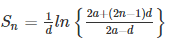
Key takeaways –
Geometric Progression
G.P. is a sequence its 1st term is non-zero and its succeeding terms is r times the previous term, r is a fixed non-zero number called as the common ratio of the G.P.
nth Term and Sum of n Terms:
‘a’ : 1st term, ‘r’ : common ratio
G.P. is a, ar, ar2, …..
nth Term ‘an’ is specified as an = arn-1
Sum Sn of the 1st n terms of the G.P. is
Sn = [a(rn -1)]/(r-1) ; r ≠1
= na, r =1
Consider -1< r <1,
Sum of the infinite G.P. is
a + ar + ar2 + ……= a/(1-r).
In case each term of a G.P. is multiplied by a fixed non-zero constant, the resulting sequence is a G.P. with a common ratio.
If each term of a G.P. is increased to the power k, the resulting sequence will be a G.P. with common ratio rk.
a1, a2, a3…… is a G.P. with common ratio r.
b1, b2, b3…… is a G.P. with common ratio r’.
The sequence will be a1b1, a2b2, a3b3 is a G.P. with common ratio rr’.
Consider 3 terms in G.P. as a/r, a, ar. In case we have to take (2k+1) terms in a
G.P. we take a/rk, a/rk-1, a, ar, ark
For 4 terms in a G.P. we take a/r3, a/r, ar, ar3. For 2k terms in a G.P. we take
a/r2k-1, a/r2k-3, ……., a/r, ar, ….ar2k-1
If a1, a2,…..,an are in G.P. then a1 an = a2 an-1 = a3 an-2 = …..
If a1, a2, a3, ………. is a G.P. then loga1, loga2, loga3…… is an AP. The converse is also true.
If {tn} is a G.P. then the common ratio r = (tp/tq)1/p-q
Harmonic Progression (H.P.)
If the sequence 1/a1, 1/a2, 1/a3, …..1/an, ……, is an AP then the sequence a1, a2, a3……an….
(ai ≠ 0) is said to be an H.P.
nth Term of H.P.
Sum of n terms,
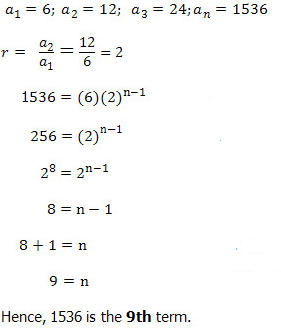
Where,
“a” is the first term of A.P
“d” is the common difference of A.P
“ln” is the natural logarithm Examples 1
If the first term is 10 and the common ratio of a GP is 3. Then write the first five terms of GP.
Solution: Given,
First term, a = 10
Common ratio, r = 3
We know the general form of GP for first five terms is given by:
a, ar, ar2, ar3, ar4
a = 10
ar = 10 x 3 = 30
ar2 = 10 x 32 = 10 x 9 = 90
ar3 = 10 x 33 = 270
ar4 = 10 x 34 = 810
Therefore, the first five terms of GP with 10 as first term and 3 as common ratio is:
10, 30, 90, 270 and 810
Examples 2
The sum of three numbers in a GP is 26 and their product is 216. ind the numbers.
Solution : Let the numbers be a/r, a, ar.
=> (a / r) + a + a r = 26
=> a (1 + r + r2) / r = 26
Also, it is given that product = 216
=> (a / r) x (a) x (a r) = 216
=> a3 = 216
=> a = 6
=> 6 (1 + r + r2) / r = 26
=> (1 + r + r2) / r = 26 / 6 = 13 / 3
=> 3 + 3 r + 3 r2 = 13 r
=> 3 r2 – 10 r + 3 = 0
=> (r – 3) (r – (1 / 3) ) = 0
=> r = 3 or r = 1 / 3
Thus, the required numbers are 2, 6 and 18.
Examples 3
Find the number of terms in the geometric progression 6, 12, 24, ..., 1536
Solution
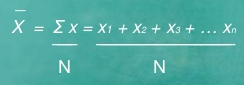
Examples 4
Determine the 4th and 8th term of the harmonic progression 6, 4, 3,…
Solution:
Given:
H.P = 6, 4, 3
Now, let us take the arithmetic progression from the given H.P
A.P = ⅙, ¼, ⅓, ….
Here, T2 -T1 = T3 -T2 = 1/12 = d
So, in order to find the 4th term of an A. P, use the formula,
The nth term of an A.P = a+(n-1)d
Here, a = ⅙, d= 1/12
Now, we have to find the 4th term.
So, take n=4
Now put the values in the formula.
4th term of an A.P = (⅙) +(4-1)(1/12)
= (⅙)+(3/12)
= (⅙)+ (¼)
= 5/12
Similarly,
8th term of an A.P = (⅙) +(8-1)(1/12)
= (⅙)+(7/12)
= 9/12
Since H.P is the reciprocal of an A.P, we can write the values as:
4th term of an H.P = 1/4th term of an A.P = 12/5
8th term of an H.P = 1/8th term of an A.P = 12/9 = 4/3
Examples 5
Compute the 16th term of HP if the 6th and 11th term of HP are 10 and 18 respectively.
Solution:
The H.P is written in terms of A.P are given below:
6th term of A.P = a+5d = 1/10 —- (1)
11th term of A.P = a+10d = 1/18 ……(2)
By solving these two equations, we get
a =13/90, and d = -2/ 225
To find 16th term, we can write the expression in the form,
a+15d = (13/90) – (2/15) = 1/90
Thus, the 16th term of an H.P = 1/16th term of an A.P = 90
Therefore, the 16th term of the H.P is 90.
Key takeaways –
A measure of central tendency is a statistical summary that represents the center point of the dataset. It indicates where most values in a distribution fall. It is also called as measure of central location.
The three most common measure of central tendency are Mean, Median, and Mode.
Definition
According to Prof Bowley “Measures of central tendency (averages) are statistical constants which enable us to comprehend in a single effort the significance of the whole.”
Requisites of a good measure of central tendency
Arithmetic mean-
a) The mean is the arithmetic average, also called as arithmetic mean.
b) Mean is very simple to calculate and is most commonly used measure of the center of data.
c) Means is calculated by adding up all the values and divided by the number of observation.
Computation of sample mean -
If X1, X2, ………………Xn are data values then arithmetic mean is given by
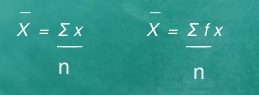
Computation of the mean for ungrouped data
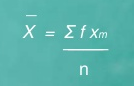
Example 1 – The marks obtained in 10 class test are 25, 10, 15, 30, 35


 The mean = X = 25+10+15+30+35 = 115 =23
The mean = X = 25+10+15+30+35 = 115 =23
5 5
Analysis – the average performance of 5 students is 23. The implication that students who got below 23 did not perform well. The students who got above 23 performed well in exam.
Example 2 – find the mean
Xi | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Freq (Fi) | 2 | 5 | 12 | 17 | 14 | 6 | 3 |
Xi | Freq (Fi) | XiFi |
9 | 2 | 18 |
10 | 5 | 50 |
11 | 12 | 132 |
12 | 17 | 204 |
13 | 14 | 182 |
14 | 6 | 84 |
15 | 3 | 45 |
| Fi = 59 | XiFi= 715 |
|
|
|
Then, N = ∑ fi = 59, and ∑fi Xi=715
 X = 715/59 = 12.11
X = 715/59 = 12.11
Mean for grouped data
Grouped data are the data that are arranged in a frequency distribution
Frequency distribution is the arrangement of scores according to category of classes including the frequency.
Frequency is the number of observations falling in a category
The formula in solving the mean for grouped data is called midpoint method. The formula is
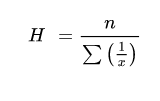
 Where,X = Mean
Where,X = Mean
Xm = midpoint of each class or category
f = frequency in each class or category
∑f Xm = summation of the product of fXm
Example 3 – the following data represent the income distribution of 100 families. Calculate mean income of 100 families?
Income | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
No. of families | 8 | 12 | 25 | 22 | 16 | 11 | 6 |
Solution
Income | No. of families | Xm (Mid point) | fXm |
30-40 | 8 | 35 | 280 |
40-50 | 12 | 34 | 408 |
50-60 | 25 | 55 | 1375 |
60-70 | 22 | 65 | 1430 |
70-80 | 16 | 75 | 1200 |
80-90 | 11 | 85 | 935 |
90-100 | 6 | 95 | 570 |
| n = 100 |
| ∑f Xm = 6198 |

X = ∑f Xm/n = 6330/100 = 63.30
Mean = 63.30
Example 4 – calculate the mean number of hours per week spent by each student in texting message.
Time per week | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 – 30 |
No. of students | 8 | 11 | 15 | 12 | 9 | 5 |
Solution
Time per week (X) | No. of students (F) | Mid point X | XF |
0 - 5 | 8 | 2.5 | 20 |
5 – 10 | 11 | 7.5 | 82.5 |
10 - 15 | 15 | 12.5 | 187.5 |
15 - 20 | 12 | 17.5 | 210 |
20 - 25 | 9 | 22.5 | 202.5 |
25 – 30 | 5 | 27.5 | 137.5 |
| 60 |
| 840 |
Mean = 840/60 = 14
Example 5 –
The following table of grouped data represents the weights (in pounds) of all 100 babies born at a local hospital last year.
Weight (pounds) | Number of Babies |
[3−5) | 8 |
[5−7) | 25 |
[7−9) | 45 |
[9−11) | 18 |
[11−13) | 4 |
Solution
Weight (pounds) | Number of Babies | Mid point X | XF |
[3−5) | 8 | 4 | 32 |
[5−7) | 25 | 6 | 150 |
[7−9) | 45 | 8 | 360 |
[9−11) | 18 | 10 | 180 |
[11−13) | 4 | 12 | 48 |
| 100 |
| 770 |
Mean = 770/100 = 7.7
Importance of mean
Demerits of mean
Key takeaways –
Harmonic mean:
Harmonic mean is quotient of “number of the given values” and “sum of the reciprocals of the given values
For ungrouped data
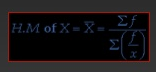
Example 1 - Calculate the harmonic mean of the numbers 13.2, 14.2, 14.8, 15.2 and 16.1
Solution
X | 1/X |
13.2 | 0.0758 |
14.2 | 0.0704 |
14.8 | 0.0676 |
15.2 | 0.0658 |
16.1 | 0.0621 |
Total | 0.3147 |
H.M of X = 5/0.3147 = 15.88
Example 2 - Find the harmonic mean of the following data {8, 9, 6, 11, 10, 5} ?
X | 1/X |
8 | 0.125 |
9 | 0.111 |
6 | 0.167 |
11 | 0.091 |
10 | 0.100 |
5 | 0.200 |
Total | 0.794 |
H.M of X = 6/0.794 = 7.560
For grouped data

Example 3 - Calculate the harmonic mean for the below data
Marks | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
F | 2 | 3 | 11 | 20 | 32 | 25 | 7 |
Solution
Marks | X | F | F/X |
30-39 | 34.5 | 2 | 0.0580 |
40-49 | 44.5 | 3 | 0.0674 |
50-59 | 54.4 | 11 | 0.2018 |
60-69 | 64.5 | 20 | 0.3101 |
70-79 | 74.5 | 32 | 0.4295 |
80-89 | 84.5 | 25 | 0.2959 |
90-99 | 94.5 | 7 | 0.0741 |
Total |
| 100 | 1.4368 |
HM = 100/1.4368 = 69.59
Example 4 – find the harmonic mean of the given class
Ages | 4 | 5 | 6 | 7 |
No. of students | 6 | 4 | 10 | 9 |
Solution
x | F | f/x |
4 | 6 | 1.50 |
5 | 4 | 0.80 |
6 | 10 | 1.67 |
7 | 9 | 1.29 |
| 29.00 | 5.25 |
HM = 29/5.25 = 5.5
Example 5 – calculate harmonic mean
class | frequency |
2-4 | 3 |
4-6 | 4 |
6-8 | 2 |
8-10 | 1 |
Solution
class | Frequency | x | f/x |
2-4 | 3 | 3 | 1 |
4-6 | 4 | 5 | 0.8 |
6-8 | 2 | 7 | 0.28 |
8-10 | 1 | 9 | 0.11 |
| 10 |
| 2.19 |
Harmonic mean = 10/2.19 = 4.55
Geometric mean
Geometric mean is a type of mean or average, which indicates the central tendency of a set of numbers by using the product of their values.
Definition
The Geometric Mean (G.M) of a series containing n observations is the nth root of the product of the values.
For ungrouped data
 Geometric Mean, GM = Antilog ∑logxi
Geometric Mean, GM = Antilog ∑logxi
N
Example 1 – find the G.M of the values
X | Log X |
45 | 1.653 |
60 | 1.778 |
48 | 1.681 |
65 | 1.813 |
Total | 6.925 |
 GM = Antilog ∑logxi
GM = Antilog ∑logxi
N
= Antilog 6.925/4
= Antilog 1.73
= 53.82
For grouped data
 Geometric Mean, GM = Antilog ∑ f logxi
Geometric Mean, GM = Antilog ∑ f logxi
N
Example 2 – calculate the geometric mean
X | F |
60 – 80 | 22 |
80 – 100 | 38 |
100 – 120 | 45 |
120 – 140 | 35 |
|
|
Solution
X | f | Mid X | Log X | f log X |
60 – 80 | 22 | 70 | 1.845 | 40.59 |
80 – 100 | 38 | 90 | 1.954 | 74.25 |
100 – 120 | 45 | 110 | 2.041 | 91.85 |
120 – 140 | 35 | 130 | 2.114 | 73.99 |
Total | 140 |
|
| 280.68 |
 GM = Antilog ∑ f logxi
GM = Antilog ∑ f logxi
N
= antilog 280.68/140
= antilog 2.00
GM = 100
Example 3 – calculate geometric mean
class | frequency |
2-4 | 3 |
4-6 | 4 |
6-8 | 2 |
8-10 | 1 |
Solution
class | frequency | X | Log x | flogx |
2-4 | 3 | 3 | 1.0986 | 3.2958 |
4-6 | 4 | 5 | 1.2875 | 6.4378 |
6-8 | 2 | 7 | 0.5559 | 3.8918 |
8-10 | 1 | 9 | 0.2441 | 2.1972 |
| 10 |
|
| 15.8226 |
 GM = Antilog ∑ f logxi
GM = Antilog ∑ f logxi
N
= antilog 15.8226/10
= antilog 1.5823
GM = 4.866
Median:
a) The points or value that divides the data into two equal parts.
b) Firstly , the data are arranged in ascending or descending order .
c) The median is the middle number depending on the data size.
d) When the data size is odd, the median is the middle value.
e) When the data size is even, median is the average of the middle two values.
f) It is also known as middle score or 50th percentile.
 For ungrouped data median is calculated by (n+1)th value
For ungrouped data median is calculated by (n+1)th value
2
Example 1 – find the median score of 7 students in science class
Score = 19, 17, 16, 15, 12, 11, 10
Median = (7+1)/2 = 4th value
Median = 15
Find the median score of 8 students in science class
Score = 19, 17, 16, 15, 12, 11, 10, 9
Median = (8+1)/2 = 4.5th value
Median = (15+12)/2 = 13.5
Example 2 – find the median of the table given below
Marks obtained | No. of students |
20 | 6 |
25 | 20 |
28 | 24 |
29 | 28 |
33 | 15 |
38 | 4 |
42 | 2 |
43 | 1 |
Solution
Marks obtained | No. of students | Cf |
20 | 6 | 6 |
25 | 20 | 26 (20+6) |
28 | 24 | 50 (26+24) |
29 | 28 | 78 |
33 | 15 | 93 |
38 | 4 | 97 |
42 | 2 | 99 |
43 | 1 | 100 |
Median = (n+1)/2 = 100+1/2 = 50.5
Median = (28+29)/2 = 28.5
Median of grouped data
Formula
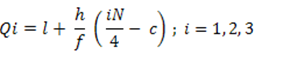
 MC = median class is a category containing the n/2
MC = median class is a category containing the n/2
Lb = lower boundary of the median class
Cfp = cumulative frequency before the median class if the scores are arranged from lowest to highest value
Fm = frequency of the median class
c.i = size of the class interval
Ex- calculate the median
Example 3-
Calculate the median
Marks | No. of students |
0-4 | 2 |
5-9 | 8 |
10-14 | 14 |
15-19 | 17 |
20-24 | 9 |
Solution
Marks | No. of students | CF |
0-4 | 2 | 2 |
5-9 | 8 | 10 |
10-14 | 14 | 24 |
15-19 | 17 | 41 |
20-24 | 9 | 50 |
| 50 |
|
n = 50
 n = 50/2= 25
n = 50/2= 25
2
The category containing n/2 is 15 -19
Lb = 15
Cfp = 24
f = 17
ci = 4

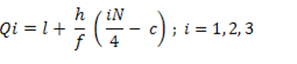
 Median = 15 + 25-24 *4 = 15.23
Median = 15 + 25-24 *4 = 15.23
17
Example 4 - Given the below frequency table calculate median
X | 60 – 70 | 70 – 80 | 80- 90 | 90-100 |
F | 4 | 5 | 6 | 7 |
Solution
X | F | CF |
60 - 70 | 4 | 4 |
70 - 80 | 5 | 9 |
80 - 90 | 6 | 15 |
90 - 100 | 7 | 22 |
n = 22
 n = 22/2= 11
n = 22/2= 11
2
The category containing n+1/2 is 80 - 90
Lb = 80
Cfp = 9
f = 6
ci = 10


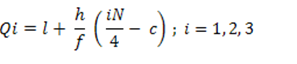
 Median = 80 + 11-9 *10 = 83.33
Median = 80 + 11-9 *10 = 83.33
6
Example 5– calculate the median of grouped data
Class interval | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
Frequency | 4 | 12 | 13 | 19 | 7 | 5 |
Solution
CI | F | CF |
1-3 | 4 | 4 |
3-5 | 12 | 16 |
5-7 | 13 | 29 |
7-9 | 19 | 48 |
9-11 | 7 | 55 |
11-13 | 5 | 60 |
n = 60
 n = 60/2= 30
n = 60/2= 30
2
The category containing n+1/2 is 7-9
Lb = 7
Cfp = 29
f = 19
ci = 2
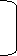

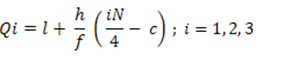
 Median = 7 + 30-29 *2 = 7.105
Median = 7 + 30-29 *2 = 7.105
19
Importance of median
Demerits of median
Key takeaways - The points or value that divides the data into two equal parts
Mode-
a) The mode is denoted Mo, is the value which occurs most frequently in a set of values.
b) Croxton and Cowden defined it as “the mode of a distribution is the value at the point armed with the item tends to most heavily concentrated. It may be regarded as the most typical of a series of value”
Mode for ungrouped data
Example 1- Find the mode of scores of section A
Scores = 25, 24, 24, 20, 17, 18, 10, 18, 9, 7
Solution – Mode is 24, 18 as both have occurred twice.
Mode for grouped data
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
L1= lower limit of the modal class,
L2= upper limit of the modal class‟
d1 =fm-f0 and d2=fm-f1
Where fm= frequency of the modal class,
f0 = frequency of the class preceding to the modal class,
f1= frequency of the class succeeding to the modal class.
Example 2 – Find the mode
Seconds | Frequency |
51 - 55 | 2 |
56 - 60 | 7 |
61 - 65 | 8 |
66 - 70 | 4 |
The group with the highest frequency is the modal group: - 61-65
D1 = 8-7 = 1
D2 = 8-4 = 4
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 61 + (65-61) 1 = 61+4 (1/5) = 61.8
mode = 61 + (65-61) 1 = 61+4 (1/5) = 61.8
1+4
Mode = 61.8
Example 3 - In a class of 30 students marks obtained by students in science out of 50 is tabulated below. Calculate the mode of the given data.
Marks obtained | No. of students |
10 -20 | 5 |
20 – 30 | 12 |
30 – 40 | 8 |
40 – 50 | 5 |
Solution
The group with the highest frequency is the modal group: - 20 -30
D1 = 12 - 5 = 7
D2 = 12 - 8 = 4
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
7+4
Mode = 61.8
Example 4- Based on the group data below, find the mode
Time to travel to work | Frequency |
1 – 10 | 8 |
11 -20 | 14 |
21 – 30 | 12 |
31 – 40 | 9 |
41 – 50 | 7 |
Solution
The group with the highest frequency is the modal group: - 11 - 20
D1 = 14 - 8 = 6
D2 = 14 - 12 = 2
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 11 + (20-11) 6 = 11+9 (6/8) = 17.75
mode = 11 + (20-11) 6 = 11+9 (6/8) = 17.75
6+2
Example 5 –
Compute the mode from the following frequency distribution
CI | F |
70-71 | 2 |
68-69 | 2 |
66-67 | 3 |
64-65 | 4 |
62-63 | 6 |
60-61 | 7 |
58-59 | 5 |
Solution
The group with the highest frequency is the modal group: - 60 - 61
D1 = 7 - 6 = 1
D2 = 7 - 5 = 2
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 60 + (61-60) 1 = 60+1 (1/3) 60.85
mode = 60 + (61-60) 1 = 60+1 (1/3) 60.85
1+2
Importance of mode
Demerits of mode
Key takeaways –
Quartiles
There are three quartiles, i.e. Q1, Q2 and Q3 which divide the total data into four equal parts when it has been orderly arranged. Q1, Q2 and Q3 are termed as first quartile, second quartile and third quartile or lower quartile, middle quartile and upper quartile, respectively. The first quartile, Q1, separates the first one-fourth of the data from the upper three fourths and is equal to the 25th percentile. The second quartile, Q2, divides the data into two equal parts (like median) and is equal to the 50th percentile. The third quartile, Q3, separates the first three-quarters of the data from the last quarter and is equal to 75th percentile.
Calculation of Quartiles:
The calculation of quartiles is done exactly in the same manner as it is in case of the calculation of median.
The different quartiles can be found using the formula given below:
Qi = l1 + 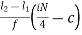 i= 1,2,3
i= 1,2,3
Where,
L1 = lower limit of ith quartile class
L2 = upper limit of ith quartile class
c = cumulative frequency of the class preceding the ith quartile class
f = frequency of ith quartile class.
Deciles
Deciles are the partition values which divide the arranged data into ten equal parts. There are nine deciles i.e. D1, D2, D3……. D9 and 5th decile is same as median or Q2, because it divides the data in two equal parts.
Calculation of Deciles:
The calculation of deciles is done exactly in the same manner as it is in case of calculation of median.
The different deciles can be found using the formula given below:
Di = l1 + 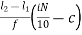 i= 1,2,3….9
i= 1,2,3….9
Where,
l1 = lower limit of ith quartile class
l2 = upper limit of ithquartile class
c = cumulative frequency of the class preceding the ithquartile class
f = frequency of ith quartile class.
Percentile
Percentiles are the values which divide the arranged data into hundred equal parts. There are 99 percentiles i.e. P1, P2, P3, ……. P99.
The 50th percentile divides the series into two equal parts and P50 = D5 = Median.
Similarly, the value of Q1 = P25 and value of Q3 = P75
Calculation of Percentiles:
The different percentiles can be found using the formula given below:
pi = l1 + 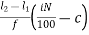 i= 1,2,3…………….99
i= 1,2,3…………….99
Where,
l1 = lower limit of ith quartile class
l2 = upper limit of ithquartile class
c = cumulative frequency of the class preceding the ithquartile class
f = frequency of ith quartile class.
Example 1
Calculate Q1, Q2 and Q3 from the following data given below:
Day | Frequency |
1 | 20 |
2 | 35 |
3 | 25 |
4 | 12 |
5 | 10 |
6 | 23 |
7 | 18 |
8 | 14 |
9 | 30 |
10 | 40 |
A1)
Arrange the frequency data in ascending order
Day | Frequency |
1 | 10 |
2 | 12 |
3 | 14 |
4 | 18 |
5 | 20 |
6 | 23 |
7 | 25 |
8 | 30 |
9 | 35 |
10 | 40 |
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (10 + 1) /4] th observation
Q1 = 2.75 th observation
Thus, 2.75 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 12 and 14
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 12 + 0.75 * (14 – 12) = 13.50
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (10 + 1) /4] th observation
Q3 = 8.25 th observation
So, 8.25 th observation lies between the 8th and 9th value in the ordered group, between frequency 30 and 35
Third quartile (Q3) is calculated as
Q3 = 8th observation +0.25 * (9th observation – 8th observation)
Q3 = 30 + 0.25 * (35 – 30) = 31.25
Example 2
Calculate Q1, D7 and P20 from the following data:
3, 13, 11, 11, 5, 4, 2
A2)
Arranging observations in the ascending order we get
2, 3, 4, 5, 11, 11, 13
Here, n = 7
Q1 = ( )th value of the observation
)th value of the observation
= ( )th Value of the observation
)th Value of the observation
= 2nd Value of the observation
= 3
D3 = (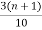 )th value of the observation
)th value of the observation
= ( )th value of the observation
)th value of the observation
= (2.4)th Value of the observation
= 2nd observation + 0.4 (3rd – 2nd)
= 3 + 0.4(4 – 3)
= 3 + 0.4
= 3.4
P20 = (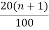 )th value of the observation
)th value of the observation
= (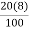 )th value of the observation
)th value of the observation
= (1.6)th value of the observation
= 1st observation + 0.6 (2nd – 1st )
= 2 + 0.6(3 – 2)
= 2 + 0.6
= 2.6
Example 3
Calculate P20 from the following data:
Class | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 |
Frequency | 3 | 4 | 2 | 1 |
A3)
In the case of Frequency Distribution, Percentiles can be calculated by using the formula:
pi = l1 + 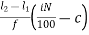
Class interval | F | CF |
2 – 4 | 3 | 3 |
4 – 6 | 4 | 7 |
6 – 8 | 2 | 9 |
8 – 10 | 1 | 10 |
Total | n = 10 |
|
Here n = 10
Class with 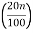 th value of the observation in CF column
th value of the observation in CF column
= 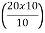 th value of the observation in CF column
th value of the observation in CF column
= 2th value of the observation in CF column and it lies in the class 2 - 4
Therefore, P20 class is 2 – 4
The lower boundary point of 2 – 4 is 2.
Therefore, L = 2
P20 = L + 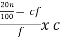
= 2 + 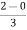 x 2
x 2
= 2 + 1.3333
= 3.3333
Example 4
Calculate D7 from the following data:
Class | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 |
Frequency | 3 | 4 | 2 | 1 |
A4)
In the case of Frequency Distribution, Deciles can be calculated by using the formula:
Di = l1 + 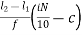
Class interval | F | CF |
2 – 4 | 3 | 3 |
4 – 6 | 4 | 7 |
6 – 8 | 2 | 9 |
8 – 10 | 1 | 10 |
Total | n = 10 |
|
Here n = 10
Class with  th value of the observation in CF column
th value of the observation in CF column
= 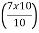 th value of the observation in CF column
th value of the observation in CF column
= 7th value of the observation in CF column and it lies in the class 6 – 8
Therefore, D7 class is 6 – 8
The lower boundary point of 6 – 8 is 6.
Therefore, L = 6
D7 = L + 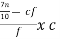
= 6 +  x 2
x 2
= 6 + 0
= 6
Example 5
Calculate Q1, Q2 and Q3 from the following data given below:
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
A5)
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:
Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
Key takeaways –
Central tendency do not reveal the variability present in the data. Dispersion measures the scatteredness of the data series around its average. It tells the variation of the data from one another and gives a clear idea about the distribution of the data.
Definition:
In statistics, dispersion is extent to which a distribution is stretched or squeezed.
Characteristics of measures of dispersion
a) It should be rigidly defined.
b) It should be easy to understand and calculate.
c) Must be based on all observation of the data.
d) Must be less affected by sampling fluctuation.
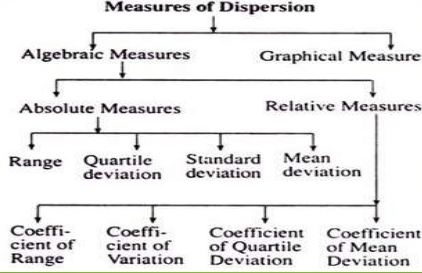
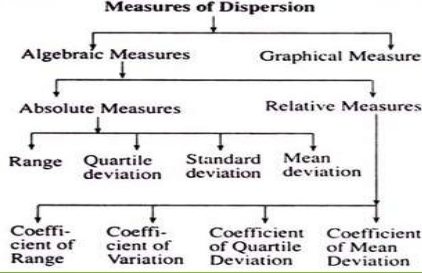
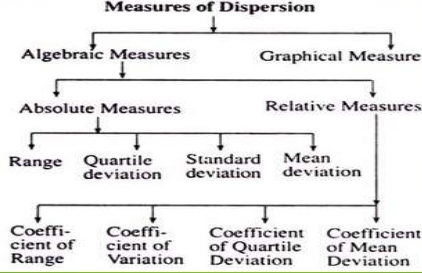
Types of measures of dispersion

Algebraic measures – It includes the mathematical way to calculate the measures of dispersion.
Graphical measures – The way to calculate the measures of dispersion by graphs and figures
Absolute measures of dispersion – It gives an idea about the amount of dispersion in a set of observations. It measures the dispersion in the same units as the units of original data. Absolute measures cannot be used for comparison of two or more data set variations.
Relative measures of dispersion – the relative measures of distribution are used for comparing the distribution of two or more data sets.
Coefficients of dispersion are used to compare two series with different measurement of unit.
Types of absolute measures of dispersion
R = H – L
Example 1 – 5, 10, 15, 20, 7, 9, 17, 13, 12, 16, 8, 6
Range = H-L
=20 – 5 = 15
Coefficient of range –
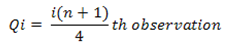
Coefficient of range = (15/(20+5))*100 = 60
Example 2 – what is the range for the following set of numbers?
15,21,57,43,11,39,56,83,77,11,64,91,18,37
Solution
Range = H-L
= 91 – 11 = 80
Therefore the range is 80
Example 3 – the frequency table shows the number of goals the lakers scored in their last twenty matches. What was the range
No. of goals | Frequency |
0 | 2 |
1 | 3 |
2 | 3 |
3 | 6 |
4 | 3 |
5 | 1 |
6 | 1 |
7 | 1 |
Solution
The range is the difference between the lowest and highest values.
The highest value was 7 (They scored 7 goals on 1 occasion)
The lowest value was 0 (They scored 0 goals on 2 occasions)
Therefore the range = 7 - 0 = 7
Example 4 – the following table shows the sales of DVD players made by a retail store each month last year
Month | No. of sales |
January | 25 |
Feb | 43 |
March | 39 |
April | 28 |
May | 29 |
June | 35 |
July | 32 |
August | 46 |
September | 28 |
October | 43 |
November | 51 |
December | 63 |
Solution
The range is the difference between the lowest and highest values.
The lowest number of sales = 25 in January
The highest number of sales = 63 in December
So the range = 63 - 25 = 38
Example 5 – what is the range for the following set of numbers?
57, -5, 11, 39, 56, 82, -2, 11, 64, 18, 37, 15, 68
Solution
The range is the difference between the lowest and highest values.
The highest value is 82.
The lowest value is -5.
Therefore the range = 82 - (-5) = 82+5 = 87
Merits
Demerits
2. Interquartile range - the interquartile range measures the range of the middle 50% of the values only. It is calculated as the difference between the upper and lower quartile.
Interquartile range = upper quartile – lower quartile
= Q3 – Q1
Examples 1– find the interquartile range for 1, 2, 18, 6, 7, 9, 27, 15, 5, 19, 12.
Solution
Arrange the numbers in ascending order
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27
Find the median
Median = 9
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27)
Q1 as median in the lower half and Q3 as median in the upper half
Q1 = median in (1, 2, 5, 6, 7)
Q1 = 5
Q3 = median in (12, 15, 18, 19, 27)
Q3 = 18
Interquartile range = 18 – 5 = 13
Example 2 – find the interquartile for the following data set: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Solution
Arrange the numbers in ascending order
3, 5, 7, 8, 9, 11, 15, 16, 20, 21
Make a mark in the center of the data:
(3, 5, 7, 8, 9,) | (11, 15, 16, 20, 21)
Find the median
Q1 = 7
Q3 = 16
Interquartile range = 16 – 7 = 9
Example 3 - find the interquartile for the following data set: 1, 3, 4, 5, 5, 6, 7, 11
Make a mark in the center of the data:
(1, 3, 4, 5,) (5, 6, 7, 11)
Find the median
Q1 = (3+4)/2 = 3.5
Q3 = (6+7)/2 = 6.5
Interquartile range = 6.5 – 3.5 = 3
Example 4 -
Find the interquartile range for odd sample size
63,64,64,70,72,76,77,81,81
Solution
Make a mark in the center of the data:
(63,64,64,70,)72,(76,77,81,81)
Find the median
Q1 = (64+64)/2 = 64
Q3 = (77+81)/2 = 79
Interquartile range = 79 – 64 = 15
3. Quartile deviation
Quartile deviation is the product of half of the difference between the upper and the lower quartiles.
QD = (Q3 - Q1) / 2
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
Quartile deviation for ungrouped data
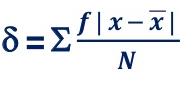
Examples 1
Day | Frequency |
1 | 20 |
2 | 35 |
3 | 25 |
4 | 12 |
5 | 10 |
6 | 23 |
7 | 18 |
8 | 14 |
9 | 30 |
10 | 40 |
Solution
Arrange the frequency data in ascending order
Day | Frequency |
1 | 10 |
2 | 12 |
3 | 14 |
4 | 18 |
5 | 20 |
6 | 23 |
7 | 25 |
8 | 30 |
9 | 35 |
10 | 40 |
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (10 + 1) /4] th observation
Q1 = 2.75 th observation
Thus, 2.75 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 12 and 14
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 12 + 0.75 * (14 – 12) = 13.50
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (10 + 1) /4] th observation
Q3 = 8.25 th observation
So, 8.25 th observation lies between the 8th and 9th value in the ordered group, between frequency 30 and 35
Third quartile (Q3) is calculated as
Q3 = 8th observation +0.25 * (9th observation – 8th observation)
Q3 = 30 + 0.25 * (35 – 30) = 31.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (31.25 – 13.50) / 2 = 8.875
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
= (31.25 – 13.50) /(31.25 + 13.50) = 0.397
Example 2 – calculate quartile deviation from the following test scores
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
Solution
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25 th observation
Thus, 2.25 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (30.25 – 23.75) / 2 = 3.25
Quartile deviation for grouped data
Where,
l = lower boundary of quartile group
h = width of quartile group
f = frequency of quartile group
N = total number of observation
C= cumulative frequency preceding quartile group
Example 3
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
Solutions
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:
Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
QD = (Q3 - Q1) / 2
QD = (61.44 – 49.19) / 2 = 6.13
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
= (61.44 – 49.19) /(61.44 + 49.19) = 0.11
Example 4 – computation of quartile deviation for grouped test scores
Class | Frequency |
9.3-9.7 | 22 |
9.8-10.2 | 55 |
10.3-10.7 | 12 |
10.8-11.2 | 17 |
11.3-11.7 | 14 |
11.8-12.2 | 66 |
12.3-12.7 | 33 |
12.8-13.2 | 11 |
Solution
Class | Frequency | Class boundaries | CF |
9.3-9.7 | 2 | 9.25-9.75 | 2 |
9.8-10.2 | 5 | 9.75-10.25 | 2 + 5 = 7 |
10.3-10.7 | 12 | 10.25-10.75 | 7 + 12 = 19 |
10.8-11.2 | 17 | 10.75-11.25 | 19 + 17 = 36 |
11.3-11.7 | 14 | 11.25-11.75 | 36 + 14 = 50 |
11.8-12.2 | 6 | 11.75-12.25 | 50 + 6 = 56 |
12.3-12.7 | 3 | 12.25-12.75 | 56 + 3 = 59 |
12.8-13.2 | 1 | 12.75-13.25 | 59 + 1 = 60 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(60)/4]th observation
Q1 = 15th observation
So, 15th value is in the interval 10.25-10.75
Group of Q1 = 10.25-10.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (10.25 + ( 0.5/ 12)* (1* (60/4) – 7)
Q1 = 10.58
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (60) /4] th observation
Q3 = 45th observation
So, 45th value is in the interval 11.25-11.75
Group of Q3 = 11.25-11.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (11.25 + ( 0.5/ 14)* (3* (60/4) – 36)
Q3 = 11.57
QD = (Q3 - Q1) / 2
QD = (11.57 – 10.58) / 2 = 0.495
Example 5 – calculate quartile deviation from the following data
CI | F |
10 – 15 | 6 |
15 – 20 | 10 |
20 – 25 | 15 |
25 – 30 | 22 |
30 – 40 | 12 |
40 – 50 | 9 |
50 – 60 | 4 |
60 – 70 | 2 |
Solution
CI | F | Cf |
10 – 15 | 6 | 6 |
15 – 20 | 10 | 16 |
20 – 25 | 15 | 31 |
25 – 30 | 22 | 53 |
30 – 35 | 12 | 65 |
35 – 40 | 9 | 74 |
45 – 50 | 4 | 78 |
55 – 60 | 2 | 80 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(80)/4]th observation
Q1 = 20th observation
So, 20th value is in the interval 20 - 25
Group of Q1 = 20 - 25
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (20 + ( 5/ 15)* (1* (80/4) – 16)
Q1 = 21.33
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (80) /4] th observation
Q3 = 60th observation
So, 60th value is in the interval 30 - 35
Group of Q3 = 30 - 35
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (30 + ( 5/ 12)* (3* (80/4) – 53)
Q3 = 32.91
QD = (Q3 - Q1) / 2
QD = (32.91 – 21.33) / 2 = 5.79
Merits
a) It provide better result than range mode.
b) It is not effected by extreme values.
Demerits
a) It is completely dependent on central item.
b) All items are not taken onto consideration.
4. Mean deviation – The average of the absolute values of deviation from the mean, median or mode is called mean deviation. This method removes shortcoming of range and QD.

OR
 =
= 
Where, ∑ is total of;
 X is the score, X is the mean, and N is the number of scores
X is the score, X is the mean, and N is the number of scores
D = Deviation of individual scores from mean
Example 1 –
Computation of mean deviation in ungrouped data
X = 55, 45, 39, 41, 40, 48, 42, 53, 41, 56
Solution
X |
| Absolute deviation (signed ignored) |
55 | 55 - 46 = 9 | 9 |
45 | 45 – 46 = -1 | 1 |
39 | -7 | 7 |
41 | -5 | 5 |
40 | -6 | 6 |
48 | 2 | 2 |
42 | -4 | 4 |
53 | 7 | 7 |
41 | -5 | 5 |
56 | 10 | 10 |
∑X = 460 |
|
|
Mean = 460/10 = 46
MD = 56/10 = 5.6
Example 2- Peter did a surveyod the number of pets owned by his classmates, with the following result. What is the mean deviation of the number of pets?
No. of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution
X | F | Fx |
|
|
0 | 4 | 0 | 1.8 | 7.2 |
1 | 12 | 12 | 0.8 | 9.6 |
2 | 8 | 16 | 0.2 | 1.6 |
3 | 2 | 6 | 1.2 | 2.4 |
4 | 1 | 4 | 2.2 | 2.2 |
5 | 2 | 10 | 3.2 | 6.4 |
6 | 1 | 6 | 3.2 | 4.2 |
| 30 | 54 | 4.2 | 33.6 |
Mean = 54/30 = 1.8
MD = 33.6/30 = 1.12
Computation of Mean deviation in grouped data
Example 3 -
Class interval | 15 – 19 | 20 – 24 | 25 – 29 | 30 – 34 | 35 – 39 | 40 – 44 | 45 - 49 |
Frequency | 1 | 4 | 6 | 9 | 5 | 3 | 2 |
Class Interval | F | X | FX | D | FD |
15 – 19 | 1 | 17 | 17 | 15 | 15 |
20 – 24 | 4 | 22 | 88 | 10 | 40 |
25 – 29 | 6 | 27 | 162 | 5 | 30 |
30 - 34 | 9 | 32 | 288 | 0 | 0 |
35 - 39 | 5 | 37 | 185 | 5 | 25 |
40 - 44 | 3 | 42 | 126 | 10 | 30 |
45 - 49 | 2 | 47 | 94 | 15 | 30 |
| N = 30 |
| ∑fx = 960 |
|
|
Mean = 960/30 = 32
MD = 170 / 30 = 5.667
Coefficient of mean deviation
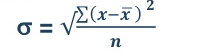
Coefficient of mean deviation = (5.67/32)*100 = 17.71
Example 4 – Calculate mean deviation from the median
Class | 5 -15 | 15 – 25 | 25 - 35 | 35 - 45 | 45 – 55 |
Frequency | 5 | 9 | 7 | 3 | 8 |
Solution
x | f | cf | Mid point x | x –median | F(x-m) |
5 -15 | 5 | 5 | 10 | 17.42 | 87.1 |
15 -25 | 9 | 14 | 20 | 7.42 | 66.78 |
25 -35 | 7 | 21 | 30 | 2.58 | 18.06 |
35 -45 | 3 | 24 | 40 | 12.58 | 37.74 |
45- 55 | 8 | 32 | 50 | 22.58 | 180.64 |
| 32 |
|
|
| 390.32 |
Since n/2 = 32/2 = 16, therefore the class is 25 – 35 is the median.
Median = 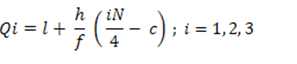
 Median = 25+16-14 *10 = 27.42
Median = 25+16-14 *10 = 27.42
7
MD from median is 390.32/32 = 12.91
Example 5 – calculate the mean deviation from continuous frequency distribution
Age group | 15 - 25 | 25 – 35 | 35 - 45 | 45 - 55 |
No. of people | 25 | 54 | 34 | 20 |
Solution
Age group (X) | Number of people (f) | Midpoint x | fx |
|
|
15 – 25 | 25 | 20 | 500 | 13.684 | 324.1 |
25 – 35 | 54 | 30 | 1620 | 3.684 | 198.936 |
35 – 45 | 34 | 40 | 1360 | 6.316 | 214.744 |
45 - 55 | 20 | 50 | 1000 | 16.316 | 352.32 |
| 133 |
|
|
| 1090.1 |
Mean = 4480/133 = 33.684
MD = 1090.1/133 = 8.196
Merits
a) It is easy to calculate
b) It helps in making comparison
c) It is not affected by extreme items
Demerits
a) It ignores algebraic sign. And are not used for mathematical treatment
b) It is not reliable
5. Standard deviation – standard deviation is calculated as square root of average of squared deviations taken from actual mean. It is also called root mean square deviation. This measure suffers from less drawbacks and provides accurate results. It removes the drawbacks of ignoring algebraic sign. We square the deviation to make them positive.
Two ways of computing SD
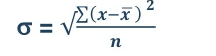
2. Shortcut method
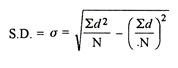
d = Deviation of the score from an assumed mean, say AM; i.e. d = (X – AM). AM is assumed mean
d2 = the square of the deviation.
∑d = the sum of the deviations.
∑d2 = the sum of the squared deviations.
N = No. of the scores
Standard deviation in ungrouped data
Example 1–
X = 12, 15, 10, 8, 11, 13, 18, 10, 14, 9
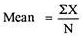
Mean = 120/10 = 12
Scores | D |
|
12 | 12-12 = 0 | 0 |
15 | 15-12 = 3 | 9 |
10 | 10 -12 = -2 | 4 |
8 | -4 | 16 |
11 | -1 | 1 |
13 | 1 | 1 |
18 | 6 | 36 |
10 | -2 | 4 |
14 | 2 | 4 |
9 | -3 | 9 |
|
|
|
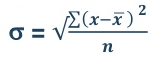
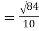 = 2.9
= 2.9
2. Shortcut method
Assumed mean (AM) = 11
Scores | D = (X- AM) |
|
12 | 12-11 = 1 | 1 |
15 | 15-11 = 4 | 16 |
10 | 10 -11 = -1 | 1 |
8 | -3 | 9 |
11 | 0 | 0 |
13 | 2 | 4 |
18 | 7 | 49 |
10 | --1 | 1 |
14 | 3 | 9 |
9 | -2 | 4 |
|
|
|
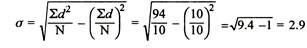
SD from short cut method = 2.9
Example 2 –Ram did a survey of the number of pets owned by his classmates, with the following results
No. of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution
x | f | Fx |
|
|
|
0 | 4 | 0 | -1.8 | 3.24 | 12.96 |
1 | 12 | 12 | -0.8 | 0.64 | 7.68 |
2 | 8 | 16 | 0.2 | 0.04 | 0.32 |
3 | 2 | 6 | 1.2 | 1.44 | 2.88 |
4 | 1 | 4 | 2.2 | 4.84 | 4.84 |
5 | 2 | 10 | 3.2 | 10.24 | 20.48 |
6 | 1 | 6 | 4.2 | 17.64 | 17.64 |
| 30 | 54 |
|
| 66.80 |
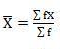
Mean = 54/30 = 1.8
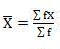
SD = √66.80/30 = 1.49
Standard deviation in grouped data
Direct method
Example 3 –
C.I. | 0 - 2 | 3 - 5 | 6- 8 | 9-11 | 12-14 | 15 -17 | 18 - 20 |
F | 1 | 3 | 5 | 7 | 6 | 5 | 3 |
Solution
C.I | f | Mid point x | Fx | d |
| fd2 |
0-2 | 1 | 1 | 1 | -10.1 | 102.01 | 102.01 |
3-5 | 3 | 4 | 12 | -7.1 | 50.41 | 151.23 |
6-8 | 5 | 7 | 35 | -4.1 | 16.81 | 84.05 |
9-11 | 7 | 10 | 70 | -1.1 | 1.21 | 8.47 |
12-14 | 6 | 13 | 78 | 1.9 | 3.61 | 21.66 |
15-17 | 5 | 16 | 80 | 4.9 | 24.01 | 120.05 |
18-20 | 3 | 19 | 57 | 7.9 | 62.41 | 187.23 |
| 30 |
| 333 |
|
| 674.70 |
Mean = 333/30 = 11.1
SD =
= 
Shortcut method
C.I | f | Mid point x | d(X-AM) | fd | fd2 |
0-2 | 1 | 1 | -9 | -9 | 81 |
3-5 | 3 | 4 | -6 | -18 | 108 |
6-8 | 5 | 7 | -3 | -15 | 45 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 3 | 18 | 54 |
15-17 | 5 | 16 | 6 | 30 | 180 |
18-20 | 3 | 19 | 9 | 27 | 243 |
| 30 |
|
| 33 | 711 |
Assumed mean = 10
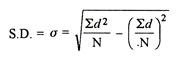
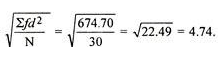
Step deviation method
C.I | f | Mid point x | D | fd | fd2 |
0-2 | 1 | 1 | -3 | -3 | 9 |
3-5 | 3 | 4 | -2 | -6 | 12 |
6-8 | 5 | 7 | -1 | -5 | 5 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 1 | 6 | 6 |
15-17 | 5 | 16 | 2 | 10 | 20 |
18-20 | 3 | 19 | 3 | 9 | 27 |
| 30 |
|
| 11 | 79 |
Here, d is calculate as (X –AM)/i, where i is length of class interval
d = (1 -10)/3 = -3 and so on
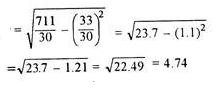
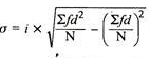
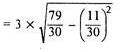
Coefficient of standard deviation
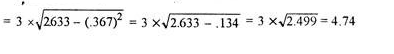
Coefficient of SD = (4.74/11.1)*100 = 42.70
Example 4 – calculate the standard deviation using the direct method
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
Solution
Class interval | Frequency | Mid point x | Fx |
|
|
|
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |
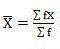
Mean = 2720/40 = 68

SD = √10510/40 = 16.20
Example 5 - calculate the mean and standard deviation of hours spent watching television by the 220 students.
Hours | No. of students |
10 – 14 | 2 |
15 – 19 | 12 |
20 – 24 | 23 |
25 – 29 | 60 |
30 – 34 | 77 |
35 – 39 | 38 |
40 - 44 | 8 |
Solution
Hours | No. of students | x | fx |
|
|
|
10 – 14 | 2 | 12 | 24 | -17.82 | 317.49 | 634.98 |
15 – 19 | 12 | 17 | 204 | -12.82 | 164.31 | 1971.67 |
20 – 24 | 23 | 22 | 506 | -7.82 | 61.12 | 1405.85 |
25 – 29 | 60 | 27 | 1620 | -2.82 | 7.94 | 476.53 |
30 – 34 | 77 | 32 | 2464 | 2.18 | 4.76 | 366.55 |
35 – 39 | 38 | 37 | 1406 | 7.18 | 51.58 | 1959.98 |
40 - 44 | 8 | 42 | 336 | 12.18 | 148.40 | 1187.17 |
| 220 |
| 6560 |
|
| 8002.73 |
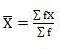
Mean = 6560/220 = 29.82
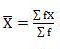
SD = √8002.73/220 = 6.03
Merits
a) It takes into account all the items and are used for future statistical analysis
b) It is suitable for making comparison
Demerits
a) It is difficult to compute
Key takeaways - Dispersion measures the scatteredness of the data series around its average.
Sources-