Unit II

Linear Programming Problem

2.1 Linear programming problem: Formulation and Graphical method. Basic terminology requirements, Applications area of Linear Programming, formulation of Linear Programming models, General mathematical formulation of Linear Programming

Introduction to Linear Programming

Preface

Optimization may be a way of life. We all have limited resources and time and need to form the foremost of them. Everything from using time productively to solving problems in your company's supply chain uses optimization. this is often a very interesting and relevant topic in data science.

This is also a really interesting topic. It starts with an easy problem, but it are often very complicated. For instance, sharing a chocolate candy between siblings may be a simple optimization problem. While solving it, we do not think mathematically. On the opposite hand, devising an e-tailer inventory and warehousing strategy are often very complex. Many SKUs with different popularity in several regions are delivered at defined times and resources.

Linear programming (LP) is one among the simplest ways to perform optimization. Making some simplified assumptions will assist you solve some very complex optimization problems. Analysts will encounter applications and problems that are solved by applied mathematics.

For some reason, LPs do not get enough attention while learning data science. So I wanted to form this excellent technique justice. i made a decision to write down a piece of writing that explains applied mathematics in simple English. The content is as simple as possible. The thought is to urge excited about applied mathematics for the primary time.

Note-If you would like to find out this during a course format, we curate this free course-Linear programming for data science professionals

What’s linear programming?

So what's linear programming? Applied mathematics may be a simple technique that uses linear functions to represent complex relationships and find the simplest points. The important words within the preamble are drawn. The particular relationship could also be far more complicated, but it is often simplified to a linear relationship.

Linear programming applications are everywhere around you. Use applied mathematics on a private and professional side. If you're driving from home to figure and need to use the shortest route, you're using applied mathematics. Or, when delivering a project, develop a technique to figure efficiently in order that your team can deliver on time.

Example of applied mathematics problem

Suppose you've got six packages delivered daily by a FedEx courier. The warehouse is at point A. The six destinations are indicated by U, V, W, X, Y, Z. The numbers on the road indicate the space between cities. To save lots of fuel and time, delivery personnel want to use the shortest route.

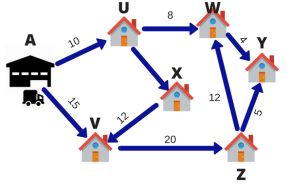
Fig 1

Therefore, the courier calculates different routes to succeed in all six destinations and comes up with the shortest route. This method of selecting the littlest way is named applied mathematics.

In this case, the deliveryman's purpose is to deliver the parcel to all or any six destinations on time. The method of selecting the simplest route is named research. Research may be a decision-making approach that has a group of methods for operating a system. Within the example above, my system was a delivery model.

Linear programming is employed to seek out the optimal solution to a given constrained problem. Applied mathematics formulates a true problem into a mathematical model. This includes objective functions and linear inequalities that are subject to constraints.

Does the 6-point linear representation above represent the important world? Yes, No. the particular route isn't a line, so it's oversimplified. Multiple turns, U-turns, traffic lights, and traffic jams can occur. However, with simple assumptions, we are creating an answer that greatly reduces the complexity of the matter and works in most scenarios.

Formulation and Graphical method

Solve applied mathematics during a graphical way

 Linear programming is often solved in multiple ways. During this section, we'll check out graphical thanks to solve applied mathematics. This method is employed to unravel two-variable applied mathematics. If you've got only two decision variables, you would like to use a graphical method to seek out the simplest solution.

The graphical method formulates a group of linear inequalities that are subject to constraints. The inequality is then plotted on the XY plane. If you plot all the inequalities on a graph, the intersecting regions offer you a feasible region. The Feasible region describes all the values a model can take. And it also gives us the simplest solution.

Let's understand this with an example.

Example: A farmer recently acquired 110 hectares of land. He decided to grow wheat and barley there. The standard of the sun and therefore the excellent climate of the region allow us to sell all wheat and barley products. He wants to understand the way to plant each variety on 110 hectares, taking under consideration costs, net, and labor requirements, consistent with the info shown below.

The farmer's budget is US $ 10,000 and 1,200 man-days are available during the design period. Find the optimal solution and value.

Solution: to unravel this problem, first create a applied mathematics method.

Formulation of linear problems

Step 1:Identify the coefficient of determination

Total area for growing wheat = X (hectare)

Total area for growing barley = Y (hectare)

X and Y are my coefficients of determination.

Step 2: Write the target function

As we can sell products from the whole land to the market. The farmer will want to maximize the profits of his total product. You’ll tend internet profit of both wheat and barley. Farmers earn a net income of $ 50 per hectare of wheat and $ 120 per hectare of barley.

Our objective function (given by Z) is up to Z = 50X + 120Y.

Step 3: Write constraints 

1. The entire budget of farmers is estimated to be US $ 10,000. The value of manufacturing wheat and barley per hectare is additionally given to us. There’s an upper limit to the entire cost a farmer can spend. Therefore, the equation is:

100X + 200Y ≤ 10,000

2. The subsequent constraint is that the upper limit of availability of total man-hours during the design period. The entire number of construction days available is 1200. As shown within the table, the man-hours per hectare of wheat and barley are shown.

10X + 30Y ≤ 1200

3. The third constraint is that the total acreage present within the plantation. The entire area available is 110 hectares. Therefore, the equation is:

X + Y ≤ 110

Step 4: Non-negative limit

The X and Y values are greater than or adequate to 0. to not mention this.

X ≥ 0, Y ≥ 0

We have formulated a applied mathematics method. it is time to unravel it.

Solve LP during a graphical way

We know that X, Y ≥ 0, so consider only the primary quadrant.

To plot the graph of the above equations, first simplify all the equations.

100X + 200Y ≤ 10,000 are often simplified to X + 2Y ≤ 100 by dividing by 100.

10X + 30Y ≤ 1200 are often simplified to X + 3Y ≤ 120 by dividing by 10.

The third equation may be a simplified sort of X + Y ≤ 110.Plot the primary two lines on the graph in quadrant 1 (see below)

Optimal feasible solutions are achieved at intersections where budget and man-hour constraints are active. This suggests that the purpose where the equations X + 2Y ≤ 100 and X + 3Y ≤ 120 intersect gives the optimal solution.

The values of X and Y that give the optimal solution are (60,20).

To increase profits, farmers got to manufacture wheat and barley on 60 hectares and 20 hectares of land, respectively.

The biggest profit the corporate gets is

Maximum Z = 50 * (60) + 120 * (20)

= US $ 5400

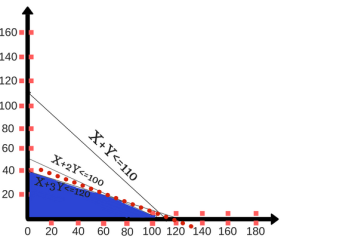
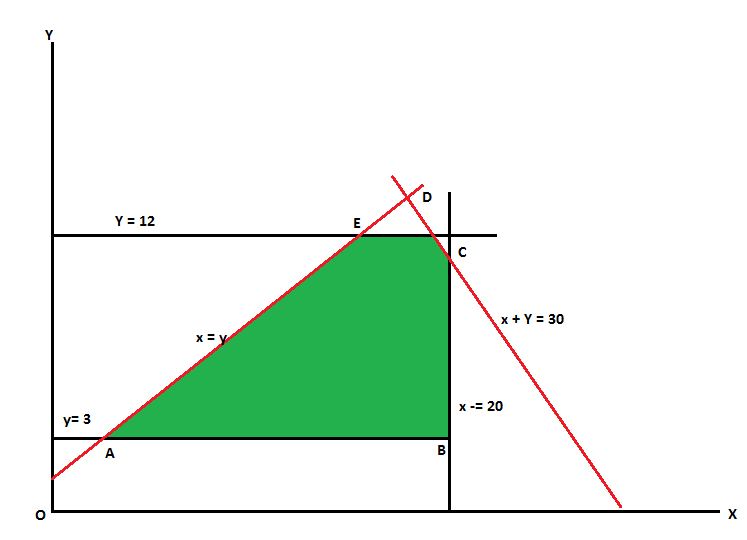
Solve the following LPP graphically-

Maximize-

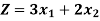
Subject to the constraints-

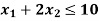
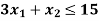
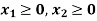
Sol.

Change the given constraints into equations-

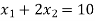
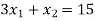
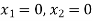
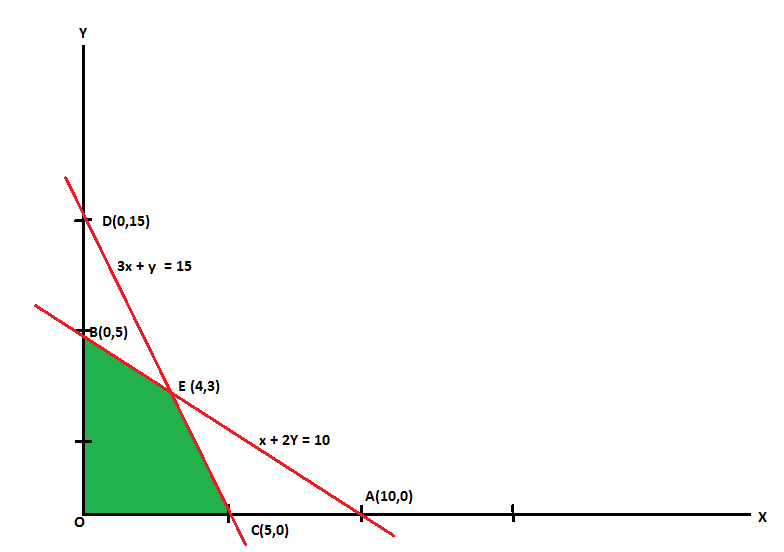
The line 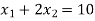  meets the x-axis at the point A(10,0) and meets the y-axis at the point B(0,5). Join A and B to get the graph for the line.             

Hence origin (0,0) satisfies the inequality 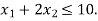so that half plane containing the origin represent the solution set of .

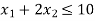And

The line 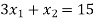meets the x-axis at the point C(5,0) and meets the y-axis at the point D(0,15). Join C and D to get the graph for the line.

Hence origin (0,0) satisfies the inequality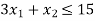   so that half plane containing the origin represent the solution set of.

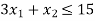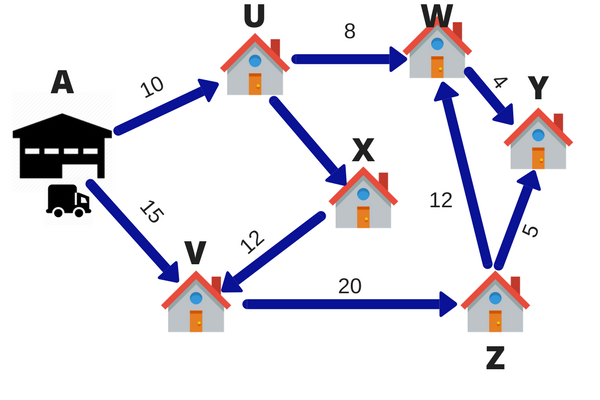
Now all the points in first quadrant satisfies  .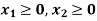

So that first quadrant is the region represented by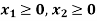

Hence the region OCEBO satisfies all the inequalities.

And each point on the region is the feasible solution of the problem.

Feasible solution-

Here in this problem the feasible solution is (5,0), (4,3) and (0,5).

Now we can obtain the optimal solution of the problem.

As we know that any point in the feasible region that gives the optimal value is called an optimal solution.

The value of the objective function 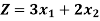at corner points of the feasible region is given below-

Here we see that the maximum value of Z is 18.

Find the maximum value of Z = 2x + 3y subject to the constraints-

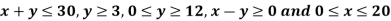
Sol.

Any point (x,y) satisfying the conditions 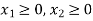lies in the first quadrant only.

Also since 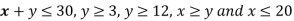the desired point (x,y) lies within the convex region ABCDE.

Its vertices are A(3,3), B(20,3), C(20,10), D(18,12) and E(12,12).

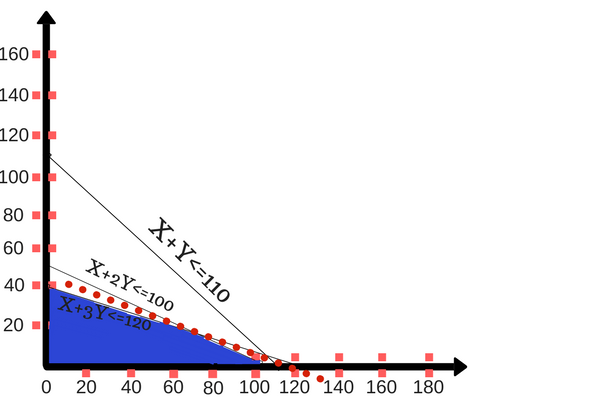
The value of Z at these points are-

Z(A) = 15

Z(B) = 49

Z(C) = 70

Z(D) = 72

Z(E) = 60

Here 72 is the maximum value which is at D.

So that the solution of the LPP is x = 18 and y = 12 and maximum Z  = 72

Example: A factory manufactures two types of items, A and B, each type requiring the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of item A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of item B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of item A at a profit of Rs. 7 and item B at a profit of Rs 10. Assuming that he can sell all the items he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit ?

Determine the maximum profit.

Sol.

We can tabulate the data as follows-

Decision variables- Let the manufacturer produce x packages of itemA and y packages of itemB per day respectively.

Objective function- SupposeZ denotes the maximum profit,

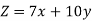
Constraints-

1st constraint-

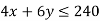
2nd constraint-

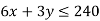
3rd constraint-

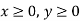
Mathematical formulation-

The mathematical form of this LPP can be written as-

Maximize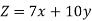
 

Subject to the constraints-

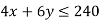
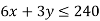
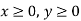
Tables for the region represented by inequalities-

For the first constraint-

For second condition-
 

Now we draw on x and y axes.

The coordinates of the vertices O, C, Eand B of the feasible region OCEBO are O(0, 0), C (40, 0), E (30, 20) and B (0, 40).The coordinates of E are obtained bysolving the equations 4x + 6y = 240 and6x + 3y = 240.             

Therefore Z is maximum at x = 30 and y = 20 and the maximum value of Z is 410.

Note: Everything taught here is additionally taught within the course format of this free course-an applied mathematics method for data science professionals.

Basic terminology Requirements

General terminology utilized in applied mathematics

Let's use the instance above to define some terms utilized in applied mathematics.

Determinants: Determinants are variables that determine the output. They represent my ultimate solution. To unravel the matter, you initially got to identify the coefficient of determination. Within the above example, the entire number of units A and B, represented by X and Y, respectively, is my coefficient of determination.

Objective function: Defined because the objective of deciding. Within the example above, the corporate wants to extend the gross profit margin, represented by Z. Therefore, profit is my objective function.

Constraint: A constraint may be a limit or limit on a choice variable. These usually limit the worth of the choice variable. Within the above example, limiting the supply of Milk and Chocó resources is my constraint.

Non-negative limit: altogether applied mathematics, the choice variable should take a non-negative value. This suggests that the worth of the choice variable must be greater than or adequate to 0.

The process of formulating an applied mathematics problem

Let's take a glance at the steps to generally define an applied mathematics problem.

For the matter to be an applied mathematics problem, the choice variables, objective functions, and constraints must all be linear functions.

If all three conditions are met, it's called an applied mathematics problem.

In order for the corporate to form the foremost profit, the above inequality must be met. When converted into a mathematical model is called formulating a real-world problem

The other two factors are resource availability and technical factors. These can be better explained using the example below. The executable solution of a linear programming problem must meet the constraints and non-negative constraints. The executable solution of LPP with the maximization problem is the optimal solution when the objective function value is maximum (maximum). Similarly, an LPP executable solution with a minimization problem is optimal when the objective function value is the minimum (minimum).

Applications of LP

Linear programming and optimization are used in a variety of industries. Manufacturing and service industries regularly use linear programming.

The application of linear programming does not end here. There are many other real-world linear programming applications, such as those applied by shareholders, sports, stock markets, and more. Please continue to explore further.

General mathematical formulation of Linear Programming

Formulation of applied mathematics model

The three components are:

1. Coefficient of determination.

2. Environmental (out of control) parameters.

3. Result (dependent) variable.

The applied mathematics model consists of equivalent components

Terminology utilized in applied mathematics problems

1. LP Problem Components: All LPPs are made from the coefficient of determination,

b. Objective function,

c. Constraints.

2. Optimization: applied mathematics attempts to maximise or minimize the worth of the target function.

3. Cost Factor Benefit: The coefficient of the target function variable represents the speed at which the worth of the target function increases or decreases by including one unit of every decision variable within the solution.

Coefficient of determination

Objective function

Constraint

4. Constraints: Maximization (or minimization) is performed consistent with a group of constraints. Therefore, LP is often defined as a constrained optimization problem. They reflect Resource limits.

5. Input / output coefficient: The coefficient of the constraint variable is named the input / output coefficient. These indicate the speed at which a specific resource is unitized or depleted. They are showed the left of the constraint.

6. Capacity: The capacity or availability of varied resources is shown to the proper of the constraint.

Formulation of LP Problem

Problem Formulation-Let's Make Some Chocolate

Example: Consider a chocolate manufacturer that produces only two sorts of chocolate, A and B. Both chocolates only require milk and chocolate. To manufacture each of the A and B units, you would like the subsequent quantities:

Each unit during a requires 1 unit of milk and three units of chocolate

Each unit in B requires 1 unit of milk and a couple of units of chocolate.

The company's kitchen features a total of 5 units of milk and 12 units of chocolate. With each sale, the corporate makes a profit

Rs6 per unit A sold

Rs5 per unit B sold.

Now the corporate wants to maximise profits. What percentage units of A and B does one got to produce respectively?

Solution: the primary thing to try to is to tabulate the matter for better understanding.

Let = X be the entire number of units generated by A.

Let = Y be the entire number of units generated by B.

Now, the entire profit is represented by Z

The company's gross profit margin is that the total number of A and B units produced multiplied by the profit per Rs6 and Rs5 units, respectively.

Profit: Maximum Z = 6X + 5Y

That is, you would like to maximize Z.

The company will attempt to produce as many A and B units as possible to maximize profits. However, Milk and Chocó resources are available in limited quantities.

As shown within the table above, each unit A and B requires 1 unit of milk. The entire amount of milk available is 5 units. To precise this mathematically,

X + Y ≤ 5

Also, each unit A and B requires 3 units and a couple of units of Chocó, respectively. The entire number of chocolates sold is 12. To precise this mathematically,

3X + 2Y ≤ 12

Also, the unit value of A can only be an integer.

Therefore, there are two constraints, X ≥ 0 and Y ≥ 0.

General mathematical formulation of Linear Programming Problems equality sign

Formulation of applied mathematics model

The three components are:

1. Coefficient of determination.

2. Environmental (out of control) parameters.

3. Result (dependent) variable.

Key takeaways:

2.2   Definitions Graphical solution method search approach: The simplex method: Introduction standard form of linear programming problem c1evelopmellt of simplex method. Simplex method (Maximization case), Simplex method (minimization case). Economic interpretation of the optimum simplex solution.

The Simplex method: Introduction standard form of linear programming problem c1evelopmellt of simplex method. Simplex method (Maximization case), Simplex method (minimization case)

Simplex method

The simplex method is one of the most powerful and popular linear programming methods. The simplex method is an iterative procedure to get the most viable solution. This method keeps transforming the values   of the fundamental variables to get the maximum value of the objective function.

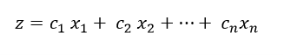
Linear programming functions are in standard form when trying to maximize the objective function. Subject to constraints,

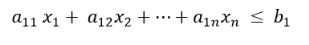
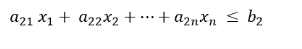
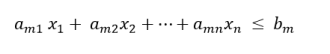
Here andafter adding the Slack variable, the system of corresponding constraint equations

Where,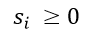

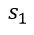
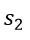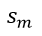……………….is called a slack variable. These are non-negative numbers that are added to remove the inequality from the equation.

The above explanation is a theoretical explanation of the simplex method. Next, I will explain how to actually use the simplex method using Excel.

Example: Company alternative ads include TV, newspaper, and radio ads. The cost of each media, including audience coverage, is as follows:

Local newspapers limit the number of ads from one company to 10. In addition, less than half of the total number of ads must occur on the radio in order to balance the ads among the three media types. And at least 10% should happen on TV. The weekly advertising budget is $ 18,200. How many ads do you need to run on each of the three media types to maximize your total audience?

Solution: First, formulate the problem for a clear understanding.

Step 1: Identify decision variables

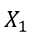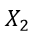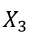, ,Represent the total number of TV, newspaper and radio ads, respectively.

Step 2: Objective function

The purpose of the company is to maximize the audience. The objective function is given by the following equation.

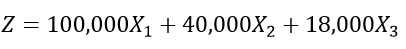
Step 3: Make a note of the constraints

Now let's look at each constraint one by one.

Clearly there are budget constraints. The total budget that can be allocated is $ 18,200. Also, the individual costs per TV, newspaper, and radio ad are $ 2000, $ 600, and $ 300, respectively. This can be expressed by the following formula.

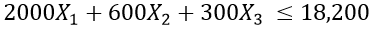
For newspaper ads, the maximum number of ads is 10. My first constraint is

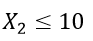
The next constraint is the number of TV ads. The company wants at least 10% of all ads to appear on TV. Therefore, it can be expressed as:

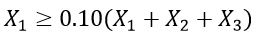
The final constraint is that the number of ads on the radio cannot exceed half the total number of ads. It can be expressed as

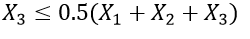
You have now formulated a linear programming problem. The simplex method is used to solve this. I will introduce the simplex method one by one.

Again, all the constraints are: We have simplified the last two equations into a standard format.

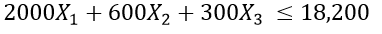
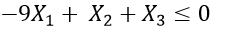
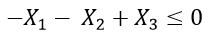
There are a total of four equations. Introduce four slack variables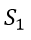,,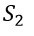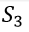and 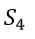to balance each equation.

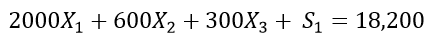
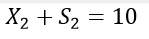
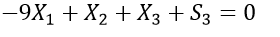
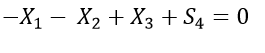
I hope you can understand the whole problem of advertising. All of the above formulas are for a better understanding. Solving these equations yields the values   X1 = 4, X2 = 10, and X3 = 14.

Solving the objective function yields a maximum audience of 1,052,000 per week. You can solve the equation by following this tutorial. Follow this tutorial to solve linear programming in Excel.

Example: Maximize

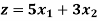
Subject to-

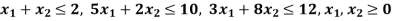
By using simplex method.

Sol. Here all b’s are positive and the objective function is to be maximized.

Step-1: Now express the problem in the standard form-

Let 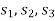are slack variables then the problem in standard form becomes-

Maximize-

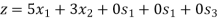
Subject to

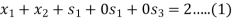
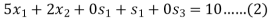
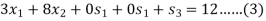
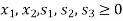
Step-2: Find the initial basic feasible solution-

There are three equations having 5 unknowns and for obtaining the solution we assign zero value to any two of the three variables.

We start with a basic solution for which we set 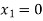and .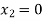

Putting  

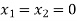in the above three equations-

We get-

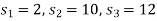
Here all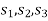
are positive, the basic solution is also feasible and non-degeneate.

The BFS is-

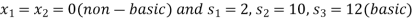
Initial BFS is given by the table below-

For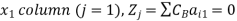

For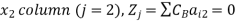

Similarly-

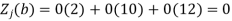
Now apply the optimality test-

As 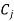is positive under some columns, the IBFS is not optimal, we move to the next step-

Step- Identify the outgoing and incoming variables-

By the above table 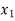is the incoming variable as its incremental contribution 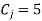is max. And the column in which it appears is the key column.

Dividing the  elements under b-column by the corresponding elements of key-column we find the mi. Positive ratio 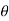in two rows.

Therefore we arbitrarily choose the row containing 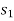as the key row.

The elements at the intersection of key row and the key column is the key element.

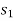is therefore the outgoing variable which will now become non-basic.

Having decided that 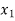is to enter the solution we have tried to find as to what maximum under 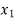could have without violating the constraints.

So that removing 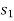, the new basis will contain 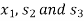as the basic variables.

Now iterate towards the optimal solution-

To transform the initial set of equations with a BFS into an equivalent set of equations with a different BFS, we make the key element unity.

We retain the key row as it is. Then to make all other elements in key column zero, we subtract proper multiples of the key row from the other rows.

Here we subtract five times the elements of key row from the second row and three times the element of key row from the third row.

These become the second and the third of the next table.

We also change the corresponding value under 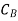column from 0 to 5.

While relacing 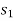by 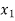under the basis.

Thus the second BFS is given below-

As is either zero or negative under all columns, the above table gives the optimal BFS.

This optimal BFS is-

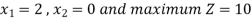
Example: Maximize-

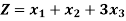
Subject to-

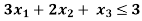
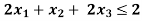
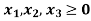
By using simplex method.

Sol.

Here we have

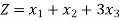
And the inequalities-

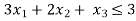...... (1)

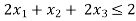........ (2)

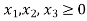  ..........(3)

By adding 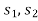we get-

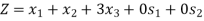  ...... (4)

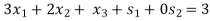....... (5)

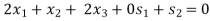...... (6)

Putting decision variables 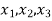equals to zero, we get-

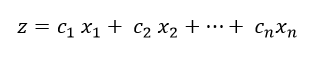
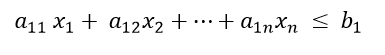
Since coefficient (–3) of 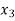is most negative, so x3 is entering variable.

The smallest ratio is 1 in the s2-row, therefore s2 is departing variable. The pivot entry (2) isat the intersection of x3-column and s2-row.

To make pivot entry (1), we multiply third row by ½, we get-

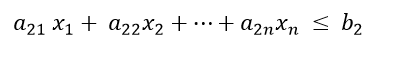
Applying R1 R1 +3R3 and R2 R2 - R1, we get

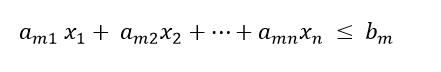
Since, Z row of the table has non-negative entries in the column of variables, therefore, this is the case of optimal solution. From the last column of the table we have x1 = 0, x2 = 0 andx3 = 1 and the maximum value of Z = 3.

Economic interpretation of the optimum simplex solution

The following economic interpretations can be made for the various terms contained in the optimal simplex solution.

1. The values   of the variables displayed in the product mix column are shown in the quantity column for them. All variables that do not appear in the product mix column are considered to have zero values. For slack variables. If some of them appear in the solution. This means that you have unused capacity / resources. Otherwise, there is no unused capacity / resources.

2. The number "aj" in the coefficient matrix indicates the marginal exchange rate between the row and column variables.

3. The numbers in the index row are known as shadow prices or accounting prices. Therefore, a positive (or negative) number in an index row indicates an algebraic decrease (or increment) in the objective function if one unit of the variable at the beginning of that column is introduced into the base (solution).

If it is under any column of the body matrix with optimal solution Cj-Zj = 0, it indicates the existence of an alternative optimal solution.

Key takeaways:

References: