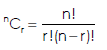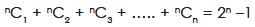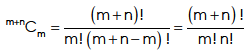Unit-2
Permutation, Combination and Linear Programming Problems
The product of the positive integers from 1 to n is denoted by n! And we read it as “factorial “
Or
“Factorial of a natural number n is the product of the first n natural numbers.”
“The continued product of first n natural numbers, i.e., 1, 2, 3, …. (n – 1) n, is generally denoted by the symbol 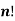 we read it as ‘factorial n”.”
we read it as ‘factorial n”.”
Expressed as-
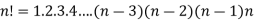
Note- 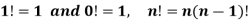
If one operation can be performed in m different ways and corresponding to any one of such operations if a second operation can be performed in n different ways, then the total number of performing the two operations is m × n.
To find the number of permutations of n different things taken r ( r £ n) at a time.
This is the same thing of finding out the number of different ways in which r places can be filled up by the n things taking one in each place. The first place can be filled up in n ways since any one of the n different things can be put in it.
When the first place has been filled up in any of these n ways, the second place can be filled up in (n – 1) ways, since any one of the remaining (n – 1) things can be put in it. Now corresponding to each of filling up the first place, there are (n – 1) ways of filling up the second, the first two places can be filled up in n (n – 1) ways. Again, when the first two places are filled up in any one of the n (n – 1) ways, the third place can be filled up by (n – 2) ways, for there are now (n – 2) things, at our disposal, to fill up the third place, Now corresponding to the each way of filling up the first two places, there are clearly (n – 2) ways of filling up the third place. Hence the first three places can be up in n (n –1) (n – 2) ways.
Proceeding similarly and noticing that the number of factors at any stage, is always equal to the number of places to be filled up, we conclude that the total number of ways in which r places can be filled up.
= n (n – 1) (n – 2) …….. To r factors
= n (n – 1) (n – 2) ……… {n – (r – 1)}
= n (n – 1) (n – 2) …….. (n – r + 1)
Using the symbol of permutation, we get,
NPr = n (n – 1) (n – 2) … (n – r + 1)
Example: Find the value of the following-
- 5!,
- 6! − 5!
Sol.
(i) 5! = 5 × 4 × 3 × 2 × 1 = 120.
(ii) 6! − 5! = 6 × 5! − 5! = (6 − 1) × 5! = 5 × 120 = 600.
Example: Simplify 
Sol.
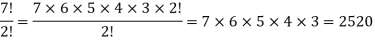
Example: What is the unit digit of the sum 2! + 3! + 4! + ..... + 22!?
Sol.
From 5! onwards for all n! the unit digit is zero and hence the contribution to the unit digit is through 2! + 3! + 4! only. Which is 2 + 6 + 24 = 32 . Therefore the required unit digit is 2.
Fundamental principal of counting:
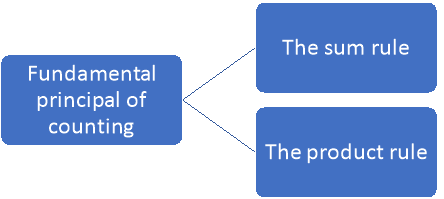
- The Sum Rule- Let us consider two tasks which need to be completed. If the first task can be completed in M different ways and the second in N different ways, and if these cannot be performed simultaneously, then there are M + N ways of doing either task. This is the sum rule of counting.
2. The Product Rule- Let us suppose that a task comprises of two procedures. If the first procedure can be completed in M different ways and the second procedure can be done in N different ways after the first procedure is done, then the total number of ways of completing the task is M × N
Example: Suppose one woman or one man has to be selected for a game from a society comprising 17 men and 29 women. In how many different ways can this selection be made?
Sol.
The first task of selecting a woman can be done in 29 ways. The second task of selecting a man can be done in 17 ways. It follows from the sum rule, that there are 17+29 = 46 ways of making this selection.
Key takeaways-
- Factorial of a natural number n is the product of the first n natural numbers.
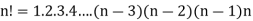
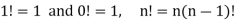
Permutations-
“The different arrangements which can be made out of a given set of things, by taking some or all of them at a time are called permutations.”
Or
A permutation is an arrangement of objects in a definite order. Since we have already studied combinations, we can also interpret Permutations as ‘ordered combinations.
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- 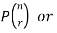
Note-
- The number of permutations of n different things taken r at a time in which p particular things never occur is-
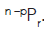
2. The number of permutations of n different things taken r at a time in which p particular things are always present is-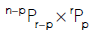
Example 1: Consider the three letters x, y, z. The arrangements of the letter x, y, ztaken two at a time are-
Xy, yx, xz, zx, yz, zy
∴The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time
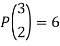
Note-A permutation of n objects taken r at a time is also called r-permutation
Binomial coefficient-
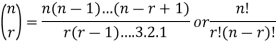
Example:
1. 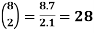

Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 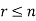 of these objects in a given order is said to be r-permutation.
of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula
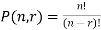
Permutation with repetitions-
The number of permutations of n objects of which are 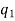 are alike,
are alike, 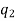 are alike,
are alike, 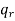
Are alike is-
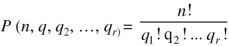
Sampling with or without replacement-
Suppose we chose the samples with repetition, from example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n = 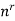
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-
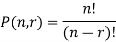
Example-
Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Example-
There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?
Solution: Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row =
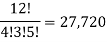
Example- A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n= 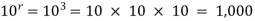
(b) P (10, 3) = 10 × 9 × 8 = 720
Example: In a sports broadcasting company, the manager must pick the top three goals of the month, from a list of ten goals. In how many ways can the top three goals be decided?
Solution: Since the manager must decide the top three goals of the month, the order of the goals is very important! It decides the first-place winner, the runner-up, and the second runner-up. Thus, we can see that the problem is of permutation formula.
Picking up three goals from a list of ten:
Possible Permutations = 10P3 = 10!(10−3)! = 10 × 9 × 8 = 720
Therefore, there are 720 ways of picking the top three goals!
Example: A license plate begins with three letters. If the possible letters are A, B, C, D and E, how many different permutations of these letters can be made if no letter is used more than once?
Solution: For the first letter, there are 5 possible choices. After that letter is chosen, there are 4 possible choices. Finally, there are 3 possible choices.
5 × 4 × 3 = 60
Using the permutation formula:
The problem involves 5 things (A, B, C, D, E) taken 3 at a time.
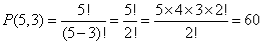
There are 60 different permutations for the license plate.
Example:
In how many ways 6 children can be arranged in a line, such that
(i) Two particular children of them are always together
(ii) Two particular children of them are never together
Sol:
(i) The given condition states that, 2 students needs to be together, hence we can consider them 1.
Thus, the remaining 7 gives the arrangement in 5! ways, i.e. 120.
Also, the two children in a line can be arranged in 2! Ways.
Hence, the total number of arrangements will be,
5! × 2! = 120 × 2 = 240 ways
(ii) The total number of arrangements of 6 children will be 6!, i.e. 720 ways.
Out of the total arrangement, we know that, two particular children when together can be arranged in 240 ways.
Therefore, total arrangement of children in which two particular children are never together will be 720 – 240 ways, i.e. 480 ways.
Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.
Hence the number of circular permutations of n different objects = (n – 1)!
Example: In how many ways 8 girls can form a ring?
Sol.
If we keep one girl fixed in any position, remaining 7 girls can be arranged in 7! ways.
Hence, the required on. Of ways = 7 ! = 7. 6. 5. 4. 3. 2. 1 = 5040.
Example: In how many ways 5 men and 5 women can take their seats in a round table, so that no two women will sit side by side.
Sol.
If one man takes his seat anywhere in a round table, then remaining 4 men can take seats in 4! = 24 ways.
In each of these 24 ways, between 5 men, if 5 women take their seats then no two women will be side by side. So in this way 5 women may be placed in 5 places in 5! = 120 ways.
Again the first man while taking seat, may take any one of the 10 seats, which means, he may take his seat in 10 ways.
Hence, reqd. Number ways = 24 × 120 × 10 = 28,800.
Key takeaways-
- A permutation of n objects taken r at a time is an arrangement of r of the objects (r≤n).
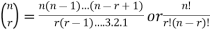
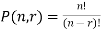
- A circular permutation of n objects is an arrangement of the objects around a circle.
- The number of circular permutations of n different objects = (n – 1)!
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
“The different groups or collection or selections that can be made of a given set of things by taking some or all of them at a time, without any regard to the order of their arrangements are called their combinations.”
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
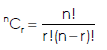
Total number of combinations:
Total number of combination of n different things taken 1, 2, 3 …. n at a time.
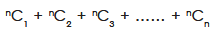
Note-
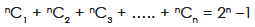
Note-
1. Property-1
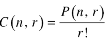
2. Property-2
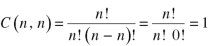
3. Property-3
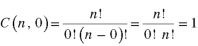
Grouping-
When we are required to form two groups out of (m + n) things,  so that one group consists of m things and the other of n things. Now formation of one group represents the formation of the other group automatically. Hence the number of ways m things can be selected from (m + n) things.
so that one group consists of m things and the other of n things. Now formation of one group represents the formation of the other group automatically. Hence the number of ways m things can be selected from (m + n) things.
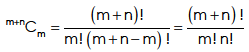
Example: From a class of 3 students, 4 students are to be chosen for competition, in how many ways they can be selected?
Sol.
The number of combinations will be-
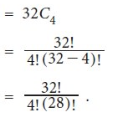
Example:
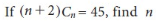
Sol.
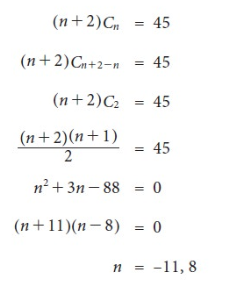
n = -11 is not possible,
Therefore, we chose-
n = 8
Example:
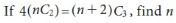
Sol.
Example: Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
Number of ways of selecting 3 consonants from 7
= 7C3
Number of ways of selecting 2 vowels from 4
= 4C2
Number of ways of selecting 3 consonants from 7 and 2 vowels from 4
= 7C3 × 4C2
= 210
It means we can have 210 groups where each group contains total 5 letters (3 consonants and 2 vowels).
Number of ways of arranging 5 letters among themselves
= 5! = 5 × 4 × 3 × 2 × 1 = 120 = 5! = 5 × 4 × 3 × 2 × 1 = 120
Hence, required number of ways
= 210 × 120 = 25200
Example: Find the values of 14C5, 10C810C8 and C(7, 2).
Solution:
We know that the formula for combination, i.e. C(n,k)C(n,k) = 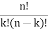
Then 14C5
= 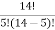 =
= 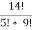 = 2002
= 2002
10C8 = 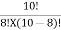 =
= 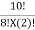 =
= 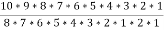 = 45
= 45
C(7, 2) = 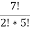 =
= = 21
= 21
Example: There are seven candidates for a post. In how many ways can a selection of four be made amongst them, so that:
- 2 persons whose qualifications are below par are excluded?
- 2 persons with good qualifications are included?
Sol.
- Excluding 2 persons, we are to select 4 out of 5 ( = 7 – 2) candidates.
Number of possible selections-
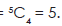
2. Here 2 persons are fixed, and we are to select only 2 persons out of (7–2), i.e. 5 candidates. Hence the required number of selection
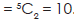
Example: In how many ways can a girl invite one or more of 5 friends?
Sol.
The number of ways will be-
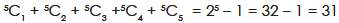
Example: In how many ways 15 things be divided into three groups of 4, 5, 6 things respectively.
Sol.
The first group can be selected as-
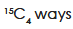
The second group can be selected as-
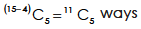
The third group can be selected as-
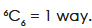
Hence the total number of ways-
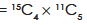
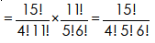
Key takeaways-
The relationship between a permutation and a combination is
nPr = nCr × r!
Or, n! ⁄ (n – r)! = nCr × r!
Or, nCr = n! ⁄ (n – r)! r!
npr= r! times nCr
Important Results Related to Combination Formula
- nCr = nCn – r
- nCn = 1 = nC0 = 1 (0! = 1)
- If nCk = nCr, then either k = r or k + r = n.
- n + 1 Cr = nCr + nC r – 1.
Example: if nPr is 11880 and nCr is 495 then find n and r.
Sol.
As we know that-
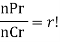
So that-
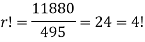
Gives r = 4.
Using this r = 4 in 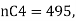
We get n = 12.
Example-1: In how many ways 6 books out of 10 different books can be arranged in a book-self so that 3 particular books are always together?
Sol.
At first 3 particular books are kept outside. Now remaining 3 books out of remaining 7 books can be arranged in 7P3 ways. In between these three books there are 2 places and at the two ends there are 2 places i.e. total 4 places where 3 particular books can be placed in 4P1 ways. Again 3 particular books can also be arranged among themselves in 3! ways.
Hence, required no. Of ways
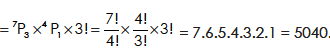
Example-2: In how many ways 8 different beads can be placed in necklace?
Sol.
8 beads can be arranged in 7 ! ways. In this 7 ! ways, arrangements counting from clockwise and anticlockwise
Are taken different. But necklace obtained by clockwise permutation will be same as that obtained from anticlockwise. So total arrangement will be half of 7 !.
Hence, required no. Of ways-
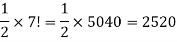
Example-3: From a company of 15 men, how many selections of 9 men can be made so as to exclude 3 particular men?
Sol.
Excluding 3 particular men in each case, we are to select 9 men out of (15 – 3) men. Hence the number of selection is equal to the number of combination of 12 men taken 9 at a time which is equal to-
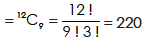
Example-4: Given n points in space, no three of which are collinear and no four coplanar, for what value of n will the number of straight lines be equal to the number of planes obtained by connecting these points?
Sol.
Since no three points, are collinear, the number of lines = number of ways in which 2 points can be selected out of n points
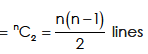
Again since three non-collinear points define a space and no four of the points are coplaner; the number of planes = number of ways in which 3 points can be selected out of n points.
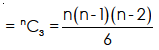
Now, we have
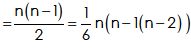
Or
6 = 2 (n – 2) Hence, n = 5
Example-5: A Science club has 15 members. In that 8 are girls. 6 of the members are to be selected for a competition and half of them should be girls. How many ways of these selections are possible?
Sol.
There are 8 girls and 7 boys in the science club. The number of ways of selecting 6 members in that half of them girls (3 girls and 3 others) is
8C3 * 7C3 = 56* 35 = 1960
Example-6: In rating 20 brands of bikes, a bike picks a first, second, third, fourth and fifth best brand and then 7 more as acceptable. In how many ways can it be done?
The picking of 5 brands for a first, second, third, fourth and fifth best brand from 20 brands in 20P5 ways. From the remaining 15 we need to select 7 acceptable in 15C7 ways. By the rule of product it can be done in 20P5 × 15C7 ways.
Sketching of graph of linear equations:
When we draw the graph of a linear equation of the form Ax + By + C = 0, we get a straight line.
We can sketch the graph of any linear equation by finding two solutions of that equation such as- 
We plot these two points on coordinates and join. We get a line.
The points where the graph cuts the x-axis and y-axis are called x-intercept and y-intercept respectively.
Note-
- When y = 0, the x-intercept occurs
- When x = 0, the y-intercept occurs
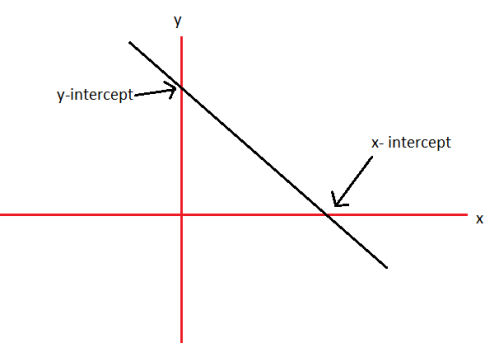
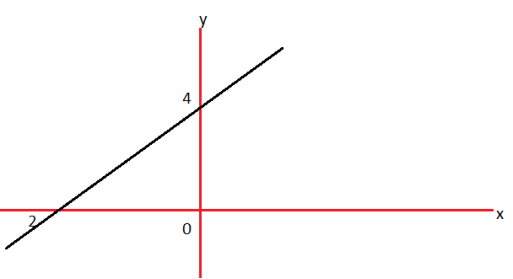
Example: Draw the graph for the linear equation 2x – y +4 = 0.
Sol.
The given equation can be written as-
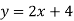
x-intercept-
When y = 0, we get-
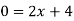
Or
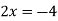
Or
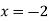
y-intercept-
When x = 0, we get-
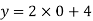
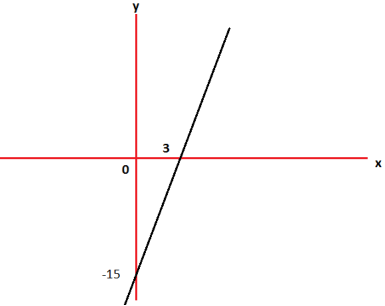
Example: Draw the graph for the linear equation y - 5x + 15=0.
Sol.
The given equation can be written as-
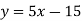
x-intercept-
When y = 0, we get-
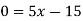
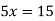
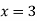
y-intercept-
When x = 0, we get-
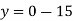
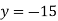
Sketching of graph of linear inequality:
A linear inequality is same as linear equation but, inequalities have signs like >, < 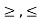 instead of =.
instead of =.
Example- 2x + 3 < 4 , 4y < 3, 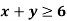 ,
, 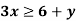 these are the linear inequalities.
these are the linear inequalities.
How to draw the graph of a linear inequality?
Step-1-
First we remove the sign of inequality and put the ‘= ‘ sign in place of inequality sign.
For example, if we need to draw the graph of linear inequality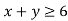 , then in first step we put it as-
, then in first step we put it as- 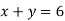 .
.
Note- We arrange the equation such as, “y” is on the left side and others are on the right side.
Like, we have 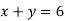 , then we put it as
, then we put it as 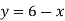
Step-2-
In second step we find the solution of the linear equation that we get from first step, and we draw the graph.
Step-
In third step, we shade the line. For 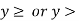 we shade above the line.
we shade above the line.
And for 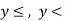 we shade below the line.
we shade below the line.
Example: Draw the graph for the inequality 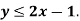
Sol.
Here we see that y is already on left side so that no need to change the position of y.
Now change the inequality sign “=”
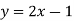
And plot the line for equation 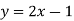
Note- The another way to shade the graph is, first we put x = 0 and y = 0 in th given inequality and we check, if the result is true then the shadow will be in side of origin and if the result is false then the shadow will be opposite to origin.
Here-
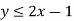
Put x = 0 and y = 0 then it becomes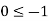
Which is false.
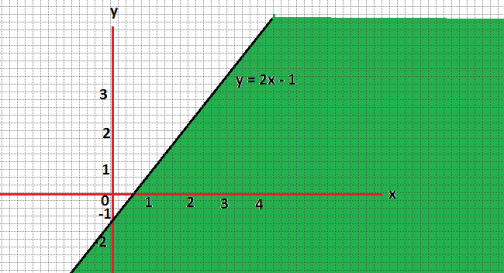
Introduction:
Optimization may be a way of life. We all have limited resources and time and need to form the foremost of them. Everything from using time productively to solving problems in your company's supply chain uses optimization. This is often a very interesting and relevant topic in data science.
This is also a really interesting topic. It starts with an easy problem, but it are often very complicated. For instance, sharing a chocolate candy between siblings may be a simple optimization problem. While solving it, we do not think mathematically. On the opposite hand, devising an e-tailer inventory and warehousing strategy are often very complex. Many SKUs with different popularity in several regions are delivered at defined times and resources.
Linear programming (LP) is one among the simplest ways to perform optimization. Making some simplified assumptions will assist you solve some very complex optimization problems. Analysts will encounter applications and problems that are solved by applied mathematics.
For some reason, LPs do not get enough attention while learning data science. So I wanted to form this excellent technique justice. i made a decision to write down a piece of writing that explains applied mathematics in simple English. The content is as simple as possible. The thought is to urge excited about applied mathematics for the primary time.
Note-If you would like to find out this during a course format, we curate this free course-Linear programming for data science professionals
What’s linear programming?
So what's linear programming? Applied mathematics may be a simple technique that uses linear functions to represent complex relationships and find the simplest points. The important words within the preamble are drawn. The particular relationship could also be far more complicated, but it is often simplified to a linear relationship.
Linear programming applications are everywhere around you. Use applied mathematics on a private and professional side. If you're driving from home to figure and need to use the shortest route, you're using applied mathematics. Or, when delivering a project, develop a technique to figure efficiently in order that your team can deliver on time.
We use linear programming to optimize the linear function subject to given linear constraints.
LPP is the popular mathematical technique which is used to make maximum profit and minimum loss.
General terminology utilized in applied mathematics
Let's use the instance above to define some terms utilized in applied mathematics.
Determinants: Determinants are variables that determine the output. They represent my ultimate solution. To unravel the matter, you initially got to identify the coefficient of determination. Within the above example, the entire number of units A and B, represented by X and Y, respectively, is my coefficient of determination.
Objective function: Defined because the objective of deciding. Within the example above, the corporate wants to extend the gross profit margin, represented by Z. Therefore, profit is my objective function.
Constraint: A constraint may be a limit or limit on a choice variable. These usually limit the worth of the choice variable. Within the above example, limiting the supply of Milk and Chocó resources is my constraint.
Non-negative limit: altogether applied mathematics, the choice variable should take a non-negative value. This suggests that the worth of the choice variable must be greater than or adequate to 0.
The process of formulating an applied mathematics problem
Let's take a glance at the steps to generally define an applied mathematics problem.
- Identify the coefficient of determination.
2. Write an objective function.
3. Mention constraints.
4. Explicitly state non-negative limits.
For the matter to be an applied mathematics problem, the choice variables, objective functions, and constraints must all be linear functions.
If all three conditions are met, it's called an applied mathematics problem.
In order for the corporate to form the foremost profit, the above inequality must be met. When converted into a mathematical model is called formulating a real-world problem
The other two factors are resource availability and technical factors. These can be better explained using the example below. The executable solution of a linear programming problem must meet the constraints and non-negative constraints. The executable solution of LPP with the maximization problem is the optimal solution when the objective function value is maximum (maximum). Similarly, an LPP executable solution with a minimization problem is optimal when the objective function value is the minimum (minimum).
Important definitions-
Linear programming problem-
We need to optimize the linear function Z subject to certain conditions, these types of problems are called Linear programming problem or in short LPP.
Objective functions-
This is a linear function of several variables, subject to the conditions.
Optimal value-
This is a maximum or minimum value of a object function which is to be calculated in a LPP.
Formulation of LPP-
Let’s consider the following example-
Example: A manufacturer produces two types of products ‘P’ and ‘Q’. Each ‘P’ type of product required 4 hours of grinding and 2 hrs of polishing, where ‘Q’ product requires 2 hrs of grinding and 5hrs of polishing.
The manufacturer has 2 grinders and 3 polishers. Each grinder works for 80hrs a week and each polisher works for 180hrs a week. Profit on ‘P’ product is Rs. 3 and profit on ‘Q’ is Rs. 4.Whatever is produced in a week is sold in the market.
How should the manufacturer allocate his capacity of production of two types of products so that he may make the maximum profit and minimum loss in a week?
Now we formulate this problem in mathematical terms as explained below-
Suppose 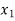 is the number of ‘P’ product and
is the number of ‘P’ product and 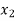 is the number of ‘Q’ product produced weekly.
is the number of ‘Q’ product produced weekly.
Then the weekly profit is-
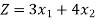
Here ‘Z’ is called the objective function which is to be maximize or minimize.
Now, to produce these number of products, the total number of grinding hours needed weekly is-
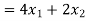
And the total number of polishing hours needed per week is-
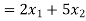
Here the number of grinding hours is not more than 80 and the number of polishing hours is not more than 180, so that we write,
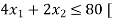 This is called the first constraint]
This is called the first constraint]
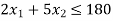 [This is the second constraint]
[This is the second constraint]
Since the number of product is non-negative, then we can write-
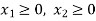
This is called the third constraint.
Hence we form the problem mathematically as follows-
To maximize- 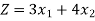
Subject to the constraints:
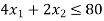
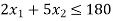
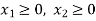
This expression is called as mathematical formulation.
Note- The variables that enter into the problem are called ‘decision variables’.
Example: A dietician mixes together two kinds of food, say, A and B in such a way that the mixture contains at least 6 units of vitamin P, 7 units of vitamin Q, 12 units of vitamin R and 9 units of vitamin S. The vitamin contents of 1 kg of food A and 1 kg of food B are given below:
Cost | Nutrition-P | Nutrition -Q | Nutrition -R | Nutrition -S |
Food-A | 1 | 1 | 1 | 2 |
Food-B | 2 | 1 | 3 | 1 |
One kg of food X costs Rs. 5, whereas one kg of food Y costs Rs. 8. Formulate the linear programming problem.
Sol.
Decision variables- Here decision variables are units of food A and B.
Let food A in the mixture be 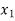 and food B in the mixture
and food B in the mixture 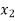 .
.
Objective function- To minimize the cost,
Total cost of food A and B = 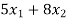
Or
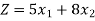
Now we will write the constraints one by one-
Constraint-1: 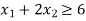
Constraint-2: 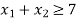
Constraint-3: 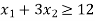
Constraint-4: 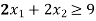
Constraint-5: 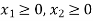
Mathematical formation will be as follows-
To minimize,
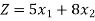
Subject to the constraints-
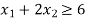
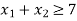
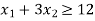
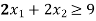
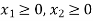
Example: A manufacturer has 3 machines 1, 2 and 3. Machines 1 and 2 are capable of being operated for at the most 12 hours whereas machine 3 must be operated at least for 5 hours a day. He produces two items each requiring the use of the three machines.
The number of hours required for producing 1 unit of each of the items X and Y on the three machines are given below:
Items | Numbers of hours required on the machines 1 2 3 |
X | 1 2 1 |
Y | 2 1 5/4 |
She makes a profit of Rs. 60 on item X and Rs. 40 on item Y. Assuming that he can sell all that he produces, how many of each item should be produced so as to maximize the profit. Formulate the above as L.P.P.
Sol.
Decision variables- Here decision variables are item X and Y.
Let the production of item X be 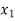 and the production of item Y be
and the production of item Y be 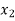 .
.
Objective function- To maximize the profit,
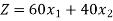
Now we will write the constraints one by one-
Constraint-1: 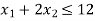
Constraint-2: 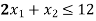
Constraint-3: 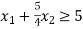
Constraint-4: 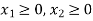
Mathematical formation will be as follows-
To maximize,
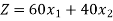
Subject to the constraints-
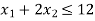
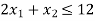
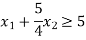
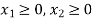
Example: A manufacturer produces two types of for children, mouth – organs and drums, each of which must be processed through two machines A and B. The Maximum availability of machines A and B per day are 12 and 18 hours respectively. The manufacturing a mouth – organ requires 4 hours in machine A and 3 hours in profit per mouth – organ is Rs 20 and per drum is Rs 50, machine A and 6 hours of machine B. If the profit per mouth-organ is RS 20 and per drum is Rs 50, formulate the problem to maximize the profit.
Sol:
Let us suppose that, the manufacturer produces X mouth- organs and y drums per day. Then tabulating the given data as follow, we observe that, if x mouth –organs and y drums are manufactured per day, he will require 4x + 2y hours of machine A and 3x + 6y hours of machine B.
Machine | Mouthorgan (x) | Drum (y) | Maximum available |
A | 4 | 2 | 12 |
B | 3 | 6 | 18 |
Since the availability of the machine A and B are not more than 12 and 18 hours respectively, we must have
4x + 2y 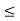 12 and 3x + 6y
12 and 3x + 6y 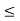 18.
18.
Note that, he may not able to complete a mouth – organ or a drum in a day Therefore, x or y need not be integers, but x and y can never be negative, since nobody can manufacture a negative number of objects.hence, the condition
X30 , y3 0 will be implemented
Thus, the problem written mathematically will be
4x +2y 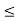 12
12
3x + 6y 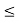 18 and
18 and
x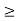 0, y
0, y 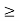 0
0
These inequalities are the constraints on the problem.
Now to find the objective function.
Since the profit per mouth – organ and drum are RS 20 RS 50 respectively, the objective function would be
Profit Z = 20x + 50y, which is to be maximized
Under the constraints mentioned above.
Example: Consider a chocolate manufacturer that produces only two sorts of chocolate, A and B. Both chocolates only require milk and chocolate. To manufacture each of the A and B units, you would like the subsequent quantities:
Each unit during a requires 1 unit of milk and three units of chocolate
Each unit in B requires 1 unit of milk and a couple of units of chocolate.
The company's kitchen features a total of 5 units of milk and 12 units of chocolate. With each sale, the corporate makes a profit
Rs6 per unit A sold
Rs5 per unit B sold.
Now the corporate wants to maximise profits. What percentage units of A and B does one got to produce respectively?
Solution: the primary thing to try to is to tabulate the matter for better understanding.
Milk | Chocó | Profit per unit | |
A | 1 | 3 | Rs 6 |
B | 1 | 2 | Rs 5 |
Total | 5 | 12 |
|
Let = X be the entire number of units generated by A.
Let = Y be the entire number of units generated by B.
Now, the entire profit is represented by Z
The company's gross profit margin is that the total number of A and B units produced multiplied by the profit per Rs6 and Rs5 units, respectively.
Profit: Maximum Z = 6X + 5Y
That is, you would like to maximize Z.
The company will attempt to produce as many A and B units as possible to maximize profits. However, Milk and Chocó resources are available in limited quantities.
As shown within the table above, each unit A and B requires 1 unit of milk. The entire amount of milk available is 5 units. To precise this mathematically,
X + Y ≤ 5
Also, each unit A and B requires 3 units and a couple of units of Chocó, respectively. The entire number of chocolates sold is 12. To precise this mathematically,
3X + 2Y ≤ 12
Also, the unit value of A can only be an integer.
Therefore, there are two constraints, X ≥ 0 and Y ≥ 0.
Applications of LPP-
Linear programming and optimization are used in a variety of industries. Manufacturing and service industries regularly use linear programming.
- Manufacturing uses linear programming to analyse supply chain operations. Their motivation is to maximize efficiency with minimal operating costs. Following the recommendations of the linear programming model, manufacturers can reconfigure their storage layouts and adjust their employees to reduce bottlenecks. This is a case study of Cequent's small warehouse based in the United States. Watch this video for a clearer understanding.
- Linear programming is also used in retail stores organized to optimize shelf space. With the number of products on the market growing exponentially, it's important to understand what your customers want. Optimization is actively used in stores such as Wal-Mart, Hyper city, Reliance, and Big Bazaar. The products in the store are strategically placed with the customer's shopping patterns in mind. The goal is to make it easier for customers to find and select the right product. This has limitations such as limited shelf space and various products.
- Optimization is also used to optimize delivery routes. The service industry uses optimization to find the best route for multiple salespeople travelling to multiple cities. With the help of clustering and greedy algorithms, delivery routes are determined by companies such as FedEx and Amazon. The goal is to minimize operational costs and time.
- Optimization is also used in machine learning. Supervised learning addresses the basics of linear programming. The system is trained to fit a mathematical model of a function from labelled input data that can predict values from unknown test data.
The application of linear programming does not end here. There are many other real-world linear programming applications, such as those applied by shareholders, sports, stock markets, and more. Please continue to explore further.
Key takeaways-
- LPP is the popular mathematical technique which is used to make maximum profit and minimum loss.
- The variables that enter into the problem are called ‘decision variables’.
LPP having two variables can be easily solved by graphical method which provides a pictorial representation of the solution and we get insights into the basic concept used in solve LPP.
There are two main methods to solve LPP- Graphical method and simplex method.
Note- LPP can be solved by using R programming.
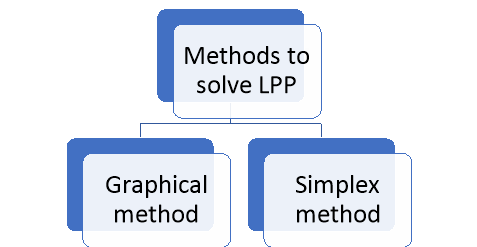
Here we will discus about graphical method.
Step by step procedure to solve LPP graphically-
- First we need to formulate the given problem as a LPP in mathematical form.
- Now plot the given constraints on
 coordinate plane and find the convex region.
coordinate plane and find the convex region. - Now determine the convex region and find the value of the objective function at each vertex. The vertex which gives the max or min value of the objective function gives the optimal solution of the LPP.
Note- The region satisfying all the constraints is called feasible region.
Example: Solve the following LPP graphically-
Maximize-
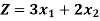
Subject to the constraints-
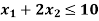
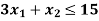
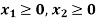
Sol.
Change the given constraints into equations-
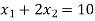
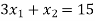
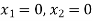
The line 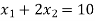 meets the x-axis at the point A(10,0) and meets the y-axis at the point B(0,5). Join A and B to get the graph for the line.
meets the x-axis at the point A(10,0) and meets the y-axis at the point B(0,5). Join A and B to get the graph for the line.
Hence origin (0,0) satisfies the inequality 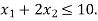 so that half plane containing the origin represent the solution set of
so that half plane containing the origin represent the solution set of 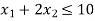 .
.
And
The line 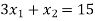 meets the x-axis at the point C(5,0) and meets the y-axis at the point D(0,15). Join C and D to get the graph for the line.
meets the x-axis at the point C(5,0) and meets the y-axis at the point D(0,15). Join C and D to get the graph for the line.
Hence origin (0,0) satisfies the inequality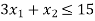 so that half plane containing the origin represent the solution set of
so that half plane containing the origin represent the solution set of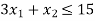 .
.
Now all the points in first quadrant satisfies 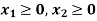 .
.
So that first quadrant is the region represented by 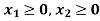
Hence the region OCEBO satisfies all the inequalities.
And each point on the region is the feasible solution of the problem.
Feasible solution-
Here in this problem the feasible solution is (5,0), (4,3) and (0,5).
Now we can obtain the optimal solution of the problem.
As we know that any point in the feasible region that gives the optimal value is called an optimal solution.
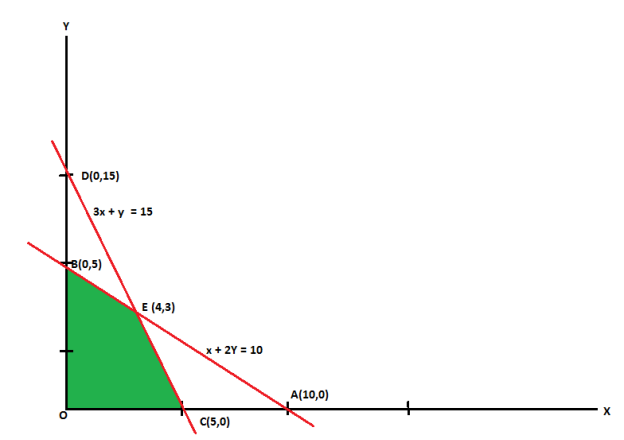
The value of the objective function 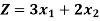 at corner points of the feasible region is given below-
at corner points of the feasible region is given below-
Vertex [ feasible region ] | Value of 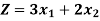 |
O(0,0) | 0 |
C(5,0) | 15 |
E(4,3) | 18 [Maximum] |
B(0,5) | 10 |
Here we see that the maximum value of Z is 18.
Note-
- This method is called corner point method-
- The optimal value of objective function must occur at a corner point (vertex) of the feasible region
- If the feasible region is bounded then the objective function Z has both maximum and minimum values on corner points of the bounded region.
Example: Find the maximum value of Z = 2x + 3y subject to the constraints-
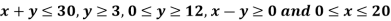
Sol.
Any point (x,y) satisfying the conditions 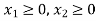 lies in the first quadrant only.
lies in the first quadrant only.
Also since 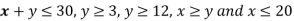 the desired point (x,y) lies within the convex region ABCDE.
the desired point (x,y) lies within the convex region ABCDE.
Its vertices are A(3,3), B(20,3), C(20,10), D(18,12) and E(12,12).
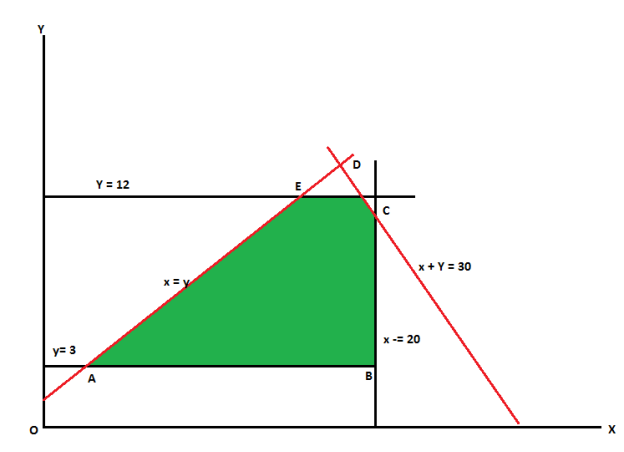
The value of Z at these points are-
Z(A) = 15
Z(B) = 49
Z(C) = 70
Z(D) = 72
Z(E) = 60
Here 72 is the maximum value which is at D.
So that the solution of the LPP is x = 18 and y = 12 and maximum Z = 72
Example: A factory manufactures two types of items, A and B, each type requiring the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of item A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of item B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of item A at a profit of Rs. 7 and item B at a profit of Rs 10. Assuming that he can sell all the items he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit ?
Determine the maximum profit.
Sol.
We can tabulate the data as follows-
Items \ Machine | Automatic operated | By hand operated | Profit |
A | 4 min | 6 min | Rs. 7 |
B | 6 min | 3 min | Rs. 10 |
| 4 hours or[240 min] | 4 hours or[240 min] |
|
Decision variables- Let the manufacturer produce x packages of item A and y packages of item B per day respectively.
Objective function- Suppose Z denotes the maximum profit,
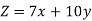
Constraints-
1st constraint-
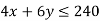
2nd constraint-
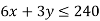
3rd constraint-
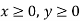
Mathematical formulation-
The mathematical form of this LPP can be written as-
Maximize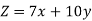
Subject to the constraints-
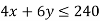
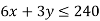
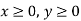
Tables for the region represented by inequalities-
For the first constraint-
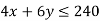
x | 60 | 0 |
y | 0 | 40 |
Points | A | B |
For second condition- 
x | 40 | 0 |
y | 0 | 80 |
Points | C | D |
Now we draw on x and y axes.
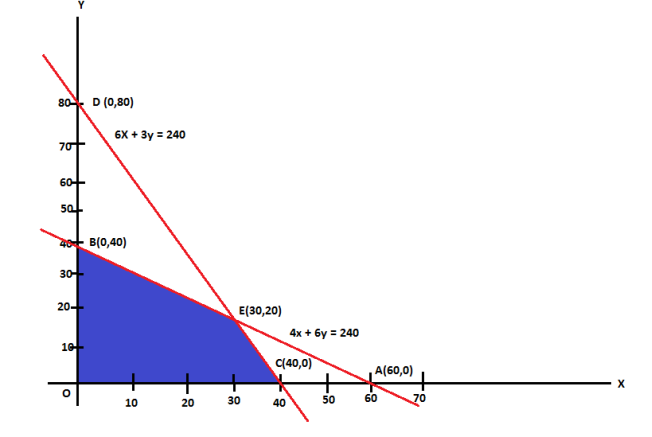
The coordinates of the vertices O, C, E and B of the feasible region OCEBO are O (0, 0), C (40, 0), E (30, 20) and B (0, 40). The coordinates of E are obtained by solving the equations 4x + 6y = 240 and 6x + 3y = 240.
Corner points of the feasible region | Value of Z = 7x + 10y |
C (40, 0) | 280 |
E(30,20) | 410 [Maximum] |
B(0, 40) | 400 |
Therefore Z is maximum at x = 30 and y = 20 and the maximum value of Z is 410.
Key takeaways:
- Linear programming is often solved in multiple ways. During this section, we'll check out graphical thanks to solve applied mathematics.
- The graphical method formulates a group of linear inequalities that are subject to constraints. The inequality is then plotted on the XY plane.
- If you plot all the inequalities on a graph, the intersecting regions offer you a feasible region.
References-
- Mathematics and Statistics for Business – R. S. Bhardwaj – Excel Books.
- Https://www.yourarticlelibrary.com/ergonomics/operation-research/operation-research-applications-methodology-and-tools/90745
- Https://kalyan-city.blogspot.com/2011/09/operations-research-definition-meaning.html
- Https://www.britannica.com/topic/operations-research/Essential-characteristics
- Https://en.wikipedia.org/wiki/Operations_research
- Https://scholar.rhsmith.umd.edu/sites/default/files/bgolden/files/introduction_to_linear_programming.pdf?m=1590769303
- Http://wwwsop.inria.fr/members/Frederic.Giroire/teaching/ubinet/pdfs/slides-linear-programming-introduction.pdf
- Https://www.courses.psu.edu/for/for466w_mem14/Ch11/HTML/Sec1/ch11sec1.htm
- Https://towardsdatascience.com/applications-of-linear-programming-problem-lpp-385bc3bb9621
- Business Mathematics and Statistics – Subhanjali Chopra – Pearson publication.
- Fundamentals of Business Mathematics and Statistics – ICAI – ICAI.
- Business Mathematics and Statistics – Dr. J K Das, N Das – McGraw Hill Education.
- Mathematical and statistical techniques, Dr. Abhilasha S. Magar & Manohar B. Bhagirath
- IGNOU