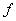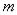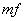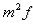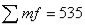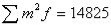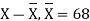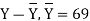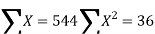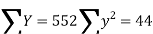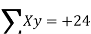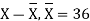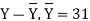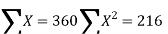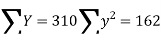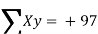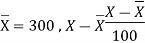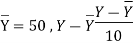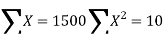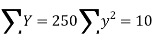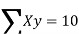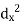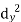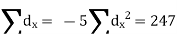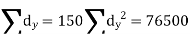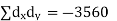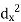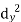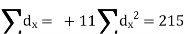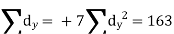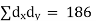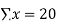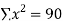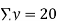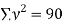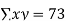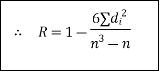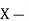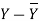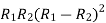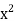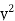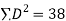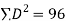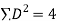Unit 2
Measures of Dispersion
As the name suggests, the measure of dispersion shows the scatterings of the data. It tells the variation of the data from one another and gives a clear idea about the distribution of the data. The measure of dispersion shows the homogeneity or the heterogeneity of the distribution of the observations.
Classification of Measures of Dispersion
The measure of dispersion is categorized as:
(i) An absolute measure of dispersion:
(ii) A relative measure of dispersion:
2.1.1 Range
A range is the most common and easily understandable measure of dispersion. It is the difference between two extreme observations of the data set. If X max and X min are the two extreme observations then
Range = X max – X min
2.1.2 Mean Deviation
Mean deviation is the arithmetic mean of the absolute deviations of the observations from a measure of central tendency. If x1, x2, …, xn are the set of observation, then the mean deviation of x about the average A (mean, median, or mode) is
Mean deviation from average A = 1⁄n [∑|xi – A|]
For a grouped frequency, it is calculated as:
Mean deviation from average A = 1⁄N [∑ fi |xi – A|], N = ∑fi
The quartiles divide a data set into quarters. The first quartile, (Q1) is the middle number between the smallest number and the median of the data. The second quartile, (Q2) is the median of the data set. The third quartile, (Q3) is the middle number between the median and the largest number.
Quartile deviation or semi-inter-quartile deviation is
Q = ½ × (Q3 – Q1)
2.2.1 Quartiles
There are three quartiles, i.e. Q1, Q2 and Q3 which divide the total data into four equal parts when it has been orderly arranged. Q1, Q2 and Q3 are termed as first quartile, second quartile and third quartile or lower quartile, middle quartile and upper quartile, respectively. The first quartile, Q1, separates the first one-fourth of the data from the upper three fourths and is equal to the 25th percentile. The second quartile, Q2, divides the data into two equal parts (like median) and is equal to the 50th percentile. The third quartile, Q3, separates the first three-quarters of the data from the last quarter and is equal to 75th percentile.
Calculation of Quartiles:
The calculation of quartiles is done exactly in the same manner as it is in case of the calculation of median.
The different quartiles can be found using the formula given below:
Qi = l1 + 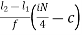 i= 1,2,3
i= 1,2,3
Where,
L1 = lower limit of ith quartile class
L2 = upper limit of ith quartile class
c = cumulative frequency of the class preceding the ith quartile class
f = frequency of ith quartile class.
2.2.2Deciles
Deciles are the partition values which divide the arranged data into ten equal parts. There are nine deciles i.e. D1, D2, D3……. D9 and 5th decile is same as median or Q2, because it divides the data in two equal parts.
Calculation of Deciles:
The calculation of deciles is done exactly in the same manner as it is in case of calculation of median.
The different deciles can be found using the formula given below:
Di = l1 + 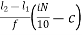 i= 1,2,3….9
i= 1,2,3….9
Where,
l1 = lower limit of ith quartile class
l2 = upper limit of ith quartile class
c = cumulative frequency of the class preceding the ith quartile class
f = frequency of ith quartile class.
2.2.3 Percentiles
Percentiles are the values which divide the arranged data into hundred equal parts. There are 99 percentiles i.e. P1, P2, P3, ……. P99.
The 50th percentile divides the series into two equal parts and P50 = D5 = Median.
Similarly, the value of Q1 = P25 and value of Q3 = P75
Calculation of Percentiles:
The different percentiles can be found using the formula given below:
pi = l1 + 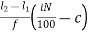 i= 1,2,3…………….99
i= 1,2,3…………….99
Where,
l1 = lower limit of ith quartile class
l2 = upper limit of ith quartile class
c = cumulative frequency of the class preceding the ith quartile class
f = frequency of ith quartile class.
In case of grouped data, modal class is determined by inspection or by preparing grouping and analysis tables. Then we apply the following formula.
Mode (Mo) = l1 + 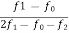 x i Or l1 +
x i Or l1 + 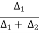 x i
x i
Where
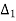 = f1-f0
= f1-f0
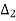 = f1-f0
= f1-f0
l1 = Lower limit of Modal class
f1 = frequency of modal class
f0= frequency of class preceding of modal class
f2= frequency of class succeeding the modal class
i = size of class
A standard deviation is the positive square root of the arithmetic mean of the squares of the deviations of the given values from their arithmetic mean. It is denoted by a Greek letter sigma, σ. It is also referred to as root mean square deviation. The standard deviation is given as
σ = [(Σ(yi – ȳ) ⁄ n] ½ = [(Σ yi 2 ⁄ n) –ȳ 2] ½
For a grouped frequency distribution, it is
σ = [(Σ fi (yi – ȳ) ⁄ N] ½ = [(Σfi yi 2 ⁄ n) –ȳ 2] ½
The square of the standard deviation is the variance. It is also a measure of dispersion.
σ 2 = [(Σ (yi – ȳ ) / n] ½ = [(Σ yi 2 ⁄ n) –ȳ 2]
For a grouped frequency distribution, it is
σ 2 = [(Σ fi (yi – ȳ) ⁄ N] ½ = [(Σ fi xi 2 ⁄ n) –ȳ 2].
If σ1, σ2 are two standard deviations of two series of sizes n1 and n2 with means ȳ1 and ȳ2. The variance of the two series of sizes n1 + n2 is:
σ 2 = (1/ n1 + n2) ÷ [n1 (σ1 2 + d1 2) + n2 (σ2 2 + d2 2)]
Where, d1 = ȳ 1 −ȳ , d2 = ȳ 2 −ȳ , and ȳ = (n1 ȳ 1 + n2 ȳ 2) ÷ ( n1 + n2).
Coefficient of Variation
100 times the coefficient of dispersion based on standard deviation is the coefficient of variation (C.V.).
C.V. = 100 × (S.D. / Mean) = (σ/ȳ ) × 100.
Q1Find the Variance and Standard Deviation of the Following Numbers: 1, 3, 5, 5, 6, 7, 9, 10.
The mean = 46/ 8 = 5.75
Step 1: (1 – 5.75), (3 – 5.75), (5 – 5.75), (5 – 5.75), (6 – 5.75), (7 – 5.75), (9 – 5.75), (10 – 5.75)
= -4.75, -2.75, -0.75, -0.75, 0.25, 1.25, 3.25, 4.25
Step 2: Squaring the above values we get, 22.563, 7.563, 0.563, 0.563, 0.063, 1.563, 10.563, 18.063
Step 3: 22.563 + 7.563 + 0.563 + 0.563 + 0.063 + 1.563 + 10.563 + 18.063
= 61.504
Step 4: n = 8, therefore variance (σ2) = 61.504/ 8 = 7.69 (3sf)
Now, Standard deviation (σ) = 2.77 (3sf)
Q2. The following gives the frequency distribution of the daily commuting time (in minutes) from home to work for all 25 employees of a company. | |||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
| Calculate the mean, variance and standard deviation of the daily commuting times. Solution : | ||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
| Mean 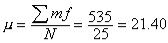 | ||||||||||||||||||||||||||||||||||||
| Variance 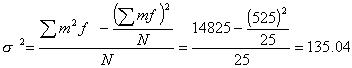 | ||||||||||||||||||||||||||||||||||||
| Standard deviation 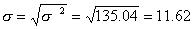
2.7 Example on quartiles deciles and percentiles:
| ||||||||||||||||||||||||||||||||||||
Q3. The number of vehicles sold by a major Toyota Showroom in a day was recorded for 10 working days. The data is given is – | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Find the Quartile Derivation and its coefficient for the given discrete distribution case. | ||||||||||||||||||||||||||||||
Solution: We first need to sort the frequency data given to us before proceeding with the quartile’s calculation | ||||||||||||||||||||||||||||||
| Sorted Data – 5, 10, 15, 17, 18, 20, 21, 25, 28 N (number of data points) = 10 | |||||||||||||||||||||||||||||
| Now, to find the quartiles, we need the logic that the first quartile lies halfway between the lowest value and the median; and the third quartile lies halfway between the median and the largest value. | |||||||||||||||||||||||||||||
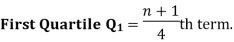 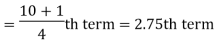 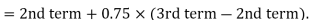
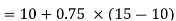 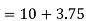 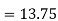
| ||||||||||||||||||||||||||||||
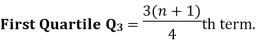  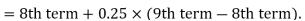
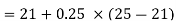 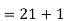 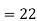 | ||||||||||||||||||||||||||||||
Using the values for Q1 and Q3, now we can calculate the Quartile Deviation and its coefficientas follows –
| ||||||||||||||||||||||||||||||
Quartile Deviation = Semi– inter Quartile Range 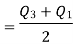 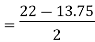 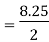 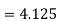 Coefficient of Quartile Deviation | ||||||||||||||||||||||||||||||
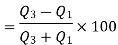
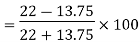
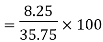
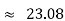 | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Q4. Given the series 3, 5, 7, 4, 6, 2 and 9. Calculate the 2nd and 4th decile. | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
Solution: To find the decile first we have to arrange the date in order. 2, 3, 4, 5, 6, 7 and 9. Here n = 7 | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
D2 | = value of 2[(n+1)/10]th item. | |||||||||||||||||||||||||||||
= value of 2[(7+1)/10]th item | ||||||||||||||||||||||||||||||
= value of 1.6th item. | ||||||||||||||||||||||||||||||
= 1st value + 0.6 of the distance between 1st and 2nd value | ||||||||||||||||||||||||||||||
= 2 + 0.6(3–2) | ||||||||||||||||||||||||||||||
D2 | = 2.6 | |||||||||||||||||||||||||||||
| Now let us find the value for D4 | |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
Solution: The ordered data is 2, 3, 4, 5, 6, 7 and 9. | ||||||||||||||||||||||||||||||
| Hence n = 7 | |||||||||||||||||||||||||||||
D2 | = value of 4[(7+1)/10]th item | |||||||||||||||||||||||||||||
= value of 4 8/10 th item. | ||||||||||||||||||||||||||||||
= value of 3.2 th item | ||||||||||||||||||||||||||||||
= 3rd value + 0.2 of the distance between 3rd and 4th value | ||||||||||||||||||||||||||||||
= 4 + 0.2(5–4) | ||||||||||||||||||||||||||||||
= 4.2 | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
Q5. Calculate the decile D1 and D3 for the following table | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
Solution: | Calculation for the first decile | |||||||||||||||||||||||||||||
D1 | = L1 + {[ k.N)/10 – F1-1]/ f1}. a1 | |||||||||||||||||||||||||||||
= 40 + {[(1.70)/ 10 – 0]/ 8}.10 | ||||||||||||||||||||||||||||||
= 40 + 70/8 | ||||||||||||||||||||||||||||||
= 390/8 | ||||||||||||||||||||||||||||||
= 48.75 | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
| Calculation for 3rd decile | |||||||||||||||||||||||||||||
D1 | = L3 + {[ k.N)/10 – F3-1]/ f3}. a3 | |||||||||||||||||||||||||||||
= 60 + {[3.70/10 – F2]/14}10 | ||||||||||||||||||||||||||||||
= 60 + (210/10) -20]/ 14}.10 | ||||||||||||||||||||||||||||||
= 60 + [(21-20)/14].10 | ||||||||||||||||||||||||||||||
= 60 + 10/14 | ||||||||||||||||||||||||||||||
= 60 + 0.71 | ||||||||||||||||||||||||||||||
= 60.71 | ||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
Q6. Find the quartiles Q1, Q2 and Q3 of the following data 20, 30, 25, 23, 22, 32, 36 | ||||||||||||||||||||||||||||||
Solution: | Arrange data in ascending form, and n =7 odd number | |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
Q7. Let us consider the percentile example problem: In a college, a list of grades of 15 students has been declared. Their grades are: 85, 34, 42, 51, 84, 86, 78, 85, 87, 69, 74, 65. Find the 80th percentile? | ||||||||||||||||||||||||||||||
Solution: | Step 1: Arrange the data in the ascending order. Ascending Order = 34, 42, 51, 65, 69, 74, 78, 84, 85, 85, 86, 87
Step 2: Find Rank, Rank = Percentile / 100 = 70/ 100 K = 0.80
Step 3: Find 80th percentile, 80th percentile = 0.80 12 = 9.6
Step 4: Since it is not a whole number, round to the nearest whole number. Therefore, 9.6 is rounded to 10 Now, count the values in the given data set from left to right until you reach the number 10. From the given data set, 10th number is 85. Hence, 80th percentile of given data set = 85
2.8 What is Skewness? Skewness is the measure of the asymmetry of an ideally symmetric probability distribution and is given by the third standardized moment. If that sounds way too complex, don’t worry! Let me break it down for you. In simple words, skewness is the measure of how much the probability distribution of a random variable deviates from the normal distribution. Now, you might be thinking – why am I talking about normal distribution here? Well, the normal distribution is the probability distribution without any skewness. You can look at the image below which shows symmetrical distribution that’s basically a normal distribution and you can see that it is symmetrical on both sides of the dashed line. Apart from this, there are two types of skewness:
2.9What is Kurtosis?
Kurtosis is a statistical measure that defines how heavily the tails of a distribution differ from the tails of a normal distribution. In other words, kurtosis identifies whether the tails of a given distribution contain extreme values.
Along with skewness, kurtosis is an important descriptive statistic of data distribution. However, the two concepts must not be confused with each other. Skewness essentially measures the symmetry of the distribution, while kurtosis determines the heaviness of the distribution tails.
| |||||||||||||||||||||||||||||
2.10 | Karl Pearson’s Coefficient of correlation | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The method of scatter diagram is descriptive in nature and gives only a general idea of correlation. The most commonly used method which gives a mathematical expression for correlation is the one suggested by Karl Pearson (1867-1936) a British Biometrician. Just as 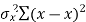 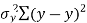 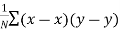 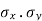 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Thus, | 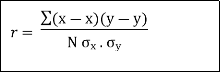 | …………… (1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But 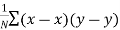 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 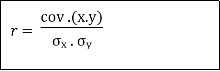 | …………… (2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we put 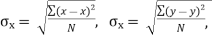 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 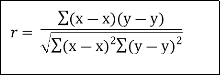 | …………… (3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If we write 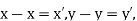 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 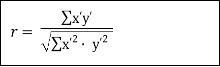 | …………… (4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The Karl Pearson’s coefficient of correlation is also called the product moment Coefficient correlation. Further, we can expand (3) and write | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 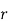 | 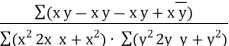 |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | 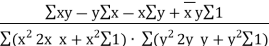 |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But 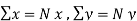 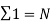 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 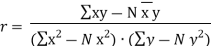 | …………… (5) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If 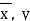 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(I) | Limits for 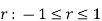 | (M.U.2004) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Proof: if we write 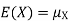 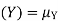 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 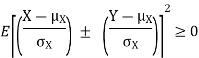 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 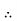 | 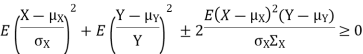 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 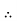 | 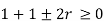 | 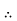 | 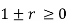 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| 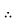 | 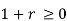 | Or | 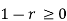 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| 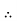 | 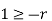 | Or | 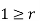 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| 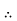 | 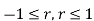 | 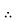 | 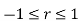 | 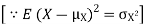 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(ii) | Theorems on correlation Theorem 1: If X, y are independent variables they are not correlated. We accept this theorem without proof. Theorem 2: Correlation coefficient is independent of change of origin and change of scale. (M.U.2002, 07) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The means if we write 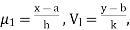 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.11. | Interpretation of the Coefficient of Correlation | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | r >0.95:If r is greater than 0.95, it indicates high degree of correlation and the value of one variable can be estimated from a known value of the other fairly accurately. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | r> 0-75 but <0.85: If r is greater than 0.75 but less than 0.85, there is probably a definite relationship between the variables and the value of one variable can be roughly estimated from a known value of the other. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | r> 040 but < 0.50: If r is greater than 0.40 but less than 0.60 there may be some relationship between the two variables. But the value of one variable calculated from a known value of the other cannot be reliable. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | r < 0.35:If =r is less than 0.35 the correlation is poor and one variable cannot be estimated from the other. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | r nearly zero: If r is nearly equal to zero, it indicates that there is probably no relation between the two variables i.e. they are independent of each other. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.12. | Computation of Coefficient of Correlation: (Ungrouped Data) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| There are three method of calculating r. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) | Actual mean method | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2) | Step deviation method | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3) | Assumed mean method | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) | Actual mean method | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The formula to be used is, | 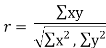 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Steps: (i) Calculate mean 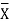 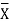 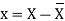 (ii) Calculate mean 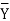 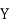 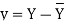 (iii) Multiply x by y and prepare the column of xy. (iv) Take the squares of x and [prepare the column of 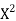 (v) Take the squares of y and [prepare the column of 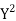 (vi) Apply the above formula.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 1: Find from the following values of the demand and the corresponding price of a commodity, the degree of correlation between the demand and price by computing Karl Pearson’s coefficient of correlation. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Let X denote the demand in Quintals and Y denote the price in paise per kg. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculation of r between demand and price
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, 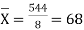 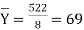 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 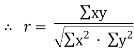 But 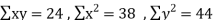 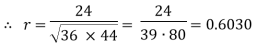 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 2: Calculate Karl Pearson’s coefficient of correlation for the following bivariate series | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(M.U. 2015) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Calculation r between X and Y
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, 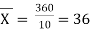 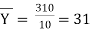 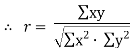 But 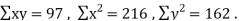 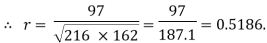 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2) | Step-deviation Method As in the case of mean and standard deviation, to simplify calculations we can use step- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 1: Calculate the co-efficient of correlation from the following data.
(M.U. 2015) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculations of r between X and Y
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, 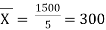 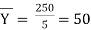 | 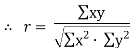 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But 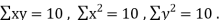 | 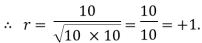 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) | Assumed Mean Method: Since in the calculation of r, deviations are to be squared the calculations will be tedious if the means are not integers but data are in integers. In such cases, we take deviations from an assumed mean conveniently chosen. The corresponding formula is | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 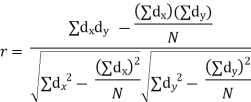 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Where, dx = deviations of X from an assumed mean, (X- A), Steps: (i) Assume any mean A for X and calculate deviations dx of X from A i.e., dx= X- A. (ii) Assume any mean B for Y and calculate deviations dy of Y from El i.e., dy=Y-B (iii) Take the squares of dx. (iv) Take the squares of dr (v) Take the products of dx and dy (vi) (vi) Apply the formula | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 4: Find the co-efficient of correlation for the prices (in As.) and sales units.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Let us assume 92 and 670 to be the means of X and Y respectively. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculations of r between price and sale
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, 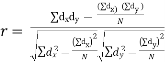 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But, 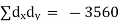 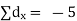 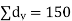 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 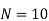 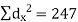 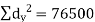 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 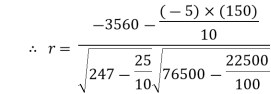 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 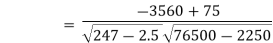 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 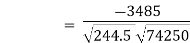 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 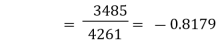 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 5: Calculate the correlation coefficient from the following data. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Let us assume 30 and 25 to be the means of X and Y respectively. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculation of r between X and Y
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, 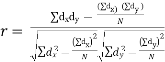 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But, 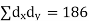 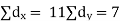 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 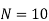 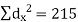 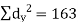 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 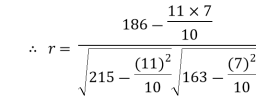 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 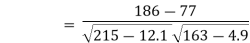 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 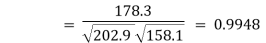 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7. | Direct Method of Calculating Coefficient of Correlation We can find the coefficient of correlation directly without taking the deviations of x and of y from their respective means. In such cases the following formula is used. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 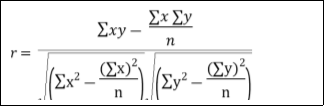 | …………… (8) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Where, x and y are the observed values of the variables and x, ji are their respective means. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 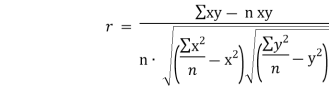 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 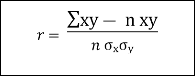 | …………… (9) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 1: Calculate the coefficient of correlation between X and Y from the following data. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Calculations of r
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.13. | Spearman’s Rank Correlation : | (M.U. 2009) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The method developed by Spearmen is simpler than Karl Pearson’s method since, it depends upon ranks of the items and actual values of the items are not required. Hence, this can be used to study correlation even when actual values are not known. For instants we can study correlation between intelligence and honesty by this method. Let xi , yi be the ranks in the two characteristics of the i-th member where i = 1,2,……n. We assume that no two members have the same rank either for x or for y. Thus x and y take all integral values between 1 and n. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 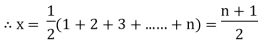 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Similarly, 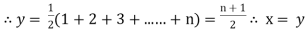 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 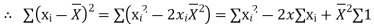 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 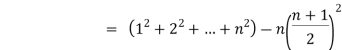 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 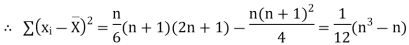 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Similarly, 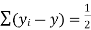 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| If 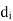  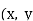 Where, 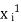 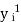 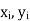 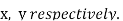 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 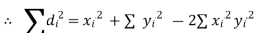 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 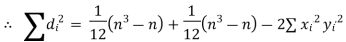 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 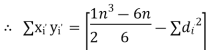 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But the coefficient of correlation | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 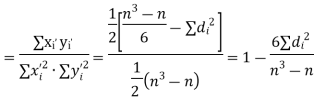 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This coefficient denoted by R | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| …………… (10) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 1: Calculate R and r from the following data. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Interpret your results. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Calculation of R and r
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 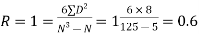 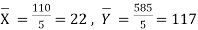 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 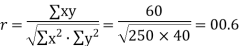 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Thus, the values of R and rare equal. It should be noted that the values of X increase by 5 and the values of Y, when arranged in ascending order also increase by the same amount 2 every time. In general, if the values of x, when arranged in ascending order increase (or decrease) by a fixed amount and if the values of y, when arranged in ascending order increase (or decrease) by another (or the same) fixed amount, then the values of r and R come out to be equal. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.14 | Computation of Correlation There are two types of problems. (i) When ranks of items are given. (ii) When the actual values of the items are given. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (i) When ranks are given: Steps: (i) Calculate the difference D = R1 - R2. (ii) Calculate: D2. (iii) Apply the formula, 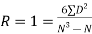 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (ii) When the actual values of the items are given.:We first ascertain the ranks of the items and follow the above procedure. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 1:Compute Spearman’s rank correlation coefficient from the following data. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Calculation of R between X and Y
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 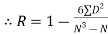 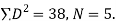 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 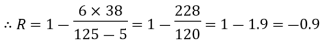 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 2: Calculate the rank correlation coefficient from the following data, relating to the ranks of 10 students in English and Mathematics. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Calculation of R between English and Mathematics
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, 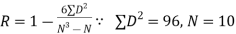 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 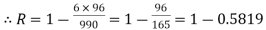 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 3: Calculate Spearman's coefficient of rank correlation from the data on height and weight of eight students.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Calculation of R between Height and Weight
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Now, 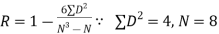 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 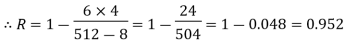 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d) | Equal Ranks In some cases, it may happen that there is a tie between two or more members i.e., they have equal values and hence equal ranks. In such cases we divide the rank among equal members. For instance, if two items have 4th rank, we divide the 4th and the next rank 5th between them equally and give 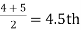 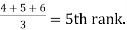 After assigning ranks in this way an adjustment is necessary. If m is the number of items having equal ranks then the factor 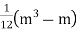 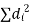 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 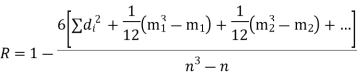 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 1: Obtain the rank correlation coefficient from the following data.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculation of R
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| There are two items in X series having equal values at the rank 4. Each is given the rank 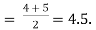 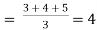 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∴ 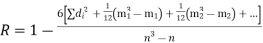 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Since, 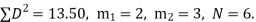 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 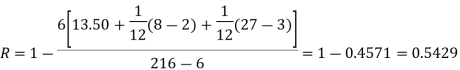 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 2: Calculate the value of rank correlation coefficient from the following data regarding marks of 6 students in statistics and accountancy in a test:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sol.: | Calculation of R
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 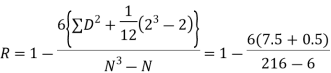 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 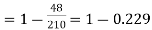 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Example 3: From the following data calculate the coefficient of rank correlation between x and Y.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculation of R between X and Y
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Since there are TV, to items in the X series having equal values at the rank 5 and two at the rank 7 they are given rank 5.5 and 7.5 each respectively. Similarly, in the Y series two items at the rank3 are given the rank 3.5 each. There are three cases where there is a tie each having 2 times.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∴ 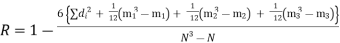 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| But, 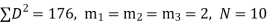 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∴ 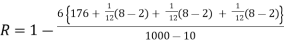 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 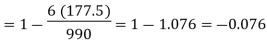
2.15 Line of Regressison | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
It is a mathematical method and with it gives a fitted trend line for the set of data in such a manner that the following two conditions are satisfied.
- The sum of the deviations of the actual values of Y and the computed values of Y is zero.
- The sum of the squares of the deviations of the actual values and the computed values is least.
This method gives the line which is the line of best fit. This method is applicable to give results either to fit a straight-line trend or a parabolic trend.
The method of least squares as studied in time series analysis is used to find the trend line of best fit to a time series data.
Secular Trend Line
The secular trend line (Y) is defined by the following equation:
Y = a + b X
Where, Y = predicted value of the dependent variable
a = Y-axis intercept i.e. the height of the line above origin (when X = 0, Y = a)
b = slope of the line (the rate of change in Y for a given change in X)
When b is positive the slope is upwards, when b is negative, the slope is downwards
X = independent variable (in this case it is time)
To estimate the constants a and b, the following two equations have to be solved simultaneously:
ΣY = na + b ΣX
ΣXY = aΣX + bΣX2
To simplify the calculations, if the midpoint of the time series is taken as origin, then the negative values in the first half of the series balance out the positive values in the second half so that ΣX = 0. In this case, the above two normal equations will be as follows:
ΣY = na
ΣXY = bΣX2
Logarithm y = aebx.
The equation is
y = aebx.
Taking log to the base e on both sides,
We get logy = loga + bx.
Which can be replaced as Y=A+BX,
Where Y = logy, A = loga, B = b and X = x.
Q1. Fit the straight line to the following data.
x | 1 | 2 | 3 | 4 | 5 |
y | 1 | 2 | 3 | 4 | 5 |
The normal equations are:
Σy = aΣx + nb
And
Σxy = aΣx2 + bΣx
Now,
x | y | x2 | Xy |
1 | 1 | 1 | 1 |
2 | 2 | 4 | 4 |
3 | 3 | 9 | 9 |
4 | 4 | 16 | 16 |
5 | 5 | 25 | 25 |
Σx = 15 | Σy = 15 | Σx2 = 55 | Σxy = 55 |
Substituting in the equations,
15 = 15a + 4b and 55 = 55a + 15b
Solving these two equations,
We get a=1 and b=0,
Therefore the required straight-line equation is y=x.
Q2. Fit the straight-line curve to the following data.
x | 75 | 80 | 93 | 65 | 87 | 71 | 98 | 68 | 84 | 77 |
y | 82 | 78 | 86 | 72 | 91 | 80 | 95 | 72 | 89 | 74 |
First drawing the table,
x | y | x2 | Xy |
75 | 82 | 5625 | 6150 |
80 | 78 | 6400 | 6240 |
93 | 86 | 8349 | 7998 |
65 | 72 | 4225 | 4680 |
87 | 91 | 7569 | 7917 |
71 | 80 | 5041 | 5680 |
98 | 95 | 9605 | 9310 |
68 | 72 | 4624 | 4896 |
84 | 89 | 7056 | 7476 |
77 | 74 | 5929 | 5698 |
798 | 819 | 64422 | 66045 |
The normal equation is:
Σy = aΣx + nb
and
Σxy = aΣx2 + bΣx.
Substituting the values, we get,
819 = 798a + 10b
66045 = 64422a + 798b
Solving, we get
a = 0.9288 and b = 7.78155
Therefore, the straight-line equation is:
y = 0.9288x + 7.78155.
Q3. Fit a second-degree parabola to the following data.
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 2 | 6 | 7 | 8 | 10 | 11 | 11 | 10 | 9 |
Solution:
Here,
x | y | x2 | x3 | x4 | Xy | x2y |
1 | 2 | 1 | 1 | 1 | 2 | 2 |
2 | 6 | 4 | 8 | 16 | 12 | 24 |
3 | 7 | 9 | 27 | 81 | 21 | 63 |
4 | 8 | 16 | 64 | 256 | 32 | 128 |
5 | 10 | 25 | 125 | 625 | 50 | 250 |
8 | 11 | 36 | 216 | 1296 | 66 | 396 |
7 | 11 | 49 | 343 | 2401 | 77 | 539 |
8 | 10 | 64 | 512 | 4096 | 80 | 640 |
9 | 9 | 81 | 729 | 6561 | 81 | 729 |
45 | 74 | 285 | 2025 | 15333 | 421 | 2771 |
The normal equations are:
Σy = aΣx2 + b Σx + nc
Σxy = aΣx3 + bΣx2 +c Σx
Σx2y = aΣx4 + bΣx3 + cΣx2
Substituting the values, we get
74 = 285a + 45b + 9c
421 = 2025 a + 285 b + 45 c
2771 = 15333a + 2025 b + 285 c
Solving them, we get the second order equation which is,
y = -0.2673x2 + 3.5232x – 0.9286.