Unit – 4

Probability and Decision Theory

4.1 Theorems on probability, including Bayes’ rule

Probability:

When the outcome of any event is not certain the theory of probability enters.

Events – Union, Intersection

1 Events 

An event is simply the outcome of a random experiment. Getting a head when we toss a coin is an event. Getting a 6 when we roll a fair die is an event. We associate probabilities to these events by defining the event and the sample space.

2. Union

We can define an event (C) of getting a 4 or 6 when we roll a fair die. Here event C is a union of two events:

Event A = Getting a 4

Event B = Getting a 6

P (C) = P (A 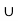B)

3. Intersection of Events

Let’s look at another example.

Let C be the event of getting a multiple of 2 and 3 when you throw a fair die.

Event A = Getting a multiple of 2 when you throw a fair die

Event B = Getting a multiple of 3 when you throw a fair die

Event C = Getting a multiple of 2 and 3

Event C is an intersection of event A & B.

Probabilities are then defined as follows.

P (C) = P (A 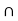B)

4. Intersection of events

If the occurrence of event A doesn’t affect the occurrence of event B, these events are called independent events.

Laws of probability

1. Addition rule

P (A ∪ B) = P(A) + P(B) – P (A ∩ B)

P (A and B) = P(A) ∙ P(B|A) = P (A ∩ B)

Some example of probability

1. Tossing of a coin/ coins: Probabilities are written as numbers between zero and one. A probability of one means that the event is certain. If you toss a coin, it will come up a head or a tail. So, there is a probability of one that either of these will happen. A probability of zero means that an event is impossible. 

Question 1

Two coins are tossed, find the probability that two heads are obtained. Note: Each coin has two possible outcomes H (heads) and T (Tails).
 

Solution
The sample space S is given by.
S = {(H,T),(H,H),(T,H),(T,T)}
Let E be the event "two heads are obtained".
E = {(H,H)}
We use the formula of the classical probability.
P(E) = n(E) / n(S) = 1 / 4

Q2. Calculate the probability of getting an odd number if a dice is rolled?

Solution: Sample space (S) = {1, 2, 3, 4, 5, 6}

Let “E” be the event of getting an odd number, E = {1, 3, 5}

So, the Probability of getting an odd number P(E) = (Number of outcomes favourable)/ (Total number of outcomes) = n(E)/n(S) = 3/6 = ½

Q3. A die is rolled and a coin is tossed, find the probability that the die shows an odd number and the coin shows a head.

Solution
Let H be the head and T be the tail of the coin. The sample space S of the experiment described in question 5 is as follows:
 

S = {(1, H), (2, H), (3, H), (4, H), (5, H), (6, H)
(1, T), (2, T), (3, T), (4, T), (5, T), (6, T)}
 

Let E be the event "the die shows an odd number and the coin shows a head".

Event E may be described as follows
 

E= {(1, H), (3, H), (5, H)}
 

The probability P(E) is given by
 

P(E) = n(E) / n(S) = 3 / 12 = 1 / 4

Q4. Two dice are rolled,  find the probability that the sum is
a) equal to 1
b) equal to 4
c) less than 13

Solution
a) the sample space S of two dice is shown below.
S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }
 

Let E be the event "sum equal to 1". There are no outcomes which correspond to a sum equal to 1, hence
P(E) = n(E) / n(S) = 0 / 36 = 0

b) Three possible outcomes give a sum equal to 4: E = {(1,3), (2,2), (3,1)}, hence.
P(E) = n(E) / n(S) = 3 / 36 = 1 / 12
 

c) All possible outcomes, E = S, give a sum less than 13, hence.
P(E) = n(E) / n(S) = 36 / 36 = 1

2. Basic concept on drawing a card:

In a pack or deck of 52 playing cards, they are divided into 4 suits of 13 cards each i.e. spades ♠ hearts ♥, diamonds ♦, clubs ♣.

Cards of Spades and clubs are black cards.

Cards of hearts and diamonds are red cards.

The card in each suit, are ace, king, queen, jack or knaves, 10, 9, 8, 7, 6, 5, 4, 3 and 2.

King, Queen and Jack (or Knaves) are face cards. So, there are 12 face cards in the deck of 52 playing cards.

Q1. A card is drawn from a well shuffled pack of 52 cards. Find the probability of:

(I) ‘2’ of spades

(ii) a jack

(iii) a king of red colour

(iv) a card of diamond

(v) a king or a queen

(vi) a non-face cards

Solution:

In a playing card there are 52 cards.

Therefore, the total number of possible outcomes = 52

(I) ‘2’ of spades:

Number of favourable outcomes i.e. ‘2’ of spades is 1 out of 52 cards.

Therefore, probability of getting ‘2’ of spade

Number of favourable outcomes
P(A)=     Total number of possible outcomes
  = 1/52

(ii) a jack

Number of favourable outcomes i.e. ‘a jack’ is 4 out of 52 cards.

Therefore, probability of getting ‘a jack’

Number of favourable outcomes
P(B) =  Total number of possible outcomes

      = 4/52
      = 1/13
(iii) a king of red colour

Number of favourable outcomes i.e. ‘a king of red colour’ is 2 out of 52 cards.

Therefore, probability of getting ‘a king of red colour’

Number of favourable outcomes
P(C) = Total number of possible outcomes

      = 2/52
      = 1/26

(iv) A card of diamond

Number of favourable outcomes i.e. ‘a card of diamond’ is 13 out of 52 cards.

Therefore, probability of getting ‘a card of diamond’

Number of favourable outcomes
P(D) =     Total number of possible outcomes

      = 13/52
      = 1/4

(v) a king or a queen

Total number of kings is 4 out of 52 cards.

Total number of queens is 4 out of 52 cards

Number of favourable outcomes i.e. ‘a king or a queen’ is 4 + 4 = 8 out of 52 cards.

Therefore, probability of getting ‘a king or a queen’

Number of favourable outcomes
P(E) =     Total number of possible outcomes

      = 8/52
      = 2/13

(vi) a non-face card

Total number of face card out of 52 cards = 3 times 4 = 12

Total number of non-face card out of 52 cards = 52 - 12 = 40

Therefore, probability of getting ‘a non-face card’

Number of favourable outcomes
P(F) =     Total number of possible outcomes

      = 40/52
      = 10/13

Q3. A card is drawn at random from a deck of cards. Find the probability of getting a queen.
Solution:
Let E be the event "getting a Queen". An examination of the sample space shows that there are 4 "Queens" so that

n(E) = 4 and n(S) = 52.

Hence the probability of event E occurring is given by
P(E) = 4 / 52 = 1 / 13 Mutually Exclusive

When two events (call them "A" and "B") are Mutually Exclusive it is impossible for them to happen together:

P (A and B) = 0

"The probability of A and B together equals 0 (impossible)"

But, for Mutually Exclusive events, the probability of A or B is the sum of the individual probabilities:

P (A or B) = P(A) + P(B)

"The probability of A or B equals the probability of A plus the probability of B"

Complementary events

The event ‘E' and the event ‘not E' are called complementary event of the latter event. If E occurs, its compliment is E which does not occur.

Compliment of an event is denoted by E’ or E or Ec.

Problems on complementary event:

1. A bag contains red and what balls. The probability of getting a red ball from the bag of balls is 1/6. What is the probability of not getting a red ball?

Solution:

The probability of getting a red ball from the bag of balls is 1/6.

Therefore, the probability of not getting a red ball

P (ball is not red) = 1 – 1/6 = 5/6

Therefore, the probability of not getting a red ball is 5/6.

2. In a box, contains blue and green marbles. The probability of getting a green marble from the box of marbles is 3/7. What is the probability of getting a blue marble?

Solution:

Let E1 be the event of getting a green marble and

E2 be the event of getting a blue marble

E2 is the probability of getting a blue marble which is also the same as the probability of not getting a green marble, Since we know that the marble are either green or blue.

Therefore, P(not getting a blue marble)

= P(E2) = 1 - P(E1)

= 1 – 3/7

= 4/7.

Therefore, the probability of getting a blue marble is 4/7.

Definition of Conditional Probability:

The probability of an event X is given then another event Y occurred is called conditional probability of X given Y.

It is denoted by P(X/Y).

P(X/Y) = P (X ∩ Y)/P(y)

Similarly, when the probability of Y given X is

P(Y/X) = P (X ∩ Y)/P(X)

Multiplication Theorem of Probability:

In an experiment suppose, X and Y are any two events then probabilities of both X and Y is given by

P (X ∩ Y) = P(X) ∙ P(Y/X) ------(I)

OR

P (X ∩ Y) = P(Y) ∙ P(X/Y) ------(II)

If X and Y are independent, then

P (X/Y) = P(X) and P(Y/X) = P(Y)

Now substituting P(Y/X) = P(Y) in “equation (I)”, we get

P (X ∩ Y) = P(X) ∙ P(Y)

Similarly, substituting P(X/Y) = P(X) in “equation (II)”, we get

P (X ∩ Y) = P(Y) ∙ P(X) = P(X) ∙ P(Y)

If X and Y are independent, then probabilities of both X and Y is given by

P (X ∩ Y) = P(X) ∙ P(Y).

Sums on conditional probability

Q1. In class X, 20% of the students are boys and 80% of them are girls. The probability that boys passed in mathematics is 0.5 and the probability that girls passed in mathematics is 0.10. One student is selected at random. What is the probability that the selected student is passed in mathematics?

Solution:

Let X denote the event that boy is selected,

Y denote the event that girl is selected and

Z denotes the event that the selected student is passed in mathematics.

P(X) = P (boy is selected) = 20/100 = 1/5

P(Y) = P (girl is selected) = 80/100 = 4/5

P(Z/X) = P (selected boy passed in mathematics) = 0.5

P(Z/Y) = P (selected girl passed in mathematics) = 0.10

P (selected student is passed in mathematics) = P (boy is selected and he is passed in mathematics or girl is selected and she is passed in mathematics)

So, required probability is

Therefore, P (selected student is passed in mathematics) = 0.18

Q2. One half percent of the population has a particular disease. A test is developed for the disease. The test gives a false positive 3% of the time and a false negative 2% of the time. (a). What is the probability that Joe (a random person) tests positive? (b). Joe just got the bad news that the test came back positive; what is the probability that Joe has the disease?

Solution:

Let D be the event that Joe has the disease. Let It be the event that Joe’s test comes back positive.

We are told that P(D) = 0.005, since 1/2% of the population has the disease, and Joe is just an average guy.

We are also told that P(T|D) = .98, since 2% of the time a person having the disease is missed (“false negative”). We are told that P (T|D) c = .03, since there are 3% false positives.

(a). We want to compute P(T).

P(T) = P(T|D) P(D) + P (T|D) c+ P (D) c = (0.98) (0.005) + (0.03) (0.995)

We do so by conditioning on whether or not Joe has the disease:

(b). We want to compute P(D|T) =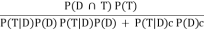

= (0.98) (0.005) / ((.98) (.005) + (.03) (.995))

=  0.14

Bayes theorem

The Bayes theorem describes the probability of an event based on the prior knowledge of the conditions that might be related to the event. If we know the conditional probability 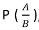, we can use the bayes rule to find out the reverse probabilities .

4.2 Random variable:

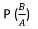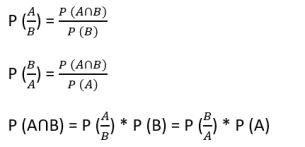
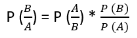
Suppose that to each point of a sample space we assign a number. We then have a function defined on the sample space. This function is called a random variable (or stochastic variable) or more precisely a random function (stochastic function). It is usually denoted by a capital letter such as X or Y. In general, a random variable has some specified physical, geometrical, or other significance.

Cumulative distribution function

Let be a discrete random variable – Let 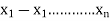be possible values
of 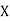with each possible outcome 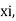we associate a number  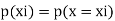 called probability of .

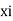(I) 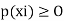for all  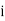            (ii)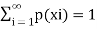

Q.1] A random variable 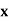has following probability distribution.

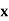	0	1	2	3	4	5	6	7
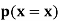	0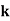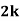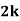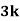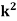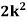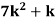

I) Find 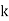   (ii)

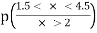
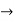 Since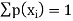

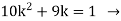Add all the terms

Solving the quadratic Equation

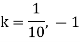
As probability can never be negative and greater than!

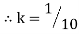 is valid

The pdf of 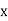   is

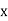	0	1	2	3	4	5	6	7
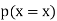	0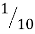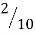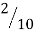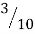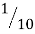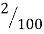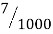

Ii]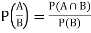 

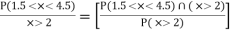
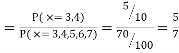
Continuous Radom Variable

A random variable is called a continue random variable if it takes all value
between an interval 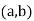e.g: Height, Weight

1] Let 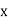be continue random variable with probability distrib

if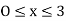

Evaluate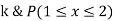

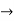
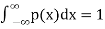
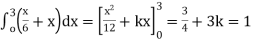
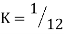
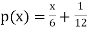if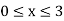 elsewhere

2]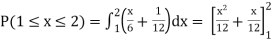 

* Expectation: If a discrete random variable 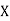assume value
with probabilities respectively then the mathematical expenses
of 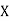denoted by

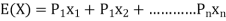
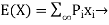For discrete

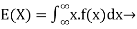For continuous

• Mean

The mean of a discrete random variable X is a weighted average of the possible values that the random variable can take. Unlike the sample mean of a group of observations, which gives each observation equal weight, the mean of a random variable weights each outcome xi according to its probability, pi. The common symbol for the mean (also known as the expected value of X) is 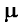, formally defined by

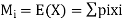
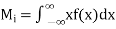
Variance

The variance of a discrete random variable X measures the spread, or variability, of the distribution, and is defined by             

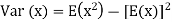
Where 

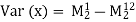
Where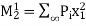 

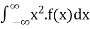
Mean and Variance of a Sum of Random Variables

Expectation is always additive; that is, if X and Y are any random variables, then

E(X+Y) =E(X)+E(Y).

If X and Y are independent random variables, then their variances will also add:

V(X+Y) =V(X)+V(Y) if X, Y independent.

More generally, if X and Y are any random variables, then

V(X+Y) =V(X)+V(Y)+2 Cov(X, Y)

Where Cov (X, Y) is the covariance between X and Y,

Cov(X, Y) =E((X−E(X)) (Y−E(Y))).

If X and Y are independent (or merely uncorrelated) then Cov (X, Y) = 0. This additive rule for variances extends to three or more random variables; e.g.,

V(X+Y+Z) =V(X)+V(Y)+V(Z)+2Cov (X, Y) +2Cov (X, Z) +2Cov (Y, Z)

With all covariances equal to zero if X, Y, and Z are mutually uncorrelated.

1] If mean of following distribution is 16 find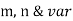   

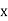	8	12	16	20	24

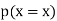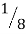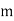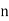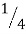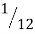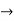 Since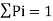

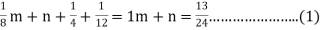
Mean 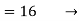given

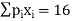
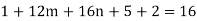
………………. (2)

Q2. In the original gambling game above, the probability distribution was defined to be:

Outcome  -1.00 0.00 3.00 5.00 

Probability                 0.30  0.40       0.2         0.10 

Mean =0.8. Calculate the variance

Solution:

The variance for this distribution, with mean = 0.8,

May be calculated as follows:
(-1 - 0.8)2 *0.3 + (0 - 0.8)2 *0.4 + (3 - 0.8)2 *0.2 + (5 - 0.3)2*0.1

= (-1.8)2 × 0.3 + (-0.8)2×0.4 + (2.2)2 ×0.2 + (4.2)2 × 0.1

= 3.24×0.3 + 0.64×0.4 + 4.84×0.2 + 17.64×0.1

= 0.972 + 0.256 + 0.968 + 1.764 = 3.960,

With standard deviation = 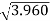= 1.990.
Since there is not a very large range of possible values, the variance is small.

Q3. As in the case of the mean, consider the gambling game in which the casino chooses to lower each pay-out by ₹1.00, then double each prize. The resulting distribution is the following:

Outcome  -₹4.00 -₹2.00 ₹4.00 ₹8.00 

Probability                   0.30  0.40   0.20   0.10 

The variance for this distribution, with mean = -0.4,

Solution:

Variance may be calculated as follows:

(-4 -(-0.4))2×0.3 + (-2 - (-0.4))2 × 0.4 + (4 - (-0.4))2 × 0.2 + (8 - (-0.4))2 × 0.1

= (-3.6)2 x 0.3 + (-1.6)2 * 0.4 + (4.4)2 * 0.2 + (8.4)2 * 0.1

= 12.96 * 0.3 + 2.56 * 0.4 + 19.36 * 0.2 + 70.56 * 0.1

= 3.888 + 1.024 + 3.872 + 7.056

= 15.84

With standard deviation = 3.980.

This is equivalent to multiplying the original value of the variance by 4, the square of the multiplying constant.

4.3 Decision theory

Definition:

A decision may be defined as the selection of the action, by the decision maker, which is considered to be the best according to some predetermined standard from amongst the available options.

Steps in Decision making

I) Identification of all possible outcomes called states of nature or events.

Ii) Identification of all courses of action called acts.

Iii) Determination of payoff function.

Iv) Choosing from among the alternatives, the best possible action on the basis of some criterion.

Criteria for decision making under uncertainty.\

• Maximax (optimistic) criterion
• Maximin (pessimistic) criterion
• Minimax Regret criterion

• Laplace criterion

a)     Maximax Criterion: In this case the decision maker does not want to miss the opportunity to achieve the largest possible profit.

Steps: 1) Locate the maximum Payoff values corresponding to each act.

2) From among the maximum choose the highest value.

This is also called the optimistic criterion because the decision maker chooses the best of the best

B) Maxima criterion: This is a conservative approach. Here the decision maker attempts in maximizing the minimum possible profits.

C) Minimax Regret criterion: The Minimax Regret Criterion is a technique used to make decisions under uncertainty. ... Under this Minimax Regret Criterion, the decision maker calculates the maximum opportunity loss values (or also known as regret) for each alternative, and then she chooses the decision that has the lowest maximum regret.

For example, suppose Geoffrey Ramsbottom is faced with the following pay-off table. He has to choose how many salads to make in advance each day before he knows the actual demand.

• His choice is between 40, 50, 60 and 70 salads.
• The actual demand can also vary between 40, 50, 60 and 70 with the probabilities as shown in the table - e.g. P (demand = 40) is 0.1.
• The table then shows the profit or loss - for example, if he chooses to make 70 but demand is only 50, then he will make a loss of $60.

The question is then which output level to choose.

Maximax

The Maximax rule involves selecting the alternative that maximizes the maximum payoff available.

This approach would be suitable for an optimist, or 'risk-seeking' investor, who seeks to achieve the best results if the best happens. The manager who employs the Maximax criterion is assuming that whatever action is taken, the best will happen; he/she is a risk-taker. So, how many salads will Geoffrey decide to supply?

Looking at the payoff table, the highest maximum possible pay-off is ₹140. This happens if we make 70 salads and demand is also 70. Geoffrey should therefore decide to supply 70 salads every day.

Maximin

The maximin rule involves selecting the alternative that maximizes the minimum pay-off achievable. The investor would look at the worst possible outcome at each supply level, then selects the highest one of these. The decision maker therefore chooses the outcome which is guaranteed to minimize his losses. In the process, he loses out on the opportunity of making big profits. 

This approach would be appropriate for a pessimist who seeks to achieve the best results if the worst happens.

So, how many salads will Geoffrey decide to supply? Looking at the payoff table,

• If we decide to supply 40 salads, the minimum pay-off is ₹80.
• If we decide to supply 50 salads, the minimum pay-off is ₹0.
• If we decide to supply 60 salads, the minimum pay-off is (80).
• If we decide to supply 70 salads, the minimum pay-off is (160).

The highest minimum payoff arises from supplying 40 salads. This ensures that the worst possible scenario still results in a gain of at least ₹80.

Minimax regret

The minimax regret strategy is the one that minimizes the maximum regret. It is useful for a risk-neutral decision maker. Essentially, this is the technique for a 'sore loser' who does not wish to make the wrong decision.

'Regret' in this context is defined as the opportunity loss through having made the wrong decision.

To solve this a table showing the size of the regret needs to be constructed. This means we need to find the biggest pay-off for each demand row, then subtract all other numbers in this row from the largest number.

For example, if the demand is 40 salads, we will make a maximum profit of ₹80 if they all sell. If we had decided to supply 50 salads, we would achieve a nil profit. The difference or 'regret' between that nil profit and the maximum of ₹80 achievable for that row is ₹80. 

Regrets can be tabulated as follows: 

The maximum regrets for each choice are thus as follows (reading down the columns):

• If we decide to supply 40 salads, the maximum regret is ₹60.
• If we decide to supply 50 salads, the maximum regret is ₹80.
• If we decide to supply 60 salads, the maximum regret is ₹160.
• If we decide to supply 70 salads, the maximum regret is ₹240

Decision making under risk

Popular methods are

1. EMV (expected monetary value)
2. EOL (Expected opportunity loss)
3. EVPI (expected value of perfect information)

Steps to calculate EMV

1. Assign a probability of occurrence for the risk.
2. Assign monetary value of the impact of the risk when it occurs.
3. Multiply the values produced by step 1 and step 2.

The formula is expressed as EMV = (Probability) x (Impact)
These sums are them added to the project cost to calculate total EMV.

Steps to calculate EOL

1. Prepare conditional profit table for each course of action and state of nature
2. Prepare conditional opportunity loss table
3. Calculate EOL for each course by multiplying the probability by pop loss.
4. Select course of action for which EOL is minimum.

Ex.1. A consumer product company is examining the introduction of a new product with new packaging or replace the existing product at much higher price (A1) or moderate change in the composition of the existing product with new packaging at a small increase in price (A2) or a small change in the composition of the existing product except the word ‘new’ with the negligible increase in price (A3). The three possible states of nature are S1: decrease in sales. The marketing department has worked out the following payoffs in terms of profits. Which strategy should be considered under (I) Minimax Regret (ii) Optimistic (iii) Equip-probability conditions?

Ans. Optimistic approach is using Maximax criterion.

Equiprobable is using Laplace criterion.

States of Nature	A1	A2	A3
S1	30,000	40,000	25,000
S2	50,000	45,000	10,000
S3	40,000	40,000	40,000
Maximum	50,000	46,000	40,000
Average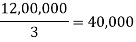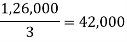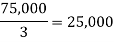

Maximum = 50,000            • decision is A1, using Maximax.

Maximum average is 42,000.            •  decision is A2, using Laplace criterion.

To find decision under minimax regret, construct the regret table first.

STATES         OF     NATURE	ACTS (STRATEGIES)
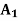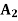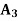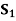	10,000	0	15,000
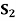	0	4,000	40,000
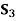	0	0	0
Maximum	10,000	4,000	40,000

Minimax = 4,000 which corresponds to .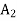

Let us tabulate the decisions using different approaches.

CRITERIA	DECISION
Optimistic	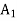: -  Replace the existing product at a higher price
Laplace         (Equiprobable)	: - make moderate change in the composition of   the existing product, with a new packaging at a small increase in price
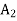
Minimax                Regret	: - make moderate change in the composition of the existing product, with a new packaging at a small increase in price

The decision depends upon which approach the decision maker wants to consider.

Decision Tree Analysis: 

In some situations, the decision maker is required to take decisions at more than one stage. Such situations are also called sequential or multi – stage decision problems.

In these problems the decision taken at one stage makes the difference in the decision making in the next stages. Hence the best decision at any stage is based on decisions taken in the previous stages. For this purpose, the decision flow diagram or tree diagram is used.

A Decision Tree presents a clear, logical model that can be understood easily by people who are not mathematically inclined. It is a diagrammatic representation of the decision problem and its solution. It enables the decision maker to see the various stages of his problems in proper sequence and perspective in a systematic manner.

However, the criteria of decision making remain the same like EMV or EOL as used in the earlier decision problems. The tree diagram consists of,

Decision Box: Denotes the course of action

Node: Show the decision branches or Course of actions

Arrows: Show the decision branches or Course of actions

For the illustrative example of TV set marketing, we can draw the decision tree as follows.

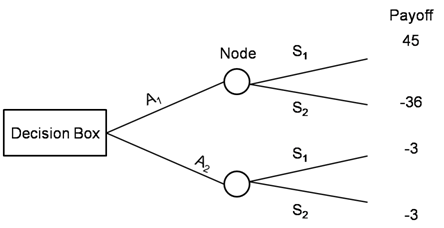
In the diagram the first set of arrows represents the 2 courses of actions A1 & A2 available with the manager. Whereas the second sets represent the events (states of nature) in terms of success of the product. These events occur on each of the course of action on the decision tree.

Question: A firm has developed a new product X. They can either test maker or Bandon the project. Test maker cost Rs.50,000. The likely outcomes are favourable (0.7) or failure (0.3). If favourable they could either abandon or produce it when the demand is given us under.

DEMAND                                     PROB                                   PROFIT RS.

Low                                            0.25                                          - 1,00,000

Medium                                      0.60                                            1,50,000

High                                          0.15                                            4,50,000

If the test market indicates failure, the project would be abandoned.   Abandoned   at any stage results in gain of rs40,000 from the special machinery used. Draw decision tree and decide the best option.

Ans.   There are two decision    and    in  this example. The decision tree is given by 

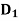  - 50,000 (test market) 1) - favorable (0.7)

-         Failure (0.3) abandon rs40,000

2) - abandon rs40,000

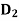  -  1) abandon - Rs40,000 low (0.25)

2)  produce - 1) medium (0.6)

2)  high (0.15)

EMV at node 2 =   0.25 (- 1,00,000) + 0.6 (1,50,000) + 0.15 (4,50,000)

=   Rs 1,32,000

The decision at  can be one of the two i.e. either abandon or produce, but EMV for producing is more:

Therefore: - The decision at  is to go for producing the product.

Question.    An investor sold his 157.4 units of a mutual fund when the NAV was Rs 20.5.  find the amount received by him if

i)                         There was no exit load

Ii)                        The exit load was 1.15%

Ans.      The number of units held by the investor = 157.4

The NAV = 20.5

i)                      When there is no exit load, he receives

(157.4 × rs20.5) = Rs 3,226.7

2)           When the exit load is 1.5%.

The actual price he received per unit 

= Rs20.5 - 1.5% of Rs20.5

=   Rs20.1925

Therefore: -   By selling 157.4 units, he gets (157.4 × rs20.1925) =n Rs 3,178.2995