Module 4
Phase Rule-Gibb’s Phase Rule
Gibbs free energy: Gibbs free energy of the system is the difference of enthalpy of the system with the product of temperature times the entropy of the system.
G=H-TS
Gibbs free energy of the system is defined in term of the thermodynamics which are state in function. Any change in the Gibbs Free Energy System is directly proportional to the difference of change in the enthalpy of the system with the products of temperature times the entropy of the system.
G= H- (TS)
While at constant temperature this reaction transform into:
G= H-T S
The Nernst Equation is derived from the Gibbs free energy under standard conditions.
E*=E*reduction-E*oxidation ………..(i)
G=-nFE ………..(ii)
Where,
n=no. Of transferred electrons in the reaction
F= Faraday constant
E=Potential Difference.
While when we see in the standard condition then, equation (ii) becomes
G*=-nFE* ………….(iii)
Hence,
Reaction is Spontaneous when E* is positive while non- spontaneous in vice-versa.
G= G*+RT lnQ ………….(iv)
Now, Substituting G=−nFE and G*=−nFE* into Equation 4, we have:
−nFE=−nFEo+RTlnQ …………….(v)
On Dividing both sides of the Equation above by −nF,
E=E*−RTnFlnQ(6) ……….(vi)
Equation (vi) in the form of log10:
E=E*−2.303RT/nF log10Q …….(vii)
At standard temperature T = 298 K, the 2.303RT/F term equals 0.0592 V and Equation
(vii) can be rewritten:
E=E*−0.0592V/n log10Q ……..(viii)
The equation (viii) clearly indicates that electric potential of cell depends on reaction quotient of reaction. The product formation leads to the increase in the concentration of the products. This tends to decrease the the potential of the cell until it reaches at the stage of equilibrium where, G=0 and G=-nFE Q=K so E=0
Then on substituting the these values to Nernst Equation we get,
0=E*-RT/nF In K …….(ix)
At room temperature it becomes;
0=E*-0.0592V/n Log10K
LogK=nE*/0.0592V
The above equation clearly indicates the equilibrium constant K is proportional to the standard potential.
The homogenous and physical part of the system is bounded by any surface which is mechanically separable is termed as phase. The phase may be the in the gaseous form, solid form or liquid form. The boundary present between the two interfaces is called as the interface. Air constitutes a single phase only as it contains a mixture of nitrogen, oxygen, carbon dioxide, water vapour etc. A system consisting of only one phase is said to be homogeneous. A mixture of two immiscible liquids such as water and benzene, will exist in two distinct liquid phases and in addition there will be a vapour phase. Thus there will be three phases each separated from the other by a well-defined bounding surface while the system consist of more than one phase is called as the heterogenous phase.
Phase Rule: If the equilibrium between any number of phases is not influenced by gravity, or electrical by surface action but are influenced only by temperature, pressure and concentration , then the number of degrees of freedom (F) of the system is related to the number of components (C ) and number of phases (P) by the following phase rule equation:
F=C-P+2
Liquid Phase:
(i) Liquid phase is depend on the number of liquids present and their miscibility.
(ii) 2 miscible liquids form 2 separate liquid phase.
(iii) 2 miscible liquids form 1 liquid phase only.
Solid Phase:
Each solid forms a separate phase while number of solid phase depends on the number of solids present in it.
Gaseous Phase:
Due to the thoroughly miscible proportions of gases they form phases only.
Eg.: N2 and H2 mixture form phases only.
Applications to water system:
In water there is only one component i.e., water and its phases: ice, water, steam that is solid, liquid and gaseous form. 
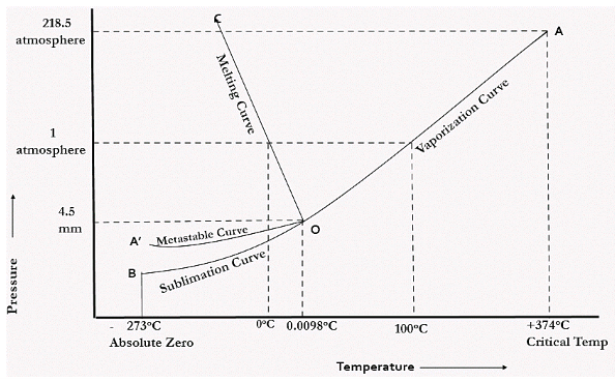
In the figure given above, the horizontal movement leads to be responsible for temperature change while the vertical curve responsible for the pressure change. In the above figure there are three curves i.e., OA,OB,OC which represents the equilibrium conditions between two phases solid with vapour, vapour with liquid and liquid with solid phase of water. Curve OC represents the equilibrium between solid and liquid phase of water. The curve is known as the fusion pressure or melting point curve. Along this curve there are two phases in equilibrium that is ice and water. At atmospheric pressure ice and water can be in equilibrium only at one temperature i.e, the freezing point of the water.
Here, C=1,
P=2
F=C-P+2
=1
Curve OB represent the equilibrium between liquid and vapor. This is called as the vaporization curve. Here also it is necessary to state either temperature or pressure. Eg.: at atmospheric pressure water and vapor can exists in equilibrium only at 1 temperature i.e., the boiling point of the water. Water vapor has also one degree of freedom.
F=C-P+2
=1
We know the phase-rule equation,
F = C – P +2 ……… (1)
For a two component system, C = 2 and hence the above equation becomes,
F = 2 – P + 2 = 4 – P ……… (2)
The minimum number of phases in any system at equilibrium is one. It is clear from the equation (2) , the maximum number of degree of freedom is three. Thus, three variables – pressure, temperature and composition of one of the components must be specified to describe the system. This will lead to three dimensional figures which cannot be conveniently represented on a paper. To make this simple, one of the three variables is kept constant.
In solid-liquid equilibrium of an alloy , practically there is no gaseous phase and the pressure will not have much influence. In the case of solid-liquid equilibrium, the experiments are generally carried out at constant pressure. Thus the system in which only the solid and liquid phases are considered and the gas phase is ignored is called a condensed system. This reduces the degree of freedom of the system by one. The phase rule equation is then written as
F’ = C – P + 1 …….. (3)
This equation is called reduced phase rule or condensed phase rule.
Lead silver system- This system has two component and four phases. These are
- Solid silver
- Solid lead
- Solution of molten silver and lead
- Vapor
But the boiling point of Ag and Pb is completely high; the vapor phase is completely absent.Since the press has nearly no affected on equilibrium so the system can be conveniently represented by temp.-conc. Diagram.
Such solid liquid system with the gas phase is absent is called condensed system.
The experimental measurements of temp and conic. In condensed system ate usually carried at under atmosphere pressure.
Since the degree of freedom in such system is reduced but one, therefore, it can be also termed as reduced phase and represented by the equation,
F=C−P+1F=C−P+1
It is more convenient to apply to solid liquid two components condensed system e.g.-Pb-Sb, Ag-Pb, Zn-Cd
The complete temp.-conc. Phase diagram of system silver-lead:
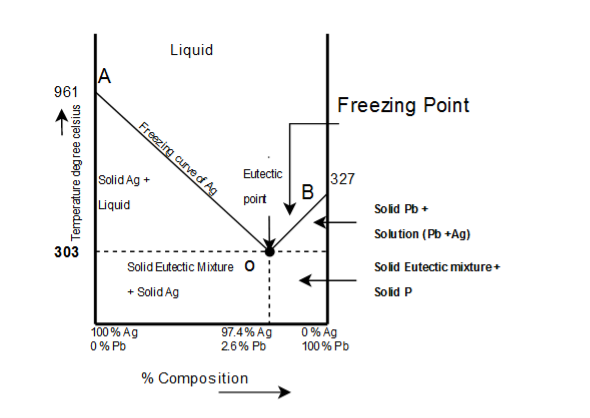
From the figure following salient features are observed:
- The curve OA(freezing curve of Ag)
- The curve BO(freezing curve of Pb)
- The eutectic point 'O'
- The Area AOB
- Curve AO →→Freezing curve of Hg.
i. It shows the effect on freezing point of Ag on addition of Pb in small quantities .
ii. The curve starts from (961)∘c(961)∘c the M.P of Ag, where pure Ag coexists as solid and liquid(Vapors being neglected)
Iii. The curve indicates that the meeting point of Ag falls gradually on adding Pb, along AO till the lowest point O(303)∘c(303)∘c is reached where solution gets saturated with request to lead. At O more Pb can go in solution and consequently, the M.P. Does not fall any further and if any Pb is added it separates as solid phase.
Along this curve, solid Ag and solution (Vapors being negligible) coexist and hence, according to reduced phase rule equation F=2−P+1F=2−P+1
i.e. system is invariant. The point O(303)∘c(303)∘c corresponds to a fixed composition of 2.62.6Ag and solution and 97.497.4 Pb and is known as eutectic composition.
On cooling the whole mass crystallizes out as such.
- Curve BO→→Freezing curve of Pb
i. It represents the effect on freezing point of Pb on gradual addition of small amount of Ag to it, point B is the M.P of pure Pb(−327)∘c(−327)∘c
Ii. Along BO, the M.P gradually falls on addition of Ag till lowest point O is reached
Iii. At this point solution gets saturated with respect to Ag and M.P of Pb does not fall any more. List item
Iv. On cooling whole mass crystallizes out. Therefore the system is univariant like AO.
3) Point O→Eutectic point Point O→Eutectic point_
The two curve AO and BO meet at O, where three phases solid Ag, solid Pb and their solution coexist and according phase rule. The point of O represents a fixed composition of Ag −2.6−2.6 is called eutectic composition.
At eutectic composition ^ temperature remains constant until the whole of melt solidifies in block to become solid of eutectic composition. However, further cooling results in simultaneous crystallization of a mixture of Ag and Pb in relative amounts corresponding to eutectic point O.
Bellow temperature line there are two regions.
Eutectic solid+ solid Ag in crystalline -stable
Eutectic + solid Pb in crystalline-stable.
It represents solution of Pb-Ag sample of Pb containing less than 2.6% Ag is taken at an arbitrary pt. On curve allowing mass cool temp gradually falls without any charge in composition till this point is reached to curve BO(pt may be P).
On lowering the temp lead begins to separate out of the composition varies along Pb till pt 0 is reached. On cooling whole mass solidifies into a block.
Limitations:
1. It can be applied only for system in equilibrium. Consequently, consequently, it is of little value in case of very slow equilibrium state attaining system.
2. It applies only to a single equilibrium system: and provided no information regarding any other possible equilibria in the system.
3. It requires utmost care in deciding the number of phases existing in an equilibrium sate, since it considers only the number of phases, rather than their amounts. Thus, even if a trace of the phase is present, it accounts towards the total number of phases.
4. It conditions that all phases of the system must be present simultaneously, under the identical conditions of temperature and pressure.
5. It conditions that solid and liquid phases must not be in finely –divided state; otherwise deviations occurs.
Applications:
1- This is used in the solubility product and potentio-metric titration.
2- It is used to calculate the potential of ion charge.
3- It is used in oxygen and aquatic environment.
Q- How many independent thermodynamic variables are required to determine the thermodynamic state of the gas in a canister of Argon.
A- The gas in the canister has only one component - Argon atoms. Furthermore, as all these atoms are in a gas there is only one phase in this system. We thus have:
F = C − π + 2
= 1 − 1 + 2
= 2
It is necessary to give the values of two thermodynamic variables in order to state the thermodynamic state of the Argon gas. Consider now the equation of state for the ideal gas:
P V = n R T
If you are given the temperature and the volume you can determine the pressure of the gas using this expression. Similarly, if you are given the pressure and the volume of the gas you can determine its temperature. In other words, once you are given the values of two thermodynamic variables you have fully characterized the gasses' thermodynamic state. The equation of state for an ideal gas is thus consistent with Gibbs Phase rule.
Q-How many intendent thermodynamic variables are required to determine the thermodynamic state of liquid water in equilibrium with its steam.
A- Once again there is only one chemical component in this particular system - water molecules. These water molecules can, however, be in one of two different phases - the liquid or the steam. As such Gibbs phase rule tells us that:
F = C − π + 2
= 1 − 2 + 2
= 1
This result is once again in line with your intuition if you think about it a little. The critical thing to realise is that the liquid and the gas must be in equilibrium in order for Gibbs phase rule to hold. In other words, the chemical potential for the gas must be equal to that of of the liquid. This only happens when the liquid is at its boiling point. Furthermore, we know that there is an relation that allows us to calculate the temperature at which a liquid will boil when the system is at a particular pressure. As the fact that there is only one independent thermodynamic variable when we have two coexisiting phases of the same substance makes total sense.
Q-How many independent thermodynamic variabls are required to determine the thermodynamic state of gaseous argon in contact with liquid water
A- In this system there are 2 components (argon and water) and 2 phases. We thus have:
F = C − π + 2
= 2 − 2 + 2
= 2
Once again the key point to recognise is that Gibbs Phase rule only holds when the gas and the solution are in equilibrium. The system will attain this equilibrium with the gas by having molecules of argon (or for that matter water) evapourate from the solution and enter the gas or condense from the gas so that they enter the solution. At any given temperature and pressure the concentration of argon (or chemical potential) will be determined through this equilibrium.
Q- How many intendent thermodynamic variables are required to determine the thermodynamic state of of a solution of Argon in water.
A- In this system there are 2 components (argon and water) but there is only 1 phase (the solution). We thus have:
F = C − π + 2
= 2 − 1 + 2
= 3
The thermodynamic variables we might use in this case could be the temperature, the volume and the chemical potential of the Argon. Incidentally, there are expressions for calculating the chemical potential of a solvent from the concentration of the solution. When analysing experiments it is often said that the thermodynamic variables are the temperature, the volume and the concentration. Strictly speaking, however, you need some way of calculating the chemical potential from the concentration, which is often far from trivial.
