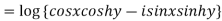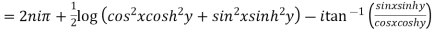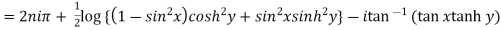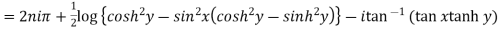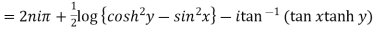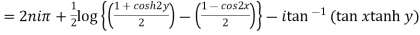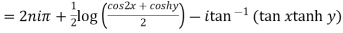Unit 2

Hyperbolic function and Logarithm of complex numbers

As we are familiar with different types of functions defined with real variable x and their properties like exponential, trigonometric or inverse trigonometric function. In this unit we shall defined these function in complex variable z and define their properties.

Separate their real and imaginary parts to get the modulus and their argument as well.

The following are the different types of complex numbers:

2.1  Exponential Function: The exponential function for the real variable x,

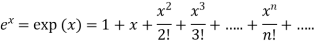
For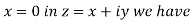

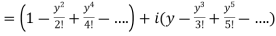
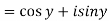
Or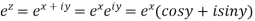   

Or  

The exponential function 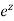of a complex variable 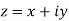as

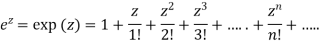
Properties:

1)    

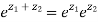
2)    

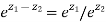
3)    

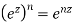
4)    

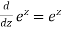
Example 1: Simplify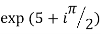

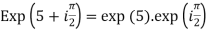
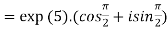
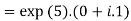
Example 2:  If 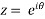, show that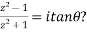

L.H.S :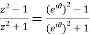 

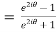
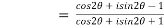
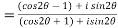
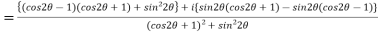
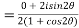
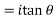
Example 3:Find the value of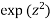

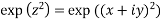
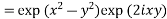
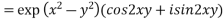
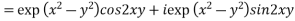
Example 4: Expand the function

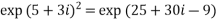
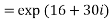
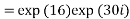
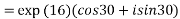
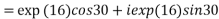
2.2Circular functions: since 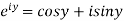and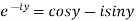

Therefore the circular function of real angles can be written as

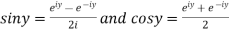and so on.

The circular function of the complex variable z is given by

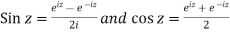
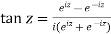
Similarly  we can find

Note: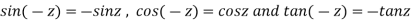

Example 1: Find out the value of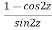

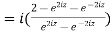
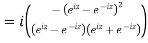
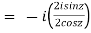
Example 2: Prove that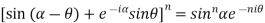

LHS

=

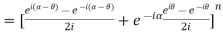
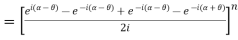
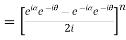
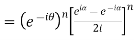
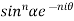
Example 3: Solve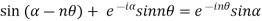

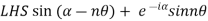
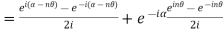
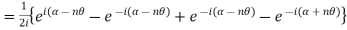
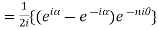
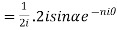
2.3Hyperbolic Function if z is any real and complex numbers:

i) 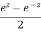                   is defined as hyperbolic sine of z and is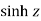

Ii) 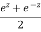                is defined as hyperbolic cosine of z and is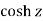

Iii)               is hyperbolic tan of z and is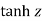

Relation between circular and hyperbolic function:

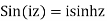
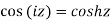
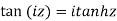
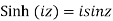
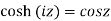
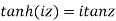
Fundamental formula of hyperbolic functions:

x =1

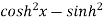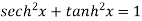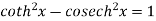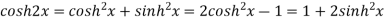
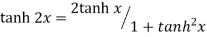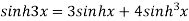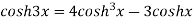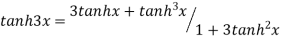Example 1: Prove that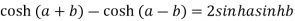

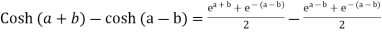
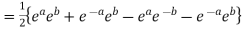
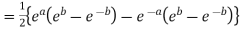
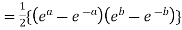
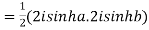
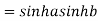
Example 2: If 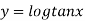,show that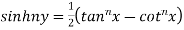

Given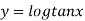

Taking exponential on both side

Taking nth power on both sides

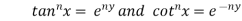
RHS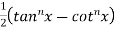  

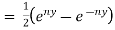
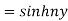
Example 3: If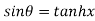 then prove that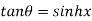

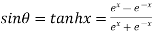……(i)

Squaring both sides

Now,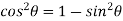

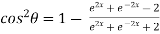
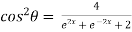
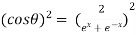
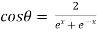……(ii)

Dividing (i) by (ii)

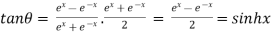
Inverse Circular and Hyperbolic functions

2.4Inverse Circular functions-

If 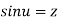,then u is called the inverse circular function of z as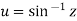 

Similarly 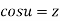then u is inverse circular function of z as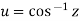

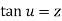then u is inverse circular function of z as

2.5Inverse Hyperbolic functions-

If 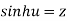, then u is called the h-yperbolic sine inverse of z as

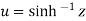
Similarly 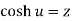then hyperbolic cosine inverse of z is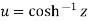

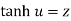then hyperbolic tan inverse of z is

The above functions are multi valued but we consider only principal value.     

Example1 : Find the value of ?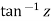

Let

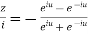
By componendo and dividendo we get

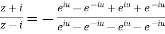
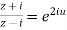
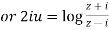
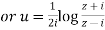
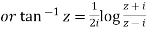
Example 2: Prove that

Let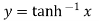

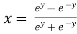
Squaring on both sides

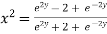
Again   

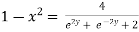
Taking square root on both side

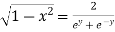
Now,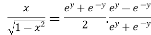

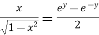
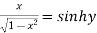
Hence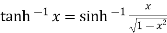 

Example 3: Prove that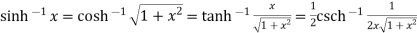

Let 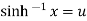   ….(i)

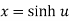
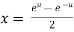
Squaring both side

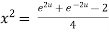
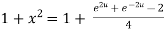
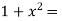
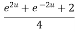
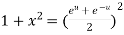
Taking square root on both side

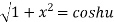
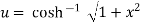  …….(ii)

Again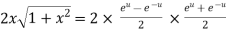  

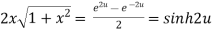
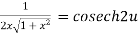
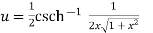……(iii)

Now,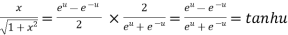 

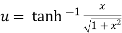   ……(iv)

From all above equation we get

2.6 Separation of Real and Imaginary Parts of Complex numbers:

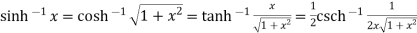
We will expand the given function in form of complex number (x+iy) and compare the real and imaginary parts of both side will give the required answer.

Example1:

Separate the real and imaginary parts of 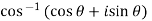and also show that the angle 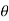is positive and acute angle?

Sol: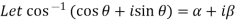  

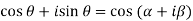
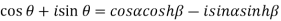
Equating real and imaginary parts we get

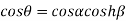   …..(1)

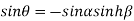     ….(2)

Squaring and adding (1) and (2) we get

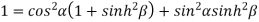
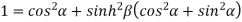
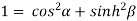
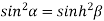     …..(3)

From equation(2)

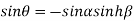
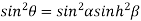
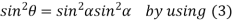
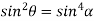
Hence 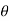is positive and acute angle.

Example 2: Separate the real and imaginary part of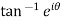

Let 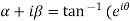)….(1)

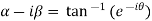…..(2)

On adding (1) and (2) we get

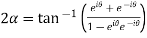
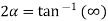
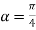
Subtracting (1) and(2) we get

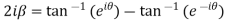
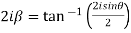
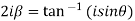
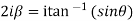
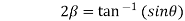
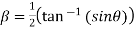
Which are the required real and imaginary parts.

Example 3:  Prove that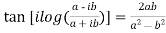

LHS :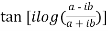       

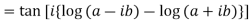
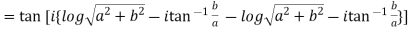
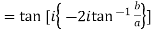
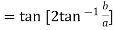
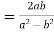
2.7 Logarithmic Function of a Complex Variable:

If 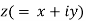and 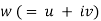be so related that 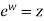, then w is said to be a logarithm of z to the base e and is written as   ….(i)

Also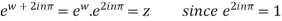   

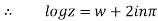   …..(ii)

i.e. the logarithm of a complex number has an infinite number of values and is, therefore, a multi-valued function.

The general value of the logarithm of z is written as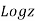

Thus from (i) and (ii)

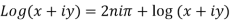
Note 1. If 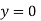, then

The logarithm of a real quantity is also multi-valued. Its  principal value is real while all other values are imaginary

Note 2. We know that the logarithm of a negative quantity has no real value.

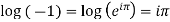
Example 1:  Find the general value of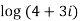       

The general value is

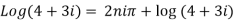
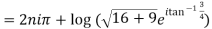
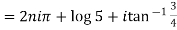
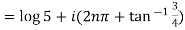
Example 2: Find the general value of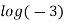 

The general value is

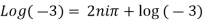
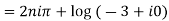
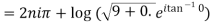
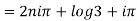
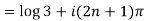
Example 3: Find the general value of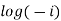

The general value is

2.8 Separation of real and imaginary parts of a logarithmic function                  

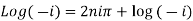
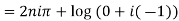
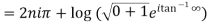
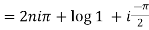
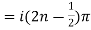
1. Real and imaginary part of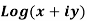

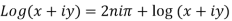
where

]

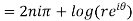
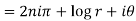
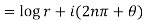
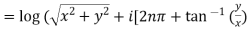Example 1: Separate the real and imaginary part of

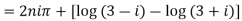
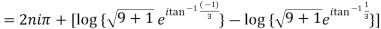
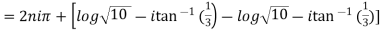
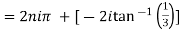
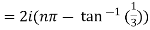
Example 2: If 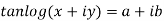where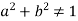 

Then Show that

Given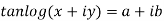

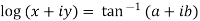
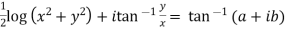
Similarly conjugate of above

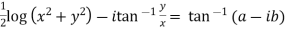
On adding above two we get

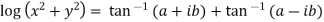
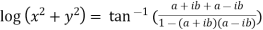
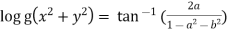
Or     

Example 3: If 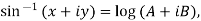show that

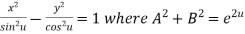
Given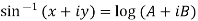  

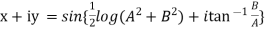
Its conjugate will be

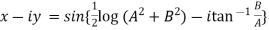
On adding above

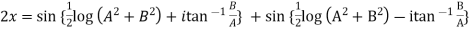
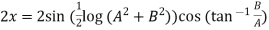
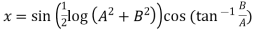
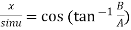     ……(i)

Similarly on Subtracting on above we get

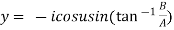
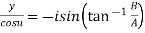     ……(ii)

Now, LHS  

=

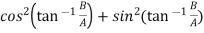
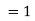
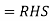
Hence proved

2.Real and Imaginary parts of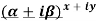

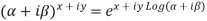
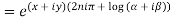
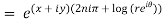  where

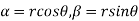
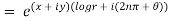
Where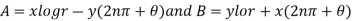

Example 1:  Find the modulus and argument of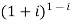

{}

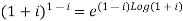
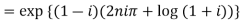
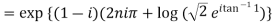
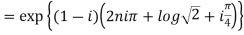
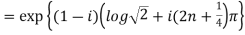
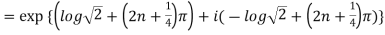
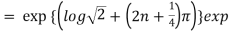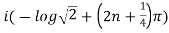Therefore  modulus of 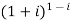 is 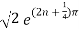 and argument is

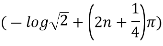
Example 3: Find all the roots of the equation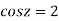

Given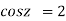

Or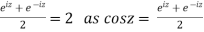        

Or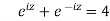

Or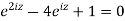  

Using formula of quadratic equation

Taking natural logarithm on both side

Or

Or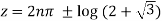 

Example 3: Separate the real and imaginary parts of

Given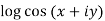

=