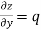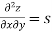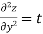Unit 3

Partial Differentiation

There are two types of quantities whose value depend on a single variables and another whose value depend on more than a single variable.

In other words : A symbol z which has a definite value for each pair of values of x and y is called a function of two independent variables x and y, denoted by

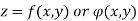
Example: velocity depends on distance and time.

Volume of cylinder depends on height and radius of cylinder.

3.1 Function of Several Variables:

Consider a function z which has a definite value for the independent variables  

Then it is called as function of several variables and is denoted by

A function whose value dependent on several independent variables is called as function of several variables.

3.2 Limit, Continuity and their Properties:

Limit :The function 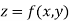is said to tend to as 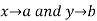if and only if the limit 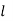is independent of the path followed by the  point x and y to approach point a and b.

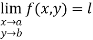
Continuity: A function 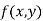is said to be continuous at a point (a,b) if

A finction is continuous at all the points of a region then it is said to be continuous in that region.

Note: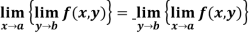

Is not always true in case of continuity.

Properties:

If 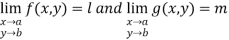then

i)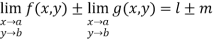                   

Ii)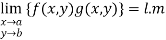                

Iii)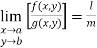              

Note: If f(x,y),g(x,y) are continuous  at (a,b) then so is their sum, difference, product and quotient.

Example 1: Find the value of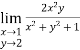

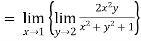
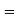
Example2 : Find the value of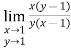

As above value tend to infinite  as x and y approaches to 1

Therefore using L-hospital rule

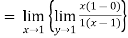
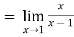
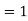
Example3 :If 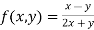   check whether

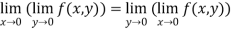or not?

LHS: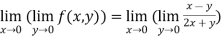

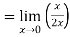
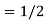
RHS: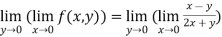

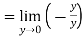
=-1

Therefore L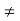HSRHS

Ans: Not

3.3 Partial Derivative: First order and Higher order  

Let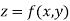 

Then partial derivative of z with respect to x is obtained by differentiating z with respect to x  treating y as constant and is denoted as

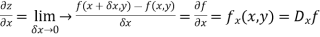
Then partial derivative of z with respect to y is obtained by differentiating z with respect to y  treating x as constant and is denoted as

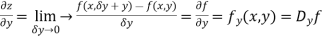
Partial derivative of higher order:

When we differentiate a function depend on more than one independent variable, we differentiate it with respect to one variable keeping other as constant.

A second order partial derivative means differentiating twice

In general 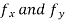are also function of x and y and so these can be further partially differentiated with respect to x and y.

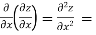
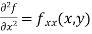
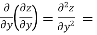
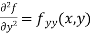
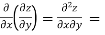
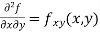
In general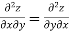

Notation:      

Generalization:         If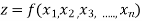

Then the partial derivative of z with respect to 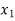is obtained by differentiating z with respect to 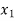treating all the other variables as constant and is denoted by

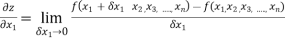
Example1: If 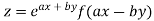. Then prove that

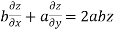
Given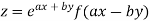 

Partially differentiating z with respect to x keeping y as constant

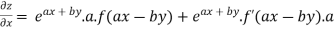
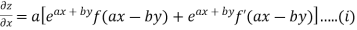
Again partially differentiating given z with respect to y keeping x as constant

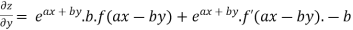
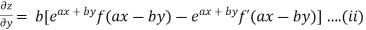
On b.eq(i) +a.eq(ii) we get

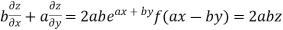
Hence proved.

Example2 : If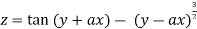

Show that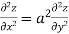

Given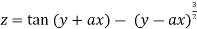 

Partially differentiating z with respect to x keeping y as constant

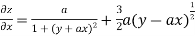
Again partially differentiating z with respect to x keeping y as constant

Partially differentiating z with respect to y keeping x as constant

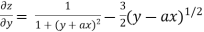
Again partially differentiating z with respect to y keeping x as constant

From eq(i) and eq(ii) we conclude that

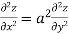
Example3  : Find the value of n so that the equation

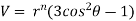
Satisfies the relation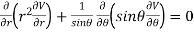 

Given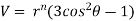   

Partially differentiating V with respect to r keeping as constant

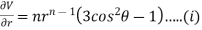
Again partially differentiating given V with respect to 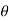keeping r as constant

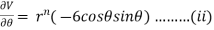
Now, we are taking the given relation

Substituting values using eq(i) and eq(ii)

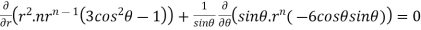
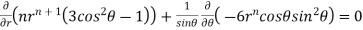
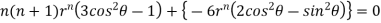
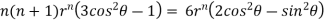
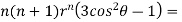
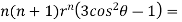
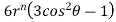
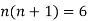
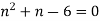
On solving we get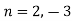 

Example 4 : If then show that when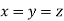

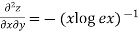
Given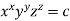 

Taking log on both side we get

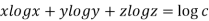
Partially differentiating with respect to x we get

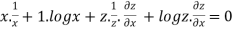
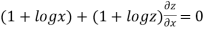
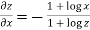  …..(i)

Similarly partially differentiating with respect y we get

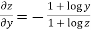    ……(ii)

LHS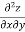 

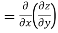
Substituting value from (ii)

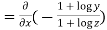
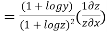
Again substituting value from (i) we get

.()                 

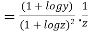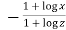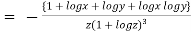
When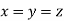

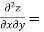
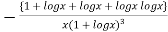
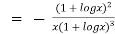
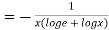
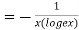
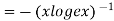
=RHS

Hence proved

Example5 :If

Then show that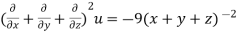 

Given 

Partially differentiating u with respect to x keeping y and z as constant

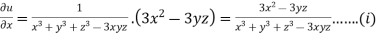
Similarly paritially differentiating u with respect to y keeping x and z as constant

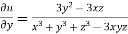  …….(ii)

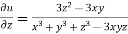  ……..(iii)

LHS: 

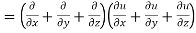
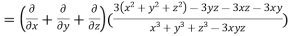
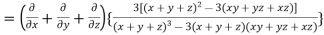
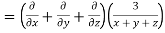
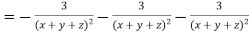
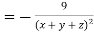
Hence proved

3.4 Composite function

A composite function is a composition / combination of the functions. In this value of one function depends on the value of another function. A composite function is created when one function is put in another.

Let

i.e

To differentiate composite function chain rule is used:

Chain rule:

1. If where x,y,z are all the function of t then

2.      If 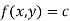be an implicit relation between x and y .

Differentiating with respect to x we get

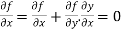
We get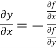            

Example1 : If 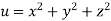where 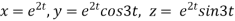then find the value of ?

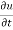Given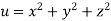  

Where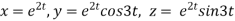 

By chain rule

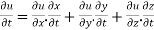
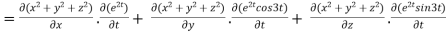
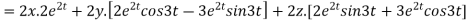
Now substituting the value of x ,y,z we get

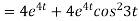-6

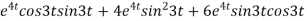
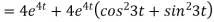
8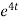

Example2 :If 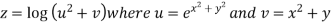then calculate

Given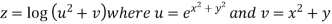

By Chain Rule

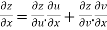
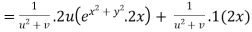
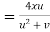
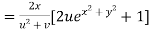
Putting the value of u =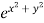

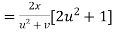
Again partially differentiating z with respect to y

By Chain Rule

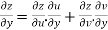
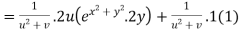
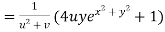
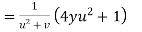by substituting value

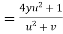
Example 3 :If .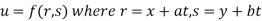

Show that    

Given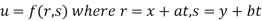

Partially differentiating u with respect to x and using chain rule

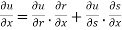
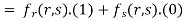
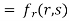………(i)

Partially differentiating z with respect to y and using chain rule

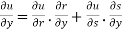
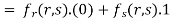
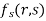=   ………..(ii)

Partially differentiating z with respect to t and using chain rule

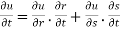
Using (i) and (ii) we get

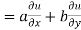
Hence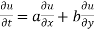   

Example4 : If 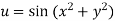where the relation is .

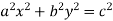Find the value of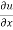

Let the given relation is denoted by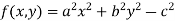

We know that

Differentiating u with respect to x and using chain rule

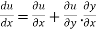
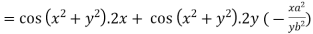
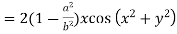
Example5 : If 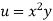and the relation is 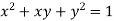. Find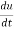

Given relation can be rewrite as

.

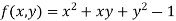We know that

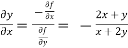
Differentiating u with respect to x and using chain rule

3.5 Euler’s theorem

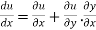
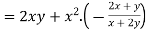
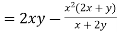
3.5.1Homogenous Function: A function of the form

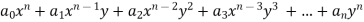
In this every term if of degree n, so it is called as homogenous function of degree n.

Rewriting the above as

= 

=

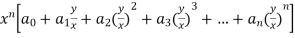
Thus every function which can be expressed as above form is called a homogenous function of degree n in x and y.

Generalization:  A function 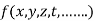is an  homogenous equation of degree n in 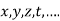if it can be expressed as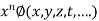

3.5.2Euler’s Theorem:

If  u be an homogenous function of degree n in x and y, then

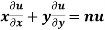
Proof: Given u is an homogenous function of degree n in x and y. So it can be rewrite as

……(i)

Partially differentiating u with respect to x we get

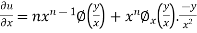
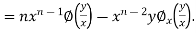
Again partially differentiating u with respect to y we get

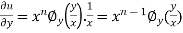
Therefore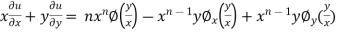

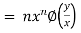
Thus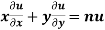                 

Hence proved

Corollary: If u is a homogenous function of degree n in x and y then

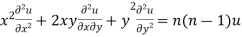
As we know that by Euler’s theorem

   ……(i)

Partially differentiating (i) with respect to x we get

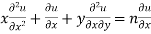
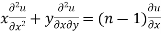   …..(ii)

Partially differentiating (i) with respect to y we get

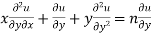
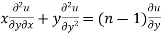      …..(iii)

Multiplying x by (ii) and y by (iii) then on adding we get

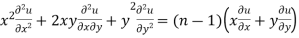
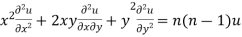by using (i)

Thus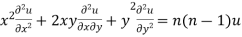    

Note: We can directly use the Euler’s theorem and its corollary to solve the problems.

Example1  Show that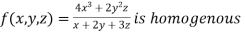

Given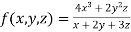

Therefore f(x,y,z) is an homogenous equation of degree 2 in x, y and z

Example2  If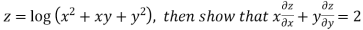

Let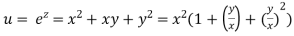

Thus u is an homogenous function of degree 2 in x and y

Therefore by Euler’s theorem

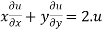
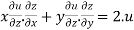
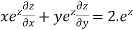      substituting the value of u

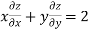
Hence proved

Example3 If 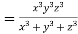, find the value of

Given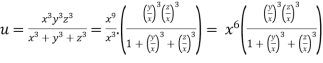 

Thus u is an homogenous function of degree 6 in x ,y and z

Therefore by Euler’s theorem

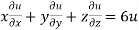
Example4 If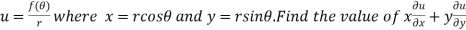 

Given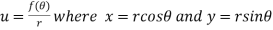 

Thus u is an homogenous equation of degree -1 in x and y

Therefore by Euler’s theorem

3.6 Deduction From Euler’s theorem    

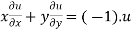
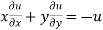
CaseI : Let u is not an homogenous function in x and y and let v be an homogenous function of degree n such that 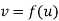 = f (x,y)

Since v is an homogenous function of degree n in x and y

By Euler’s theorem

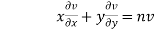
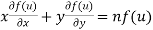
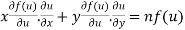
     provided

Where u is a non homogenous function and f(u) is an homogenous function of degree n in x and y

Thus for an non homogenous function u the Euler’s theorem will be

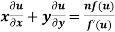     provided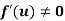

Where f(u) is an homogenous function of degree n in x and y

Example1: If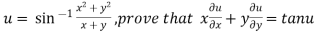

Let

Thus z is a homogenous function of degree 1 in x and y

Therefore by deduction of Euler’s theorem

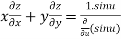
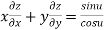
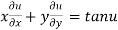
Hence proved

Example2 If 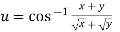. Prove that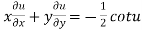

Let 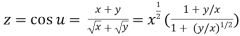    ….(i)

Thus  z is an homogenous equation of degree (1/2) in x and y

Therefore by deduction of Euler’s theorem

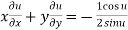
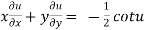
Hence proved 

Example3 If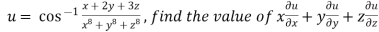

Let 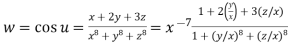       …(i)

Thus w is an homogenous function of degree -7 in x, y and z

Therefore by Euler’s theorem

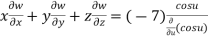
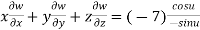
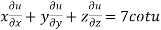
CaseII   Let u is not an homogenous function in x and y and let f(u) be an homogenous function                        of degree n    x and y then 

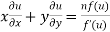     provided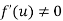

Now let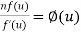

So, 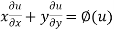      …..(i)

Partially differentiating (i) with respect to x we get

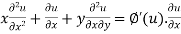
     ….(ii)

Partially differentiating (i) with respect to y we get

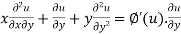
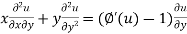   ….(iii)

Multiplying x by (ii) and y by (iii) and then on adding we get

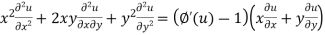
      {by using (i)}

Thus if u is an non homogenous equation in a x and y then

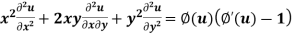
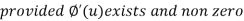
Note: we observe that 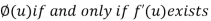is the necessary and sufficient condition for existence of above theorem.

Example1  If 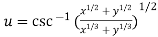, prove that

Let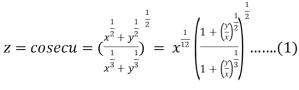

Thus z is an homogenous equation of degree 1/12 in x and y

Therefore by deduction of Euler’s theorem

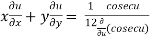
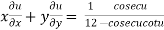
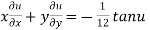    ……(2)

Partially differentiating (2) with respect to x we get

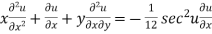
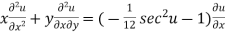       …..(3)

Partially differentiating (2) with respect to y we get

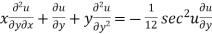
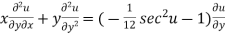    …(4)

Multiplying x by (3)  and y by (4) and the on adding we get

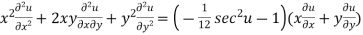
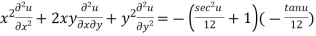   {by using (1)}

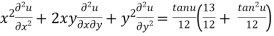
Hence proved

Example2 If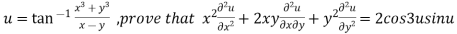

Let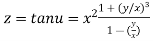

Thus z is an homogenous function of degree 2 in x and y

      …..(1)

Applying the deduction of Euler’s theorem

Using (1) we get

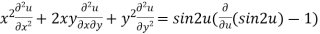
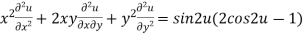
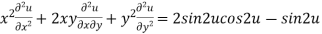
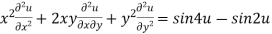
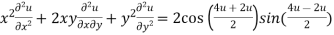
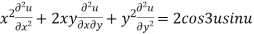
Example3 If 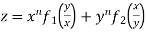.then prove that

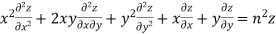
Let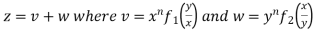

Here  v is an homogenous equation of degree n in x and y

Therefore by Euler’s theorem

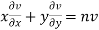      ….(i)

Also w is an homogenous function of degree (-n) in x and y

Therefore by Euler’s theorem

    ….(ii)

Now, Applying Euler’s theorem on z we get

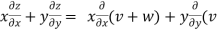+w)

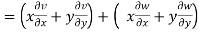
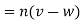           by using (i) and (ii)

Thus 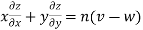          ……(iii)

Partially differentiating  (iii) with respect to x we get

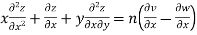        …..(iv)

Again partially differentiating (iii) with respect to y we get

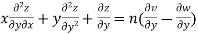       ….(v)

Multiplying x by (iv) and y by (v) and the on adding we get

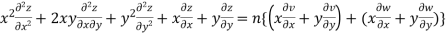
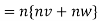
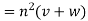
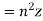
Hence proved