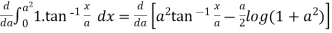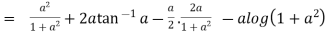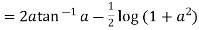Unit – 4
Application of Partial Differentiation and Successive Differentiation
In this unit we are going to calculate the value of a maximum value and minimum value of a function with or without given relation between the variables. We will also calculate the nth order derivative of the given function. With the help of Leibnitz’s method we will differentiate and integrate a function simultaneously.
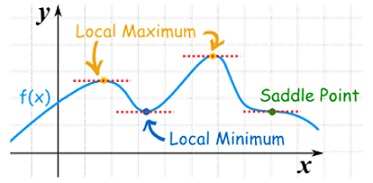
As we know that the value of a function at maximum point is called maximum value of a function. Similarly the value of a function at minimum point is called minimum value of a function.
The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other.
Maxima and Minima of a function of one variables
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point  if and only if
if and only if 
Minima is a minimum point  if and only if
if and only if 


Maxima and Minima of a function of two independent variables
Let 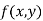 be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point  is said to be a maximum point of
is said to be a maximum point of 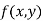 if
if

Or 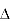 =
= 
For all positive and negative values of h and k.
Similarly the point 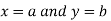 is said to be a minimum point of
is said to be a minimum point of 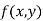 if
if
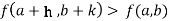
Or  =
= 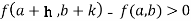
For all positive and negative values of h and k.
Saddle point:Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643192145_554638.png)
At the point.
Stationary Value
The value 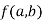 is said to be a stationary value of
is said to be a stationary value of 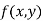 if
if
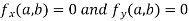
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of 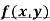
- Calculate
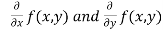 .
. - Form and solve
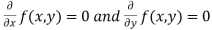 , we get the value of x and y let it be pairs of values
, we get the value of x and y let it be pairs of values 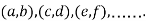
- Calculate the following values :
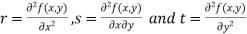
4. (a) If 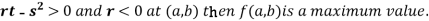
(b) If 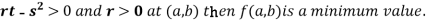
(c) If 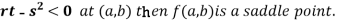
(d) If 
Example1 Find out the maxima and minima of the function
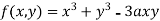
Given  …(i)
…(i)
Partially differentiating (i) with respect to x we get
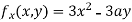 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
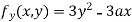 ….(iii)
….(iii)
Now, form the equations 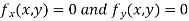
Using (ii) and (iii) we get
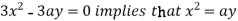
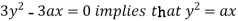
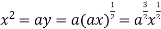 using above two equations
using above two equations
Squaring both side we get

Or 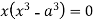
This show that 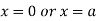
Also we get 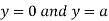
Thus we get the pair of value as 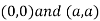
Now, we calculate
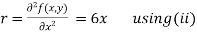
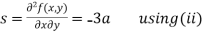
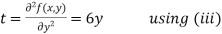
Putting above values in
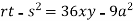
At point (0,0) we get
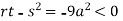
So, the point (0,0) is a saddle point.
At point 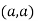 we get
we get

So the point  is the minimum point where
is the minimum point where 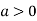
In case 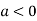

So the point  is the maximum point where
is the maximum point where 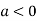
Example2 Find the maximum and minimum point of the function
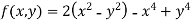
Partially differentiating given equation with respect to and x and y then equate them to zero


On solving above we get 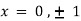
Also 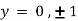
Thus we get the pair of values (0,0), (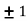 ,0) and (0,
,0) and (0,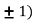
Now, we calculate

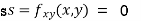

At the point (0,0)
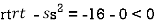
So function has saddle point at (0,0).
At the point (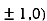
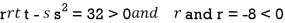
So the function has maxima at this point (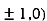 .
.
At the point (0,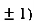
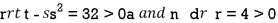
So the function has minima at this point (0,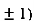 .
.
At the point (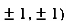

So the function has an saddle point at (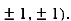
Example3 Find the maximum and minimum value of 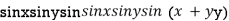
Let 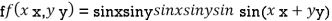
Partially differentiating given function with respect to x and y and equate it to zero
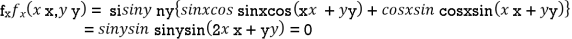 ..(i)
..(i)
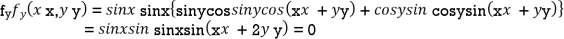 ..(ii)
..(ii)
On solving (i) and (ii) we get
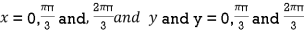
Thus pair of values are 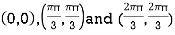
Now, we calculate

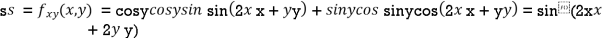
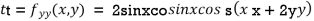
At the point (0,0)
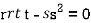
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x, 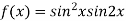
At the point 
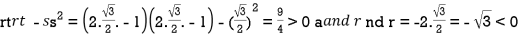
So that the given function has maximum value at 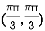
Therefore maximum value of given function
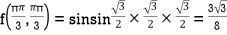
At the point 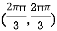
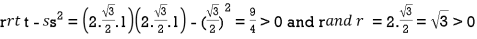
So that the given function has minimum value at 
Therefore minimum value of the given function
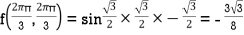
Generally to calculate the stationary value of a function with some relation by converting the given function into the least possible independent variables and then solve them. When this method fail we use Lagrange’s method.
This method is used to calculate the stationary value of a function of several variables which are all not independent but are connected by some relation.
Let 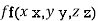 be the function in the variable x, y and z which is connected by the relation
be the function in the variable x, y and z which is connected by the relation 
Rule: a) Form the equation
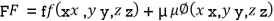
Where 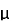 is a parameter.
is a parameter.
b) Form the equation using partial differentiation is

(We always try to eliminate )
)
c) Solve the all above equation with the given relation 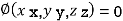
These give the value of 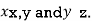
These value obtained when substituted in the given function will give the stationary value of the function.
Example1 Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.
Let first number be x, second be y and third be z.
According to the question
Let the given function be f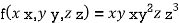
And the relation 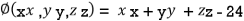
By Lagrange’s Method
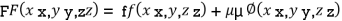
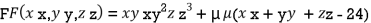 ….(i)
….(i)
Partially differentiating (i) with respect to x,y and z and equate them to zero
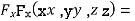
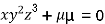 ….(ii)
….(ii)
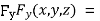
 ….(iii)
….(iii)
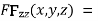
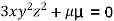 ….(iv)
….(iv)
From (ii),(iii) and (iv) we get
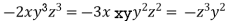
On solving
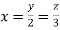
Putting it in given relation we get
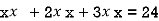
Or 
Or 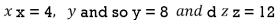
Thus the first number is 4 second is 8 and third is 12
Example2 The temperature T at any point 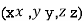 in space is
in space is 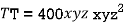 .Find the highest temperature on the surface of the unit sphere.
.Find the highest temperature on the surface of the unit sphere.
Given function is 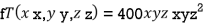
On the surface of unit sphere given 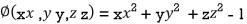 [
[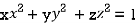 is an equation of unit sphere in 3 dimensional space]
is an equation of unit sphere in 3 dimensional space]
By Lagrange’s Method
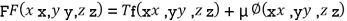
 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
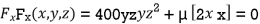 or
or 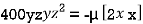 …(ii)
…(ii)
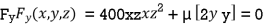 or
or 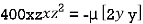 …(iii)
…(iii)
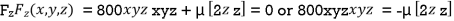 …(iv)
…(iv)
Dividing (ii) and (ii) by (iv) we get
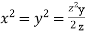
Using given relation 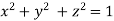
Or 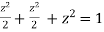
Or 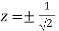
So that 
Or 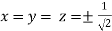
Thus points are 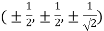
The maximum temperature is 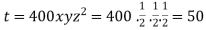
Example3 If 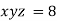 ,Find the value of x and y for which
,Find the value of x and y for which 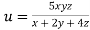 is maximum.
is maximum.
Given function is 
And relation is 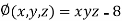
By Lagrange’s Method
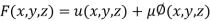
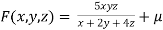 [
[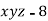 ] ..(i)
] ..(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
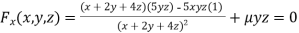
Or 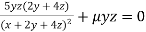 …(ii)
…(ii)
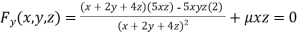
Or 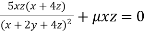 …(iii)
…(iii)
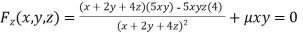
Or 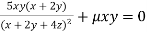 …(iv)
…(iv)
On solving (ii),(iii) and (iv) we get
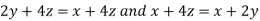
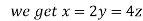
Using the given relation we get 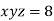
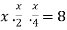

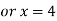
So that 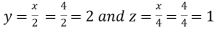
Thus the point for the maximum value of the given function is 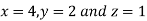
Example4 Find the points on the surface  nearest to the origin.
nearest to the origin.
Let 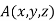 be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin 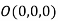 is
is
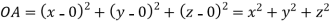
Thus the given equation will be
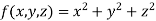
And relation is 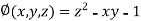
By Lagrange’s Method

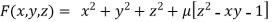 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero

Or 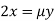 …(ii)
…(ii)
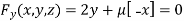
Or  …(iii)
…(iii)
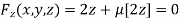
Or 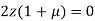
Or 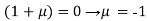
On solving equation (ii) by (iii) we get
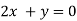
And 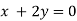
On subtracting we get 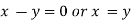
Putting in above 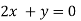
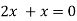
Or 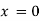
Thus 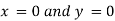
Using the given relation we get
 = 0.0 +1=1
= 0.0 +1=1
Or 
Thus point on the surface nearest to the origin is 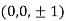
4.3.1 Successive Differentiation with nth derivative:
It is the process of differentiating the given function simultaneously many times and the result obtained are called successive derivative.
Let 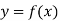 be a differentiable function.
be a differentiable function.
First derivative is denoted by 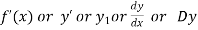
Second derivative is 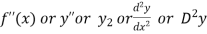
Third derivative is 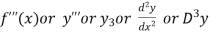
Similarly the nth derivative is 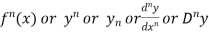
Example:
Function | Derivaties |
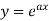 |
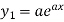
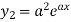
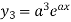 …………..
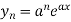 |
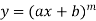 |
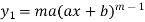
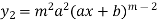
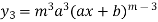 ………..
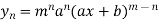 |
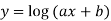 |
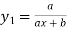

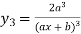 …………
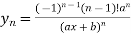 |
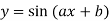 |
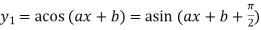
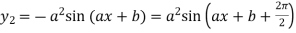
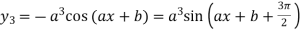 ………….
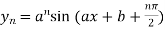
|
Example1: Find the nth derivative of 
Since 
Differentiating both side with respect to x
 [
[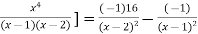
Again differentiating with respect to x
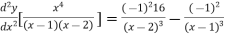
Again differentiating with respect to x
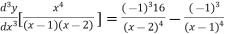
Similarly the nth derivative is
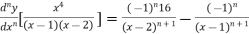
Example2: Find the nth derivative of 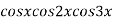
Let 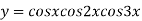
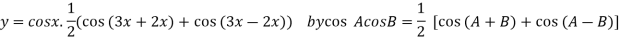
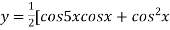 ]
]
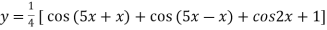
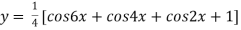
Differentiating with respect to x we get
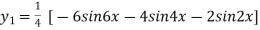
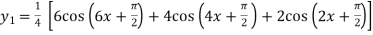
Again differentiating with respect to x we get

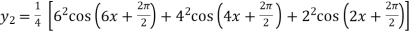
Again differentiating with respect to x we get
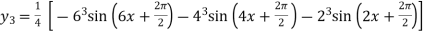

Similarly Again differentiating with respect to x we get
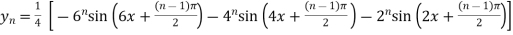
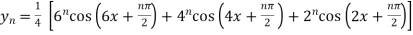
Example3: Find the nth derivative 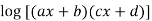
Let 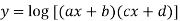
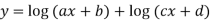
Differentiating with respect to x.
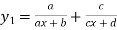
Again differentiating with respect to x.
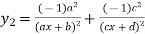
Again differentiating with respect to x.
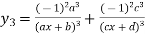
Again differentiating with respect to x.

Again differentiating with respect to x.
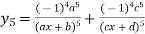
Similarly the nth derivative with respect to x.
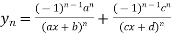
4.3.2Leibnitz’s theorem:
If u and v are the function of x such that their nth derivative exists, then the nth derivative of their product will be
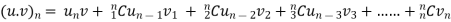
Example1:Find the nth derivative of 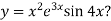
Let 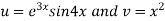
Also 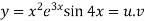
By Leibnitz’s theorem
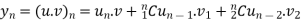
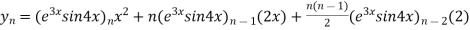
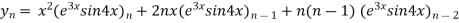 …(i)
…(i)
Here 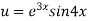
Differentiating with respect to x, we get
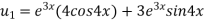
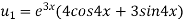
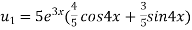

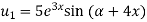
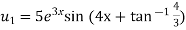
Again differentiating with respect to x, we get
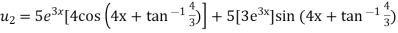
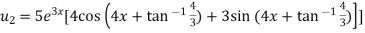
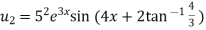
Similarly the nth derivative will be
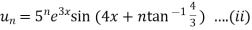
From (i) and (ii) we have,
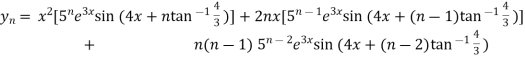

Example2: If 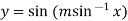 , then show that
, then show that
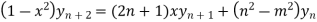
Also, find 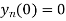
Here 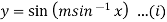
Differentiating with respect to x, we get
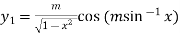 …(ii)
…(ii)
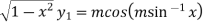
Squaring both side we get
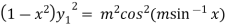


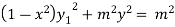 …(iii)
…(iii)
Again differentiating with respect to x ,we get
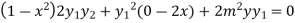
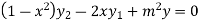
Using Leibnitz’s theorem we get
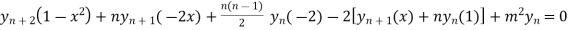

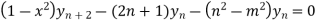 …(iv)
…(iv)
Putting x=0 in equation (i),(ii) and (iii) we get

Putting n=1,2,3,4….
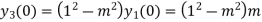

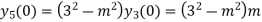
………………
Hence 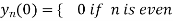
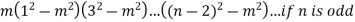
Example3: If 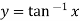 then show that
then show that
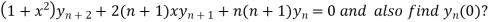
Given 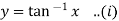
Differentiating both side with respect to x.
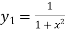 …..(ii)
…..(ii)
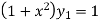
Again differentiating with respect to x, we get
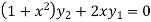 …(iii)
…(iii)
By Leibnitz’s theorem
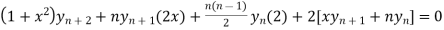

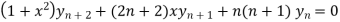
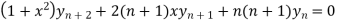 …(iv)
…(iv)
Putting x=0 in equation (i),(ii),(iii) and (iv) we get
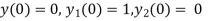
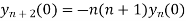
Putting n=1,2,3,4… so we get
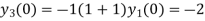
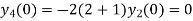
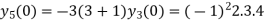
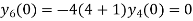

Hence we have
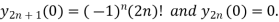
This method is used to differentiate the given function under integral sign.
Let 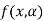 be a function defined in two variables x and
be a function defined in two variables x and  (is a parameter) .
(is a parameter) .
Define 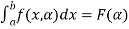
To find the derivative of 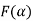 , when exist is not always possible to first evaluate this integral and then find the derivative, Such type of problems are solved by using Leibnitz’s Rules.
, when exist is not always possible to first evaluate this integral and then find the derivative, Such type of problems are solved by using Leibnitz’s Rules.
Leibnitz’s First Rule
 This rule is applicable when the limits of the given integral are constant.
This rule is applicable when the limits of the given integral are constant.
This rule helps us to calculate the value of the definite integrals which are difficult or even impossible to find out by other methods.
Note: The rule for differentiation under integral sign of an infinite integral is the same as for a definite integral.
Important To solve the integral problem many times we are going to use partial fraction method to split the fraction. Some standard form are given below:
S. No. | Form of rational fraction | Partial fraction form |
1 | 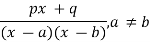 | 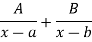 |
2 |  | 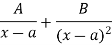 |
3 | 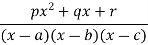 | 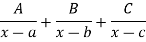 |
4 | 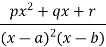 | 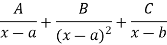 |
5 | 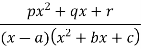 |  |
Example1 Find the value of 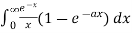
Let 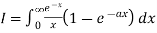
Differentiating both side with respect to a we get
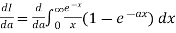
Using Leibnitz’s Rule
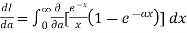
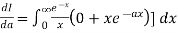
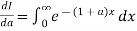
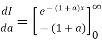
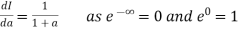
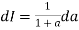
Now, integrating both side
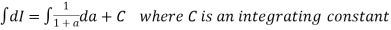
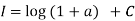
As given integral 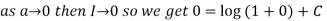
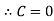
Thus 
Example2 Differentiating under the integral sign ,find the value of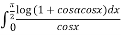
Let 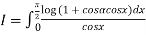
Differentiating both side with respect to parameter 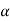
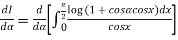
Using Leibnitz’s theorem
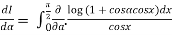
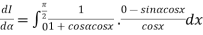
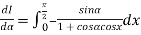
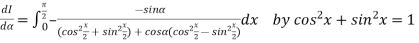
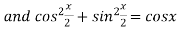
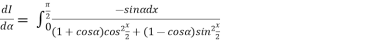
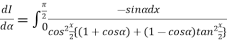
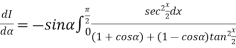
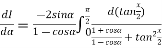
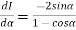
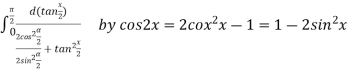
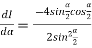
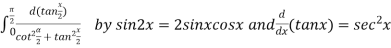
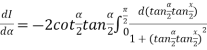

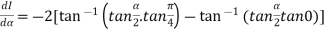
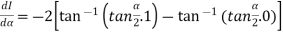
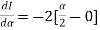
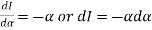
On integrating both side
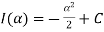
When 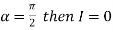
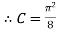
Hence 
Leibnitz’s Second rule for variable limits of integration
 This method is applicable when limits of integration are variable.
This method is applicable when limits of integration are variable.
Example1 If 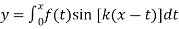 ,prove that y satisfied the differential equation
,prove that y satisfied the differential equation
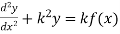
Given 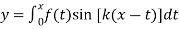
Differentiating both side with respect to x

By Leibnitz’s Rule
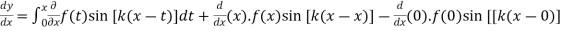
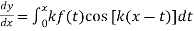
Again differentiating with respect to x we get
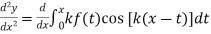
Using Leibnitz’s Rule
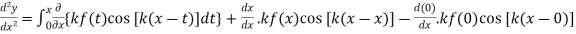
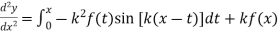

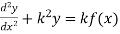
Hence proved
Example2 Verify by direct integration and prove that
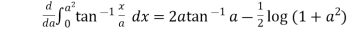
Let 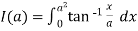
Differentiating both side with respect to a, we get
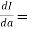
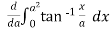
By Leibnitz’s theorem

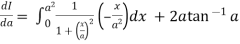

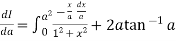
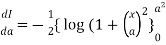 +
+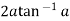
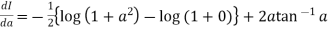
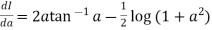
Hence proved
Direct integration

By product of two function under integration
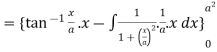

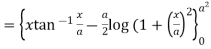

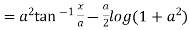
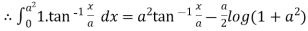
So that,