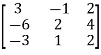Unit-5
Matrices
A matrix is an ordered rectangular array of numbers or functions. The number or the functions are called the element or the entries of the matrix.
Notation: Let 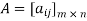 i.e. A is a matrix of order
i.e. A is a matrix of order 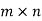 .
.
Or 
Is a matrix of order 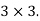 It has 3 rows and 3 columns.
It has 3 rows and 3 columns.
5.1.1. Special Matrices:
a) Row matrix: A matrix with only one single row and many columns can be possible.
A = 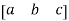
b) Column matrix: A matrix with only one single column and many rows can be possible.
A = 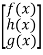
c) Square matrix: A matrix in which number of rows is equal to number of columns is called a square matrix. Thus an 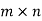 matrix is square matrix then m=n and is said to be of order n.
matrix is square matrix then m=n and is said to be of order n.
The determinant having the same elements as the square matrix A is called the determinant of the matrix A. Denoted by |A|.
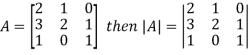
The diagonal elements of matrix A are 2, 2 and 1 is the leading and the principal diagonal.
The sum of the diagonal elements of square matrix A is called the trace of A.
A square matrix is said to be singular if its determinant is zero otherwise non-singular.
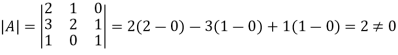
Hence the square matrix A is non-singular.
d) Diagonal matrix: A square matrix is said to be diagonal matrix if all its non diagonal elements are zero.
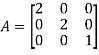
e) Scalar matrix: A diagonal matrix is said to be scalar matrix if its diagonal elements are equal.
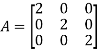
f) Identity matrix: A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an identity matrix or Unit matrix.
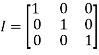
h) Null Matrix: If all the elements of a matrix are zero, it is called a null or zero matrixes.
Ex: 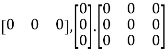 etc.
etc.
5.1.2 Operation on matrices:
a) Equality of matrices: Two matrices A and B are said to be equal if and only if
(i) They are of the same order
(ii) Each element of A is equal to the corresponding element of B.
b) Addition and Subtraction of matrices:
If A,B be two matrices of the same order , then their sum and difference is the sun or difference of t heir corresponding elements.
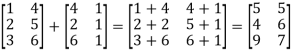
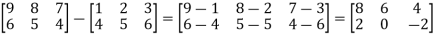
Note: i) For addition or subtraction matrices must be of same order.
Ii) Also A+B=B+A
Iii) (A+B)-C=A+ (B-C) =B+(C-A)
c) Multiplication of matrix by a scalar: The product of a matrix A by a scalar k is a matrix whose each element is k times the corresponding elements of A.
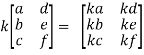
d) Multiplication of matrices: Two matrices can be multiplied only when the number of column of first is equal to number of rows in the second. Such matrix are said to be conformable.
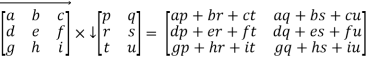
In this case first matrix is of order 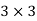 and second is of order
and second is of order 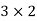 and new matrix obtained is of order
and new matrix obtained is of order 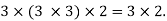
Note: a) Generally 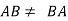
b) 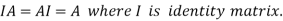
c) 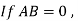 It does not necessarily imply that A or B is a null matrix.
It does not necessarily imply that A or B is a null matrix.
d) Associative law holds in multiplication 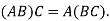
e) Distributive law holds 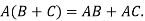
f) Power of a matrix: If A be a square matrix , then the product
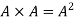
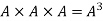 and so on.
and so on.
If 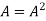 then the matrix A is called idempotent.
then the matrix A is called idempotent.
e) Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 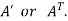
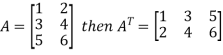
The transpose of matrix 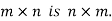 Also
Also 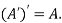
Note: 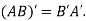
f) Adjoint of a square matrix: The determinant of the square matrix
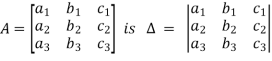
The matrix formed by the cofactors of elements in 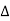 is
is
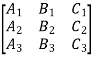 . Then the transpose of this matrix i.e.
. Then the transpose of this matrix i.e. 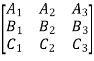
Is called adjoint of the matrix A.
Example: let A = 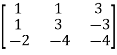
Then 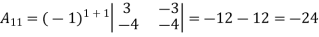
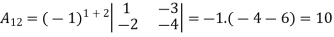
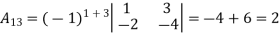
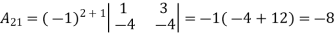
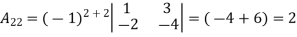
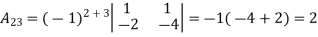
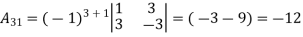
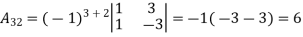
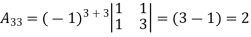
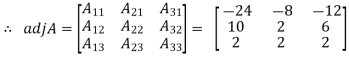
g) Inverse of a matrix:
If A be any matrix, then a matrix B if it exists, such that
AB=BA=I
Is called inverse of A. The matrix A and B should both be square matrices of the same order.
|AB|=|BA|=|I|=1
i.e. both |A| and |B| must be non zero or non singular.
The inverse of a matrix A is denoted by 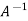
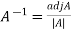
Note: 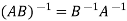
Example: let A = 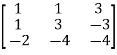
Then 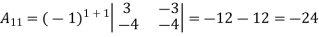
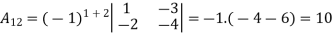
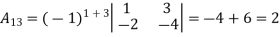
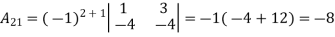
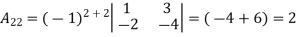
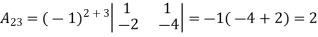
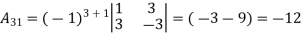
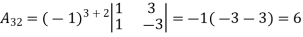
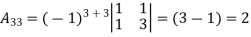
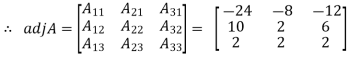
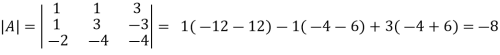
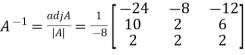
5.2.1 Symmetric and Skew-Symmetric Matrices:
A square matrix 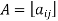 is said to be symmetric if
is said to be symmetric if 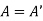 , that is,
, that is,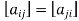 for all possible values of i and j.
for all possible values of i and j.
Example: A = 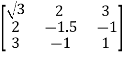 is a symmetric matrix as
is a symmetric matrix as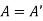 .
.
A square matrix 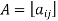 is said to be skew- symmetric if
is said to be skew- symmetric if 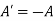 , that is,
, that is,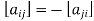 for all possible values of i and j.
for all possible values of i and j.
In case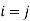 , we have
, we have 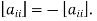 Therefore
Therefore 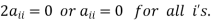
This shows that all the diagonal elements of a skew-symmetric matrix is zero.
Example: 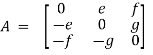 is skew symmetric as
is skew symmetric as 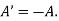
Theorem1: For any square matrix A with real number entries, A+A’ is symmetric and A-A’ is skew symmetric matrix.
Theorem2: Any Square matrix can be expressed as sum of symmetric matrix and skew symmetric matrix.
Let A be any square matrix then we can write
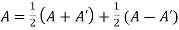
Where A+A’ is a symmetric matrix and A-A’ is a skew symmetric matrix.
Example1: Express the matrix  as sum of a symmetric and skew symmetric matrix.
as sum of a symmetric and skew symmetric matrix.
Let A = 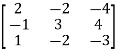 therefore A’ =
therefore A’ = 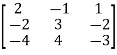
Suppose 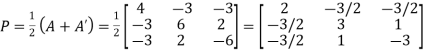
We calculate 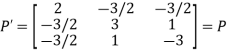
Hence P is the required symmetric matrix.
Again let 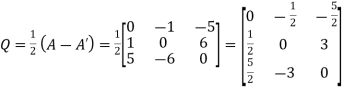
We find 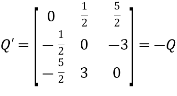
Hence Q is the required skew -symmetric matrix.
Now, we check
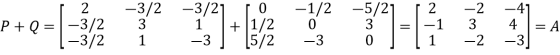
This implies that square matrix A can be represented as sum of symmetric and skew symmetric matrices.
Example2: Express the matrix 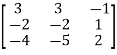 as sum of a symmetric and skew symmetric matrix.
as sum of a symmetric and skew symmetric matrix.
Let A = 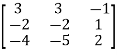 therefore A’ =
therefore A’ = 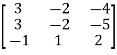
Suppose 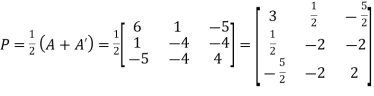
We can find P’ =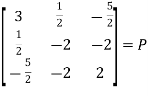
Hence P is the required symmetric matrix.
Again let 
We find Q’ = 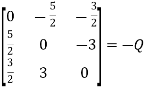
Hence Q is the required skew symmetric matrix.
Now, we check
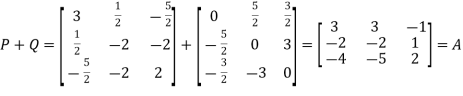
This implies that square matrix A can be represented as sum of symmetric and skew symmetric matrices.
Example3: Express the matrix 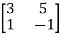 as sum of a symmetric and skew symmetric matrix.
as sum of a symmetric and skew symmetric matrix.
Let A = 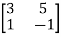 therefore A’ =
therefore A’ = 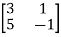
Suppose 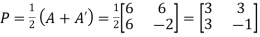
We find P’= 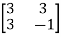 = P
= P
Hence P is the required symmetric matrix.
Again let 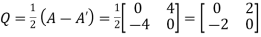
We find Q’ = 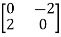 = -Q’
= -Q’
Hence Q is the required skew symmetric matrix.
Now, we check
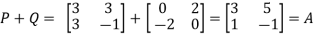
This implies that square matrix A can be represented as sum of symmetric and skew symmetric matrices.
5.2.2. Hermitian and Skew-Hermitian Matrices:
A matrices with complex number or functions entries are called complex matrices.
Conjugate matrix: If 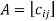 have a complex elements of form
have a complex elements of form 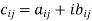 where
where 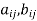 are the real then
are the real then
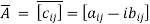
Is called conjugate matrix of A.
Hermitian Matrix: A square matrix A such that 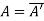 is called a Hermitian matrix. All the element of the principal diagonal are real where as element are transpose conjugate in other position.
is called a Hermitian matrix. All the element of the principal diagonal are real where as element are transpose conjugate in other position.
Example1: 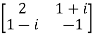 is a Hermitian Matrix as
is a Hermitian Matrix as
A = 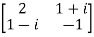 therefore A’=
therefore A’=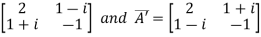
So that 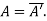
Example2: Show that 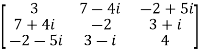 is a Hermitian matrix.
is a Hermitian matrix.
Let A = 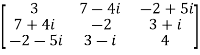 therefore A’ =
therefore A’ = 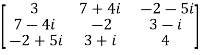
Now, 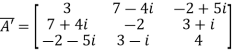
Here 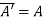
Hence given matrix is a Hermitian matrix.
Skew –Hermitian Matrix: A square matrix A such that 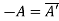 is called a Skew- Hermitian matrix. All the element of the principal diagonal are either zero or purely imaginary where as element are transpose conjugate in other position.
is called a Skew- Hermitian matrix. All the element of the principal diagonal are either zero or purely imaginary where as element are transpose conjugate in other position.
Example1: A = 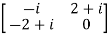 and A’ =
and A’ = 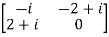
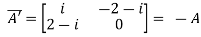
Hence A is an skew-hermitian matrix.
Example2: Show that 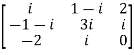
Let A = 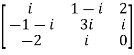 and then A’=
and then A’=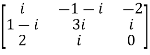
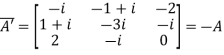
It is clear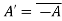 , hence the given matrix is skew-hermitian matrix.
, hence the given matrix is skew-hermitian matrix.
Note: A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.
Similarly a Skew- Hermitian matrix is a generalization of a Skew symmetric matrix and also every Skew- symmetric matrix is Skew –Hermitian.
Theorem: Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
Or If A is given square complex matrix then 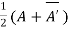 is hermitian and
is hermitian and 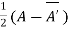 is skew-hermitian matrices.
is skew-hermitian matrices.
Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where 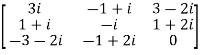
Let A =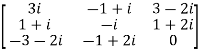
Therefore 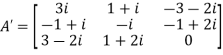 and
and 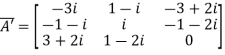
Let 
Again 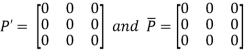
Hence P is a hermitian matrix.
Let 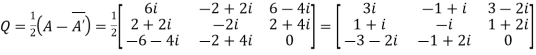
Again 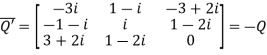
Hence Q is a skew- hermitian matrix.
We Check
P +Q=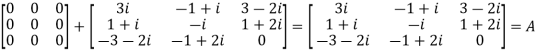
Hence proved.
Example2: If A = 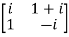 then show that
then show that
(i) 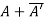 is hermitian matrix.
is hermitian matrix.
(ii) 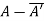 is skew-hermitian matrix.
is skew-hermitian matrix.
Given A = 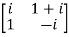
Then 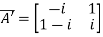
Let 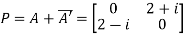
Also 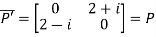
Hence P is a Hermitian matrix.
Let 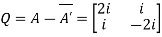
Also 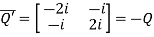
Hence Q is a skew-hermitian matrix.
5.2.3 Orthogonal Matrices:
A real square matrix A is said to be orthogonal if 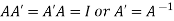
Since 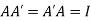 .
.
Taking determinant we get 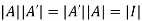
As we know that 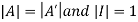
So,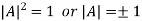 .
.
This implies that determinant of an orthogonal matrix is either 1 or -1.
Note: i) If A is orthogonal, A’ and inverse of A is also orthogonal.
Ii) If A and B are orthogonal then AB is also orthogonal.
Example1: Prove that the following matrix is orthogonal:
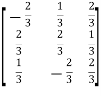
Let A = 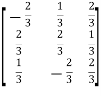 then A’=
then A’= 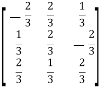
Now, AA’=
Thus AA’=  = I
= I
Hence the matrix is orthogonal.
Example2: Is the following matrix is orthogonal:
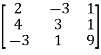
Let A = 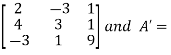
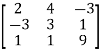
Now, AA’= 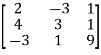 .
. 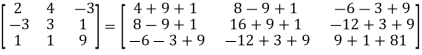
AA’= 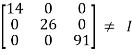
Hence given matrix is not orthogonal.
Example3: Is the following matrix is orthogonal:
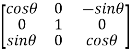
Let A = 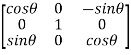 therefore A’ =
therefore A’ =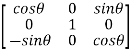
Now AA’ =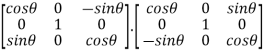
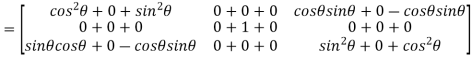
=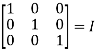
Hence the given matrix is orthogonal.
5.2.4.Unitary matrices:
A square matrix U such that 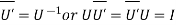 is called a unitary matrix. The Unitary matrix is a generalization of an orthogonal matrix in complex field.
is called a unitary matrix. The Unitary matrix is a generalization of an orthogonal matrix in complex field.
Note: i) Inverse of an unitary matrix is unitary matrix.
Ii) Product of two unitary matrices is unitary matrix.
Example1: Prove that 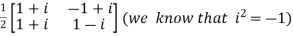
Let U = 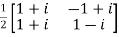 therefore U’=
therefore U’= 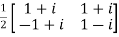
Also 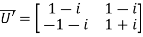
Now, UU’= 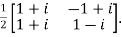
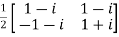
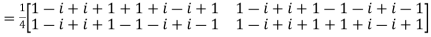
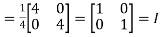
Hence the given matrix is a unitary matrix.
Example2: Given that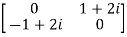 , show that
, show that 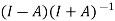 is a unitary matrix.
is a unitary matrix.
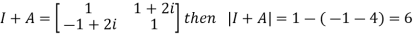
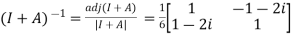
Also 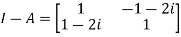
Now, 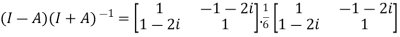
=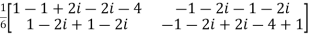
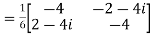 ..(i)
..(i)
Its transpose conjugates 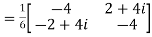 ... (ii)
... (ii)
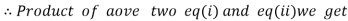
=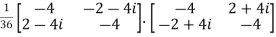
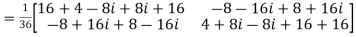
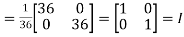
Hence the above matrix is a unitary matrix.
A matrix is said to be of rank r when
(i) It has at least one nonzero minor of order r,
(ii) Every minor of higher order than order r vanishes.
Equivalently the rank of a matrix is the largest order of any non vanishing minor of the matrix.
Elementary transformation n of a matrix:
- The interchange of any two rows (columns).
- The multiplication of any row (column) by a nonzero number.
- The addition of a constant multiple of the elements of any row(column)to the corresponding elements of any other row(column).
Echelon form of a matrix:
The echelon form of a matrix consist of row echelon form and any matrix can be reduced into row echelon form with help of elementary transformation. The row echelon form consists of:
- The first non zero in each row i.e. leading element is 1.
- Each leading entry is in a column to the right of the leading entry of the previous row.
- Rows with all zero elements, if any, are below to the rows with non zeros entries.
Example: 
Example1: Find the rank of the following matrices?
Let A = 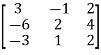
Applying 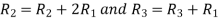
A 
Applying 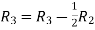
A 
Applying 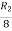
A 
Applying 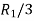
A 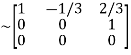
It is clear that minor of order 3 vanishes but minor of order 2 exists as 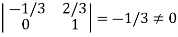
Hence rank of a given matrix A is 2 denoted by 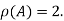
2. 
Let A = 
Applying 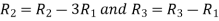

Applying 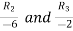
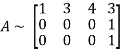
Applying 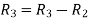
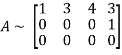
The minor of order 3 vanishes but minor of order 2 non zero as 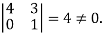
Hence the rank of matrix A is 2 denoted by 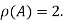
3. 
Let A = 
Apply 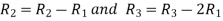

Apply 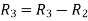

Apply 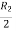
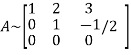
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 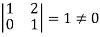
Hence the rank of given matrix is 2 i.e. 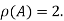
Every non zero matrix A of rank r can be reduced by sequence of elementary transformations, to the form

Called the normal form of A.
Example1: Reduce the matrix into normal form and find the rank of matrix:
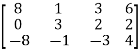
Let A = 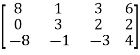
Apply 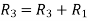

Apply 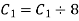

Apply 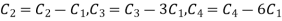

Apply 
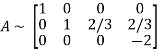
Apply 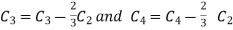

Apply 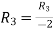
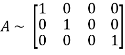
Apply 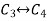
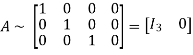
Hence the rank of the matrix is 3.
Example2: Reduce the matrix in to normal form and find its rank:

Let A = 
Apply 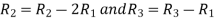
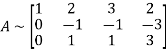
Apply 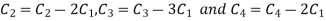
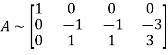
Apply 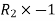

Apply 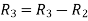

Apply 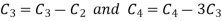
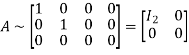
Hence the rank of the matrix A is 2.
Example3: Find the rank of a matrix using normal form,

Let A = 
Apply 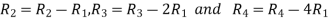
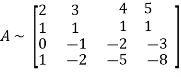
Apply 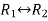
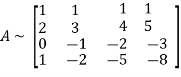
Apply 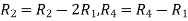
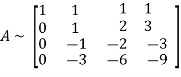
Apply 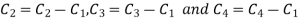
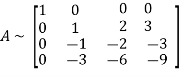
Apply 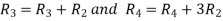

Apply 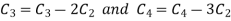

Hence the rank of the given matrix A is 2.
From the normal form of a matrix A of rank r, corresponding to matrix A there exists non singular matrices P and Q such that
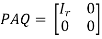
If A be a 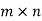 matrix with m rows and n columns, then P is square matrix of order
matrix with m rows and n columns, then P is square matrix of order 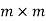 and Q is a square matrix of order
and Q is a square matrix of order 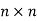 repectively. Also P is an elementary matrix obtained by the elementary row transformations and also Q is an elementary matrix obtained by the elementary column transformations.
repectively. Also P is an elementary matrix obtained by the elementary row transformations and also Q is an elementary matrix obtained by the elementary column transformations.
Note: 1. P and Q are non singular matrices i.e. 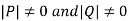 .
.
2. P and Q are not unique. Different elementary transformation in normal form gives different P and Q.
Example1: Find the non-singular matrices P and Q such that PAQ is in normal form:
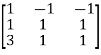
Let A = 
Also we know that A =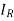 A
A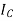 where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
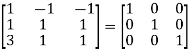 A
A
Apply 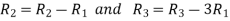
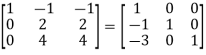 A
A
Apply 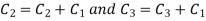
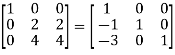 A
A
Apply 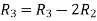
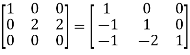 A
A
Apply 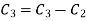
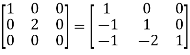 A
A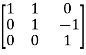
Apply 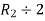
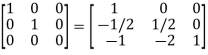 A
A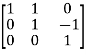
Or 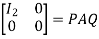 where P=
where P=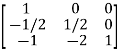 , Q=
, Q=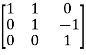
Hence the rank of matrix A is 2.
Example2: Find the non-singular matrices P and Q such that PAQ is in normal form:
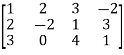
Let A = 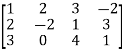
Also we know that A =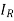 A
A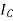 where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
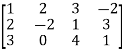
 A
A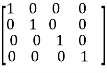
Apply 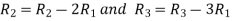
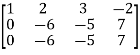
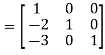 A
A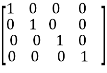
Apply 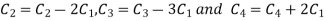
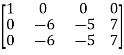
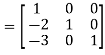 A
A
Apply 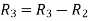
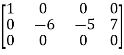
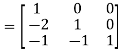 A
A
Apply 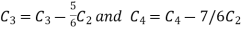
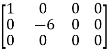
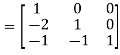 A
A
Apply 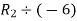
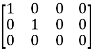
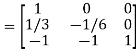 A
A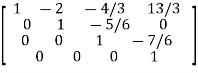
Or 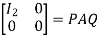 where P=
where P=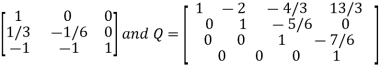
Hence the rank of the matrix A is 2.
Example3: Find the non-singular matrices P and Q such that PAQ is in normal form:

Let A= 
Also we know that A =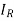 A
A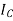 where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.
where all row elementary transformation is applied in identity matrix pre multiplied where as column elementary transformation is applied in identity matrix post multiplied.

 A
A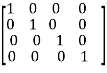
Apply 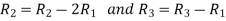
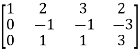
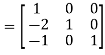 A
A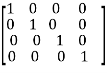
Apply 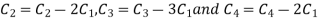

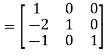 A
A
Apply 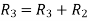
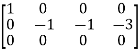
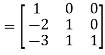 A
A
Apply 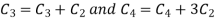
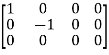
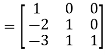 A
A
Apply 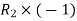
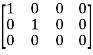
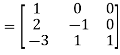 A
A
Or 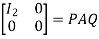 where P=
where P=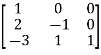 and Q=
and Q=
Hence the rank of matrix A is 2.
The standard form of system of homogenous linear equation is
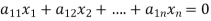
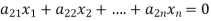 (1)
(1)
…………………………………
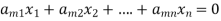
It has m number of equations and n number of unknowns.
Let the coefficient matrix be A = 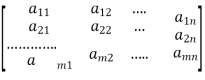
By elementary transformation we reduce the matrix A in triangular form we calculate the rank of matrix A, let rank of matrix A be r.
The following condition helps us to know the solution (if exists consistent otherwise inconsistent) of system of above equations:
- If r = n i.e. rank of coefficient matrix is equal to number of unknowns then system of equations has trivial zero solution by
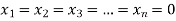
II. If r < n i.e. rank of coefficient matrix is less than the number of unknowns then system of equations has (n-r) linearly independent solutions.
In this case we assume the value of (n-r) variables and other are expressed in terms of these assumed variables. The system has infinite number of solutions.
III. If m < n i.e. number of equations is less than the number of unknowns then system of equations has non zero and infinite number of solutions.
IV. If m=n number of equations is equal to the number of unknowns then system of equations has non zero unique solution if and only if |A|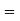 0. The solution is consistent. The |A| is called eliminant of equations.
0. The solution is consistent. The |A| is called eliminant of equations.
Example1: Solve the equations:
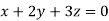
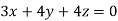
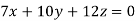
Let the coefficient matrix be A = 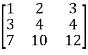
Apply 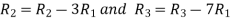
A 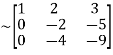
Apply 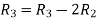
A 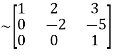
Since |A|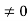 ,
, 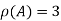
Also number of equation is m=3 and number of unknowns n=3
Since rank of coefficient matrix A = n number of unknowns
The system of equation is consistent and has trivial zero solution.
That is 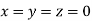
Example2: Solve completely the system of equations
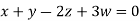
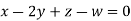
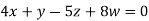
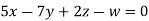
Solution: We can write the given system of equation as AX=0
Or 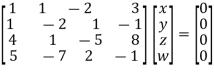
Where coefficient matrix A = 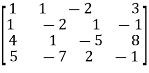
Apply 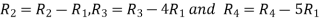
A 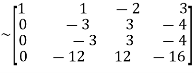
Apply 
A 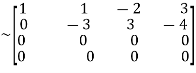 …(i)
…(i)
Since |A|=0 and also 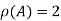 , number of equations m =4 and number of unknowns n=4.
, number of equations m =4 and number of unknowns n=4.
Here 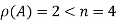
So that the system has (n-r) linearly independent solution.
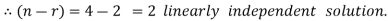
Let 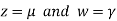
Then from equation (i) we get
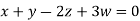
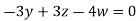
Putting 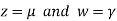
We get 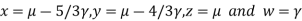 has infinite number solution.
has infinite number solution.
Example 3: find the value of λ for which the equations
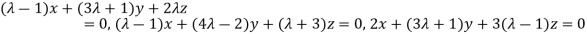
Are consistent, and find the ratio of x: y: z when λ has the smallest of these values. What happen when λ has the greatest o these values?
The system of equation is consistent only if the determinant of coefficient matrix is zero.
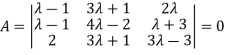
Apply 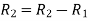
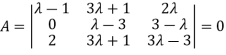
Apply 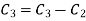
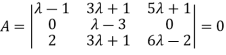
Or 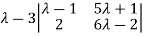 =0
=0
Or 
Or (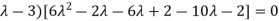
Or (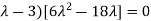
Or 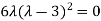
Or 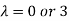 ………….(i)
………….(i)
- When λ =0, the equation become
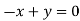
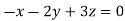
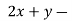 3z=0
3z=0
On solving we get
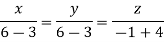
Hence x=y=z
II. When λ=3, equation become identical.
The standard form of system of non- homogenous linear equation is
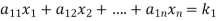
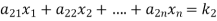 (1)
(1)
…………………………………
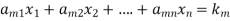
It has m number of equations and n number of unknowns.
Let the coefficient matrix be A = 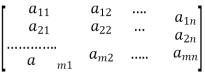
And the augmented matrix be K = 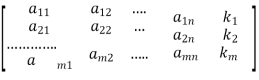
By elementary transformation we reduce the matrix A and K in triangular form we calculate the rank of matrix A and K.
Rouche’s Theorem: The system of equations(1) is consistent if and only if the coefficient matrix A and the augmented matrix K are the same rank otherwise the system is inconsistent.
The following condition helps us to know the solution (if exists consistent otherwise inconsistent) of system of above equations:
Let the rank of matrix A is r and matrix K is r’, number of equations be m and number of unknowns be n.
- If
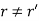 , then system of equations is inconsistent i.e. has no solution.
, then system of equations is inconsistent i.e. has no solution. - If
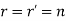 , then system of equations is consistent i.e. has unique solution.
, then system of equations is consistent i.e. has unique solution. - If
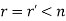 , then system of equations is consistent i.e. has infinite number solution. It has (n-r) linearly independent solutions i.e. we assume arbitrary values for (n-r) variable and rest variable are expressed in terms of these.
, then system of equations is consistent i.e. has infinite number solution. It has (n-r) linearly independent solutions i.e. we assume arbitrary values for (n-r) variable and rest variable are expressed in terms of these.
Example1: Solve the system of equations:
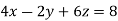
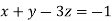
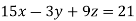
We can write the system as 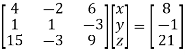
Apply 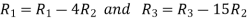
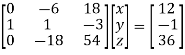
Apply 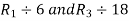
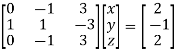
Apply 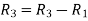
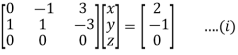
Here coefficient matrix A= 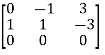 then
then 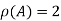
And augmented matrix K= 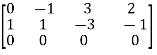 then
then 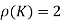
Since rank of coefficient matrix and augmented matrix are equal and is less than the number of unknowns. Therefore system have (n-r) =3-2=1, linearly independent solutions.
From equation (i) we have

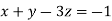
Let 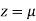
So, 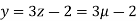

Hence 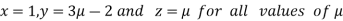
Hence system has infinite number of solutions.
Example2: Investigate for what value of λ and µ the simultaneous equations:
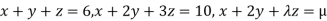
Have (i) no solution
(ii) Unique solution
(iii) An infinite number of solutions.
We can write the given system as
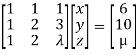
Apply 
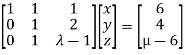
Apply 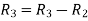
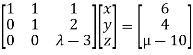
Here the coefficient matrix is A= 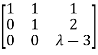 and augmented matrix K=
and augmented matrix K=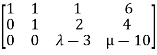
- The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if
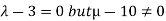 .
.
So, λ=3 and µ≠10 in case of no solution.
II. In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.
This is possible only if 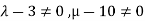 as n=3
as n=3
This implies that 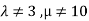 for unique solution.
for unique solution.
III. In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns
This is possible only if 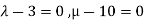 as n=3.
as n=3.
This implies that 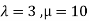 for infinite solution.
for infinite solution.
Example3: Find the values of a and b for which the equations
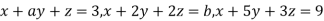
Are consistent. When will these equations have a unique solution?
We can write the above system as
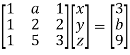
Apply 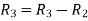
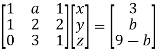
Apply 
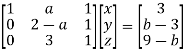
Apply 
Here the coefficient matrix is A = 
And augmented matrix K is 
- The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if
 .
.
So, a=-1 and b≠6 in case of no solution
II. In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.
This is possible only if 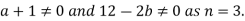
So, 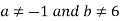 for unique solution.
for unique solution.
III. In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns
This is possible only if 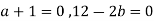 as n=3.
as n=3.
This implies that 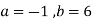 for infinite solution.
for infinite solution.