Unit – 1
Forces
Classification of forces system: - When two or more forces act on a body, they are called to form of system of forces. It to be divided in following manner.
1. Coplanar Forces
2. Non-Coplanar Forces
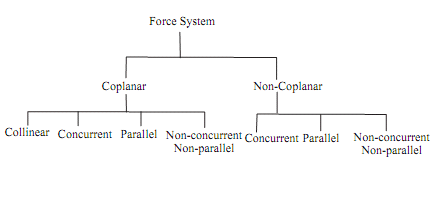
Coplanar forces:-The forces, the lines of action of which lie on the same plane, are known as coplanar forces.
There is different type of coplanar forces. They are:
• Collinear Force: When the lines of action of all the forces of a system act along the same line, this force system is called collinear force system.

• Concurrent Force: All forces of this kind, which act at one point, are known as concurrent forces.
• Parallel Forces: If all the forces are parallel to each other and lay an single plane then they are parallel forces.
• Non-Coplanar Parallel Forces: All forces are parallel to each other but not lie in single plane then they are non-coplanar parallel forces.
• Non-Coplanar Concurrent Forces: All forces do not lie in same plane but line of action passes through single point, and then they are non-coplanar concurrent forces.
• Non-Coplanar, Non-Concurrent Forces: All forces do not lie in a single plane and line of action does not pass through single point, then they are “non-coplanar non-concurrent forces.
Principle of transmissibility:- The state of rest of motion of a rigid body in unaltered if the force acting on the body replace by another force of the same magnitude and direction but acting anywhere on the body along the line of action of the applied force.
In the following figure, two rigid bodies A and B are joined by a rigid rod. If the system is moving in frictionless, the acceleration in both cases is given by,
Acceleration = Applied force/total mass
It is independent of point of application.
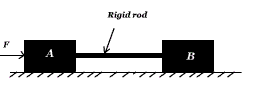

When the block is connected by the springs, the system becomes non-rigid. In this case, point of application matters. If the forces applied at B, initially the acceleration of A will be much compared B. Thus, the point of application of force matters.
To conclude, the principle of transmissibility is valid for rigid body only.
Composition of forces: The process finding out resultant of force, of a number of forces, is called composition of forces or compounding of forces.
Method for the Resultant Forces:-Though there are many methods for finding out the resultant force of a number of given forces, yet the following are important from the subject point of view:
• Analytical method
• Graphical method
Analytical method for Resultant Force: The resultant of force, of a given forces, may be found out analytically by the following method:
• Parallelogram law of forces.
• Method of resolution.
Parallelogram law of forces:
If the two coplanar forces meet at a point, their resultant may be found by the law of parallelogram of forces, which states that, "If two forces acting at a point are such that they can be represented in magnitude and direction by the two adjacent sides of parallelogram, the diagonal of the parallelogram passing through their point of intersection gives the resultant in magnitude and direction".
Consider two forces P and Q acting at point 0 in the body as shown in Figure. Their combined effect can be found out by constructing a parallelogram using vector P and vector Q as two adjacent sides of the parallelogram as shown in Figure.
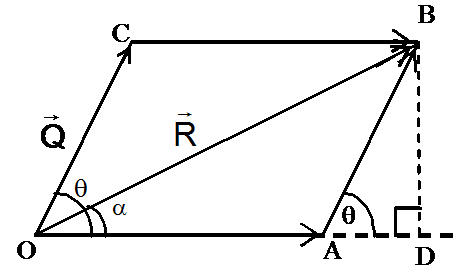
The diagonal passing through 0 represents their resultant in magnitude and direction. You can prove by: fie geometry of the figure that the magnitude R of the resultant and the angle it makes with P are given by
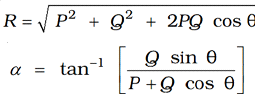
P and Q = Force whose resultant is required to find out.
Special Case:
• If θ = 0 i.e., When the force act along the same line,
R= P+Q
• If θ =90 i.e., When the force act as right angle then,
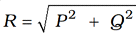
Resolution of forces:
It is desirable to resolve a force into rectangular components. His process of splitting the force into components is called the resolution of a force whereas the process of finding the resultant of any number of forces is called the composition of forces. The resolution of forces helps in determining the resultant of a number of forces acting on a body as it reduces vectorial addition to algebraic addition.
Method of Resolution for the resultant forces:
• Resolve all the forces horizontally and find the algebraic sum of all the horizontal components (i.e., ∑H).
• Resolve all the forces vertically and find the algebraic sum of all the vertical components (i.e., ∑V).
• The resultant R of the given forces will be given by the equation :
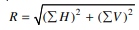
• The resultant force will be inclined at an angle θ, with the horizontal, such that
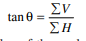
Notes: The value of the angle θ will vary depending upon the value of ∑V and ∑H
As discussed below:
1. When ∑V is +ve, the resultant makes an angle between 0° and 180°.But when ∑V is –ve, the resultant makes an angle between 180° and 360°.
2. When ∑H is +ve, the resultant makes an angle between 0° to 90° or 270° to 360°. But when ∑H is –ve, the resultant makes an angle between 90° to 270°.
Q1. A force of 80 N is acting on a bolt as shown in Figure. Find the horizontal and vertical components of the force.
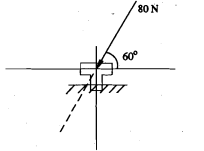
Solution: By principle of transmissibility of a force, the force can be considered acting at any
Point on the line of action of the force.
:. θ = 68" + 180" = 240"
With respect to positive x axis measured in anticlockwise direction
:. Fx=Fcos 0=80cos240°=-40N
Fy = F sin 0 = 80 sin 240" = - 69.28 N.
:. F = (-40~15 + (-69.28~);
= -407 - 69.28 5
Q2. A force of 120 N is exerted on a hook in the ceiling as shown in Figure. Determine the horizontal and vertical components of the force.
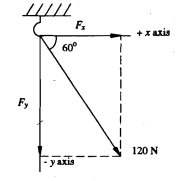
Solution: As is to be measured in anticlockwise direction from positive x axis, then θ = 300'
Fx=Fcos0=120cos 300"=+60N.
FY=Fsin8=120 sin300"=-103.92N.
The vector components of force F are
Fx= (+ 60 N )i and Fy=(-130.92N)j
Therefore F can be expressed as
F=+60i-103.92j
Resultant of coplanar concurrent forces:
The technique of resolution of a force can be used to determine the resultant of coplanar concurrent forces. If 'n' concurrent forces F! , F2 , F3 , ... , F, are acting at a point in a body then each force can be resolved into two mutually perpendicular directions. Thus, we get '2n' components. Each set of 2n components acts in one direction only. Therefore, we can algebraically add all these components to get the components of the resultant.
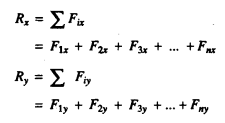
Finally, combining the components Rx and Ry, vector ally, we get the resultant R

Where, 8 is the angle of inclination of the resultant with respect to positive x axis.
Resultant of non-coplanar concurrent forces:
In case of non-coplanar force system also, the technique of resolution of forces can be used to determine the resultant. If three non-coplanar forces F1, F2 & F3 are acting at a point o in a body, the resultant R12 of the two forces F1, and F2 can be determined by law of parallelogram of forces. The force R, can next be combined with F3 by means of the parallelogram, giving the resultant of three forces F1, F2 and F3 as R. If there are more forces in the system, the same process can be continued until all the forces have been covered. Here, note that the resultant of non-coplanar force system must pass through the point of concurrence. The resultant of concurrent force system can also be determined as vector sum of the forces of the system. The vector sum of the forces can be obtained very easily if each force is resolved into rectangular component. Thus, the vector sum of non-coplanar system of concurrent forces F1, F2 &F3 is

Which can be written rectangular component form as
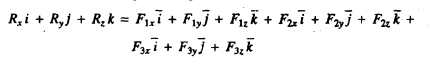
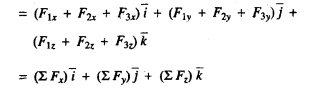
Therefore
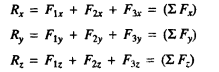
Finally, combining the component Rx, Ry and Rz vectorally, we get the resultant R
Thus
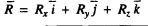
And 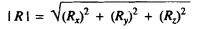

Where θx, θy & θz are the angle which the resultant R makes with x, y and z axis respectively.
Moment of force about a Point:
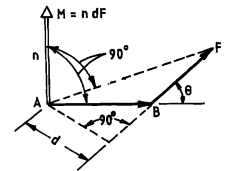
The moment of force can be determine with respect to about a point. The moment of force F with respect to point A is defined as a vector with a magnitude equal to the product of the perpendicular distance from A to F and the magnitude of the force and with a direction perpendicular to the plane containing A and F. The sense of the moment vector is given by the direction a right-hand screw would advance if turned about A in the direction indicated by F as shown in figure.
Couple:
A couple is a force system consisting of two equal, coplanar, parallel forces acting in opposite direction. Since a couple constitutes two equal and parallel forces, their resultant is zero and hence a couple has no tendency to produce translator motion but produces rotation in the body on which it acts.

Figure shows two equal and opposite forces, each equal to P and acting at A and B along parallel lines, thus constituting a couple. The perpendicular distance AB is called the arm of the couple and is denoted by p.
Varignon’s Theorem:
It state, “If a number of coplanar forces are acting simultaneously on a particle, the algebraic sum of the moments of all the forces about any point is equal to the moment of their resultant force about the same point.”
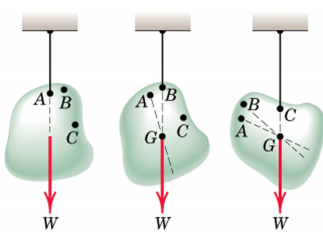
Centroid:
A body of mass M in equilibrium under the action of tension in the cord, and resultant W of the gravitational forces acting on all a particles of the body. The resultant is collinear with the cord suspended the body from different points on the body- Dotted lines show line of action will be concurrent at a single point G. As long as dimensions of the body are smaller compared with these of the earth.
We assume uniform and parallel force field due to the gravitational attraction of the earth.
The unique point G is called the Centre of Gravity of the body (CG).
First moment of area:
The first moment of an area quantified the distribution of an area about an axis. It is calculated as the summation of the product of each area and its distance from the axis. While it may seem mostly mathematical, one fantastic application of the first moment is to check if an area is “symmetry distributed” about an axis. That is, all points are evenly spread out from that axis. This symmetry has deep implication in structural analysis.
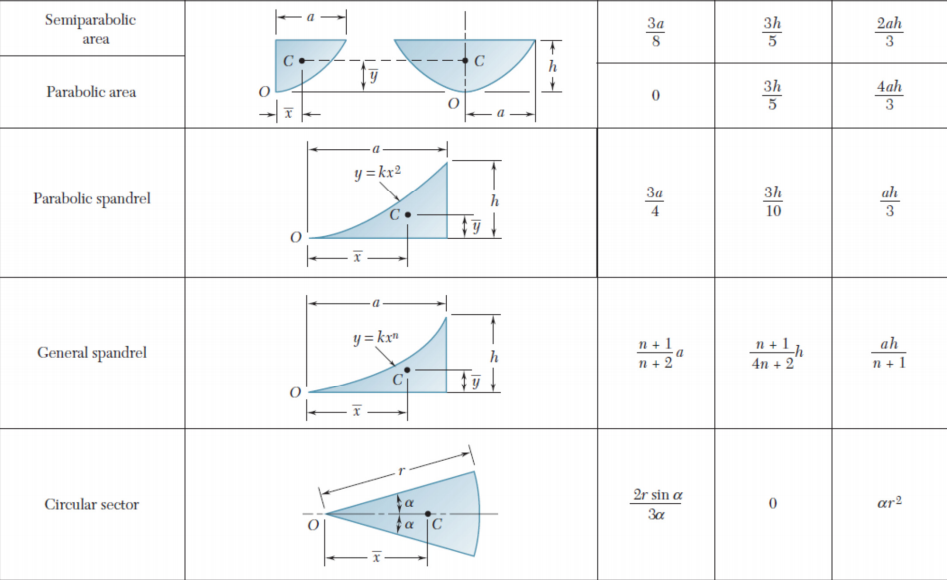
Centroid of composite plane laminas:


Reference book:
- Engineering Mechanics of PROF. M.D.DAYAL
- Engineering Mechanics of PROF.MANISH NADKARNI
- Engineering Mechanics of PROF.RAM KUMAR
- Engineering Mechanics of PROF.THUBE SIR