Unit – 3

Friction

3.1 Revision of Static friction: -

Static friction is force that keeps an object at rest. The friction experienced when individuals try to move a stationary object on surface, without actually triggering any elative motion between the body and the surface which it is on.

It is the friction experienced by the body when it is a rest. In others words it is the friction when the body tends to move.

Ex: - Papers on the tabletop.

Fig. Revision of Static Friction

3.2 Dynamic Friction: - If the value of applied force exceeds the limiting friction, the body starts moving over the other body and the friction at resistance experienced by the body while moving is known as Dynamic friction.

It is the friction experienced by a body when it is in motion. Dynamics friction is also called kinetic friction. It is always less than the static friction.

Ex: - A car moves on road.

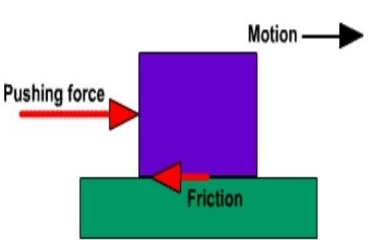
Fig. Dynamic Friction

3.3 Kinetic friction: - It’s defined as a force that acts between moving surfaces. A body moving on the surface experiences a force in the opposite direction of its movement. The magnitude of the force will depend on the coefficient of kinetic friction between the two materials.

Kinetic friction that arises in the region of slip is essentially an irreversible process. It is not surprising; therefore, that shear traction in the contact during tangential unloading differs from that during loading. 

Ex: - Rubbing both hands together to create heat.

Fig. Kinetic Friction

3.4 Coefficient of friction: - It is experimentally found that the magnitude of limiting friction bears a constant ratio to the normal reaction between the two surfaces and this ratio is called Coefficient of friction. It is denoted by µ.

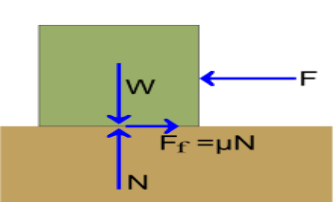
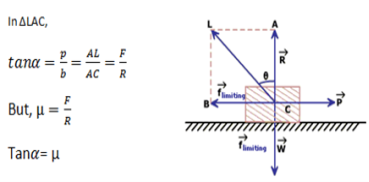
It is defined as the ratio of limiting friction to the normal friction between the surfaces of contact.

Coefficient of friction = F/N

F = limiting friction.

N = normal reaction between the contact surfaces.

Thus,                        

µ=F/N

There are two values of. When there is limiting equilibrium, the coefficient of friction is called static and is denoted by S.

When the bodies are in relative motion, the coefficient of friction is called Kinetic and is denoted by K.             

Example. A 5 kg box on a horizontal table is pushed by a horizontal force of 15 N as shown on the right.

If the coefficient of friction is 0.4, will the box move?

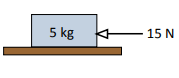
Ans.  Given, weight of the box 5 kg

Vertical force is in equilibrium R=5g

Maximum possible friction F = 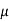R= 0.4 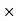5g= 19.6 N

The pushing force, 15 N, is less than this and so cannot overcome the friction. The box will          not move.

3.5 Angle of Friction: - Angle of friction is defined as the angle made between the normal reaction force and resultant force of normal reaction force and friction. If the force is small, the static friction between the surfaces would prevent the block from moving.

Let the angle of inclination (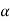) be gradually increased, till the body just starts sliding down the plane. This angle of inclined plane, at which a body just begins to slide down the plane, is called the angle of friction. This is also equal to the angle, which the normal reaction makes with the vertical.

Ex: - Box moving on a plane.

Example. A body of weight 300 N is lying on a rough horizontal plane having a coefficient of friction as 0.3. Find the magnitude of the force, which can move the body, while acting at an angle of 25° with the horizontal.

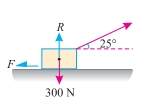
Ans. Given: Weight of the body (W) = 300 N; Coefficient of friction (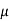) = 0.3 and angle made by the force with the horizontal ( 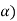= 25°

P= Magnitude of the force which can be move

F= Friction of the force

Resolving the force horizontally

F = P cos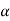 = Pcos25° = P 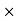0.9063

Resolving the force vertically

R = 300 N – P sin25°

= 300 – P 0.4226

We know that force of the friction (F)

F= 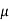R

P 0.9063 = 0.3 (300 – P 0.4226)

P = 87.1N

Example. Two blocks A and B of weights 1 KN and 2 KN respectively are in equilibrium position as shown in Fig.

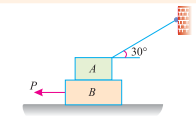
If the coefficient of friction between the two blocks as well as the block B and the floor is 0.3, find the force (P) required moving the block B.

Ans. Given: Weight of block A (WA) = 1 KN; Weight of block B (WB) = 2 KN and coefficient of friction (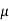) = 0.3.

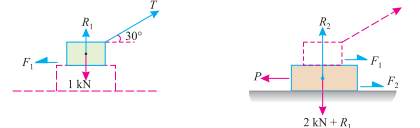
(i)                Block A    (ii) Block B

The forces acting on the two blocks A and B are shown in Fig. (A) and (B) respectively. First of all, consider the forms acting in the block A.

Resolving the force vertically

R1 + T sin 30° = 1

T sin30° = 1- R1 ………………………………            (i)

And resolving the force horizontally

Tcos30° = F1 =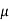R1 =0.3 R1    ...............................                      (ii)

Dividing equation (i) by (ii)

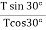=  or tan30° =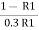

0.5774 = 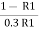 or   0.5774 0.3R1 = 1- R1

R1 = 0.85 KN

And   F1 = 0.3 0.85 = 0.255 KN

Resolving the force vertically

R2 = 2 + R1 = 2 + 0.85 = 2.85 KN

F2 = 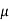R2 = 0.3 2.85 = 0.855 KN

Now resolving the force horizontally

P = F1 + F2 = 0.255+0.855 = 1.11KN

Example. What is the maximum load (W) which a force P equal to 5 KN will hold up, if the coefficient of friction at C is 0.2 in the arrangement shown in Fig. Neglect other friction and weight of the member.

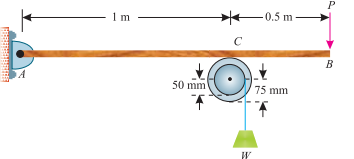
If W = 3 KN and P = 4.5 KN, what are the normal and tangential forces transmitted at C?

Ans. Given: Force (P) = 5 KN and coefficient of friction at C () = 0.2 Maximum load W

Let R = Normal reaction of the pulley on the beam at C

First of all, consider the equilibrium of the beam AB. Taking moments about the hinge A and equating the same,                           

R × 1 = 5 × 1.5 = 7.5 or R = 7.5 KN

Now consider the equilibrium of the pulley. It is subjected to a normal reaction of 7.5 KN (as calculated above). We know that maximum force of friction at C.

= . R = 0.2 × 7.5 = 1.5 KN

Now taking moments about the center of the pulley and equating the same

W × 50 = 1.5 × 75 = 112.5

W = 2.25 KN

Normal and tangential forces transmitted at C

Now consider a weight W equal to 3 KN suspended from the pulley and a force P equal to 4.5 KN applied at B.

Let R1 = Normal force or normal reaction at C, and

F1 = Tangential force at C.

Taking moments about the hinge A and equating the same,

R1 × 1 = 4.5 × 1.5 = 6.75 or R1 = 6.75 KN

3.6 Laws of friction: - Some laws of friction, which may be grouped under the following heads.

1. Laws of static friction
2. Laws of kinetic or dynamic friction

1. Laws of static friction

• The force of friction always acts in a direction opposite to that in which the body tends to move.
• Till the limiting values are reached, the magnitude of friction is exactly equal to the force which tends to move the body.
• The magnitude of the limiting friction bears a constant ratio to the normal reaction between the two surfaces.
• The force of friction depends upon the roughness/smoothness of the surfaces.
• After the body starts moving, the dynamic friction comes into play, the magnitude of which is less than that of limiting friction and its bears a constant ratio with normal force. This ratio is called coefficient of dynamic friction.
• The magnitude of the force of friction is exactly equal to the applied force.
• The magnitude of the maximum static friction (limiting friction) bears a constant ratio to the normal reaction between the two surfaces.

2.     Laws of kinetic or dynamic friction

• The force of friction always acts in a direction, opposite to that in which the body is moving.
• The magnitude of kinetic friction bears a constant ratio to the normal reaction between the two surfaces. But this ratio is slightly less than that in case of limiting friction
• For moderate speeds, the force of friction remains constant. But it decreases slightly with the increase of speed.
• The dynamic friction bears a constant ratio to the normal reaction between the two surfaces.
• The force of friction remains constant for moderate speeds. But it decreases slightly with the increases speed.

3.7 Cone of Friction:-

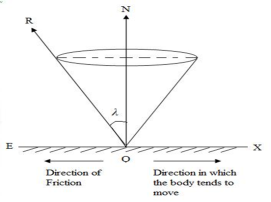
Suppose a body is at the point of sliding in the other direction, it is easily seen that the resultant reaction will make the same angle  with the normal. Hence, when limiting friction is offered the line of action of the resultant reaction should always lie on the surface of an inverted right circular cone whose semi-vertex is ().With R as axis and O as vertex if the line OA is revolved around the axis, the cone is so formed called Cone of Friction.

Equilibrium of bodies of inclined plane: - A body resting on a plane inclined at an angle  to the horizontal plane is in a state of equilibrium when the gravitational force tending to the slide the body down the inclined plane is balanced by an equal and opposite frictional force acting up the inclined plane.

• When the body is just on the point of motion down the plane

P=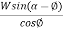

• When the body is just on the point of motion up the plane

P=

Ex: Sloping road and hills, chisels.

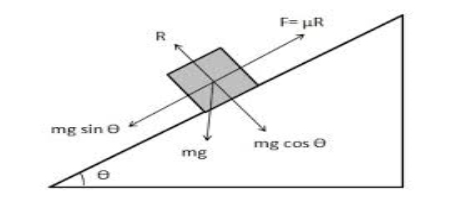
Example 1:- The force required to pull the body of weight 50 N on a rough horizontal surface 20N where is applied at an angle of 25 with the horizontal as shown. Determine the coefficient of friction and the magnitude of reaction N between the body and the horizontal surfaces. Does the reaction pass through the center of gravity of the body?

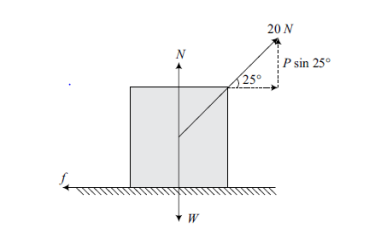
Ans: -          The body is in equilibrium

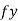 = 0

N = W – P Sin 25

= 50 – 20  0.42

= 41.55 N

 = 0

 = 20 Cos 25 = 18.13 N

Now                                               µ =  / N = 18.13 / 41.55 =0.436                             Ans.

The reaction passes through the center of gravity of the body as it is equal and opposite to weight of body W.

Example 2:- A block of weight 5 KN is pulled by a force P as shown. The coefficient of friction between the contact surfaces of 0.35. Find the direction  for which P is minimum and find the corresponding value of P.

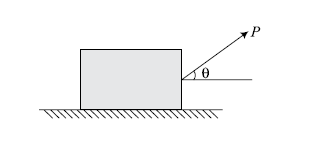
Ans: - (1) Draw the free body diagram of the block.

(2)  Apply equilibrium conditions.

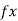 = 0

 = P Cos 



W = N + P Sin 

(3) The angle of inclination of force P will be equal to the angle of friction for minimum value of P.

 =  = =  

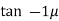= 20.48

                                                 P = W Sin 

Cos ( -) 

For P to be minimum, cos ( - ) = 1

P = W Sin  = 5 Sin 20.48 = 1.75 KN                                 Ans.                                                   

3.8 Application of problems involving wedges and ladders:-

WEDGE FRICTION: - A wedge is, usually, of a triangular or trapezoidal in cross-section. It is, generally, used for slight adjustments in the position of a body i.e. for tightening fits or keys for shafts. Sometimes, a wedge is also used for lifting heavy weights as shown in Fig.

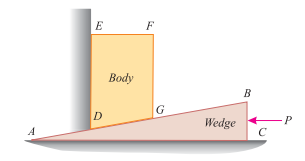
Thus these problems may be solved either by the equilibrium method or by applying Lami’s theorem. Now consider a wedge ABC, which is used to lift the body DEFG.

The forces acting on the load are:

• Weight of the load, W
• Resultant act on the body in term of R.

Let W = Weight of the body DEFG,

P = Force required to lift the body, and

= Coefficient of friction on

The planes AB, AC and DE such that

Tan =

A little consideration will show that when the force is sufficient to lift the body, the sliding will take place along three planes AB, AC and DE will also occur as shown in Fig. (a) and (b)

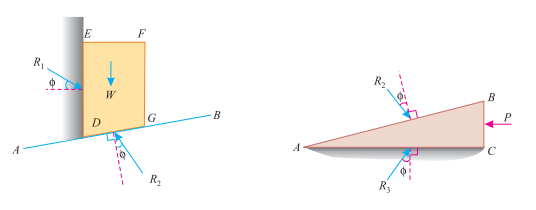
The three reactions and the horizontal force (P) may now be found out analytical method as discussed below:

1. First of all, consider the equilibrium of the body DEFG. And resolve the forces W, R1 and R2 horizontally as well as vertically.
2. Now consider the equilibrium of the wedge ABC. And resolve the forces P, R2 and R3 horizontally as well as vertically.

Example 1:- A uniform ladder of weight of 300 N rests against a smooth vertical wall a rough horizontal floor making at angle 60 with the horizontal. Determine the force of friction at floor.

Ans: - Draw free body diagram of ladder AB..

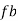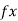As the wall is smooth, = 0

 = 0

FA = RA

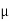RA = RB

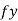 = 0

RA = W = 300N

FA = 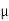RA = 300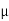

Assume µ = 0.3 between ladder and floor

FA = 90 N                                              Ans.

Example 2:- A uniform ladder of weight 800 N and length 7 m rests on a horizontal ground and leans against a smooth vertical wall. It make the angle by ladder with horizontal is 60. When a man of weight 60N on the ladder is 4m from the top, the ladder is at the point of slipping. Determine the coefficient of friction between the ladder and the floor.

Ans: - Draw the free body diagram of the ladder.

(1)                              = 0

FA = RB

(2)                             = 0       ˚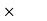

RA = 800 + 600 = 1400 N

FA = RB = 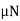= 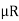A

= 1400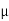

∑MB = 0

RA7cos 60˚ = FA7 sin60˚ + 8003.5 cos 60˚ + 600 3cos 60˚

14007cos 60˚ = 1400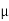 7 sin60˚ + (8003.5 +600 3) cos 60˚

0.3

Example 3. A uniform ladder 3 m long weighs 200 N. It is placed against a wall making an angle of 60° with the floor as shown in Fig.

The coefficient of friction between the wall and the ladder is 0.25 and that between the floor and ladder is 0.35. The ladder, in addition to its own weight, has to support a man of 1000 N at its top at B. Find out:

• The horizontal force P to be applied to ladder at the floor level to prevent slipping.
• If the force P is not applied, what should be the minimum inclination of the ladder with the horizontal, so that there is no slipping of it with the man at its top?

Ans. Given: Length of the ladder (l) = 3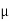 ; Weight of the ladder (W) = 200 N; Coefficient of friction between the wall and the ladder (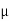w) = 0.25 and coefficient of friction between the floor and ladder (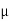f) = 0.35.

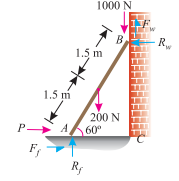
(A)                           (B)

Horizontal force (P) applied to the ladder at floor level to prevent slipping                

Resolving the forces horizontally,

P + Ff = Rw           …………… (i)

And now resolving the forces vertically

Rf + Fw = 1000 + 200 = 1200N      …………… (ii)

(200 × 1.5 cos 60°) + 1000 × 3 cos 60°)

= (Fw× 3 cos 60°) + (Rw × 3 sin 60°)

Dividing both side by cos 60°,

300 + 3000 = (3 × Fw) + (3 × Rw tan 60°)

1100 = Fw + Rw tan 60°       …………. (iii)

FW = 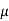W × RW = 0.25 RW  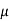                 (W =0.25)

Substituting this value of Fw in equation (iii)        

1100 = (0.25 Rw) + (Rw tan 60°) = Rw (0.25 + 1.732) = Rw × 1.982 

Rw = 555 KN

Fw= 0.25 Rw = 0.25 × 555 = 138.7 N  

Now substituting the value of Fw in equation (ii), 

Rf + 138.7 = 1200 

Rf = 1200 – 138.7 = 1061.3 N

Ff = 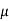f Rf = 0.35 × 1061.3 = 371.5 N

Now substituting the value of Ff in equation (i),

P + 371.5 = 555

P = 555 – 371.5 = 183.5 N

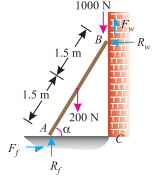
Inclination of the ladder with the horizontal for no slipping

Now consider the ladder inclined at angle (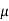) and without any horizontal force acting at the floor as shown in Fig. (B).

Resolving the forces horizontally

Rw = Ff = 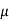f × Rf = 0.35 × Rf     ......... (iv)

And now resolving the forces vertically,

Rf + Fw = 1000 + 200 = 1200 N

Fw =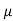w × Rw = 0.25(0.35 Rf) = 0.09 Rf

Rf + 0.09 Rf = 1200

Rf = 1101 N

And  Rw= 0.35Rf = 0.35 × 1101 = 385.4 N

Similarly  Ff = 0.09 Rf = 0.09 × 1101 = 99.1 N

Taking moments about A and equating the same,

(1000 × 3 cos) + (200 × 1.5 cos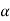) = (Fw × 3 cos 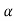+ (Rw × 3 sin)

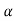Dividing both sides by 3 cos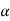

1000 + 100 = Fw + Rw tan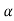

1100 = 99.1 + 385.4 tan

385. Tan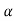 = 1100 – 99.1 = 1000.9         

Tan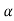= 2.5970 or 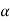= 68.9° Ans.

Example 4. A block weighing 1500 N, overlying a 10° wedge on a horizontal floor and leaning against a vertical wall, is to be raised by applying a horizontal force to the wedge. Coefficient of friction between the entire surface in contact to be 0.3, determine the minimum horizontal force required to raise the block.

Ans. Given: Weight of the block (W) = 1500 N; Angle of the wedge (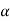) = 10° and coefficient of friction between all the four surfaces of contact (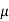) = 0.3 = tan or = 16.7°.

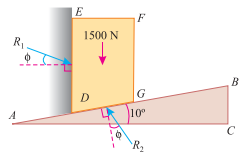
We know that it is in equilibrium under the action of the following forces as shown in Fig. (a).

• Its own weight 1500 N acting downwards.
• Reaction R1
• Reaction R2.

Resolving the forces horizontally,

R1 cos (16.7°) = R2 sin (10 + 16.7°) = R2 sin 26.7°

R1 × 0.9578 = R2 × 0.4493

R2 = 2.132 R1

And now resolving the forces vertically

R1 × sin (16.7°) + 1500 = R2 cos (10° + 16.7°) = R2 cos 26.7°

R1 × 0.2874 + 1500 = R2 × 0.8934 = (2.132 R1)0.8934

= 1.905 R1

R1 (1.905 – 0.2874) = 1500

R1= 927.3 N

We know that it is in equilibrium under the action of the following forces as shown in Fig. (b).

• Reaction R2 of the block on the wedge
• Force (P) acting horizontally, and
• Reaction R3 on the face AC of the wedge.

Resolving the forces vertically,

R3 cos 16.7° = R2 cos (10° + 16.7°) = R2 cos 26.7°

R3 × 0.9578 = R2 × 0.8934 = 1977 × 0.8934 = 1766.2

R3 = 1844 N

And now resolving the forces horizontally,

P = R2 sin (10° + 16.7°) + R3 sin 16.7° = 1977 sin 26.7° + 1844 sin 16.7° N

= (1977 × 0.4493) + (1844 × 0.2874) = 1418.3 N Ans.

Video link:- https://youtu.be/dsW4FSIXuTE

Reference books:

• I. H. Shames, Engineering Mechanics.
• J. L. Meriam and L. G.
• R. C. Hibbler, Engineering Mechanics