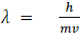Unit-1

QUANTUM PHYSICS

1.1             De Broglie hypothesis of matter waves:

According to de Broglie’s hypothesis, massless photons as well as massive particles must satisfy one common set of relations that connect the energy E with the frequency f, and the linear momentum p with the wavelength ʎ We have discussed these relations for photons in the context of Compton’s effect. We are recalling them now in a more general context. Any particle that has energy and momentum is a de Broglie wave of frequency f and wavelengthʎ:

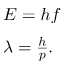
Here, E and p are, respectively, the relativistic energy and the momentum of a particle. De Broglie’s relations are usually expressed in terms of the wave vector:

And the wave frequency 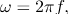 as we usually do for waves:

Wave theory tells us that a wave carries its energy with the group velocity. For matter waves, this group velocity is the velocity u of the particle. Identifying the energy E and momentum p of a particle with its relativistic energy mc2 and its relativistic momentum mu, respectively, it follows from de Broglie relations that matter waves satisfy the following relation:

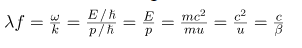
Where β=u/c When a particle is massless, we have u=c and becomes ʎf=c 

If an electron in the nth Bohr orbit moves as a wave, its wavelength must be equal to  Assuming that is valid, the electron wave of this wavelength corresponds to the electron’s linear momentum  In a circular orbit, therefore, the electron’s angular momentum must be:

This equation is the first of Bohr’s quantization conditions, providing a physical explanation for Bohr’s quantization condition is a convincing theoretical argument for the existence of matter waves.

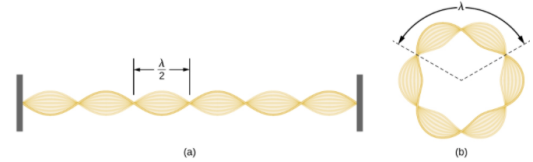
Standing-wave pattern: (a) a stretched string clamped at the walls; (b) an electron wave trapped in the third Bohr orbit in the hydrogen atom.

• De Broglie’s hypothesis of matter waves postulates that any particle of matter that has linear momentum is also a wave. The wavelength of a matter wave associated with a particle is inversely proportional to the magnitude of the particle’s linear momentum. The speed of the matter wave is the speed of the particle.
• De Broglie’s concept of the electron matter wave provides a rationale for the quantization of the electron’s angular momentum in Bohr’s model of the hydrogen atom.
• In the Davisson–Germer experiment, electrons are scattered off a crystalline nickel surface. Diffraction patterns of electron matter waves are observed. They are the evidence for the existence of matter waves. Matter waves are observed in diffraction experiments with various particles.

Expression for de- Broglie wavelength 

The expression of the wavelength associated with a material particle can be derived on the analogy of radiation as follows:

Considering the plank’s theory of radiation, the energy of photon (quantum) is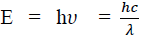

Where c is the velocity of light in vacuum and is its wave length.

According to Einstein energy – mass relation

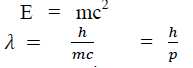
Where mc = p is momentum associated with photon.

If we consider the case of material particle of mass m and moving with a velocity v ,i.e momentum mv, then the wave length associated with this particle ( in analogy to wave length associated with photon ) is given by

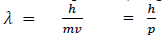
Different expressions for de-Broglie wavelength

(a) If E is the kinetic energy of the material particle then

There for de Broglie wavelength is—

(b) When a charged particle carrying a charge ‘q’ is accelerated by potential difference v, then its kinetic energy K.E is given by

E = qV

Hence the de-Broglie wavelength associated with this particle is

For an electron

1.2. Properties of matter waves:

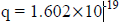
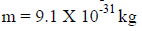
(a) Lighter is the particle, greater is the wavelength associated with it.

(b) Smaller is the velocity of the particle, greater is the wavelength associated with it.

(c) When v = 0, then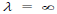 i.e. wave becomes indeterminate and if v =∞, then

. This shows that matter waves are generated only when material particles are in motion.

(d) Matter waves are produced whether the particles are charged particles or not

i.e., matter waves are not electromagnetic waves but they are a new kind of waves.

(e) It can be shown that the matter waves can travel faster than light i.e. the velocity of matter waves can be greater than the velocity of light.

(f) No single phenomenon exhibits both particle nature and wave nature simultaneously.

Distinction between matter waves and electromagnetic waves

S.no.	Matter wave	Electromagnetic wave
1   2   3   4   5	Matter waves are associated with moving particles (charged or uncharged)   Wavelength depends on the mass of the particle and its velocity   Matter waves can travel with a velocity greater than the velocity of light.   Matter wave is not electromagnetic wave.       Matter wave require medium for propagation i.e., they cannot travel through vacuum.	Electromagnetic waves are produced only by accelerated charged particles   Wavelength depends on the energy of photon   Travel with velocity of light c= 3×108 m/s   Electric field and magnetic field oscillateperpendicular to each other.   Electromagnetic waves do not require medium

1.3. Wave Packet:

We know that by Heisen­berg’s prin­ci­ple, in or­der to get some lo­cal­iza­tion of the po­si­tion of a par­ti­cle, some un­cer­tainty must be al­lowed in mo­men­tum. That means that you must take the ini­tial mo­men­tum space wave func­tion 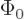 to be nonzero over at least some small in­ter­val of dif­fer­ent mo­men­tum val­ues . Such a com­bi­na­tion of com­po­nent waves is called a wavepacket.

The wave func­tion for a typ­i­cal wave packet is sketched below. The red line is again the real part of the wave func­tion, and the black lines are the en­ve­lope en­clos­ing the wave; they equal plus and mi­nus the mag­ni­tude of the wave func­tion.

The real part (red) and mag­ni­tude or en­ve­lope (black) of a wave packet. (Schematic).

If the en­ve­lope changes lo­ca­tion with time, and it does, then so does the re­gion where the par­ti­cle can be found. This then fi­nally is the cor­rect pic­ture of mo­tion in quan­tum me­chan­ics: the re­gion in which the par­ti­cle can be found prop­a­gates through space.

The clas­si­cal de­scrip­tion also re­quires that the par­ti­cle moves with ve­loc­ity

u=p/m

Which is twice the speed p/2m of the wave. So, the en­ve­lope should move twice as fast as the wave. Like as in fig. Below

That the en­ve­lope does in­deed move at speed p/m can be seen if you de­fine the rep­re­sen­ta­tive po­si­tion of the en­ve­lope to be the ex­pec­ta­tion value of po­si­tion. That po­si­tion must be some­where in the mid­dle of the wave packet.

1.4. Phase velocity and group velocity:

To understand the difference between phase and group velocity of waves, consider the following analogy.

A group of people, say city marathon runners, start from the starting at the same time. Initially it would appear that all of them are running at the same speed. As time passes, group spreads out (disperses) simply because each runner in the group is running with different speed.

If you think of phase velocity to be like the speed of an individual runner, then the group velocity is the speed of the entire group as a whole. Obviously and most often, individual runners can run faster than the group as a whole.

To stretch this analogy, we note that the phase velocity vp of waves are typically larger than the group velocity vg of waves. However, this really depends on the properties of the medium. The media in which vg = vp is called the non-dispersive medium. But the media in which vg<vp is called normal dispersion. The media in which vg>vp is called anomalous dispersive media. It must be emphasized that dispersion is a property of the medium in which a wave travel. It is not the property of the waves themselves. The relation between phase and group velocity is given by

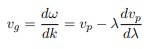
Generally, ω(k) is called the dispersion relation and indicates the dispersion properties of a medium.

As this formula predicts, if the phase velocity does not depend on the wavelength of the propagating wave, then vg = vp.

For example, sound waves are non-dispersive in air, i.e., all the individual components that make up the sound wave travel at same speed. Phase velocity of sound waves is independent of the wavelength when it propagates in air.

Monochromatic wave with angular frequency

ω = 2πν (ν is the frequency) travelling in +ve x-direction is given by

y = A sin(ωt − kx).

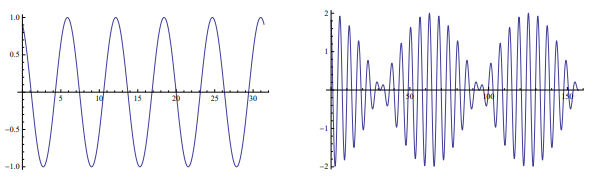
On the other hand, group velocity refers to a group composed of waves within a frequency band ∆ω.

Group velocity is the velocity with which the entire group of waves would travel.

In above fig--

y = sin (2 +t)

y = sin (2 +t) + sin(2 + 1.1t).

The last form is the sum of two waves whose frequencies differ by 0.1.

Notice that the amplitude of the group is modulated as a function of t. The example here shows the waves as a function of t, but similar scenario holds good for waves as a function of x. For the travelling wave shown in the left panel of the figure, phase velocity is the velocity with which any one of the peaks progresses. However, for the right panel of the figure, the speed of any of the peaks would give the group velocity.

Relation between group velocity and phase velocity:

For a wave group formed by the superposition of number of waves, the group velocity and phase velocity are given by

For any propagating wave packet –

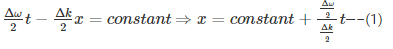
Velocity is the rate of change of displacement given by--

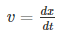
Hence, group velocity is got by differentiating equation (1) with respect to time…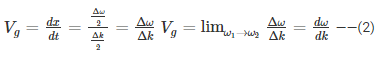

We know that phase velocity is given by

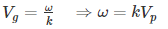
Substituting?? = kVp in equation (2) we get-

Thus, we arrive at the equation relating group velocity and phase velocity –

1.5. Wave function:

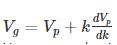
The quantity that characterizes the de–Broglie wave or matter wave is called the wave function. It is usually denoted asΨ = (x, y,z, t). This gives complete information about the state of a physical system at a particular time.

It is also called the state function and represents the probability amplitude. If ‘Ψ’ is large, the probability of finding the particle is also large and if ‘Ψ’ is small then the probability of finding the particle is small. The wave function gives the likelihood of finding the particle at a given instant and at a given position inside the wave packet.

Properties of wave functions:

There are certain properties that an acceptable wave function ‘Ψ ‘must satisfy:

1. In order to avoid infinite probabilities, Ψ must be finite for all values of x, y, z.

2.     In order to avoid multiple values of the probability, Ψ must be single valued. i.e., for each set of x, y and z, Ψ must have a unique value.

3.     For finite potentials, Ψ and 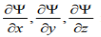must be continuous in all regions.

4.     In order to normalize the wave function, Ψ must approach to zero as ‘x’ approaches to ± infinity.

1.6. Physical interpretation of wave function

In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus, Ψ2 is a measure of particle density.

According to Max Born ΨΨ* = |Ψ|2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume dv (= dxdydz) is given by |Ψ|2 dv or |Ψ |2 dx.dy.dz.

Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space.

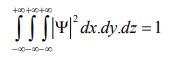or

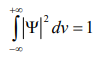
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.

1.7. Heisenberg uncertainty principle

Statement: It is impossible to determine simultaneously both the position and momentum of a quantum mechanical particle moving inside the wave packet with equal accuracy. In any simultaneous determination of the position and momentum of a particle, the product of the corresponding uncertainties inherently present in the measurement is equal to, greater than (h/4π).

Explanation: Consider a quantum particle moving inside a wave packet of width Δx. Then inside the wave packet it is not possible to find the exact position of the particle and any attempt to measure it will have an uncertainty (error) which less than or equal to Δx.

The maximum uncertainty involved in measuring the position of the particle within the wave packet is Δx. Since position cannot be measured accurately, there will be an uncertainty in measuring momentum also. According to Heisenberg’s uncertainty principle, the product of uncertainty involved in the measurement of these two quantities is given by the relation,

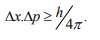
Where ∆x = uncertainty in position.

∆p = uncertainty in momentum.

It can be applied to any conjugate physical quantities such as energy and time, angular position and angular momentum etc.

Other forms of Uncertainties are:

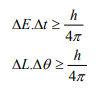
Where, ΔE, Δt are the uncertainties in the measurement of energy and time, and ΔL, Δθ are the uncertainties in the measurement of angular momentum and angular position.

1.8. Non-existence of electron in nucleus:

The Heisenberg uncertainty principle based on quantum physics explains a number of facts which could not be explained by classical physics.

Non-existence of electrons in the nucleus:

But to prove it, let us assume that electrons exist in the nucleus. As the radius of the nucleus in approximately 10-14 m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by:

∆x= 10-14 m

According to uncertainty principle,

∆x∆px =h/2∏

Thus                            ∆px=h/2∏∆x

Or                               ∆px =6.62 x10-34/2 x 3.14 x 10-14

∆px=1.05 x 10-20 kg m/ sec

If this is p the uncertainty in the momentum of electron ,then the momentum of electron should be at least of this order, that is p=1.05*10-20 kg m/sec.

An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formula

E=  √ m20 c4 + p2c2

E =  √(9.1*10-31)2 (3*108)4 + (1.05*10-20)2(3*108)2

= √(6707.61*10-30) +(9.92*10-24)

=(0.006707*10-24) +(9.92*10-24)

= √9.9267*10-24

E= 3.15*10-12 J

Or                                  E=3.15*10-12/1.6*10-19 eV

E= 19.6* 106 eV

Or                                  E= 19.6 MeV

Therefore, if the electron exists in the nucleus, it should have an energy of the order of 19.6 MeV. However, it is observed that beta-particles (electrons) ejected from the nucleus during b –decay have energies of approximately 3 Me V, which is quite different from the calculated value of 19.6 MeV. Second reason that electron cannot exist inside the nucleus is that experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.

Therefore, it is confirmed that electrons do not exist inside the nucleus.

1.9. Schrodinger ‘s time dependent wave equation:

It was observed that the wave function of a particle of fixed energy E could most naturally be written as a linear combination of wave functions of the form:

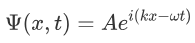
Now the hemiltonian of this system:

H=T+V

Where V is the potential energy and T is the kinetic energy. As we already know that ‘H’ is the total energy, we can rewrite the equation as:

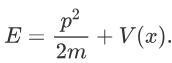
Now taking the derivatives:

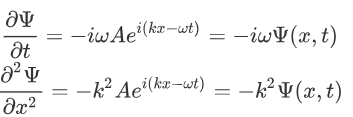
We know that:

Where ‘λ’ is the wavelength and ‘k’ is the wavenumber.

We have:

Therefore:

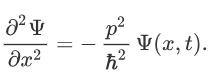
Now multiplying Ψ (x, t) to the Hamiltonian we get:

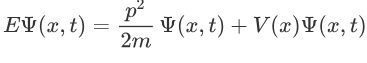
The above expression can be written as:

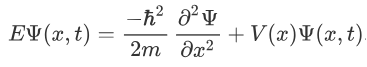
We already know that the energy wave of a matter wave is written as:

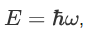
So, we can say that

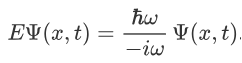
Now combining the right parts, we can get the Schrodinger Wave Equation.

1.10. Schrodinger ‘s time independent wave equation:

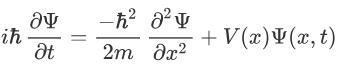
According to de-Broglie theory, for a particle of mass ‘m’, moving with a velocity ‘v’, the wavelength associated with it is

λ=h/p

The wave equation for a de-Broglie wave can be written in complex notation as:

…………1

Where, A is the amplitude, ω is angular frequency and k is the wave vector.

Differentiate equation (1) with respect to‘t’ twice, we get

We have differential equation for the traveling wave as,

……….3

Where, y is displacement and ‘v’ is velocity of wave.

By analogy, we can write the wave equation for de-Broglie wave associated with the motion of a free particle as,

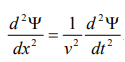………4

This represents the de-Broglie wave propagating along x-direction with a velocity ‘v’ and ‘Ψ’ is the displacement.

From equation (2) and (4),

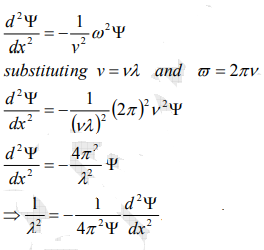…………..5

The kinetic energy of a moving particle of mass ‘m’ and velocity ‘v’ is given by

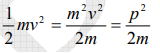
But we have from equation (1), p = (h/λ)

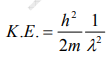
Substitute for (1/ λ)2 from equation (5),

…………….6

Let there be a field where the particle is present. Depending on its position in the field, the particle will possess certain potential energy. Then we can write:

Total energy = Kinetic energy + Potential energy

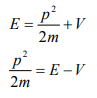
From equation (6), we can write

This is the time independent Schrödinger’s wave equation in one-dimension.

1.11. Particle trapped in one dimensional infinite potential well:

We will now look at the solutions of a particle of mass m confined to move along the x-axis between 0 to L. This is achieved by making the potential 0 between x = 0 and x = L and V = ∞ for x < 0 and x > L. In quantum mechanics this model is referred to as particle in a box (PIB) of length L.

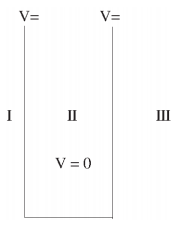
The one-dimensional infinite potential well of length L. It is divided into three regions, with regions I and III having V = ∞ and region II having V = 0

Before we set up and solve the Schrodinger equation let us apply de Broglie’s approach to this problem. De Broglie associates a wave with every material particle traveling with momentum p. The wavelength of the wave is

The classical analog of a particle in a box is a string that is fixed at both ends. When such a string is plucked, we know that the amplitude of the oscillations at the fixed ends is zero. In other words, an integer number of half-wavelengths must fit in the length of the box. Applying this idea to the present case, we find that

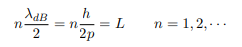
Solving for p we get

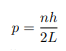
The particle feels no potential energy so all its energy is in the form of kinetic energy. As a result

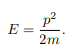
Substituting for p, we get

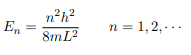
The Schrodinger equation is-

Hψˆ (x) = Eψ(x)

Where V (x) = ∞ in regions I and III and V (x) = 0 in region II. The results are in no way affected if in region II the potential is V because it only has the effect of altering the zero of energy and so without of generality, we will assume that V = 0 within the box. In regions I and III the wave function is identically zero since the potential is infinite so we will only have to consider the solution within the box. We are looking for the solutions to the equation.

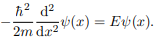
We rewrite this differential equation in the form:

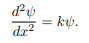
Wave equation

ψ(x) = A cos(kx) + B sin(kx)

The boundary conditions that the wave function should satisfy are

ψ (0) = 0 and ψ(L) = 0. The

First of these conditions implies that A = 0.

The second condition yields

B sin(kL) = 0

Which implies that kL = nπ, n = 1, 2, 3, ···

Or in other words k = nπ/L. Because E is related to k we hence obtain that

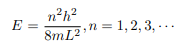
You will notice that the application of the boundary conditions naturally leads to quantization. In addition, observe that we do not consider n = 0 as a possibility because that would imply that the wave function is identically zero for all x or in other words there is no particle! The constant B is yet to be determined. The normalization condition on the wave function yields B.

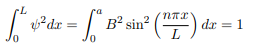
In cases where the wave function is not an eigen function of the operator corresponding to the observable, we will be concerned with the statistical mean of the measured values, averaged over a large number of measurements, the expectation value. The expectation value is defined of an operator is defined a: 

The average momentum is the

1.12         Quantum Computing:

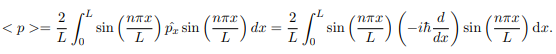
Quantum computing is essentially harnessing and exploiting the amazing laws of quantum mechanics to process information. A traditional computer uses long strings of “bits,” which encode either a zero or a one.

A quantum computer, on the other hand, uses quantum bits, or qubits. What's the difference? Well a qubit is a quantum system that encodes the zero and the one into two distinguishable quantum states. But because qubits behave quantumly

Quantum computer can process a vast number of calculations simultaneously. Think of it this way: whereas a classical computer works with ones and zeros, a quantum computer will have the advantage of using ones, zeros and “superpositions” of ones and zeros. Certain difficult tasks that have long been thought impossible (or “intractable”) for classical computers will be achieved quickly and efficiently by a quantum computer.

When you enter the world of atomic and subatomic particles, things begin to behave in unexpected ways. In fact, these particles can exist in more than one state at a time. It’s this ability that quantum computers take advantage of.