Unit-2
CRYSTALLOGRAPHY
It is necessary to have some method of identifying and visualising the most useful planes. Crystallographers use an identification system referred to as Miller, or hkl, indices (a sort of zip-code for the planes).
Miller indices are simply a set of three numbers, hkl, which can take on any combination of three integer values between +∞ and −∞, e.g. (111), (-501) and (7-2-2). Each combination of hkl describes a unique set of planes filling the crystal and so hkl is often presented as a subscript to a property: e.g. dhkl which therefore means the d spacing between the planes defined by hkl. The Miller indices, hkl, also provide a useful means for visualising the planes. The convention is that if you have three axis, x,y,z, with three unit spacings, a,b,c, on each then one of these hkl planes can be visualised as the plane which intersects the x,y,z-axes at distances of a/h, b/k, c/l respectively
The next such plane parallel to this would pass through the origin. The illustration below shows an example of such a set of planes for the case of hkl = (222)
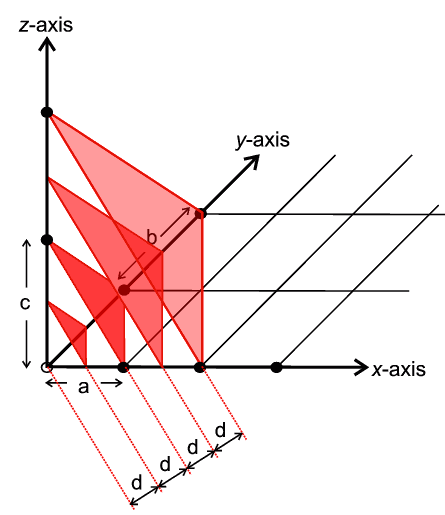
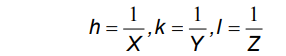
The inter-planar spacing (dhkl) between crystallographic planes belonging to the same family (h,k,l) is denoted (dhkl) Distances between planes defined by the same set of Miller indices are unique for each material dhkl Inter-planar spacings can be measured by x-ray diffraction (Bragg’s Law) The lattice parameters a, b, c of a unit cell can then be calculated The relationship between d and the lattice parameters can be determined geometrically and depends on the crystal system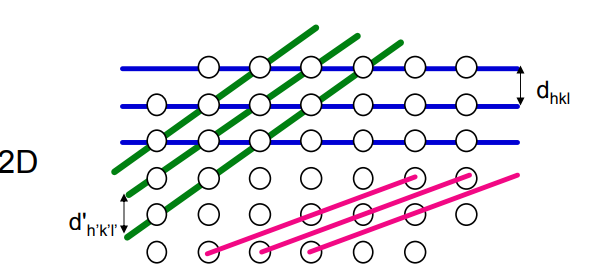
Bragg’s Law can be derived using simple geometry by considering the distances travelled by two parallel X-rays reflecting from adjacent planes. The X-ray hitting the lower plane must travel the extra distance AB and BC. To remain in phase with the first X-ray, this distance must be a multiple of the wavelength thus:
nλ = AB+BC = 2AB(since the two triangles are identical)
The distance AB can be expressed in terms of the interplanar spacing (d) and incident angle (θ) because d is the hypotenuse of right triangle ZAB shown at right.
Sin(θ) = AB/d
Thus AB = d sin(θ)
Therefore:
nλ = 2 d sin(θ)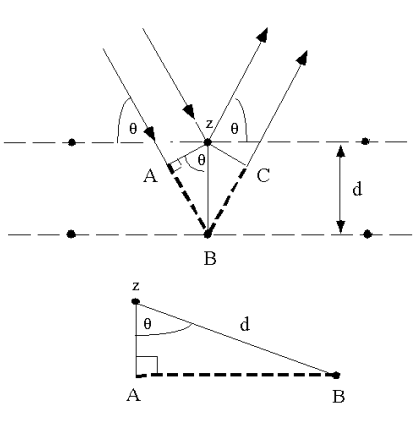
Reflection (signal) only occurs when conditions for constructive interference between the beams are met
These conditions are met when the difference in path length equals an integral number of wavelengths, n. The final equation is the
BRAGG’S LAW n λ = 2 d sin θ
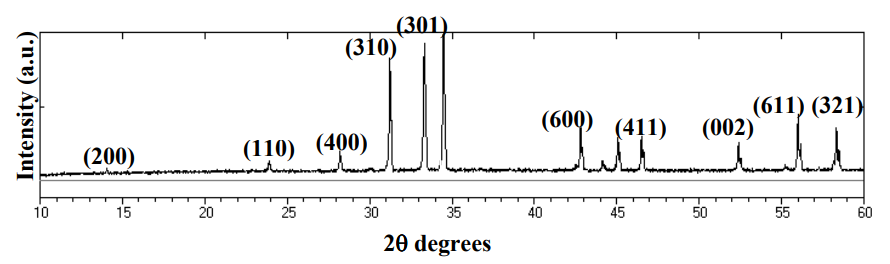
Bragg’s law relates the diffraction angle, 2θ, to dhkl
– In most diffractometers, the X-ray wavelength λ is fixed.
– Consequently, a family of planes produces a diffraction peak only at a specific angle 2θ.
• dhkl is a geometric function of the size and shape of the unit cell
– dhkl is the vector drawn from the origin to the plane (hkl) at a 90° angle.
– dhkl, the vector magnitude, is the distance between parallel planes of atoms in the family (hkl)
– Therefore, we often consider that the position of the diffraction peaks are determined by the distance between parallel planes of atoms
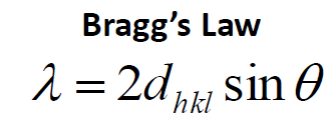

The diffraction peak intensity is determined by the arrangement of atoms in the entire crystal
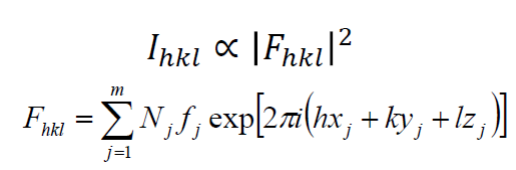
• The structure factor Fhkl sums the result of scattering from all of the atoms in the unit cell to form a diffraction peak from the (hkl) planes of atoms.
• The amplitude of scattered light is determined by:
– where the atoms are on the atomic planes
• this is expressed by the fractional coordinates xj yj zj – what atoms are on the atomic planes
• the scattering factor f j quantifies the efficiency of X-ray scattering at any angle by the group of electrons in each atom
– The scattering factor is equal to the number of electrons around the atom at 0° θ, the drops off as θ increases
• Nj is the fraction of every equivalent position that is occupied by atom j
Bragg’s law provides a simplistic model to understand what conditions are required for diffraction.
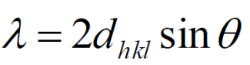
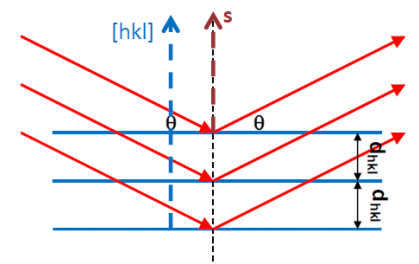
• For parallel planes of atoms, with a space dhkl between the planes, constructive interference only occurs when Bragg’s law is satisfied.
– In our diffractometers, the X-ray wavelength λ is fixed.
– A family of planes produces a diffraction peak only at a specific angle 2θ.
• Additionally, the plane normal [hkl] must be parallel to the diffraction vector s
– Plane normal [hkl]: the direction perpendicular to a plane of atoms
– Diffraction vector s: the vector that bisects the angle between the incident and diffracted beam
Many powder diffractometers use the Bragg-Brentano Para focusing geometry


A single crystal specimen in a Bragg-Brentano diffractometer would produce only one family of peaks in the diffraction pattern.
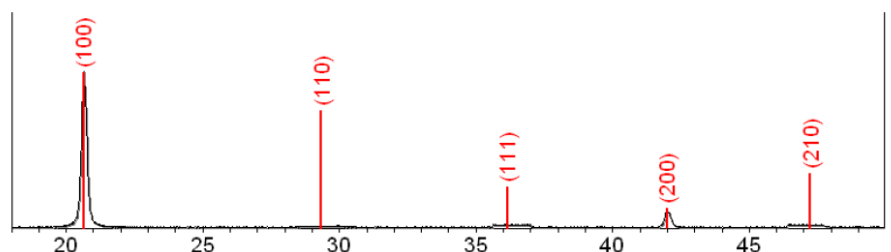
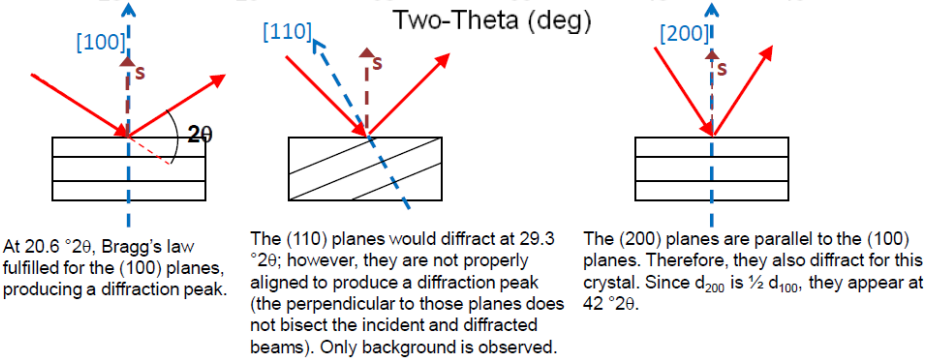
•For every set of planes, there will be a small percentage of crystallites that are properly oriented to diffract (the plane perpendicular bisects the incident and diffracted beams).
•Basic assumptions of powder diffraction are that for every set of planes there is an equal number of crystallites that will diffract and that there is a statistically relevant number of crystallites, not just one or two.