Unit 5
SUPERCONDUCTORS AND SUPERCAPACITORS
A superconductor is a material that can conduct electricity or transport electrons from one atom to another with no resistance. This means no heat, sound or any other form of energy would be released from the material when it has reached "critical temperature" (Tc), or the temperature at which the material becomes superconductive. Unfortunately, most materials must be in an extremely low energy state (very cold) in order to become superconductive.
Research is underway to develop compounds that become superconductive at higher temperatures. Currently, an excessive amount of energy must be used in the cooling process making superconductors inefficient and uneconomical.
Superconductors come in two different flavours: type I and type II.
5.1.1 Critical temperature
The CRITICAL TEMPERATURE is the temperature at which the normal state of a conductor changes to superconducting state. Critical temperature is different for different superconductors.
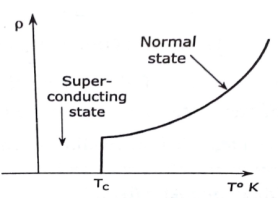
5.1.2 Critical magnetic field:
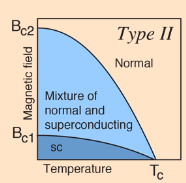
The superconducting state cannot exist in the presence of a magnetic field greater than a critical value, even at absolute zero. This critical magnetic field is strongly correlated with the critical temperature for the superconductor, which is in turn correlated with the bandgap. Type II superconductors show two critical magnetic field values, one at the onset of a mixed superconducting and normal state and one where superconductivity ceases.
It is the nature of superconductors to exclude magnetic fields (Meissner effect) so long as the applied field does not exceed their critical magnetic field. This critical magnetic field is tabulated for 0K and decreases from that magnitude with increasing temperature, reaching zero at the critical temperature for superconductivity. The critical magnetic field at any temperature below the critical temperature is given by the relationship
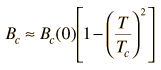
5.1.3 Meissner ‘s effect:
When a material makes the transition from the normal to superconducting state, it actively excludes magnetic fields from its interior; this is called the Meissner effect.
This constraint to zero magnetic field inside a superconductor is distinct from the perfect diamagnetism which would arise from its zero electrical resistance. Zero resistance would imply that if you tried to magnetize a superconductor, current loops would be generated to exactly cancel the imposed field (Lenz's law). But if the material already had a steady magnetic field through it when it was cooled trough the superconducting transition, the magnetic field would be expected to remain. If there were no change in the applied magnetic field, there would be no generated voltage (Faraday's law) to drive currents, even in a perfect conductor. Hence the active exclusion of magnetic field must be considered to be an effect distinct from just zero resistance. A mixed state Meissner effect occurs with Type II materials.
One of the theoretical explanations of the Meissner effect comes from the London equation. It shows that the magnetic field decays exponentially inside the superconductor over a distance of 20-40 nm. It is described in terms of a parameter called the London penetration depth.
Perfect Diamagnet
If a conductor already had a steady magnetic field through it and was then cooled through the transition to a zero resistance state, becoming a perfect diamagnet, the magnetic field would be expected to stay the same.
Superconductor
Remarkably, the magnetic behaviour of a superconductor is distinct from perfect diamagnetism. It will actively exclude any magnetic field present when it makes the phase change to the superconducting state.
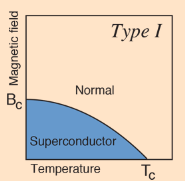
5.1.4 Type I and Type II and high Tc superconductors
Type I Superconductors
A type I superconductor consists of basic conductive elements that are used in everything from electrical wiring to computer microchips. At present, type I superconductors have Tcs between 0.000325 °K and 7.8 °K at standard pressure. Some type I superconductors require incredible amounts of pressure in order to reach the superconductive state. One such material is sulphur which, requires a pressure of 9.3 million atmospheres (9.4 x 1011 N/m2) and a temperature of 17 °K to reach superconductivity. Some other examples of type I superconductors include Mercury - 4.15 °K, Lead - 7.2 °K, Aluminium - 1.175 °K and Zinc - 0.85 °K. Roughly half of the elements in the periodic table are known to be superconductive.
Type II Superconductors
A type II superconductor is composed of metallic compounds such as copper or lead. They reach a superconductive state at much higher temperatures when compared to type I superconductors. The cause of this dramatic increase in temperature is not fully understood. The highest Tc reached at standard pressure, to date, is 135 °K or -138 °C by a compound (HgBa2Ca2Cu3O8) that falls into a group of superconductors known as cuprite perovskites. This group of superconductors generally has a ratio of 2 copper atoms to 3 oxygen atoms, and is considered to be a ceramic. Type II superconductors can also be penetrated by a magnetic field whereas a type I can not
A supercapacitor is similar to a capacitor except for the bigger area of its plates and the smaller distance between these plates. The plates are metallic and are soaked in electrolytes and are separated by a very thin insulator. An electric double layer is created in the supercapacitor as opposite charges are formed on both sides of the separator when the plates are charged. This results in a supercapacitor with greater capacitance. In other words, the combination of plates and the larger effective surface area enables a supercapacitor to have greater capacitance and higher energy density. Unlike a battery, a supercapacitor has an unlimited life cycle, with little wear and tear on long-term use. Thus, it can be charged and discharged an unlimited number of times.
A supercapacitor has many advantages. It can deliver high power and enable high load currents owing to its low resistance. Its charging mechanism is simple and fast and is not subject to overcharging. Compared to a battery, a supercapacitor has excellent high- and low-temperature charge and discharge performance. It is also highly reliable and has low impedance.
A supercapacitor has certain limitations including its high cost and the high self-discharge involved. Moreover, unlike a regular battery, it has low specific energy and its use of the full energy spectrum is hindered by linear discharge voltage.
Because of their properties, supercapacitors are used in many applications. They are widely deployed to deliver power and bridge power gaps. They are a replacement for batteries in certain settings such as in battery-free devices
Principal:
In an ordinary capacitor, the plates are separated by a relatively thick dielectric made from something like mica (a ceramic), a thin plastic film, or even simply air (in something like a capacitor that acts as the tuning dial inside a radio). When the capacitor is charged, positive charges form on one plate and negative charges on the other, creating an electric field between them. The field polarizes the dielectric, so its molecules line up in the opposite direction to the field and reduce its strength. That means the plates can store more charge at a given voltage.
Construction:
Similar to a normal capacitor, the supercapacitor also has two parallel plates with a bigger area. But the difference is, the distance between the plates is small. The plates are made up of metals and soaked in electrolytes. The plates are separated by a thin layer called an insulator.
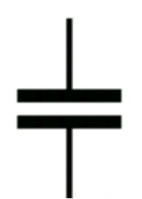
When opposite charges are formed on both sides of the insulator, an electric double layer is formed and the plates are charged. Hence the supercapacitor is charged and has higher capacitance. These capacitors are used to provide high power and enable high load currents with low resistance. The cost of the supercapacitor is high because of its high charging and discharging capacitance.
An electric-double layer is created when the plates are changed and opposite charges are formed on both sides of the plates. Hence the supercapacitors are also called double-layer capacitors or electric double-layer capacitors (EDLC’S). When the area of the plates increases and the distance between the plates decreases, then the capacitance of the capacitor increases.
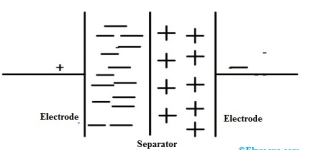
When the supercapacitor is not charged, all the charges are distributed randomly within the cell. When the supercapacitor is charged, all the positive charges are attracted to the negative terminal and negative charges are attracted to the positive terminal. Generally, supercapacitors are available with 420F capacitance, charging and discharging current 4-2Amps with a room temperature of -22 degrees centigrade.
Applications
The applications of supercapacitor include the following.
- To deliver high power and bridge power gaps
- Industrial and electronic applications
- Used in wind turbines, electric and hybrid vehicles
- Regenerative braking to release the power in acceleration
- To start power in start-stop systems
- Regulate voltage in the energy grid
- To capture and assist the power in lower loads and lifted loads
- Back-ups the power in a quick discharging state.
The batteries are widely used with a specific volume and weight, also have better energy density. Supercapacitors are high-capacity capacitors with high power density. When compared to a battery, the supercapacitor has a fast charging-discharging capacity, can handle low-high temperature, high reliability, and low impedance.
The cost of the battery is low whereas the cost of a supercapacitor is high. Supercapacitors have the self-discharging capacity. In the battery, the operating voltage determines the charging and discharging modes. In a supercapacitor, the allowable voltage depends on the type of dielectric material used between the plates. And also, the electrolyte in the capacitor may increase the capacitance.
Batteries are available in lead-acid batteries, Ni-MH, Li-Po, Li-ion, LMP, etc. Supercapacitors are available with organic electrolyte, aqueous electrolyte, ionic liquid, hybrid, and pseudo supercapacitors. Batteries are used to store large amounts of energy and supercapacitors are used to deliver high power density.
To gain insight into how this energy may be expressed (in terms of Q and V), consider a charged, empty, parallel-plate capacitor; that is, a capacitor without a dielectric but with a vacuum between its plates. The space between its plates has a volume Ad, and it is filled with a uniform electrostatic field E. The total energy UCUC of the capacitor is contained within this space. The energy density Ue in this space is simply UCUC divided by the volume Ad. If we know the energy density, the energy can be found as
UC=uE (Ad)UC=uE (Ad).
The amount of energy that can be stored in a capacitor per mass of that capacitor is called its specific energy. Specific energy is measured gravimetrically (per unit of mass) in watt-hours per kilogram (Wh/kg).
The amount of energy can be stored in a capacitor per volume of that capacitor is called its energy density. Energy density is measured volumetrically (per unit of volume) in watt-hours per litre (Wh/l).
As of 2013 commercial specific energies range from around 0.5 to 15 Wh/kg. For comparison, an aluminium electrolytic capacitor stores typically 0.01 to 0.3 Wh/kg, while a conventional lead-acid battery stores typically 30 to 40 Wh/kg and modern lithium-ion batteries 100 to 265 Wh/kg. Supercapacitors can therefore store 10 to 100 times more energy than electrolytic capacitors, but only one tenth as much as batteries. For reference, petrol fuel has a specific energy of 44.4 MJ/kg or 12300 Wh/kg (in vehicle propulsion, the efficiency of energy conversions should be considered resulting in 3700 Wh/kg considering a typical 30% internal combustion engine efficiency).
Commercial energy density (also called volumetric specific energy in some literature) varies widely, but in general range from around 5 to 8 Wh/l. Units of litres and dm3 can be used interchangeably. In comparison, petrol fuel has an energy density of 32.4 MJ/l or 9000 Wh/l
If a system has a high-power density, then it can output large amounts of energy based on its mass. For example, a tiny capacitor may have the same power output as a large battery. However, since the capacitor is so much smaller, it has a higher power density. Since they release their energy quickly, high power density systems can also recharge quickly. An example application of this type of energy storage is a camera flash. It has to be small enough to fit inside the camera (or cell phone) but have a high enough power output to light up the subject of your photo. This makes a system with a high-power density ideal.
The specific energy of supercapacitors is insufficient compared with batteries, capacitors have the important advantage of the specific power. Specific power describes the speed at which energy can be delivered to/absorbed from the load. The maximum power is given by the formula
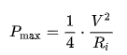
With V = voltage applied and Ri, the internal DC resistance of the capacitor.
Specific power is measured either gravimetrically in kilowatts per kilogram (kW/kg, specific power) or volumetrically in kilowatts per litre (kW/l, power density).
The described maximum power Pmax specifies the power of a theoretical rectangular single maximum current peak of a given voltage. In real circuits the current peak is not rectangular and the voltage is smaller, caused by the voltage drop. IEC 62391–2 established a more realistic effective power Peff for supercapacitors for power applications:
Supercapacitor specific power is typically 10 to 100 times greater than for batteries and can reach values up to 15 kW/kg.
