Unit-2
Matrices and determinants
Matrices have wide range of applications in various disciplines such as chemistry, Biology, Engineering, Statistics, economics, etc.
Matrices play an important role in computer science also.
Matrices are widely used to solving the system of linear equations, system of linear differential equations and non-linear differential equations.
First time the matrices were introduced by Cayley in 1860.
Definition-
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-
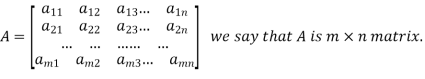
The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Notation of a matrix-
A matrix ‘A’ is denoted as-
A = 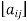
Where, i = 1, 2, …….,m and j = 1,2,3,…….n
Here ‘i’ denotes row and ‘j’ denotes column.
Types of matrices-
1. Rectangular matrix-
A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.
Example:
A = 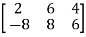
The order of matrix A is 2×3 , that means it has two rows and three columns.
Matrix A is a rectangular matrix.
2. Square matrix-
A matrix which has equal number of rows and columns, is called square matrix.
Example:
A = 
The order of matrix A is 3 ×3 , that means it has three rows and three columns.
Matrix A is a square matrix.
3. Row matrix-
A matrix with a single row and any number of columns is called row matrix.
Example:
A = 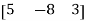
4. Column matrix-
A matrix with a single column and any number of rows is called row matrix.
Example:
A = 
5. Null matrix (Zero matrix)-
A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by O
Example:
A = 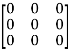
6. Diagonal matrix-
A matrix is said to be diagonal matrix if all the elements except principal diagonal are zero
The diagonal matrix always follows- 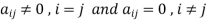
Example:
A = 
7. Scalar matrix-
A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.
Example-
A = 
8. Identity matrix-
A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.
It is denoted by – ‘I’
I = 
9. Triangular matrix-
If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.
There are two types of triangular matrices-
(a) Lower triangular matrix-
If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example:
A = 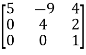
(b) Upper triangular matrix-
If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example-
A = 
Special types of matrices-
Symmetric matrix-
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 and
and 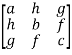
Example: check whether the following matrix A is symmetric or not?
A = 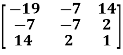
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
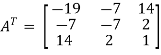
Here,
A = 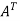
The matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix.
Then,
A = 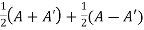
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Hermitian matrix:
A square matrix A = 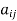 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
It means,
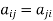
For example:
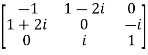
Necessary and sufficient condition for a matrix A to be hermitian –
A = (͞A)’
Skew-Hermitian matrix-
A square matrix A = 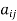 is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
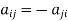
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
For example:
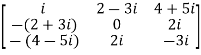
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-
- A = (͞A)’
Note: A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.
Similarly a Skew- Hermitian matrix is a generalization of a Skew symmetric matrix and also every Skew- symmetric matrix is Skew –Hermitian.
Theorem: Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
Or If A is given square complex matrix then 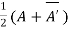 is hermitian and
is hermitian and 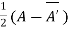 is skew-hermitian matrices.
is skew-hermitian matrices.
Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where 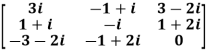
Let A =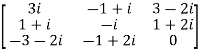
Therefore 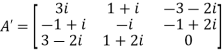 and
and 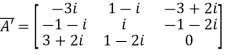
Let 
Again 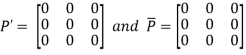
Hence P is a hermitian matrix.
Let 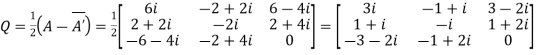
Again 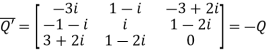
Hence Q is a skew- hermitian matrix.
We Check
P +Q=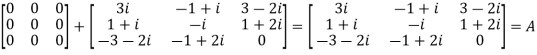
Hence proved.
Example2: If A = 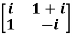 then show that
then show that
(i) 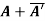 is hermitian matrix.
is hermitian matrix.
(ii) 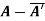 is skew-hermitian matrix.
is skew-hermitian matrix.
Sol.
Given A = 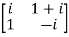
Then 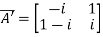
Let 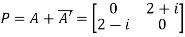
Also 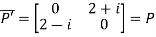
Hence P is a Hermitian matrix.
Let 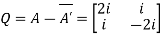
Also 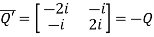
Hence Q is a skew-hermitian matrix.
Skew-symmetric matrix-
A square matrix A is said to be skew symmetrix matrix if –
1. A’ = -A, [ A’ is the transpose of A]
2.all the main diagonal elements will always be zero.
For example-
A = 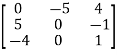
This is skew symmetric matrix, because transpose of matrix A is equals to negative A.
Example: check whether the following matrix A is symmetric or not?
A = 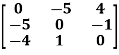
Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.
-A = A’
Orthogonal matrix-
Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
Such that,
A. A’ = I
Matrix × transpose of matrix = identity matrix
Note- if |A| = 1, then we can say that matrix A is proper.
Examples: 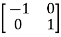 and
and 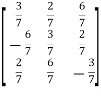 are the form of orthogonal matrices.
are the form of orthogonal matrices.
Unitary matrix-
A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Such that,
( ͞A)’. A = I
For example:
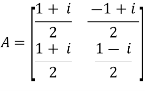
and its
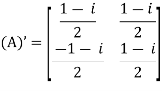
Then (͞A)’ . A = I
So that we can say that matrix A is said to be a unitary matrix.
Key takeaways-
A = 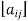
Where, i = 1, 2, …….,m and j = 1,2,3,…….n
Here ‘i’ denotes row and ‘j’ denotes column.
3. Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
4. Square matrix = symmetric matrix + anti-symmetric matri
5. A square matrix A = 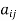 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
6. All the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
7. A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian
8. Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
9. A square matrix A is said to be skew symmetrix matrix if –
(a) A’ = -A, [ A’ is the transpose of A]
(b) all the main diagonal elements will always be zero.
10. Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
11. if |A| = 1, then we can say that matrix A is proper.
12. A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Algebra on Matrices:
Addition and subtraction of matrices is possible if and only if they are of same order.
We add or subtract the corresponding elements of the matrices.
Example: 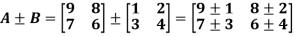
Example: Add 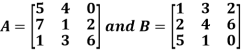 .
.
Sol.
A + B = 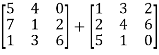
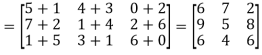
2. Scalar multiplication of matrix:
In this we multiply the scalar or constant with each element of the matrix.
Example: 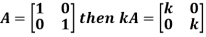
3. Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
Example: 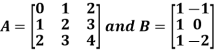
Then 
4. Power of Matrices: If A is A square matrix then
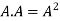
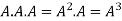 and so on.
and so on.
If 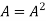 where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent.
5. Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 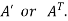
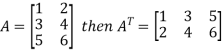
The transpose of matrix 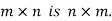 Also
Also 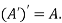
Note: 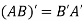
6. Trace of a matrix-
Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.
Example- If we have a matrix A-
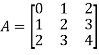
Then the trace of A = 0 + 2 + 4 = 6
Key takeaways-
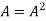
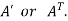
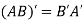
If A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix
The determinant of a square matrix is a number that associated with the square matrix. This number may be positive, negative or zero.
The determinant of the matrix A is denoted by det A or |A| or D
For 2 by 2 matrix-
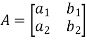
Determinant will be
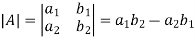
For 3 by 3 matrix-
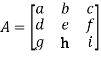
Determinant will be
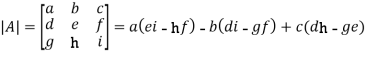
Example: If A = 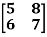 then find |A|.
then find |A|.
Sol.
As we know that-
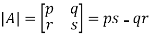
Then-
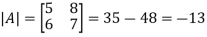
Example: Find out the determinant of the following matrix A.
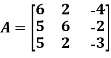
Sol.
By the rule of determinants-
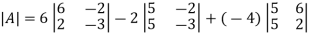
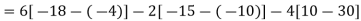
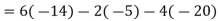
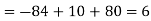
Example: expand the determinant:

Sol. As we know
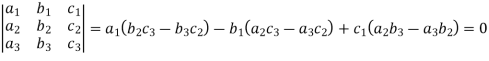
Then,
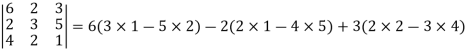
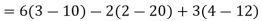
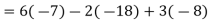
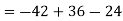
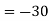
Minor –
The minor of an element is define as determinant obtained by deleting the row and column containing the element.
In a determinant,
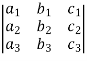
The minor of 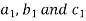 are given by
are given by
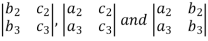
Cofactor –
Cofactors can be defined as follows,
Cofactor = 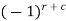 minor
minor
Where r is the number of rows and c is the number of columns.
Example: Find the minors and cofactors of the first row of the determinant.

Sol. (1) The minor of element 2 will be,
Delete the corresponding row and column of element 2,
We get,
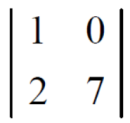
Which is equivalent to, 1 × 7 - 0 × 2 = 7 – 0 = 7
Similarly the minor of element 3 will be,
4× 7 - 0× 6 = 28 – 0 = 28
Minor of element 5,
4 × 2 - 1× 6 = 8 – 6 = 2
The cofactors of 2, 3 and 5 will be,
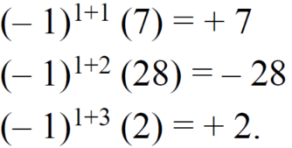
Properties of determinants-
(1) If the rows are interchanged into columns or columns into rows then the value of determinants does not change.
Let us consider the following determinant:
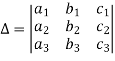
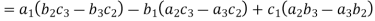
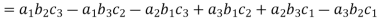
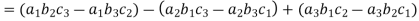
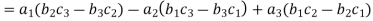
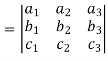
(2) The sign of the value of determinant changes when two rows or two columns are interchanged.
Interchange the first two rows of the following, we get
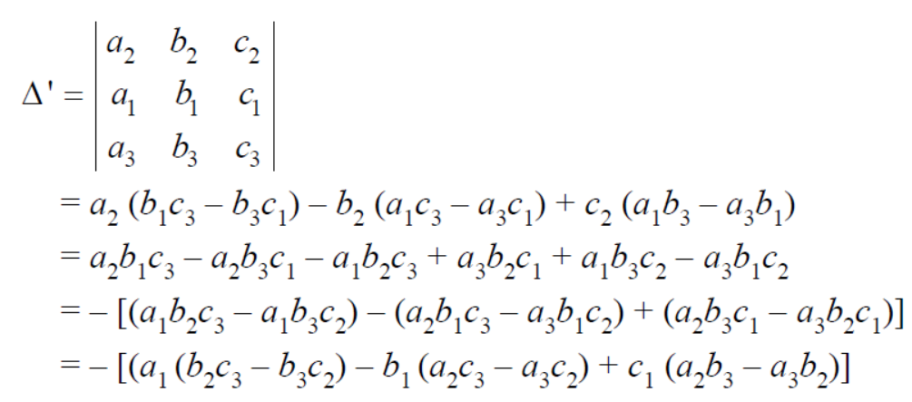
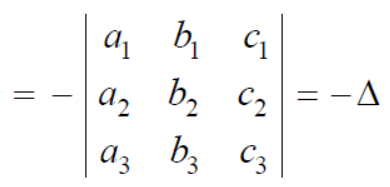
(3) If two rows or two columns are identical the the value of determinant will be zero.
Let, the determinant has first two identical rows,
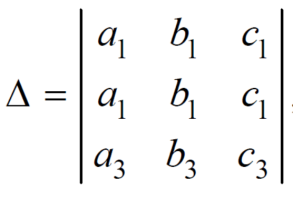
As we know that if we interchange the first two rows then the sign of the value of the determinant will be changed, so that
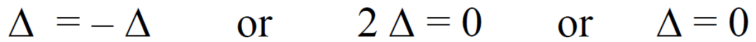
Hence proved
(4) if the element of any row of a determinant be each multiplied by the same number then the determinant multiplied by the same number,
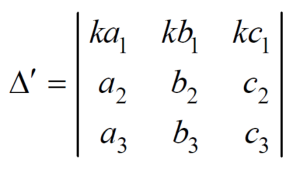
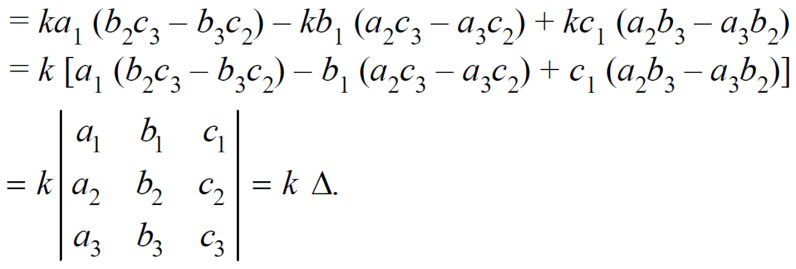
Example: Show that,
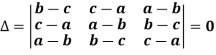
Sol. Applying
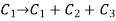
We get,
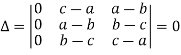
Example: Solve-
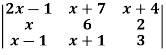
Sol:
Given
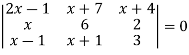
Apply- 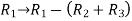
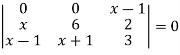
We get-
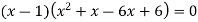
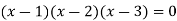
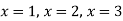
Applications of determinants-
Determinants have various applications such as finding the area and condition of collinearity.
Area of triangles-
Suppose the three vertices of a triangle are 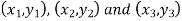 respectively, then we know that the area of the triangle is given by-
respectively, then we know that the area of the triangle is given by-
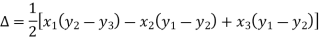
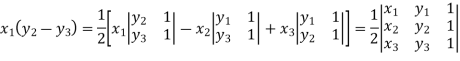
This is how we can find the area of the triangle.
Condition of collinearity-
Let there are three points 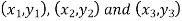
Then these three points will be collinear if -
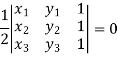
Example: Show that the points given below are collinear-
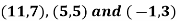
Sol.
First we need to find the area of these points and if the area is zero then we can say that these are collinear points-
So that-
We know that area enclosed by three points-
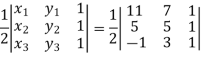
Apply- 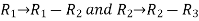
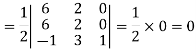
So that these points are collinear.
Key takeaways-
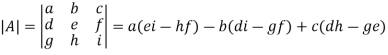
In a determinant,
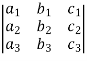
The minor of 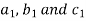 are given by
are given by
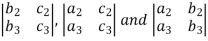
4. Cofactors can be defined as follows,
Cofactor = 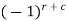 minor
minor
Where r is the number of rows and c is the number of columns.
5. If the rows are interchanged into columns or columns into rows then the value of determinants does not change.
6. The sign of the value of determinant changes when two rows or two columns are interchanged.
7. If two rows or two columns are identical the the value of determinant will be zero.
8. if the element of any row of a determinant be each multiplied by the same number then the determinant multiplied by the same number
9. If the three vertices of a triangle are 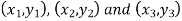 respectively, then we know that the area of the triangle is given by-
respectively, then we know that the area of the triangle is given by-
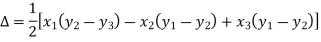
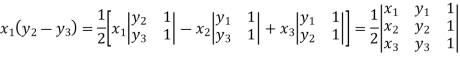
10. Condition of collinearity-
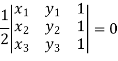
This method was introduced by Gabriel Cramer (1704 – 1752).
Suppose we have to solve the following equations,
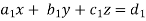
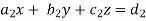
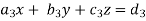
Now, let-
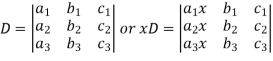
Multiply the second column by y and 3rd column by z and adding to the first column then we have-
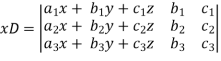
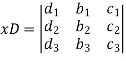
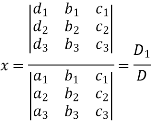
Similarly we get-
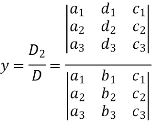
And
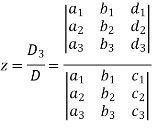
Example: Solve the following equations by using Cramer’s rule-
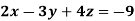
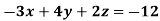
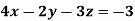
Sol.
Here we have-
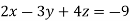
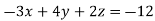
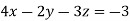
And here-
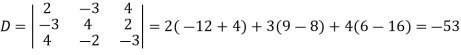
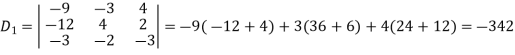
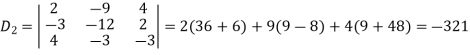
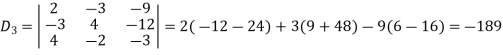
Now by using cramer’s rule-
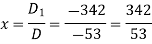
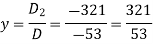
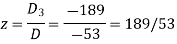
Example: Solve the following system of linear equations-
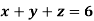
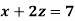
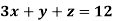
Sol.
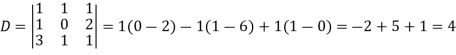

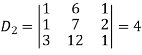

By using cramer’s rule-
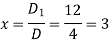
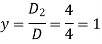
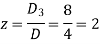
Adjoint of a matix-
Transpose of a co-factor matrix is known as the disjoint matrix.
If the following is a co-factor of matrix A-
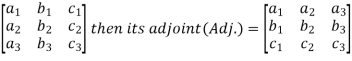
Inverse of a matrix-
The inverse of a matrix ‘A’ can be find as-
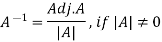
Example: Find the inverse of matrix ‘A’ if-
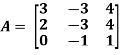
Sol.
Here we have-
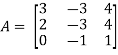
Then
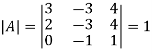
And the matrix formed by its co-factors of |A| is-
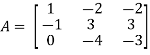
Then
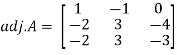
Therefore-
We know that-
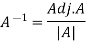
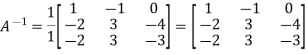
Inverse of a matrix by using elementary transformation-
The following transformation are defined as elementary transformations-
1. Interchange of any two rows (column)
2. Multiplication of any row or column by any non-zero scalar quantity k.
3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar.
The symbol ~ is used for equivalence.
Elementary matrices-
If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.
Note- Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
The method of finding inverse of a non-singular matrix by using elementary transformation-
Working steps-
1. Write A = IA
2. Perform elementary row transformation of A of the left side and I on right side.
3. Apply elementary row transformation until ‘A’ (left side) reduces to I, then I reduces to 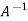
Example-1: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
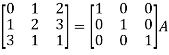
Apply 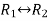 , we get
, we get
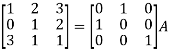
Apply 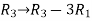
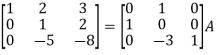
Apply 
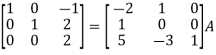
Apply 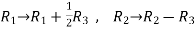
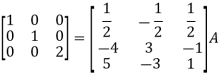
Apply 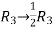
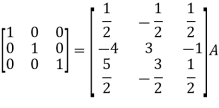
So that,
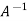 =
= 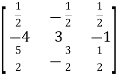
Example-2: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
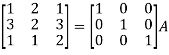
Apply 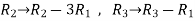
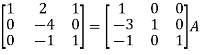
Apply 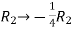
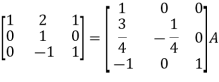
Apply 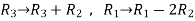
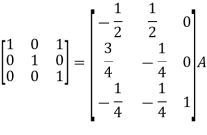
Apply 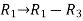
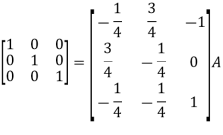
So that
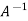 =
= 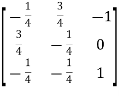
Key takeaways-
If the following is a co-factor of matrix A-
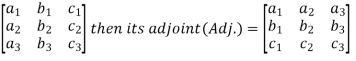
2. 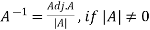
3. If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.
4. Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
5. The symbol ~ is used for equivalence.
Input –Output analysis is a form of economic analysis based on the interdependencies between economic sectors.
The method is most commonly used for estimating the impacts of positive or negative economic shocks and analyzing the ripple effects throughout an economy.
Input –Output analysis technique was invented by Prof. Wassily W.Leontief.
Leontief imagines an economy in which goods like iron, coal, alcohol, etc. are produced in their respective industries by means of a primary factor, viz., labour, and by means of other inputs such as iron, coal, alcohol, etc. For the production of iron, coal is required.
Leontief imagines an economy in which goods like iron, coal, alcohol, etc. are produced in their respective industries by means of a primary factor, viz., labour, and by means of other inputs such as iron, coal, alcohol, etc. For the production of iron, coal is required.
Input–output tables can be constructed for whole economies or for segments within economies. They are useful in planning the production levels in various industries necessary to meet given consumption goals and in analyzing the effects throughout the economy of changes in certain components. They have been most widely used in planned economies and in developing countries.
Let 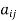 be the value of the output
be the value of the output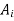 consumed by
consumed by 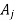 where i ,j = 1,2
where i ,j = 1,2
Let 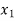 and
and 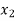 be the value of the current outputs of
be the value of the current outputs of 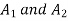 respectively.
respectively.
And
Let 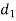 and
and 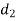 be the value of the final demands for the outputs of
be the value of the final demands for the outputs of 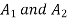 respectively.
respectively.
We get the following equation by the assumption-
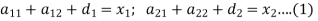
Let-
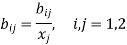
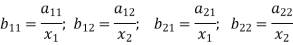
Then the equation (1) becomes-
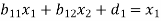
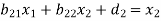
These equations can be arranged as-
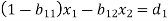
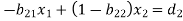
We can write it in matrix form as-
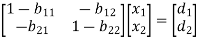
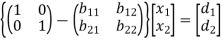
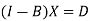
Where-
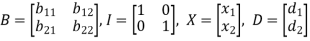
We get by solving-
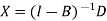
The matrix B is called Technology matrix.
The Hawkins –Simon conditions-
If B is the technology matrix then Hawkins- Simon conditions are-
i. The main diagonal elements in I – B must be positive and
ii. |I – B| must be positive.
Example: Suppose [A] = 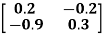
Sol.
Here
[I - A] = 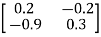
And the value of |I – A| is less than zero then the Hawkins-Simon conditions are not satisfied so that no solution is possible in this case.
Example: The following inter-industry transactions table was constructed for an economy of the year 2019-
Industry | 1 | 2 | Final consumption | Total output |
1 | 500 | 1600 | 400 | 2500 |
2 | 1750 | 1600 | 4650 | 8000 |
Labours | 250 | 4800 | - | - |
Now construct the technology co-efficient matrix showing direct requirement.
Sol.
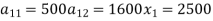
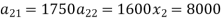
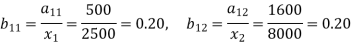
The technology matrix is-
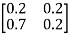
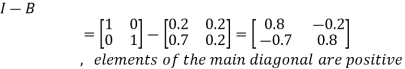
Now-
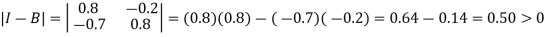
Since the diagonal elements are positive and 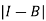 is positive.
is positive.
Here Hawkins-Simon conditions are satisfied.
Hence the system has a solution.
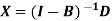
If B is the technology matrix then Hawkins- Simon conditions are-
i. The main diagonal elements in I – B must be positive and
ii. |I – B| must be positive.
References-