UNIT 1

Matrices and Determinant

1.1 Algebra of matrices

1     Addition and subtraction of matrices:

Addition and subtraction of matrices is possible if and only if they are of same order.

We add or subtract the corresponding elements of the matrices.

 Example: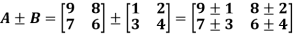

Example: Add .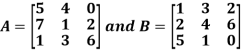

Sol.

A + B =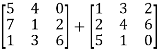

2     Scalar multiplication of matrix:

In this we multiply the scalar or constant with each element of the matrix.

        Example: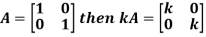

3     Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.

Example: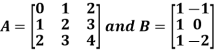

Then

4     Power of Matrices: If A is a square matrix then

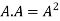
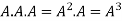and so on.

 If where A is square matrix then it is said to be idempotent.

5. Transpose of  a  matrix: The  matrix  obtained  from  any  given  matrix A ,  by interchanging rows  and   columns is  called the  transpose of  A and is  denoted  by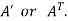

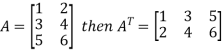
The transpose of matrix 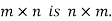 Also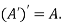 

Note: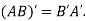

6. Trace of a matrix-

Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.

Example- If we have a matrix A-

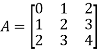
Then the trace of A = 0 + 2 + 4 = 6

Key takeaways-

1.2 Inverse of a matrix

Inverse of a matrix-

The inverse of a matrix ‘A’ can be find as-

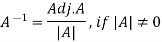
Example: Find the inverse of matrix ‘A’ if-

Sol.

Here we have-

Then

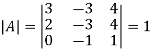
And the matrix formed by its co-factors of |A| is-

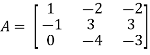
Then

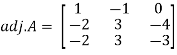
Therefore-

We know that-

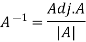
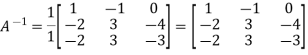
Inverse of a matrix by using elementary transformation-

The following transformation are defined as elementary transformations-

1. Interchange of any two rows (column)

2. Multiplication of any row or column by any non-zero scalar quantity k.

3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar.

The symbol ~ is used for equivalence.

Elementary matrices-

If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.

Note- Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.

The method of finding inverse of a non-singular matrix by using elementary transformation-

Working steps-

1. Write A = IA

2. Perform elementary row transformation of A of the left side and I on right side.

3. Apply elementary row transformation until ‘A’ (left side) reduces to I, then I reduces to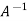

Example-1: Find the inverse of matrix ‘A’ by using elementary transformation-

A =

Sol.  Write the matrix ‘A’ as-  

A = IA

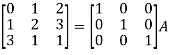
Apply , we get

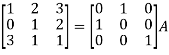
Apply

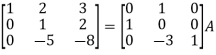
Apply

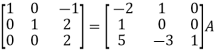
Apply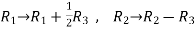

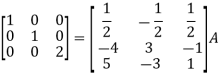
Apply

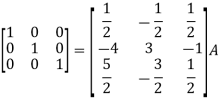
So that,

  =

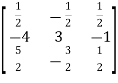
Example-2: Find the inverse of matrix ‘A’ by using elementary transformation-

A =

Sol.  Write the matrix ‘A’ as-  

A = IA

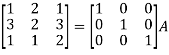
Apply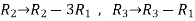

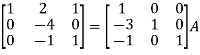
Apply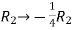

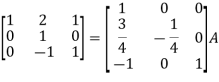
Apply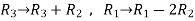

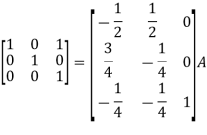
Apply

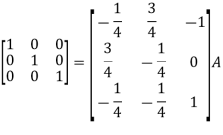
So that

  = 

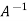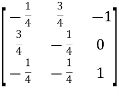
Key takeaways-

1.3 Matrix Operation – Business Application Solution of system of linear equations (having unique solution and involving not more than three variables) using matrix inversion Method and Cremer’s Rule.

There are two types of linear equations-

1.  Consistent                                    2. Inconsistent

Let’s understand about these two types of linear equations

Consistent –

If a system of equations has one or more than one solution, it is said be consistent.

There could be unique solution or infinite solution.

For example-

A system of linear equations-

2x + 4y = 9

x + y = 5

has unique solution,

where as,

A system of linear equations-

2x + y = 6

4x + 2y = 12

Has infinite solutions.

Inconsistent-

If a system of equations has no solution, then it is called inconsistent.

Consistency of a system of linear equations-

Suppose that a system of linear equations is given as-

This is the format as AX = B

Its augmented matrix is-

[A:B] = C

(1) consistent equations-

if  Rank of A = Rank of C

here,  Rank of A = Rank of C = n ( no. of unknown) – unique solution

and Rank of A = Rank of C = r , where r<n   -  infinite solutions

(2) inconsistent equations-

If Rank of A ≠ Rank of C

Solution of homogeneous system of linear equations-

A system of linear equations of the form AX = O is said to be homogeneous , where A denotes the coefficients and of matrix and and O denotes the null vector.

Suppose the system of homogeneous linear equations is ,

It means ,

AX = O

Which can be written in the form of matrix as below,

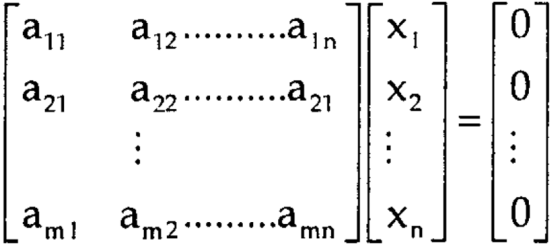
 Note-  A system of homogeneous linear  equations always has a solution if

1. r(A) = n then there will be trivial solution, where n is the number of unknown,

2. r(A) < n , then there will be an infinite number of solution.

Example: Find the solution of the following homogeneous system of linear equations,

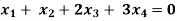
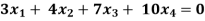
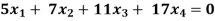
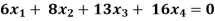
Sol. The given system of linear equations can be written in the form of matrix as follows,

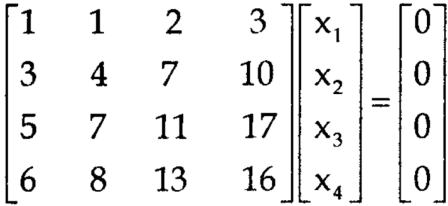
Apply the elementary row transformation,

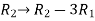
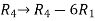  , we get,

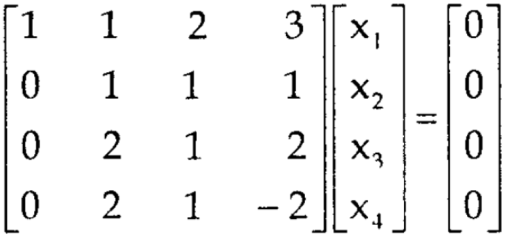
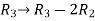
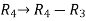    , we get

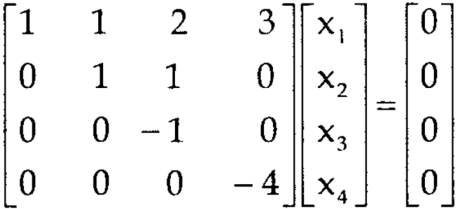
  Here r(A) = 4, so that it has trivial solution,

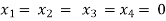
Example: Find out the value of ‘b’ in the system of homogenenous equations-

2x + y + 2z = 0

x + y + 3z = 0

4x + 3y +  bz = 0

Which has

(1) trivial solution

(2) non-trivial solution

Sol. (1)

For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value.

Now for non-trivial solution-

(2)

Convert the system of equations into matrix form-

AX = O

Apply 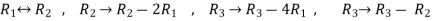respectively , we get the following resultant matrices

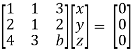
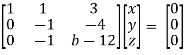
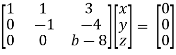
For non-trivial solutions , r(A) = 2 < n

b – 8 = 0

b = 8

Solution of non-homogeneous system of linear equations-

Example-1: check whether the following system of linear equations is consistent of not.

2x + 6y = -11

6x + 20y – 6z = -3

6y – 18z = -1

Sol. Write the above system of linear equations in augmented matrix form,

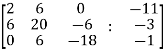
Apply  , we get

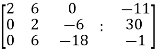
Apply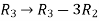

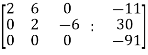
Here the rank of C is 3 and the rank of A is 2

Therefore both ranks are not equal. So that the given system of linear equations is not consistent.

Example: Check the consistency and find the values of x , y and z of the following system of linear equations.

2x + 3y + 4z = 11

X + 5y + 7z = 15

3x + 11y + 13z = 25

Sol. Re-write the system of equations in augmented matrix form.

C = [A,B]

That will be,

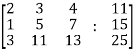
Apply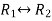 

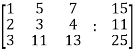
Now apply ,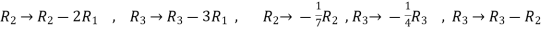

We get,

~~

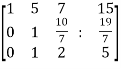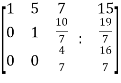
Here rank of A = 3

And rank of C = 3, so that the system of equations is consistent,

So that we can can solve the equations as below,

That gives,

x + 5y + 7z = 15  ……………..(1)

y + 10z/7 = 19/7 ………………(2)

4z/7 = 16/7 ………………….(3)

From eq. (3)

z = 4,

from 2,

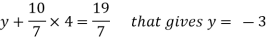
From eq.(1), we get

x + 5(-3) + 7(4) = 15

That gives,

x = 2

Therefore the values of x , y , z are    2 , -3 , 4  respectively.

Solving a system of linear equations using cramer’s rule

This method was introduced by Gabriel Cramer (1704 – 1752).

Suppose we have to solve the following equations,

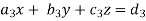
Now, let-

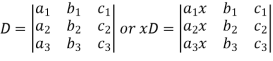
Multiply the second column by y and 3rd column by z and adding to the first column then we have-

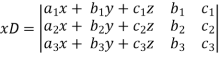
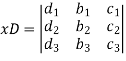
Similarly we get-

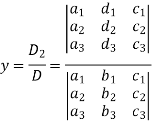
And

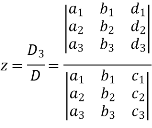
Example: Solve the following equations by using Cramer’s rule-

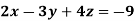
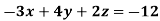
Sol.

Here we have-

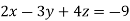
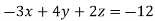
And here-

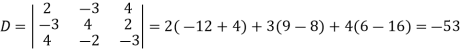
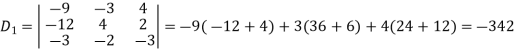
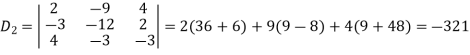
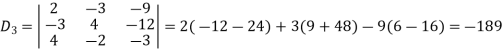
Now by using cramer’s rule-

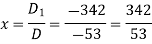
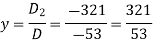
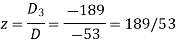
Example: Solve the following system of linear equations-

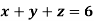
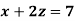
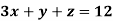
Sol.

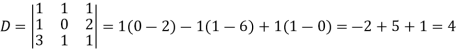
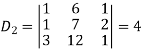
By using cramer’s rule-

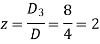
References-