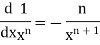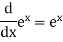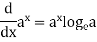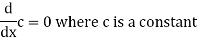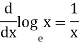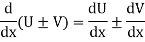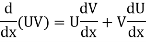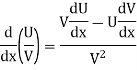UNIT 2

Calculus I

2.1 Mathematical functions and their types- linear, quadratic, polynomial, exponential, logarithmic and logistic function.

There are two broad types of functions- algebraic and transcendental functions.

Algebraic function: A function in the form of a polynomial with finite number of terms is known as algebraic function.

Domain and Range of a Function:

The set of values of independent variables x is called the ‘Domain’ of the function and the set of corresponding values of f(x) i.e. the dependent variable y is called the ‘Range’ of the function. These functions can be constructed using only a finite number of elementary operations, such as plus, minus, multiplication and division.

Polynomial Function-

A polynomial in the variable x is a function that can be written in the form-

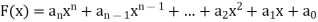
Here 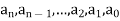are constant.

The term containing the highest power of x are called the leading term

The degree of the polynomial is the power of x in the leading term. degree 0, 1, and 2 are polynomials which are constant, linear and quadratic functions while degree 3, 4, and 5 are polynomials with special names: cubic, quartic, and quintic functions. Polynomials with degree n > 5 are just called 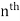degree polynomials.

Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used.

Linear Function: Linear functions are those whose graph is a straight line.

A linear function has the following form. y = f(x) = a + bx.

Quadratic Function: A quadratic function is one of the forms: f(x) = 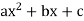, where a, b, and c are numbers with a ≠ 0

Power Function: A power function is a function that can be represented in

the form:

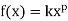
where k and p are real numbers, and x is known as the coefficient

Rational Function-

A rational function is defined by a rational fraction, i.e., an algebraic fraction such that both the numerator and the denominator are polynomials.

Note- the value of denominator should not be equal to zero.

Example: Find the domain and range of the function f(x) =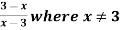

Sol.

f(0) = 3/-3  = -1

f(1) = -1

f(2) = -1

f(3) = -1

so that the domain is = {-1, 0, 1, 2, 4,….} and range = {-1, -1, -1, -1,…..}

Example: find the value of f(2), f(0) and f(3) of the given function-

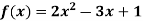
Sol.

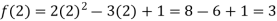
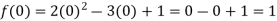
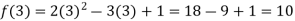
Example: if f(x) = 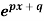then prove that

Sol.

By taking LHS-

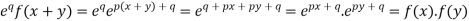
Hence proved

Key takeaways-

Domain and Range of a Function:

A polynomial in the variable x is a function that can be written in the form-

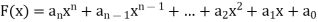
Here 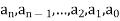are constant.

The term containing the highest power of x are called the leading term

3.        Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used.

4.        Power Function: A power function is a function that can be represented in

the form:

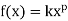
where k and p are real numbers, and x is known as the coefficient.

2.2 Concepts of limit, and continuity of a function, Concept and rules of differentiation, Maxima and Minima involving second order

The rate of change of one variable of function with respect to another on which it depends is called the derivative of the function.

A derivative is the limit of the ratio of the small increment in one variable of the function corresponding to a small increment in the argument (other variable) as the later tends to zero.

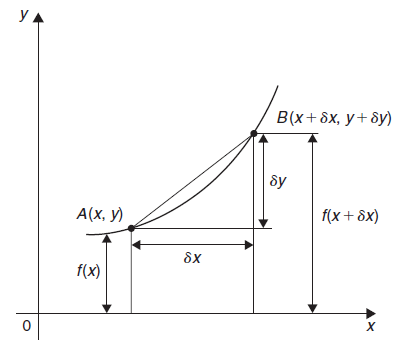
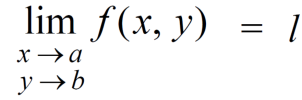
Differentiation from first principal-

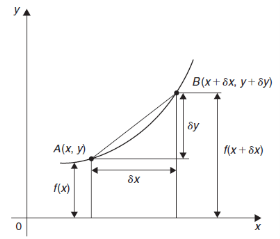
A and B are the two point on a curve representing small increment in the x and y directions respectively.

Gradient of chord-

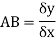
However-

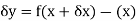
Hence-

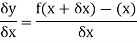
Here 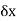which approaches to 0, 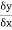approches a limiting value of the gradient of the chord approaches the gradient of the tangent A.

When determining the gradient of a tangent to a curve there are two notations used. The gradient of the curve at A can either be written as,

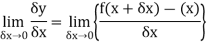
Where

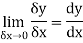
Or we can write it as-

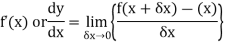
Example: Differentiate the function f(x) = 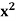by using the first principal method.

Solution.

We know that-

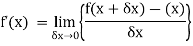
Here

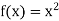
Substituting (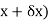 for x gives-

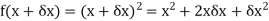
Hence-

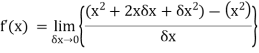
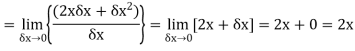
Limits-

The function f(x,y) is said to tend to limit ‘l’ , as x →a and  y→bIff the limit is dependent on point (x,y) as  x →a and  y→b

We can write this as,

Example-1: evaluate the

Solution. We can simply find the Solutionution as follows,

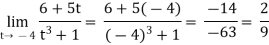
Example-2:  evaluate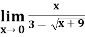

Solution.

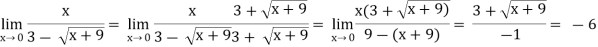
Example-3: evaluate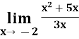

Solution.

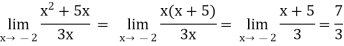
Increment-

Increment of a variable means the difference of initial value from the final value

Increment = final value – initial value

Let x change its value from 2 to 8, increment of x = 8 – 2 = 6

Note- increment can be negative or positive.

Here we will denote the increment of x by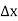

If in y = f(x), the independent variable x changes to 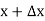then the increment of x =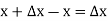

So y = f(x) changes to y = f(x +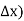

Increment of y = f(x +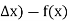

Then the increment ratio-

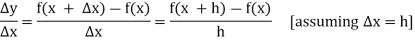
If the ratio 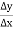tends to a limit, as ® 0 from either side, then this limit is known as the derivative of

y [ = f(x)] with respect to x.

A function y = f(x) is said to be derivable at x if

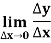
Or

Or

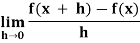
Derivative of y = f(x) with respect to x is denoted by dy/dx or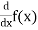

Some useful derivatives-

Example: Find dy/dx of the following functions-

   

   

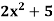
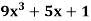
Sol.

Let y =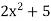

Then-

And

Let y =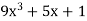

Then-

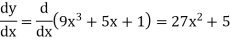
Example: Differentiate 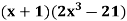with respect to x.

Sol.

Let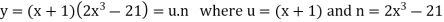

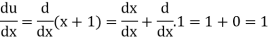
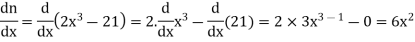
Now

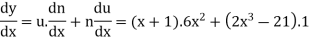
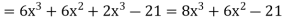
Example: if 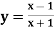then find dy/dx.

Solution.

Suppose y = u/v where u = x - 1 and v = x + 1 

Then

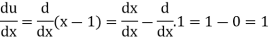
And

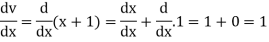
So that-

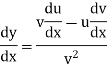
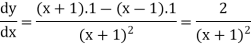
Derivative of function of a function-

If y = f(z),  z = 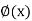then y = f{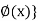

Now if y = f(z) and z = z = 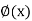then-

Derivative of logarithmic function and exponential function-

If y = log x then its derivative will be-

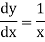
If y = then its derivative-

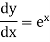
Note- derivative of a constant is always zero.

Example:  if y = 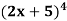then find dy/dx.

Sol.

Suppose z =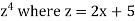

Now-

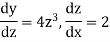
So that-

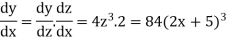
Example: if y =

Sol.

Suppose y = 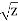where z =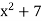

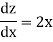
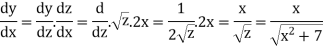
Example: If y = log loglog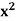 then find dy/dx.

Sol.

Suppose y = log u where u = log v and v = log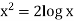

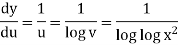
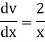
So that-

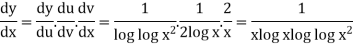
Example: if y =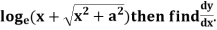

Sol.

Let y = log u where u =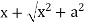

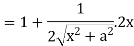
Now

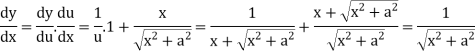
Example: find the derivative of the function f(x) = .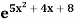

Sol.

Let y = f(x) then

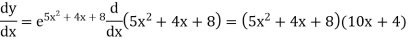
Example: Find the derivative of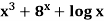

Sol.

Let y = then-

Second order derivative-

The derivative of dy/dx is known as the second order derivative of y.

It is denoted by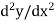

Example: if y = log x/ x a then find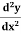

Solution. First we will find the first derivative-

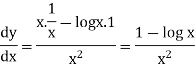
Now

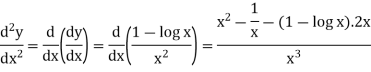
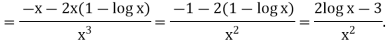
Example: if y = 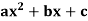then find

Sol.

Here

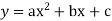
Difference with respect to x, we get-

Now

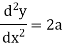
Example: if y = 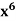then find .

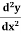Sol.

Here

y =

Then

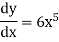
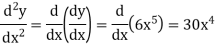
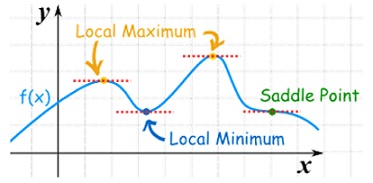
Maximum and minimum-

A function f(x) is said to be maximum at x = a if f(a) is greater than every other value of f(x) in the immediate neighbourhood of x = a (i.e., f(x) ceases to increase but begins to increase at x = a. Similarly the minimum value of f(x) will be that value at x = b which is less than other values in the immediate neighbourhood of x = b.

Maxima and minima of function of two variables-

As we know that the value of a function at maximum

 point is called maximum value of a function. Similarly the value of a function at minimum point is called minimum value of a function.

The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other.

Maxima and Minima of a function of one variables

If  f(x) is a single valued function defined in a region R then

Maxima is a maximum point 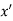if and only if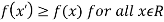

Minima is a minimum point 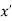if and only if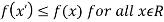

Maxima and Minima of a function of two independent variables

Let 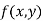be a defined function of two independent variables.

Then the point 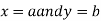is said to be a maximum point o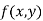f if

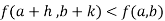
Or   =

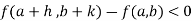
For all positive and negative values of h and k.

Similarly the point 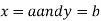is said to be a minimum point o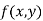f if

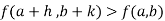
 Or   =

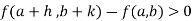
For all positive and negative values of h and k.

Saddle point:

Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.

Note-

Increasing and decreasing functions-

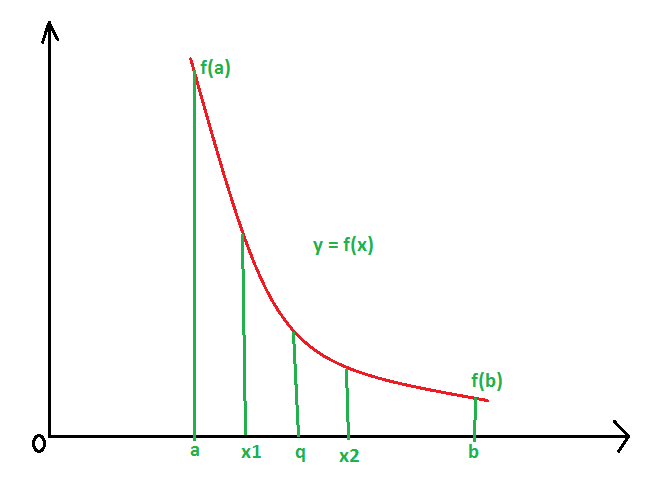
A function is said to be increasing function in an interval [a, b] if y increases as well as x increases from a to b.

Or in other words, A function is said to be an increasing function in [a, b] if its first derivative is greater than zero for all values of x in an interval [a, b].

And

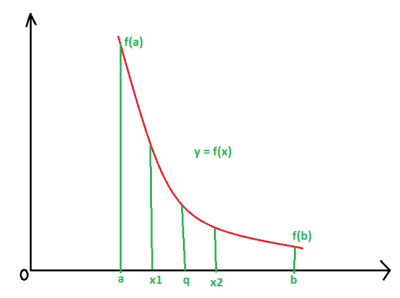
A function is said to be decreasing function in an interval [a, b] if y decreases as well as x increases from a to b.

“If the first derivative is less than zero for all values of x in an interval [a, b] then the function y = f(x) is a decreasing function in [a, b].

Criteria for maximum and minimum-

For a function y = f(x) to attain a maximum point at x = a,

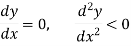
For minimum point-

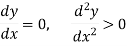
Conditions for maximum and minimum-

Necessary Condition-

If a function f(x) is maximum or minimum at a point x = b and if f’(b) exists then f’ (b) = 0.

Sufficient Condition-

If b is a point in an interval where f(x) is defined and if f ‘(b) = 0 and f’’(b) 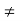0, then  f(b) is maximum if f’’(b) < 0 and is minimum if f’’(b) > 0. (The proof is not shown at present).

Working Rule:

First derivative method

To find the maximum or minimum point of a curve y = f(x).

Find f ‘(x) and equate it to zero. From the equation f ‘(x) = 0, find the value of x, say a and b.

Here the number of roots of f ‘(x) = 0 will be equal to the number of degree of f ‘(x) = 0.

Then find f ‘(a – h) and f ‘(a + h), then note the change of sign if any (here h is very small).

If the change is from positive to negative, f(x) will be maximum at x = a. If again the change of sign is from negative to positive, f(x) will be maximum at x = a.

Similarly for x = b.

Second derivative method-

First we find the first derivative of y = f(x) i.e dy/dx and make it zero.

From the equation 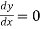find the value of x say a and b.

The again we find the second derivative of y or .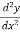

Put x = a in 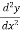, if 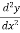at x = a is negative then the function is maximum at x = a and maximum value will be f(a).

If the value of 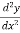at x = a is positive, then the function is minimum and the minimum value will be f(a)

Similarly we take for x = b.

Example: Examine for maximum and minimum for the function f(x) =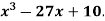

Sol.

Here the first derivative is-

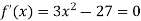
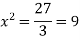
So that, we get-

Now we will get to know that the function is maximum or minimum at these values of x.

For x = 3

Let us assign to x, the values of 3 – h and 3 + h (here h is very small) and put these values at f(x).

Then-

Which is negative for h is very small

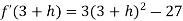Which is positive

Thus f’(x) changes sign from negative to positive as it passes through x = 3.

So that f(x) is minimum at x = 3 and the minimum value is-

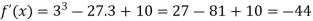
And f(x) is maximum at x = -3.

Example: Find out the value of x for which the function f(x) = is minimum of maximum.

Sol.

Let

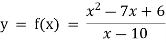
Then the first derivative will be-

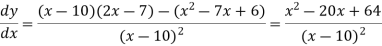
Putting  , we get-

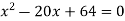
By using middle term splitting-

We get-

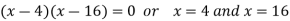
Now we will find the second derivative-

We get-

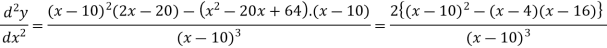
Here

At x = 4,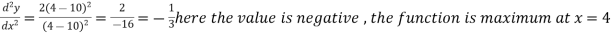

At x = 16,

Example: Find all points of maxima and minima of the function f(x) =.

Sol.

 Here,

f(x) =.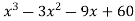

f’(x) =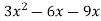

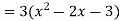
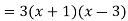
Put, f’(x) = 0

We get,

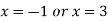
Hence x = -1 and x = 3 are the critical values of the given function.

Now take,

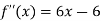
Where x = -1, then f’’(x) = -12

Since f’’(x) < 0 at x = -1, the function has maxima at x = -1

And when x = 3, then f’’(x) = 12

Since f’’(x) > 12 at x = 3, the function has minima at x =

Key takeaways-

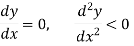
For minimum point-

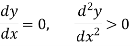
3.        Necessary Condition- If a function f(x) is maximum or minimum at a point x = b and if f’(b) exists then f’ (b) = 0.

Sufficient Condition- If b is a point in an interval where f(x) is defined and if f ‘(b) = 0 and f’’(b) 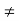0, then  f(b) is maximum if f’’(b) <0 and is minimum if f’’(b) > 0. (The proof is not shown at present).

References-