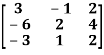Unit - 3
Matrices
Matrix (Introduction)
Matrices have wide range of applications in various disciplines such as chemistry, Biology, Engineering, Statistics, economics, etc.
Matrices play an important role in computer science also.
Matrices are widely used to solving the system of linear equations, system of linear differential equations and non-linear differential equations.
First time the matrices were introduced by Cayley in 1860.
Definition-
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-
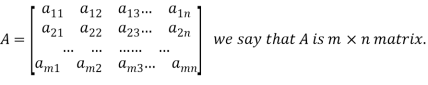
The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Notation of a matrix-
A matrix ‘A’ is denoted as-
A = 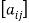
Where, i = 1, 2, …….,m and j = 1,2,3,…….n
Here ‘i’ denotes row and ‘j’ denotes column.
Types of matrices-
1. Rectangular matrix-
A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.
Example:
A = 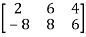
The order of matrix A is 2×3 , that means it has two rows and three columns.
Matrix A is a rectangular matrix.
2. Square matrix-
A matrix which has equal number of rows and columns, is called square matrix.
Example:
A = 
The order of matrix A is 3 ×3 , that means it has three rows and three columns.
Matrix A is a square matrix.
3. Row matrix-
A matrix with a single row and any number of columns is called row matrix.
Example:
A = 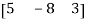
4. Column matrix-
A matrix with a single column and any number of rows is called row matrix.
Example:
A = 
5. Null matrix (Zero matrix)-
A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by O
Example:
A = 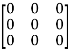
6. Diagonal matrix-
A matrix is said to be diagonal matrix if all the elements except principal diagonal are zero
The diagonal matrix always follows- 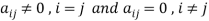
Example:
A = 
7. Scalar matrix-
A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.
Example-
A = 
8. Identity matrix-
A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.
It is denoted by – ‘I’
I = 
9. Triangular matrix-
If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.
There are two types of triangular matrices-
(a) Lower triangular matrix-
If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example:
A = 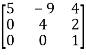
(b) Upper triangular matrix-
If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example-
A = 
Algebra on Matrices:
- Addition and subtraction of matrices:
Addition and subtraction of matrices is possible if and only if they are of same order.
We add or subtract the corresponding elements of the matrices.
Example: 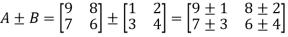
2. Scalar multiplication of matrix:
In this we multiply the scalar or constant with each element of the matrix.
Example: 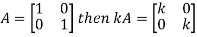
3. Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
Example: 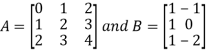
Then 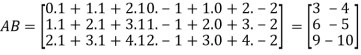
4. Power of Matrices: If A is A square matrix then
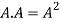
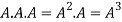 and so on.
and so on.
If 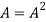 where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent.
5. Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 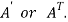
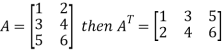
The transpose of matrix  Also
Also 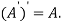
Note: 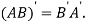
6. Trace of a matrix-
Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.
Example- If we have a matrix A-
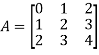
Then the trace of A = 0 + 2 + 4 = 6
Special types of matrices
Symmetric matrix-
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 and
and 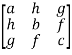
Example: check whether the following matrix A is symmetric or not?
A = 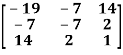
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
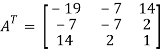
Here,
A = 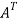
So that, the matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix
Then,
A = 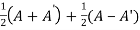
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Hermitian matrix:
A square matrix A =  is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
It means,
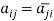
For example:
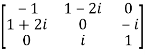
Necessary and sufficient condition for a matrix A to be hermitian –
A = (͞A)’
Skew-Hermitian matrix-
A square matrix A = 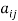 is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
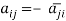
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
For example:
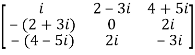
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-
- A = (͞A)’
Note: A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.
Similarly a Skew- Hermitian matrix is a generalization of a Skew symmetric matrix and also every Skew- symmetric matrix is Skew –Hermitian.
Theorem: Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
Or If A is given square complex matrix then 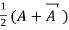 is hermitian and
is hermitian and 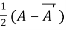 is skew-hermitian matrices.
is skew-hermitian matrices.
Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where 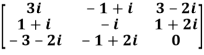
Let A =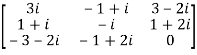
Therefore 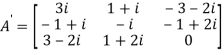 and
and 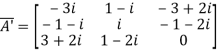
Let 
Again 
Hence P is a hermitian matrix.
Let 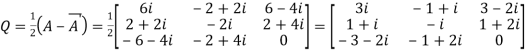
Again 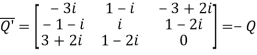
Hence Q is a skew- hermitian matrix.
We Check
P +Q=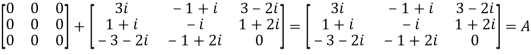
Hence proved.
Example2: If A =  then show that
then show that
(i) 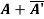 is hermitian matrix.
is hermitian matrix.
(ii) 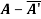 is skew-hermitian matrix.
is skew-hermitian matrix.
Sol.
Given A = 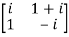
Then 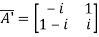
Let 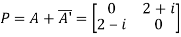
Also 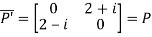
Hence P is a Hermitian matrix.
Let 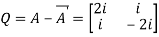
Also 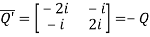
Hence Q is a skew-hermitian matrix.
Skew-symmetric matrix-
A square matrix A is said to be skew symmetrix matrix if –
1. A’ = -A, [ A’ is the transpose of A]
2.all the main diagonal elements will always be zero.
For example-
A = 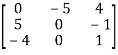
This is skew symmetric matrix, because transpose of matrix A is equals to negative A.
Example: check whether the following matrix A is symmetric or not?
A = 
Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.
-A = A’
Orthogonal matrix-
Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
Such that,
A. A’ = I
Matrix × transpose of matrix = identity matrix
Note- if |A| = 1, then we can say that matrix A is proper.
Examples: 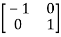 and
and 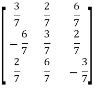 are the form of orthogonal matrices.
are the form of orthogonal matrices.
Unitary matrix-
A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Such that,
( ͞A)’ . A = I
For example:
A =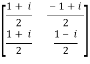 and its ( ͞A)’ =
and its ( ͞A)’ = 
Then (͞A)’ . A = I
So that we can say that matrix A is said to be a unitary matrix.
Key takeaways-
- The matrices were introduced by Cayley in 1860.
- A matrix ‘A’ is denoted as-
A = 
Where, i = 1, 2, …….,m and j = 1,2,3,…….n
Here ‘i’ denotes row and ‘j’ denotes column.
3. Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
4. Square matrix = symmetric matrix + anti-symmetric matri
5. A square matrix A = 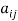 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
6. All the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
7. A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian
8. Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
9. A square matrix A is said to be skew symmetrix matrix if –
(a) A’ = -A, [ A’ is the transpose of A]
(b) all the main diagonal elements will always be zero.
10. Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
11. if |A| = 1, then we can say that matrix A is proper.
12. A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
13. Addition and subtraction of matrices is possible if and only if they are of same order.
14. Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
15. If  where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent.
16. The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 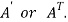
17. : 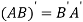
If A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix
Let’s consider the two linear equations,
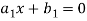

From first eq. , we get,
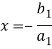
Put this value in second equation, we get
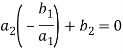
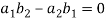
This can be written as,
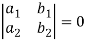
The expansion of the determinant is given as,
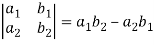
In other words,
The determinant of a square matrix is a number that associated with the square matrix. This number may be positive, negative or zero.
The determinant of the matrix A is denoted by det A or |A| or D
For 2 by 2 matrix-
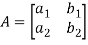
Determinant will be
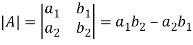
For 3 by 3 matrix-
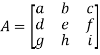
Determinant will be

Example: Expand the determinant

Sol. As we know, expansion of the determinant is given by,
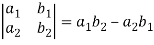
Then we get,
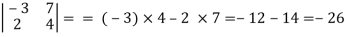
Example: If A = 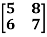 then find |A|.
then find |A|.
Sol.
As we know that-

Then-
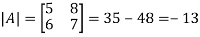
Example: Find out the determinant of the following matrix A.

Sol.
By the rule of determinants-

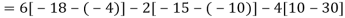
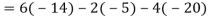
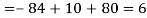
Example: Expand the determinant:

Sol. As we know
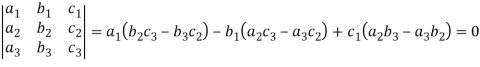
Then,
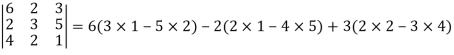
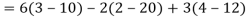

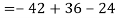

Minor –
The minor of an element is define as determinant obtained by deleting the row and column containing the element.
In a determinant,
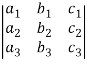
The minor of 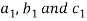 are given by
are given by
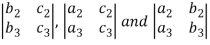
Cofactor –
Cofactors can be defined as follows,
Cofactor = 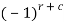 minor
minor
Where r is the number of rows and c is the number of columns.
Example: Find the minors and cofactors of the first row of the determinant.

Sol. (1) The minor of element 2 will be,
Delete the corresponding row and column of element 2,
We get,
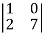
Which is equivalent to, 1 × 7 - 0 × 2 = 7 – 0 = 7
Similarly the minor of element 3 will be,
4× 7 - 0× 6 = 28 – 0 = 28
Minor of element 5,
4 × 2 - 1× 6 = 8 – 6 = 2
The cofactors of 2, 3 and 5 will be,
(-1)1+1(7) = +7
(-1)1+2(28) = -28
(-1)1+3(2) =+2
Example: Expand the determinant:

Sol. As we know
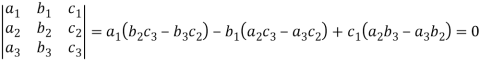
Then,
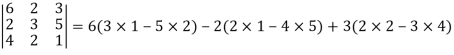
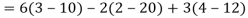
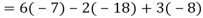

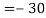
Properties of determinants-
(1) If the rows are interchanged into columns or columns into rows then the value of determinants does not change.
Let us consider the following determinant:
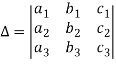
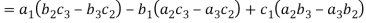
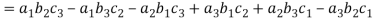
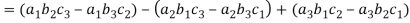
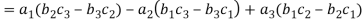

(2) The sign of the value of determinant changes when two rows or two columns are interchanged.
Interchange the first two rows of the following, we get
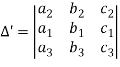
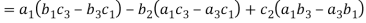
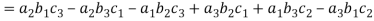
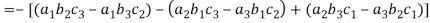
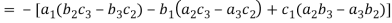
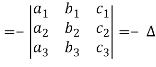
(3) If two rows or two columns are identical the the value of determinant will be zero.
Let, the determinant has first two identical rows,

As we know that if we interchange the first two rows then the sign of the value of the determinant will be changed.
(4) if the element of any row of a determinant be each multiplied by the same number then the determinant multiplied by the same number,
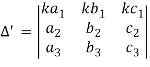
= ka1(b2c3 – b3c2) – kb1 (a2c3 – a3c2) + kc1 (a2b3 – a3b2)
= k[a1 (b2c3 – b3c2) – b1(a2c3 – a3c2) + c1 (a2b3 – a3b2)]
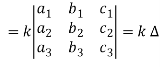
Example: prove the following without expanding the determinant.
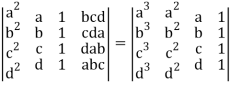
Sol. Here in order to prove the above result, we follow the steps below,
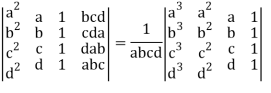


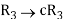
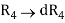
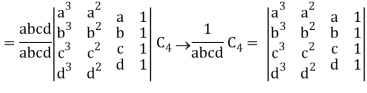
Hence proved.
Example: Prove that (without expanding) the determinant given below is equal zero.

Sol. Applying the operation,
C1 C1 – C3 and C2 C2 – C3
We get,

Now applying the operation,
C1 C1 – 2C2 and C3 C3 – 10 C2
We get,

Apply,
R1 R1 – R3 and R2 R2 + 3R3
We get,

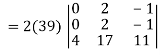
Here first and second row are identical then we know that by property it becomes zero.
Example: Show that,
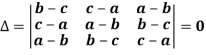
Sol. Applying
C1 C1 + C2 + C3
We get,
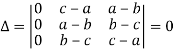
Example: Solve-
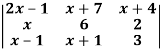
Sol:
Given-
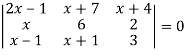
Apply- 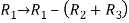
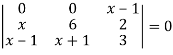
We get-

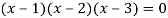
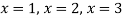
Applications of determinants-
Determinants have various applications such as finding the area and condition of collinearity.
Area of triangles-
Suppose the three vertices of a triangle are  respectively, then we know that the area of the triangle is given by-
respectively, then we know that the area of the triangle is given by-

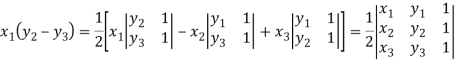
This is how we can find the area of the triangle.
Condition of collinearity-
Let there are three points 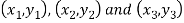
Then these three points will be collinear if -
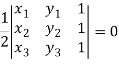
Example: Show that the points given below are collinear-
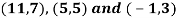
Sol.
First we need to find the area of these points and if the area is zero then we can say that these are collinear points-
So that-
We know that area enclosed by three points-
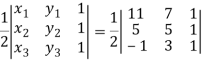
Apply- 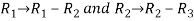
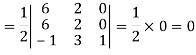
So that these points are collinear.
Key takeaways-
- The determinant of the matrix A is denoted by det A or |A| or D
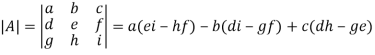
- The minor of an element is define as determinant obtained by deleting the row and column containing the element.
In a determinant,
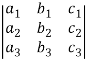
The minor of 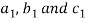 are given by
are given by
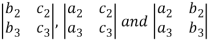
4. Cofactors can be defined as follows,
Cofactor = 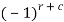 minor
minor
Where r is the number of rows and c is the number of columns.
5. If the rows are interchanged into columns or columns into rows then the value of determinants does not change.
6. The sign of the value of determinant changes when two rows or two columns are interchanged.
7. If two rows or two columns are identical the the value of determinant will be zero.
8. if the element of any row of a determinant be each multiplied by the same number then the determinant multiplied by the same number
9. If the three vertices of a triangle are 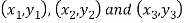 respectively, then we know that the area of the triangle is given by-
respectively, then we know that the area of the triangle is given by-
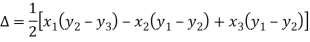
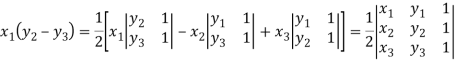
10. Condition of collinearity-
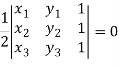
Adjoint of a matix-
Transpose of a co-factor matrix is known as the disjoint matrix.
If the following is a co-factor of matrix A-
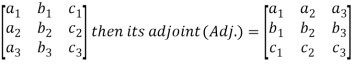
Inverse of a matrix-
The inverse of a matrix ‘A’ can be find as-

Example: Find the inverse of matrix ‘A’ if-
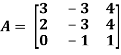
Sol.
Here we have-
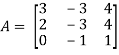
And the matrix formed by its co-factors of |A| is-
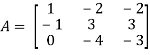
And
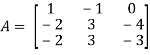
Therefore-
We know that-
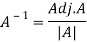
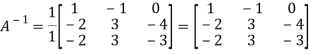
Inverse of a matrix by using elementary transformation-
The following transformation are defined as elementary transformations-
1. Interchange of any two rows (column)
2. Multiplication of any row or column by any non-zero scalar quantity k.
3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar.
The symbol ~ is used for equivalence.
Elementary matrices-
If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.
Note- Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
The method of finding inverse of a non-singular matrix by using elementary transformation-
Working steps-
1. Write A = IA
2. Perform elementary row transformation of A of the left side and I on right side.
3. Apply elementary row transformation until ‘A’ (left side) reduces to I, then I reduces to 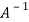
Example-1: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
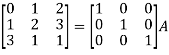
Apply 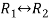 , we get
, we get

Apply 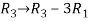
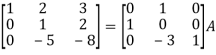
Apply 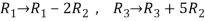
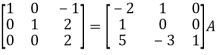
Apply 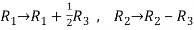
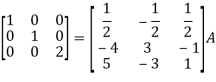
Apply 
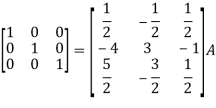
So that,
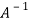 =
= 
Example-2: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
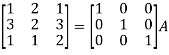
Apply 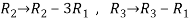

Apply 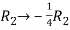
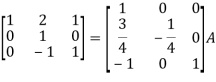
Apply 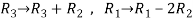
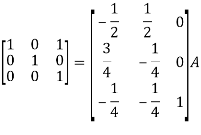
Apply 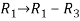
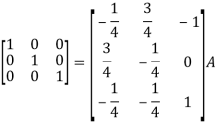
So that
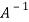 =
= 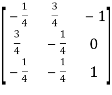
Gauss –Jordan Method of finding the inverse:
We know that X will be the inverse of a matrix A if
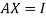
Where I is an identity matrix of order same as A.
We write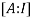 , using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution.
, using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution.
The determinant of this coefficient matrix is the product of the diagonal elements of the upper triangular matrix.
If this |A|=0 then inverse does not exist.
Example1: Find the inverse of the matrix  by row transformation?
by row transformation?
Let A=
By Gauss-Jordan method
We have 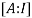
=
Apply 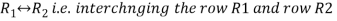

Apply 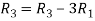 we get
we get

Apply 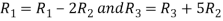 we get
we get
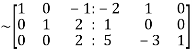
Apply 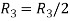

Apply 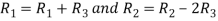
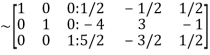
Hence 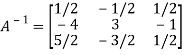
Example2: Find the inverse of 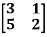
Let A=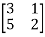
By Gauss-Jordan method
We have 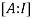
=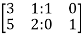
Apply 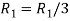
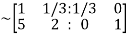
Apply 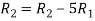
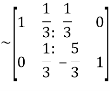
Apply 
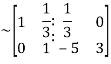
Apply 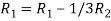
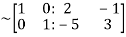
Hence 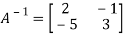
Example3: Find the inverse of the matrix 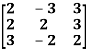 by row transformation?
by row transformation?
Let A= 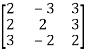
By Gauss-Jordan method
We have 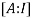
=
Apply 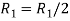 we get
we get
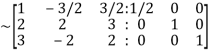
Apply 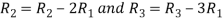
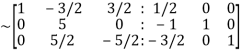
Apply 
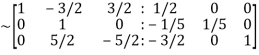
Apply 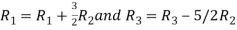
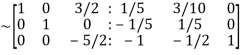
Apply 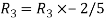
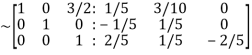
Apply 
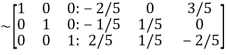
Hence 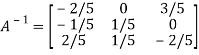
Example4: Find the inverse of 
Let A=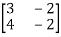
By Gauss Jordan method
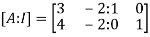
Apply 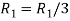
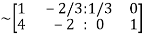
Apply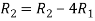
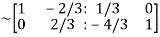
Apply 

Apply 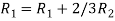
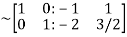
Hence the inverse of matrix A is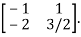
Example5: Find the inverse of 
Let A= 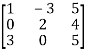
By Gauss-Jordan Method [A:I]
=
Apply 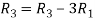
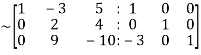
Apply 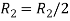
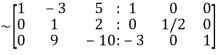
Apply 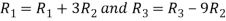

Apply 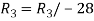
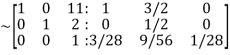
Apply 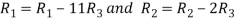
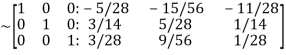
Hence the inverse of matrix A is 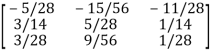
Rank of a matrix
Rank of a matrix by echelon form-
The rank of a matrix (r) can be defined as –
1. It has at least one non-zero minor of order r.
2. Every minor of A of order higher than r is zero.
Example: Find the rank of a matrix M by echelon form.
M = 
Sol. First we will convert the matrix M into echelon form,
M = 
Apply, 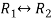 , we get
, we get
M = 
Apply 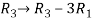 , we get
, we get
M = 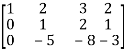
Apply 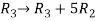
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Example: Find the rank of a matrix A by echelon form.
A = 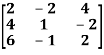
Sol. Convert the matrix A into echelon form,
A = 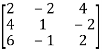
Apply 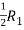
A = 
Apply 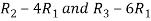 , we get
, we get
A = 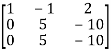
Apply 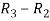 , we get
, we get
A = 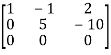
Apply 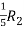 ,
,
A = 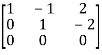
Apply 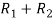 ,
,
A = 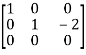
Therefore the rank of the matrix will be 2.
Example: Find the rank of a matrix A by echelon form.
A = 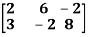
Sol. Transform the matrix A into echelon form, then find the rank,
We have,
A = 
Apply, 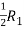
A = 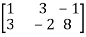
Apply 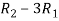 ,
,
A = 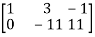
Apply 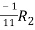
A = 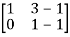
Apply 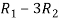
A = 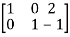
Hence the rank of the matrix will be 2.
Example: Find the rank of the following matrices by echelon form?
Let A = 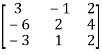
Applying 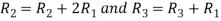
A 
Applying 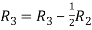
A 
Applying 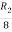
A 
Applying 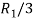
A 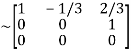
It is clear that minor of order 3 vanishes but minor of order 2 exists as 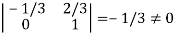
Hence rank of a given matrix A is 2 denoted by 
2. 
Let A = 
Applying 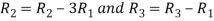

Applying 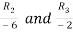
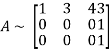
Applying 
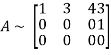
The minor of order 3 vanishes but minor of order 2 non zero as 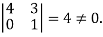
Hence the rank of matrix A is 2 denoted by 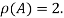
3. 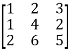
Let A = 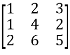
Apply 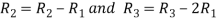

Apply 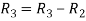

Apply 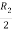
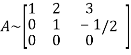
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 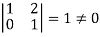
Hence the rank of given matrix is 2 i.e. 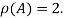
Rank of a matrix by normal form-
Any matrix ‘A’ which is non-zero can be reduced to a normal form of ‘A’ by using elementary transformations.
There are 4 types of normal forms –

The number r obtained is known as rank of matrix A.
Both row and column transformations may be used in order to find the rank of the matrix.
Note-Normal form is also known as canonical form
Example: reduce the matrix A to its normal form and find rank as well.
A = 
Sol. We have,
A = 
We will apply elementary row operation,
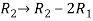
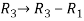
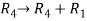
We get,
A = 
Now apply column transformation,
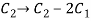
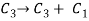
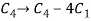
We get,
A - 
Apply
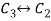 , we get,
, we get,

Apply 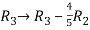 and
and 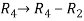

Apply 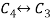
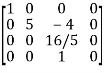
Apply 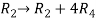 and
and 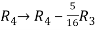

Apply 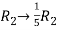 and
and 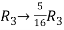

As we can see this is required normal form of matrix A.
Therefore the rank of matrix A is 3.
Example: Find the rank of a matrix A by reducing into its normal form.
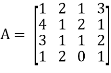
Sol. We are given,
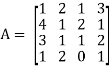
Apply
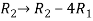
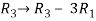
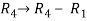
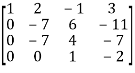

Apply
C2 C2 – 2 C1, C3 C3 + C1, C4 C4 – 3 C1
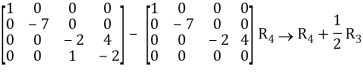
C3 C3 + 6/7 C2, C4 C4 – 11/7 C2
C4 C4 + 2C3 - 
R2 - 1/7 R2
R3 - ½ R3
This is the normal form of matrix A.
So that the rank of matrix A = 3
Rank-Nullity theorem
Let A is a matrix of order m by n, then-
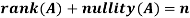
Proof: If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let  represent these free variables and let
represent these free variables and let 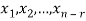 denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here 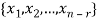 is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 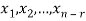

Which shows that 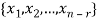 spans null-space (A).
spans null-space (A).
Thus 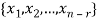 is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
There are two types of linear equations-
1. Consistent
2. Inconsistent
Let’s understand about these two types of linear equations.
Consistent –
If a system of equations has one or more than one solution, it is said be consistent.
There could be unique solution or infinite solution.
For example-
A system of linear equations-
2x + 4y = 9
x + y = 5
Has unique solution,
Whereas,
A system of linear equations-
2x + y = 6
4x + 2y = 12
Has infinite solutions.
Inconsistent-
If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations-
Suppose that a system of linear equations is given as-
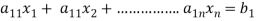
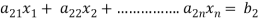
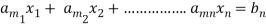
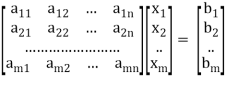
This is the format as AX = B
Its augmented matrix is-
[A:B] = C
(1) Consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
(2) Inconsistent equations-
If Rank of A ≠ Rank of C
Solution of homogeneous system of linear equations-
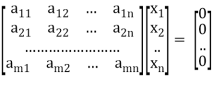
A system of linear equations of the form AX = O is said to be homogeneous, where A denotes the coefficients and of matrix and O denotes the null vector.
Suppose the system of homogeneous linear equations is,

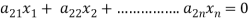
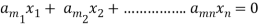
It means
AX = O
Which can be written in the form of matrix as below,
Note- A system of homogeneous linear equations always has a solution if
1. r(A) = n then there will be trivial solution, where n is the number of unknown,
2. r(A) < n , then there will be an infinite number of solution.
Example: Find the solution of the following homogeneous system of linear equations,
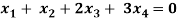
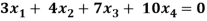
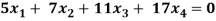
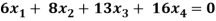
Sol. The given system of linear equations can be written in the form of matrix as follows,
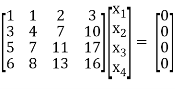
Apply the elementary row transformation,
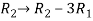
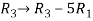
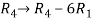 , we get,
, we get,
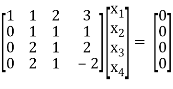

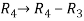 , we get
, we get
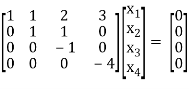
Here r(A) = 4, so that it has trivial solution,
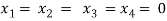
Example: Find out the value of ‘b’ in the system of homogenenous equations-
2x + y + 2z = 0
x + y + 3z = 0
4x + 3y + bz = 0
Which has
(1) Trivial solution
(2) Non-trivial solution
Sol. (1)
For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value.
Now for non-trivial solution-
(2)
Convert the system of equations into matrix form-
AX = O
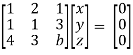
Apply  Respectively , we get the following resultant matrices
Respectively , we get the following resultant matrices

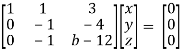
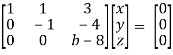
For non-trivial solutions, r(A) = 2 < n
b – 8 = 0
b = 8
Solution of non-homogeneous system of linear equations-
Example-1: check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
Sol. Write the above system of linear equations in augmented matrix form,
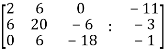
Apply 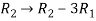 , we get
, we get
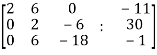
Apply 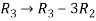
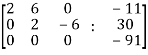
Here the rank of C is 3 and the rank of A is 2
Therefore both ranks are not equal. So that the given system of linear equations is not consistent.
Example: Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form.
C = [A,B]
That will be,
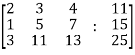
Apply 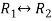
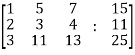
Now apply ,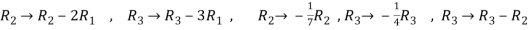
We get,
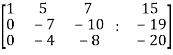 ~
~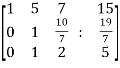 ~
~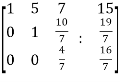
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can can solve the equations as below,
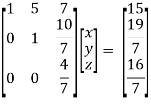
That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,

From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x , y , z are 2 , -3 , 4 respectively.
Solution of system of linear equation by gauss elimination and gauss Jordan method-
The matrix that we make from the coefficient x,y and z of of the linear equations is reduced into echelon form by elementary row operation.
At the end, we calculate the value of z, and value of y and x are calculated by backward substitution.
Example: find the solution of the following linear equations.
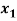 +
+ 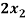 -
- 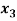 = 1
= 1
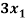 -
-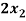 +
+ 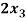 = 2
= 2
 -2
-2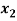 +
+ 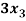 = 5
= 5
Sol. These equations can be converted into the form of matrix as below-

Apply the operation,  and
and 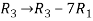 , we get
, we get
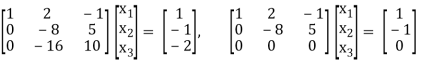 R3 R3 – 2R2
R3 R3 – 2R2
We get the following set of equations from the above matrix,
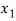 +
+  -
- 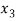 = 1 …………………..(1)
= 1 …………………..(1)
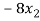 + 5
+ 5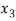 = -1 …………………(2)
= -1 …………………(2)
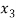 = k
= k
Put x = k in eq. (1)
We get,
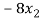 + 5k = -1
+ 5k = -1
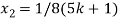
Put these values in eq. (1), we get
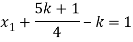
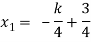
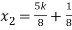 and
and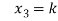
These equations have infinitely many solutions.
Guass- Jordan method –
This method is the modification of gauss elimination method
Example: solve the following system of equations by gauss-jordan method
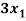 +
+ 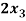 - 2
- 2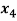 = 0
= 0
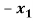 +
+ 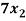 +
+ 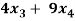 = 0
= 0
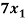 - 7
- 7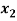 +
+ 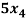 = 0
= 0
Sol. The given system of equations can be written in the form of matrices as follows,
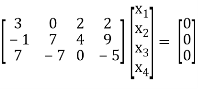
By applying operation - we get,
we get,
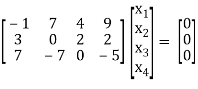
Now apply, 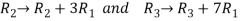
We get,
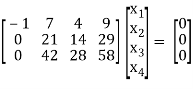
Apply, 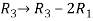
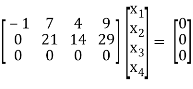
The set of the equations we get from above matrices,
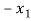 +
+ 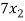 +
+  = 0 …………………..(1)
= 0 …………………..(1)
21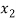 +
+ 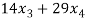 = 0 …………………………..(2)
= 0 …………………………..(2)
Suppose 
From equation-2, we get
21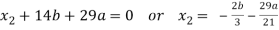
Now from equation-1:
-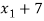 (
(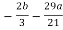 ) + 4b + 9a = 0
) + 4b + 9a = 0
We get,
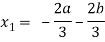
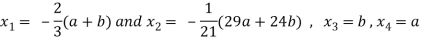
Example: solve the following system of equations by gauss-jordan method
2x + y + 2z = 10
X + 2y + z = 8
3x + y – z = 2
Sol. We will write the equations in matrix form as follows,
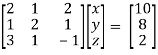
Now apply operation, 
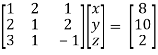
Apply  , we get,
, we get,
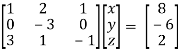
Apply,  , we get,
, we get,
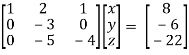
Apply,  / -3 , we get
/ -3 , we get
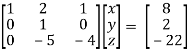
Apply 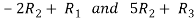
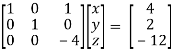
Apply  / -4, we get
/ -4, we get
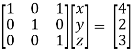
Finally apply 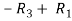
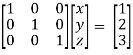
Therefore the solution of the set of linear equations will be,
x = 1 , y = 2 , z = 3
Example: solve the following system of equations by gauss-jordan method.
6a + 8b +6c + 3d = -3
6a – 8b + 6c – 3d = 3
8b - 6d = 6
Sol. Change the system of linear equations into matrix form,
The augmented matrix format will be,
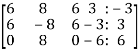
Apply 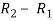

Apply 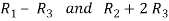
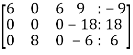
Apply 

Apply 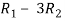 and
and 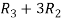
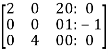
Apply 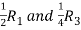

Apply 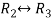

This is the reduced row echelon form,
The system of linear equations becomes,
a + c = 0
b = 0
d = -1
Suppose c = t be a free variable,
Then the solution will be,
a = -t
b = 0
c = t
d = -1
For any number ‘t’.
Solving a system of linear equations using cramer’s rule
This method was introduced by Gabriel Cramer (1704 – 1752).
Suppose we have to solve the following equations,
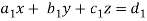
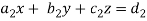
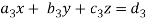
Now, let-
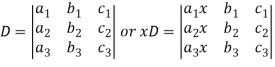
Multiply the second column by y and 3rd column by z and adding to the first column then we have-
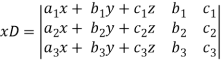
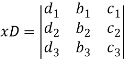
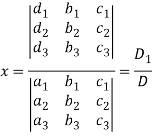
Similarly we get-
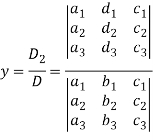
And
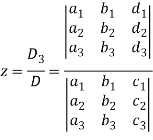
Example: Solve the following equations by using Cramer’s rule-
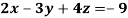
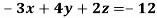
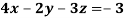
Sol.
Here we have-
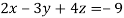
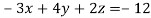
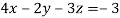
And here-
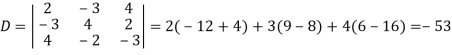
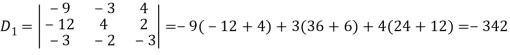
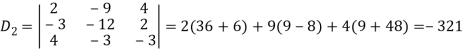
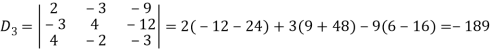
Now by using cramer’s rule-
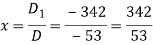
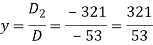
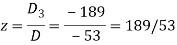
Example: Solve the following system of linear equations-
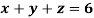
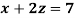

Sol.
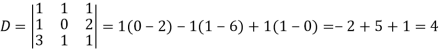

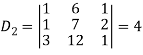

By using cramer’s rule-
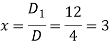

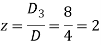
Gauss seidel iteration method
Step by step method to solve the system of linear equation by using Gauss Seidal iteration method-
Suppose,
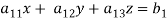
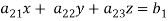
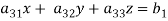
This system can be written as after dividing it by suitable constants,
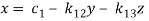
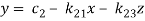

Step-1 Here put y = 0 and z = 0 and x = 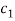 in first equation
in first equation
Then in second equation we put this value of x that we get the value of y.
In the third eq. We get z by using the values of x and y
Step-2: we repeat the same procedure
Example: solve the following system of linear equations by using Guassseidel method-
6x + y + z = 105
4x + 8y + 3z = 155
5x + 4y - 10z = 65
Sol. The above equations can be written as,
 ………………(1)
………………(1)
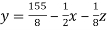 ………………………(2)
………………………(2)
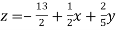 ………………………..(3)
………………………..(3)
Now put z = y = 0 in first eq.
We get
x = 35/2
Put x = 35/2 and z = 0 in eq. (2)
We have,
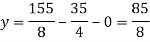
Put the values of x and y in eq. 3
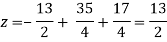
Again start from eq.(1)
By putting the values of y and z
y = 85/8 and z = 13/2
We get
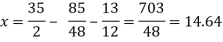
The process can be showed in the table format as below
Iterations | 1 | 2 | 3 | 4 |
x = 35/2 – y/6 – z/6 | 35/2 = 17.5 | 14.64 | 15.12 | 14.98 |
y = 155/8 – x/2 – 3z/8 | 85/8 = 10.6 | 9.62 | 10.06 | 9.98 |
z = - 13/2 + x/2 +2y/5 | 13/2 = 6.5 | 4.67 | 5.084 | 4.98 |
At the fourth iteration, we get the values of x = 14.98, y = 9.98 , z = 4.98
Which are approximately equal to the actual values
As x = 15 , y = 10 and y = 5 ( which are the actual values)
Example: solve the following system of linear equations by using Guass seidel method-
5x + 2y + z = 12
x + 4y + 2z = 15
x + 2y + 5z = 20
Sol. These equations can be written as,
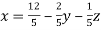 ………………(1)
………………(1)
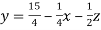 ………………………(2)
………………………(2)
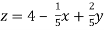 ………………………..(3)
………………………..(3)
Put y and z equals to 0 in eq. 1
We get,
x = 2.4
Put x = 2.4, and z = 0 in eq. 2 , we get
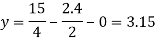
Put x = 2.4 and y = 3.15 in eq.(3) , we get
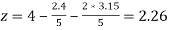
Again start from eq.(1), put the values of y and z , we get
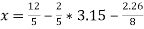 = 0.688
= 0.688
We repeat the process again and again
The following table can be obtained –
Iterations | 1 | 2 | 3 | 4 | 5 |
x = 12/5 – 2/5 y – z/5 | 2.4 | 0.688 | 0.84416 | 0.962612 | 0.99426864 |
y = 15/4 – x/4 – z/2 | 3.15 | 2.448 | 2.09736 | 2.013237 | 2.00034144 |
x = 4-x/5 – 2y/5 | 2.26 | 2.8832 | 2.99222 | 3.0021828 | 3.001009696 |
We see that the values are apprx. Equal to exact values.
Exact values are x = 1 , y = 2, z = 3.
Applications of system of linear equations:
Linear systems in Economics
A country's economy is usually divided into sectors, a few that come to mind might be: manufacturing, services, energy and fuel, transportation, and other public or private sectors. Each of these sectors has a total output (which we will measure in dollars) for one year. This total output is the total amount of earnings for a year and is represented by the letter p, this particular revenue is then used, some or all of it may be invested by exchanging or buying from the other sectors in the economy.
For all of this trade, there must exist an equilibrium price where each sector has:
Income = expenses (expenditures)
Which means that the total amount of income in a sector must be equal to the total amount of expenses, or in other words, the total amount of income is the most that a sector can spend either buying, trading, or even keeping its own capital.
In economics, we can use linear algebra to determine the equilibrium price of outputs for each sector.
Linear systems with Network Flow
Network flow refers to a connected system, named the network, which has elements going in and going out (thus the term flow). A network in itself has a set of points called nodes which are the connections in a set of branches. In this way, each branch has a flow direction pointing to a node, and each node has flow in and flow out, meaning the elements traveling through the network will be passing through each node and the same amount of elements that arrive to each of them are the same ones that get out and go away (there are no losses).
And so, we can use linear algebra to study the flow of some quantity through a network. Just keep in mind the rule for the nodes:
Flow in = Flow out
Applications of Linear equations in Real life
- Finding unknown age
- Finding unknown angles in geometry
- For calculation of speed, distance or time
- Problems based on force and pressure
Row reduction and echelon forms:
Elementary transformation of matrices
It contains three operations one on the rows or columns of the matrix:
- Interchanging- It contain interchange of any two rows or columns .i.e.
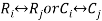
b. Scalar multiplication-It contains scalar multiplication of any scalar quantity with any row or column.

c. Linear combination: we form a linear combination by multiplying a scalar with any row or column and then add the corresponding elements with another row or column.
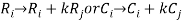 t
t
NOTE: Elementary transformation does not change/affect the order or rank of the matrix.
Elementary matrix: It is obtained from an identity matrix by applying any elementary transformation to it
Row echelon from-
Any matrix is said to be in row echelon form if it follows the term mentioned below:
1. The first non-zero element in each row , is called leading coefficient , is 1. ( some prefers it is not necessary that it should be 1. It can be any number)
2. Each leading entry is in a column to the right of the leading entry in the previous row.
3. Rows with all zero elements are below rows having a non-zero element.
Example of a row echelon form-
 and
and 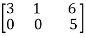
Row reduced form-
A matrix is said to be in reduced row echelon form if it satisfies the following terms-
1. The first non-zero entry in each row is 1.
2. The columns containing this 1 has all the other entries 0.
A matrix in row reduced form is known as row reduced matrix.
For example:

The above matrices are row reduced matrix
Important definition-
Leading term-the first non-zero entry of any row is called leading term.
Leading column-the column containing the leading term is known as leading column.
Row reduced echelon from-
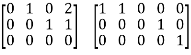
A matrix is said to be in row reduced echelon form if it has following properties,
1. If the given matrix is already in row reduced form.
2. The row consisting of all zeroes comes below all non zero rows
3. The leading term appear from left to right in successive rows
Some of the examples of row reduced echelon form of the matrices are given below,
Key takeaways-
- If a system of equations has one or more than one solution, it is said be consistent.
- If a system of equations has no solution, then it is called inconsistent.
- Consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
4. Inconsistent equations-
If Rank of A ≠ Rank of C
Suppose we have A = 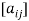 be an n × n matrix , then
be an n × n matrix , then
Characteristic equation- The equation |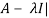 = 0 is called the characteristic equation of A , where |
= 0 is called the characteristic equation of A , where |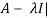 is called characteristic matrix of A. Here I is the identity matrix.
is called characteristic matrix of A. Here I is the identity matrix.
The determinant |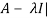 is called the characteristic polynomial of A.
is called the characteristic polynomial of A.
Characteristic roots-the roots of the characteristic equation are known as characteristic roots or Eigen values or characteristic values.
Important notes on characteristic roots-
1. The characteristic roots of the matrix ‘A’ and its transpose A’ are always same.
2. If A and B are two matrices of the same type and B is invertible then the matrices A and 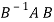 have the same characteristic roots.
have the same characteristic roots.
3. If A and B are two square matrices which are invertible then AB and BA have the same characteristic roots.
4. Zero is a characteristic root of a matrix if and only if the given matrix is singular.
Solved examples to find characteristics equation-
Example-1: Find the characteristic equation of the matrix A:
A = 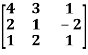
Sol. The characteristic equation will be-
|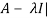 = 0
= 0
 = 0
= 0
On solving the determinant, we get
(4-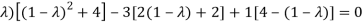
Or 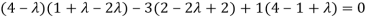
On solving we get,

Which is the characteristic equation of matrix A.
Example-2: Find the characteristic equation and characteristic roots of the matrix A:
A = 
Sol. We know that the characteristic equation of the matrix A will be-
|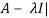 = 0
= 0
So that matrix A becomes,
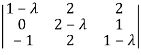 = 0
= 0
Which gives , on solving
(1-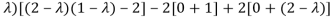 = 0
= 0
Or 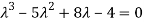
Or (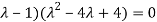
Which is the characteristic equation of matrix A.
The characteristic roots will be,
(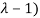 (
(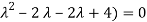
(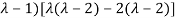
(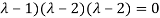
Values of 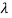 are-
are-
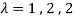
These are the characteristic roots of matrix A.
Example-3: Find the characteristic equation and characteristic roots of the matrix A:
A = 
Sol. We know that, the characteristic equation is-
|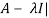 = 0
= 0
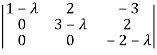 = 0
= 0
Which gives,
(1-
Characteristic roots are- 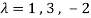
Eigen values and Eigen vectors-
Let A is a square matrix of order n. The equation formed by
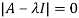
Where I is an identity matrix of order n and 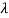 is unknown. It is called characteristic equation of the matrix A.
is unknown. It is called characteristic equation of the matrix A.

The values of the 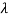 are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
Corresponding to each Eigen value there exist vectors X,
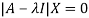
Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.
Note: Corresponding to distinct Eigen value we get distinct Eigen vectors but in case of repeated Eigen values we can have or not linearly independent Eigen vectors.
If 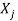 is Eigen vectors corresponding to Eigen value
is Eigen vectors corresponding to Eigen value 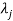 then
then 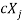 is also Eigen vectors for scalar c.
is also Eigen vectors for scalar c.
Properties of Eigen Values:
- The sum of the principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.
Let A be a matrix of order 3 then 
2. The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then 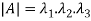 .
.
3. If 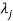 is the Eigen value of the matrix A then 1/
is the Eigen value of the matrix A then 1/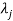 is the Eigen value of the
is the Eigen value of the 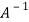 .
.
4. If  is the Eigen value of an orthogonal matrix, then 1/
is the Eigen value of an orthogonal matrix, then 1/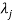 is also its Eigen value.
is also its Eigen value.
5. If 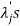 are the Eigen values of the matrix A then
are the Eigen values of the matrix A then 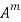 has the Eigen values
has the Eigen values 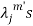 .
.
Example1: Find the sum and the product of the Eigen values of 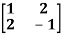 ?
?
Sol. The sum of Eigen values = the sum of the diagonal elements
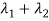 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
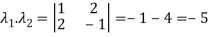
On solving above equations we get 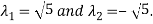
Example2: Find out the Eigen values and Eigen vectors of  ?
?
Sol. The Characteristics equation is given by 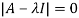

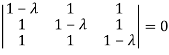
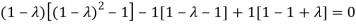
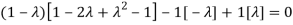

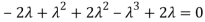
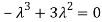

Or 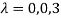
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 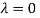 is
is
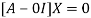
Where X is the column matrix of order 3 i.e.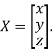
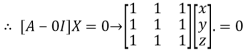
This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1) = 2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value 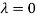 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value  is
is
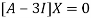
Where X is the column matrix of order 3 i.e.
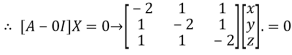
This implies that 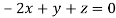
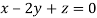

Taking last two equations we get
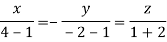
Or 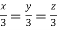
Thus the Eigen vectors corresponding to the Eigen value 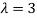 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Example3: Find out the Eigen values and Eigen vectors of 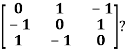
Sol. Let A =
The characteristics equation of A is 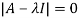 .
.
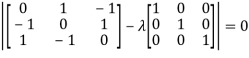
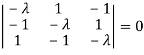
Or 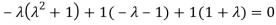
Or 
Or 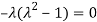
Or 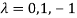
The Eigen vector corresponding to Eigen value  is
is
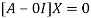
Where X is the column matrix of order 3 i.e.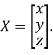

Or 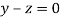

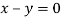
On solving we get 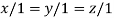
Thus the Eigen vectors corresponding to the Eigen value 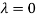 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 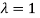 is
is
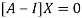
Where X is the column matrix of order 3 i.e.
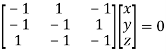
Or 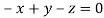
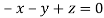
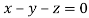
On solving 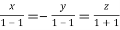 or
or 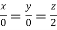 .
.
Thus the Eigen vectors corresponding to the Eigen value 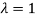 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 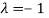 is
is

Where X is the column matrix of order 3 i.e.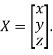
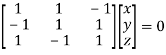
Or 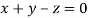
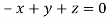
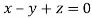
On solving we get 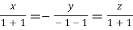 or
or 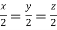 .
.
Thus the Eigen vectors corresponding to the Eigen value 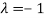 is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Example-4:
Determine the Eigen values of Eigen vector of the matrix.
Determine the Eigen values of Eigen vector of the matrix.
A = 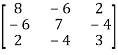
Solution:
Consider the characteristic equation as, |A – λI| = 0
i.e., 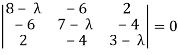
i.e. (8 – 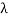 )(21 - 10λ + λ2 – 16) + 6(-18 + 6 λ + 8) + 2(24 – 14 + 2 λ) = 0
)(21 - 10λ + λ2 – 16) + 6(-18 + 6 λ + 8) + 2(24 – 14 + 2 λ) = 0
(8 – λ)( λ2 - 10 λ + 5) + 6(6 λ – 10) + 2(2 λ + 10) = 0
8 λ2 - 80 λ + 40 – λ3 + 10 λ2 - 5 λ + 36 λ – 60
- λ3 + 18 λ - 45 λ = 0
i.e. λ3 - 18 λ + 45 λ = 0
Which is the required characteristic equation
λ(λ2 - 18 λ + 45) = 0
λ(λ – 15)( λ – 3) = 0
λ = 0, 15, 3 are the required Eigen values.
Now consider the equation
[A – λI]x = 0 ............(1)
Case I:
If λ = 0 Equation (1) becomes
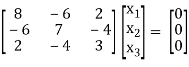
R1 + R2
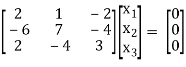
R2 + 3R1, R3 – R1
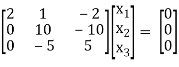
-1/1 R2
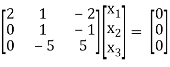
R3 + 5 R2
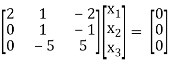
R3 + 5R2
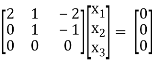
Thus [A – λ I] = 2 & n = 3
3 – 2 = 1 independent variable.
Now rewrite equation as,
2x1 + x2 – 2x3 = 0
x2 – x3 = 0
Put x3 = t
x2 = t &
2x1 = -x2 + 2x3
2x1 = -t + 2t
x1 = t/2
Thus x1 = 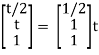 ∀ t ∈ R.
∀ t ∈ R.
Is the eigen vector corresponding to λ = t.
Case II:
If λ = 3 equation (1) becomes,
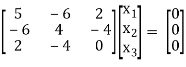
R1 - 2R3
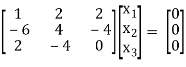
R2 + 6R1, R3 – 2R1
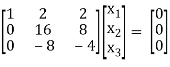
½ R2
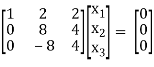
R + R2
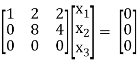
Here [A – λI] = 2, n = 3
3 – 2 = 1 Independent variables
Now rewrite the equations as,
x1 + 2x2 + 2x3 = 0
8x2 + 4x3 = 0
Put x3 = t
x2 = ½ t &
x1 = - 2 x2- 2x3
= - 2( ½ )t – 2(t)
= -3t
x2 = 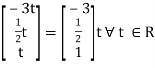
Is the eigen vector corresponding to λ = 3.
Case III:
If λ = 15 equation (1) becomes,
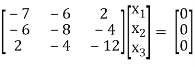
R1 + 4R3
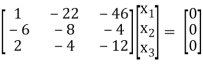
½ R3
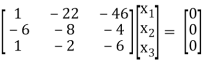
R13
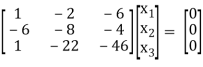
R2 + 6 R1 , R3 – R1
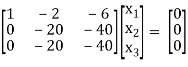
R3 – R2
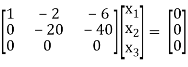
Here rank of [A – λI] = 2 & n = 3
3 – 2 = 1independent variable
Now rewrite the equation as,
x1 – 2x2 – 6x3 = 0
-20x2 – 40x3 = 0
Put x3 = t
x2 = -2t & x1 = 2t
Thus x3 = 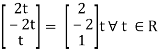
Is the eigen vector for λ = 13.
Example-5:
Find the Eigen values of Eigen vector for the matrix.
A = 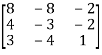
Solution:
Consider the characteristic equation as |A – λI| = 0
i.e., 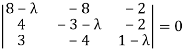
(8 – λ)[-3 + 3 λ – λ + λ2 – 8] + 8[4 - 4 λ + 6] – 2[-16+9+3 λ] = 0
(8 – λ)[ λ2 + 2 λ – 11] + 8[+0 - 4 λ] – 2[ 3 λ – 7] = 0
8 λ2 + 16 λ – 88 – λ3 - 2 λ2 + 11 λ + 80 - 32 λ - 6 λ + 14 =0
i.e. – λ3 + 6 λ2 - 11 λ + 6 = 0
λ3 - 6 λ2 + 11 λ + 6 = 0
(λ – 1)( λ – 2)( λ – 3) = 0
λ = 1,2,3 are the required eigen values.
Now consider the equation
[A – λI]x = 0 .......(1)
Case I:
λ = 1 Equation (1) becomes,
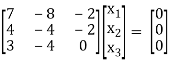
R1 – 2R3
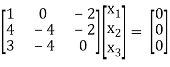
R2 – 4R1, R3 – 3R1
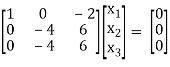
R3 – R2
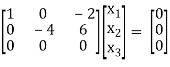
Thus [A – λI] = 2 and n = 3
3 – 2 =1 independent variables
Now rewrite the equations as,
x1 – 2x3 = 0
- 4 x2+ 6 x3 = 0
Put x3 = t
x2 = 3/2 t , x1 = 2b
x1 = 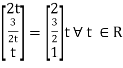
I.e.
The Eigen vector for λ = 1
Case II:
If λ = 2 equation (1) becomes,
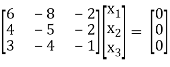
1/6 R1
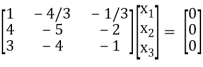
R2 – 4R1 , R3 – 3R1
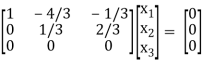
Thus (A – λI) = 2 & n = 3
3 – 2 = 1
Independent variables.
Now rewrite the equations as,
x1 – 4/3 x2 – 1/3 x3 = 0
1/3 x2 + 2/3 x3 = 0
Put x3 = t
1/3 x2 = - 2/3 t
x2 = - 2t
x1 = -4/3 x2 + 1/3 x3
= (-4)/3 (-2t) + 1/3 t
= 3t
x2 = 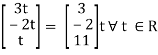
Is the Eigen vector for λ = 2
Now
Case III:-
If λ = 3 equation (1) gives,
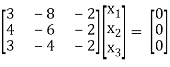
R1 – R2
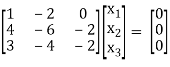
R2 – 4R1, R3 – 3R1
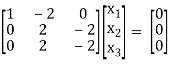
R3 – R2
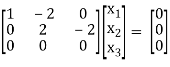
Thus [A – λI] = 2 & n = 3
3 – 2 = 1
Independent variables
Now x1 – 2x2 = 0
2x – 2x3 = 0
Put x3 = t, x2 = t, x1 = 25
Thus
x3 = 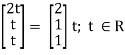
Is the Eigen vector for λ = 3
Key takeaways-
- Let A he a square matrix, λ be any scalar then |A- λ I| = 0 is called characteristic equation of a matrix A.
- If two are more Eigen values are identical then the corresponding Eigen vectors may or may not be linearly independent.
- The Eigen vectors corresponding to distinct Eigen values of a real symmetric matrix are orthogonal
References:
1. Edgar G. Goodaire and Michael M. Parmenter, Discrete Mathematics with Graph Theory, 3rd Ed., Pearson Education (Singapore) P. Ltd., Indian Reprint, 2005.
2. Kenneth Rosen Discrete mathematics and its applications Mc Graw Hill Education 7th edition.
3. V Krishna Murthy, V. P. Mainra, J. L. Arora, An Introduction to Linear Algebra, Affiliated East-West Press Pvt. Ltd.
4. J. L. Mott, A. Kendel and T.P. Baker: Discrete mathematics for Computer Scientists and
5. Mathematicians, Prentice Hall of India Pvt Ltd, 2008.
6. Schaum’s outlines discrete mathematics.
7. Discrete mathematics structures by G.Shanker rao.