Unit - 4

Equilibrium points

4.1 Equilibrium points, interpretation of the phase plane

A single first order differential equation of the form

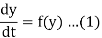
Makes no mention of t in the function f.

Such a differential equation is called autonomous, that is time independent variable t does not appear explicitly. When the independent variable is time, then the system is also known as time invariant.

Example: Consider the autonomous differential equation

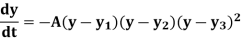
With y1 < y2 < y3. We can give the qualitative behavior using the phase line. This is a line with arrow in the plane pointing to the right at y if f(y) is positive and to the left if f(y) is negative. Thus.

Solutions y(t) move the direction of the arrows as time increases. • A point y0 are called an equilibrium of critical point if f(y0) = 0. This give the trivial solution

y(t) = y0 for all t.

Example: Describe the equilibrium points of

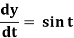
For the equilibrium points.

If both arrows point toward the critical point, it is called stable or a sink. Nearby solutions will converge to the equilibrium point. The solution is stable under small perturbations, meaning that if the solution is disturbed, it will return. y2 is a stable point.

If both arrows point away from the critical point, it is called unstable or source. Nearby solutions will diverge from the equilibrium point, The solution is unstable under small perturbations, meaning that if the solution is disturbed, it will not return. y1 is an unstable point.

If one arrow points towards the equilibrium point, and one points away, it is semi-stable or a node: It is stable in one direction (where the arrow points towards the point), and unstable in the other direction (where the arrow points away from the point). y2 is a node.

More generally, if f has a derivative-

• f’(y) < 0 at stable equilibria,

• f’ (y) > 0 at unstable equilibria.

• f’(y) = 0 at nodes.

Representation as a System of First Order Equations:

For the second order linear ordinary differential equation-

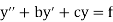
We can write this as system of two first order equations

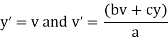
In the case of mass-spring oscillator, v is the velocity. In the case of a circuit in series, we typically write the equation in terms of the charge q,

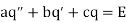
We can write this as the system

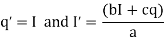
In this case I is the current.

The Phase Plane Equation:

A system of two first order linear ordinary differential equations-

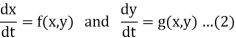
This system is also called autonomous and time invariant.

Exercise:

If (x(t), y(t)) is a solution of (2), and t0 is a real number, then so is (x(t0 + t), y(t0 + t)). By the chain rule

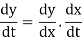
Or

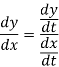
For time invariant systems in (2), this allows us to consider the phase plane equation,

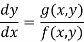
Let us review what the phase plane equation tells us and what it does not tell us.

• A plot of (x(t), y(t)) is a solution of (2) is a curve in the plane, known as a trajectory.

• If (x(t), y(t)) is a solution of (2), then the derivatives of the solution are vectors

(dx/dt, dy/dt) = (f(x, y), g(x, y))

With

– slope dy/dx = g(x, y)/f(x, y)  and

– magnitude (or speed)

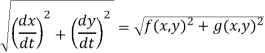
• The trajectory itself does not tell us when the solution arrives at a position (x, y) in the plane, not does it tell us the speed. Indeed, if we were t0 multliply both f and g by a constant α 6= 0, it would not change the trajectory. It would change the speed and it would change the direction of the solution curve is α < 0.

• It does tell us the slope dy/dx which is the tangent line to the trajectory at a position (x, y).

• The solutions to (3) give us these trajectories.

• However, for (2), t is the independent variable. x and y are dependent variables

• The direction fields give us solutions to differential equations with x the independent variable and y dependent. So, even though these plots look very similar, they reveal different information.

Example: An LC circuit, also called a resonant circuit, tank circuit, or tuned circuit, is an electric circuit consisting of an inductor, having inductance L, and a capacitor, having capacitance C, the governing equations for the chage q are

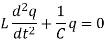
If we have the initial value problem, q(0) = 0, q 0 (0) = I0, then the solution is

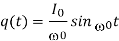
Where 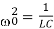 . The current,

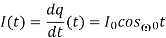
Thus the trajectory

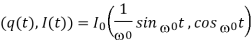
Is an ellipse.

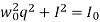
In addition,

In the qIplane the solution (q(t), I(t)) has slope

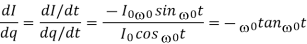
If now, we look at this same equation at a first order system, we have that

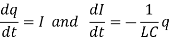
Thus

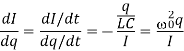
From the solution to the differential equation, we have

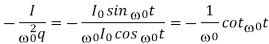
As before.

If we focus on a solution to

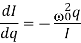
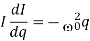
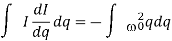
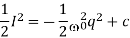
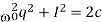
If the trajectory has the point (0, I0), then 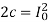, the ellipse we saw before. The difference is that we do not have the time course for the trace of the differential equation along the ellipse.

Equilibrium Points:

As in the of one equation, a point x0, y0 satisfying

f(x0, y0) = 0 and g(x0, y0) = 0

Called a critical point, or equilibrium point, of the autonomous system (2) The corresponding constant solution (x(t), y(t)) = (x0, y0) is called an equilibrium solution.

The set of all critical points is called the critical point set.

Example: for

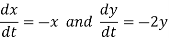
The direction field,

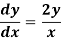
Gives vectors with positive slope in quadrants I and III and negative slope in quadrants I and IV.

So the vector etiher aim toward the equilibrium point (0, 0) or away. Since both x and y are decreasing with time in quadrant I, we can add arrows that point to the origin and the origin is stable.

To solve the phase plane equation

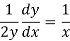
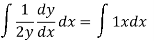
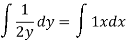
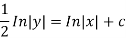
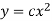
For

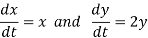
We have the same equilibrium point and the same phase plane equation, but the origins is unstable and the arrows point outward.

Key takeaways:

1. The Phase Plane Equation: A system of two first order linear ordinary differential equations-

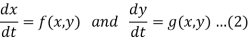
2.     Equilibrium Points: As in the of one equation, a point x0, y0 satisfying

f(x0, y0) = 0 and g(x0, y0) = 0

Called a critical point, or equilibrium point, of the autonomous system (2) The corresponding constant solution (x(t), y(t)) = (x0, y0) is called an equilibrium solution.

4.2 Predatory-prey model and its analysis

Predatory-prey equation is also known as the Lotka-Volterra equations.

The first order non-linear differential equations used to describe the dynamics of biological systems, one as predator and other is prey.

The populations change is represented as-

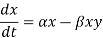
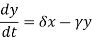
Where

x is the number of prey

y is the number of predator

instantaneous growth rates of the two populations;

t = time

are the parameters.

Physical meaning of the equations:

Predatory-prey model makes a number of assumptions, not necessarily realizable in nature, about the environment and evolution of the predator and prey populations

1. The prey population finds ample food at all times.
2. The food supply of the predator population depends entirely on the size of the prey population.
3. The rate of change of population is proportional to its size.
4. During the process, the environment does not change in favour of one species, and genetic adaptation is inconsequential.
5. Predators have limitless appetite.

Prey:

The prey equation reduces, when multiplied out

The prey are assumed to have an unlimited food supply and to reproduce exponentially, unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet, this is represented above by βxy. If either x or y is zero, then there can be no predation.

With these two terms the equation above can be interpreted as follows: the rate of change of the prey's population is given by its own growth rate minus the rate at which it is preyed upon.

Predator:

The predator equation becomes

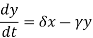
In this equation, δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used, as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). The term γy represents the loss rate of the predators due to either natural death or emigration, it leads to an exponential decay in the absence of prey.

Hence the equation expresses that the rate of change of the predator's population depends upon the rate at which it consumes prey, minus its intrinsic death rate.

Solution of the equations:

The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.

If none of the non-negative parameters α, β, γ, δ vanishes, three can be absorbed into the normalization of variables to leave only one parameter: since the first equation is homogeneous in x, and the second one in y, the parameters β/α and δ/γ are absorbable in the normalizations of y and x respectively, and γ into the normalization of t, so that only α/γ remains arbitrary. It is the only parameter affecting the nature of the solutions.

A linearization of the equations yields a solution similar to simple harmonic motion with the population of predators trailing that of prey by 90° in the cycle.

Example:

Let there are two species of animals, rat (prey) and a snake (predator). If the initial conditions are 10 rats and 10 snakes, one can plot the progression of the two species over time; given the parameters that the growth and death rates of rat are 1.1 and 0.4 while that of snakes are 0.4 and 0.1 respectively. The choice of time interval is arbitrary.

This corresponds to eliminating time from the two differential equations above to produce a single differential equation

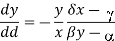
Relating the variables x and y. The solutions of this equation are closed curves. It is amenable to separation of variables: on integrating

Yields the implicit relationship

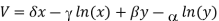
Where V is a constant quantity depending on the initial conditions and conserved on each curve.

Population equilibrium:

Population equilibrium occurs in the model when neither of the population levels is changing, which means when both of the derivatives are equal to 0:

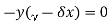
The above system of equations yields two solutions:

{x = 0, y = 0}

And

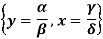
Hence there are two equilibriums.

The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters α, β, γ, and δ.

Key takeaways:

1. The populations change is represented as-

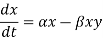
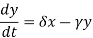
2.     Prey:

The prey equation reduces, when multiplied out

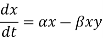
3.     Predator:

The predator equation becomes

4.3 Epidemic model of influenza and its analysis

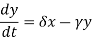
Overview (Influenza):

Every year, influenza causes high morbidity and mortality especially among the immune-compromised persons worldwide. The emergence of drug resistance has been a major challenge in curbing the spread of influenza.

Influenza is a contagious respiratory illness caused by influenza viruses. There are three major types of flu viruses: types A, B, and C. The majority of human infections are caused by types A and B. Of major concern is influenza A virus which is clinically the most vicious. It is a negative-sense single-stranded RNA virus with eight gene segments. The segmented nature of influenza A virus genome allows the exchange of gene segments between viruses that coinfect the same cell

This process of genetic exchange is termed reassortment. Reassortment leads to sudden changes in viral genetics and to susceptibility in hosts. Influenza A virus has a wide range of susceptible avian hosts and mammalian hosts such as humans, pigs, horses, seals, and mink. In addition, the virus is able to repeatedly switch hosts to infect multiple avian and mammalian species. The unpredictability of influenza A virus evolution and interspecies movement creates continual public health challenges.

Influenza can be prevented by getting vaccination each year. However, given that the virus mutates rapidly, a vaccine made for one year may not be useful in the following year. In addition, antigenic drift in the virus may occur after the year’s vaccine has been formulated, rendering the vaccine less protective, and hence, outbreaks can easily occur especially among high-risk individuals. According to, other preventive actions include staying away from people who are sick, covering coughs and sneezes, and frequent handwashing.

Influenza spreads rapidly around the world during seasonal epidemics and pandemics.

It has afflicted the human population for centuries. For instance, the 1918 influenza pandemic infected nearly one quarter of the world’s population and resulted in the deaths of about 100 million people.

Studies show that this pandemic is especially responsible for the high morbidity and mortality among vulnerable groups such as children, the elderly, and patients with underlying health conditions.

Within the past one hundred years, there have been four pandemics resulting from the emergence of a novel influenza strain for which the human population possessed little or no immunity. 

Mathematical formulation:

The model subdivides the total population into five compartments: Susceptible (S), Vaccinated (V), Infected with Wild-type strain 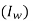Infected with Resistant strain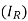, and Recovered (R). Individuals in a given compartment are assumed to have similar characteristics. Parameters vary from compartment to compartment but are identical for all individuals in a given compartment. Individuals enter the population at the rate of π, and all recruited individuals are assumed to be susceptible. The Susceptible get infected after effective contact with either the Infected with Wild-type strain or the Infected with Resistant strain. The force of infection is given by either (Infection by Wild-type strain) or 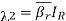  (Infection by Resistant strain), where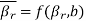

Parameters 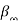 and 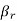 refer to the transmission rate of wild-type strain and resistant strain, respectively. Parameter b is the rate of developing drug resistance. The susceptible can only be infected by one strain at a time. The rate of vaccination is ϕ. The vaccinated can also become infected with either the wild-type strain or the resistant strain. This depends on the vaccine efficacy. When the vaccine efficacy is 100%, the vaccinated cannot become infected. Individuals who are infected with the wild-type strain are treated and recover at the rate of α, while those who are infected with the resistant strain recover at the rate of  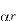. The wild-type strain is assumed to mutate to resistant strain, and hence, those infected with the wild type join those infected with the resistant strain at the rate of b. Individuals with wild-type strain and those with resistant strain suffer disease-induced death at the rates   and 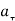, respectively. The recovered lose immunity at the rate of ϑ joins the susceptible class. Individuals in all the epidemiological compartments suffer natural death at the rate of μ. The model diagram is given in Figure-

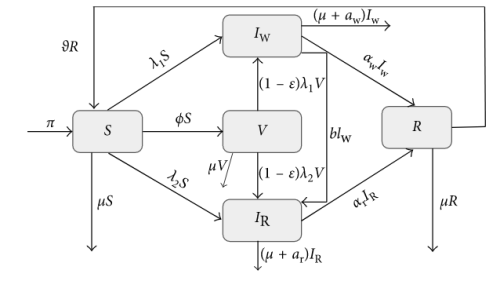
Model equation:

The following system of nonlinear ordinary differential equations, with nonnegative initial conditions, describes the dynamics of influenza:

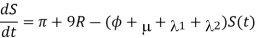
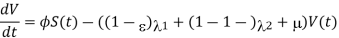
Where 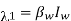and 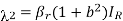We assume that all the model parameters are positive and the initial conditions of the model system (1) are given by

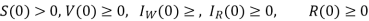
The parameters are given below

Parameter	Description	Value
	Transmission rate of wild-type strain	0.00102 da
	Transmission rate of resistant strain	0.00102 da
	Vaccination efficacy	0.77
	Vaccination rate	0.00027375 da
B	Rage of developing drug resistance	0.118
	Recovery rate for individual in 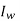class	0.1998 da
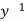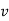	Recovery rate for individual in class	0.0714 da
	Rate of losing immunity	0.00833 da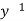
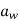	Death rate due to infection with wild-type strain	0.01
	Average human life span	70×365 days
Π	Recruitment rate	0.0381
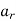	Death rate due to infection with resistant rain	0.021

Model analysis:

Positivity of Solutions:

The model system (1) monitors the changes in human population. It is therefore important to prove that the solutions of system (1) with nonnegative initial conditions will remain nonnegative for all  t > 0. Thus, we have the following theorem:

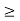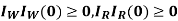Theorem: Given that the initial conditions of system (1) are S(0) > 0, V(0) 0, and 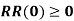the solutions S(t), V(t),   and R(t) are non-negative for all t > 0.

Proof:

Assume that

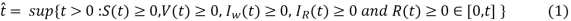
Thus 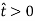 , and it follows directly from the first equation of system (1) that

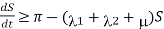……… (2)

Using the integrating factor method to solve inequality (2), we have

………(3)

Integrating both sides, we get

…………(4)

Where C is the constant. Hence,

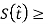S(0)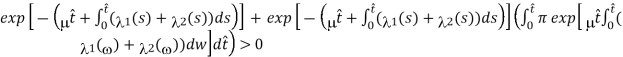……….. (5)

Hence, 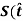)>0

From the second equation in system (1), we obtain

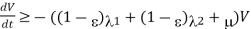………. (6)

Hence

……… (7)

Similarly, it can be shown that

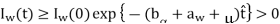
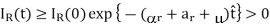
…….. (8)

Therefore, all the solutions of system (1) with nonnegative initial conditions will remain nonnegative for all time t > 0.

Invariant Region:

We show that the total population is bounded for all time t > 0. The analysis of system (1) will therefore be analyzed in a region  of biological interest. Thus, we have the following theorem on the region that system (1) is restricted to.

Theorem:

The feasible region  defined by

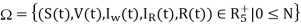
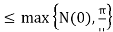…….. (i)

The initial conditions is positively invariant and attracting with respect to system (1) for all t > 0.

Proof. Summing up the equations in (1) [above], we obtain that the total population satisfies the following differential equation:

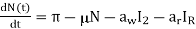……. (ii)

In the absence of influenza infection, it follows that

…….. (iii)

It can easily be seen that

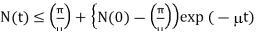…….. (iv)

From (iv), we observe that as t , , so if then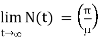

On other hand if 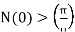then N will decrease to 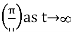This means that 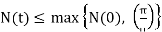therefore N(t) is bounded above. Subsequently are bounded above. Thus, in  system (1) is well posed. Hence, it is sufficient to study the dynamics of the system in 

Existence of Equilibrium Points

In the absence of influenza 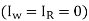, system (1) has a disease-free equilibrium, which is given by

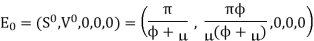
References:

1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
2. P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
4. W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
5. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
7. T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
8. J. Sinha Roy and S Padhy: A course of Ordinary and Partial differential equation Kalyani
9. Martin Braun, Differential Equations and their Applications, Springer International, Student Ed. Publishers, New Delhi.
10. Higher engineering mathematics, HK Dass