Unit - 1
Review of Algebraic and Order Properties of R
In this unit we will discuss about the real number system.
You already know that- the set N of natural numbers, the set Z of integers, and the set Q of rational numbers. You know that N 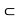 Z
Z 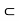 Q. You also know the arithmetic operations, addition and multiplication of two natural numbers, integers, and rational numbers. You also know the order relation m < n between two integers, more generally between two rational numbers.
Q. You also know the arithmetic operations, addition and multiplication of two natural numbers, integers, and rational numbers. You also know the order relation m < n between two integers, more generally between two rational numbers.
The system of real numbers has been evolved in different ways by different mathematicians. In the late 19th Century, the two famous German mathematicians Richard Dedekind [1815-1897] and George Cantor [1845-1918] gave two independent approaches for the construction of real numbers. During the same time, an Italian mathematician, G. Peano [1858-1932] defined the natural numbers by the well-known Peano Axioms. However, we start with the set of natural numbers as the foundation and build up the integers. From integers, we construct the rational numbers and then through the set of rational numbers, we reach the stage of real numbers. This development of number system culminates into the set of complex numbers. A detailed study of the system of numbers leads us to a beautiful branch of Mathematics namely.
Algebra of the Real Number System:
The set R of real numbers is a set which contains Q and on which we continue to have arithmetic operations and an order relation. There are some properties of the real number system listed below
The properties of the addition of real numbers are
- x + y = y + x for x, y
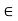 R. (Commutativity of Addition)
R. (Commutativity of Addition) - (x + y) + z = x + (y + z) for all x, y, z
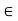 R. (Associativity of Addition)
R. (Associativity of Addition) - There exists a unique element 0
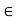 R such that x + 0 = 0 + x = x for all x
R such that x + 0 = 0 + x = x for all x 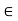 R. (Existence of Additive Identity or Zero)
R. (Existence of Additive Identity or Zero) - For every x
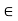 R, there exists a unique element y
R, there exists a unique element y 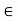 R such that x + y = 0 We denote this y by -x. (Existence of Additive Inverse)
R such that x + y = 0 We denote this y by -x. (Existence of Additive Inverse)
The properties of the multiplication of real numbers are
- x . y = y . x for all x, y
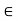 R. (Commutativity of Multiplication)
R. (Commutativity of Multiplication) - x . (y . z) = (x . y) . z for all x, y, z
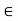 R. (Associativity of Multiplication)
R. (Associativity of Multiplication) - There exists a unique element 1
 R such that x . 1 = 1 . x = x for all x
R such that x . 1 = 1 . x = x for all x 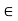 R. (Existence of Multiplicative Identity)
R. (Existence of Multiplicative Identity) - Given x
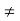 0 in R, there exists a unique y such that xy = 1 = yx.We denote this y by 1/x or
0 in R, there exists a unique y such that xy = 1 = yx.We denote this y by 1/x or  (Existence of Multiplicative Inverse or Reciprocal)
(Existence of Multiplicative Inverse or Reciprocal)
For all x, y, z  R, we have x . (y + z) = x . y + x . z. (Distributivity of multiplication . Over addition +.)
R, we have x . (y + z) = x . y + x . z. (Distributivity of multiplication . Over addition +.)
There is an order relation on R which satis_es the Law of Trichotomy. Given
Any two real numbers x and y, one and exactly one of the following is true:
Law of Trichotomy: x = y, x < y, or y < x.
We often write y > x to denote x < y. Also, the symbol x _ y means either x = y
Or x < y, and so on.
Some of the important facts about order relation in R-
(1) If x < y and y < z, then x < z. (Transitivity)
(2) If x < y and z 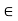 R, then x + z < y + z.
R, then x + z < y + z.
(3) If x < y and z > 0, then xz < yz.
(4) If x < y, then -y < -x.
(5) For any x 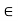 R,
R, 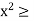 0. In particular, 0 < 1.
0. In particular, 0 < 1.
(6) If x > 0 and y < 0, then xy < 0.
(7) If 0 < x < y, then 0 < 1/y < 1/x.
Key takeaways:
- The set R of real numbers is a set which contains Q and on which we continue to have arithmetic operations and an order relation.
- x + y = y + x for x, y
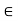 R. (Commutativity of Addition)
R. (Commutativity of Addition) - (x + y) + z = x + (y + z) for all x, y, z
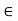 R. (Associativity of Addition)
R. (Associativity of Addition) - Law of Trichotomy: x = y, x < y, or y < x.
The Real Line
A convenient and familiar geometric interpretation of the real number system is the real line. In this interpretation, the absolute value jaj of an element a in R is regarded as the distance from a to the origin 0. More generally, the distance between elements a and b in R is |a - b|. If a is a given real number, then saying that a real number x is ‘‘close to’’ a should mean that the distance jx _ aj between them is ‘‘small.’’ A context in which this idea can be discussed is provided by the terminology of neighborhoods, which we now define.
ε-neighborhood of a point in R-
Let a 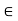 R and
R and 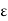 > 0. Then the
> 0. Then the 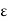 -neighborhood of a is the set-
-neighborhood of a is the set-
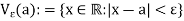
For a 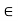 R, the statement that x belongs to
R, the statement that x belongs to 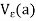 is equivalent to either of the statements
is equivalent to either of the statements
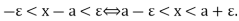

Examples (a) Let U := {x : 0 < x < 1}. If a 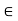 U, then let e be the smaller of the two numbers a and 1 - a. Then it is an exercise to show that
U, then let e be the smaller of the two numbers a and 1 - a. Then it is an exercise to show that  is contained in U. Thus each element of U has some e-neighborhood of it contained in U. (b) If I := {x : 0
is contained in U. Thus each element of U has some e-neighborhood of it contained in U. (b) If I := {x : 0 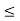 x
x 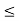 1}, then for any
1}, then for any 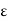 > 0, the e-neighborhood
> 0, the e-neighborhood 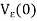 of 0 contains points not in I, and so
of 0 contains points not in I, and so 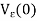 is not contained in I. For example, the number
is not contained in I. For example, the number 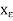 := - e/2 is in
:= - e/2 is in 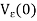 but not in I.
but not in I.
Key takeaways:
Let a  R and
R and 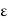 > 0. Then the
> 0. Then the 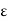 -neighborhood of a is the set-
-neighborhood of a is the set-
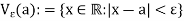
Definition of ordered field:
We defined the order relation 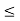 in R. It is easy to see that this order relation satisfies the following properties:
in R. It is easy to see that this order relation satisfies the following properties:
Let x, y, z be any elements of R. Then
O1: For any two elements x and y of R, one and only of the following holds:
(i) x < y, (ii) y < x, (iii) x = y,
O2: x 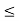 y, y
y, y 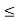 x implies x
x implies x  z,
z,
O3: x 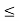 y implies x
y implies x 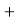 z
z 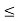 y + z,
y + z,
O4: x 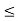 y, 0 < z implies x.z
y, 0 < z implies x.z 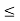 y.z
y.z
Complete Ordered Field
Although R and Q are both ordered fields, yet there is a property associated with the order relation which is satisfied by R but not by Q. This property is known as the Order-Completeness, introduced for the first time by Richard Dedekind.
Suppose set S = {1, 3, 5, 7). You can see that each element of S is less than or equal to 7. That is x  7, for each x
7, for each x  S. Take another set S, where S = {x
S. Take another set S, where S = {x  R : x
R : x 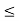 17). Once again, you see that each element of S is less than 18. That is, x < 18, for each x
17). Once again, you see that each element of S is less than 18. That is, x < 18, for each x 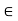 S. In both the examples, the sets have a special property namely that every element of the set is less than or equal to some number.
S. In both the examples, the sets have a special property namely that every element of the set is less than or equal to some number.
This number is called an upper bound of the corresponding set and such a set is said to be bounded above.
Upper Bound of a Set
Let S 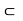 R. If there is a number u
R. If there is a number u 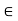 R such that x
R such that x 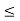 u, for every x
u, for every x 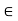 S, then S is said to be bounded above. The number u is called an upper bound of S.
S, then S is said to be bounded above. The number u is called an upper bound of S.
Example: Verify whether the following sets are bounded above. Find an upper bound of the set, if it exists.
(i) The set of negative integers
{–1, –2, –3, ......}.
(ii) The set N of natural numbers.
(iii) The sets Z, Q and R.
Sol:
(i) The set is bounded above with –1 as an upper bound,
(ii) The set N is not bounded above.
(iii) All these sets are not bounded above.
Now consider a set S = {2, 3, 4, 5, 6, 7). You can easily see that this set is bounded above because 7 is an upper bound of S. Again this set is also bounded below because 2 is a lower bound of S.
Thus S is both bounded above as well as bounded below. Such a set is called a bounded set.
Consider the following sets:
S1 = {... –3, –2, –1, 0, 1, 2, ......},
S2 = {0, 1, 2, ......},
S3 = (0, –1, –2, ......}.
You can easily see that S, is neither bounded above nor bounded below. The set S4 is not bounded above while S, is not bounded below. Such sets are known as Unbounded Sets.
Bounded Sets
A set S is bounded if it is both bounded above and bounded below.
In other words, S has an upper bound as well as a lower bound. Thus, if S is bounded, then there exist numbers u (an upper bound) and v (a lower bound) such that v 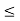 x
x  u, for every x
u, for every x 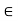 S.
S.
If a set S is not bounded then S is called an unbounded set. Thus S is unbounded if either it is not bounded above or it is not bounded below.
Example:
(i) Any finite set is bounded.
(ii) The set Q of rational numbers is unbounded.
(iii) The set R of real numbers is unbounded.
(iv) The set P = {sin x, sin 2x, sin 3x,......, sin nx, ......} is bounded because –1 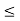 sin nx
sin nx 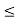 1, for every n and x.
1, for every n and x.
Key takeaways:
- Although R and Q are both ordered fields, yet there is a property associated with the order relation which is satisfied by R but not by Q. This property is known as the Order-Completeness
- Let S
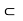 R. If there is a number u
R. If there is a number u 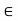 R such that x
R such that x  u, for every x
u, for every x 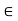 S, then S is said to be bounded above. The number u is called an upper bound of S.
S, then S is said to be bounded above. The number u is called an upper bound of S. - A set S is bounded if it is both bounded above and bounded below.
If a set S is bounded above, then it has an infinite number of upper bounds. Choose the least of these upper bounds. This is called the least upper bound of the set S and is known as the Supremum of the set S. (The word ’Supremum’ is a Latin word).
The Supremum of a Set:
Let S be a set bounded above. The least of all the upper bounds of S is called the least upper bound or the Supremum of S. Thus, if a set S is bounded above, then a real number m is the supremum of S if the following two conditions are satisfied:
(i) m is an upper bound of S,
(ii) if k is another upper bound of S, then m 5 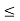 k.
k.
The greatest lower bound, in Latin terminology, is called the Infimum of a set.
Example: Each of the intervals ]a, b[, [a, b] ]a, b], [a, b[ has both the supremum and the infimum. The number a is the infimum and b is the supremum in each case. In case of [a, b] the supremum and the infimum both belong to the set whereas this is not the case for the set ]a, b[.
In case of the set ]a, b], the infimum does not belong to it and the supremum belongs to it. Similarly, the infimum belongs to [a, b[ but the supremum does not belong to it.
Theorem 1: Prove that the supremum of a set, if it exists, is unique.
Proof: If possible, let there be two supremums (Suprema) say m and m’ of a set $.
Since m is the least upper bound of S, therefore by definition, we have
m  m’
m’
Similarly, since m’ the least upper bound of S, therefore, we must have
M’  m.
m.
This shows that m = m’ which proves the theorem.
Do by yourself- Prove that the infimum of a set, if it exists, is unique.
Note- If the supremum of a set belongs to the set, then it is called the greatest member of the set. Similarly, if the infimum of a set belongs to it, then it is called the least member of the set.
Completeness Property:
Every non-empty subset S of R which is bounded above, has the supremum.
Similarly, we have every non-empty subset S of R that is bounded below, has the infimum.
In fact, it can be easily shown that the above two statements are equivalent.
Now, if you consider a non-empty subset S of Q, then S considered as a subset of R must have, by property, a supremum. However, this supremum may not be in Q. This fact is expressed by saying that Q considered as a field in its down right is not Order-Complete. We illustrate this observation as follows:
Construct a subset S of Q consisting of all those positive rational numbers whose squares are less than 2 i.e.
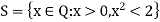
Since the number 1 ES, therefore S is non-empty. Also, 2 is an upper bound of S because every element of S is less than 2. Thus the set S is non-empty and bounded, above. According to the
Axiom of Completeness of R, the subset S must have the supremum in R. We claim that this supremum does not belong to Q.
Archimedean Property:
If x 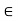 R, then there exists
R, then there exists 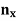
 N such that x
N such that x 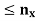
Proof:
If the assertion is false, then n 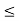 x for all n
x for all n 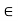 N; therefore, x is an upper bound of N. Therefore, by the Completeness Property, the nonempty set N has a supremum u
N; therefore, x is an upper bound of N. Therefore, by the Completeness Property, the nonempty set N has a supremum u 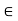 R. Subtracting 1 from u gives a number u - 1, which is smaller than the supremum u of N. Therefore u - 1 is not an upper bound of N, so there exists m
R. Subtracting 1 from u gives a number u - 1, which is smaller than the supremum u of N. Therefore u - 1 is not an upper bound of N, so there exists m 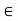 N with u - 1 < m. Adding 1 gives u < m + 1, and since m + 1
N with u - 1 < m. Adding 1 gives u < m + 1, and since m + 1 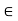 N, this inequality contradicts the fact that u is an upper bound of N.
N, this inequality contradicts the fact that u is an upper bound of N.
Corollary: If S := {1/n : n  N}, then inf S = 0.
N}, then inf S = 0.
Proof:
Since S  is bounded below by 0, it has an infimum and we let w := inf S. It is clear that w
is bounded below by 0, it has an infimum and we let w := inf S. It is clear that w 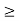 0. For any
0. For any 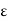 > 0, the Archimedean Property implies that there exists n
> 0, the Archimedean Property implies that there exists n 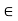 N such that 1/
N such that 1/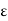 < n, which implies 1/n <
< n, which implies 1/n < 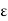 . Therefore we have
. Therefore we have
0 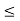 w
w  1/n <
1/n < 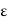 : But since
: But since  > 0 is arbitrary
> 0 is arbitrary
Corollary If t > 0, there exists 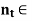 N such that 0 < 1/
N such that 0 < 1/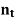 < t.
< t.
Proof:
Since inf {1/n : n  N} = 0 and t > 0, then t is not a lower bound for the set
N} = 0 and t > 0, then t is not a lower bound for the set
{1/n : n 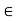 N}. Thus there exists
N}. Thus there exists 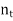
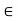 N such that 0 < 1/
N such that 0 < 1/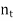 < t.
< t.
Key takeaways:
- If a set S is bounded above, then it has an infinite number of upper bounds.
- The supremum of a set, if it exists, is unique.
- If the supremum of a set belongs to the set, then it is called the greatest member of the set.
- Every non-empty subset S of R which is bounded above, has the supremum. Similarly, we have every non-empty subset S of R that is bounded below, has the infimum.
- Archimedean Property:
If x 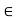 R, then there exists
R, then there exists 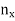
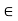 N such that x
N such that x 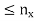
The importance of the Supremum Property lies in the fact that it guarantees the existence of real numbers under certain hypotheses. We shall make use of it in this way many times. At the moment, we shall illustrate this use by proving the existence of a positive real number x such that  = 2; that is, the positive square root of 2. We know that an x cannot be a rational number; thus, we will be deriving the existence of at least one irrational number.
= 2; that is, the positive square root of 2. We know that an x cannot be a rational number; thus, we will be deriving the existence of at least one irrational number.
Theorem- There exists a positive real number x such that 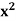 = 2.
= 2.
Proof:
Let S :{s 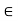 R : 0
R : 0 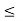 s;
s; 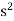 < 2}. Since 1
< 2}. Since 1 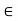 S, the set is not empty. Also, S is bounded above by 2, because if t > 2, then
S, the set is not empty. Also, S is bounded above by 2, because if t > 2, then  > 4 so that t does not belongs to S. Therefore the Supremum Property implies that the set S has a supremum in R, and we let x := sup S. Note that x > 1.
> 4 so that t does not belongs to S. Therefore the Supremum Property implies that the set S has a supremum in R, and we let x := sup S. Note that x > 1.
We will prove that 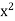 = 2 by ruling out the other two possibilities:
= 2 by ruling out the other two possibilities: 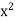 < 2 and
< 2 and 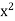 > 2.
> 2.
First assume that  < 2. We will show that this assumption contradicts the fact that
< 2. We will show that this assumption contradicts the fact that
x = sup S by finding an n 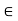 N such that x + 1/n
N such that x + 1/n 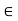 S, thus implying that x is not an upper bound for S. To see how to choose n, note that 1/
S, thus implying that x is not an upper bound for S. To see how to choose n, note that 1/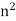
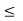 1/n so that
1/n so that
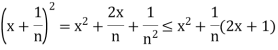
Hence if we can choose n so that
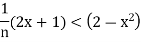
Then we get 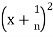 <
< 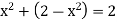 . By assumption we have 2 -
. By assumption we have 2 - 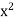 > 0, so that (2-
> 0, so that (2-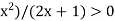 . Hence the Archimedean Property can be used to
. Hence the Archimedean Property can be used to
Obtain n 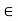 N such that
N such that
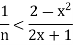
These steps can be reversed to show that for this choice of n we have x + 1=n 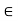 S, which contradicts the fact that x is an upper bound of S. Therefore we cannot have
S, which contradicts the fact that x is an upper bound of S. Therefore we cannot have 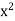 < 2.
< 2.
Now assume that 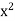 > 2.We will show that it is then possible to find m
> 2.We will show that it is then possible to find m  N such that
N such that
x - 1=m is also an upper bound of S, contradicting the fact that x = sup S. To do this, note that
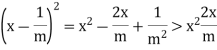
Hence if we can choose m so that
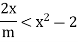
Then 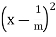 >
> >
> 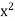 – (
– (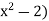 equals 2Now by assumption we have
equals 2Now by assumption we have 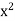 - 2 > 0, so that
- 2 > 0, so that 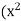 - 2)/2x > 0. Hence, by the Archimedean Property, there exists m
- 2)/2x > 0. Hence, by the Archimedean Property, there exists m 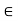 N such that
N such that
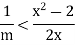
These steps can be reversed to show that for this choice of m we have 
Now if s 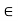 S, then
S, then 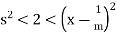 , whence it follows that s < x – 1/m. This implies that x - 1/m is an upper bound for S, which contradicts the
, whence it follows that s < x – 1/m. This implies that x - 1/m is an upper bound for S, which contradicts the
Fact that x = sup S. Therefore we cannot have 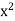 > 2. Since the possibilities
> 2. Since the possibilities 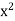 < 2 and
< 2 and 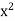 > 2 have been excluded, we must have
> 2 have been excluded, we must have 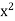 = 2. By slightly modifying the preceding argument, the reader can show that if a > 0, then there is a unique b > 0 such that
= 2. By slightly modifying the preceding argument, the reader can show that if a > 0, then there is a unique b > 0 such that 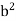 = a.We call b the positive square root of a and denote it by b =
= a.We call b the positive square root of a and denote it by b = 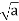 or b =
or b = 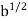 A slightly more complicated argument involving the binomial theorem can be formulated to establish the existence of a unique positive nth root of a.
A slightly more complicated argument involving the binomial theorem can be formulated to establish the existence of a unique positive nth root of a.
Density of Rational Numbers in R-
We now know that there exists at least one irrational real number, 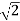 .
.
Actually there are ‘‘more’’ irrational numbers than rational numbers in the sense that the set of rational numbers is countable, while the set of irrational numbers is uncountable.
However, we next show that in spite of this apparent disparity, the set of rational numbers is ‘‘dense’’ in R in the sense that given any two real numbers there is a rational number between them (in fact, there are infinitely many such rational numbers).
The Density Theorem-
If x and y are any real numbers with x < y, then there exists a rational number r 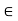 Q such that x < r < y.
Q such that x < r < y.
Note- If x and y are real numbers with x < y, then there exists an irrational number z such that x < z < y.
Intervals: An interval in R is an non-empty subset of R which has the property that, whenever two numbers a and b belong to it, all numbers between a and b also belong to it.
Or in other words, A subset J 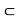 R is said to be an interval if a, b
R is said to be an interval if a, b 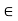 J and if
J and if
a < x < b, we then have x 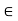 J:
J:
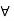 a, b
a, b  J and a < x < b =) x
J and a < x < b =) x  J
J
A real number x such that a < x < b is said to be between a and b.
The set N of natural numbers is not an interval because while 1 and 2 belong to N, but 1.5 which lies between 1 and 2, does not belong to N.
Let a, b 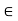 R with a
R with a 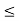 b.
b.
(i) Consider the set {x 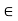 R : a
R : a 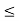 x
x 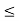 b}. This set is denoted by ]a, b[, and is called a closed interval. Note that the-end points a and b are included in it.
b}. This set is denoted by ]a, b[, and is called a closed interval. Note that the-end points a and b are included in it.
(ii) Consider the set{x 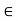 R : a < x < b}. This set is denoted by [a, b], and is called an open interval. In this case the end points a and b are not included in it,
R : a < x < b}. This set is denoted by [a, b], and is called an open interval. In this case the end points a and b are not included in it,
(iii) The interval {x 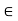 R: a
R: a 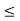 x < b} is denoted by [a, b[.
x < b} is denoted by [a, b[.
(iv) The interval {x 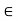 R : a < x
R : a < x  b} is denoted by ]a, b].
b} is denoted by ]a, b].
Example: Let a 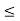 b be real numbers. We define
b be real numbers. We define
[a, b] {x
{x 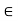 R: a
R: a 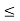 x
x 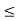 b}
b}
(a, b)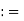 {x
{x 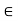 R: a < x < b}
R: a < x < b}
[a, b)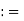 {x
{x 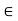 R: a
R: a 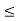 x < b}
x < b}
[a, b)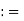 {x
{x 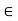 R: a < x
R: a < x 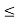 b}
b}
[a, )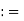 {x
{x 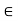 R: x
R: x 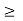 a}
a}
(a, ) {x
{x 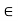 R: x > a}
R: x > a}
(-, b] {x
{x 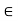 R: x
R: x 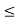 b}
b}
(-, b)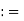 {x
{x 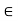 R: x < b}
R: x < b}
(-, ) R
R
Intervals of these types are called bounded intervals. But remember that these are not finite sets. In fact these are infinite sets except for the case [a, a] = {a}.
We can easily verify that an open interval ]a, b[ as well as ]a, b] and [a, b[ are always contained in the closed interval [a, b].
Open set: X a set S is said to be open if it is a neighbourhood of each of its points. Thus, a set S is open if for each x in S, there exists an open interval ]x – 6, x +  [,
[, > 0 such that
> 0 such that
x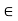 ] x –
] x – 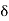 , x +
, x + 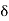 [
[ 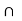 S.
S.
It follows at once that a set S is not open if it is not a neighbourhood of even one of its points.
Example: An open interval is an open set
Sol:
Let ]a, b[ be an open interval. Then a < b. Let c] a, b[. Then a < c < b and therefore
c – a > 0 and b – c > 0
Choose
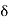 = Minimum of {b – c, c – a)
= Minimum of {b – c, c – a)
= Min (b – c, c – a).
Note that b – c > 0, c – a > 0. Therefore 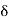 > 0.
> 0.
Now 
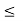 c – a
c – a 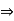 a
a 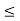 c –
c –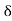
And 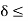 b – c
b – c 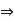 c +
c + 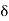 < b.
< b.
i.e.
Therefore,]c – 6, c +  [
[ 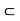 ]a, b[ and hence ]a, b[ is a neighbourhood of c.
]a, b[ and hence ]a, b[ is a neighbourhood of c.
Example:
(i) The sat R of real numbers is an open set
(ii) The null set f is an open set
(iii) A finite set is not an open set
(iv) The interval ]s, b] is not an open set.
Example: Prove that the intersection of any two open sets is an open set.
Sol:
Let A and B be any two open sets. Then we have to show that A B is also an open set.
If A 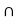 B =
B =  , then obviously A
, then obviously A 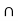 B is an open set. Suppose A
B is an open set. Suppose A 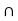 B
B 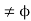 .
.
Let x be an arbitrary element of A 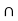 B.
B.
Then x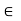 A
A 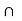 B
B  x
x A and x
A and x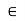 B.
B.
Since A and B are open sets, therefore A and B are both neighbourhoods of x. Hence A 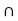 B is a neighbourhood of x. But x
B is a neighbourhood of x. But x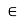 A
A  B is chosen arbitrarily. Therefore, A
B is chosen arbitrarily. Therefore, A  B is a NBD of each of its points and hence A
B is a NBD of each of its points and hence A  B is an open set. This proves the result.
B is an open set. This proves the result.
Do by yourself- Prove that the union of any two open sets is an open set.
Closed sets: Suppose the set S = {x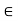 R : 0
R : 0 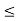 5 x < 1}. In this set, 1 is a limit point of S but it does not belong to S. But if you take S = {x: 0
5 x < 1}. In this set, 1 is a limit point of S but it does not belong to S. But if you take S = {x: 0  x
x 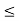 1}, then all the limit points of S belong to S. Such a set is called a closed set.
1}, then all the limit points of S belong to S. Such a set is called a closed set.
A closed set can be defined as follows:
“A set is said to be closed if it contains all its limit points.”
Example: (i) Every closed and bounded interval such as [a, b] and [0, 1] is a closed set.
(ii) An open interval is not a closed set.
(iii) The set R is a closed set because every real number is a limit point of R and it belongs to R.
(iv) The null set is a closed set
(v) The set S = {1 / n: n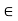 N} is not a closed set.
N} is not a closed set.
(vi) The set ]a, 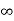 [ is not a closed set, but ] –
[ is not a closed set, but ] –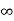 , a] is a closed set
, a] is a closed set
Note - there is a fundamental connection between open and closed sets. Consider, the following subsets of R:
(i) ]0, 4[
(ii) [–2, 5]
(iii) ]0, = 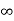 [
[
(iv) ] –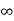 > 6].
> 6].
The sets (i) and (iii) are open while (ii) and (iv) are closed. If you consider their complements, then the complements of the open sets are closed while those of the closed sets are open.
Theorem: A set is closed if and only if its complement is open.
Proof: We assume that S is a closed set. Then we prove that its complement Sc is open.
To show that 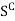 is open, we have to prove that
is open, we have to prove that  is a NBD of each of its points. Let x
is a NBD of each of its points. Let x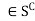 . Then, x
. Then, x 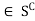 implies x
implies x  S. This means x is not a limit point of S because S is given to be a closed set. Therefore, there exists a
S. This means x is not a limit point of S because S is given to be a closed set. Therefore, there exists a 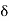 > 0 such that ]x –
> 0 such that ]x – 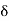 , x +
, x + 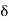 [ contains no points of S. This means that ]x –
[ contains no points of S. This means that ]x –  , x +
, x + 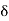 [ is contained in Sc. This further implies that Sc is a NBD of x. In other words,
[ is contained in Sc. This further implies that Sc is a NBD of x. In other words,  is an open set, which proves the assertion.
is an open set, which proves the assertion.
Conversely, let a set S be such that its complement 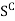 is open. Then we prove that S is closed. To show that S is closed, we have to prove that every limit point x of S belongs to S. Suppose x
is open. Then we prove that S is closed. To show that S is closed, we have to prove that every limit point x of S belongs to S. Suppose x  S, Then x
S, Then x  .
.
This implies that 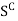 is a NBD of x because Sc is open. This means that there exists an open interval
is a NBD of x because Sc is open. This means that there exists an open interval
]x – 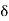 , x +
, x + 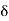 [, for some 6 > 0, such that
[, for some 6 > 0, such that
]x – 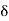 , x +
, x + 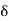 [
[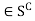
In other words, ]x –  , x +
, x + 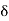 [ contains no point of S. Thus x is not a limit point of S, which is a contradiction. Thus our supposition is wrong and hence, x
[ contains no point of S. Thus x is not a limit point of S, which is a contradiction. Thus our supposition is wrong and hence, x 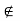 S is not possible. In other words, the (limit) point x belongs to S and thus S is a closed set.
S is not possible. In other words, the (limit) point x belongs to S and thus S is a closed set.
Limit point of a set: A number p is said to be a limit point of a set S of real numbers if every neighbourhood of p contains at least one point of the set S different from p.
Examples:
- Every point in Q, (the set of rational numbers), is a limit point of Q, because for every rational number r and
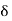 > 0, i.e. ] r – 6, r +
> 0, i.e. ] r – 6, r +  [ has at least one rational number different from r. This is because of the reason that there are infinite rationals between any two real numbers.
[ has at least one rational number different from r. This is because of the reason that there are infinite rationals between any two real numbers. - The set N of natural numbers has no limit point because for every real number a, you can always find
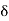 > 0 such that ]a – 6, a +
> 0 such that ]a – 6, a + 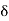 [ does not contain a point of the set N other than a.
[ does not contain a point of the set N other than a. - Every point of the interval ]a, b] is its limit point. The end points a and b are also the limit points of ]a, b]. But the limit point a does not belong to it whereas the limit point b belongs to it.
- Every point of the set [a,
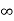 [ is a limit point of the sets. This is also true for ] –
[ is a limit point of the sets. This is also true for ] –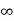 , a[.
, a[.
Note-
(i) A limit point of set may or may not belong to the set,
(ii) A set may have no limit point,
(iii) A set may have only one limit point.
(iv) A set may have more than one limit point.
Key takeaways:
- An interval in R is an non-empty subset of R which has the property that, whenever two numbers a and b belong to it, all numbers between a and b also belong to it.
- X a set S is said to be open if it is a neighbourhood of each of its points.
- “A set is said to be closed if it contains all its limit points.”
Statement: Every infinite bounded set has a limit point.
Proof:
Let S be a infinite bounded set and m, M its infimum and supremum respectively.
Suppose P is a set of real numbers defined as follows:
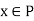 iff it exceeds at the most a finite number of members of S.
iff it exceeds at the most a finite number of members of S.
The set P is non-empty for  . Also M is an upper bound of P. For no number greater than or equal to M can belong to P. Thus the real number set P is non-empty and is bounded above.
. Also M is an upper bound of P. For no number greater than or equal to M can belong to P. Thus the real number set P is non-empty and is bounded above.
Therefore by the order-completeness property, P has a supremum say 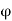 .
.
We shall now show that 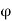 is a limit point of S.
is a limit point of S.
Consider any neighbourhood ] 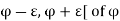 where
where 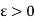
Since 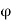 is the supremum of P, there exists at least one member say
is the supremum of P, there exists at least one member say of P such that
of P such that 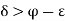 .
.
Now 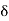 belongs to P, therefore it exceeds at the most a finite number of members of S, and consequently
belongs to P, therefore it exceeds at the most a finite number of members of S, and consequently  can exceed at the most a finite number of members of S.
can exceed at the most a finite number of members of S.
Again as 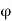 is the supremum of P,
is the supremum of P, 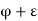 can not belong to P, and consequently
can not belong to P, and consequently 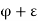 must exceed an infinite number of members of S.
must exceed an infinite number of members of S.
Now 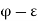 exceeds at the most a finite number of members of S and
exceeds at the most a finite number of members of S and 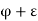 exceeds infinitely many members of S,
exceeds infinitely many members of S,
Implies that- [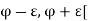 contains an infinite number of members of S.
contains an infinite number of members of S.
Consequently  is a limit point of S.
is a limit point of S.
Example: If S, T are the subsets of R, then show that
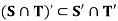
Sol:
Now
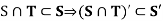
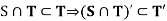
Consequently
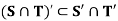
Example: Give an example to show that  may not be equal.
may not be equal.
Sol:
Let
S = ] 1, 2 [ and T = ] 2, 3 [
So that
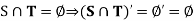
Also
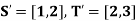
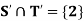
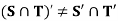
Closure of a Set:
Let S be any set of real numbers (S 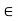 R). The closure of S is defined as the union of the set S and its derived set S. It is denoted by
R). The closure of S is defined as the union of the set S and its derived set S. It is denoted by  , Thus
, Thus

In other words, the closure of a set is obtained by the combination of the elements of a given set S and its derived set S'.
For example, 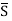 of S = { 1/ n: n
of S = { 1/ n: n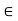 N} is given by.
N} is given by.
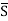 = { 1/n , n
= { 1/n , n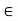 N}
N}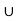 {0} = {0, 1, ½, 1/3….}
{0} = {0, 1, ½, 1/3….}
Interior of a Set:
Let (X,τ)be the topological space and A⊆X, then a point x∈A is said to be an interior point of set A, if there exists an open set U such that
x∈U⊆A
In other words let A be a subset of a topological space X, a point x∈A is said to be an interior points of A if x is in some open set contained in A.
Interior of a Set
Let (X,τ) be a topological space and A be a subset of X, then the interior of A is denoted by Int(A) or Ao is defined to be the union of all open sets contained in A.
In other words let (X,τ) be a topological space and A be a subset of X. The interior of A is the union of all open subsets of A, and a point in the interior of A is called an interior point of A.
Notes:
• The interior of A is the union of all open sets contained in A. The union of open sets is again an open set. Hence the interior of A is the largest open set contained in A.
• ϕo=ϕand Xo=X
• The interior of sets is always open.
• Ao⊆A
Example:
Let X={a,b,c,d,e} with topology τ={ϕ,{b},{a,d},{a,b,d},{a,c,d,e},X}. If A={a,b,c}, then find Ao. Since there is no open set containing aa and a subset of A, so a is not an interior point of A. Similarly, c is not an interior point of A. Since {b} is an open set containing b and is a subset of A, so bb is an interior point of A. Hence Ao={b}.
Theorems
• Each point of a non empty subset of a discrete topological space is its interior point.
• The interior of a subset of a discrete topological space is the set itself.
• The interior of a subset A of a topological space X is the union of all open subsets of A.
• The subset A of topological space X is open if and only if A=Ao.
• If A is a subset of a topological space X, then (Ao)o=Ao.
• Let (X,τ) be a topological space and A and B are subsets of X, then
(1) A⊆B⇒Ao⊆Bo
(2) (A∩B)o=Ao∩Bo
(3) (A∪B)o⊇Ao∩Bo
Boundary of a Set:
Let A be a subset of a topological space X, a point x∈X is said to be boundary point or frontier point of A if each open set containing at x intersects both A and Ac
The set of all boundary points of a set A is called the boundary of A or the frontier of A. It is denoted by Fr(A). Since, by definition, each boundary point of A is also a boundary point of Ac and vice versa, so the boundary of A is the same as that of Ac, i.e. Fr(A)=Fr(Ac).
Key takeaways:
- The closure of a set is obtained by the combination of the elements of a given set S and its derived set S'
- Let A be a subset of a topological space X, a point x∈A is said to be an interior point of A if x is in some open set contained in A.
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. Advanced engineering mathematics, by HK Dass
3. Mathematical analysis by Dr. Anju panwar
4. Real analysis by Dr. Sachin Kaushal
5. Real analysis by Ajit kumar & S.Kumaresan
6. Principles of real analysis by S.C Malik
7. A BASIC COURSE IN REAL ANALYSIS- AJIT KUMAR