Unit - 4
Differentiability of a function at a point & in an interval
Derivability in an interval:
A function f(x) defined on [a, b] is derivable at the end point a which means f’(a) exists if
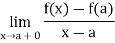
Or
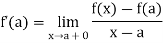
Similarly it is derivable at the end point b, if
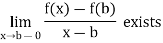
If a function is derivable at all points of an interval except the end points, it is said to be derivable in the open interval.
A function is derivable in the closed interval [a, b] if it is derivable in the open interval ]a, b[ and also at the end points a and b.
Example: A function f is defined on R by
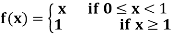
Consider the derivability at x = 1.
Sol:
Lf’(1) = 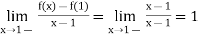
Rf’(1) = 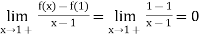
Hence
Lf’(1) and Rf’(1) are not equal.
Thus
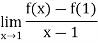
Does not exists. Which means f’(1) does not exists.
Example: A function f is defined as
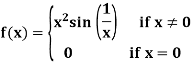
Is derivable at x = 0 but 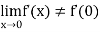

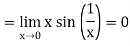
We know that from elementary calculus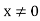 ,
,
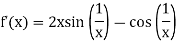
Clearly  does not exists and therefore there is no possibility of
does not exists and therefore there is no possibility of 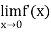 being equal to f’(0).
being equal to f’(0).
Thus
f’(x) is not continuous at x = 0 but f’(0) exists.
Theorem: A function which is derivable at a point is necessarily continuous at that point.
Proof:
Let a function f be derivable at x = c.
So that
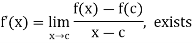
Now
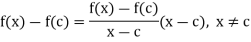
Taking limits as x tends to c, we get
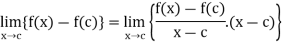
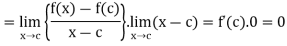
So that 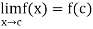 and therefore f is continuous at x = c.
and therefore f is continuous at x = c.
Key takeaways:
- A function f(x) defined on [a, b] is derivable at the end point a which means f’(a) exists if
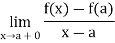
2. If a function is derivable at all points of an interval except the end points, it is said to be derivable in the open interval.
3. A function which is derivable at a point is necessarily continuous at that point.
Caratheodory's theorem:
Let f be defined on an interval I containing the point c.
Then f is differentiable at c if and only if there exists a function w on I that is continuous at c and satisfies
 ……….(1)
……….(1)
In this case, we have 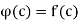
Proof:
If f’(c) exists, we can define  by
by

The continuity of w follows from the fact that 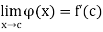 If x = c, then both sides of
If x = c, then both sides of
(1) equal 0,while if x 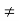 c, then multiplication of
c, then multiplication of 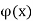 by x - c gives (1) for all other x
by x - c gives (1) for all other x 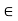 I.
I.
Now assume that a function w that is continuous at c and satisfying (1) exists. If
We divide (10) by x - c  0, then the continuity of
0, then the continuity of 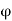 implies that
implies that
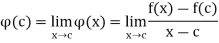
Exists. Therefore f is differentiable at c and f’(c) = 
Example: we consider the function f defined by f(x) = 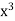
For x 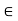 R. For c
R. For c 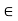 R, we see from the factorization
R, we see from the factorization
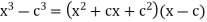
That 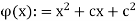 satisfies the conditions of the theorem. Therefore, we conclude that f is differentiable at c
satisfies the conditions of the theorem. Therefore, we conclude that f is differentiable at c  R and that f’(c) =
R and that f’(c) = 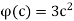
Chain rule:
Let I, J be intervals in R, let g : I 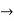 R and f : J
R and f : J 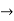 R be functions such that f(J)
R be functions such that f(J)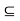 I, and let c
I, and let c 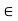 J. If f is differentiable at c and if g is differentiable at f (c), then the composite function g o f is differentiable at c and
J. If f is differentiable at c and if g is differentiable at f (c), then the composite function g o f is differentiable at c and
(g o f)’ (c) = g’(f(c)) . f’(c) ……(1)
Proof:
Since f’(x) exists, Caratheodory’s Theorem implies that there exists a function w on J such that 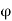 (c) is continuous at c and f(x)- f(c) =
(c) is continuous at c and f(x)- f(c) = 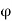 (x) (x – c) for x
(x) (x – c) for x 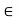 J, and where
J, and where 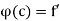 (c). Also, since g’(f(c)) exists, there is a function
(c). Also, since g’(f(c)) exists, there is a function 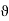 defined on I such that
defined on I such that 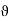 is continuous at d := f f(c) and g(y) – g(d) =
is continuous at d := f f(c) and g(y) – g(d) = 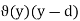 for y
for y 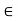 I, where
I, where
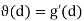 . Substitution of y = f(x) and d = f(c) then produces
. Substitution of y = f(x) and d = f(c) then produces
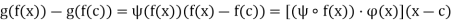
For all x 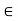 J such that f (x)
J such that f (x)  I. Since the function
I. Since the function 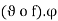 is continuous at c and its
is continuous at c and its
Value at c is g’(f(c)).f’(c) Caratheodory’s Theorem gives (1).
If g is differentiable on I, if f is differentiable on J, and if f(J) 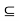 I, then it follows from the Chain Rule that (g o f)’ = (g’ o f). f’ which can also be written in the form
I, then it follows from the Chain Rule that (g o f)’ = (g’ o f). f’ which can also be written in the form
D(g o f) = (Dg o f) .Df
Example: If f : I 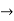 R is differentiable on I and g(y) =
R is differentiable on I and g(y) =  for y
for y 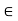 R and
R and
n 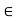 N, then since g’(y) =
N, then since g’(y) = 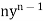 , it follows from the Chain Rule
, it follows from the Chain Rule
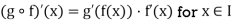
Therefore we have
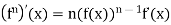
Example: Suppose that f is defined by
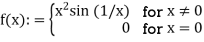
If we use the fact that Dsin x = cos x for all x 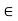 R and apply the Product Rule and the Chain Rule
R and apply the Product Rule and the Chain Rule
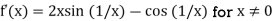
If x = 0, none of the calculational rules may be applied.
Consequently, the derivative of f at x = 0 must be found by applying the definition of derivative.
We find that
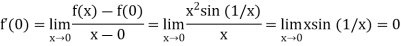
Hence, the derivative f’ of f exists at all x  R. However, the function f’ does not have a limit at x = 0, and consequently f’ is discontinuous at x = 0. Thus, a function f that is differentiable at every point of R need not have a continuous derivative f’.
R. However, the function f’ does not have a limit at x = 0, and consequently f’ is discontinuous at x = 0. Thus, a function f that is differentiable at every point of R need not have a continuous derivative f’.
Algebra of differentiable function:
The existence of the derivative of a function at a point depends on the existence of a limit
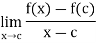
Therefore keeping in view the corresponding theorem on limits, we can establish the following fundamental theorem on derivative.
In the function f, g are derivable at c then the functions f + g, f – g, fg anf f/g (note- g(c) should be non-zero) are also derivable at c, and
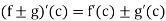
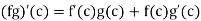
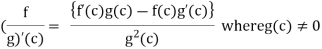
In order to illustrate the procedure, we will go through the following theorem:
Theorem: if f is derivable at c and f(c) is non-zero then the function 1/f is also derivable thereat, and
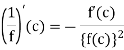
Since f is derivable at c, it is also continuous.
Again since f(c) is non-zero, there exists a neighbourhood of N of c wherein f does not vanish,
Now

Proceeding to limits when x tends to c, we have
Thus the limit exists and equals 
Mean value theorem
As we know that, the function f : I  R is said to have a relative maximum [respectively, relative minimum] at c
R is said to have a relative maximum [respectively, relative minimum] at c  I if there exists a neighborhood V :=
I if there exists a neighborhood V := 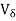 (c) of c such that f(x)
(c) of c such that f(x) 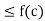 [respectively, f(c)
[respectively, f(c) 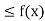 ] for all x in V
] for all x in V 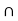 I. We say that f has a relative extremum at c
I. We say that f has a relative extremum at c 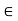 I if it has either a relative maximum or a relative minimum at c.
I if it has either a relative maximum or a relative minimum at c.
Mean value theorem:
Suppose that f is continuous on a closed interval
I := [a, b], and that f has a derivative in the open interval (a, b). Then there exists at least one point c in (a, b) such that
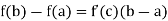
Proof:
Consider the function 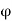 defined on I by
defined on I by
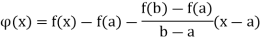
[The function w is simply the difference of f and the function whose graph is the line segment joining the points (a, f (a)) and (b, f (b))]
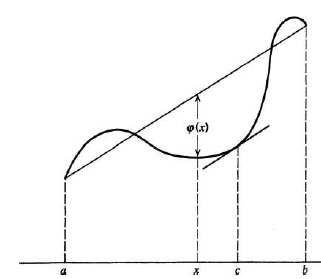
The hypotheses of Rolle’s Theorem are satisfied by  since w is continuous on [a, b], differentiable on (a, b), and
since w is continuous on [a, b], differentiable on (a, b), and 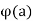 =
=  . Therefore, there exists a point c in (a, b) such that
. Therefore, there exists a point c in (a, b) such that
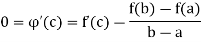
Hence, f(b) – f(a) = f’(c) (b –a)
Theorem:
Suppose that f is continuous on the closed interval I := [a, b], that f is differentiable on the open interval (a, b), and that f’(x) = 0 for x  Then f is constant on I.
Then f is constant on I.
Proof:
We will show that f(x) = f(a) for all x  I. Indeed, if x
I. Indeed, if x 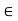 I, x > a, is given, we apply the Mean Value Theorem to f on the closed interval [a, x]. We obtain a
I, x > a, is given, we apply the Mean Value Theorem to f on the closed interval [a, x]. We obtain a
Point c (depending on x) between a and x such that f(x) – f(a) = f’(c) (x – a) since f’(c) = 0 (by hypothesis), we deduce that f(x) – f(a) = 0. Hence, f(x) = f(a) for any x 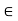 Suppose that f and g are continuous on I := [a, b], that they are differentiable on (a, b), and that f’(x) = g’(x) for all x
Suppose that f and g are continuous on I := [a, b], that they are differentiable on (a, b), and that f’(x) = g’(x) for all x 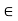 (a, b). Then there exists a constant C such that f = g + C on I.
(a, b). Then there exists a constant C such that f = g + C on I.
Key takeaways:
- The existence of the derivative of a function at a point depends on the existence of a limit

2. Suppose that f is continuous on a closed interval I := [a, b], and that f has a derivative in the open interval (a, b). Then there exists at least one point c in (a, b) such that
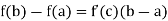
Interior Extremum Theorem:
Let c be an interior point of the interval I at which f : I 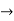 R has a relative extremum. If the derivative of f at c exists, then f’(c) = 0.
R has a relative extremum. If the derivative of f at c exists, then f’(c) = 0.
Proof:
We will prove the result only for the case that f has a relative maximum at c; the
Proof for the case of a relative minimum is similar.
If f’(c)> 0, then there exists a neighborhood V 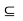 I of c such that
I of c such that
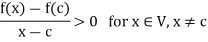
If x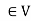 and x > c, then we have
and x > c, then we have
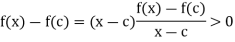
But this contradicts the hypothesis that f has a relative maximum at c. Thus we cannot
Have f’(c) > 0. Similarly, we cannot have f’(c) < 0. Therefore we must have f’(c) = 0.
Rolle’s theorem-
Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions
1. f(x) is continuous in [a , b]
2. f(x) is differentiable in (a , b)
3. f(a) = f(b)
Then there exists atleast a point point c ϵ (a , b) , where a<b , such that f’(c) = 0
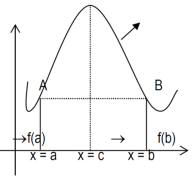
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-
1.f(x) is a continuous function in[a , b] , from the figure without breaks in between A&B on y = f(x).
2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.
Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.
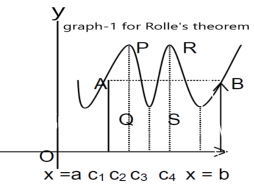
Slope of the tangent at P or Q,R,S , will be 0 ,even the curve y = f(x) decreases or increases, that means f(x) is constant.
Derivative of f(x),
f’(c) = 0
That’s why, f’(c) = 0
3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.
So that, f(a) = f(b)
Example: Verify Rolle’s theorem for the function f(x) = x(x+3) 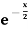 in interval [-3, 0].
in interval [-3, 0].
Sol. First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x) 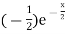 + (2x + 3)
+ (2x + 3)
= 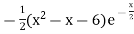
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
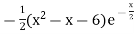 = 0
= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Example: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Sol:
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+ 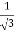 and 2 -
and 2 - 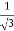
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Example: Verify the Rolle’s theorem for sin x in the interval [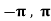 ]
]
Sol. Suppose f(x) = sin x
We know that sin x is continuous for all x.
Now, f’(x) = cos x exists for all x in (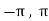 ) and
) and
f(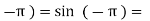 0
0
f( 0
0
Thus f(x) satisfies all the conditions of Rolle’s theorem.
Now,
f’(x) = 0 that gives, cos x = 0
x = 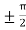
Here we notice that both intervals lie in (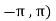 .
.
There exists, c = 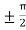
So that, f’(c) = 0
The Rolle’s theorem has been verified.
Key takeaways:
1. Let c be an interior point of the interval I at which f : I 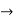 R has a relative extremum. If the derivative of f at c exists, then f’(c) = 0.
R has a relative extremum. If the derivative of f at c exists, then f’(c) = 0.
2. Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions
1. f(x) is continuous in [a , b]
2. f(x) is differentiable in (a , b)
3. f(a) = f(b)
Then there exists atleast a point point c ϵ (a , b) , where a<b , such that f’(c) = 0
The Intermediate Value Property of Derivatives:
Lemma: Let I 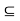 R be an interval, let f : I
R be an interval, let f : I 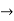 R, let c
R, let c 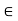 I, and assume that f has a derivative at c. Then:
I, and assume that f has a derivative at c. Then:
(a) If f’(c) > 0, then there is a number 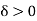 such that f(x) > f(c) for
such that f(x) > f(c) for 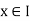 such that c < x < c +
such that c < x < c + 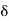
(b) If f’(c) < 0, then there is a number 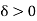 such that f(x) > f(c) for
such that f(x) > f(c) for  such that c -
such that c -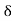 < x < c.
< x < c.
Proof:
Since
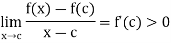
It follows that there is a number  such that if c
such that if c  and 0 < |x – c| <
and 0 < |x – c| < 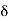
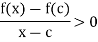
If x 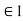 also satisfies x
also satisfies x 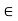 c, then we have
c, then we have
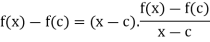
Hence, if  and c < x < c +
and c < x < c + 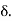
Similarly we can prove the second part.
Darboux’s theorem:
If f is differentiable on I = [a, b] and if k is a number between f’(a) and f’(b), then there is at least one point c in (a, b) such that f’(c) = k.
Proof: Suppose that f’(a) < k < f’(b). We define g on I by g(x) : = kx – f(x) for x 
Since g is continuous, it attains a maximum value of I. Since g’(a) = k – f’(a) > 0, it follows from above lemma that the maximum of g does not occur at x = a.
Similarly since g’(b) = k – f’(b) < 0, it follows from lemma (b) that the maximum does not occur at x = b.
Therefore, g attains its maximum at some c in (a, b).
Then we have 0 = g’(c) = k – f’(c).
Hence f’(c) = k.
Example: The function g: [-1, 1] 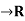 defined by
defined by
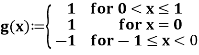
(which is a restriction of the signum function) clearly fails to satisfy the intermediate value property on the interval [-1, 1]. Therefore, by Darboux’s Theorem, there does not exist a function f such that f’(x) = g(x) for all 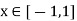
In other words, g is not the derivative on [-1,1] of any function.
One very important use of the Mean Value Theorem is to obtain certain inequalities.
Whenever information concerning the range of the derivative of a function is available, this information can be used to deduce certain properties of the function itself.
Let’s illustrate by the following example:
Example-1: The exponential function f(x) =  has the derivative f’(x) =
has the derivative f’(x) = 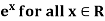 . Thus f’(x) > 1 for x > 0 and f’(x) < 1 for x < 0. From these relationships, we drive the inequality,
. Thus f’(x) > 1 for x > 0 and f’(x) < 1 for x < 0. From these relationships, we drive the inequality,
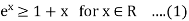 with equality occurring if and only if x = 0.
with equality occurring if and only if x = 0.
If x = 0, we have equality with both sides equal to 1. If x > 0, we apply the Mean
Value Theorem to the function f on the interval [0, x]. Then for some c with 0 < c < x we have
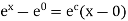
Since 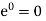 and
and 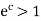 . This becomes
. This becomes  > x so that we have
> x so that we have 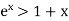 for x > 0.
for x > 0.
A similar argument establishes the same strict inequality for x < 0.
Thus the inequality (1) holds for all x, and equality occurs only if x = 0.
Example-2: The function g(x) := sin x has the derivative g’(x) = cos x for all x 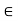 R. On the basis of the fact that -1
R. On the basis of the fact that -1 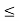 cos x
cos x 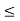 1 for all x
1 for all x 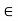 R, we will show that
R, we will show that
-x 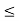 sin x
sin x  for all x
for all x 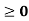 …….. (1)
…….. (1)
Indeed, if we apply the Mean Value Theorem to g on the interval [0, x], where x > 0, we Obtain
Sin x - sin 0 = (cos c)(x – 0)
For some c between 0 and x. Since sin 0 = 0 and -1 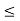 cos c
cos c  1, we have -x
1, we have -x  sin x
sin x  since equality holds at x = 0, the inequality (1) is established.
since equality holds at x = 0, the inequality (1) is established.
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. Advanced engineering mathematics, by HK Dass
3. Mathematical analysis by Dr. Anju panwar
4. Real analysis by Dr. Sachin Kaushal
5. Real analysis by Ajit kumar & S.Kumaresan
6. Principles of real analysis by S.C Malik
7. A BASIC COURSE IN REAL ANALYSIS- AJIT KUMAR