Unit - 1
L’ Hospital’s Rules
Let we have two functions f(x) and g(x) and-
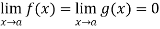
Then-
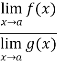
Is an expression of the form  .
.
In that case we can say that f(x)/g(x) is an indeterminate for of the type  at x = a.
at x = a.
Now, Let we have two functions f(x) and g(x) and-
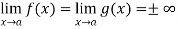
Then-
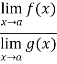
Is an expression of the form  , in that case we can say that f(x)/g(x) is an indeterminate for of the type
, in that case we can say that f(x)/g(x) is an indeterminate for of the type  at x = a.
at x = a.
Some other indeterminate forms are 
L’ Hospital’s rule for  form-
form-
Working steps-
1. Check that the limits f(x)/g(x) is an indeterminate form of type  .
.
(Note- we cannot apply L’ Hospital rule if it is not in indeterminate form)
2. Differentiate f and g separately.
3. Find the limits of the derivatives. If the limit is finite, then it is equal to the limit of f(x)/g(x).
then it is equal to the limit of f(x)/g(x).
Example-1: Evaluate 
Sol. Here we notice that it is an indeterminate form of  .
.
So that, we can apply L’ Hospital rule-
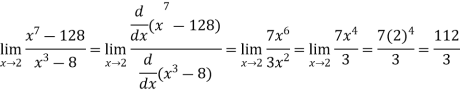
Example-2: Evaluate 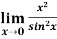 .
.
Sol. Let f(x) = 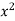 and g(x) =
and g(x) = 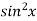 .
.
Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’ Hospital rule, we get-

= 
= 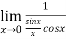
=  = 1
= 1
Note- Suppose we get an indeterminate form even after finding first derivative, then in that case, we use the other form of L’ Hospital’s rule.
If we have f(x) and g(x) are two functions such that 
 .
.
If 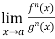 exist or (∞, -∞), then
exist or (∞, -∞), then
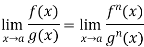
Example-3: Evaluate 
Sol.
Let f(x) = 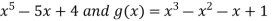 , then
, then
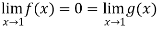
And
 = 0
= 0
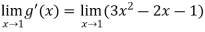 = 0
= 0
But if we use L’ Hospital rule again, then we get-
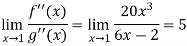
Example-4: Evaluate 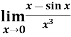
Sol. We can see that this is an indeterminate form of type 0/0.
Apply L’ Hospital’s rule, we get
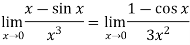
But this is again an indeterminate form, so that we will again apply L’ Hospital’s rule-
We get
 =
= 
L’ Hospital’s rule for  form-
form-
Let f and g are two differentiable functions on an open interval containing x = a, except possibly at x = a and that

If  has a finite limit, or if it is
has a finite limit, or if it is 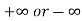 , then
, then

Theorem- If we have f(x) and g(x) are two functions such that 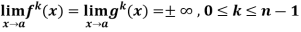 .
.
If 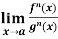 exist or (∞, -∞), then
exist or (∞, -∞), then
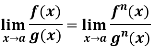
Example-5: Find 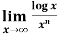 , n>0.
, n>0.
Sol. Let f(x) = log x and g(x) = 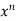
These two functions satisfied the theorem that we have discussed above-
So that,
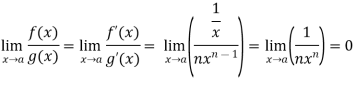
Example-6: Evaluate 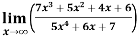
Sol.
Apply L’ Hospital rule as we can see that this is the form of 
 =
= 
Note- In some cases like above example, we cannot apply L’ Hospital’s rule.
Other types of indeterminate forms-
Example-7: Evaluate 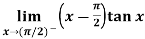
Sol. Here we find that-
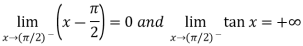
So that this limit is the form of 0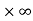 .
.
Now,
Change 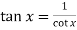 to obtain the limit-
to obtain the limit-

Now this is the form of 0/0,
Apply L’ Hospital’s rule-
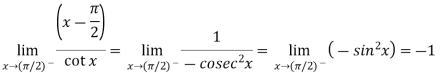
Key takeaways-
If we have f(x) and g(x) are two functions such that  .
.
If  exist or (∞, -∞), then
exist or (∞, -∞), then
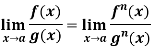
Cauchy’s mean value theorem-
Suppose we have two functions f(x) and g(x) of x, such that,
1. Both functions are continuous in [a, b]
2. Both functions are differentiable in (a, b)
3. g’(x) ≠ 0 for any x ϵ (a, b)
These three exists atleast, x = c ϵ (a, b), at which
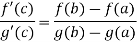
Proof:
Suppose, we define a functions,
h(x) = f(x) – A.g(x) …………………….(1)
So that h(a) = h(b) and A is a constant to be determined.
Now,
h(a) = f(a) – Ag(a)
h(b) = f(b) – Ag(b)
So that,
f(a) – Ag(a) = f(b) – A.g(b),
Which gives
A = 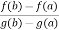 …………………………….(2)
…………………………….(2)
Now, h(x) is continuous in [a, b] as RHS of eq. (1) is continuous in [a, b] and h(x) is diff. In (a, b) as RHS of eq. (1) is diff. In (a, b)
Also,
h(a) = h(b)
Therefore all the conditions of Rolle’s theorem are satisfied then there exists a Value x = cϵ (a, b)
So that h’(c) = 0
Differentiate eq.(1) w.r.t. x , we get
h’(x) = f’(x) – A.g’(x)
At x = c
h’(c) = f’(c) – A.g’(c)
0 = f’(c) – A.g’(c)
A = 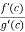
So that, we get
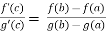 where a<c<b
where a<c<b
Hence the Cauchy’s mean value theorem is proved.
Example: Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cosx in [ 0, π/2]
Sol. It is given that,
f(x) = sin x and g(x) = cos x
Now,
f’(x) = cos x and g’(x) = - sin x
We know that both the functions are continuous in [ 0, π/2] and differentiable in (0, π/2).
Also, g’(x) = - sin x ≠ 0 for all x ϵ (0, π/2)
By Cauchy’s mean value theorem, we get
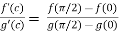 for some c: 0< c <
for some c: 0< c <
That means
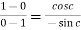 which gives,
which gives,
Cot c = 1
c = 
Now we see that  lies between 0 and
lies between 0 and 
Example: Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]
Sol. We are given, f(x) = x⁴ and g(x) = x
Derivative of these functions,
f’(x) = 4x³ and g’(x) = 2x
Put these values in Cauchy’s formula, we get
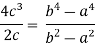
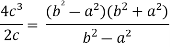
2c² = 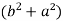
c² = 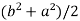
c = 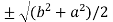
Now put the values of a = 1 and b = 2, we get
c = 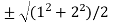 =
=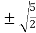 =
= 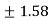 (approx)
(approx)
Hence the Cauchy’s theorem is verified.
Key takeaways
Suppose we have two functions f(x) and g(x) of x, such that,
1. Both functions are continuous in [a, b]
2. Both functions are differentiable in (a, b)
3. g’(x) ≠ 0 for any x ϵ (a, b)
These three exists atleast, x = c ϵ (a, b), at which

If a function f is defined on [a, a + h] is such that
The (n-1)th derivative 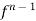 is continuous on [a a+h] and (ii) the nth derivative
is continuous on [a a+h] and (ii) the nth derivative 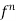 exists on ] a, a+h [ then for every for all at least one real number
exists on ] a, a+h [ then for every for all at least one real number  between 0 and 1, such that
between 0 and 1, such that
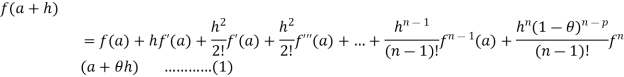
Where p is the given positive integer.
We see that the condition (i) in the statement implies all the derivatives f’ f’’….. And are continuous on [a, a + h]
Consider the function 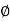 defined on [a, a + h] as
defined on [a, a + h] as
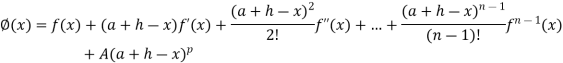
Where A is a constant to be determined such that
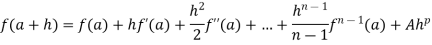
The function satisfies all the conditions of Rolle’s theorem and hence for every for all at least one real number  between 0 to 1, such that
between 0 to 1, such that
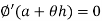
But
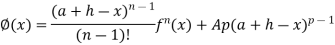
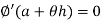
We get
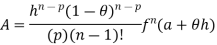
The term
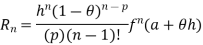
Which occurs after n terms is called Taylor’s remainder.
Cauchy form of remainder
P=1, we get
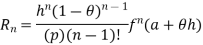
Lagrange’s form of remainder
P=n, we get
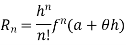
Suppose c is the interior point of the domain [a, b] of a function f. Then the point c is said to be stationary if f’(c) = 0.
Maximum value- The function f is said to have a maximum value at c if f(c) is the greatest value of the function in a small neighbourhood c – 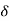 , c +
, c + [,
[, of c.
of c.
Thus

We have
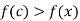
Such that, f(x) – f(c) is negative for all values of x in c – 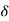 , c +
, c +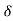 [ other than c.
[ other than c.
Minimum value- The function f is said to have a minimum value at c if f(c) is the least value of the function in a small neighbourhood c – 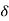 , c +
, c + [,
[, of c.
of c.
Thus

We have
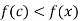
Such that, f(x) – f(c) is positive for all values of x in ] c – 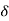 , c +
, c +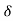 [ other than c.
[ other than c.
Extreme value- The function is said to have an extreme value at c if f(c) is either a maximum or a minimum value.
Thus at an extreme point c, f(x) – f(c) keeps the same sign for all values of x is a deleted neighborhood ] c –  , c +
, c + [ of c.
[ of c.
Method to find out the points of maximum and minimum values
Let c be an extreme point of a function f with domain [a, b]. If c is a point of maximum value, then for every for all a neighborhood ] c –  , c +
, c + [ of c such that
[ of c such that
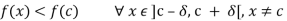
So that

f is increasing from f(c) in a small interval to the right of c.
We can conclude that
C is a point of maximum value if the function changes from an increasing to a decreasing function as x passes through c.
Therefore if f is derivable, the derivative changes sign from positive to negative as x passes through c.
It is clear that c is a point of minimum value if f changes from decreasing to an increasing function and in case f is derivable, the derivative f’ changes sign from negative to positive as x passes through c.
Theorem- if c is an interior point of the domain of a function and f’(c) = 0, then the function has a maximum or a minimum at c as f’’(c) is negative or positive.
F’’(c) implies that f and f’ exists and are continuous at c and continuity at c implies the existence of f and f’ in a neighbourhood ] c – 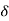 , c +
, c +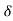 [,
[,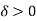 of c, the neghbourhood being itself contained in a domain D of f.
of c, the neghbourhood being itself contained in a domain D of f.
Suppose

This implies that f’(x) is an increasing function atc,
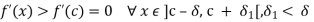
And
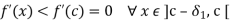
First one implies that f’(x) is positive and hence f is an increasing function in ] c, c + 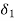 [ .
[ .
Similarly, f(x) > f(c) in 
These last results imply that
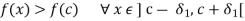
Has a minima at c.
Similarly

Note- Extreme values exists only if the first non-zero derivative is of even order.
Example: Examine the function  for extreme values.
for extreme values.
Sol.
Suppose
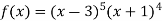
Then
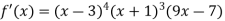
Hence the function is derivable for all x  and the derivative f’ vanishes for x = -1, 3 and 7/9 which we may test for extreme values.
and the derivative f’ vanishes for x = -1, 3 and 7/9 which we may test for extreme values.
- For x = -1
f’ is positive for a value of x less than -1 and negative for greater than -1.
Thus f’ changes sign from + to – as x passes through -1.
Hence -1 is a point of maximum
2. X = 3
F’ remains positive as x passes through 3.
So that x= 3 is
Key takeaways
- Minimum value- The function f is said to have a minimum value at c if f(c) is the least value of the function in a small neighbourhood ] c –
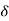 , c +
, c +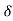 [,
[,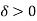 of c.
of c. - Extreme value- the function is said to have an extreme value at c if f(c) is either a maximum or a minimum value
- If c is an interior point of the domain of a function and f’(c) = 0, then the function has a maximum or a minimum at c as f’’(c) is negative or positive.
- Extreme values exists only if the first non-zero derivative is of even order.
Maclaurin’s Series Expansions
Statement:-
Maclaurin’s series of f(x) at x = 0 is given by,
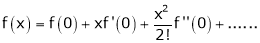
Expansion of some standard functions
i) f(x) = ex then
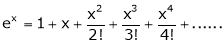
Proof:-
Here
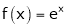



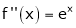
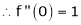
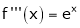
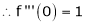
 By Maclaurin’s series we get,
By Maclaurin’s series we get,
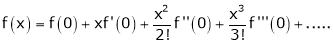
i.e. 
Note that
- Replace x by –x we get
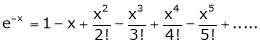
2. f(x) = sin x then
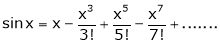
Proof:
Let (x) = sin x
Then by Maclaurin’s series,
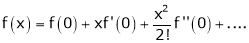 … (1)
… (1)
Since
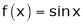

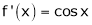
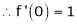


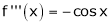
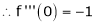
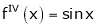
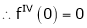
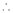 By equation (i) we get,
By equation (i) we get,
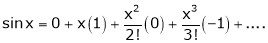
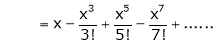
3. 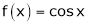 Then
Then
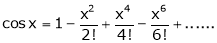
Proof:
Let f(x) = cos x
Then by Maclaurin’s series,
 … (1)
… (1)
Since
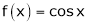
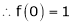
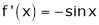
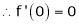

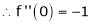
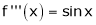
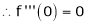
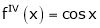

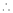 From Equation (1)
From Equation (1)
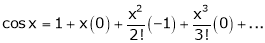
4. 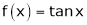 then
then

Proof:
Here f(x) = tan x
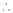 By Maclaurin’s expansion,
By Maclaurin’s expansion,
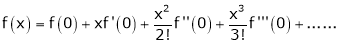 … (1)
… (1)
Since
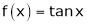
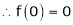
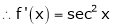

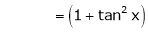

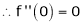
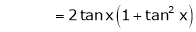

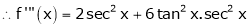
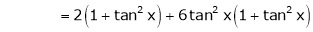
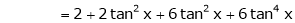
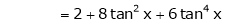
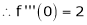

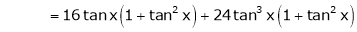
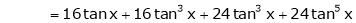

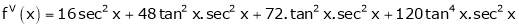
 …..
…..
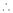 By equation (1)
By equation (1)

5.  Then
Then

Proof:-
Here f(x) = sin hx.
 By Maclaurin’s expansion,
By Maclaurin’s expansion,
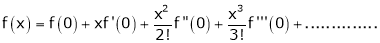 (1)
(1)


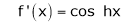


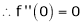
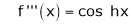
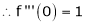
 By equation (1) we get,
By equation (1) we get,
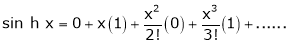
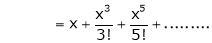
6. 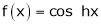 . Then
. Then
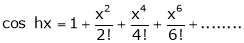
Proof:-
Here f(x) = cos hx
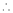 By Maclaurin’s expansion
By Maclaurin’s expansion
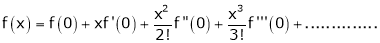 (1)
(1)
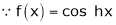
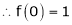
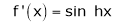
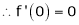
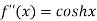

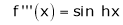
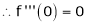
 By equation (1)
By equation (1)
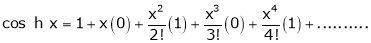
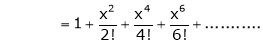
7. f(x) = tan hx
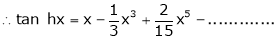
Proof:
Here f(x) = tan hx
 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
 … (1)
… (1)
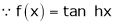
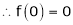


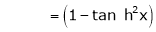
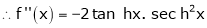


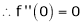
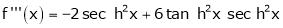
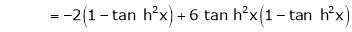



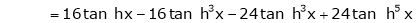
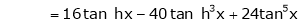
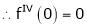
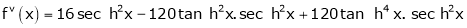
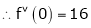
 By equation (1)
By equation (1)

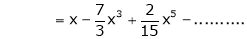
8. 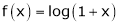 then
then
Proof:-
Here f(x) = log (1 + x)
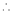 By Maclaurin’s series expansion,
By Maclaurin’s series expansion,
 … (1)
… (1)


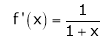
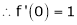


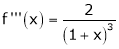
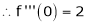

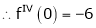
 By equation (1)
By equation (1)
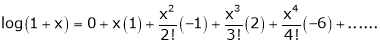
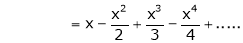
9. 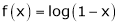
In above result we replace x by -x
Then
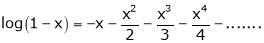
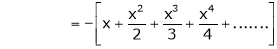
10. Expansion of tan h-1x
We know that
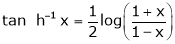
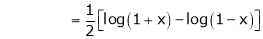
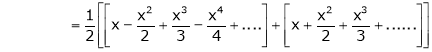

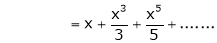
Thus
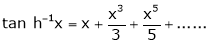
11. Expansion of (1 + x)m
Proof:-
Let f(x) = (1 + x)m
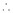 By Maclaurin’s series.
By Maclaurin’s series.
 … (1)
… (1)

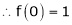
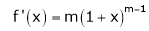
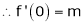
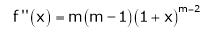
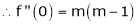
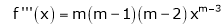
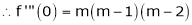
 By equation (1) we get,
By equation (1) we get,
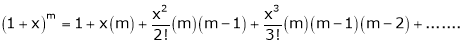

Note that in above expansion if we replace m = -1 then we get,
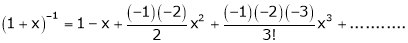
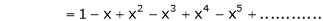
Now replace x by -x in above we get,
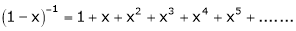
Expand by, Maclaurin’s theorem

Solution:
Here f(x) = log (1 + sin x)
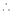 By Maclaurin’s Theorem,
By Maclaurin’s Theorem,
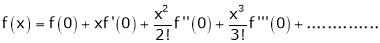 … (1)
… (1)
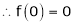
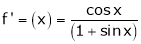

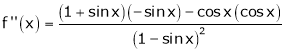
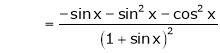
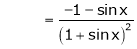
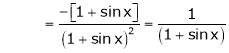
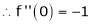
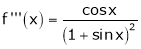

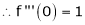
 ……..
……..
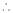 equation (1) becomes,
equation (1) becomes,
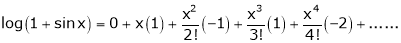
Expand by Maclaurin’s theorem,
Log sec x
Solution:
Let f(x) = log sec x
 By Maclaurin’s Expansion’s,
By Maclaurin’s Expansion’s,
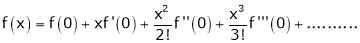 (1)
(1)
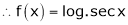

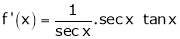

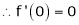
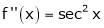
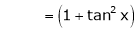
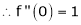
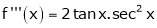
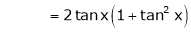
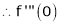
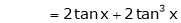
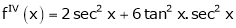
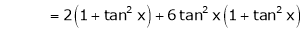
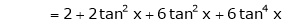


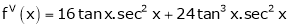
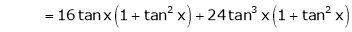
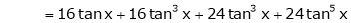
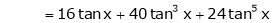
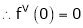

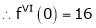
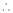 By equation (1)
By equation (1)
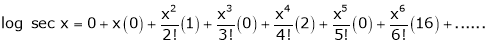
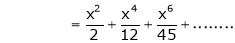
Example: Prove that 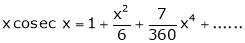
Solution:
Here f(x) = x cosec x
= 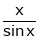
Now we know that
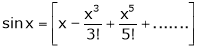
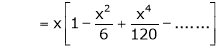
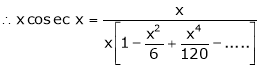
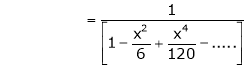
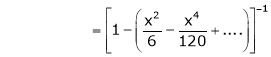
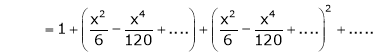
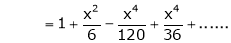
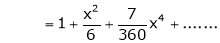
Example: Expand 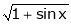 upto x6
upto x6
Solution:
Here 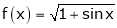
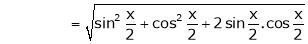
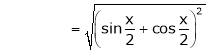

Now we know that
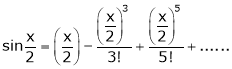 … (1)
… (1)
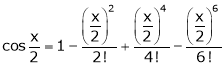 … (2)
… (2)
Adding (1) and (2) we get

Example: Show that 
Solution:
Here 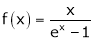
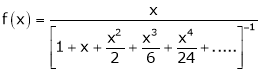
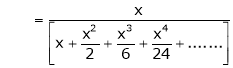
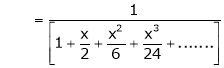
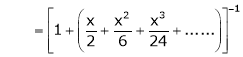
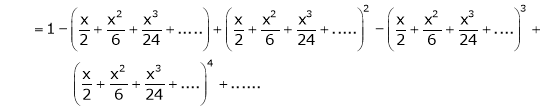
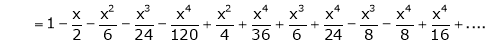
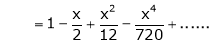
Thus
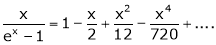
Expand  by using Maclaurin’s series. C
by using Maclaurin’s series. C
Sol.
Let

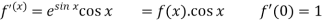

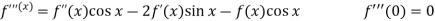
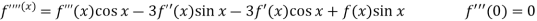
Put these values in Maclaurin’s series-
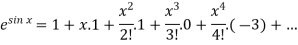
Or

Taylor’s Series Expansion:
a) The expansion of f(x+h) in ascending power of x is
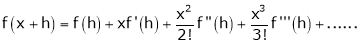
b) The expansion of f(x+h) in ascending power of h is
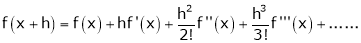
c) The expansion of f(x) in ascending powers of (x-a) is,
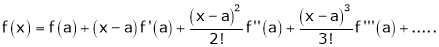
Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions
Example: Expand 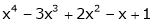 in power of (x – 3)
in power of (x – 3)
Solution:
Let 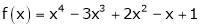
Here a = 3
Now by Taylor’s series expansion,
 … (1)
… (1)
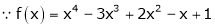
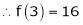
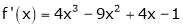
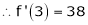

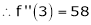
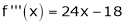
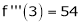
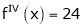
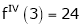
 equation (1) becomes.
equation (1) becomes.
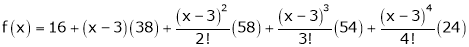
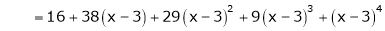
Example: Using Taylors series method expand
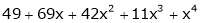 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 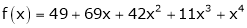
a = -2
 By Taylors series,
By Taylors series,
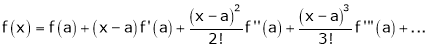 … (1)
… (1)
Since

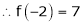
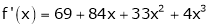
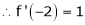
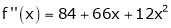
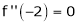
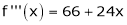
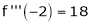
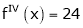
 ,
, 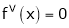 , …..
, …..
Thus equation (1) becomes
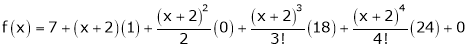

Example: Expand 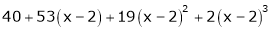 in ascending powers of x.
in ascending powers of x.
Solution:
Here
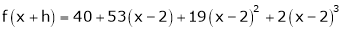
i.e. 
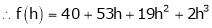
Here h = -2
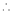 By Taylors series,
By Taylors series,
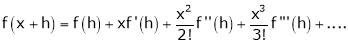 … (1)
… (1)
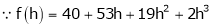
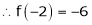
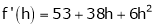
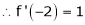

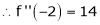
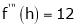
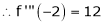
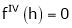

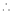 equation (1) becomes,
equation (1) becomes,


Thus
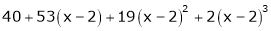
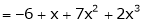
Example: Expand 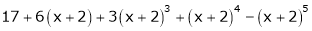 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
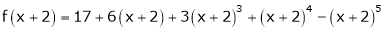
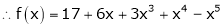
i.e. 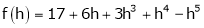
Here
h = 2
 By Taylors series
By Taylors series
 … (1)
… (1)


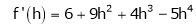


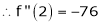
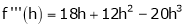
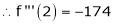
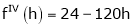

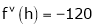
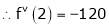

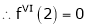
 By equation (1)
By equation (1)
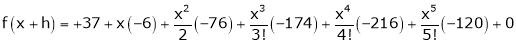
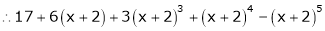
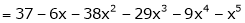
Key takeaways-
- Maclaurin’s Series Expansions

2. Taylor’s Series Expansion:-

Let’s first define the exponential functions-
A function which contains 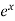 where e is the constant, called an exponential function.
where e is the constant, called an exponential function.
Here ‘e’ is the exponent which has an approximate value 2.7183
The power series for 
The value of 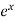 can be defined in terms of the following power series:
can be defined in terms of the following power series:
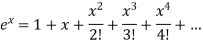
If we obtain an actual value of  by adding all the terms of the series, then the series is said to be convergent.
by adding all the terms of the series, then the series is said to be convergent.
The more terms we take in the series, the closer will be the value of 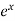 to its actual value.
to its actual value.
Example: Find the value of 5 , correct to five decimal places by using the power series for
, correct to five decimal places by using the power series for 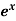 .
.
Sol. As we know that the exponential series is-
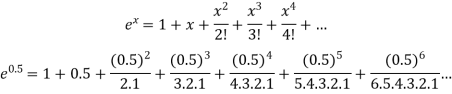
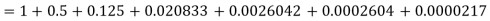
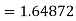
Here we get-
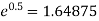
Now
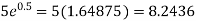
Example: Expand 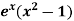 as far as the term in
as far as the term in 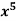 .
.
Sol. We know that the power series for  is-
is-
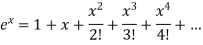
Here we have to find- 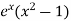
So that-
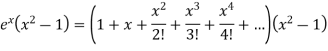
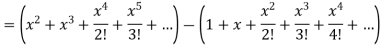
On solving, we get-
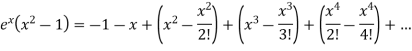
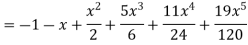
Trigonometric and log function-
As we know that,
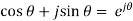
And
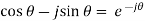
By adding these equations-

And subtracting (2) from (1), we get-
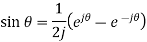
Note- 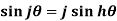
Example-1: Verify 
Sol.
As we know that
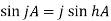
And
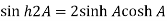
Hence,

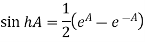
And
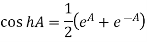
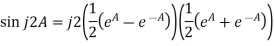

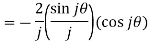
 since
since 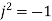
That means
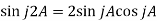
The following function is a logarithmic function-
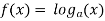
‘a’ is any value which is greater than 0, except 1
The natural logarithmic function is-
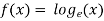
The value of
e = 2.71828182….
Properties of logarithms-
1.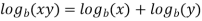
2. 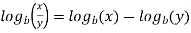
3. 
4.  then x = y
then x = y
Example: Simply the logarithm 
Sol. We can write this as-
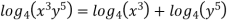
= 3
Example: Simplify 
Sol. We know that-
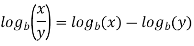
So that
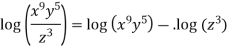
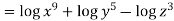
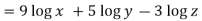
Key takeaways
- A function which contains
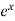 where e is the constant, called an exponential function.
where e is the constant, called an exponential function. 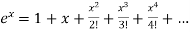
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. Advanced engineering mathematics, by HK Dass
3. Mathematical analysis by Dr. Anju panwar
4. Real analysis by Dr. Sachin Kaushal
5. Real analysis by Ajit kumar & S.Kumaresan
6. Principles of real analysis by S.C Malik