Unit - 2
Riemann integration
The definite integral is the key tool in calculus for defining and calculating quantities like volumes, areas, length of curved paths, probabilities and weights of many objects.
Historically the idea of integration was initially given by Archimedes in 287-212 BC.
This can be extended to the area of wide class of planar region such as the region R = { (x, y): 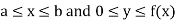 } under a curve y = f(x), where f: [a, b]
} under a curve y = f(x), where f: [a, b]  is a bounded function. Such that
is a bounded function. Such that 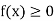 .
.
A formal setup for these is the theory of Riemann integration.
Suppose [a, b] be a closed interval.
The partition of [a, b] means a finite set P of points 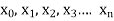 where
where

The partition P consists of n+1 points.
Example: P = {a, b} is a partition of [a, b]
P = {0, 1/3, 2/3, 1} is the partition of [0, 1].
Note- the consecutive points of a partition are not necessary of equidistant.
The i’th sub interval is denoted by 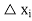

Let f be a bounded real function on [a, b].
Evidentally f is bounded on each sub-interval corresponding to each partition P,
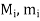 be the supremum and infimumof f in
be the supremum and infimumof f in  .
.
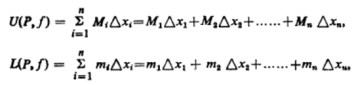
These are called the upper and lower sums of f corresponding to the partition P.
If M and m are the bounds of f in [a, b], we have,
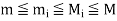
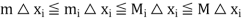
Put I = 1,2,….n and adding all inequalities, we obtain

Now each partition gives rise to a pair of sums, the upper and lower sums, by considering all partitions of [a, b], we get a set U of upper sums and a set L of lower sums.
The above inequality shows that both these sets are bounded and so each set has the supremum and infimum.
The infimum of the set of upper sums is called the upper integral and supremum of the set of lower sums is called the lower integral of f over [a, b]. Thus

The above integrals may or may not be equal.
Note- Lower sums increases and upper sums decreases as the partition becomes finer and finer.
Let f: [a, b] 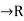 be a bounded function
be a bounded function
- If P is the partition of [a, b] and p* is a refinement of P, which means
 *
*
Then
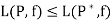
And
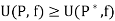
2. If 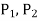 are any two partitions of [a, b], then
are any two partitions of [a, b], then
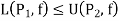
3. Let P be any partition of [a, b] then

Definition-
Let f: [a, b] 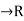 be a bounded function and P = {a =
be a bounded function and P = {a = 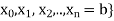 be a partition of [a, b].
be a partition of [a, b].
The lower Riemann integral of f on [a, b] is defined as Sup {L(P, f) | P is a partition of [a, b]} and is defined by

i.e.
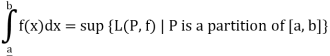
The upper Riemann integral of f on [a, b] is defined as Sup {U(P, f) | P is a partition of [a, b]} and is defined by

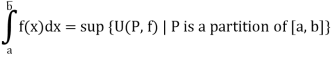
Definition of Riemann integrable
A bounded function f: [a, b]  is said to be “Riemann integrable” over [a, b] if
is said to be “Riemann integrable” over [a, b] if
For each 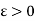 for every partition of P of [a, b] such that
for every partition of P of [a, b] such that
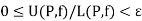
And it is denoted by 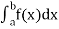
Note-
- If f: [a, b]
 is a bounded function, then
is a bounded function, then
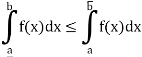
2. A bounded function f is Riemann integrable on [a, b]
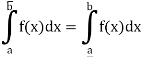
3. If bounded function f is such that
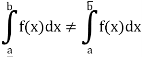
Then f is not Riemann integrable on [a, b].
[x] = the greatest integer not greater than x.
Since x belongs to [0, 3], f(x) = [x] is bounded on [0, 3], further f(x) = [x] is discontinuous at x = 1, 2
So that f(x) = [x] is bounded and has finite number of points of discontinuity.
Example: A constant function is Riemann integrable on [a, b].
Sol:
Let f(x) = k for every x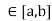 , where
, where  be a constant.
be a constant.
Clearly f is bounded on [a, b] and inf f = sup f = k
Let  be a partition on [a, b].
be a partition on [a, b].
Let 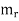 and
and 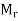 be the inf and sup of f on
be the inf and sup of f on 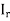 , where
, where 
Since f(x) = k for every x
 =
= 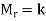
So that

And

Hence
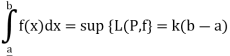
Similarly
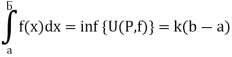
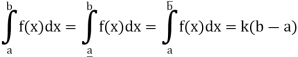
So that f is Riemann integrable on [a, b].

Note-
- A function need not be Reimann integrable on [a, b], even though it is bounded on [a, b].
- If f is Riemann integrable on [a, b] and m and M are the infimum and supremum of f on [a, b], then
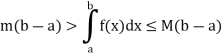
3. If f: [a, b] 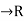 is a bounded function, then for each
is a bounded function, then for each 
(i) U(P, f) <  and
and
(ii) L(P, f) > 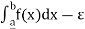
For each P - set of all partitions on [a, b] with ||P|| <
- set of all partitions on [a, b] with ||P|| <  .
.
Note- This result is known as Darboux’s theorem.
4. Let If f: [a, b] 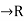 be a bounded function. As the norm of a partition, ||P||, becomes small, the number of partition points becomes large in such a way that n
be a bounded function. As the norm of a partition, ||P||, becomes small, the number of partition points becomes large in such a way that n  and ||P||
and ||P|| 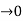 . Hence
. Hence
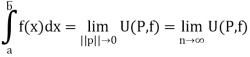
Similarly

Example: Show that the function f defined by
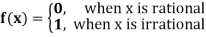
Is not integrable on any interval.
Sol.
Suppose we consider a partition P of an interval [a, b].
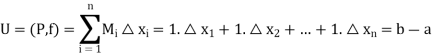
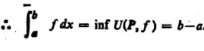
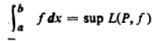
= sup{ }
}
= 0
Thus

Ex: Show that (3x + 1) is integrable on [1, 2] and
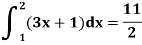
Key takeaways:
- The partition of [a, b] means a finite set P of points
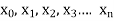 where
where

2. Lower sums increases and upper sums decreases as the partition becomes finer and finer.
3. The lower Riemann integral of f on [a, b] is defined as Sup {L(P, f) | P is a partition of [a, b]} and is defined by
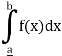
4. The upper Riemann integral of f on [a, b] is defined as Sup {U(P, f) | P is a partition of [a, b]} and is defined by

5. A bounded function f: [a, b]  is said to be “Riemann integrable” over [a, b] if
is said to be “Riemann integrable” over [a, b] if
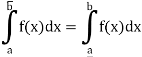
We know that a bounded function is said to be integrable when the upper and lower integrals are equal.
Here we will give the necessary and sufficient conditions for the integrability of a function in two forms.
Form-1:
The necessary and sufficient condition for the integrability of a bounded function f is that to every 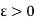 , there corresponds
, there corresponds  such that for every partition P of [a, b] with norm
such that for every partition P of [a, b] with norm 
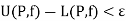
The condition is necessary-
The bounded function f is integrable,
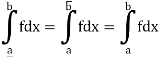
Let 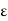 be any positive number.
be any positive number.
By the Darboux’stheoem there exists 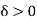 such that for every partition P with norm
such that for every partition P with norm 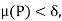
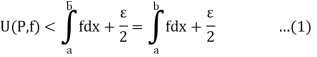
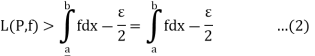
Or
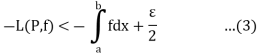
From (1) and (3), we get on adding,
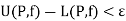
For every partition P with norm 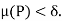
The condition is sufficient –
Let 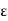 be any positive number. For any partition P with norm
be any positive number. For any partition P with norm  , where
, where
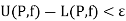
Also for any partition P. We know that-

Since 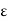 is an arbitrary positive number, so that we see that a non-negative number is less than every positive number, so that it must be equal to zero.
is an arbitrary positive number, so that we see that a non-negative number is less than every positive number, so that it must be equal to zero.
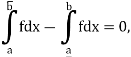
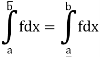
So that f is integrable.
Form-2:
A bounded function f is integrable on [a, b] if and only if for every 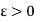 there exists a partition P such that
there exists a partition P such that

The condition is necessary
Let the function f is integrable, so that
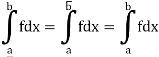
Let  be any positive number.
be any positive number.
Since the upper and lower integral are the infimum and the supremum respectively of the upper and lower sums, therefore 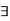 partitions
partitions  and
and 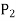 such that
such that

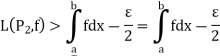
Let P be the common refinement of 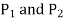 .
.

Thus 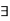 a partition P such that,
a partition P such that,
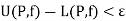
The condition is sufficient
Let  be any positive number, P be a partition for which
be any positive number, P be a partition for which
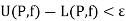
For any partition
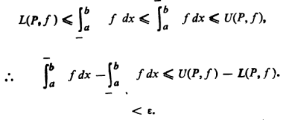
The non-negative number, being less than every positive numbers 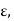 must be zero
must be zero

So that f is integrable.
Example: Prove that f(x) =  is integrable on [0, a] and
is integrable on [0, a] and 
Sol:
f(x) =  is bounded on [0, a].
is bounded on [0, a].
Let us consider the partition P = {0, a/n, 2a/n,….,ra/n,…,na/n}

Length of each sub-interval = 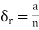
Since f(x) =  is increasing function in [0, a],
is increasing function in [0, a],
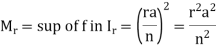

So that
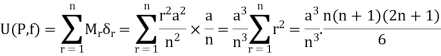
And
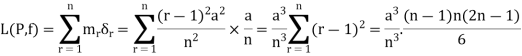
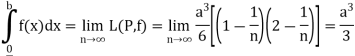
And
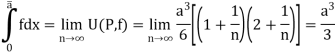
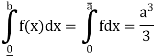
f(x) = 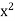 is integrable on [0, a] and
is integrable on [0, a] and 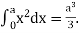

Key takeaways:
- The necessary and sufficient condition for the integrability of a bounded function f is that to every
 , there corresponds
, there corresponds  such that for every partition P of [a, b] with norm
such that for every partition P of [a, b] with norm 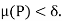
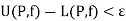
2. A bounded function f is integrable on [a, b] if and only if for every  there exists a partition P such that
there exists a partition P such that
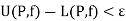
Integral as a limit of sums (Riemann sums)
Corresponding to a partition P of [a, b], suppose we chose points 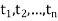 such that
such that 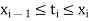 , let consider the sum
, let consider the sum

The above sum is called a Riemann sum of f over [a, b] relative to P.
Definition of integrability (Second)
A function f is said to be integrable on[a, b] if lim S(P, f) exists as 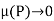 , and then
, and then

Theorem- if 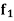 and
and  are two bounded and integrable functions on [a, b] then f =
are two bounded and integrable functions on [a, b] then f = 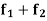 is also integrable on [a, b] and
is also integrable on [a, b] and
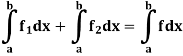
Proof:
Here f is bounded on [a, b].
Suppose  be any partition of [a, b] and
be any partition of [a, b] and 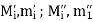 ;
; be the bounds of
be the bounds of 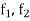 and f respectively in
and f respectively in 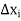
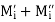 and
and 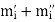 are the rough upper and lower bounds whereas
are the rough upper and lower bounds whereas 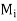 and
and 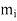 are the supremum and infimum of of f in
are the supremum and infimum of of f in  .
.
So that
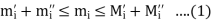
Multiply by 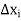 and adding all these inequalities for i = 1, 2, 3,…,n, we obtain
and adding all these inequalities for i = 1, 2, 3,…,n, we obtain

Suppose  be a positive number.
be a positive number.
Since  are integrable therefore we can choose
are integrable therefore we can choose  such that for any partitions P with norm
such that for any partitions P with norm 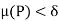 we have
we have
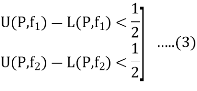
Thus for any partition P with norm 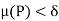 , we have, from equation (2) and (3)
, we have, from equation (2) and (3)
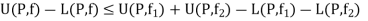
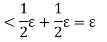
Thus the function f is integrable.
Since 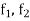 are integrable and
are integrable and 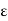 is any positive number, therefore by using Darboux’s theorem, for every
is any positive number, therefore by using Darboux’s theorem, for every 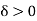 such that for all partitions P whose norm
such that for all partitions P whose norm 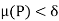 , we have
, we have
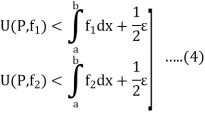
Also
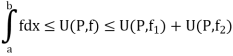
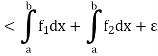
Since 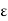 is arbitrary,
is arbitrary,

Proceeding with 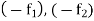 in place of
in place of  respectively, we get
respectively, we get

Or

From equation (5) and (6)

Theorem- if  and
and  are two bounded and integrable functions on [a, b] then f =
are two bounded and integrable functions on [a, b] then f = 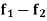 is also integrable on [a, b] and
is also integrable on [a, b] and

Proof:
Let f = 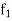 +
+ 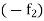 so that f is bounded on [a, b].
so that f is bounded on [a, b].
Suppose  be any partition of [a, b] and
be any partition of [a, b] and 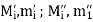 ;
;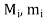 be the bounds of
be the bounds of 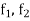 and f respectively in
and f respectively in 
The bounds of
So that 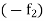 are
are 

Multiply by 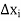 and adding all these inequalities for i = 1, 2, 3,…,n, we obtain
and adding all these inequalities for i = 1, 2, 3,…,n, we obtain
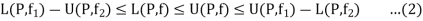
Suppose 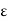 be a positive number.
be a positive number.
Since  are integrable therefore we can choose
are integrable therefore we can choose 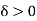 such that for any partitions P with norm
such that for any partitions P with norm  we have
we have
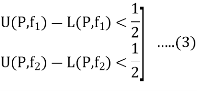
Thus for any partition P with norm 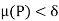 , we have, from equation (2) and (3)
, we have, from equation (2) and (3)

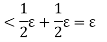
Thus the function f is integrable.
Since 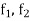 are integrable and
are integrable and  is any positive number, therefore by using Darboux’s theorem, for every
is any positive number, therefore by using Darboux’s theorem, for every  such that for all partitions P whose norm
such that for all partitions P whose norm  , we have
, we have
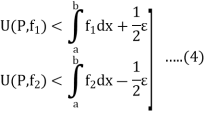
Also
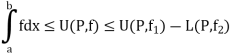
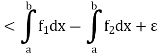
Since 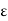 is arbitrary,
is arbitrary,

Proceeding with 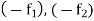 in place of
in place of 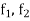 respectively, we get
respectively, we get
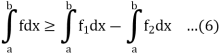
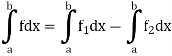
Equivalence of two definitions
We have two definitions of integrability, now we will show the equivalency of these two definitions.
Suppose f is the bounded function and integrable, so that
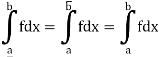
Suppose 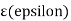 be any positive number.
be any positive number.
By using Darboux’s theorem, there exists 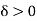 such that for every partition P with norm
such that for every partition P with norm  ,
,

And
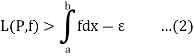
If  is any point of
is any point of 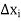 , we have
, we have
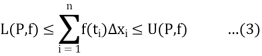
From (1), (2) and (3), we obtain that for any 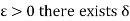 , such that for every partition with norm
, such that for every partition with norm  ,
,

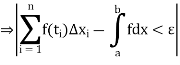
Thus the function is integrable according to the second definition also.
Applications:
- If the functions
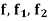 where
where  are bounded and integrable on [a, b], then
are bounded and integrable on [a, b], then

Proof:
Let 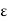 be any positive number and
be any positive number and 
Since  are integrable, therefore for every
are integrable, therefore for every 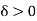 such that for every partition
such that for every partition 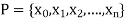 with norm
with norm  and for every choice of points
and for every choice of points  in
in 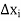 ,
,
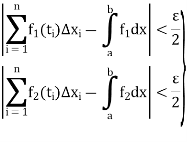

Thus
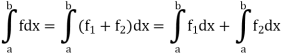
Similarly we can prove for  .
.
2. If a function f is bounded and integrable on each of the intervals [a, c], [c, b], [a, b] where c is a point of [a, b], then

Proof:
Let 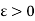 be given
be given
As f is integrable on each of the intervals [a, c], [c, b], [a, b], there exists 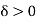 such that for every partition
such that for every partition  containing the point c with norm
containing the point c with norm 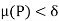 and for every choice of points
and for every choice of points 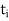 in
in 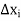 .
.

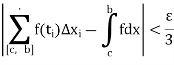
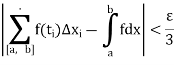
But
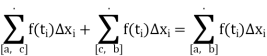
There we deduce
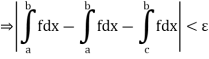
Which gives
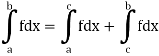
Key takeaways:
- If
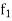 and
and  are two bounded and integrable functions on [a, b] then f =
are two bounded and integrable functions on [a, b] then f = 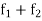 is also integrable on [a, b] and
is also integrable on [a, b] and
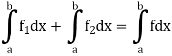
2. If 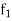 and
and  are two bounded and integrable functions on [a, b] then f =
are two bounded and integrable functions on [a, b] then f = 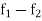 is also integrable on [a, b] and
is also integrable on [a, b] and
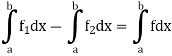
3. A function f is said to be integrable on[a, b] if lim S(P, f) exists as  , and then
, and then
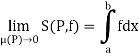
- If f:
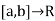 is monotonic on [a, b], then f is integrable on [a, b].
is monotonic on [a, b], then f is integrable on [a, b]. - If the set of points of discontinuity of a bounded function
 is finite, then f is Riemann integrable on [a, b].
is finite, then f is Riemann integrable on [a, b]. - If the set of points of discontinuity of a bounded function f:
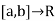 has a finite number of limit points, then f is integrable on [a, b].
has a finite number of limit points, then f is integrable on [a, b].
Theorem- Every monotonic function is integrable.
Proof:
We will prove the theorem for the case where I: [a,b]  R is a monotonically increasing function. The function is bounded. f(a) and f(b) being g.l.b. And l.u.b. Let Î > 0 be given number, Let n be a positive integer such that
R is a monotonically increasing function. The function is bounded. f(a) and f(b) being g.l.b. And l.u.b. Let Î > 0 be given number, Let n be a positive integer such that
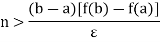
Divide the interval [a,b] into n equal sub-intervals, by the partition P = 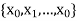 of [a, b]. Then
of [a, b]. Then


This proves that f is integrable.
Theorem: Every continuous function is integrable.
Proof:
Here we will prove that a function f which is continuous on [a, b] is also integrable on [a, b].
Suppose 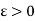 be given
be given
Let we choose a positive number 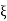 , such that
, such that

Since f is continuous on [a, b], therefore it is bounded and is uniformly continuous on [a, b].
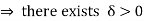 , such that
, such that
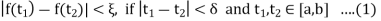
Now choose a partition P with norm 
Then by equation (1), we get

Hence

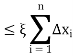

Thus f is integrable.
Note- Continuity is sufficient but not necessary condition for integrability.
Theorem: A bounded function f, having a finite number of points of discontinuity on [a, b] is integrable on [a, b].
Proof:
Suppose M and m be the bounds of f.
Suppose 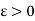 be given
be given
Let there be p points of discontinuity of f on [a, b].
Here we consider a partition P of [a, b] such that all the points of the sum of whose length  .
.
The oscillation of f in each of these sub-intervals being 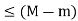 , their total contribution to {U(P, f) - L(P, f)} is less than
, their total contribution to {U(P, f) - L(P, f)} is less than

The function f is continuous in the remaining portion of [a, b], which means in the (p+1) sub-intervals of [a, b] excluding the sub-intervals taken above.
The contribution to the {U(P, f) - L(P, f)} from each of these (p+1) sub-intervals can be made  , so that the total contribution to {U(P, f) - L(P, f)} yby these (p+1) sub-intervals is less than
, so that the total contribution to {U(P, f) - L(P, f)} yby these (p+1) sub-intervals is less than
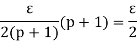
Thus, for the partition P of [a, b].
U(P, f) - L(P, f)} 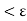
Hence the function f is integrable.
Key takeaways:
- Every monotonic function is integrable.
- Every continuous function is integrable.
- A bounded function f, having a finite number of points of discontinuity on [a, b] is integrable on [a, b].
Property-1: if f and g are integrable on [a, b], then so is f + g, and

Proof:
Any Riemann sum of f+g over a partition P = of [a, b]can
of [a, b]can
Be written as

Here  are the Riemann sums for f and g.
are the Riemann sums for f and g.
Above definition(property), implies that if  > 0 there are positive numbers
> 0 there are positive numbers 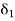 and
and  such that
such that
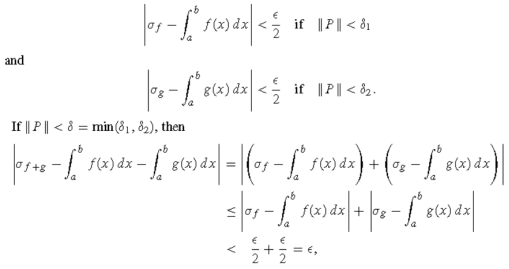
So the conclusion follows from the above definition.
Property-2: If f is integrable on [a, b] and c is a constant, then cf is integrable on [a, b] and
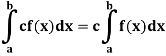
Property-3: If f and g are integrable on [a, b] and 
Then

Proof:
Since  , every lower sum of g – f over any partition of [a, b] is non-negative, therefore,
, every lower sum of g – f over any partition of [a, b] is non-negative, therefore,

Hence

Property-4: if f is integrable on [a, b], then so is |f|, and
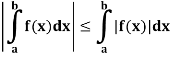
Key takeaways:
- If f and g are integrable on [a, b], then so is f + g, and
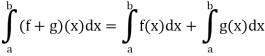
2. If f is integrable on [a, b] and c is a constant, then cf is integrable on [a, b] and
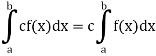
3. If f and g are integrable on [a, b] and 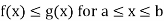
Then
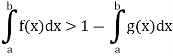
Definition of piecewise continuous functions-
A piecewise continuous function is a function that is continuous except at a finite number of points in its domain.
We usually write piecewise continuous functions by defining them case by case on different intervals. For example,
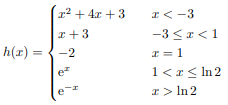
Is a piecewise continuous function
Note- Let f(x) be a real valued function. Suppose that f(x) has both a left limit S and a right limit R at x = a. Suppose further that f(x) is defined at x = a, and that R and S are both equal to f(a). We write this in limit notation as
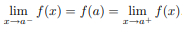
And f(x) is continuous at x = a.
If we approach x = a from either the left or the right, f(x) approaches f(a).
In this section, we will show that functions f : [a, b] → R which are either piecewise monotonic or piecewise continuous are integrable.
f : [a, b] → R is increasing if f(x) ≤ f(y) whenever x < y for any x, y ∈ [a, b]. Similarly, f : [a, b] → R is decreasing if f(x) ≥ f(y) whenever x < y for any x, y ∈ [a, b]. The function f : [a, b] → R is called monotonic if it is either increasing or decreasing.
Theorem: If f : [a, b] → R is monotonic, then f ∈ R(a, b).
Here we are going to prove the theorem for the case that f is increasing, as the argument for the case that f is decreasing is almost identical.
Since f is increasing, by definition, f(a) ≤ f(x) ≤ f(b) for all x ∈ [a, b]. It follows that f is bounded on [a, b] by the value f(b). In order to prove that f ∈ R(a, b), we will show that the Cauchy criterion is satisfied. To this end, for > 0, we choose
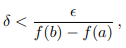
And choose any partition Pδ. Then

Theorem: If f : [a, b] → R is continuous, then f ∈ R(a, b).
Here we will use the Cauchy criterion. Since [a, b] is closed, f is uniformly continuous on [a, b]; therefore, for any > 0, we can choose δ > 0 such that
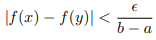
Whenever x, y ∈ [a, b] and |x − y| < δ
Let Pδ denote any partition of [a, b]. Since f is continuous, we can replace the inf and sup with min and max, respectively, in the definitions of mi and Mi , so that for each i = 1, ..., N(δ),

For each i = 1, ..., N(δ)
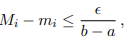
So that
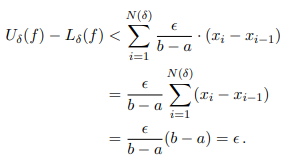
Definition of monotone functions-
A function f is monotone increasing on (a, b) if f(x)  f(y) whenever x < y. A function f is monotone decreasing on (a, b) if f(x)
f(y) whenever x < y. A function f is monotone decreasing on (a, b) if f(x)  f(y) whenever x < y.
f(y) whenever x < y.
A function f is called monotone on (a, b) if it is either always monotone increasing or monotone decreasing.
Note-
- If f is a monotonic function defined on an interval I, then f is differentiable almost everywhere on I, i.e. the set of numbers x in I such that f is not differentiable in x has Lebesgue measure zero.
- If f is a monotonic function defined on an interval [a, b], then f is Riemann integrable.
- A function is unimodal if it is monotonically increasing up to some point (the mode) and then monotonically decreasing.
Integrability of monotone function
Let the partition of the interval-
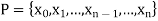
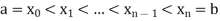
If we divide the interval into n equal parts then the width of each rectangle will be
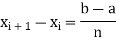
We calculate an upper bound of integral as
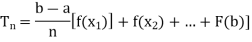
We consider the decreasing function
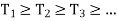
With the same partition this is a lower bound of the integral
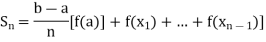
We consider the increasing function

If this two sequences converges towards one and same limit, we can call this limit the definite integral, and we write
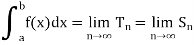
When we consider an increasing function which is monotonic, we have anincreasing sequence { and decreasing sequence {
and decreasing sequence {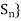 .
.
Then the question is only whether we can verify

We can calculate 
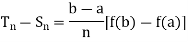
Then the limit
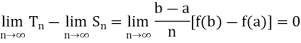
We conclude that if f is monotonic in the interval [a, b], then the definite integral exists.

Key takeaways:
- A function f is called monotone on (a, b) if it is either always monotone increasing or monotone decreasing.
- If f is a monotonic function defined on an interval [a, b], then f is Riemann integrable.
Intermediate Value Theorem
Let f be a continuous function on an interval containing a and b.
If K is any number between f(a) and f(b) then there is a number c, a 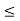 c S b such that f(c) = K
c S b such that f(c) = K
Proof:
Either f(a) = f(b) or f(a) < f(b) or f(b) < f(a). If f(a) = f(b) then K = f(a) = f(b) and so c can be taken to be either a or b. We will assume that f(a) < f(b). (The other case can be dealt with similarly.) We can, therefore, assume that f(a) < K < f(b).
Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S 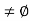 and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a
and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a  c
c 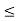 b. We want to show that f(c) = K. Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S
b. We want to show that f(c) = K. Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S 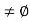 and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a
and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a  c
c 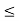 b. We want to show that f(c) = K.
b. We want to show that f(c) = K.
Since f is continuous on [a, b], f is continuous at c. Therefore, given 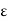 > 0, there exists a 6 > 0 such that whenever x is in [a, b] and |x – c| < 6, |f(x) – f(c) ( < G,
> 0, there exists a 6 > 0 such that whenever x is in [a, b] and |x – c| < 6, |f(x) – f(c) ( < G,
i.e., f(c) – 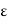 < f(x) < f(c) +
< f(x) < f(c) + 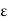 .
.
If c  b, we can clearly assume that c + 6 < b. Now c is the least upper bound of S. So c –
b, we can clearly assume that c + 6 < b. Now c is the least upper bound of S. So c –  is not ‘an upper bound’ of S. Hence, there exists a y in S such that c – 6 < y
is not ‘an upper bound’ of S. Hence, there exists a y in S such that c – 6 < y 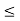 c. Clearly |y – c| <
c. Clearly |y – c| <  and so by (4) above, we have
and so by (4) above, we have
f(c) – 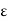 < f(y) < f(c) +
< f(y) < f(c) +  .
.
Since y is in S, therefore f(y) < K. Thus, we get
f(c) – S < K
If now c = b then K – 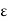 < K < f(b) = f(c), i.e., K < f(c) + E. If c
< K < f(b) = f(c), i.e., K < f(c) + E. If c 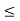 b, then c < b; then there exists an x such that c < x < c + 6, 6, x
b, then c < b; then there exists an x such that c < x < c + 6, 6, x 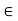 [a, b] and for this x, f(x) < f(c) +
[a, b] and for this x, f(x) < f(c) + 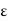 by (4) above. Since x > c, K
by (4) above. Since x > c, K  f(x), for otherwise x would be in S which will imply that c is not an upper bound of S. Thus, again we have K
f(x), for otherwise x would be in S which will imply that c is not an upper bound of S. Thus, again we have K 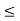 f(x) < f(c) + E.
f(x) < f(c) + E.
In any case,
K < f(c) + 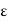 ...(6)
...(6)
Combining (5) and (6), we get for every 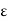 > 0
> 0
f (c) – 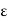 < K < f(c) +
< K < f(c) + 
Which proves that K = f(c), since 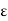 is arbitrary while K, f(c) are fixed. In fact, when f(a) < K < f(b)
is arbitrary while K, f(c) are fixed. In fact, when f(a) < K < f(b)
And f(c) = K, then a < c < b.
Note-
- If f is a continuous function on the closed interval [a, b] and If f(a) and f(b) have opposite signs (i.e., f(a) f(b) < 0), then there is a point x0 in ]a, b[ at which f vanishes. (i.e., f(
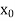 ) = 0).
) = 0). - Let f be a continuous function defined on a bounded closed interval [a, b] with values in [a, b]. Then there exists a point c in [a, b] such that f(c) = c. (i.e., there exists a fixed point c for the function f on [a, b]).
Example: The equation 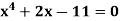 has a real root lying between 1 and 2.
has a real root lying between 1 and 2.
Sol:
The function 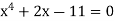 is a continuous function on the closed interval [1, 2], f(1) = –8 and f(2) = 9. Hence, by Corollary 1, there exists an
is a continuous function on the closed interval [1, 2], f(1) = –8 and f(2) = 9. Hence, by Corollary 1, there exists an  such that
such that  ) = 0.
) = 0.
Which means 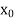 is the real root of the equation
is the real root of the equation 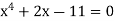 lying in the interval ]1, 2[.
lying in the interval ]1, 2[.
Key takeaways:
- Let f be a continuous function on an interval containing a and b. If K is any number between f(a) and f(b) then there is a number c, a
 c S b such that f(c) = K
c S b such that f(c) = K - If f is a continuous function on the closed interval [a, b] and If f(a) and f(b) have opposite signs (i.e., f(a) f(b) < 0), then there is a point x0 in ]a, b[ at which f vanishes. (i.e., f(
 ) = 0).
) = 0).
Theorem- A function f is bounded and integrable on [a, b] and there exists a function F such that F’ = f on [a, b], then

Since the function F’ = f is bounded and integrable. So that every given 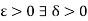 such that for every partition P =
such that for every partition P = 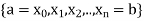 , with the norm
, with the norm 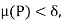

Or
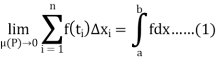
For every choice of the point 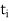 in
in 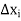 .
.
By Lagrange’s mean value theorem, we have


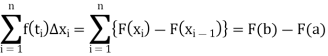
From equation (1),

This is also called second fundamental theorem of integral calculus.
Properties:
If f is a continuous function on [a, b], then 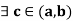 such that
such that

This result is also known as “Mean-value theorem”.
Proof: f is continuous on [a, b]
f is bounded on [a, b] and 
If m, M be the inf and sup of f on [a, b].
We know that

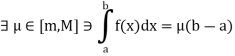
Since f is continuous on [a, b] and 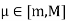 .
.
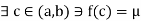
So that

Example: Prove that 
Sol:
Let us consider
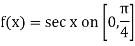
Clearly sec x is continuous on 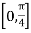 and hence integrable on
and hence integrable on 
By the above theorem, 
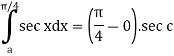
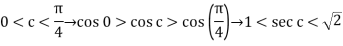

Also
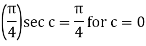
And
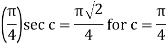
Hence
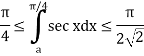
Key takeaways:
- A function f is bounded and integrable on [a, b] and there exists a function F such that F’ = f on [a, b], then

2. If f is a continuous function on [a, b], then 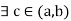 such that
such that

References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. Advanced engineering mathematics, by HK Dass
3. Mathematical analysis by Dr. Anju panwar
4. Real analysis by Dr. Sachin Kaushal
5. Real analysis by Ajit kumar & S.Kumaresan
6. Principles of real analysis by S.C Malik
.