Unit - 3
Improper integrals
Definite integrals-
When we apply limits in indefinite integrals are called definite integrals.
If an expression is written as 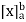 , here ‘b’ is called upper limit and ‘a’ is called lower limit.
, here ‘b’ is called upper limit and ‘a’ is called lower limit.
If f is an increasing or decreasing function on interval [a , b], then
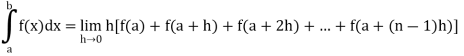

Where 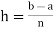
Properties-
1. The definite integral applies only if a<b, but it would be appropriate to include the case a = b and a>b as well, in that case-
If a = b, then
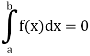
And if a>b, then
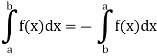
2. Integral of a constant function-

3. Constant multiple property-
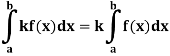
4. Interval union property-
If a < c < b, then
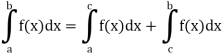
5. Inequality-
If c and d are constants such that 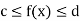 for all x in [a , b], then
for all x in [a , b], then
c(b – a)
Note- if a function f:[a , b]→R is continuous, then the function ‘f’ is always Integrable.
Example-1: Evaluate .
.
Sol. Here we notice that f:x→cos x is a decreasing function on [a , b],
Therefore by the definition of the definite integrals-
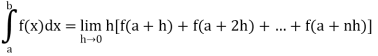
Then

Now,
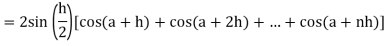
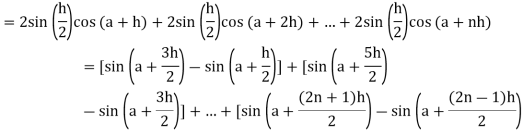
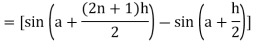

Here 
Thus
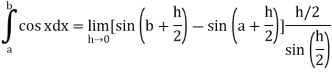
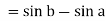
Example-2: Evaluate 
Sol. Here 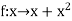 is an increasing function on [1 , 2]
is an increasing function on [1 , 2]
So that,



 …. (1)
…. (1)
We know that-
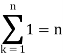
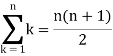
And
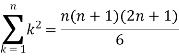
Then equation (1) becomes-


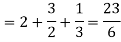
Note- we can find the definite integral directly as-

Example-3: Evaluate-

Sol. 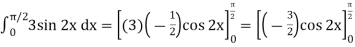
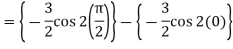
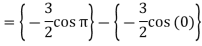
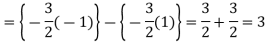
Improper integrals
(1) Let f is function defined on [a, ∞) and it is integrable on [a , t] for all t >a, then
If  exists, then we define the improper integral of f over [a, ∞) as follows-
exists, then we define the improper integral of f over [a, ∞) as follows-
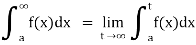
(2) Let f is function defined on (-∞,b] and it is integrable on [t , b] for all t >b, then
If 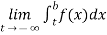 exists, then we define the improper integral of f over (-∞ , b] as follows-
exists, then we define the improper integral of f over (-∞ , b] as follows-

(3) Let f is function defined on (-∞, ∞] and it is integrable on [a , b] for every closed and bounded interval [a , b] which is the subset of R., then
If 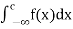 and
and 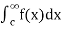 exist for some c belongs to R , then we define the improper integral of f over (-∞ ,∞ ) as follows-
exist for some c belongs to R , then we define the improper integral of f over (-∞ ,∞ ) as follows-
 =
= 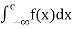 +
+ 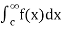
(4) Let f is function defined on (a ,∞) and  exists for all t>a , then
exists for all t>a , then
If  exists , then we define the improper integral of f over (a , ∞) as follows-
exists , then we define the improper integral of f over (a , ∞) as follows-
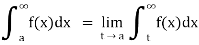
(5) Let f is function defined on (-∞ , b) and 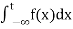 exists for all t<b , then
exists for all t<b , then
If 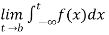 exists, then we define the improper integral of f over (-∞ , b) as follows-
exists, then we define the improper integral of f over (-∞ , b) as follows-
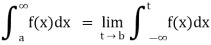
Improper integrals over finite intervals-
(1) Let f is function defined on (a, b] and  exists for all t ∈(a,b) , then
exists for all t ∈(a,b) , then
If  exists, then we define the improper integral of f over (a , b] as follows-
exists, then we define the improper integral of f over (a , b] as follows-
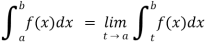
(2) Let f is function defined on [a, b) and 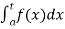 exists for all t ∈(a,b) , then
exists for all t ∈(a,b) , then
If 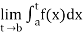 exists, then we define the improper integral of f over [a , b) as follows-
exists, then we define the improper integral of f over [a , b) as follows-

(3) Let f is function defined on [a, c) and (c, b] . If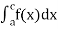 and
and 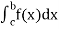 exist then we define the improper integral of f over [a, b] as follows-
exist then we define the improper integral of f over [a, b] as follows-
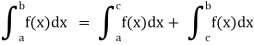
We will read more about the uses of improper integrals in the next topic.
Integration of Unbounded Function with finite limits of integration-
Let a function f be defined in an interval [a, b] everywhere except possible at finite number of points.
Convergence at left –end-
Let a be the only points of infinite discontinuity of f so that according to assumption made in the last section, the integral

𝑇ℎ𝑒 𝑖𝑚𝑝𝑟𝑜𝑝𝑒𝑟 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑙  is defined as the
is defined as the
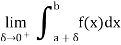
So that
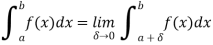
If this Limit exists and is finite, the improper integral  is said to converge at (a) if otherwise, it is called divergent.
is said to converge at (a) if otherwise, it is called divergent.
Convergence at right-end
Suppose b be the only point of infinite discontinuity the improper integral is then defined by the relation
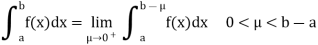
If the limit exists, the improper integral is said to be convergent at 𝑏. Otherwise
Is called divergent.
Convergence at both the end points-
If the end points a and b are the only points of infinite discontinuity of f , then for any
Point c, a < c < b,
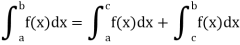
Convergence at Interior points-
If an interior point c, a < c < b, is the only point of infinite discontinuity of f, we get
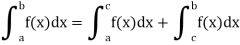
Comparison test for the convergence and divergence
If f and g are two positive functions and ‘a’ is only singular point of f and g on [a. b], such that
f(x) ≤𝑔(𝑥), 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑥∈[𝑎,𝑏]
 converges if
converges if 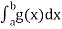 converges.
converges. diverges, if
diverges, if 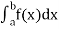 converges.
converges.
Comparison test in limit form
If f and g are two positive functions [a, b] and ‘a’ is the only singular point of f and g in [a, b], such that
𝑙𝑖𝑚𝑥→𝑎+(𝑥)𝑔(𝑥) = l
Where ‘l’ is a non – zero finite number.
Then, the two integrals 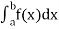 and
and 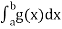 converges and diverges
converges and diverges
Together at ‘a’.
Note- The improper integral 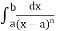 Converges if and only if n < 1.
Converges if and only if n < 1.
Example: test the convergence of
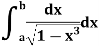
Sol:
Here we have

Here we can see that 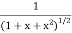 is a bounded function.
is a bounded function.
Suppose M is its upper bound then

Also since
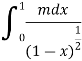
Is convergent as n = ½ < 1. Therefore,
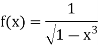
Is convergent.
Example: Show that 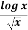 is divergent.
is divergent.
Sol:
Let us suppose
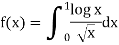
Here x=1 is only singular point.
Take (𝑥) =1/x-1
Then


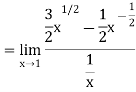
Thus,  and
and  are same.
are same.
Since  is divergent, hence
is divergent, hence  is divergent.
is divergent.
Convergence of beta and gamma functions
Beta function- Show that

Exists if and only if m and n both are positive.
Proof:
It is a proper integral for 𝑚≥1,≥1 ,0 and 1 are the only points of infinite discontinuity; 0 when m < 1 and 1. When n < 1, we have
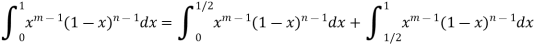
Converges at 0, when m < 1,
Suppose
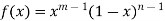

Take g(x) = 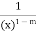
Then
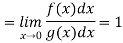
Since 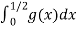 converges iff. 1 – m < 1 or m > 0.
converges iff. 1 – m < 1 or m > 0.
Thus
 converges for m > 0.
converges for m > 0.
Converges at x = 1,
We take

Take
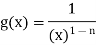
Then

Also 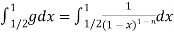 converges if and only if 1−n < 1 or n > 0.
converges if and only if 1−n < 1 or n > 0.
Thus,  converges if n > 0.
converges if n > 0.
Hence 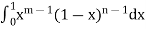 converges if m > 0 , n > 0 .
converges if m > 0 , n > 0 .
Absolute convergence
The improper integral 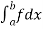 is said to be absolutely convergent if
is said to be absolutely convergent if  is convergent
is convergent
Note- Every absolutely convergent integral is convergent.
Example: Show that 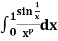 , p>0 converges absolutely for p<1.
, p>0 converges absolutely for p<1.
Sol:
Suppose

‘0’ is the only point of infinite discontinuity and f does not keeps the same sign in [0, 1].
So that
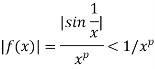
Also 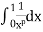 converges for 𝑝 < 1.
converges for 𝑝 < 1.
Thus
 converges if and only if p > 0.
converges if and only if p > 0.
Hence
 is absolutely convergent if and only if 𝑝 < 1.
is absolutely convergent if and only if 𝑝 < 1.
Convergent at infinity
The symbol  , 𝑥≥ 𝑎 is defined as limit of
, 𝑥≥ 𝑎 is defined as limit of 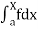 when x tends to infinity, so that
when x tends to infinity, so that

If the limit exists and is finite then the improper integral (1) is said to be divergent.
Example: Show that  is divergent.
is divergent.
Sol:
For X > 0, we have
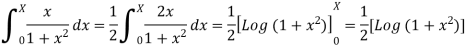
Here
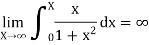
So that 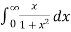 is divergent.
is divergent.
Gamma function-
The integral
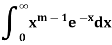
Is convergent if and only if 𝑚>0.
Proof:
Suppose
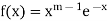
If 𝑚 < 1, the ‘0’ infinite discontinuity.
So we need to examine the convergence of above improper integral at both 0 and ∞.
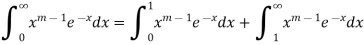
Convergence at 0 for 𝒎<1:
Let
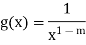
Then
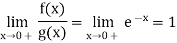
Since 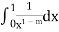 converges, if and only if m>0.
converges, if and only if m>0.
Therefore 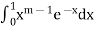 converges if and only if 𝑚>0.
converges if and only if 𝑚>0.
Convergence at 
Let
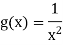
So that
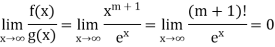
Since 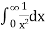 is divergent
is divergent
Thus 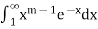 is convergent for every m.
is convergent for every m.
Hence 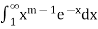 is convergent if and only if 𝑚> 0 and is denoted by < 𝑚) .
is convergent if and only if 𝑚> 0 and is denoted by < 𝑚) .
Thus

Thus Γ(0), Γ(-1), etc. are not exists .
Key takeaways:
- If an expression is written as
 , here ‘b’ is called upper limit and ‘a’ is called lower limit.
, here ‘b’ is called upper limit and ‘a’ is called lower limit. - If a function f:[a , b]→R is continuous, then the function ‘f’ is always Integrable.
- 𝑇ℎ𝑒 𝑖𝑚𝑝𝑟𝑜𝑝𝑒𝑟 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑙
 is defined as the
is defined as the

4. If f and g are two positive functions and ‘a’ is only singular point of f and g on [a. b], such that
f(x) ≤𝑔(𝑥),𝑓𝑜𝑟 𝑎𝑙𝑙 𝑥∈[𝑎,𝑏]
 converges if
converges if 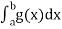 converges.
converges.
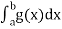 diverges, if
diverges, if 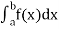 converges.
converges.
The improper integral 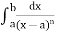 Converges if and only if n < 1.
Converges if and only if n < 1.
5. The improper integral 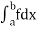 is said to be absolutely convergent if
is said to be absolutely convergent if 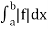 is convergent
is convergent
6. Every absolutely convergent integral is convergent
Sequence and series of a function:
Let  be a real valued function defined on an interval I and for each
be a real valued function defined on an interval I and for each  , then <
, then < is called a sequence of real valued function on I.
is called a sequence of real valued function on I.
We denote it by { } or <
} or < >
>
If 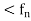 > is a sequence of real valued function on an interval I, then
> is a sequence of real valued function on an interval I, then 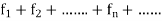 is called the series of real valued function defined on an interval I.
is called the series of real valued function defined on an interval I.
This series is denoted by 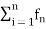
That is, we shall consider sequences whose terms are functions rather than real numbers. These sequences are useful in obtaining approximations to a given function.
Point-wise convergence-
Let 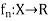 be a sequence of functions from a set X to R.
be a sequence of functions from a set X to R.
We say that  converges to f pointwise on X if for each
converges to f pointwise on X if for each 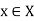 the sequence (
the sequence ( of real numbers converges to the real number f(x) in R.
of real numbers converges to the real number f(x) in R.
Like we say a sequence ( is convergent on X. We may also define a sequence of function (
is convergent on X. We may also define a sequence of function (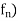 is pointwise convergent on X.
is pointwise convergent on X.
This means that there exists a function 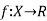 such that (
such that (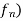 is pointwise convergent to f. There is an another problem for us. We need to find the limit function f and then show that
is pointwise convergent to f. There is an another problem for us. We need to find the limit function f and then show that  pointwise.
pointwise.
This means that we fix first and form the sequence
first and form the sequence 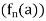 of real numbers.
of real numbers.
For any given 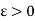 , we have to find an
, we have to find an  such that
such that 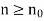 we have |
we have |
Thus 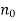 may depend not only on
may depend not only on 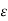 but also on a.
but also on a.
Example: A sequence of continuous functions whose limit function is discontinuous.
Let
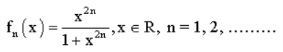
We note that
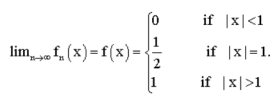
Each  is continuous on R but the limit function f is discontinuous at x = 1 and x = -1.
is continuous on R but the limit function f is discontinuous at x = 1 and x = -1.
Example: A double sequence in which limit process cannot be interchanged:
For m =1, 2,….,
n = 1, 2,3,..., let us consider the double sequence
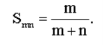
For every fixed n, we have

And so
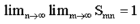
On the other hand, for every fixed m, we have
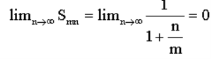
And so
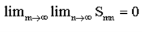
Hence
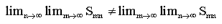
Example: A sequence of differentiable functions { 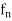 } with limit 0 for which {
} with limit 0 for which {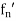 } diverges
} diverges
Let
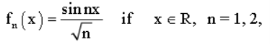
Then

But

And so

Uniform convergence-
A sequence of function { is said to converge uniformly to a function f on a set E if for every
is said to converge uniformly to a function f on a set E if for every  there exists and integer N such that n > N implies
there exists and integer N such that n > N implies

If each tern of the sequence <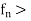 is real-valued, then the expression (1) can be written as
is real-valued, then the expression (1) can be written as
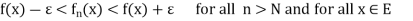
Definition: A series  is said to be uniformly convergent on E if the sequence
is said to be uniformly convergent on E if the sequence 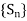 of partial sums defined by
of partial sums defined by  converges uniformly on E.
converges uniformly on E.
Note- Every uniformly convergent sequence is pointwise convergent but not conversely.
Example: Consider the sequence < defined by
defined by
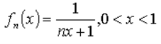
Then
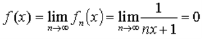
Hence 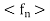 converence pointwise to 0 for all 0 < x < 1.
converence pointwise to 0 for all 0 < x < 1.
Let 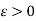 be given, then for convergence, we have
be given, then for convergence, we have
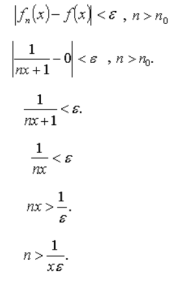
If 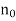 is taken as integer greater than 1/x
is taken as integer greater than 1/x , then
, then
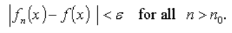
Since 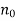 depends both on
depends both on  in (0, 1), so
in (0, 1), so  does not converge uniformly on (0, 1).
does not converge uniformly on (0, 1).
Example: Consider the sequence< defined by
defined by
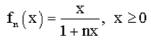
Then
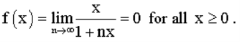
Then <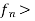 converges pointwise to 0 for all
converges pointwise to 0 for all  Let
Let  then for convergence we must have
then for convergence we must have
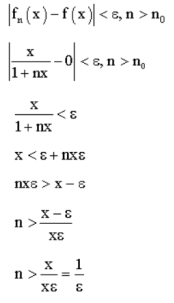
If  is taken as integer greater than 1/
is taken as integer greater than 1/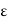 , then
, then
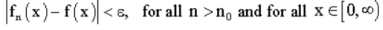
Hence 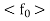 converges uniformly to f on [0,
converges uniformly to f on [0, 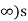
Example: Consider the sequence <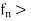 defined by
defined by

Then
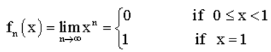
Let 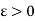 be given. Then for convergence, we must have
be given. Then for convergence, we must have
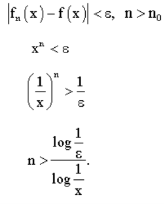
Thus we should take 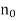 to be an integer next higher to
to be an integer next higher to  .
.
If we take x = 1 then m does not exists.
Thus the sequence is not uniformly convergent to f in the interval which contains 1.
Cauchy’s principal of uniform convergence
The necessary and sufficient condition for a sequence of functions  defined on A to converge uniformly on A is that for every
defined on A to converge uniformly on A is that for every  > 0, there exists a positive integer m such that
> 0, there exists a positive integer m such that
|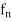 (x) –
(x) –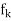 (x)| <
(x)| <  for n > k
for n > k  m and " x
m and " x 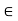 A
A
Key takeaways:
- Let
 be a real valued function defined on an interval I and for each
be a real valued function defined on an interval I and for each 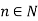 , then <
, then <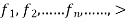 is called a sequence of real valued function on I.
is called a sequence of real valued function on I. - We say that
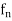 converges to f pointwise on X if for each
converges to f pointwise on X if for each  the sequence (
the sequence ( of real numbers converges to the real number f(x) in R.
of real numbers converges to the real number f(x) in R. - A series
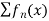 is said to be uniformly convergent on E if the sequence
is said to be uniformly convergent on E if the sequence 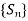 of partial sums defined by
of partial sums defined by 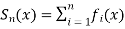 converges uniformly on E.
converges uniformly on E. - Every uniformly convergent sequence is pointwise convergent but not conversely.
Uniform Convergence and Continuity
Definition- A sequence of functions  on D is uniformly convergent on D if and only if, for all > 0, there exists a N ∈ N such that |fn(x) − f(x)| <
on D is uniformly convergent on D if and only if, for all > 0, there exists a N ∈ N such that |fn(x) − f(x)| < 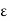 for all x ∈ D and n ≥ N.
for all x ∈ D and n ≥ N.
Definition of supremum norm-
Suppose f : D → R is a function with domain D. We define the sup-norm of f over D as:
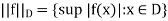
a function f is bounded if and only if ||f|| < ∞, which follows immediately from the definitions. The connection between sup-norm and uniform convergence is also straight-forward.
Theorems on continuity:
Theorem-1: If f, g are two continuous functions at a point c then the functions f + g, f – g and fg are also continuous at c and g(c) is non-zero then f/g is also continuous at c.
Theorem-2: A function f is defined on an interval I, is continuous at a point c belongs to I, is continuous at point  iff for every sequence
iff for every sequence 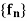 converging to c, we have
converging to c, we have

Proof:
First let us suppose that the function f is continuous at a point  , and {
, and {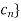 is a sequence such that
is a sequence such that 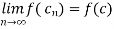
Since f is continuous at c, therefore for any given 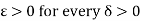 such that
such that
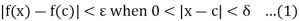
Again since 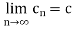 , therefore for every, a positive integer m, such that
, therefore for every, a positive integer m, such that
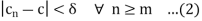
From equation (1), put  , we have
, we have


The sequence { converges to f(c).
converges to f(c).
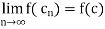
Now suppose that that f is not continuous at c.
We will now show that through 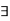 a sequence {
a sequence {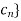 converging to c yet the sequence {
converging to c yet the sequence {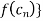 does not converges to f(c).
does not converges to f(c).
Since f is not continuous at c, therefore there exists an  .
.
Such that for every 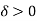 ,
, 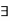 an x such that
an x such that

Also

By putting 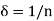 , we find that for each positive integer n,
, we find that for each positive integer n,
There is an  such that
such that
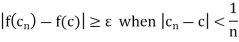
Thus the sequence {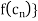 does not converge to f(c).
does not converge to f(c).
Example: Examine the continuity at the origin
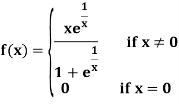
Sol:
Now,


Thus
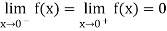
Also
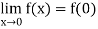
Thus the function is continuous at origin.
Theorem: If a function f is continuous on a closed interval [a, b], then it attains its bounds at least once in [a., b]
Proof:
If f is a continuous function, then it attains its bounds at every point of the interval.
Suppose f is a function which is not constant.
Since f is continuous on the interval which is closed [a, b], so that it is bounded.
Let m and M are the infimum and supremum of f.
It is to be shown that for every points p and q of [a, b] such that
f(p) = m and f(q) = M
Now consider the supremum case-
Let f does not attains the supremum M so that the function does not take the value M for any point 
Which means
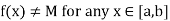
Now consider

Which is positive for all values of x in [a, b].
Evidently the function g is continuous and so bounded in [a, b].
Let k(>0) be its supremum
So that
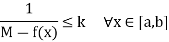
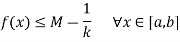
Which is a contradiction that M is the supremum of f in [a, b].
Hence our superposition that f does not attains the value M leads to a contradiction and hence f attains its supremum for at least one value in [a, b].
Similarly we can show that the function also attains its infimum m.
Therefore the function attains its bounds at least once in [a, b].
Theorem: if a function f is continuous at an interior point c of [a, b] and  such that f(x) has the same sign as f(c) for every
such that f(x) has the same sign as f(c) for every 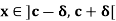
Proof:
Since the function f is continuous at an interior point c of [a, b], therefore for any 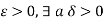 such that
such that

Or
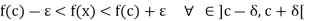
When f(c) > 0, taking 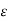 to be less than f(c) we find that
to be less than f(c) we find that
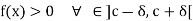
When f(c) > 0, taking 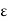 to be less than -f(c) we find that
to be less than -f(c) we find that
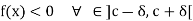
Theorem: if a function f is continuous on [a, b] and 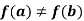 , then it assumes every value between f(a) and f(b).
, then it assumes every value between f(a) and f(b).
Proof:
Suppose A is any number between f(a) and f(b). Now we show that there exists a number  such that f(c) = A.
such that f(c) = A.
Let consider a function 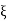 defined on [a, b] such that
defined on [a, b] such that

Hence it it clear 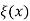 is continuous on [a, b].
is continuous on [a, b].
Also

And
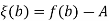
So that 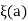 and
and 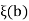 has positive signs.
has positive signs.
Thus the function 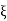 is continuous on [a, b] and
is continuous on [a, b] and 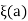 and
and  are of opposite signs, therefore for every
are of opposite signs, therefore for every 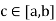 , such that
, such that
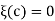
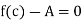

Theorem- Let 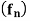 be a sequence of continuous functions on a set E
be a sequence of continuous functions on a set E 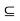 R and suppose that
R and suppose that 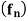 converges uniformly on E to a function f : E
converges uniformly on E to a function f : E  R . Then the limit function f is continuous.
R . Then the limit function f is continuous.
Proof:
Suppose c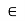 E be an arbitrary point. If c is an isolated point of E, then f is automatically continuous at c. So suppose that c is an accumulation point of E. We shall show that f is continuous at c. Since
E be an arbitrary point. If c is an isolated point of E, then f is automatically continuous at c. So suppose that c is an accumulation point of E. We shall show that f is continuous at c. Since  uniformly, for every
uniformly, for every  > 0 there is an integer N such that n
> 0 there is an integer N such that n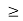 N implies
N implies
|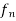 (x) –f(x)| <
(x) –f(x)| <  for all x
for all x 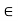 E
E
Since  is continuous at c, there is a neighbourhood
is continuous at c, there is a neighbourhood  such that x
such that x 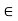
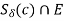 (since c is limit point) implies
(since c is limit point) implies
|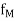 (x) –
(x) –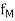 (c)| <
(c)| < 
By triangle inequality, we get


Hence
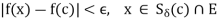
Which is the proof of continuity of f at arbitrary point  .
.
Theorem- If the sequence of continuous function  is uniformly convergent to a function f on [a, b] then f is continuous on [a, b].
is uniformly convergent to a function f on [a, b] then f is continuous on [a, b].
Proof:
Suppose 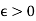 be given.
be given.
The sequence  is uniformly convergent to f on [a, b], then there exists a positive integer m such that
is uniformly convergent to f on [a, b], then there exists a positive integer m such that
|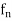 (x) –f(x)| <
(x) –f(x)| <  for every
for every 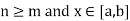 ….(1)
….(1)
Let 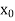 be any point of [a, b].
be any point of [a, b].
In particular then from (1),
|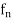 (
(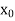 ) –f(
) –f(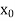 )| <
)| <  for every
for every  ……(2)
……(2)
Now 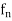 is continuous at
is continuous at 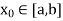
So there exists  such that
such that
| (
(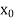 ) –f(
) –f( )| <
)| <  whenever |x -
whenever |x - 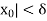 …….(3)
…….(3)
Hence for |x -  , we have
, we have
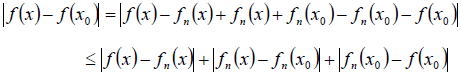
From (1), (2) and (3)
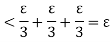
We get |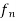 (x) – f(
(x) – f( )| <
)| < 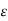 whenever |x -
whenever |x - 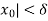
Hence f is continuous at 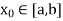
f is continuous on [a, b].
Theorem-1:
Uniform convergence and continuity-
If  be a sequence of continuous functions defined on [a, b] and
be a sequence of continuous functions defined on [a, b] and  f uniformly on [a, b], then
f uniformly on [a, b], then
f is continuous on [a, b].
Theorem -2:
Uniform Convergence and Differentiation
Let 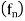 be a sequence of functions, each differentiable on [a, b] such that
be a sequence of functions, each differentiable on [a, b] such that 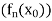 converges for some point
converges for some point  of [a, b]. If
of [a, b]. If 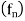 converges uniformly on [a, b] then
converges uniformly on [a, b] then  converges uniformly on [a, b] to a function f such that
converges uniformly on [a, b] to a function f such that
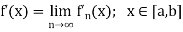
Theorem-3:
Uniform Convergence and Integration
If a sequence  converges uniformly to f on [a, b] and each function
converges uniformly to f on [a, b] and each function 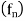 is integrable on [a, b], then f is integrable on [a, b] and
is integrable on [a, b], then f is integrable on [a, b] and
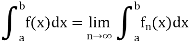
Theorems on derivability-
In the function f, g are derivable at c then the functions f + g, f – g, fg and f/g where g(c) is non-negative are also derivable at c.
Theorem: if f is derivable at c and f(c) is non-zero then the function 1/f is also derivable thereat, and

Proof:
Since f is derivable at c, it is also continuous thereat.
Again since 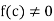 , there exists a neighbourhood N of c wherin f does not vanish.
, there exists a neighbourhood N of c wherin f does not vanish.
Now
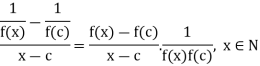
Finding limits when x tends to c, we get
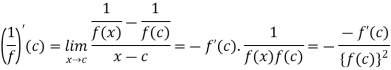
Hence the limit exists and equals to 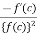 .
.
Key takeaways:
- Let
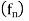 be a sequence of continuous functions on a set E
be a sequence of continuous functions on a set E  R and suppose that
R and suppose that  converges uniformly on E to a function f : E
converges uniformly on E to a function f : E 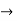 R . Then the limit function f is continuous.
R . Then the limit function f is continuous. - If the sequence of continuous function
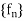 is uniformly convergent to a function f on [a,b] then f is continuous on [a,b]
is uniformly convergent to a function f on [a,b] then f is continuous on [a,b]
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. Advanced engineering mathematics, by HK Dass
3. Mathematical analysis by Dr. Anju panwar
4. Real analysis by Dr. Sachin Kaushal
5. Real analysis by Ajit kumar & S.Kumaresan
6. Principles of real analysis by S.C Malik
.
.
.