Unit - 4

Series of functions

4.1 Series of functions

A series is the sum of the terms of a sequence. Thus if 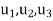is a sequence then the sum 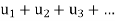of all the terms is called an infinite series and it is denoted by

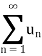
The sequence is called the sequence of partial sums of the series and the partial sums 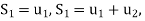so on, is regarded as the approximation to the full infinite sum 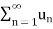of the series.

If the sequence { of partial sums converges the series is termed as convergent and lim 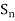is said to be the sum of the series.

Note- an infinite series is said to converge, diverge if its sequence of partial sums converges, diverges respectively.

Necessary condition for convergence

Theorem- A necessary condition for convergence of an infinite series 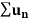is that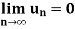

Let

So that { is the sequence of partial sums.

Since the series converges, therefore the sequence 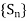also converges.

Consequently

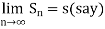
Now

So that

Hence for a convergent series

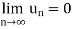
i.e. series cannot converge if its n’th term does not tend to zero.

Example: Show that the series given below is not convergent.

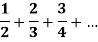
Sol:

Here we have

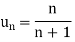
Here is not zero, therefore the given series is not convergent.

Key takeaways

1. A series is the sum of the terms of a sequence. Thus if is a sequence then the sum 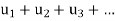of all the terms is called an infinite series and it is denoted by

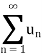
2.     An infinite series is said to converge, diverge if its sequence of partial sums converges, diverges respectively.

4.2 Theorems on the continuity and derivability of the sum function of a series of functions

Continuous function-

Suppose f is the function, then it is said to be continuous at a point c, a < c < b, if

Note- A function f is said to be continuous from the left at c if

A function f is said to be continuous from the right at c if

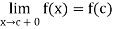
Hence a function is continuous at c if it is continuous from the left as well as from right.

Continuity at an end point- A function f defined on interval [a, b] is said to be continuous at the end point ‘a’ if it is continuous from the right at ‘a’

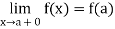
Similarly, the function is continuous at the end point b of [a, b] if

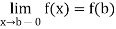
Continuity in an interval- A function f is said to be continuous in an interval [a, b] if it is continuous at every point of the interval.

Theorems on continuity-

Theorem- if f and g be two functions continuous at a point c then the function f + g, f – g, fg are also continuous at c.

Theorem- A function f defined on an interval I, is continuous at a point c 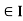, and 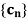is a sequence such that

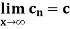
Since f is continuous at c, so that for any given

Such that

Again since , therefore a positive integer m, such that

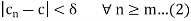
From equation (1), put , we get

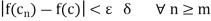
The sequence 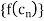converges to f(c).

Or

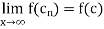
Now let f is not continuous at c.

We will now show that through 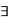a sequence converging to c yet the sequence 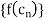does not converges to f(c).

Since f is not continuous at c, therefore there exists an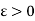

Such that for every, there exists an x such that

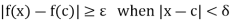
Also

By taking 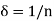, we find that for each positive integer n, there is a 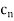, such that

Thus the sequence does not converges to f(c).

Example: Prove that the function defined by

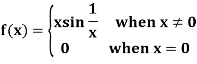
Is continuous at x = 0

Sol:

Now

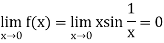
So that

Therefore, the function is continuous at x = 0.

Types of discontinuities-

1. A function f is said to be a removable discontinuity at x = c if  exists but it is not equal to the value of f(c) of the function.

Such a discontinuity can be removed by assigning a value to the function at x = c.

2.     The function f is said to have a discontinuity of the first kind at x = c if 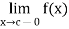and both exists but unequal.

3.     The function f is said to have a discontinuity of the first kind from left at x = c if 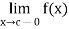exists but not equal to f(c).

4.     The function f is said to have a discontinuity of the second kind at x = c if neithe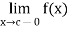r nor exists.

5.     The function f is said to have a discontinuity of the second kind from left at x = c if does not exists

Example: Discuss the kind of discontinuity if any, of the following function-

Sol:

The function is continuous at all points except the origin.

Let’s test at x = 0

And

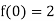
Thus the function has discontinuity of the first kind from the right at x = 0.

Example: When [x] denotes the largest integer, then discuss the continuity at x = 3 for the function,

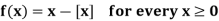
Sol:

Here

And

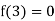
Thus the function has a discontinuity of the first kind from the left at x = 3.

Example: Show that the following function is continuous at origin-

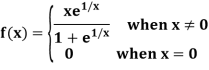
Sol:

Here

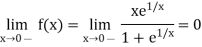
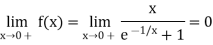
Thus

Also

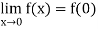
Therefore, the function is continuous at the origin.

Uniform continuity

A function f defined on an interval I is said to be uniformly continuous on I if to each 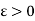there exists a 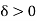, such that

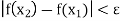
Theorem: A function which is uniformly continuous on an interval, is continuous on that interval

Suppose the function f is uniformly continuous on an interval I, so that for a given 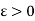, there exists a 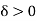such that

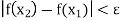
Where 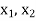are any two points of I for which |

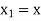Let , then by taking we find that for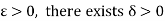

Such that

Hence the function is continuous at every point , which means the functions  f is continuous on I.

Derivability in an interval

A function defined on [a, b] is derivable at the end point a, which means f’(a) exists if

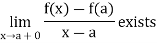
Or we can say that

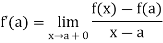
Similarly the function is derivavble at the end point b, if
 

Or

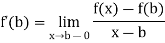
Example: Show that the function f(x) = |x| is not derivable at x = 0.

Sol:

Left hand derivative –

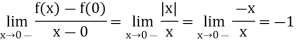
Right hand derivative –

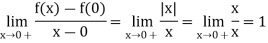
Thus

Hence the function is not derivable at x = 0.

Theorem- A function which is derivable at a point is necessarily continuous at that point.

Poof:

Suppose the function is derivable at x = c

So that

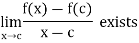
Now

Taking limits as x tends to c, we get

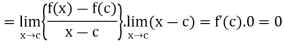So that , therefore the function f is continuous t x = c.

Note-

If the functions f, g are derivable at c then the functions f + g, f – g, fg and f/g [are also derivable at c and

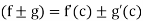
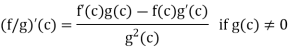
Key takeaways:

1. Suppose f is the function, then it is said to be continuous at a point c, a < c < b, if

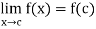
2.     If f and g be two functions continuous at a point c then the function f + g, f – g, fg are also continuous at c.

3.     A function f defined on an interval I, is continuous at a point c 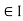, and 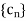is a sequence such that

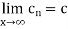
4.     A function f defined on an interval I is said to be uniformly continuous on I if to each 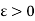there exists a 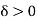, such that

5.     A function defined on [a, b] is derivable at the end point a, which means f’(a) exists if

4.3 Cauchy criterion for uniform convergence and Weierstrass M-Test Limit superior and Limit inferior

Cauchy’s convergence theorem-

A series of real function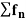, each defined on a set X converges uniformly on X iff for every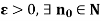, such that

Proof:

Let 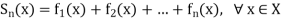be a partial sum.

So that 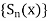is a sequence of partial sums of the series  . Now the series 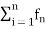is uniformly convergent iff the sequence 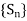is uniformly convergent.

It means for the given a positive integer m such that n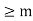

By Cauchy’s criteria of uniform convergence of sequence

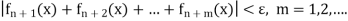
Which is the complete proof of Cauchy’s criterion for series.

Weierstrass M-Test

Let <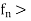 be a sequence of functions defined on E and suppos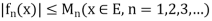e where is independent of x.

Then converges uniformly as well as absolutely on E if 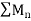converges.

Proof:

In order to prove uniform convergence, we see that

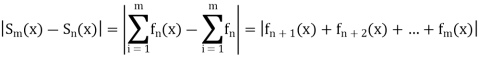
But since 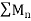is convergent, given , there exists N(which is independent of x) such that

Hence

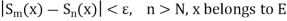
And so converges uniformly by the Cauchy’s criterion for uniform convergence.

Example: Prove that

Is uniformly convergent.

Sol.

We assume that x is positive, for if x is negative.

We can change the signs of all terms.

We have

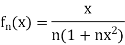
And

Thus maximum value of is

Hence

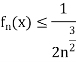
Since

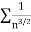is convergent, Weirstrass’s M-test implies that is uniformly convergent for all

4.4. Power series, radius of convergence, Cauchy Hadamard Theorem

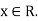
Power series

A series of the form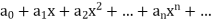

Where all the ‘a’ are independent of x, is known as power series in x

A power series is an infinite series of the form 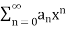where 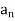are the coefficients.

Convergence of power series

For x = 0, every power series is convergent.

There are three cases about the convergence of power series

1. The series converges for only x = 0 which is trivial point of convergence, then it is called “nowhere convergent”.

2. The series converges absolutely for all values of x, then it is called “everywhere convergent”.

3. The series converges for some values of x and diverges for others.

Note- the collection of points x for which the series is convergent is called its region of convergence.

Definition: let 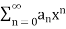be a power series. Then applying Cauchy’s root test we see that the power series 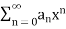is convergent if

Where

The series is divergent if

Taking

We will prove that the power series is absolutely convergent if |x| < R and divergent if |x| > R.

If 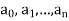are real and if x is real, we get an interval –R < x < R inside which the series is convergent.

If x is replaced by a complex number z then the power series converges absolutely at all points z inside the circle |z| = R and does not converge at any point outside the circle.

This circle is called the circle of convergence and R is known as the radius of convergence.

The interval (-R, R) is called interval of convergence.

Definition:  For the power series the radius of convergence is defined as

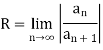
Provided the limit exists.

Interval for convergence-

In this power series-

D’Almbert’s ratio test-

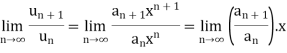
If 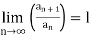, then by ratio test, the power series is convergent, when 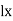is less than 1.

Or in other way if |x|<1/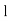 then the series converges and diverges for other values.

Thus the interval of convergence of power series is-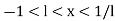

Example: Find the radius of convergence of the following series

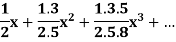
Sol.

Here we have

The n’th term of the series will be

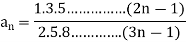
We know that

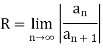
Then

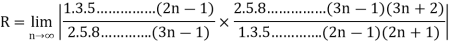
So series converges for all x where |x| < 3/2.

Example: Find the radius of convergence of the following series

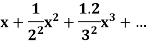
Sol:

Here we have

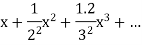
Now, the n’th term of the series will be

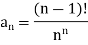
We know that

So the series is convergent for all x where |x| < e.

Example-1: If the series 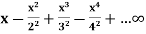converges, then find the value of x.

Sol. Here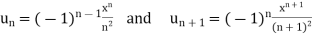

Then,

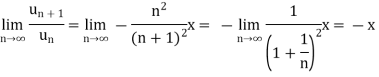
By D’Almbert’s ratio test the series is convergent for |x|<1 and divergent if |x|>1.

So at x = 1

The series becomes-

At x = -1

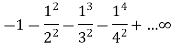
This is an alternately convergent series.

This is also convergent series, p = 2

Here, the interval of convergence is

Example-2: If the series converges, then find the value of x.

Sol. Here

Then,

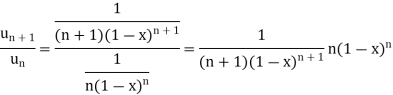
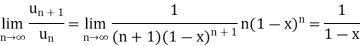
By D’Almbert’s ratio test the series is convergent for ||<1 or |1-x|>1

Or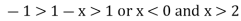

At x = 0, the series becomes- 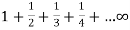 which is divergent harmonic series.

At x = 2, the series becomes-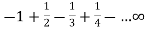 

It is an alternate series which is convergent by Leibnitz rule.

So that the series.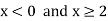

Cauchy-Hadamdard theorem- If R is the radius of convergence of the power series 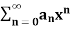, then the series is absolutely convergent if |x| < R and divergent if |x| > R.

Proof:

Since the n’th term of the serie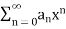s is 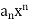, for each x belongs to R, let

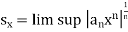, then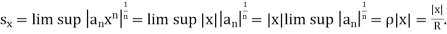 

Case-1: suppose 0 < R < +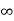

In this case,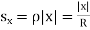

So if |x| < R, then 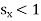and hence the power series is convergent by Cauchy root test, and

If |x| > R, then 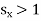. So power series 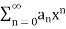is divergent by Cauchy root test.

Case-2: suppose R = +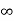

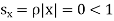Then , therefore for each x belongs to R. Hence by Cauchy root test, power series 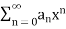is convergent for each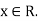

Case-3: Suppose R = 0

In this case, 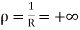, so that for x 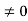, therefore by Cauchy root test, the power series 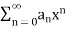is divergent for x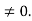

Example: Find the interval of convergence of the following power series-

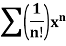
Sol:

Consider the series
 

Here

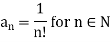
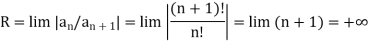
Hence, the series converges for all 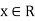. So that the interval of convergence  is (-

Example: Find the interval of convergence of the following power series-

Sol:

Consider the series,

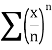
Here

Therefore

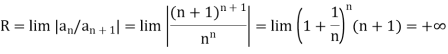
Hence, the series converges for all . So the interval of convergence is

Key takeaways

1. A series of the form

Where all the ‘a’ are independent of x, is known as power series in x

2.     This circle is called the circle of convergence and R is known as the radius of convergence.

3.     Cauchy-Hadamdard theorem- If R is the radius of convergence of the power series 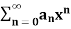, then the series is absolutely convergent if |x| < R and divergent if |x| > R.

4.5. Differentiation and integration of power series

What is power series?

A power series is a type of series with terms involving a variable. Evidently, if the variable is x, then all the terms of the series involve powers of x. So we can say that a power series can be design of as an infinite polynomial.

Let the power series 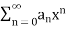have the radius of convergence R > 0.

Let

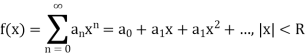
Then for |x| < R the function 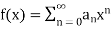is continuous.

Differentiation of power series-

The differentiation of power series is given by

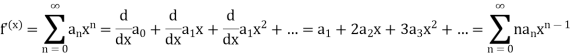
Integration of power series-

The power series can also be integrated term-by-term on an interval lying inside the interval of convergence.

Hence if –R < b < x < R,

When the series is integrated on the interval [0, x], it can be written as

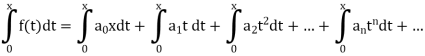
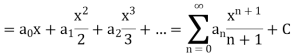
Where C is the constant.

Evaluating the derivative and indefinite integral in this manner is called term-by-term differentiation of a power series and term-by-term integration of a power series respectively.

4.6. Abel's Theorem

Abel’s theorem (first form)

If a power series 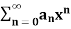converges at the point R of the interval of convergence (-R, R), then it uniformly converges in the interval [0, R].

Proof:

Let us consider the sum

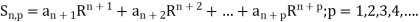
Then we have

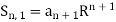
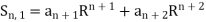
And so on.

This gives

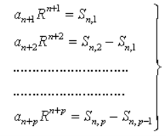…..(1)

Let e > 0 be given

Now the series 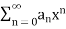is convergent at x = R.

The series of numbers 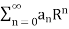is convergent and hence by Cauchy’s general principal of convergence, there exists an integer N such that

Now if we take 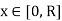, then we have

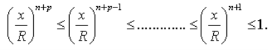……(3)

Consider for all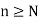

Thus we have proved

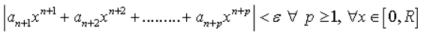
Hence by Cauchy’s criterion of convergence of series, the series 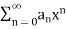converges uniformly on [0, R].

Note-

1. In case, a power series with interval of convergence (-R, R) converges at x = -R , then the series is uniformly convergent in [-R, 0].

Similarly, if a series convergent at the end points -R and R, then the series is uniformly convergent on [-

R, R].

2. If a power series with interval of convergence (-R, R) diverges at end point x  R , then it cannot be uniformly convergent on [0, R].

Abel’s theorem (Second form)

Let be a power series with finite radius of convergence R and let .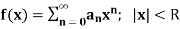

If the series 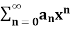converges at end point x = R then

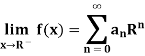
Proof:

If we take R = 1, then there is no loss of generality,

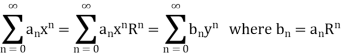
This is the power series with radius R’, where

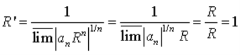
So if any series is given we can transform it in another power series with unit radius of convergence.

We can take R = 1.

Thus, now it is sufficient to prove that let be a power series with unit radius of convergence and

Let

If the series converges then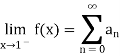
 

Now let’s prove the same.

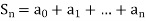
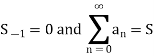
Then

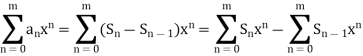
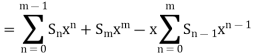
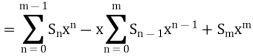
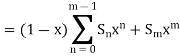
Now for |x| < 1;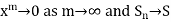

So that

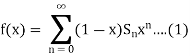
Now since 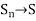, therefore for , there exists an integer N such that

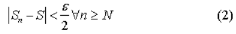
Also we have

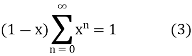
Hence for all 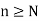, we have

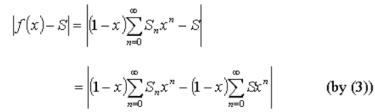
Now for a fixed N, 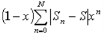is a continuous function of x having zero value at x = 1.

Thus there exists 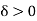such that 1 -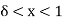

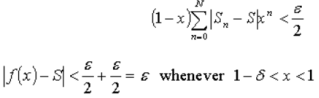
Hence

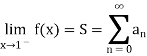
Abel’s test for uniform convergence-

The series converges uniformly on E if

1. 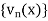is a positive decreasing sequence for all values of x

2. 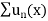is uniformly convergent

3. is bounded for all x

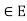
Example: Let us consider the series

Here we note that if p > 1, then 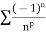is absolutely convergent and is independent of x.

Hence by Weierstrass’s M-test, the given series is uniformly convergent for all x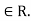

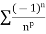If , the series is convergent but not absolutely.

Let

Then <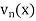> is monotonically decreasing sequence for |x| < 1, because

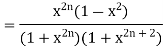
Also

Hence, by Abel’s test, the series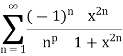
 

Is uniformly convergent for 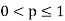and |x| < 1.

Example: Prove that the given series

Is converges uniformly in (0, 1).

Sol.

Here we have

Since n/n+1 tends to 0 as n tends to infinity, taking n sufficient large

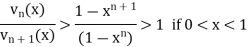
Hence < is monotonically decreasing and positive.

Hence by Abel’s test, the given series is uniformly convergent in (0, 1).

Key takeaways

1. Abel’s theorem (first form)

If a power series converges at the point R of the interval of convergence (-R, R), then it uniformly converges in the interval [0, R].

2.     Abel’s theorem (Second form)

Let 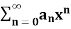be a power series with finite radius of convergence R and let .

If the series 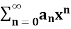converges at end point x = R then

4.7. Weierstrass Approximation Theorem

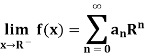
This theorem was given by Karl weierstrass in 1885. He proved this theorem on the approximation by polynomials of continuousreal valued functions defined on closed intervals.

Statement- if f is real function defined on [a, b] then there exists a sequence of real polynomials which converges uniformly to f(x) on [a, b], which means

Proof:

If a = b, then f(x) = f(a)

Then the theorem is true by taking to be a constant polynomial defined by

Thus we assume that a < b

We take a = 0, b = 1.

Now we know that for positive integer n and k where 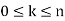, the binomial coefficient 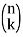, which is defined as

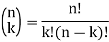
Now we define the polynomial 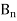where

The polynomial (1) is known as Bernstain polynomial.

We shall prove that certain Bernstain polynomial exists which uniformly converges to f on [0, 1].

Consider the identity

Diff w.r.t. x, we get

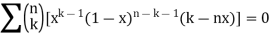
Multiply by x(1-x) both sides, we get

Diff. w.r.t. x, we get

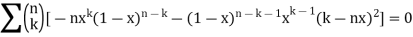
On applying (2) we get

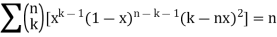
Multiply by x(1-x), we get

Since the maximum value of x(1-x) in [0, 1] is ¼.

So the equation (4) can be written as

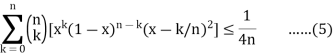
Now f is continuous on [0,1]. So, f is bounded and uniformly continuous on [0, 1].

such that

And by uniform continuity for given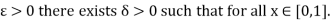

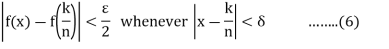
Now for any fixed but arbitrary x in [0,1], then n-values 0,1,2,3,….,n of k can be divided into two parts as follows

Let A be the set of values of k for which and B be the set of remaining values for which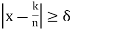

Now for 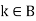, we get by (5)

.

Now

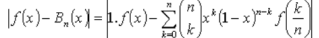
By (2)

We split the summation on RHS into two parts accordingly as

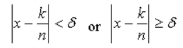
Let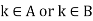

Thus we have

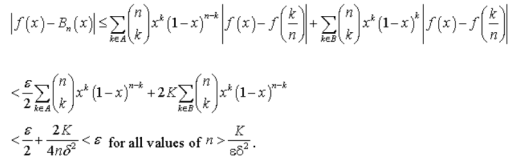
Thus converges uniformly to f(x) on [0, 1].

Which is the proof of the theorem.

Example: Find a continuous function f: (-1, 1) that can not be approximated by a polynomial.

Sol:

Suppose f: (-1 1) be given by f(x) = 1/(1+x). Then f will also be a continuous function.

If possible, for , let there exists a polynomial p(x) such that

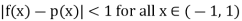
Since p(x) is bounded on (-1, 1), there exists a constant M > 0 such that

Now

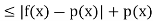
Therefore, f is bounded on (-1, 1) which is a contradiction.

Key takeaways

1. If f is real function defined on [a, b] then there exists a sequence of real polynomials which converges uniformly to f(x) on [a, b], which means

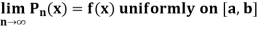
References

1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.

2. Advanced engineering mathematics, by HK Dass

3. Mathematical analysis by Dr. Anju panwar

4. Real analysis by Dr. Sachin Kaushal

5. Real analysis by Ajit kumar & S.Kumaresan

6. Principles of real analysis by S.C Malik