Unit - 2
Rate of convergence of the above methods
Convergence-
A sequence of iterates 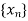 is said to converge with order
is said to converge with order 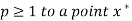 if
if

For some constant c > 0.
Note-
- If p = 1, the sequence is said to be linearly convergent to
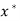 .
. - If p = 2, the sequence is said to be quadratically convergent to
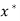 .
. - If p = 3, the sequence is said to be cubically convergent to
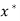 . And so on.
. And so on.
Order and Rate of Convergence
Let 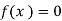 be the given equation. Let α be its exact root.
be the given equation. Let α be its exact root.
Then 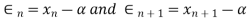
Then the positive number p is said to be order of convergence if,
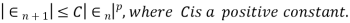
If p=1 , then convergence is linear and if p=2 , then it is quadratic.
a) Bisection Mehtod: The percentage error 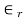 defined by
defined by
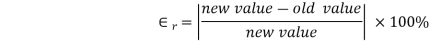
The rate of convergence for bisection method is 
i.e. it converges linearly.
b) Regula-Falsi Method: The rate of convergence is
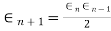
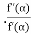
Here p=1.618 and is linear.
c) Newton Raphson Method: The rate of convergence is
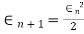
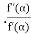
Here p=2 so the convergence is quadratic
d) Secant Method: The rate of convergence is
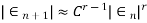
Order of convergence is non integer and is greater than one , so is super linear.
Note: Order of Convergence
1) Bisection Method : p=1 (linear)
2) Regula-Falsi Method: 1 < p < 2 (superlinear).
3) Newton Raphson Method: p = 2 (quadratic).
4) Secant Method: p=1.618 (superlinear).
Gaussian Elimination Method
In this method we eliminate successively the unknown 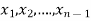 so that the equation (1) remain with the single unknown
so that the equation (1) remain with the single unknown 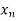 and reduce to upper triangular system. At last with help of back substitution we calculate the values of the remaining unknowns.
and reduce to upper triangular system. At last with help of back substitution we calculate the values of the remaining unknowns.
Consider a system of n linear equation in n unknown 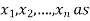
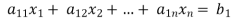
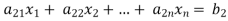
… …… ….. … (1)
… …… …. …
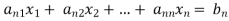
To convert the above system into upper triangular matrix we eliminate 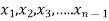 from the second, third, fourth …., n equations above by multiplying the first equation by
from the second, third, fourth …., n equations above by multiplying the first equation by 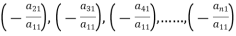 added them to the corresponding equations second, third, fourth,…., n equation. We get
added them to the corresponding equations second, third, fourth,…., n equation. We get
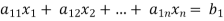
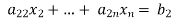
… …… ….. …
… …… …. …
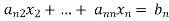
Repeating the above method for 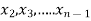 we get finally the upper triangular form.
we get finally the upper triangular form.
Upper Triangular form of above
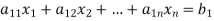
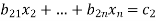
……………………….. (i)
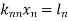
Thus 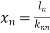 .
.
Then we calculate the values of  .
.
Note: In (i) the coefficient 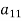 is the pivot element and the equation is called the pivot equation. If
is the pivot element and the equation is called the pivot equation. If 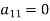 then the above method fails and if it is close to zero the round off error may occur.
then the above method fails and if it is close to zero the round off error may occur.
If  or very small compared to other coefficient of the equation, then we find the largest available coefficient in the column given below the pivot equation and then interchange the two rows to obtain new pivot variable this is known as partial pivoting.
or very small compared to other coefficient of the equation, then we find the largest available coefficient in the column given below the pivot equation and then interchange the two rows to obtain new pivot variable this is known as partial pivoting.
Example1 Apply Gauss Elimination method to solve the equations:
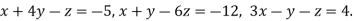
Given Check Sum (sum of coefficient and constant)
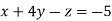 -1 …. (I)
-1 …. (I)
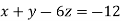 -16 …. (ii)
-16 …. (ii)
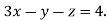 5 …. (iii)
5 …. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
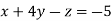 -1 ….(i)
-1 ….(i)
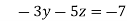 -15 ….(iv)
-15 ….(iv)
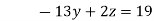 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 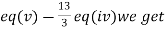
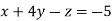 -1 ….(i)
-1 ….(i)
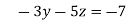 -15 ….(iv)
-15 ….(iv)
 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 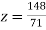
From (iv) we get 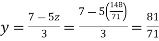
From (i) we get 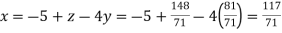
Hence the solution of the given equation is 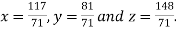
Example2 Solve the equation by Gauss Elimination Method:
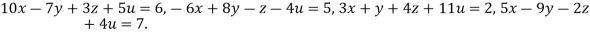
Given 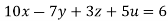
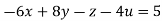
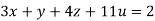
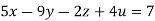
Rewrite the given equation as
 … (i)
… (i)
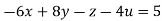 ….(ii)
….(ii)
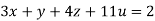 ….(iii)
….(iii)
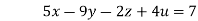 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
 …(i)
…(i)
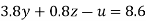 ….(v)
….(v)
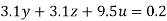 ….(vi)
….(vi)
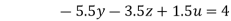 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
 …(i)
…(i)
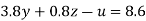 ….(v)
….(v)
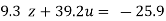 …(viii)
…(viii)
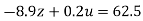 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
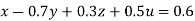 … (i)
… (i)
 ….(v)
….(v)
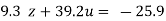 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 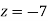
Form eq(v), we get 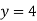
From eq(i), 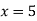
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Example3 Apply Gauss Elimination Method to solve the following system of equation:
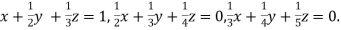
Given 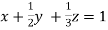 … (i)
… (i)
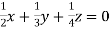 … (ii)
… (ii)
 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply 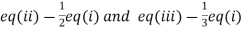 we get
we get
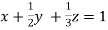 … (i)
… (i)
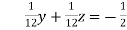 … (iv)
… (iv)
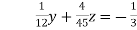 … (v)
… (v)
(II) We eliminate y from (v)
Apply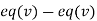 we get
we get
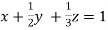 … (i)
… (i)
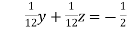 … (vi)
… (vi)
 … (vii)
… (vii)
(III) Back substitution
From (vii) 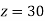
From (vi) 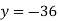
From (i) 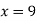
Hence the solution of the equation is 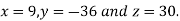
Example4: Solve the system by Gauss Elimination method using partial pivoting
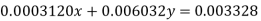

Given exact solution is 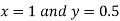
Given equations are 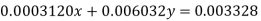
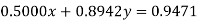
Using partial pivoting we rewrite the given equations as
 (1)
(1)
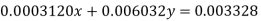 (2)
(2)
Using Gauss elimination method
Multiplying (1) by (-0.0003120/0.5000) + (2) we get

Or 
Substituting value of y in equation (1) we get 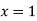
Hence 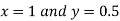
Example5: Solve the system of linear equations
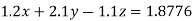
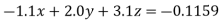
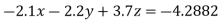
Using partial pivoting by Gauss elimination method we rewrite the given equations as
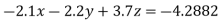 (1)
(1)
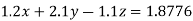 (2)
(2)
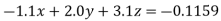 (3)
(3)
Apply 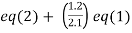 and
and 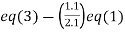
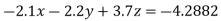 (1)
(1)
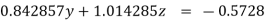 (4)
(4)
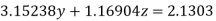 (5)
(5)
Apply  )
)
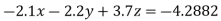 (1)
(1)
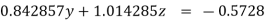 (4)
(4)
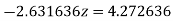
Or 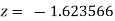 .
.
Putting value of z in 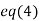 we get
we get 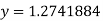 .
.
Putting values of y and z in 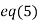 we get
we get 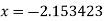 .
.
Hence the solution of the equation is 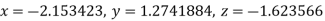 .
.
Gauss-Jordan method-
In this method we reduce the given system of equations AX = b to a diagonal system of equations Ix = d, here I is the identity matrix.
The reduced system gives the solution vector X.
Example: By using Gauss-Jordan method, solve the system of equations-
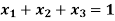
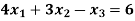
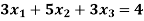
Sol:
Here the augmented matrix will be-
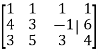
By performing elementary row transformation, and eliminations, we get-
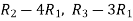
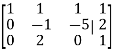
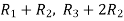
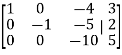
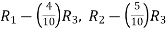
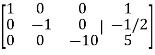
Now making the pivots as 1, ((
We obtain,
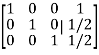
Hence the solution of the system is-
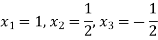
Matrix Inversion using Gauss Jordan method-
We know that X will be the inverse of a matrix A if
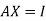
Where I is an identity matrix of order same as A.
We write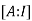 , using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution.
, using elementary operation we covert the matrix A in to a upper triangular matrix. Then compare this matrix with each corresponding column and using back substitution.
The determinant of this coefficient matrix is the product of the diagonal elements of the upper triangular matrix.
If this |A|=0 then inverse does not exist.
Example1
Solve the system of equations
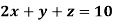
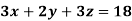

Here A =

The augmented system is

Apply 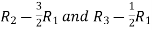
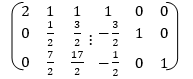
Apply 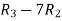
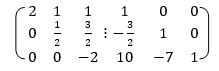
Here 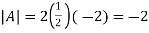
Which is non zero so the inverse exists.
Comparing the diagonal matrix with corresponding columns.
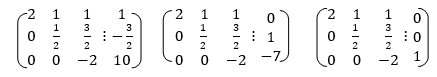
By back Substitution we get
Form first part of above 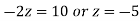
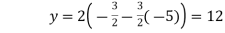

Similarly we solve second and third part and obtain a matrix whose columns are
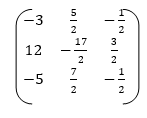
Which is the required inverse 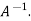
Example2: Find the inverse and determinant of-
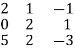
Let [A:I]= 
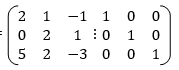
Apply 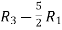
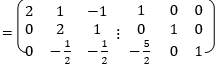
Apply 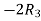
= 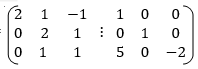
Apply 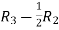
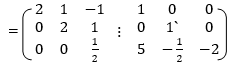
Here 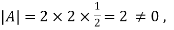 therefore
therefore 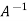 exist.
exist.
On comparing the coefficient matrix with each column of RHS matrix.
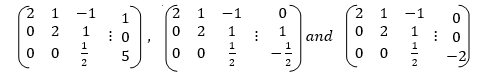
From first term back substitution

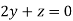
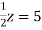
We get 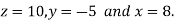
From second and third we get 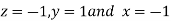
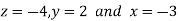
Hence 
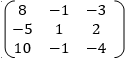
Jacobi’s Iteration method:
Let us consider the system of simultaneous linear equation
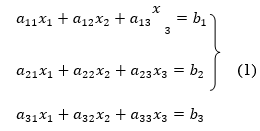
The coefficients of the diagonal elements are larger than the all other coefficients and are non zero. Rewrite the above equation we get
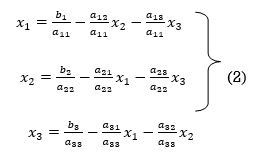
Take the initial approximation 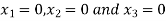 we get the values of the first approximation of
we get the values of the first approximation of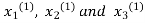 .
.
By the successive iteration we will get the desired the result.
Example: Use Jacobi’s method to solve the system of equations:
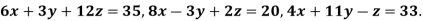
Since 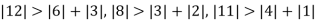
So, we express the unknown with large coefficient in terms of other coefficients.
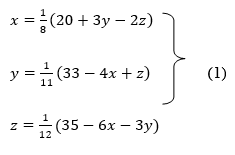
Let the initial approximation be 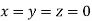
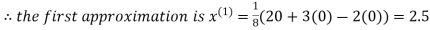
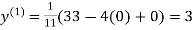
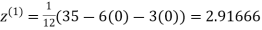
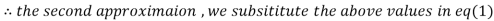
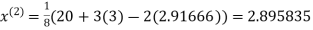
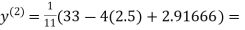 2.35606
2.35606
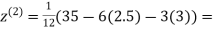 0.91666
0.91666

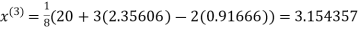
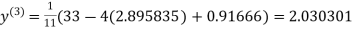
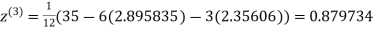
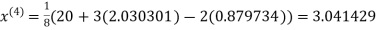
 1.932936
1.932936
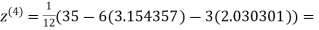 0.831912
0.831912
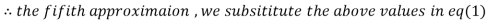
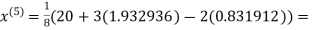 3.016873
3.016873
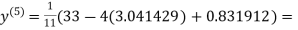 1.969654
1.969654
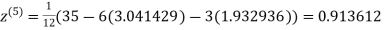
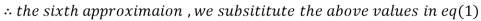
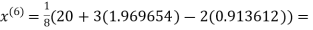 3.010217
3.010217
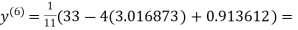 1.986010
1.986010
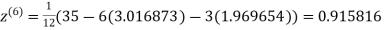
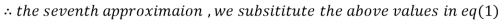
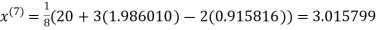
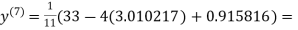 1.988631
1.988631
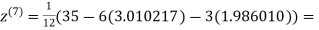 0.915055
0.915055
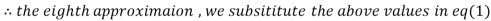

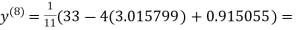 1.986532
1.986532
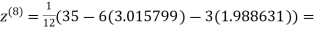 0.911609
0.911609
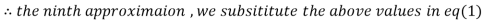
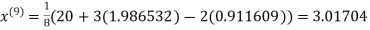
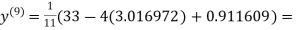 1.985792
1.985792
 0.911547
0.911547
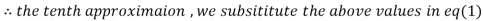

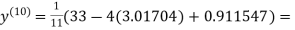 1.98576
1.98576
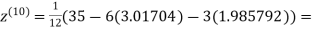 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 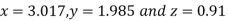
Example: Solve by Jacobi’s Method, the equations
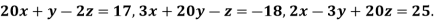
Given equation can be rewrite in the form
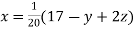 … (i)
… (i)
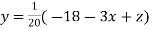 ..(ii)
..(ii)
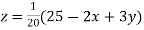 ..(iii)
..(iii)
Let the initial approximation be 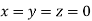
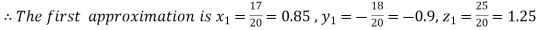
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
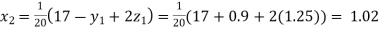
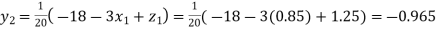
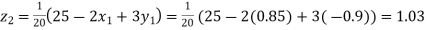
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
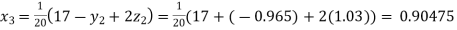
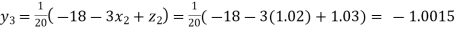
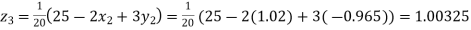
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
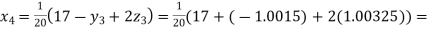 0.90025
0.90025
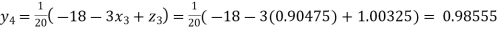
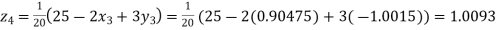
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
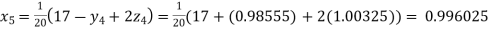
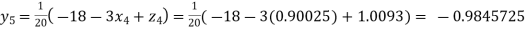
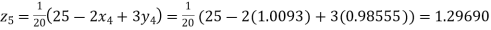
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
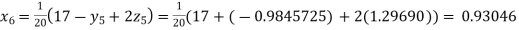
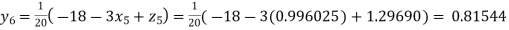
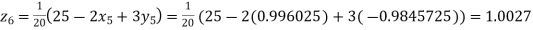
Hence solution approximately is 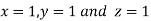
Example: Use Jacobi’s method to solve the system of the equations
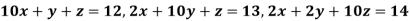
Rewrite the given equations
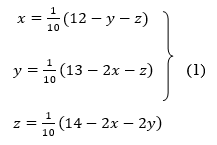
Let the initial approximation be 
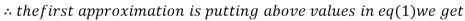
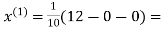 1.2
1.2
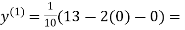 1.3
1.3
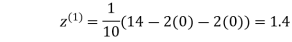
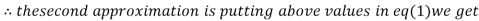
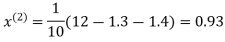

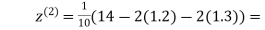 0.9
0.9

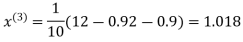
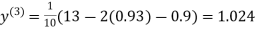
 1.03
1.03
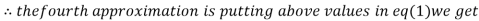
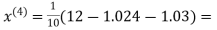 0.9946
0.9946
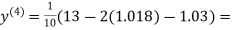 0.9934
0.9934
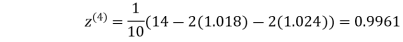

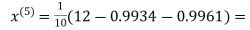 1.0015
1.0015
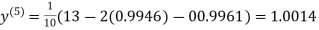
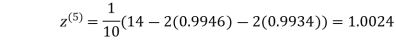
Hence the solution of the above equation correct to two decimal places is
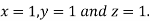
Gauss Seidel method:
This is the modification of the Jacobi’s Iteration. As above in Jacobi’s Iteration, we take first approximation as 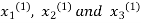 and put in the right hand side of the first equation of (2) and let the result be
and put in the right hand side of the first equation of (2) and let the result be 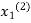 . Now we put
. Now we put 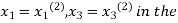 right hand side of second equation of (2) and suppose the result is
right hand side of second equation of (2) and suppose the result is  now put
now put 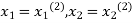 in the RHS of third equation of (2) and suppose the result be
in the RHS of third equation of (2) and suppose the result be 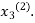 the above method is repeated till the values of all the unknown are found up to desired accuracy.
the above method is repeated till the values of all the unknown are found up to desired accuracy.
Example: Use Gauss –Seidel Iteration method to solve the system of equations
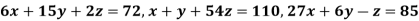
Since 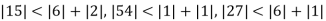
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
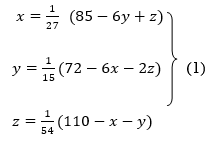
Let the initial approximation be 

 3.14814
3.14814
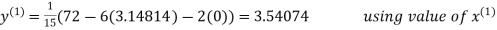
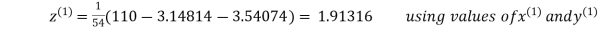
 2.43217
2.43217

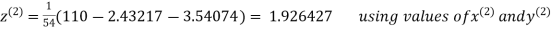
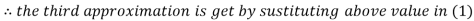
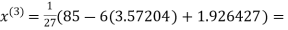 2.42571
2.42571
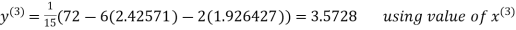
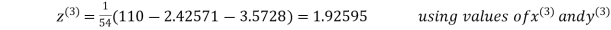

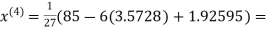 2.4260
2.4260
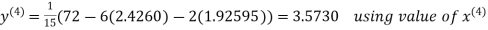
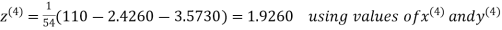
Hence the solution correct to three decimal places is
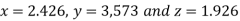
Example: Solve the following system of equations
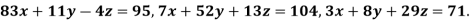 By Gauss-Seidel method.
By Gauss-Seidel method.
Rewrite the given system of equations as
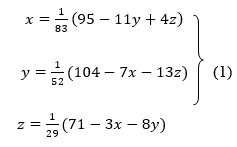
Let the initial approximation be 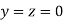
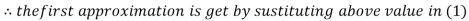
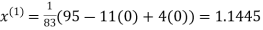
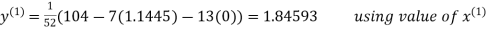
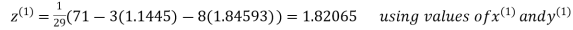
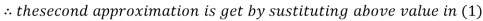
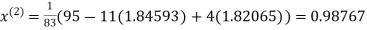
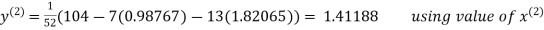
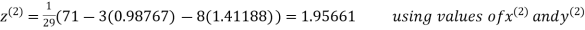
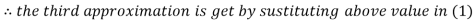
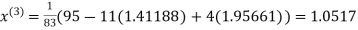
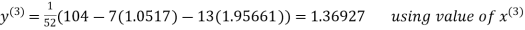
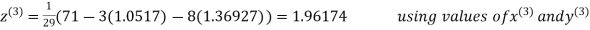

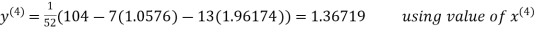
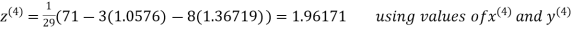
Thus the required solution is 
Example: Solve the following equations by Gauss-Seidel Method
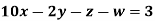
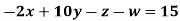

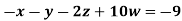
Rewrite the above system of equations
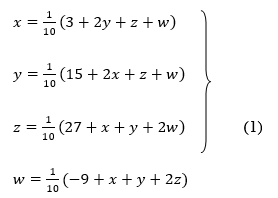
Let the initial approximation be 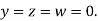

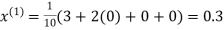
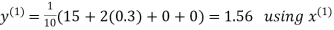
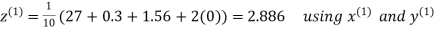
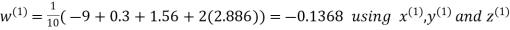

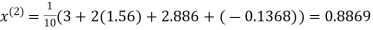
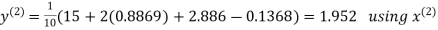
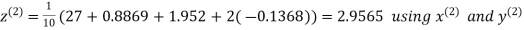
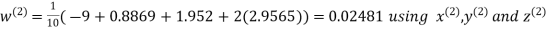

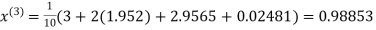
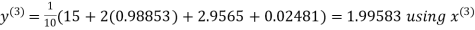




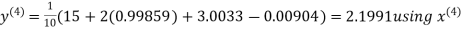
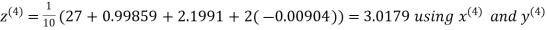
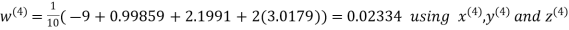

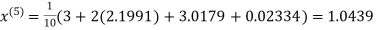
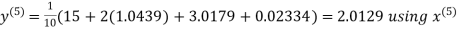

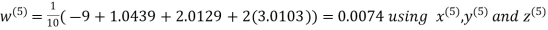
Hence the required solution is 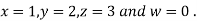
Solving Eigen value problems (Power method)-
Consider the eigen value problem
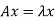
The Eigen values of a matrix A are given by the roots of the characteristic equation
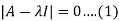
If the matrix A is of order n, then expanding the determinant, we obtain the characteristic equation as
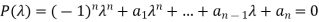
For the given matrix we write the characteristic equation, by expanding we find the roots 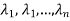 . These are called the Eigen values.
. These are called the Eigen values.
Now suppose 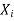 be the solution of the system of homogeneous equations, corresponding to the Eigen value
be the solution of the system of homogeneous equations, corresponding to the Eigen value 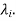
These vectors 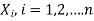 are called the Eigen vectors.
are called the Eigen vectors.
To find the approximate values of all the Eigen values and Eigen vectors, iteration method or power method is used.
Power method is used when only the largest and/or the smallest Eigen values of a matrix are desired.
Procedure for Power method-
Step-1: First we choose an arbitrary real vector 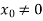 , basically
, basically  is chosen as-
is chosen as-

Step-2: Compute 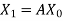 ,
, 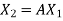 ,
, 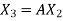 ,
, 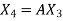 , …………
, …………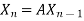 Put
Put 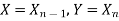
Step-3: Compute 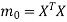 ,
, 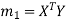 ,
, 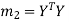
Step-4: The largest Eigen value is
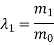
The error in 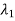 can be find as-
can be find as-
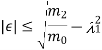
The Eigen vector corresponding to 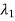 is
is 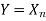
How do we determine the smallest Eigen value?
If 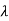 is the Eigen value of A, then the reciprocal
is the Eigen value of A, then the reciprocal 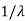 is the Eigen value of
is the Eigen value of 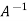 , then the reciprocal of the largest Eigen value of
, then the reciprocal of the largest Eigen value of  will be the smallest Eigen value of A.
will be the smallest Eigen value of A.
Example: Find the largest Eigen value and the corresponding Eigen vector of the matrix
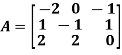
Also find the error in the value of the largest Eigen value.
Sol.
Let us choose the initial vector
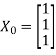
Then
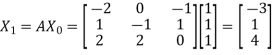
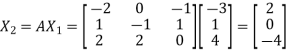
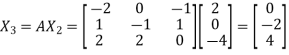
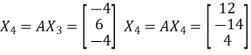
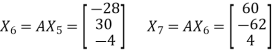
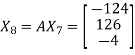 and
and 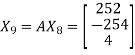
Now put 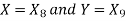 , then-
, then-
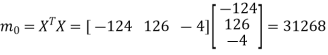
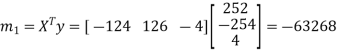

Hence the largest Eigen value is-
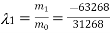
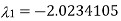
And the corresponding Eigen vector is-
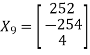
The error can be calculated as-
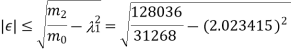
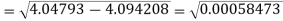
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction to Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.