Unit - 2
Prime and maximal ideals
The purpose of this section is to define those ideals of commutative rings with identity that correspond to integral domains or fields of factor rings.
Definition 3.4.1 Let R be a ring. A two-sided ideal I of R is called maximal if I 6= R and no proper ideal of R properly contains I.
EXAMPLES
- In Z, the ideal h6i = 6Z is not maximal since h3i is a proper ideal of Z properly containing h6i (by a proper ideal we mean one which is not equal to the whole ring).
- In Z, the ideal h5i is maximal. For suppose that I is an ideal of Z properly containing h5i. Then there exists some m ∈Iwith m ∈6 h5i, i.e. 5 does not divide m. Then gcd(5,m) =1 since 5 is prime, and we can write
1 = 5s + mt
For integers s and t. Since 5s ∈I and mt∈I, this means 1 ∈I. Then I = Z, and h5i is a maximal ideal in Z.
3. The maximal ideals in Z are precisely the ideals of the form hpi, where p is prime.
The following is a generalization of the statement that Z/nZis a field precisely when n is prime.
Theorem 3.4.2 Let R be a commutative ring with identity, and let Mbe an ideal of R. Then the factor ring R/M is a field if and only if M is a maximal ideal of R.
COMMENT ON PROOF: There are two things to be shown here. We must show that if R/M is a field (i.e. if every non-zero element of R/M is a unit), then M is a maximal ideal of R. A useful strategy for doing this is to suppose that I is an ideal of R properly containing M, and try to show that I must be equal to R. We must also show that if M is a maximal ideal of R, then every non-zero element of R/M is a unit. A strategy for doing this is as follows : if a ∈R does not belong to M (so a+Mis not the zero element in R/M), then the fact that M is maximal as an ideal of R means that the only ideal of R that contains both M and the element a is R itself. In particular the only ideal of R that contains both M and the element a contains the identity element of R.
Proof of Theorem 4.2.6: (⇐=) Suppose that R/M is a field and let I be an ideal of R properly containing M. Let a ∈I, a 6∈M. Then a + M is not the zero element of R/M, and so (a + M)(b + M) = 1 + M, for some b ∈R. Then ab −1 ∈M; let m = ab −1. Now 1 = ab − m and so 1 ∈I since a ∈I and m∈I. It follows that I = R and so M is a maximal ideal of R.
(=⇒): Suppose that M is a maximal ideal of R and let a+Mbe a non-zero element of R/M. We need to show the existence of b + m ∈R/M with (a + M)(b + M) = 1 + M. This means ab + M = 1 + M, or ab −1 ∈M.
So we need to show that there exists b ∈R for which ab −1 ∈M. Let M0 denote the set of elements of R of the form
Ar + s, for some r ∈R and s ∈M.
Then M0 is an ideal of R (check), and M0 properly contains M since a ∈M0 and a ∈6 M. Then M0 = R since M is a maximal ideal of R. In particular then 1 ∈M0 and 1 = ab + m for some b∈R and m ∈M. Then ab −1 ∈M and
(a + M)(b + M) = 1 + M in R/M.
So a + M has an inverse in R/M as required.
We will now characterize those ideals I of R for which R/I is an integral domain. Definition 3.4.3 Let R be a commutative ring. An ideal I of R is called prime if I 6= R and whenever ab ∈I for elements a and b of R, either a∈I or b∈I.
EXAMPLE: The ideal h6i is not a prime ideal in Z, since 2×3 ∈h6i although neither 2 nor 3 belongs to h6i. However the ideal h5i is prime in Z, since the product of two integers is a multiple of 5 only if at least one of the two is a multiple of 5. The prime ideals of Z are precisely the maximal ideals; they have the form hpifor a prime p.
Theorem 3.4.4 Let R be a commutative ring with identity, and let I be an ideal of R. Then the factor ring R/I is an integral domain if and only if I is a prime ideal of R.
Proof: R/I is certainly a commutative ring with identity, so we need to show that R/I contains zero-divisors if and only if I is not a prime ideal of R. So let a+I, b+Ibe non-zero elements of R/I. This means neither a norb belongs to I. We have
(a + I)(b + I) = 0 + I in R/I if and only if ab ∈I. This happens for some pair aandbif and only if I is not prime.
Corollary 3.4.5 Let R be a commutative ring with identity. Then every maximal ideal of R is prime.
Proof: Let M be a maximal ideal of R. Then R/M is a field so in particular it is an integral domain. Thus M is a prime ideal of R.
It is not true that every commutative ring with identity has a maximal prime ideal. As an example, 1. The zero ideal of Z is prime but not maximal, as we have seen.
In Z[x], let I denote the ideal consisting of all elements whose constant term is 0 (I is the principal ideal generated by x). The Iis a prime ideal of Z[x] but it is not maximal, since it is contained for example in the ideal of Z[x] consisting of all those polynomials whose constant term is even.
Theorem 3.4.6 Let F be a field and let I be an ideal of the polynomial ring F[x]. Then 1. I is maximal if and only if I = hp(x)ifor some irreducible polynomial p(x) in F[x].
2. I is prime if and only if I = {0} or I = hp(x)ifor an irreducible p(x) ∈F[x].
Proof: By Lemma 3.2.3 I is principal, I = hp(x)ifor some p(x) ∈F[x]. 1. (⇐=) Assume p(x) is irreducible and let I1 be an ideal of F[x] containing
1. Then I1 = hf(x)ifor some f(x) ∈F[x]. Since p(x) ∈I1 we have p(x) = f(x)q(x) for some q(x) ∈F[x]. Since p(x) is irreducible this means that either f(x) has degree zero (i.e. is a non-zero element of F) or q(x) has degree zero.
If f(x) has degree zero then f(x) is a unit in F[x] and I1 = F[x]. If q(x) has degree zero then p(x) = af(x) for some nonzero a ∈F, and f(x) = a−1p(x); then f(x) ∈I and I1 = I. Thus either I1 = I or I1 = F[x], so I is a maximal ideal of F[x].
(=⇒): Suppose I = hp(x)iis a maximal ideal of F[x]. Then p(x) 6= 0. If p(x) = g(x)h(x) is a proper factorization of p(x) then g(x) and h(x) both have degree at least 1 and hg(x)iandhh(x)iare proper ideals of F[x] properly containing I. This contradicts the maximality of I, so we conclude that p(x) is irreducible. This proves 1.
2. Certainly the zero ideal of F[x] and the principal ideals generated by irreducible polynomials are prime. Every other ideal has the form hf(x)ifor a reducible f(x). If I = hf(x)iandf(x) = g(x)h(x) where g(x) and h(x) both have degree less than that of f(x) then neither g(x) nor h(x) belongs to I but their product does. Thus I is not prime.
2.1.1 Maximal ideal:
Properties
• The Jacobson radical, an essential ring ideal, can be formulated using maximal right (or maximal left) ideals.
• If R is a unital commutative ring with a maximal ideal, k = R/m is a field if and only if m is a maximal ideal. R/m is referred to as the residue field in this situation. In non-unital rings, this fact may fail. In the case of, for example, is a maximum ideal but not a field.
R/L is a simple left R-module if L is a maximal left ideal. In rings with unity, on the other hand, any simple left R-module emerges in this manner. This also demonstrates that a collection of representatives of simple left R-modules is a set because it corresponds to a subset of the set of R's maximal left ideals.
Krull's theorem (1929): There is a maximal ideal for every nonzero unital ring. If "ideal" is replaced with "right ideal" or "left ideal," the same result is obtained. In a broader sense, any nonzero finitely produced module has a maximal submodule. Assume I am an ideal that isn't R. (respectively, A is a right ideal which is not R). Then R/I is a ring with unity (respectively, R/A is a finitely generated module), and the quotient can be used to prove that there is a maximal ideal (respectively, maximum right ideal) of R containing I using the previous theorems (respectively, A).
- For rings with no unity, Krull's theorem can fail. There are no simple modules in a radical ring, i.e. a ring in which the Jacobson radical is the entire ring, and hence no maximal right or left ideals. Look at regular ideals to see if there are any ways to get around this issue.
- Every maximal ideal in a commutative ring with unity is a prime ideal. The opposite is not necessarily true: in any non field integral domain, for example, the zero ideal is a prime ideal that is not maximum. Zero-dimensional rings are commutative rings with maximal prime ideals, where the dimension utilised is the Krull dimension.
- A maximal ideal of a noncommutative ring might not be prime in the commutative sense. For example, let
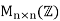 be the ring of all n×n matrices over
be the ring of all n×n matrices over . This ring has a maximal ideal
. This ring has a maximal ideal 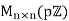 for any prime 𝑃, but this is not a prime ideal since
for any prime 𝑃, but this is not a prime ideal since 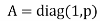 and
and  for n=2 are not in
for n=2 are not in 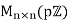 , but
, but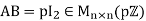
 . However, maximal ideals of noncommutative rings are prime in the generalized sense below.
. However, maximal ideals of noncommutative rings are prime in the generalized sense below.
2.1.2 Prime ideal:
- If and only if the factor ring R/I is an integral domain, an ideal I in the ring R (with unity) is prime. If and only if (0) is a prime ideal, a commutative ring (with unity) is an integral domain.
- A prime I is multiplicatively closed if and only if its set-theoretic complement is prime.
- Krull's theorem states that any nonzero ring includes at least one prime ideal (indeed, it contains at least one maximal ideal).
- More generally, if S is any multiplicatively closed set in R, then a lemma essentially due to Krull shows that there exists an ideal of R maximal with respect to being disjoint from S, and moreover the ideal must be prime. This can be further generalized to noncommutative rings (see below).[4] In the case {S} = {1}, we have Krull's theorem, and this recovers the maximal ideals of R. Another prototypical m-system is the set, {x, x2, x3, x4, ...}, of all positive powers of a non-nilpotent element.
- The set of all prime ideals (the spectrum of a ring) contains minimal elements (called minimal prime). Geometrically, these correspond to irreducible components of the spectrum.
- The preimage of a prime ideal under a ring homomorphism is a prime ideal.
- The sum of two prime ideals is not necessarily prime. For an example, consider the ring
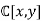
 with prime ideals P = (x2 + y2 − 1) and Q = (x) (the ideals generated by x2 + y2 − 1 and x respectively). Their sum P + Q = (x2 + y2 − 1, x) = (y2 − 1, x) however is not prime: y2 − 1 = (y − 1)(y + 1) ∈ P + Q but its two factors are not. Alternatively, the quotient ring has zero divisors so it is not an integral domain and thus P + Q cannot be prime.
with prime ideals P = (x2 + y2 − 1) and Q = (x) (the ideals generated by x2 + y2 − 1 and x respectively). Their sum P + Q = (x2 + y2 − 1, x) = (y2 − 1, x) however is not prime: y2 − 1 = (y − 1)(y + 1) ∈ P + Q but its two factors are not. Alternatively, the quotient ring has zero divisors so it is not an integral domain and thus P + Q cannot be prime. - Not every ideal which cannot be factored into two ideals is a prime ideal; e.g.
 cannot be factored but is not prime.
cannot be factored but is not prime. - In a commutative ring R with at least two elements, if every proper ideal is prime, then the ring is a field. (If the ideal (0) is prime, then the ring R is an integral domain. If q is any non-zero element of R and the ideal (q2) is prime, then it contains q and then q is invertible.)
• If and only if a prime element generates a nonzero primary ideal, it is prime. Every nonzero prime ideal in a UFD has a prime element.
Numericals:
1) In each part of this question, give examples of the specified type. No justification is needed, but incorrect examples will be counted negatively
(a) Two integral domains which are not principal ideal domains
SOLUTION: One such integral domain is the ring Z[ √ −5]. Another example of such an integral domain is the ring Z[X]
(b) A field with 27 elements
SOLUTION Let F = Z/3Z, a field with three elements. Let g(X) ∈ F[X] be an irreducible element such that deg g(X) = 3. Since F[X] is a PID, the ideal I = g(X) is a maximal ideal in F[X] and therefore the quotient ring S = F[X] / I I is a field. d. Furthermore, the elements of S can be uniquely expressed in the form,

Where a0, a1, a2 ∈ F. Since F has three elements, it follows that S has 33 = 27 elements. Hence S is a field with 27 elements.
We must just show that such a polynomial g(X) ∈ F[X] actually exists. Let g(X) = α+βX +αX3 , where α = 1 + 3Z and β = 2 + 3Z. The additive identity in F is 0F = 0 + 3Z. The unity element in F is α. The other nonzero element in F is β. One checks easily that g(0F ) = α 6= 0F , g(α) = α 6= 0F , and g(β) = α 6= 0F . Hence g(a) 6= 0 for all a ∈ F. Since g(X) has degree 3, it follows that g(X) is an irreducible element of F[X].
(c) Three examples of maximal ideals in the ring R = Z[ √ 2].
SOLUTION:
Let p be a prime. We can define a homomorphism ϕ : R → /p
/p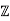 by ϕ(a + b √ 2) = a + bγ for all a, b ∈
by ϕ(a + b √ 2) = a + bγ for all a, b ∈ if γ is an element in
if γ is an element in 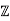 /p
/p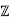 such that γ2 = 2 + p
such that γ2 = 2 + p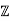 . Such a homomorphism is clearly surjective. Hence, if I = ker(ϕ), then R/I ∼=
. Such a homomorphism is clearly surjective. Hence, if I = ker(ϕ), then R/I ∼=  /p
/p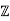 . Thus, R/I is a field. Hence I is a maximal ideal.
. Thus, R/I is a field. Hence I is a maximal ideal.
If p = 2, one can take γ = 0 + 2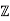 . If p = 7, one can take γ = 3 + 7
. If p = 7, one can take γ = 3 + 7 . If p = 23, one can take γ = 5 + 23
. If p = 23, one can take γ = 5 + 23 . In each case, one obtains a different maximal ideal I in the ring R because the corresponding quotient rings are not isomorphic.
. In each case, one obtains a different maximal ideal I in the ring R because the corresponding quotient rings are not isomorphic.
An alternative approach is to use a result proved in class. If α = a+b√ 2, where a, b ∈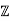 , and
, and 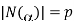 where p is a prime, then we proved that R/() is isomorphic to
where p is a prime, then we proved that R/() is isomorphic to 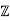 /p
/p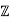 which is a field. Hence (α) is a maximal ideal. Note that
which is a field. Hence (α) is a maximal ideal. Note that

And hence the following ideals in R are maximal ideals:

(d) An example of a prime ideal in the ring 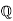 [x] which is not a maximal.
[x] which is not a maximal.
SOLUTION:
Since  [x] is an integral domain, the zero ideal is a prime ideal. However,
[x] is an integral domain, the zero ideal is a prime ideal. However,  [x] is not a field and hence the zero ideal is not a maximal ideal in that ring.
[x] is not a field and hence the zero ideal is not a maximal ideal in that ring.
Key takeaways:
- A prime is an ideal P in a ring A.
- A maximal m in a ring A is an ideal m.
- Maximal ideals are essential because the quotients of rings by maximal ideals are simple rings, and in the special case of unital commutative rings, the quotients of rings by maximal ideals are unital commutative rings.
2.2.1 Ring homomorphisms:
Definition
A map f : R→ S between rings is called a ring homomorphism if
f(x + y) = f(x) + f(y) and f(xy) + f(x)f(y) for all x, y ∈ R.
Remarks
- The operations on the left are in the ring R; those on the right are in S.
- Since such a homomorphism is a group homomorphism from (R, +) to (S, +) it maps 0R to 0S.
Even if the rings R and S have multiplicative identities a ring homomorphism will not necessarily map 1R to 1S.
c. It is easy to check that the composition of ring homomorphisms is a ring homomorphism.
Definition
A ring isomorphism is a ring homomorphism that is a bijection (one-one and onto).
If f : R → S is such an isomorphism, we call the rings R and S isomorphic and write R ≅ S.
Remarks
- Isomorphic rings have all their ring-theoretic properties identical. One such ring can be regarded as "the same" as the other.
The inverse map of the bijection f is also a ring homomorphism.
Examples
- The map from Z to Zn given by x ↦ x mod n is a ring homomorphism. It is not (of course) a ring isomorphism.
- The map from Z to Z given by x ↦ 2x is a group homomorphism on the additive groups but is not a ring homomorphism.
- The map from Z to the ring of 2 × 2 real matrices given by x ↦
 is a ring homomorphism which does not map the multiplicative identity to the multiplicative identity.
is a ring homomorphism which does not map the multiplicative identity to the multiplicative identity. - Of course the map x ↦ x mod n is a homomorphism which does map the identity to the identity.
- The "evaluation at 1/2 map" from the ring of continuous real-valued functions on the interval [0, 1] to R given by (e½)f = f (1/2) for f belongs C[0, 1] is a ring homomorphism.
- The "evaluation at 1 map" from the ring Q[x] to Q given by (e1)p = p(1) for p ∈ Q[x] is a ring homomorphism.
That is: e1(a0 + a1x + a2x2 + ... + anxn) = a0 + a1 + a2 + ... + an.
7. The "evaluation at √2 map" from Z[x] to R given by p ↦ p(√2) is a ring homomorphism.
This will turn out to be a surprisingly important example.
8. The map from C to ring of 2 × 2 real matrices given by a + bi ↦ 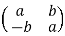 is a ring isomorphism.
is a ring isomorphism.
9. Let R be the field with 9 elements {a + bx | a, b ∈ Z3} and the multiplication rule x2 = -1.
Let S be the field with 9 elements {a + by | a, b ∈ Z3 } and the multiplication rule y2 = y + 1.
Then the map defined by 1 ↦ 1 and x ↦ y + 1 defines a ring isomorphism.
Proof: We'll see a neat way of proving this later.
The connection of this with the last section is given by:
Definition
The kernel of a (ring) homomorphism is the set of elements mapped to 0.
That is, if f: R→ S is a ring homomorphism, ker(f) = f-1(0) = {r ∈ R | f(r) = 0S }.
Theorem
The kernel of a ring homomorphism is an ideal.
Proof
An easy verification.
Remarks
a. Notice the resemblance to the related result for groups: a group homomorphism's kernel is a normal subgroup.
b. The kernel is a two-sided ideal if the ring R is not commutative.
Examples
- The kernel of the above map from Z to Zn is the ideal nZ.
- Just as in the group-theory case, the kernel of a homomorphism is {0} if and only if the homomorphism is one-one.
Proof
(=>) If f(r) = f(s) then f(r - s) = 0 and so r - s belongs ker(f) and we have r - s = 0.
(<=) If a ∈ ker(f) and a ≠ 0 then a, 0 ↦ 0 and so the map is not one-one.
- The kernel of the "evaluation at 0" map from R[x] to R is the ideal < x > of polynomials with zero constant terms.
- The kernel of the "evaluation at 0 taken modulo 2" map from Z[x] to Z2 is the ideal < 2, x > of polynomials with even constant terms.
Remark
Every ideal is the kernel of a ring homomorphism, as we will discover later. This is analogous to the group theory result that every normal subgroup is a group homomorphism's kernel.
This section's final result is also similar to the comparable example in Group theory,
Theorem
The image of a ring homomorphism f: R→ S is a subring of S.
Proof
The image is the set im(f) = {s ∈ S | s = f(r) for some r ∈ R }. It is easy to do the verification.
Example
The image of e from Z[x] to R is the subring {a + b √2 | a, b ∈ Z } we met earlier.
from Z[x] to R is the subring {a + b √2 | a, b ∈ Z } we met earlier.
2.2.2 Properties:
A ring homomorphism is a map 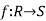 between two rings such that
between two rings such that
1. Addition is preserved: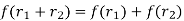
2. The zero element is mapped to zero:  , and
, and
3. Multiplication is preserved: 
Where the operations on the left-hand side is in R and on the right-hand side in S. Note that a homomorphism must preserve the additive inverse map because 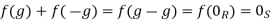 so
so  .
.
A ring homomorphism for unit rings (i.e., rings with a multiplicative identity) satisfies the additional property that one multiplicative identity is mapped to the other, i.e.,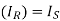 .
.
Numericals:
1) In each case determine if the map θ is a ring homomorphism.
(a) θ :z3→ 12, θ(r) = 4r.
12, θ(r) = 4r.
Answer:
No, this is not a ring homomorphism. Indeed, θ([1]3) = [4]12 [1]12.
[1]12.
(b) θ : Z4→ 12, θ(r) = 3r.
12, θ(r) = 3r.
Answer:
No, this is not a ring homomorphism. Indeed, θ([1]4) = [3]12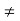 [1]12.
[1]12.
(c) θ : R × R → R, where θ(r, s) = r + s.
Answer:
No, this is not a ring homomorphism. Indeed, 1R×R = (1R, 1R) but
θ(1R×R) = θ(1R, 1R) = 1R + 1R 1R when R
1R when R 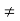 0.
0.
(d) θ : R × R → R, where θ(r, s) = rs.
Answer:
No, this is not a ring homomorphism
Indeed, θ(1, 0) = θ(0, 1) = 0. But θ((1, 0) + (0, 1)) = θ(1, 1) = 1 6= 0 + 0.
(e) θ : F( ) → R where θ(f) = f(1).
) → R where θ(f) = f(1).
Answer:
Yes, this is a ring homomorphism. Indeed, for f, g ∈F( ) we have (fg)(x) = f(x)g(x) and (f + g)(x) = f(x) + g(x) for every x ∈ R. Hence
) we have (fg)(x) = f(x)g(x) and (f + g)(x) = f(x) + g(x) for every x ∈ R. Hence
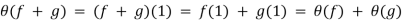
And
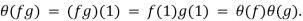
Also, for the function 1 : →
→ , 1(x) = 1 for all x ∈
, 1(x) = 1 for all x ∈ we have θ(1) = 1(1) = 1. Thus θ is indeed a ring homomorphism.
we have θ(1) = 1(1) = 1. Thus θ is indeed a ring homomorphism.
2) Show that x 3 − 8x 2 + 5x + 3 = 0 has no solutions x ∈ Z.
Solution:
Suppose, on the contrary, that there exists x ∈ such that x 3−8x 2+ 5x+ 3 = 0. Consider the ring homomorphism φ :
such that x 3−8x 2+ 5x+ 3 = 0. Consider the ring homomorphism φ : →
→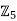 defined by φ(n) = n where n ∈
defined by φ(n) = n where n ∈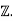
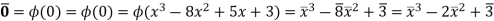
Thus 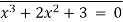 in
in 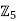 . By substituting the possible values of
. By substituting the possible values of 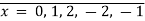 into the left-hand side of the above equation, we get:
into the left-hand side of the above equation, we get:
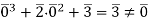
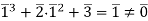

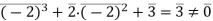

Since  , this yields a contradiction with the fact that
, this yields a contradiction with the fact that 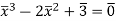 in
in  .
.
Hence there does not exist x ∈ such that x 3− 8x 2 + 5x + 3 = 0.
such that x 3− 8x 2 + 5x + 3 = 0.
2.3.1 The First Isomorphism Theorem
Theorem 1.1 (An image is a natural quotient). Let
f:G −→Ge
Be a group homomorphism. Let its kernel and image be
K = ker(f), He = im(f),
Respectively a normal subgroup of G and a subgroup of Ge. Then there is a natural isomorphism f˜: G/K −∼→H,˜gK7−→f(g).
Proof. The map f˜is well defined because if g0K = gK then g0 = gk for some k ∈K and so
f(g0) = f(gk) = f(g)f(k) = f(g)e˜ = f(g).
The map f˜ is a homomorphism because f is a homomorphism,
f˜(gK g0K) = f˜(gg0K) by definition of coset multiplication
= f(gg0) by definition of f˜
= f(g)f(g0) because f is a homomorphism
= f˜(gK)f˜(g0K) by definition of f.˜
To show that f˜ injects, it suffices to show that ker(f˜) is only the trivial element K of G/K. Compute that if f˜(gK) = e˜ then f(g) = e˜, and so g ∈K, making gK= K as desired. The map f˜ surjects because He = im(f).
The following is a diagrammatic representation of the theorem that captures the idea that an image is isomorphic to a quotient:

For a familiar example of the theorem, let
T :V−→W
Be a linear transformation. The theorem says that there is a resulting natural isomorphism
Te:V/nullspace(T) −→range(T).
The quotient vector space V/nullspace(T) is the set of translates of the nullspace.
If we expand a basis of the nullspace,
{v1,···,vν} (whereνis the nullity of T),
To a basis of V,
{v1,···,vν,vν+1,···,vn},
Then a basis of the quotient (now denoting the null space N for brevity) consists of the cosets
{vν+1 + N,···,vn+ N},
Thus the isomorphism V/N −→T(V ) encompasses the basic result from linear algebra that the rank of T and the nullity of T sum to the dimension of V . The dimension of the original codomain W is irrelevant here.
Often the First Isomorphism Theorem is applied in situations where the original homomorphism is an epimorphism f:G−→Ge. The theorem then says that consequently the induced map f˜: G/K −→Ge is an isomorphism. For example,
- Since every cyclic group is by definition a homomorphic image of Z, and since the nontrivial subgroups of Z take the form nZ where n ∈Z>0, we see clearly now that every cyclic group is either
G ≈Z or G ≈Z/nZ.
Consider a finite cyclic group,

Consider also a subgroup,
G = hgki.
Then π−1(H) = kZ, so that
H ≈ kZ/(kZ∩nZ) = kZ/lcm(k,n)Z.
The multiply-by-k map followed by a natural quotient map gives an epimorphism Z−→kZ/lcm(k,n)Z, and the kernel of the composition is (lcm(k,n)/k)Z = (n/gcd(k,n))Z. Thus
H ≈Z/(n/gcd(k,n))Z.
Hence the subgroup H = hgkiof the order-n cyclic group G = hgihas order
|hgki| = n/gcd(k,n).
Especially, H is all of G when gcd(k,n) = 1, and so G has ϕ(n) generators.
- The epimorphism|| : C× −→R+ has as its kernel the complex unit circle, denoted T,
T = {z ∈C× :|z| = 1}.
The quotient group C×/T is the set of circles in C centered at the origin and having positive radius, with the multiplication of two such circles returning the circle whose radius is the product of the radii. The isomorphism

Takes each circle to its radius.
- The epimorphism exp: C−→C× has as its kernel a dilated vertical copy of the integers,
K = 2πiZ.
Each element of the quotient group C/2πiZisa translate of the kernel. The quotient group overall can be viewed as the strip of complex numbers with imaginary part between 0 and 2π, rolled up into a tube. The isomorphism

Takes each horizontal line at height y to the ray making angle y with the positive real axis. Loosely, the exponential maps shows us a view of the tube looking “down” it from the end.
- The epimorphism det :GLn(R) −→R× has as its kernel the special linear group SLn(R). Each element of the quotient group GLn(R)/SLn(R) is the equivalence class of all n-by-n real matrices having a given nonzero determinant. The isomorphism

Takes each equivalence class to the shared determinant of all its members.
- The epimorphisms gn :Sn−→ {±1} has as its kernel the alternating group An. The quotient group Sn/An can be viewed as the set
{even,odd},
Forming the group of order 2 having even as the identity element. The isomorphism

Takes even to 1 and odd to −1.
2.3.2 The Second Isomorphism Theorem
Theorem 2.1. Let G be a group. Let H be a subgroup of G and let K be a normal subgroup of G. Then there is a natural isomorphism
HK/K −→H/(H ∩K), hK7−→h(H ∩K).
Proof. Routine verifications show that HK is a group having K as a normal subgroup and that H ∩K is a normal subgroup of H. The map
H −→HK/K, h 7−→hK
Is a surjective homomorphism having kernel H ∩K, and so the first theorem gives an isomorphism
H/(H ∩K) −→HK/K, h(H ∩K) 7−→hK.
The intended isomorphism is inverse to the display's isomorphism.
Before continuing, it's worth noting that HK = KH if G is a group, H is a subgroup, and K is a normal subgroup. Because K is a regular person,
HK = {hK:h∈H} = {Kh: h ∈H} = KH.
This fact will be mentioned later in the article.
Consider a general linear group, its special linear subgroup, and its centre as an illustration of the second ismorphism theorem.

Then
HK = G, H ∩K = {±I2}.
The isomorphism given by the theorem is therefore

The projective general and special linear groups are the groups on both sides of the isomorphism. The gap between the general and special linear groups vanishes after projectivizing, despite the fact that the general linear group is larger.
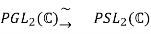
2.3.3 The Third Isomorphism Theorem
Theorem 3.1 (Absorption property of quotients). Let G be a group. Let K be a normal subgroup of G, and let N be a subgroup of K that is also a normal subgroup of G. Then
K/N is a normal subgroup of G/N,
And there is a natural isomorphism
(G/N)/(K/N) −→G/K, gN·(K/N) 7−→gK.
Proof. The map
G/N −→G/K, gN7−→gK
Is well defined because if g0N = gNtheng0 = gn for some n ∈N and so because N ⊂K we have g0K = gK. The map is a homomorphism because
GN g0N = gg0N 7−→gg0K = gK g0K.
The map clearly surjects. Its kernel is K/N, showing that K/N is a normal subgroup of G/N, and the first theorem gives an isomorphism
(G/N)/(K/N) −→G/K, gN·(K/N) 7−→gK,
As claimed.
For example, let n and m be positive integers with n | m. Thus
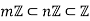
And all subgroups are normal since Z is abelian. The third isomorphism theorem gives the isomorphism
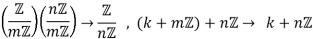
And so the following diagram commutes because both ways around are simply k →7 k + nZ:
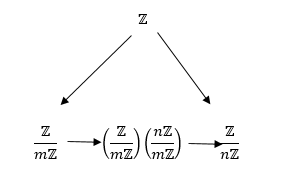
In other words, if modulo m is reduced and then modulo n is reduced, the second reduction subsumes the first.
2.3.4 The Quotient Field of an Integral Domain:
The rationals  are constructed from the integers
are constructed from the integers  by "forming fractions". This amounts to making all the nonzero elements of
by "forming fractions". This amounts to making all the nonzero elements of 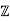 invertible. In fact, you can perform this construction for an arbitrary integral domain.
invertible. In fact, you can perform this construction for an arbitrary integral domain.
Theorem. Let R be an integral domain.
(a) There is a field Q, the quotient field of R, and an injective ring map .
.
(b) If F is a field and 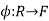 is an injective ring map, there is a unique ring map
is an injective ring map, there is a unique ring map such that the following diagram commutes:
such that the following diagram commutes:
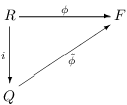
Heuristically, this means that Q is the "minimal" way of inverting the nonzero elements of R.
Proof. The first step is to form the fractions. Let

(Think of 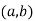 as corresponding to the fraction
as corresponding to the fraction  . The elements of Q aren't actually fractions, but equivalence classes of fractions. Think of the situation in the rationals
. The elements of Q aren't actually fractions, but equivalence classes of fractions. Think of the situation in the rationals 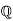 :
: and
and are really the same element of
are really the same element of  .)
.)
Two rational fractions and
and 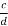 are equal if and only if
are equal if and only if  . I'll use this idea to put an equivalence relation on S.
. I'll use this idea to put an equivalence relation on S.
If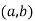 ,
,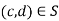 , write
, write 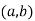 ~(c,d)if and only if ad=bc . I claim this is an equivalence relation.
~(c,d)if and only if ad=bc . I claim this is an equivalence relation.
(a) Since ab=ba , I have 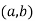 =
=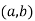 .
.
(b) If  ~(c,d) , then ad=bc . So bc=ad , and hence (c,d)~
~(c,d) , then ad=bc . So bc=ad , and hence (c,d)~ .
.
(c) Suppose 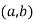 ~(c,d) and (c,d)~
~(c,d) and (c,d)~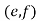 .
.
Then ad=bc and cf=de . I want to show thataf=be . The first equation yields adf=bcf , while the second equation yields bcf=bde. Therefore, adf=ade . Now 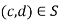 implies
implies  , and since R is a domain, I may cancel d to obtain af=be . Hence,
, and since R is a domain, I may cancel d to obtain af=be . Hence, 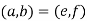 , which completes the proof of transitivity.
, which completes the proof of transitivity.
Let Q be the set of equivalence classes. Let 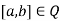 denote the equivalence class of
denote the equivalence class of  . I want to show that Q is a field with the appropriate properties.
. I want to show that Q is a field with the appropriate properties.
First, I'll define the operations. For  , define
, define
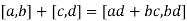
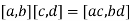
Note that in each case 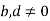 so
so  , and the expressions on the right at least make sense.
, and the expressions on the right at least make sense.
I now have some normal but time-consuming verifications to complete. Because these operations are defined on equivalence classes, I must ensure that they are well-defined —- that is, that they are independent of the equivalence classes' representative choices.
I have to check all the axioms for a field once I have well-defined operations. Checking all of the ring axioms, commutativity, and the existence of inverses for nonzero elements are all part of this process. For example, I'll show that [0,1] functions as an additive identity, while [1,1] is the multiplicative identity.
Expecting you to wade through all of the ugliness is maybe a little much. Regardless, I'll post all of my work below. I recommend checking that one of the two operations is well-defined and working through the proof for at least one of the ring axioms.
First, I'll prove that addition and multiplication are well-defined. Suppose that , so
, so 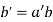 , and
, and 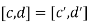 so
so  .
.
1. Addition is well-defined.
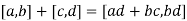 and
and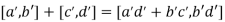
Now
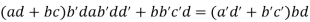
Hence, 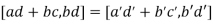
2. Multiplication is well-defined.
 and
and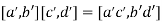
Now
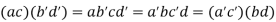
Hence,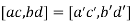 .
.
Next, I'll double-check that Q is a field. I need to double-check the ring axioms, as well as the fact that multiplication is commutative and nonzero elements have inverses.
3. Addition is associative.
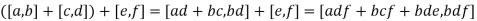

4. Addition is commutative.
 and
and 
5. 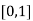 is the additive identity.
is the additive identity.
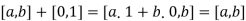
6.  .
.

However,  , since
, since 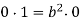
7. Multiplication is associative.

8. Multiplication is commutative.

9. [1,1] is the multiplicative identity.
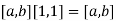
10. Multiplication distributes over addition.
By commutativity of multiplication, it suffices to check this on one side.

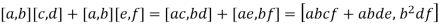
However,
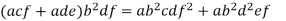 and
and
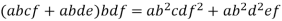
Therefore, 
11. Nonzero elements have multiplicative inverses.
Suppose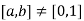 , so
, so 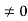 . Then using
. Then using  , I have
, I have

Hence, 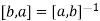 .
.
This completes the verification that Q is a field. Next, I'll construct the imbedding of R into Q.
Define  by
by 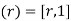 . I'll check that i is a ring map. First,
. I'll check that i is a ring map. First, 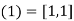 .
.
Next,

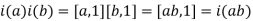
Next, I'll show that i is injective. Suppose  (since [0,1] is the zero element of Q). Then
(since [0,1] is the zero element of Q). Then 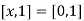 , or x=0 . Therefore, ker i={0} , so i is injective.
, or x=0 . Therefore, ker i={0} , so i is injective.
Finally, I'll complete the proof by verifying the universal property. Suppose that F is a field and 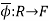 is an injective ring map. Define
is an injective ring map. Define  by
by

Observe that since  ,
,  (injectivity), so
(injectivity), so 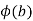 is invertible in the field F.
is invertible in the field F.
I have to check that the map is well-defined. Suppose that 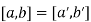 , so
, so  . Then
. Then
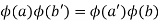


Next, I'll check that  is a ring map. First,
is a ring map. First,
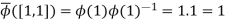
Next,
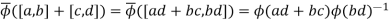


Finally,

I need to check that 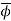 makes the diagram commute. If
makes the diagram commute. If 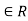 ,
,
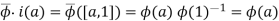
Finally, I'll show that 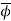 is the only map which could satisfy these conditions. If
is the only map which could satisfy these conditions. If 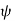 was another injective ring map filling in the diagram, then for
was another injective ring map filling in the diagram, then for  ,
,
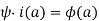
Hence, 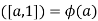 .
.
Now let 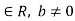 . Since
. Since  is a ring map,
is a ring map,
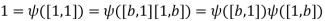
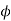 is injective, so
is injective, so 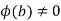 , and it's invertible in F. Therefore,
, and it's invertible in F. Therefore,

Now put the results of the last two paragraphs together, again using the fact that  is a ring map:
is a ring map:
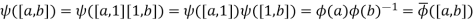
Thus,  is the unique map filling in the diagram, and the proof is (finally!) complete.
is the unique map filling in the diagram, and the proof is (finally!) complete.
The quotient field of an integral domain is unique up to ring isomorphism, according to the usual argument for objects defined by universal characteristics. That is, if R is a domain and Q and Q’ are fields satisfying the universal property for the quotient field of R, then Q≈Q’ .
If R is a field, then it is its own quotient field. To prove this, use uniqueness of the quotient field, and the fact that the identity map 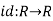 satisfies the universal property.
satisfies the universal property.
In most cases, it is easy to see what the quotient field "looks like". For example, let R be the domain 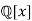 of polynomials with rational coefficients. The quotient field is
of polynomials with rational coefficients. The quotient field is 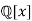 , the field of rational functions with rational coefficients. It consists of all quotients
, the field of rational functions with rational coefficients. It consists of all quotients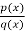 , where
, where 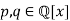 and
and 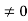 , under the usual operations.
, under the usual operations.
This may seem like a lot of work to produce something that is "obvious". But the reason this may seem "obvious" to you is that you've had lots of experience working with the the rational numbers 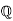 , the quotient field of the integers
, the quotient field of the integers  .
.
Numericals:
1) Prove the Second Isomorphism Theorem: If A is an ideal of R, and S is a subring of R then S + A = {s + a|s∈ S, a ∈ A} is a subring of R, and, moreover, A and S ∩ A are ideals of S + A and S respectively and (S + A)/A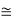 S/(S ∩ A).
S/(S ∩ A).
Solution:
First check that S + A = {s + a|s∈ S, a ∈ A} is a subring of R. Indeed, 1 = 1+0 ∈ S+A. Also, for any s1, s2 ∈ S, a1, a2 ∈ A we have (s1+a1)+(s2+a2) = (s1 + s2) + (a1 + a2) ∈ S + A since s1 + s2 ∈ S and a1 + a2 ∈ A. Similarly, in the above situation we have
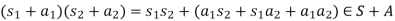
Since s1s2 ∈ S (because S is a subring of R) and a1s2 + s1a2 + a1a2 ∈ A (because A is an ideal in R). Thus indeed, S + A is an ideal in R and, moreover A ⊆ S + A since for every a ∈ A we have a = 0 + a ∈ S + A.
Since A is an ideal in R and A ⊆ S + A ⊆ R, it follows from the definition of an ideal that A is an ideal in S + A.
We now have to show that (S + A)/A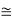 S/(S ∩ A).
S/(S ∩ A).
Define f : S → (S + A)/A by f(s) = s + A for s ∈ S.
We claim that f is a ring homomorphism. Indeed,
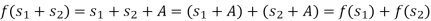
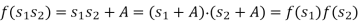
Finally, f(1) = 1 + A. Thus indeed f is a ring homomorphism.
We claim that f is onto. Indeed, for any s ∈ S, a ∈ A we have f(s) = s + A = s + a + A, so that f is indeed onto.
We also claim that Ker(f) = S ∩ A. Indeed for s ∈ S we have

Thus f: S → (S + A)/A is an onto ring homomorphism with Ker(f) = S ∩ A. Therefore S ∩ A is an ideal in S and, by the Isomorphism Theorem, (S + A)/A S/(S ∩ A), as required.
S/(S ∩ A), as required.
2) Let φ: 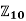 →
→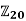 be the homomorphism with φ(1) = 4. Then, by the homomorphism property, φ(x) = 4x (mod 20). In particular
be the homomorphism with φ(1) = 4. Then, by the homomorphism property, φ(x) = 4x (mod 20). In particular


Observe that kerφ =  ≤ Z10 is isomorphic to C2 and Imφ =
≤ Z10 is isomorphic to C2 and Imφ =  ≤
≤  is isomorphic to C5. The factor group is
is isomorphic to C5. The factor group is

The function
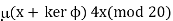
Is the isomorphism from the Theorem.
References:
1. M. Artin, Abstract Algebra, 2nd Ed., Pearson, 2011.
2. Joseph 1. Rotman, An Introduction to the Theory of Groups, 4th Ed., Springer Verlag, 1995.
3. I. N. Herstein, Topics in Algebra, Wiley Eastern Limited, India, 1975.