Unit - 3
Polynomial rings over commutative rings
Let R be a commutative ring. A polynomial of degree n in an indeterminate (or variable) x with coefficients in R is an expression of the form f = f(x) = a0 + a1x + ···+ anxn, where a0,···,an ∈R and an ≠0. We say that a0,···,an are the coefficients of f and that anxnis the highest degree term of f. A polynomial is determined by its coeffiecients. Two polynomials 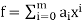 and
and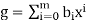 are equal if m = n and ai= bi for i= 0,1,···,n.
are equal if m = n and ai= bi for i= 0,1,···,n.
A polynomial's degree is a non-negative integer. Constant polynomials, or simply constants, are polynomials of degree zero that are just the elements of R. The set of all polynomials in the variable x with coefficients in R is denoted as R[x]. Polynomial addition and multiplication are defined in the usual way: If f(x) = a0 + a1x + a2x2 + a3x3+···and g(x) = b0+b1x+b2x2+b3x3 +···are two elements of R[x], then their sum is f(x) + g(x) = (a0 + b0) + (a1 + b1)x + (a2 + b2)x2 + (a3 + b3)x3 + ···and their product is defined by f(x)·g(x) =
a0b0+(a0b1+a1b0)x+(a0b2+a1b1+a2b0)x2+(a0b3+a1b2+a2b1+a3b0)x3+···
Let 1 denote the constant polynomial 1 and 0 denote the constant polynomial zero. Then (R[x],+,·,0,1) is a commutative ring. The ring axioms are easily verified.
Lemma
Let R be a domain. Then deg(fg) = deg(f) + deg(g).
Proof. Suppose deg(f) = m and deg(g) = n. Then f and g has the form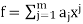 and
and 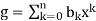 where am ≠0 and bn≠0. From the definition of polynomial multiplication,
where am ≠0 and bn≠0. From the definition of polynomial multiplication,
One notices that the highest degree term of fgis ambnxm+n. Since R is a domain, ambn≠0 , so fghas degree m + n. !
Corollary.
Let R be a domain.
(a) Then R[x] is a domain.
(b) The units in R[x] are precisely the constant polynomials that are also units in R.
Proof. (a) Let f,g∈R[x] such that fg= 0. Thendeg(f) + deg(g) = deg(0) = 0 ( since the zero polynomial is a constant, so it has degree zero). Since degree is a nonzero integer, it follows that deg(f) = 0 and deg(g) = 0, so f and g are constants, i.e, f and g are just elements of R. Now, since R is a domain, it follows that f = 0 or g = 0.
(b) Let u be an unit of R[x]. Then there exists v ∈R[x] such that uv= 1, so deg(u) + deg(v) = deg(1) = 0, so deg(u) = deg(v) = 0, that is, u and v are constants, that is, u and v are elements of R. Now uv= 1 says that u is an unit of R. !
Definition (evaluation at a point).
Let f(x) = a0 + a1x + ···+ anxn∈R[x] be a polynomial and r ∈R. Then we let f(r) = a0 + a1r + ···+ anrn. We say that f(r) is the value of the polynomial f(x) at r. We say that a ∈R is a root of the polynomial f if f(a) = 0. This way each polynomial f(x) determines a function f :R →R that takes r ∈R to f(r). Notice that if f = g, then f(r) = g(r) for all r ∈R. Define a function evr:R[x] →R given by evr(f) = f(r). One verifies that evris a ring homomorphism from R[x] to R; it is called the evaluation homomorphism. We also say that evr(f) = f(r) is the element of R obtained by evaluating f at r.
For the rest of this section, we let F be a field and we consider polynomial ring in one variable over the field F. If p ∈Z is a prime number, then Z/pZis a field with p elements. We write Fp= Z/pZ.
Theorem (Euclidean algorithm).
Let f(x),g(x) ∈F[x] with g(x) ≠0. Then there exists unique polynomials q(x) and r(x) such that f(x) = g(x)q(x) + r(x) and deg(r(x)) <deg(q(x)).
Sketch of proof. Follows from the Euclidean algorithm for division of polynomials.
Example
Examples of polynomial division in Q[X]:
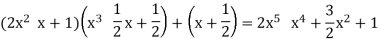
Divide the right hand side by 2x2 −x + 1 and check that (x3 − 21x + 21) is the quotient and 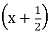 is the remainder.
is the remainder.
Corollary. F[x] is a PID.
Sketch of proof. Given an ideal I find the polynomial of least degree in I and show that it generates I.
Corollary
Let F be a field. A polynomial f ∈F[x] has a root a ∈F if and only if (x −a) divides f in F[x].
Proof. If (x −a) divides f in F[x], then f(x) = (x −a)g(x) for some g ∈F[x], so f(a) = (a −a)g(a) = 0, so a is a root of f. Conversely, suppose a is a root of f. By Euclidean algorithm, we can divide f by (x −a) and write f(x) = (x −a)g(x) + r where g,r∈F[x] and deg(r) <deg(x −a) = 1, so deg(r) = 0, that is r ∈F is a constant. Evaluating both sides at a we obtain 0 = f(a) = (a−a)g(a)+r = r, so r = 0, hence f(x) = (x−a)g(x). !
Reducing coefficients modulo an ideal:
Let φ:R →S be a ring homomorphism. Then verify that φ determines a ring homomorphism Φ:R[x] →S[x] given by Φ(a0 +a1x+ ···+anxn) = φ(a0)+φ(a1)x+···+φ(an)xn. In particular, if I is an ideal in R, then we have the natural quotient homomorphism π :R →R/I and hence we have a ring homomorphsim R[x] →R/I[x] obtained by taking a polynomial and reducing its coefficients modulo I. This homomorphism takes f = a0+a1x+···+anxn∈R[x] to f mod I, where f mod I is defined to be f mod I = (a0 mod I)+(a1 mod I)x+···+(an mod I)xn. If a is a root of fin R, then reducing coefficients modulo I, we find that a mod I is a root of fmod I. In particular, if f has a root in R, then f mod I has a root in R/I.
Recall that an element f is a PID R is called irreducible, if f = uv with u,v ∈ R implies that either u or v is an unit. An element is called reducible if it is not irreducible. The units in F[x] are just the nonzero constants (since F is a field). Given any f ∈F[x] and a constant u ∈F \{0}, we can always write f = u(u−1f); this is called a trivial factorization. So a non-trivial factorization of f∈F[x] is a factorization f = gh where both g and h has degree at least 1. The irreducible polynomials in F[x] are the polynomials that “cannot be non-trivially factored”.
Exercise: (a) Show that f(x) = x3 −3x + 3 is irreducible in Q[x]. (b) Show that f(x) = x3 −3x + 3 is reducible in F5[x]
Sketch of proof. Suppose f is reducible. If f = gh is a nontrivial factorization of f, then deg(g)+deg(h) = 3, so either g has degree 1 and h has degree 2 or vice versa (since g and h are not constants). So f has a factor of the form (ax+b) where a, b∈Q and a ̸=0. It follows that −b/a is a root of f, so f has a root in Q. Write the root of f in the form m/n where m,n∈Z with gcd(m,n) = 1. Then f(m/n) = 0 implies m3 −3mn2 + n3 = 0. So n divides 3mn2−n3 = m3 but gcd(m,n) = 1, so n = 1. It follows that f has an integer root. Now since f ∈Z[x], we can reduce coefficients modulo 2 and obtain a polynomial f mod 2 ∈F2[x]. Note that f mod 2 does not have a solution in F2, since f(0) ≡1 mod 2 and f(1) ≡1 mod 2. It follows that f does not have an integer root, which is a contradiction. So f is irreducible in Q[x]. On the other hand, note that f(2) ≡0 mod 5. So 2 is a solution of fin F5. Divide f by (x −2) in F5[x], to find the factorization f(x) ≡(x + 1)2(x −2) mod 5.
The division algorithm for Z
If a, b ∈ Z with b ≠ 0 then ∃ q, r ∈ Z such that a = bq + r with |r| <|b|.
The element q is called the quotient and r is the remainder.
Proof
Assume a > b > 0. Subtract multiples of b from a until just before things go negative. The quotient q is the number of times you subtract and r = a - bq.
Remarks
a. The divisor is smaller than the remainder. We use absolute value to measure "size" in Z.
b. It's worth noting that you have a choice of remainders: you can take it as positive or negative.
Definition
The greatest common divisor (or highest common factor) of two integers a, b ∈ Z is the largest integer which divides them both.
Remarks
a. We use the absolute value to determine the "largeness."
b. The gcd is only unique up to the point where it is multiplied by 1. The invertible elements or units of Z are these.
To prove our point, we can use the division algorithm.
The Euclidean algorithm
If d is the gcd of a, b there are integers x, y such that d = ax + by.
Proof
Here is an example: Take a = 76, b = 32:
| 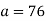  |  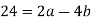 |
|
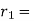 | 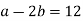  | 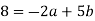 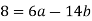 | 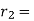 |
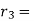 | 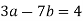 | 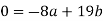 |
|
In general, use the procedure: divide (say) a by b to get remainder r1. Note that one can write r1 in terms of a and b.
Then divide b by r1 to get remainder r2. Note that one can write r2 in terms of b and r1 and hence in terms of a and b.
Repeat the process getting smaller and smaller remainders r1 , r2 , ... Which must eventually lead to a remainder of 0.
Ri may be stated in terms of a and b at each stage since the latest non-zero remainder d divides all the previous ones, and hence both a and b. As a result, it divides gcd (a, b). Because d may be expressed in terms of a and b, gcd(a, b) divides d and must be d.
As a result of this technique, we can now demonstrate:
Theorem
Every ideal of Z is principal.
Proof
Let I be a non-zero ideal. Choose the smallest (non-zero) element a in the ideal I. If b is any other element then the gcd(a, b) is in I and this must be either ±a. So b is a multiple of a.
Thus I = < a >.
We now prove similar results for another ring.
The division algorithm for R[x]
If a(x), b(x) ∈ R[x] with b(x) ≠ 0 then ∃ q(x), r(x) ∈ R[x] such that a(x) = b(x)q(x) + r(x) with either r(x) = 0 or deg(r(x)) < deg(b(x)).
Remarks
a. You'll notice that this is nearly identical to the Z example.
b. The divisor is smaller than the remainder. We use the degree to gauge "size" in R[x].
Proof
We use the (slightly less well-known) process of dividing one polynomial by another (of lower degree). It is just like long division.
One example will suffice!
Take a(x) = 3x4 + 2x3 + x2 - 4x + 1 and b = x2 + x + 1
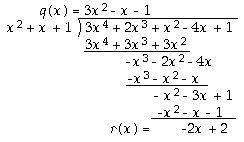
Definition
The greatest common divisor of two polynomials a(x), b(x) ∈ R[x] is a polynomial of highest degree which divides them both.
Remarks
a. This is the greatest polynomial dividing both, where the degree is used to measure "largeness."
b. The gcd is only determined up to the point where a non-zero real number is multiplied by it. R[xinvertible ]'s elements or units are these.
b. It's worth noting that calculating the gcd of (say) 2 and 4 as polynomials yields 1, whereas doing it as integers yields 2.
The following can then be demonstrated:
The Euclidean algorithm for polynomials.
If d(x) is the gcd of a(x), b(x) there are polynomials p(x), q(x) such that d = a(x)p(x) + b(x)q(x).
Proof
Just the same as for Z -- except that the divisions are more tedious.
Remarks
In the calculating package Maple the integer gcd is implemented with igcd and the Euclidean algorithm with igcdex. For polynomials use gcd and gcdex.
The above result on principal ideals follows for this ring.
Every ideal of R[x] is principal.
Proof
Just as in the Z case, an ideal is generated by its smallest (in degree) element.
Remarks
A principal ideal domain, or PID, is an integral domain in which every ideal is principal.
b. For the ring of polynomials F[x] over any field F, the foregoing facts about real polynomials can be proved. F[x] is a PID, as we have just demonstrated.
Let us now demonstrate the same conclusion for a different ring.
Definition
The ring of Gaussian integers is the subring {a + bi | a, b ∈ Z} of C. It is denoted Z[i].
We'll prove the division and Euclidean algorithms for this ring later, but first we must determine whether one Gaussian integer is greater than another.
Definition
The norm (or length) of the Gaussain integer a + bi is a2 + b2. We will write it as N(a + bi).
Remarks
a) This is, of course, |z|2 with z = a + bi. It is more convenient not to take the square root, since it keeps the norm as an integer.
b) If u, v are Gaussian integers, the norm satisfies N(uv) = N(u)N(v).
The division algorithm for Z[i]
If u, v ∈ Z[i] with v ≠ 0 then ∃ q, r ∈ Z[i] such that u = vq + r with N(r) < N(v).
Remarks
- The remainder is smaller than the divisor. In Z[i] we measure "size" by the norm.
- We will see that in fact there is sometimes a choice of remainders.
Proof
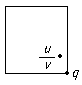
This proof is very different to the other proofs above.
First divide u by v in C. You get a complex number u /v which lies in one of the "cells of the integer lattice".
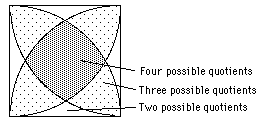
At least one corner of the square is within distance 1 of u/v. This is the quotient q. The remainder is then r = u - vq and since |u/v - q| < 1 we have |u - qv| < |v| and so N(r) < N(v) as required.
Remark
For most positions of u/v there will be a choice of 2, 3 or even four Gaussian integers for the quotient.
Definition
The greatest common divisor of two Gaussian integers u, v ∈ Z[i] is a Gaussian integer of largest norm which divides them both.
Remarks
- Note that we measure the "largeness" using the norm.
- The gcd is only determined up to multiplication by an invertible Gaussian integer. These units of Z[i] are ±1 and ±i.
Then we can calculate just as before and prove:
The Euclidean algorithm for Gaussian integers.
If w is the gcd of u, v there are Gaussian integers g, h such that w = ug + vh.
And then we can deduce:
Every ideal of Z[i] is principal.
Remark
A Euclidean ring is a ring in which one may specify a meaningful notion of size that leads to a Euclidean algorithm.
Definition A principal ideal domain (PID) is an integral domain in which every ideal is principal.
Lemma  is a PID
is a PID
NOTE: Showing that  is a PID means showing that if I is an ideal of
is a PID means showing that if I is an ideal of  , then there is some integer n for which I consists of all the integer multiples of n.
, then there is some integer n for which I consists of all the integer multiples of n.
Proof: Suppose that I ⊆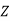 is an ideal. If I = {0} then I is the principal ideal generated by 0 and I is principal. If I
is an ideal. If I = {0} then I is the principal ideal generated by 0 and I is principal. If I 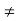 {0} then I contains both positive and negative elements. Let m be the least positive element of I. We will show that
{0} then I contains both positive and negative elements. Let m be the least positive element of I. We will show that
I = 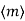 .
.
Certainly 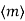 ⊆ I as I must contain all integer mulitples of m. On the other hand suppose a ∈ I. Then we can write
⊆ I as I must contain all integer mulitples of m. On the other hand suppose a ∈ I. Then we can write

Where q ∈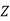 and 0
and 0 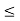 r < m. Then r = a −qm. Since a ∈ I and −qm∈ I, this means r ∈ I. It follows that r = 0, otherwise we have a contradiction to the choice of m. Thus a = qm and a ∈
r < m. Then r = a −qm. Since a ∈ I and −qm∈ I, this means r ∈ I. It follows that r = 0, otherwise we have a contradiction to the choice of m. Thus a = qm and a ∈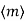 . We conclude I =
. We conclude I =  .
.
Note: In fact every subring of Z is an ideal - think about this.
Lemma
Let F be a field. Then the polynomial ring F[x] is a PID
NOTE: Recall that F[x] has one important property in common with 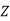 , namely a division algorithm. This is the key to showing that F[x] is a PID.
, namely a division algorithm. This is the key to showing that F[x] is a PID.
Proof: Let I ⊆ F[x] be an ideal. If I = {0} then I =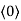 and I is principal. If I
and I is principal. If I  {0}, let f(x) be a polynomial of minimal degree m in I. Then
{0}, let f(x) be a polynomial of minimal degree m in I. Then 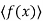 ⊆ I since every polynomial multiple of f(x) is in I.
⊆ I since every polynomial multiple of f(x) is in I.
We will show that I =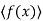 . To see this suppose g(x) ∈ I. Then
. To see this suppose g(x) ∈ I. Then
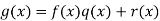
Where q(x), r(x) ∈ F[x] and r(x) = 0 or deg(r(x)) < m. Now
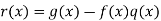
And so r(x) ∈ I. It follows that r(x) = 0 otherwise r(x) is a polynomial in I of degree strictly less than m, contrary to the choice of f(x).
Thus g(x) = f(x)q(x), g(x) ∈hf(x)i and I = 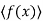
Or
A major ideal domain is an integral domain in which a single element can generate all proper ideals. The acronym P.I.D. Stands for "principal ideal domain." Integers, Gaussian integers, and a collection of polynomials in one variable with real coefficients are examples of P.I.Ds.
The reverse is not true: every Euclidean ring is a major ideal domain. Nonetheless, the Euclidean algorithm's concept of greatest common divisor can be extended to the more comprehensive context of principal ideal domains as follows. Given two nonzero elements 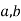 of a principal ideal domain
of a principal ideal domain 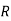 , a greatest common divisor of
, a greatest common divisor of  and
and 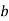 is defined as any element
is defined as any element 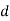 of
of  such that
such that

Every primary ideal domain is a distinct factorization domain, but not the other way around. Every polynomial ring over a field is a unique factorization domain, but if the number of indeterminates is one, it is a principal ideal domain.
Factoring is a valuable tool for solving higher degree equations and is required for the simplification of many algebraic expressions. In fact, factoring is so crucial that it is impossible to progress in algebra beyond this stage without first mastering it.
The contrast between terms and factors has been emphasised in previous chapters. It's important to understand that phrases are multiplied and factors are added or withdrawn. There are three key definitions that follow.
Terms appear in a sum or difference that is stated. Factors can be found in the indicated product.
Only if the entire expression is an indicated product is it in factored form.
In Factored form Not in Factored Form
Example 1 
Example 2 
Example 3 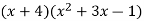
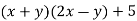
It's worth noting that in these situations, we must always consider the complete statement. Factors can be built up of words, and terms can contain factors, but the factored form must meet the requirements outlined above.
Factoring is the process of converting an expression into a product of factors from a sum or difference of terms.
It's worth noting that the value of the expression isn't altered in this definition; only its form is.
REMOVING COMMON FACTORS
OBJECTIVES
You should be able to:
1. Determine which factors are common to all terms in an expression after finishing this section.
2. Compile a list of common factors.
We multiplied an expression like 5(2x + 1) to get 10x + 5 in the previous chapter. Factoring, in general, "undoes" multiplication. 10x + 5 contains 5 as a factor in each phrase, therefore 10x + 5 = 5(2x + 1).
Example 1 shows how to factor an expression by removing common factors.
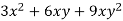
Solution
First list the factors of each term.
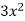 has factors
has factors 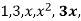 and
and 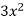
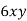 has factors
has factors  and so on
and so on
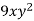 has factors
has factors  and so on
and so on
3x is the greatest common factor of all three terms.
After that, look for factors that are common to all phrases and find the best of them. This is the most prevalent factor. The highest common factor in this situation is 3x.
Place 3x before a set of parenthesis to continue.

Divide each phrase of the original equation by 3x to find the terms within the parenthesis.
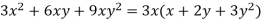
Note that this is the distributive property. It is the reverse of the process that we have been using until now.
The original expression has now been factorised. When checking the factoring, keep in mind that factoring only changes the shape of an expression, not the value. If the answer is correct, the following must be true:

To see if this is correct, multiply. For factoring, a second check is required to ensure that the phrase has been factored completely. To put it another way, "Have we eliminated all common factors? Is it possible to factor in some more?"
3(x2 + 2xy + 3xy2) would be the solution if the factor "3" had been deleted from 3x2 + 6xy + 9xy2.
When we multiply to see if the answer is equal to the original phrase, we discover that it is. The factor x, on the other hand, is still present in all words. As a result, the phrase is not fully factored.
This expression is factored but not completely factored.
For factoring to be correct the solution must meet two criteria:
1. The original expression must be able to be multiplied to get the factored expression.
2. F The phrase must be factored entirely.
Example 2 Factor 12x3 + 6x2 + 18x.
Solution
It should not be required to list the elements of each phrase at this point. You should be able to figure out the most common component in your head. Individualizing the pieces is a smart practise to follow. To put it another way, don't try to acquire all of the common components at once; instead, get the number first, then each letter involved. 6 is a factor of 12, 6, and 18, for example, and x is a factor of each phrase. As a result, 6x(2x2 + x + 3) = 12x3 + 6x2 + 18x. We can see that the terms within the parenthesis have no other common factor when we multiply, therefore we know the solution is accurate.
Say to yourself, "What is the largest common factor of 12, 6, and 18?"
Then, "What is the largest common factor of x3, x2, and x?"
Remember, this is a check to make sure we have factored correctly.
Example 3
Factor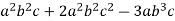
Solution
We note that 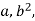 and c are common factors
and c are common factors
Hence 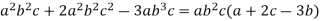
Check:
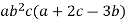
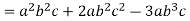
Again, multiply out as a check.
Example 4
Factor 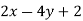
Solution
The only common factor is 2.
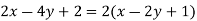
Example 5
Factor 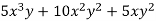
Solution

Again, find the greatest common factor of the numbers and each letter separately.
If an expression cannot be factored it is said to be prime.
Example 6
Factor 
Solution
Since there is no common factor (except 1), this expression is prime.
Remember that 1 is always a factor of any expression.
FACTORING BY GROUPING
OBJECTIVES
You should be able to:
1. Factor expressions where the common factor involves more than one term after finishing this section.
2. Use grouping as a factor.
A method of factoring known as grouping is an extension of the notions described in the previous section.
To begin, it's important to understand that a common element does not have to be a single term. For example, there are two terms in the formula 2y(x + 3) + 5(x + 3). They are 2y(x + 3) and 5(x + 3), respectively. We have a factor (x + 3) that is made up of terms in each of these terms. This factor (x + 3) is quite common.
Example 1
Factor 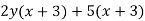
Solution
Since 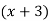 is a common factor, we have
is a common factor, we have 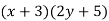
Multiplying as in the previous chapter, we find 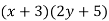
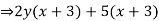
Example 2
Factor 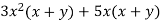
Solution
We see that x and x+y are common factors.
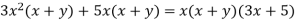
Example 3
Factor 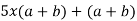
Solution

Note that the expression  is similar to the expression
is similar to the expression
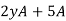
Factoring 2yA+5A, we obtain
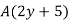
So, factoring  , we have
, we have
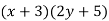
When there are four or more terms, we may need to add an intermediary step or two to factor them.
Example 4
Factor 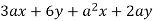
Solution
To begin, keep in mind that not all four terms in the statement share a common component, but some do. For example, the first two terms can be factored to provide 3(ax + 2y). We get a(ax + 2y) by factoring a from the remaining two terms. The expression is now 3(ax + 2y) + a(ax + 2y), and we can factor as (axe + 2y)(3 + a) because we have a common factor of (axe + 2y). We get the original expression 3ax + 6y + a2x + 2ay by multiplying (axe + 2y)(3 + a) and observe that the factoring is valid.
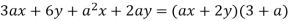
The first two terms
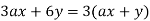
The remaining two terms
 is now a factoring problem
is now a factoring problem
Because we "grouped" the terms two at a time, this is an example of factoring by grouping.
Example 5
Factor 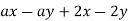
Solution
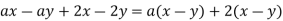
Example 6
Factor 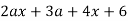
Solution

Multiply (x - y)(a + 2) and see if you get the original expression.
Again, multiply as a check. Before factoring by grouping can be done, the terms may need to be rearranged first.
Example 7 Factor 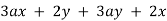
Solution
The first two terms have no common element, but the first and third terms have, so the third term will be placed after the first. Always keep an eye on the future to see how the terms might be arranged.

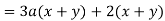
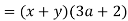
It is critical to ensure that the factors within parenthesis are identical in all circumstances. This may need the use of a negative number or letter as a factor.
Remember, the commutative property allows us to rearrange these terms.
Multiply as a check.
Example 8 Factor ax - ay - 2x + 2y.
Solution
It's worth noting that if we subtract a from the first two terms, we get a. (x - y). When we factor +2 into the last two numbers, we get 2(-x + y), but when we factor "-2," we get - 2 (x - y). We proceed in this manner because we want the terms within parenthesis to be (x - y).
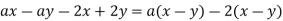
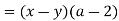
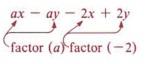
FACTORING TRINOMIALS
OBJECTIVES
You should be able to:
1. Mentally multiply two binomials after completing this section.
2. Factor a trinomial with a coefficient of 1 in the first term.
3. Find the factors of any trinomial that can be factored.
Factoring trinomials as products of two binomials will appear in a huge number of future problems. You learnt how to multiply polynomials in the previous chapter. Now we'll look at the special case of multiplying two binomials and see if we can come up with a pattern for it.
Example 1
Find the product of 
Solution
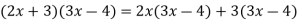
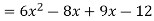
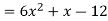
Because this form of multiplication is so common, knowing how to reach the answer without going through so many steps is helpful. Let's take a look at a pattern.
Note that the first term of the answer (6x2) came from the product of the two first terms of the factors, i.e. (2x + 3)(3x - 4) = 6x2 + x - 12. (3x).
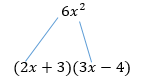
Also note that the third term (-12) came from the product of the second terms of the factors, that is ( + 3)(-4).

We now have the following part of the pattern:
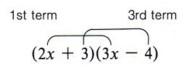
Now looking at the example again, we see that the middle term (+x) came from a sum of two products (2x)( -4) and (3)(3x).
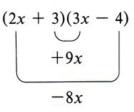
We now have four products for any two binomials:
1. First-to-first-to-first-to-first-to-first-
2. External terms
3. In-depth terminology
4. From last to last, last to last, last to last, last to last, last
These products are shown by this pattern.
When the products of the outside terms and inside terms give like terms, they can be combined and the solution is a trinomial.
This method of multiplying two binomials is sometimes called the FOIL method.
FOIL stands for First, Outer, Inner, Last.
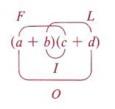
It is a shortcut method for multiplying two binomials and its usefulness will be seen when we factor trinomials.
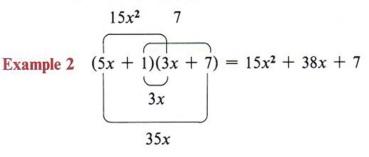
You should memorize this pattern.
Again, maybe memorizing the word FOIL will help.
Not only should this pattern be memorized, but the student should also learn to go from problem to answer without any written steps. This mental process of multiplying is necessary if proficiency in factoring is to be attained.
Example 3
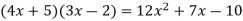
As you work the following exercises, attempt to arrive at a correct answer without writing anything except the answer. The more you practice this process, the better you will be at factoring.
Now that we have established the pattern of multiplying two binomials, we are ready to factor trinomials. We will first look at factoring only those trinomials with a first term coefficient of 1.
Example 4
Factor 
Solution
Because this is a trinomial with no common factor, we'll factor it using the multiplication pattern.
We will actually be working in reverse the process developed in the last exercise set.
First write parentheses under the problem.
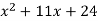
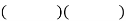
We now wish to fill in the terms so that the pattern will give the original trinomial when we multiply. The first term is easy since we know that (x)(x) = x2.
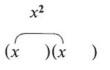
Remember, the product of the first two terms of the binomials gives the first term of the trinomial.
Now we must discover integers that multiply to provide 24 while also adding to get the middle term. It's worth noting that the first and last terms in each of the following examples are correct.

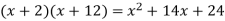

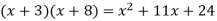
Only the last product has a middle term of 11x, and the correct solution is
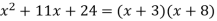
This method of factoring is called trial and error - for obvious reasons.
Some number facts from arithmetic might be helpful here.
- The product of two odd numbers is odd.
- The product of two even numbers is even.
- The product of an odd and an even number is even.
- The sum of two odd numbers is even.
- The sum of two even numbers is even.
- The sum of an odd and even number is odd.
Therefore, when we factor an expression such as x2 + 11x + 24, we know that the product of the last two terms in the binomials must be 24, which is even, and their sum must be 11, which is odd.
Thus, only an odd and an even number will work. We need not even try combinations like 6 and 4 or 2 and 12, and so on.
Example
Factor 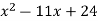
Solution
Here the problem is only slightly different. We must find numbers that multiply to give 24 and at the same time add to give - 11. You should always keep the pattern in mind. The last term is obtained strictly by multiplying, but the middle term comes finally from a sum. Knowing that the product of two negative numbers is positive, but the sum of two negative numbers is negative, we obtain
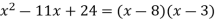
Example
Factor 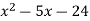
Solution
For the third term, we're dealing with a negative integer, which makes the task significantly more challenging. We must conceptualise in terms of a difference because -24 can only be the product of a positive and a negative number, and the middle word must originate from the sum of both numbers. We need to discover numbers with a product of 24 and a difference of 5. Furthermore, the greater number must be negative, because when a positive and negative number are added, the result will bear the sign of the larger number. With all of this in mind, we arrive to
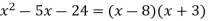
The order of factors is insignificant.
 by the commutative law of multiplication.
by the commutative law of multiplication.
When factoring trinomials, keep the following points in mind:
1. When the third term's sign is positive, both signs in the factors must be the same—and they must be the same as the middle term's sign.
2. When the penultimate term's sign is negative, the components' signs must be unlike-and the larger term's sign must be like the middle term's sign.
The coefficient of each of the first terms in the preceding exercise was 1. When the first term's coefficient is not 1, factoring becomes significantly more difficult since the number of alternatives increases dramatically.
Example
Factor 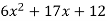
Solution
Factors of 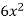 are
are 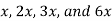 . Factors of 12 are
. Factors of 12 are 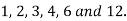
Notice that there are twelve ways to obtain the first and last terms, but only one has 17x as a middle term.
 Middle term
Middle term 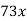
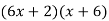 Middle term
Middle term 
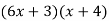 Middle term
Middle term 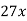
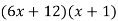 Middle term
Middle term 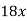
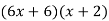 Middle term
Middle term 
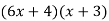 Middle term
Middle term 
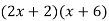 Middle term
Middle term 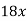
 Middle term 22
Middle term 22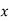
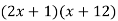 Middle term
Middle term 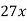
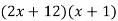 Middle term
Middle term 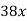
 Middle term
Middle term 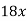
 Middle term 17
Middle term 17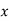
You could, of course, try each of these mentaly instead of writing them out.
There is only one way to obtain all three terms:
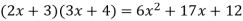
In this case, one of the twelve options is right. As a result, trial and error can take a long time.
Even when guessing is employed, it should be "informed guessing," in which we apply all of our numerical knowledge and engage in a significant amount of mental arithmetic. Many of the combinations in the above example would be quickly dismissed. Because we're looking for 17x as a middle term, we won't try multiplying 6 by 6, 3 by 12, 6 by 12, and so on, because the resulting products will be larger than 17. We also know that 17 is the sum of an even and an odd number because it is odd. All of these factors contribute to a reduction in the number of options to explore.
First find numbers that give the correct first and last terms of the trinomial. Then add the outer and inner product to check for the proper middle term.
Example
Factor 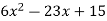
Solution
First, we must assess the situation.
1. Because the last term is positive, there are two similar signals.
2. Both signals will be negative since the middle phrase is negative.
3. The 6x2 factors are x, 2x, 3x, and 6x. The 15 factors are 1, 3, 5, and 15.
4. Multiply the result of 15 by 2x, 3x, or 6x to eliminate it as being too large. Experiment with some suitable combinations.
These would automatically give too large a middle term.
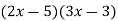 Middle term incorrect(-21x)
Middle term incorrect(-21x)
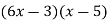 Middle term incorrect(-33x)
Middle term incorrect(-33x)
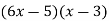 Middle term correct(-23x)
Middle term correct(-23x)
See how the number of possibilities is cut down.
Example
Factor 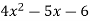
Solution
Analyze:
1. The last term is negative, indicating that the signs are unlike.
2. We need to look for goods that differ by 5 with the greater value being negative.
3. We rule out a product of 4x and 6 as being likely too huge.
4. Experiment with different combinations.
Remember to run over all of the possible combinations in your head. This is the "trial and error" method of factoring. Through practise, you will improve your ability to perform this task.

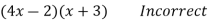
(4x - 3)(x + 2) : Here the middle term is + 5x, which is the right number but the wrong sign. Be careful not to accept this as the solution, but switch signs so the larger product agrees in sign with the middle term.
 gives the correct sign for the middle term.
gives the correct sign for the middle term.
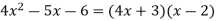
SPECIAL CASES IN FACTORING
OBJECTIVES
You should be able to:
1. Identify and factor the differences of two perfect squares after finishing this section.
2. Find a perfect square trinomial and factor it.
In this section, we'll look at several unique examples of factoring that crop up frequently in difficulties. When these specific instances are recognised, factoring becomes much easier.
The difference of two perfect squares is the first particular example we'll look at.
Remember that the middle word in multiplying two binomials by the pattern originates from the sum of two products.
From our experience with numbers we know that the sum of two numbers is zero only if the two numbers are negatives of each other.
When the sum of two numbers is zero, one of the numbers is said to be the additive inverse of the other.
For example: ( + 3) + (-3) = 0, so + 3 is the additive inverse of - 3, also -3 is the additive inverse of +3.
Example 1 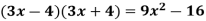
Example 2 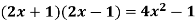
Example 3 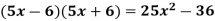
In each example the middle term is zero. Note that if two binomials multiply to give a binomial (middle term missing), they must be in the form of (a - b) (a + b).
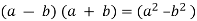
The rule may be written as 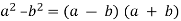 . This is the form you will find most helpful in factoring.Reading this rule from right to left tells us that if we have a problem to factor and if it is in the form of
. This is the form you will find most helpful in factoring.Reading this rule from right to left tells us that if we have a problem to factor and if it is in the form of 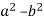 , the factors will be (a - b)(a + b).
, the factors will be (a - b)(a + b).
Example 4
Factor 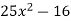
Solution
Here both terms are perfect squares and they are separated by a negative sign.
The form of this problem is 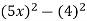 (the form of
(the form of 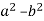 )
)
So 
Where a = 5x and b = 4.
Special cases make factoring easier, but keep in mind that a particular case is exactly that—a special case. Both terms must be perfect squares in this situation, and the sign must be negative, resulting in "the difference of two perfect squares."
The sum of two squares is not factorable.
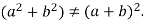 Why?
Why?
Example 5: 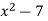 Not the special case. Why?
Not the special case. Why?
Example 6: 4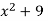 Not the special case. Why?
Not the special case. Why?
You must also be cautious while identifying flawless squares. Keep in mind that perfect square numbers are integers with integer square roots. Exponents with perfect square exponents are also even.
Example 7: 4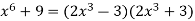
Example 8: 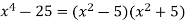
Example 9: 
Example 10: 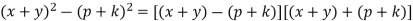
Students often overlook the fact that (1) is a perfect square. Thus, an expression such as x2 - 1 is the difference of two perfect squares and can be factored by this method.
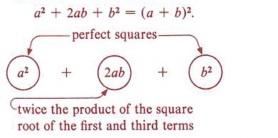
The perfect square trinomial is another unique situation in factoring. It's worth noting that this example is caused by squaring a binomial.

We recognise this scenario by noting the distinguishing characteristics. Three things stand out.
1. A perfect square is the first term.
2. A perfect square is the third term.
3. The middle term is equal to the square root of the first and third terms multiplied by two.
For factoring purposes it is more helpful to write the statement as
Example 11
Factor 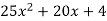
Solution
- 25x2 is a perfect square-principal square root = 5x.
- 4 is a perfect square-principal square root = 2.
- 20x is twice the product of the square roots of 25x2 and
- 20x = 2(5x)(2).
- Form a binomial with the square root of the first term, the square root of the last term, and the sign of the middle term to create a perfect square trinomial, and indicate the square of this binomial.
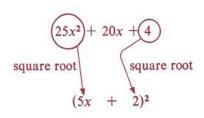
Thus, 25x2 + 20x + 4 = (5x + 2)2
Always square the binomial as a check to make sure the middle term is correct.
Example 12: 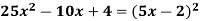
Example 13: 9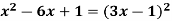
Example 14: 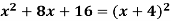
Example 15: 4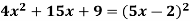
Not the special case of a perfect square trinomial.
15 ≠ 2(2x)(3)
3.5.1 Introduction
There is no straightforward way to determine whether an arbitrary polynomial in F[T] is irreducible for a broad field F. We'll concentrate on the scenario F = Q and offer two helpful irreducibility tests for monic polynomials in Z[T] in Q[T]. Let

The two tests are
- Reduction mod p: for a prime p, reducing coefficients of f(T) modulo p leads to

If f(T) is irreducible in (Z/pZ)[T] for some p, then f is irreducible in Q[T].
- Eisenstein criterion: call f(T) Eisenstein at p if p | aifor all iand p2 - a0. If f is Eisenstein for some p, then f is irreducible in Q[T].
These tests each depend on a choice of a prime number, but they use the prime number in different ways.
Example The polynomial T3 +T +1 is irreducible in (Z/2Z)[T], so every monic cubic in Z[T] that reduces modulo 2 to T3+T +1 is irreducible in Q[T], such as T3−4T2+3T +1.
Example The polynomial T6 + T + 1 is irreducible in Q[T] because it is irreducible in (Z/2Z)[T]. To show irreducibility in (Z/2Z)[T], we just have to check it is not divisible by any irreducibles of degree 1, 2, or 3 in (Z/2Z)[T]: there are two irreducibles of degree 1 (T and T + 1), one irreducible of degree 2 (T2 + T + 1), and two irreducibles of degree 3 (T3 + T + 1 and T3 + T2 + 1). This leaves us with a finite amount of computation, which you should go through yourself.
Example
Let 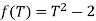 . Then
. Then
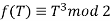

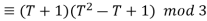
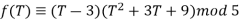
Sof is reducible mod p for p = 2,3,5. However f(T) mod 7 is irreducible since f mod 7 has degree 3 in (Z/7Z)[T] and has no root in Z/7Z: that is a finite check since Z/7Z is finite. By the reduction mod p test at p = 7, T3 −2 is irreducible in Q[T].
Remark There are monic polynomials in Z[T] that are irreducible in Q[T] but are reducible mod p for all p, e.g., T4 −10T2 +1. So the reduction mod p test does not always apply.
Example T3 −2 is Eisenstein at 2, so it’s irreducible in Q[T]. This is a much easier method for T3 −2 than reduction mod p
Example Tn−2 is Eisenstein at 2 for any n ≥ 1, so it is irreducible in Q[T].
The usefulness of the Eisenstein criterion is that it lets us create irreducibles in Q[T] of any degree we wish. (Note T −2 is Eisenstein at 2: the test could be used in degree 1, but it is not necessary since all linear polynomials over a field are irreducible.)
3.5.2 Gauss’ Lemma
To prove the reduction mod p test and the Eisenstein criterion, we will prove the polynomial in each test can’t be decomposed into lower-degree factors in Z[T]. How come that implies irreducibility in Q[T]? For comparison, T2 + 1 is irreducible in R[T] but if we enlarge R to C then T2 +1 = (T +i)(T −i) in C[T] and the polynomial becomes reducible. Passing from Z[T] to Q[T] never turns irreducibility into reducibility. This is traditionally called Gauss’ lemma.
Theorem (Gauss). If f(T) ∈Z[T] is monic and f(T) = g(T)h(T) in Q[T] where degg<degf and degh<degf then we can write f(T) = g1(T)h1(T) in Z[T], where g1(T) and h1(T) are scalar multiples of g(T) and h(T), respectively; in particular, degg1(T) = degg(T) <degf(T) and degh1(T) = degh(T) <degf(T).
Therefore if a monic polynomial in Z[T] can’t be written as a product of lower-degree polynomials in Z[T], it is irreducible in Q[T].
As an example, T2 −1 in Q[T] is ((4/3)T −4/3)((3/4)T + 3/4), having linear factors, and in Z[T] it is (T + 1)(T −1), also having linear factors.
Proof. Step 1: Use common denominators to factor a scalar multiple of f(T) in Z[T].
Let d and e be common denominators of the coefficients of g(T) and h(T), respectively, so 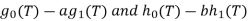 where g0(T) and h0(T) are both in Z[T]. Thus
where g0(T) and h0(T) are both in Z[T]. Thus
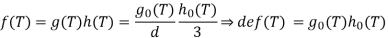
This last equation takes place in Z[T].
Step 2: Use greatest common divisors to get factors of f(T) whose coefficients are relatively prime.
Factor out the greatest common divisor of the coefficients of g0(T) and of the coefficients of h0(T):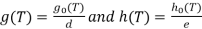 where a,b∈Z+, the coefficients of g1(T) are relatively prime, and the coefficients of h1(T) are relatively prime. Then
where a,b∈Z+, the coefficients of g1(T) are relatively prime, and the coefficients of h1(T) are relatively prime. Then
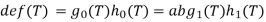
Step 3: Obtain a factorization of f(T) in Z[T].
We will show de = ab, so cancelling this (nonzero) factor from both sides gives us f(T) = g1(T)h1(T) in Z[T] where g1(T) = g0(T)/a = (d/a)g(T) and h1(T) = h0(T)/b = (e/b)h(T) are scalar multiples of g(T) and h(T).
Since f(T) is monic, looking at the leading coefficient on both sides of (2.1) we get
De = ab(lead g1) (lead h1) in Z,
Soab | de. Let c = de/ab ∈Z+, so c ≥ 1 and (2.1) implies
(2.2) cf(T) = g1(T)h1(T).
If c >1 then it has a prime factor, say p. Reduce both sides of (2.2) modulo p: this turns (2.2) into 0 = g1(T)h1(T) in (Z/pZ)[T]. Since (Z/pZ)[T] is an integral domain, one of g1(T)
Orh1(T) is 0, which is another way of saying all the coefficients of g1(T) are divisible by p or all the coefficients of h1(T) are divisible by p. Neither is possible, since the coefficients of g1(T) are relatively prime and the coefficients of h1(T) are relatively prime. Therefore c has no prime factor, so c = 1 and f(T) = g1(T)h1(T) is a factorization of f(T) in Z[T] where the factors g1(T) and h1(T) are scalar multiples of g(T) and h(T).
A good way to think about the later part of this proof is that we applied the reduction mod p homomorphism to turn an equation in Z[T] into an equation in (Z/pZ)[T] for a suitably chosen prime p. We will apply this same idea in the proofs of both the reduction mod p test and the Eisenstein criterion.
3.5.3 Reduction mod p:
Theorem If f(T) ∈Z[T] is monic and there is a prime p such that f(T) is irreducible in (Z/pZ)[T] then f(T) is irreducible in Q[T].
Proof. By Gauss’ lemma, to prove f(T) is irreducible in Q[T] it suffices to show we can’t write f(T) as a product of lower-degree factors in Z[T].
Assume f = ghfor some g,h∈Z[T] with degg<degfand degh<degf. We will get a contradiction from this.
Looking at the leading coefficients on both sides of f = ghwe have 1 = (lead g)(lead h) in Z, so g and h both have leading coefficient 1 or both have leading coefficient −1. Therefore, after changing the signs on g and h if necessary, we can assume g and h are both monic in Z[T]. Reduction mod p is a ring homomorphism Z[T] →(Z/pZ)[T], so it turns the equation f = ghin Z[T] into f = ghin (Z/pZ)[T]. Since f is irreducible, one of g or h has degree 0 and the other has degree equal to that of f. Because f, g and h are all monic,
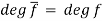
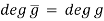
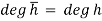
Therefore one of g or h has degree equal to the degree of f, but this contradicts g and h both having degree less than deg f.
3.5.4 Enough prime values implies irreducibility
The polynomial T2 +1 is irreducible in Z[T], but that doesn’t mean its values at integers have to be prime numbers: a2 + 1 is composite for all odd a ≥ 3 since m2 + 1 is even and greater than 2. However, a2 +1 is prime for many values of a, such as a = 1,2,4,6, and 10. It turns out if a polynomial in Z[T] takes enough prime values that proves its irreducibility!
Theorem If f(T) ∈Z[T] is monic of degree d ≥ 1 and there are 2d+1 integers a such that f(a) is ±1 or a positive or negative prime number then f(T) is irreducible in Q[T].
Proof. By Gauss’ lemma it suffices to prove f(T) is irreducible in Z[T] to know it is irreducible in Q[T]. Suppose f(T) = g(T)h(T) in Z[T] where degg<degfand degh<degf. Then f(a) = g(a)h(a). If f(a) is ±1 or a positive or negative prime then g(a) = ±1 and h(a) = ±1. Since g(T) assumes a value on Z at most deggtimes and h(T) assumes a value on Z at most deghtimes, the number of integers n such that g(a) = ±1 or h(a) = ±1 is at most 2degg +2degh = 2degf = 2d, so if f(a) is ±1 or a positive or negative prime 2d+1 times then we have a contradiction so f(T) is irreducible in Q[T].
Example The polynomial T4 −10T2 + 1 is ±1 or has a positive or negative prime value at T = 0,±2,±4,±6,±8, which is 2 ·4 + 1 = 9 values. Therefore T4 −10T2 + 1 is irreducible in Q[T].
Theorem, like the reduction mod p test and Eisenstein criterion, it is not always directly applicable to prove irreducbility. For example, T2+T +2 is irreducible but takes only even values when T runs over the integers. There is a conjecture, due to Bunyakovsky, that describes when a polynomial in Z[T] should take prime values infinitely often, and a change of variables can convert any irreducible polynomial to a form where Bunyakovsky’s conjecture is expected to apply (see the end of [1]). However, Theorem 5.1 appears to be limited to proving irreducibility of individual polynomials rather than families of polynomials such as Tn−2 as n varies, which can be treated by the Eisenstein criterion.
3.5.5 Reducibility tests
Some calculations provide shortcuts that can be used to speed up the process. Consider the operation of increasing a positive integer number to a higher power. It is possible, for example, to calculate 138 by multiplying 13 by itself seven times,
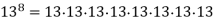
However, the shortcut of squaring three times considerably speeds up the computation,
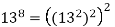
It's generally difficult to tell whether a particular computation can be sped up using this method. Computational irreducibility refers to the inability of a computation to be sped up.
3.6.1 Eisenstein's Irreducibility Criterion:
The irreducibility criterion of Eisenstein is a way for proving irreducibility of a polynomial with integer coefficients (that is, cannot be written as a product of two polynomials of smaller degree with integer coefficients). It is not generally relevant to most polynomials due to its unique requirements, but it is useful for displaying examples of properly chosen irreducible polynomials.
Let 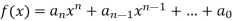 be a polynomial with integer coefficients. Suppose that there exists a prime pp, such that
be a polynomial with integer coefficients. Suppose that there exists a prime pp, such that
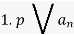


Then f(x) is irreducible over the integers.
3.6.2 Proof of Eisenstein's Irreducibility Criterion:
Suppose not, then
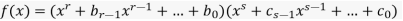
With 0 <r and s < n. Take ii least such that p∣bi (where we allow the case i = r and br=1), and j least such that p∣cj (where we allow the case j=s and cs=1). Now the (i+j)th coefficient ai+j of the product is
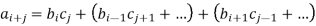
And so is a sum of bicj and terms divisible by p. As p∣bicj, p∣ai+j. But ,p2∣a0=b0c0, so p cannot divide both b0 and c0. Thus, either i=0 or ,j=0, so i+j<n. So we contradict p∣ai+j.
Thus, by contradiction, Eisenstein's irreducibility criterion holds true.
3.6.3 Extended Eisenstein's Criterion
Let 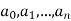 be integers. Then, Eisenstein's Criterion states that the polynomial
be integers. Then, Eisenstein's Criterion states that the polynomial 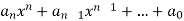 has an irreducible factor of degree more than
has an irreducible factor of degree more than 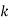 if:
if:
1)  is a prime which divides each of
is a prime which divides each of 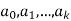
2) 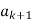 is not divisible by
is not divisible by 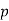
3) 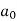 is not divisible by
is not divisible by 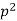
Proof
Let  , where
, where 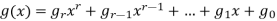 and
and  . Since
. Since  has only one factor of p, we know that or
has only one factor of p, we know that or 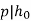 . WLOG, assume
. WLOG, assume 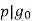 . Then, we know that
. Then, we know that 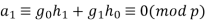 . This means
. This means 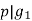 . Similarily, we see, if
. Similarily, we see, if 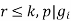 for all
for all 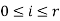 . This means that
. This means that  , so
, so 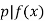 . However, we know that
. However, we know that 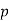 does not divide by
does not divide by 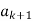 a contradiction. Therefore,
a contradiction. Therefore, 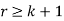 .
.
3.6.4 Advanced explanation:
Applying the theory of the Newton polygon for the p-adic number field, for an Eisenstein polynomial, we are supposed to take the lower convex envelope of the points
(0, 1), (1, v1), (2, v2), ..., (n − 1, vn−1), (n, 0),
Where vi is the p-adic valuation of ai (i.e. the highest power of p dividing it). Now the data we are given on the vi for 0 < i < n, namely that they are at least one, is just what we need to conclude that the lower convex envelope is exactly the single line segment from (0, 1) to (n, 0), the slope being −1/n.
This means that each root of Q has a p-adic valuation of 1/n, implying that Q is irreducible over the p-adic field (because no product of any appropriate subset of the roots has integer value, for example) and, a fortiori, over the rational number field.
This argument is far more difficult than the direct reduction mod p argument. It does, however, allow one to observe how frequently Eisenstein's criterion might apply, in terms of algebraic number theory, after a change of variable, and so severely limit the available choices of p with respect to which the polynomial may have an Eisenstein translation (that is, become Eisenstein after an additive change of variables as in the case of the p-thcyclotomic polynomial).
In fact only primes p ramifying in the extension of Q generated by a root of Q have any chance of working. These can be found in terms of the discriminant of Q. For example, in the case x2 + x + 2 given above, the discriminant is −7 so that 7 is the only prime that has a chance of making it satisfy the criterion. Modulo 7, it becomes (x − 3)2— a repeated root is inevitable, since the discriminant is 0 mod 7. Therefore the variable shift is actually something predictable.
Again, for the cyclotomic polynomial, it becomes
(x − 1)p−1 mod p;
The discriminant can be shown to be (up to sign) pp−2, by linear algebra methods.
For the polynomial, only entirely ramified primes have a possibility of being Eisenstein primes. (Ramification is always total in quadratic fields, therefore the distinction is not seen in the quadratic case like x2 + x + 2 above.) In fact, Eisenstein polynomials are directly linked to totally ramified primes, as follows: if the root of an Eisenstein polynomial at p generates a field extension of the rationals, then p is totally ramified in the extension, and vice versa, if p is totally ramified in a number field, then the field is generated by the root of an Eisenstein polynomial at p.
Examples:
1) The polynomial ring D = k[u] in the variable u over the field k is one of the most basic instances of an integral domain after Z. The primary ideal created by u in this situation is a prime ideal. Eisenstein's criterion can then be used to prove the irreducibility of a polynomial such as Q(x) = x3 + ux + u in D[x]. Indeed, u does not divide a3, u2 does not divide a0, and u divides a0, a1 and a2. This shows that this polynomial satisfies the hypotheses of the generalization of Eisenstein's criterion for the prime ideal p = (u) since, for a principal ideal (u), being an element of (u) is equivalent to being divisible by u.
2) The polynomial 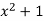 is irreducible, but does not fulfil the above property, since no prim62 +e number divides 1. However, substituting
is irreducible, but does not fulfil the above property, since no prim62 +e number divides 1. However, substituting  for
for  produces the polynomial
produces the polynomial 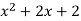 , which does fulfill the Eisenstein criterion (with
, which does fulfill the Eisenstein criterion (with 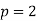 ) and shows the polynomial is irreducible.
) and shows the polynomial is irreducible.
Domains of Factorization That Aren't Found Anywhere Else ( UFDs )
R will be used to denote an integral domain throughout this section (i.e. a commutative ring with identity containing no zero-divisors). Remember that a R unit is an element that has the inverse of multiplication. We can write if an is any R element and u is a unit
a = u(u−1a).
This isn't regarded as a valid factorization of a. We don't regard 5 = 1(5) or 5 = (1)(5) to be correct factorizations of 5 in Z, for example. We don't think about it.
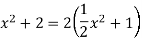
To be a proper factorization of 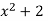 in
in 
Definition 4.1.1 If an element an in an integral domain R is not zero or a unit, and if an is expressed as the product of two elements of R, one of them is a unit, it is said to be irreducible.
If p is neither zero or a unit, and p divides ab for elements a,b of R, either p divides an or p divides b, an element p of an integral domain R is considered prime.
Note
- Elements r and s are called associates of each other if s = ur for a unit u of R. So a ∈R is irreducible if it can only be factorized as the product of a unit and one of its own associates.
- If R is an integral domain, every prime element of R is irreducible. To see this let p ∈R be prime and suppose that p = rs is a factorisation of p in R. Then since p divides rs, either p divides r or p|s. There is no loss of generality in assuming p divides r. Then r = pa for some element a of R, and p = rsso p = pas. Then p −pas = 0 so p(1−as) = 0 in R. Thus as = 1 since R is an integral domain and p 6=0. Then s is a unit and p = rs is not a proper factorisation of p. Hence p is irreducible in R.
It is not true that every irreducible element of an integral domain must be prime, as we will shortly see.
Examples:
- In Z the units are 1 and −1 and each non-zero non-unit element has two associates, namely itself and its negative. SO 5 and −5 are associates, 6 and −6 are associates, and so on. The irreducible elements of Z are p and −p, for p prime.
- In Q[x], the units are the non-zero constant polynomials. The associates of a non-zero non-constan2 t polynomial f(x) are the polynomials of the form af(x) where a ∈Q×.
So x + 2 is associate to 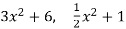 , etc.
, etc.
3. In Z the irreducible elements are the integers p and −p where p is a prime numbers. The prime elements of Z are exactly the irreducible elements - the prime numbers and their negatives.
Definition 4.1.2 An integral domain R is a unique factorization domain if the following conditions hold for each element a of R that is neither zero nor a unit.
- a can be written as the product of a finite number of irreducible elements of R.
- This can be done in an essentially unique way. If a = p1p2 ...prand a = q1q2 ...qsare two expressions for a as a product of irreducible elements, then s = r and q1,...,qscan be reordered so that for each i, qi is an associate of pi.
Example 4.1.3 Z is a UFD.
(This is the Fundamental Theorem of Arithmetic).
Example 4.1.4 Let denote the set of complex numbers of the form a+b√−5 wher√−e a and b are integers (and
denote the set of complex numbers of the form a+b√−5 wher√−e a and b are integers (and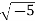 denotes the complex number
denotes the complex number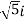 . We will show that Z
. We will show that Z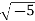
Is not a UFD (it is easily shown to be a ring under the usual addition and multiplication of complex numbers).
Claim: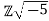 is not a UFD.
is not a UFD.
The proof if this claim will involve a number of steps.
- We define a function
 where
where 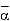 denotes the complex conjugate of α. Thus
denotes the complex conjugate of α. Thus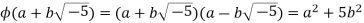
Let α,  . Then
. Then
φ(αβ) = αβαβ= αβα¯β¯ = αα¯ββ¯ = φ(α)φ(β).
So φis multiplicative.
2. Suppose α is a unit of  and let β be its inverse. Then φ(αβ) = φ(1) = 1 = φ(α)φ(β). Since φ(α) and φ(β) are positive integers this means φ(α) = 1 and φ(β) = 1. So φ(α) = 1 whenever αis a unit.
and let β be its inverse. Then φ(αβ) = φ(1) = 1 = φ(α)φ(β). Since φ(α) and φ(β) are positive integers this means φ(α) = 1 and φ(β) = 1. So φ(α) = 1 whenever αis a unit.
On the other hand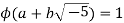 implies a2 + 5b2 = 1 for integers a andb which means b = 0 and a = ±1. So the only units of
implies a2 + 5b2 = 1 for integers a andb which means b = 0 and a = ±1. So the only units of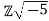 are 1 and −1.
are 1 and −1.
3. Suppose φ(α) = 9 for some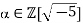 is not irreducible in
is not irreducible in 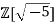 then it factorizes as α1α2 where α1 and α2 are non-units. Then we must have
then it factorizes as α1α2 where α1 and α2 are non-units. Then we must have
φ(α1) = φ(α2) = 3.
Now this would means 3 = c2 + 5d2 for integers c and d which is impossible. So if φ(α) = 9 then αis irreducible in 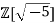
4. Now 9 = 3 × 3 and 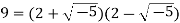 in
in 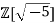 . The elements 3, 2 + √−5 and
. The elements 3, 2 + √−5 and  are all irreducible in
are all irreducible in 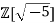 by item 3 above. Furthermore 3 is not an associate of either
by item 3 above. Furthermore 3 is not an associate of either 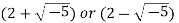 as the only units in
as the only units in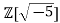 are 1 and -1 We conclude that the factorizations of 9 above are genuinely different, and Z[√−5] is not a UFD.
are 1 and -1 We conclude that the factorizations of 9 above are genuinely different, and Z[√−5] is not a UFD.
Note that 3 is an example of an element of Z[√−5] that is irreducible but not prime. Remark: The ring Z[i] = {a + bi :a,b∈Z} is a UFD.
Theorem 4.1.5 Let F be a field. Then the polynomial ring F[x] is a UFD.
Proof: We need to show that every non-zero non-unit in F[x] can be written as a product of irreducible polynomials in a manner that is unique up to order and associates.
So let f(x) be a polynomial of degree n ≥ 1 in F[x]. If f(x) is irreducible there is nothing to do. If not then f(x) = g(x)h(x) where g(x) and h(x) both have degree less than n. If g(x) or h(x) is reducible further factorization is possible; the process ends after at most n steps with an expression for f(x) as a product of irreducibles. To see the uniqueness, suppose that
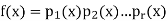 and
and
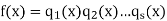
Are two such expressions, with s ≥ r. Then q1(x)q2(x)...qs(x) belongs to the ideal hp1(x)iof F[x]. Since this ideal is prime (as p1(x) is irreducible) this means that either q1(x) ∈hp1(x)ior q2(x)...qs(x) ∈hp1(x)i. Repeating this step leads to the conclusion that at least one of the qi(x) belongs to hp1(x)i. After reordering the qi(x) if necessary we have q1(x) ∈hp1(x)i. Since q1(x) is irreducible this means q1(x) = u1p1(x) for some unit u1. Then
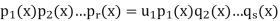
Since F[x] is an integral domain we can cancel p1(x) from both sides to obtain
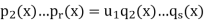
After repeating this step a further r −1 times we have
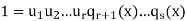
Whereu1,...,ur are units in F[x] (i.e. non-zero elements of F). This means s = r, since the polynomial on the right in the above expression must have degree zero. We conclude that q1(x),...,qs(x) are associates (in some order) of p1(x),...,pr(x). This completes the proof.
Unique Factorization in 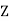 [X] Every polynomial in
[X] Every polynomial in  [X] that is not the zero polynomial or a unit in
[X] that is not the zero polynomial or a unit in 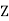 [X] can be written in the form cp1(X)p2(X) ····· pm(X), where c is a constant and the pi(X) ′ s are irreducible polynomials of positive degree. Furthermore, if
[X] can be written in the form cp1(X)p2(X) ····· pm(X), where c is a constant and the pi(X) ′ s are irreducible polynomials of positive degree. Furthermore, if
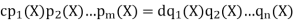
Then c = ±d, n = m, and after renumbering the q(x) ′ s, pi(x) = ±qi(x), for i = 1, 2, . . . , m.
In the above example, c = 2, p1(X) = X − 0, p2(X) = X + 4, and p3(X) = X + 2.
We need not restrict ourselves to polynomials over  . It is common to consider polynomials with coefficients over
. It is common to consider polynomials with coefficients over 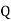 or
or 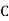 .
.
In our second example, we cannot factor X2 + 1 over Z or Q, but we CAN factor it over C , into 
Let’s consider factorization over Q
Eisenstein’s Irreducibility Criteria (1850) Let 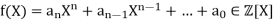 If there is a prime p such that
If there is a prime p such that 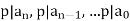 and
and  then f(X) is irreducible over
then f(X) is irreducible over 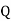 .
.
References:
1. M. Artin, Abstract Algebra, 2nd Ed., Pearson, 2011.
2. Joseph 1. Rotman, An Introduction to the Theory of Groups, 4th Ed., Springer Verlag, 1995.
3. I. N. Herstein, Topics in Algebra, Wiley Eastern Limited, India, 1975.