Unit - 2

Subspaces

2.1 Subspaces

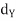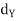Let (X, d) be a metric space and Y a nonempty subset of X. If denotes the restriction of the function d to the set Y Y, then is a metric for Y and (Y, ) is a metric space.

Lemma- Let (X, d) be a metric space and Y a subspace of X. Let z 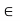 Y and r > 0. Then

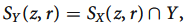
Where 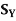(z, r) (respectively 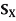(z, r)) denotes the ball with centre z and radius r in Y (respectively X).

Proof:
here we have-

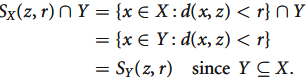
Let and .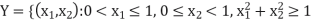

Here the open ball in Y with centre (1, 0) and radius 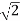is the entire space of Y.

Note-

Let (X, d) be a metric space and Ya subspace of X. Let Z be a subset of Y. Then

(i) Z is open in Y if and only if there exists an open set G 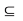X such that

Z = G 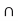Y;

(ii) Z is closed in Y if and only if there exists a closed set F 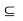X such that

Z = F Y

Proposition: Let Y be a subspace of a metric space (X, d). Every subset of Y that is open in Y is also open in X if and only if Y is open in X.

Proof:
Suppose every subset of Y open in Y is also open in X. We want to show that Y is open in X. Since Y is an open subset of Y, it must be open in X. Conversely, suppose Y is open in X. Let Z be an open subset of Y. By above result (given in note), there exists an open subset G of X such that Z = G 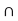Y. Since G and Y are both open subsets of X, their intersection must be open in X, i.e., Z must be open in X.

Proposition- If Y is a nonempty subset of a metric space (X, d), and (Y, d) is complete, then Y is closed in X.

Proof:

Let x be any limit point of Y. Then x is the limit of a sequence 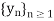in Y. The sequence 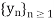is Cauchy, and hence, by assumption, converges to a point y of Y. But following Definition 1.3.2, y = x.

Therefore, x 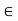Y. This shows that Y is closed in X.

2.2 Countability Axioms and Separability

Def:

Let (X, d) be a metric space and x 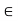X. Let 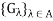be a family of open sets, each containing x. The family  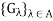 is said to be a local base at x if, for every nonempty open set G containing x, there exists a set 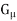in the family 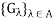such that

Let x 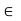R. Consider the family of all open intervals (r,s) containing x and having rational endpoints r and s. This family is a local base at x. It consists of open balls, not necessarily centred at x. Moreover, the family is countable and thus constitutes what is called a countable base at x.

Proposition: In any metric space, there is a countable base at each point.

Proof:

Let (X, d) be a metric space and x 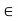X. The family of open balls centred at x and having rational radii, i.e., {S(x, ): 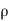rational and positive} is a countable base at x. In fact, if G is an open set and x G, then by the definition of an open set, there exists an 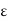> 0 (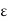 depending on x) such that x S(x, 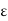) 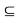G. Let 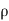be a positive rational number less than 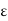. Then

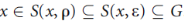
Proposition: The collection {S(x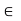, ): x X, 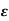> 0} of all open balls in X is a base for the open sets of X.

Proof:

Let G be a nonempty open subset of X and let x 2 G. By the definition of an open subset, there exists a positive e(x) (depending upon x) such that

Which is the proof.

Definition- A metric space is said to be second countable if it has a countable base for its open sets.

Definition- Let (X, d) be a metric space and G be a collection of open sets in X. If for each x 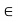X there is a member G 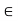G’ such that x 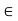G, then G’ is called an open cover (or open covering) of X. A sub-collection of G’ which is itself an open cover of X is called a sub-cover.

Example: The union of the family { . . . , ( -3, -1), (-2, 0), (- 1, 1), (0, 2), . . . } of open intervals is R. The family is therefore an open covering of R. However, the family of open intervals { . . . , (-2, -1), (- 1, 0), (0, 1), (1, 2), . . . } is not an open covering, because the intervals’ union does not contain the integers. The aforementioned cover contains no sub-covering besides itself, because, if we delete any interval from the family, the midpoint of the deleted interval will not belong to the union of the remaining intervals.

Example: Let X be the discrete metric space consisting of the five elements a, b, c, d, e. The union of the family of subsets {{a}, {b, c}, {c, d}, {a, d, e}} is X and all subsets are open. Therefore the family is an open cover. The family {{b, c}, {c, d}, {a, d, e}} is a proper sub-cover.

Note- A metric space is said to be Lindelo¨f if each open covering of X contains a countable sub-covering.

Definition-

A subset 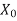of a metric space (X, d) is said to be everywhere dense or simply dense if = X, which means if every point of X is either a point or a limit point of 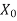. This means that, given any point x of X, there exists a sequence of points of 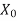that converges to x.

Note- X is always a dense subset of itself; interest centres around what proper subsets of a metric space are dense.

Example: The set of rationals is a dense subset of R and so is the set of irrationals. Note that the former is countable whereas the latter is not.

Definition- The metric space X is said to be separable if there exists a countable, everywhere dense set in X. In other words, X is said to be separable if there exists in X a sequence

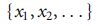
Such that for every x X, some sequence in the range of the above converges to x.

Theorem- Let (X, d) be a metric space and Y 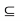X. If X is separable, then Y with the induced metric is separable, too.

Proof:

Let E = {xi : i =  1, 2, . . . } be a countable dense subset of X. If E is contained in Y, then there is nothing to prove. Otherwise, we construct a countable dense subset of Y whose points are arbitrarily close to those of E. For positive integers n and m, let 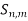=  S(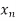, 1/m) and choose  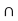Y whenever this set is nonempty. We show that the countable set {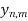: n and m positive integers} of Y is dense in Y.

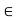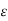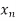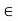
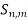
For this purpose, let y Y and > 0. Let m be so large that 1/m < /2 and find  2 S(y, 1/m). Then y  Y and

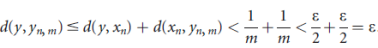
Thus, 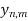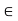S(y, 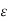). Since y 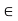Y and 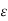> 0 are arbitrary, the assertion is proved.

2.3 Baire’s Category theorem

It is an important theorem in general topology.

Let (X, d) be a metric space. A subset YX is said to be nowhere dense if 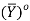is empty, it means 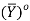has no interior point.

A subset F X is said to be of category I if it is a countable union of nowhere dense subsets. Subsets that are not of category I are said to be of category II.

Notes-

1. A subset Y of X is nowhere dense if and only if the complement 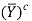is dense in X, or 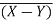=X
2. If d denotes the discrete metric, the only nowhere dense set is the null set.
3. The notion of being nowhere dense is not the opposite of being everywhere dense, i.e., not being nowhere dense does not imply that the set is everywhere dense.
4. Every subset must be either of category I or of category II.
5. Since a denumerable union of denumerable sets is again a denumerable set, it follows that, if Y1, Y2, . . . Are each of category I, then so must be
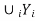
6. A subset of a nowhere dense set is nowhere dense and, therefore, a subset of a set of category I is again of category I.

Definition

A subset A X of a (metric/topological) space is said to be nowhere dense in X, if given any nonempty open set U, we can find a nonempty open subset V 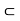U such that A 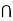v = O.

Baire’s category theorem-

Let (X, d) be a complete metric space.

(1) Let 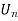, be open dense subsets of X, for n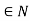. Then 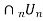is dense in X.

(2) Let 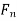, be nonempty closed subsets of X such that X = 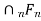Then at least one of 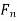's has nonempty interior. In other words, a complete metric space cannot be a countable union of nowhere dense closed subsets.

Proof:

We first observe that both the statements are equivalent. For, G is open and dense if its complement F:= X \ G is closed and nowhere dense. Hence any one of the statements of the theorem follows from the other by taking complements. So, we confine ourselves to proving the first.

Let U:= 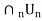. We have to prove that U is dense in X. Let x X and r > 0 be given. We need to show that B(x,r) O. Since U1 is dense and B (x, r) is open there exists x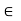 B (x , r) 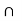U . Since B (x, r) 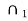is open, there exists r1 such that 0< r1 < 1/2 and B[ x1, r1] 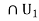  We repeat this argument for the open set B(x i, r 1 ) and the dense set 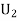to get B[ x1, r1].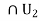

Again we find r2 such that 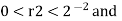B[ x2, 2]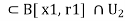

Proceeding this way, for each n  N, we get 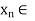X and an 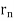, with the properties

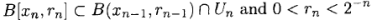
Clearly, the sequence 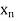is Cauchy: if m 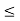n,

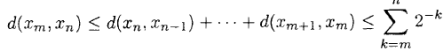
Since 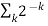is convergent, it follows that () is Cauchy.

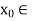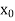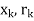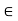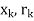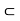Since X is complete, there exists X such that . Since is the limit of the sequence in the closed set B[], we deduce that B[] B[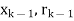] 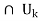for all k. In particular, 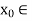B(x, r)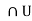

References:

1. S. Kumaresan, Topology of Metric Spaces, Narosa Publishing House, Second Edition 2011
2. Topology of metric spaces, S. Kumarsen, Alpha science international Ltd.
3. Metric spaces, Satish shirali and Harkrishan L. Vasudeva, Springer.

.

.

.