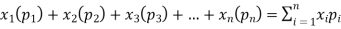Unit - 2
Mathematical Expectation
Expectation:
Let a random variable X has a probability distribution which assumes the values say with their associated probabilities
with their associated probabilities  then the mathematical expectation can be defined as-
then the mathematical expectation can be defined as-

The expected value of a random variable X is written as E(X).
Expected value for a continuous random variable is
Example: If a random variable X has the following probability distribution in tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | ¼ | 1/2 | 1/4 |
Sol.
We know that-

So that-
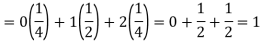
Example: Find the expectations of the number of an unbiased die when thrown.
Sol. Let X be a random variable which represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-
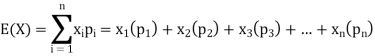
So that-

Key takeaways:
Moment word is very popular in mechanical sciences. In science moment is a measure of energy which generates the frequency. In Statistics, moments are the arithmetic means of first, second, third and so on, i.e. rth power of the deviation taken from either mean or an arbitrary point of a distribution. In other words, moments are statistical measures that give certain characteristics of the distribution. In statistics, some moments are very important. Generally, in any frequency distribution, four moments are obtained which are known as first, second, third and fourth moments. These four moments describe the information about mean, variance, skewness and kurtosis of a frequency distribution. Calculation of oments gives some features of a distribution which are of statistical importance. Moments can be classified in raw and central moment. Raw moments are measured about any arbitrary point A (say). If A is taken to be zero then raw moments are called moments about origin. When A is taken to be Arithmetic mean we get central moments. The first raw moment about origin is mean whereas the first central moment is zero. The second raw and central moments are mean square deviation and variance, respectively. The third and fourth moments are useful in measuring skewness and kurtosis.
Moments-
The rth moment of a variable x about the mean x is usually denoted by is given by
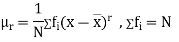
The rth moment of a variable x aboutany point a is defined by
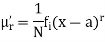

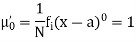

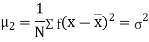
Relation between moments about mean and moment about any point:

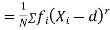 where
where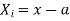 and
and 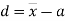


In particular
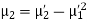
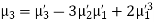
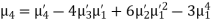
Note. 1. The sum of the coefficients of the various terms on the right‐hand side is zero.
3. The dimension of each term on right‐hand side is the same as that ofterms on the left.
4.
Relationship between moments about mean and moment about any point-

When two variables are related in such a way that change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is correlation between two variables.
Example- Height and weight of the persons of a group.
The correlation is said to be perfect correlation if two variables vary in such a way that their ratio is constant always.
Sheppard’s Corrections for Moments
The fundamental assumption that we make in farming class intervals is that the frequencies are uniformly distributed about the mid points of the class intervals. All the moment calculations in case of grouped frequency distributions rely on this assumption. The aggregate of the observations or their powers in a class is approximated by multiplying the class mid point or its power by the corresponding class frequency.
For distributions that are either symmetrical or close to being symmetrical, this assumption is acceptable. But it is not acceptable for highly skewed distributions or when the class intervals exceed about 1/20th of the range. In such situations, W. F. Sheppard suggested some corrections to be made to get rid of the so called “grouping errors” that enter into the calculation of moments.
Sheppard suggested the following corrections known as Sheppard’s corrections in the calculation of central moments assuming continuous frequency distributions if the frequency tapers off to zero in both directions
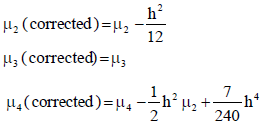
Where, h is the width of class interval.
Chebyshev’s inequality
If X is any random variable then for any b>0 we have
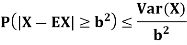
Chebyshev’s inequality states that the difference between X and EX is somehow limited by Var (X). This is intuitively expected as variance shows on average how far we are from the mean.
Example. Let X ~ binomial (n, p). Using Chebyshev's inequality, find an upper bound on P(X ≥n), where  . Evaluate the ground for
. Evaluate the ground for 
Solution.
One way to obtain a bound is to write
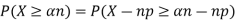
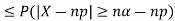

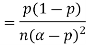
For p = ½ and  , we obtain
, we obtain
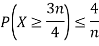
Example. Let X be a random variables such that

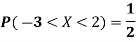
Find a lower bound to its variance.
Solution.
The lower bound can be derived thanks to Chebyshev’s inequality
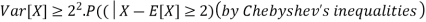

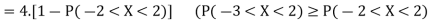
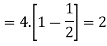
Thus, the lower bound is Var[X]≥2
Example: A individual is selected from a population randomly who has average income of 40,000 dollars with SD 20,000 dollars, what will be the probability of selecting an individual whose income is either less than 10,000 dollars or greater than 70,000 dollars.
Sol.
Here we use Chebyshev inequality to solve such problems.
If X denotes income then X is less than 10,000 dollars or greater than 70,000 dollars only if-
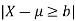
Where  and b = 30,000 the the probability-
and b = 30,000 the the probability-
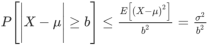
= 400,000,000/900,000,000 = 4/9
Key takeaways:
- The rth moment of a variable x about the mean x is usually denoted by is given by
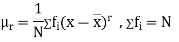
2. If X is any random variable then for any b>0 we have
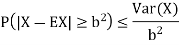
The moment generating function (m.g.f) of the discrete probability distribution of the variate X about the value x = a is defined as the expected value of  is denoted by
is denoted by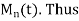
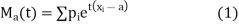
Which is a function of the parameters t only.
Expanding the exponential in (1) we get
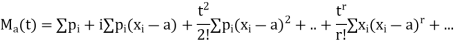

Where 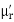 is the moment of order r and a. Thus
is the moment of order r and a. Thus 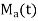 generates moment and that is why it is called the moment generating function. From (2) we find
generates moment and that is why it is called the moment generating function. From (2) we find
 = coefficient of
= coefficient of  In the expansion of
In the expansion of 
Otherwise differentiating (2) r X with respect to t and then putting t = 0, we get
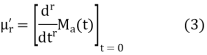
Thus the moment about any point x = a can be found from (2) or more conveniently from the formula (3).
Rewriting (1) as
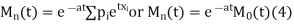
Thus the m.g.f about point 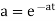 (m.g.f about the origin).
(m.g.f about the origin).
If f(x) is the density function of a continuous variate X then the moment generating function of this continuous probability distribution about x =a is given by
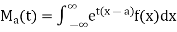
Example. Find the moment generating function of the exponential distribution 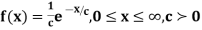 . Hence find its mean and S.D.
. Hence find its mean and S.D.
Solution. The moment generating function about the origin is
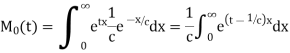

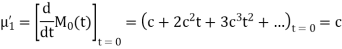
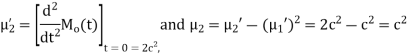
Hence the mean is c wand S.D. Is also c
MGF of linear combinations
If X1,X2,…,Xn are n independent random variables with respective moment generating functions MXi(t)=E(etXi) for i=1,2,…,n, then the moment-generating function of the linear combination:
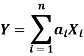
Is
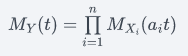
Proof:

The first equality comes from the definition of the moment-generating function of the random variable Y. The second equality comes from the given definition of Y. The third equality comes from the properties of exponents, as well as from the expectation of the product of functions of independent random variables. The fourth equality comes from the definition of the moment-generating function of the random variables Xi, for i=1,2,…,n. And, the fifth equality comes from using product notation to write the product of the moment-generating functions.
While the theorem is useful in its own right, the following corollary is perhaps even more useful when dealing not just with independent random variables, but also random variables that are identically distributed — two characteristics that we get, of course, when we take a random sample.
The conditional expectation (or conditional mean, or conditional expected value) of a random variable is the expected value of the random variable itself, computed with respect to its conditional probability distribution
Definition:
Let X and Y be two random variables. The conditional expectation of X given Y = y is the weighted average of the values that X can take on, where each possible value is weighted by its respective conditional probability (conditional on the information that Y = y
The expectation of a random variable X conditional on Y = y is given by E[X|Y = y]
In the case in which X and Y are two discrete random variables and, considered together, they form a discrete random vector the formula for computing the conditional expectation of X given Y = y is a straightforward implementation of the above informal definition of conditional expectation: the weights of the average are given by the conditional probability mass function of X.
Definition Let X and Y be two discrete random variables. Let  be the support of X and let pX|Y-y(X) be the conditional probability mass function of X given Y = y. The conditional expectation of X given Y = y is
be the support of X and let pX|Y-y(X) be the conditional probability mass function of X given Y = y. The conditional expectation of X given Y = y is

Provided that

Example: Let the support of the random vector [X, Y] be
 and its joint probability mass function be
and its joint probability mass function be
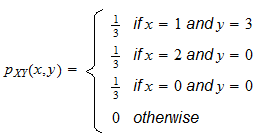
Let us compute the conditional probability mass function of X given Y = 0. The marginal probability mass function of Y evaluated at Y = 0 is
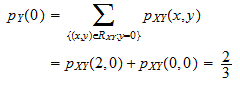
The support of X is,
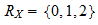
Thus, the conditional probability mass function of X given Y = 0 is

The conditional expectation of X given Y = 0 is
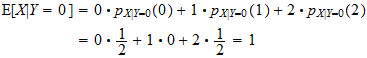
Professor Bowley defines the average as-
“Statistical constants which enable us to comprehend in a single effort the significance of the whole”
An average is a single value that is the best representative for a given data set.
Measures of central tendency show the tendency of some central values around which data tend to cluster.
The following are the various measures of central tendency-
1. Arithmetic mean
2. Median
3. Mode
4. Weighted mean
5. Geometric mean
6. Harmonic mean
The arithmetic mean or mean-
The arithmetic mean is a value which is the sum of all observation divided by a total number of observations of the given data set.
If there are n numbers in a dataset- 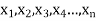 then the arithmetic mean will be-
then the arithmetic mean will be-
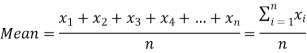
If the numbers along with frequencies are given then mean can be defined as-
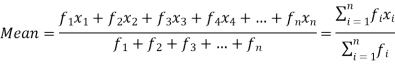
Example-1: Find the mean of 26, 15, 29, 36, 35, 30, 14, 21, 25.
Sol.
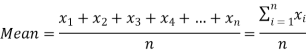

Example-2: Find the mean of the following dataset.
x | 20 | 30 | 40 |
f | 5 | 6 | 4 |
Sol.
We have the following table-
X | F | Fx |
20 | 5 | 100 |
30 | 6 | 180 |
40 | 7 | 160 |
| Sum = 15 | Sum = 440 |
Then Mean will be-


Short cut method
Let a be the assumed mean, d the deviation of the variate x from a. Then

Example1. Find the arithmetic mean for the following distribution:
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
Solution. Let assumed mean (a) = 25
Class | Mid value  | Frequency | 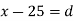 | 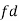 |
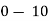 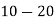  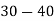 40— 50 |  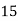 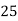 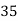 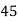 |  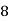  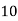 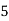 |  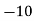  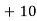  | 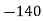  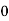   |
Total |
|  |
| 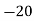 |

(c) Step deviation method
Let  be the assumed mean,
be the assumed mean,  the width ofthe class interval and
the width ofthe class interval and

Example 2. Find the arithmetic mean of the data given in example by step deviation method
Solution. Let 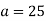
Class | Mid‐value  | Frequency  | 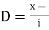 | 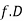 |
  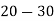 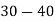  |     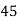 | 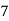  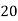  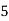 |      | 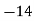   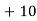  |
Total |
| 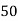 |
| 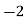 |

Median-
Median is the mid-value of the given data when it is arranged in ascending or descending order.
1. If the total number of values in the data set is odd then the median is the value of 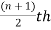 item.
item.
Note-The data should be arranged in ascending r descending order
2. If the total number of values in the data set is even then the median is the mean of the  item.
item.
Example: Find the median of the data given below-
7, 8, 9, 3, 4, 10
Sol.
Arrange the data in ascending order-
3, 4, 7, 8, 9, 10
So there total 6 (even) observations, then-

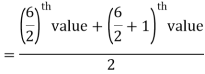

Median for grouped data-
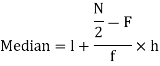
Here,
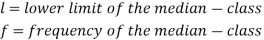
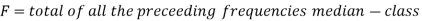


Example: Find the median of the following dataset-

Sol.
Class interval | Frequency | Cumulative frequency |
0 - 10 | 3 | 3 |
10 – 20 | 5 | 8 |
20 – 30 | 7 | 15 |
30 – 40 | 9 | 24 |
40 – 50 | 4 | 28 |

So that median class is 20-30.
Now putting the values in the formula-
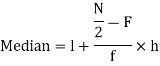
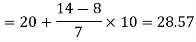
So that the median is 28.57
Example: Find the value of Median from the following data:
No. Of days for which absent (less than) |  |  |  | 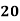 | 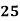 | 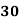 | 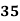 | 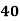 |  |
No. Of students |  | 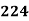 |  | 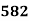 | 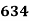 |  |  |  | 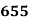 |
Solution. The given cumulative frequency distribution will first be converted into ordinary frequency as under
Class Interval | Cumulative frequency | Ordinary frequency |
0-5 5-10 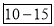 15-20 20-25 25-35 30-35 35-40 40-45 | 29 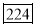 465 582 634 644 650 653 655 | 29=29 224-29=195 465-224=  582-465=117 634-582=52 644-634=10 650-644=6 653-650=3 655-653=2 |
Median  size of
size of or 327.
or 327. Item
Item
327.  Item lies in 10‐15 which is the median class.
Item lies in 10‐15 which is the median class.
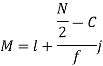
Where stands for the lower limit of the median class,
stands for the lower limit of the median class,
 stands for the total frequency,
stands for the total frequency,
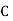 stands for the cumulative frequency just preceding the median class,
stands for the cumulative frequency just preceding the median class,  stands for class interval
stands for class interval
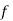 stands for frequency for the median class.
stands for frequency for the median class.
Median 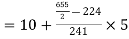
Mode-
A value in the data which is most frequent is known as mode.
Example: Find the mode of the following data points-
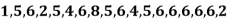
Sol. Here 6 has the highest frequency so that the mode is 6.
Mode for grouped data-
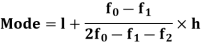
Here,
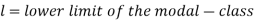
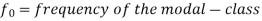



Example: Find the mode of the following dataset-

Sol.
Class interval | Frequency |
0 - 10 | 3 |
10 – 20 | 5 |
20 – 30 | 7 |
30 – 40 | 9 |
40 – 50 | 4 |
Here the highest frequency is 9. So that the modal class is 40-50,
Put the values in the given data-
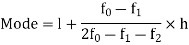

Hence the mode is 42.86
Example: Find the mode from the following data:
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
Solution.
Age | Frequency | Cumulative frequency |
0-6 6-12 12-18 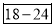 24-30 30-36 36-42 | 6 11 25 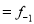 35   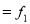 12 6 | 6 17 42 77 95 107 113 |
Mode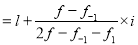
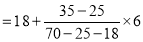

GEOMETRIC MEAN
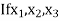 , ,
, ,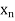 be
be 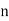 values of variates
values of variates 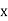 , then the geometric mean
, then the geometric mean
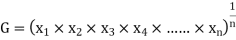
Example 7. Find the geometric mean of 4, 8, 16.
Solution. .
.
HARMONIC MEAN
The harmonic mean of a series of values is defined as the reciprocal of the arithmetic mean of their reciprocals. Thus 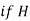 be the harmonic mean, then
be the harmonic mean, then

Example 8: Calculate the harmonic mean of 4, 8, 16.
Solution:
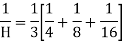

Measures of dispersion
According to Spiegel-
“The degree to which numerical data tend to spread about an average value is called the variation or dispersion of data”
The different measures of dispersion are-
1. Range
2. Quartile deviation
3. Mean deviation
4. Standard deviation
5. Variance
Range-
This is one of the simplest measures of dispersion. The difference between the maximum and minimum value of the dataset is known as the range.
Range = Max. Value – Min. Value
Example- Find the range of the data- 8, 5, 6, 4, 7, 10, 12, 15, 25, 30
Sol. Here the maximum value is 30 and the minimum value is 4 so that the range is-
30 – 4 = 26
Coefficient of range-
The coefficient of range can be calculated as follows-
Coefficient of Range = 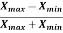
Quartile deviation-


Example- Find the quartile deviation of the following data-
Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 3 | 5 | 7 | 9 | 4 |
Sol.
Here N/4 = 28/4 = 7 so that the 7’th observation falls in class 10 – 20.
And
3N/4 = 21, and 21’st observation falls in the interval 30 – 40 which is the third quartile.
The quartiles can be calculated as below-
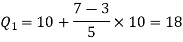
And

Hence the quartile deviation is-

Mean deviation-
The mean deviation can be defined as-
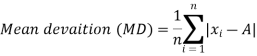
Here A is assumed mean.
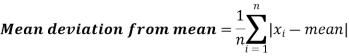
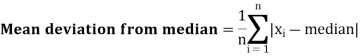
Example: Find the mean deviation from the mean of the following data-
Class interval | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
Sol.
Class interval | Mid-value | Frequency | d = x – a | f.d | |x - 14| | f |x - 14| |
0-6 | 3 | 8 | -12 | -96 | 11 | 88 |
6-12 | 9 | 10 | -6 | -60 | 5 | 50 |
12-18 | 15 | 12 | 0 | 0 | 1 | 12 |
18-24 | 21 | 9 | 6 | 54 | 7 | 63 |
24-30 | 27 | 5 | 12 | 60 | 13 | 65 |
Total |
| 44 |
| -42 |
| 278 |
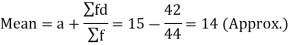
Then mean deviation from mean-
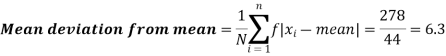
Standard deviation:
It is defined as the positive square root of the arithmetic mean of the square of the deviation of the given values from their arithmetic mean. It is denoted by the symbol 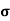 .
.

Where  is A.M of the distribution
is A.M of the distribution 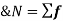 . We have more formulae to calculate the standard deviation.
. We have more formulae to calculate the standard deviation.


 ….
…. 
In frequency distribution from, we put 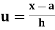 where H is generally taken as width of class interval
where H is generally taken as width of class interval
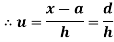
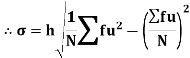
Shortcut formula to calculate standard deviation-
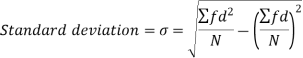
The square of the standard deviation is called known as a variance.
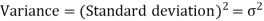
Example-1: Compute the variance and standard deviation.
Class | Frequency |
0-10 | 3 |
10-20 | 5 |
20-30 | 7 |
30-40 | 9 |
40-50 | 4 |
Sol.
Class | Mid-value (x) | Frequency (f) | 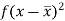 |
0-10 | 5 | 3 | 1470.924 |
10-20 | 15 | 5 | 737.250 |
20-30 | 25 | 7 | 32.1441 |
30-40 | 35 | 9 | 555.606 |
40-50 | 45 | 4 | 1275.504 |
Sum |
| 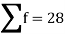 | 4071.428 |
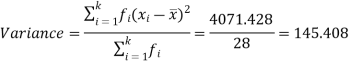
Then standard deviation,
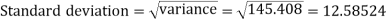
Example-2: Calculate the standard deviation of the following frequency distribution-
Weight | 60 – 62 | 63 – 65 | 66 – 68 | 69 – 71 | 72 – 74 |
Item | 5 | 18 | 42 | 27 | 8 |
Sol.
Weight | Item (f) | X | d = x – 67 | f.d |  |
60 – 62 | 5 | 61 | -6 | -30 | 180 |
63 – 65 | 18 | 64 | -3 | -54 | 162 |
66 – 68 | 42 | 67 | 0 | 0 | 0 |
69 – 71 | 27 | 70 | 3 | 81 | 243 |
72 – 74 | 8 | 73 | 6 | 48 | 288 |
Total |
100 |
|
|
45 |
873 |
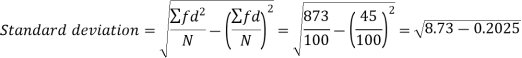
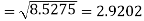
Example: Calculate S.D for the following distribution.
Wages in rupees earned per day | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
No. Of Labourers | 5 | 9 | 15 | 12 | 10 | 3 |
Solution:
Wages earned C.I | Mid value 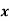 | Frequency |  |  | 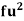 |
52 | 5 | 5 | -2 | -10 | 20 |
153 | 15 | 9 | -1 | -9 | 9 |
25 | 25 | 15 | 0 | 0 | 0 |
35 | 35 | 12 | 1 | 12 | 12 |
45 | 45 | 10 | 2 | 20 | 40 |
55 | 55 | 3 | 3 | 9 | 27 |
Total | - | 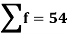 | 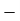 | 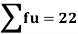 |  |
Using formula,

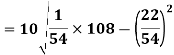
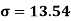
Key takeaways-

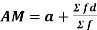
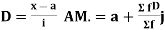
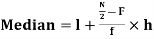

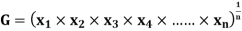
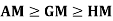

- Mean – Mode = [Mean - Median]
- Range = Max. Value – Min. Value
- Coefficient of Range =






16. 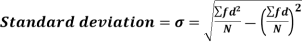
References:
1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
2. P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
4. W. Feller, “An Introduction to Probability Theory and its Applications”, Vol. 1, Wiley, 1968.
5. N.P. Bali and M. Goyal, “A text book of Engineering Mathematics”, Laxmi Publications, 2010.
6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
7. T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010.
8. BV ramana mathematics.