Unit - 1
Complex Numbers and Complex plane
1.1.1 Complex Numbers:
Overview:
The sum of a real and an imaginary number is a complex number. A complex number is denoted by the letter z and has the form a + ib. Both a and b are genuine numbers in this case. The value 'a' is known as the real component and is indicated by Re(z), while 'b' is known as the imaginary part and is denoted by Im (z). Ib is also known as an imaginary number.
Some of the examples of complex numbers are- 2 + 3i, -2+i, ½ + 1/5i.
Definition:
A complex number takes the form z = x + iywhere x and y are real,and iis an imaginary number that satisfies 
We call x and y the real part and the imaginary part of z, respectively, and we write
x = Re(z) and y = Im(z).
The real numbers are precisely those complex numbers with zero imaginaryparts. A complex number with zero real part is said to be purelyimaginary.
Throughout our presentation, the set of all complex numbers is denotedby C. The complex numbers can be visualized as the usual Euclideanplane by the following simple identification: the complex numberz = x + iy∈C is identified with the point (x, y) ∈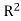
. For example, 0corresponds to the origin and icorresponds to (0, 1). Naturally, the xand y axis of R2 are called the real axis and imaginary axis, becausethey correspond to the real and purely imaginary numbers, respectively.
Power of i
The letter I often known as the iota, is used to denote the imaginary component of a complex number. Additionally, the iota(i) can be used to find the square root of negative values. We have the value of i2 = -1, and this is used to find the value of √-4 = √i24 = +2i The value of i2 = 1 is the fundamental aspect of a complex number. Let us try and understand more about the increasing powers of i.
- i = √-1
- i2 = - 1
- i3 = i.i2 = i(-1) = -i
- i4 = (i2)2 = (-1)2 = 1
- i4n = 1
- i4n+1 = i
- i4n+2 = -1
- i4n+3 = -i
Graphing of Complex Numbers
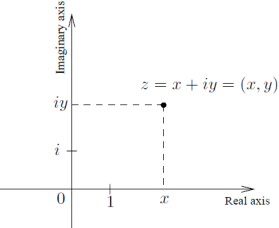
The real and imaginary parts of a complex number can be thought of as an ordered pair (Re(z), Im(z)) and can be represented as coordinate points in the euclidean plane. The complex plane, or Argand Plane, is the euclidean plane with regard to complex numbers, named after Jean-Robert Argand. The real part - a, with reference to the x-axis, and the imaginary part - ib, with reference to the y-axis, are used to depict the complex number z = a + ib. Let's try to grasp the meaning of two key words related to the argand plane representation of complex numbers. The argument and modulus of a complex number.
Modulus of the Complex Number: The modulus of a complex number is the distance between a point in the argand plane (a, ib) and the complex number. This distance is defined as r = |a2+b2a2+b2| and is measured from the origin (0, 0) to the point (a, ib). Furthermore, this may be deduced from Pythagoras' theorem, in which the hypotenuse is represented by the modulus, the real component is the base, and the imaginary part is the altitude of the right-angled triangle.
Argument of the Complex Number: The argument of the complex number is the anticlockwise angle formed by the line connecting the geometric representation of the complex number and the origin, with the positive x-axis. The inverse of the tan of the imaginary component divided by the real part of the complex number is the argument of the complex number.
Argz (θ) = Tan-1 
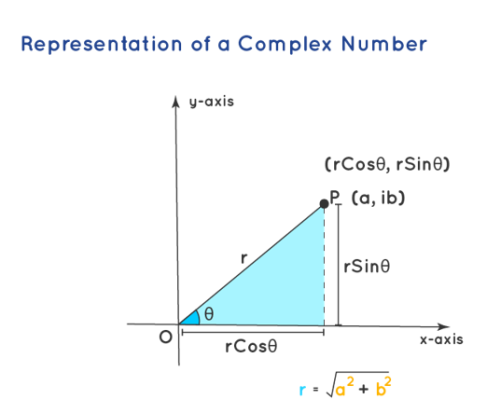
Polar Representation of a Complex Number: With the modulus and argument of a complex number and the representation of the complex number in the argand plane, we have a new form of representation of the complex number, called the polar form of a complex number. The complex number z = a + ib, can be represented in polar form as z = r(Cosθ + iSinθ). Here r is the modulus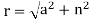
, and θ is the argument of the complex number
(θ = Tan-1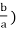 
Properties of Complex Numbers
The following properties of complex numbers are helpful to better understand complex numbers and also to perform the various arithmetic operations on complex numbers.
Conjugate of a Complex Number: By taking the identical real component of the complex number and altering the imaginary part of the complex number to its additive inverse, the conjugate of the complex number is generated. Conjugate complex numbers are those in which the sum and product of two complex numbers are both real numbers. For a complex number z = a + ib, its conjugate is ¯zz¯ = a - ib.
The sum of the complex number and its conjugate is z+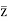
= ( a + ib) + (a - ib) = 2a, and the product of these complex numbers z.
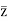= (a + ib) × (a - ib) = a2 + b2.
Reciprocal of a complex Number: In the process of dividing one complex number by another, the reciprocal of complex numbers comes in handy. The product of one complex number with the reciprocal of another complex number is the process of division of complex numbers. The reciprocal of the complex number z = a + ib is
Z-1 = 
This also shows that z≠z−1.
Equality of Complex Numbers: Complex numbers are equal in the same way that real numbers are equal. When the real parts of two complex numbers z1=a1+ib1 and z2=a2+ib2 are equal, a1=a2, and the imaginary parts of both complex numbers are equal, b1=b2, they are said to be equal. Also, in the polar form, two complex numbers are equal if and only if they have the same magnitude and their argument (angle) differs by an integral multiple of the magnitude 2π.
Ordering of Complex Numbers: It is impossible to organise complex numbers. Complex numbers, unlike real numbers and other related number systems, cannot be sorted. There is no ordering of complex numbers that is compatible with addition and multiplication, thus they do not have the structure of an ordered field. In an ordered field, the non-trivial sum of squares is 0; however, in a complex integer, the non-trivial sum of squares is i2 + 12 = 0. The magnitude of complex numbers, which is their distance from the origin, can be measured and represented in a two-dimensional argrand plane.
Euler's Formula: As per euler's formula for any real value θ we have eiθ = Cosθ + iSinθ, and it represented the complex number in the coordinate plane where Cosθ is the real part and is represented with respect to the x-axis, Sinθ is the imaginary part that is represented with respect to the y-axis, θ is the angle made with respect to the x-axis and the imaginary line, which is connecting the origin and the complex number. As per Euler's formula and for the functional representation of x and y we have ex + iy = ex(cosy + isiny) = excosy + iexSiny. This decomposes the exponential function into its real and imaginary parts.
Operations on Complex Numbers
The addition, subtraction, multiplication, and division operations that can be done on natural numbers may likewise be performed on complex numbers. The following are the details of the various arithmetic operations on complex numbers.
Addition: Complete numbers are added in the same way as natural numbers are added. The real part is added to the real part, while the imaginary part is added to the imaginary part in complex numbers. The sum of complex numbers z1+z2=(a+c)+i(b+d) given two complex numbers of the form z1=a+id and z2=c+id. All of the properties of addition apply to complex numbers.
• The sum of two complex numbers is also a complex number, according to the Closure Law. The sum of two complex numbers, z1 and z2, is also a complex number.
• Commutative Law: We have z1+z2=z2+z1 for two complex integers z1, z2.
• Associative Law: We have z1+(z2+z3)=(z1+z2)+z3 for the three complex numbers z1,z2,z3.
• Additive Identity: There exists 0 = 0 + i0 for a complex integer z = a + ib, such that z + 0 = 0 + z = 0.
• Additive Inverse: There is a complex number -z = -a -ib such that z + (-z) = (-z) + z = 0 for the complex number z = a + ib. The additive inverse is -z in this case.
Subtraction: The subtraction of complex numbers follows a similar process of subtraction of natural numbers. Here for any two complex numbers, the subtraction is separately performed across the real part and then the subtraction is performed across the imaginary part. For the complex numbers z1 = a + ib, z2=c+id, we have z1−z2 = (a - c) + i(b - d)
Multiplication: Multiplication of complex numbers differs from multiplication of natural numbers in a few ways. We must utilise the formula i2=1 in this case. The product is z1.z2 = (ca - bd) + i(ad + bc) for the two complex numbers z1 = a + ib, z2 = c + id.
The polar form of multiplication for complex numbers differs slightly from the above-mentioned form of multiplication. To get the product of the complex numbers, multiply the absolute values of the two complex numbers and add their arguments.
For the complex numbers z1=r1(Cosθ1+iSinθ1), and z2 = z2=r1(Cosθ2+iSinθ2), the product of the complex numbers is z1.z2=r1.r2(Cos(θ1+θ2)+iSin(θ1+θ2)).
Division: The division of complex numbers makes use of the formula of reciprocal of a complex number. For the two complex numbers z1 = a + ib, z2 = c + id, we have the division as z1z2=(a+ib)×1(c+id)=(a+ib)×(c−id)(c2+d2).
Algebraic Identities of Complex Numbers
For complex numbers, all algebraic identities hold true. Using algebraic identities of complex numbers, the addition and subtraction of complex numbers with exponents of 2 or 3 can be easily solved.
- (z1 +z2)2 = z12+ 2z1z2 + z22
- (z1 -z2)2 = z12- 2z1z2 + z22
- (z1 +z2)3 = z13+ 3z12 z2 + 3z22 z1 + z32
- (z1 -z2)3 = z13- 3z12 z2 + 3z22 z1 - z32
- (z1 +z2) (z1 -z2) = z12 - z22
- (z1 +z2+z3)2 = z12+ z22 + z32+ 2z1z2+ 2z2z3+ 2z3z1
Complex numbers are points in the plane endowed with additional structure. We consider the set R2 = {(x, y): x, yR}, i.e., the set of ordered pairs of real numbers. Two such pairs are equal if their corresponding components coincide:
(x1, y1) = (x2, y2) iff x1 = x2 and y1 = y2.
With two operations - addition and multiplication - defined below, the set R2 becomes the set C of complex numbers. R2 considered as a set of complex numbers C is called Argand diagram or Argand plane or Gauss plane.
Addition
(x1, y1) + (x2, y2) = (x1 + x2, y1 + y2).
Multiplication
(x1, y1)(x2, y2) = (x1x2 - y1y2, x1y2 + x2y1).
Addition is defined componentwise in a relatively standard way that extends to spaces of higher dimension. Multiplication on the other hand is peculiar to complex numbers. It only has weakened analogues in R4 (quaternions) and R8 (octonions).
Addition and multiplication of complex numbers inherit most of the properties of addition and multiplication of real numbers:
z + w = w + z and zw = wz (Commutativity),
z + (u + v) = (z + u) + v and z(uv) = (zu)v (Associativity),
z(u + v) = zu + zv (Distributive Law).
Several complex numbers play exclusive roles. For example, the number (0, 0) has the properties of 0:
(x, y) + (0, 0) = (x, y) and
(x, y)(0, 0) = (0, 0).
As a result, it's only logical to associate it with the number 0. The sign is the same as the one used to denote the "true" zero. We'll see why it's a good idea to think of the two zeros - real and complex - as one and the same number in a moment.
Another complicated number of outcomes is (1, 0). Because of the following feature, this number plays a significant role in multiplication:
(x, y)(1, 0) = (x·1 - y·0, x·0 + y·1)
= (x, y).
Among complex numbers (1, 0) behaves like the real unit 1 among the real numbers. Again, there is a good reason to say that the two are one and the same. It is customary to write (1, 0) = 1.
The third number of importance is (0, 1). It has the remarkable feature of having a negative square. More accurately,
(0, 1)(0, 1) = (0·0 - 1·1, 0·1 + 1·0)
= (-1, 0).
In engineering sciences, the number (0, 1) is sometimes denoted as j. Elsewhere, it is standard to denote it i: i = (0, 1). Multiplication by i has a curious effect:
(x, y)(0, 1) = (x·0 - y·1, x·1 + y·0)
= (-y, x).
When you compare two points in the plane (x, y) and (y, -x) and join them to the origin (even if for only a few specific values of a and y), you'll see that the two segments are perpendicular to each other. Furthermore, the latter is obtained by rotating the former by 90 degrees in a positive (counterclockwise) direction.
Landau, for example, constructed the idea of complex numbers entirely in algebraic terms. Drawing from geometric intuition is often quite useful, both on an elementary and sophisticated level. Points on the horizontal x-axis are represented by numbers (x, 0). The points on the horizontal number line would be connected with plain real numbers if the y-axis was not present. A real value x would be assigned to the position corresponding to (x, 0). As a result, it's only logical to distinguish between the two representations of the same point:
(1) x = (x, 0).
Note that previously we already did this for x = 0 and x = 1. The identification (1) is also supported algebraically. For, algebraically, x and (x, 0) are indistinguishable:
(x1, 0) + (x2, 0) = (x1 + x2, 0) and
(x1, 0)(x2, 0) = (x1x2, 0),
As if the second component (0) was not present. With (1) in mind, we can write
(x, y) = (x, 0) + (0, y)
= (x, 0) + (y, 0)(0, 1)
= x + yi,
Which is called the algebraic form of complex number (x, y):
x + yi = (x, y).
With (1), we easily multiply complex numbers by real:
r(x, y) = (r, 0)(x, y) = (rx, ry),naturally. Of fact, this adds nothing new to the equation except for the convenience of notations. Addition and multiplication are redefined in algebraic form as
(x1 + y1i) + (x2 + y2i) = (x1 + x2) + (y1 + y2)i and
(x1 + y1i)(x2 + y2i) = (x1x2 - y1y2) + (x1y2 + x2y1)i.
Without (1), i2 would for ever remain (-1, 0). Taking (1) into account we obtain the famous identity
(2) i2 = (0, 1)2 = (-1, 0) = -1.
The idea of embedding the real-number set R into the complex-number set C is possibly the most important property of complex numbers, as stated by (1). Because the theory of complex numbers would not be complete without (1) and (2), the branch of algebra that drove much of its development, namely the search for the roots of polynomial equations, would be incomplete.
The two parts of the complex number z = x + yi have special notations:
x = Re(z), y = Im(z).
Both real and imaginary parts of a complex number are real and any complex number can be written as
z = Re(z) + i·Im(z).
Real and Imaginary are represented by the mnemonics Re and Im. Neither of them is less genuine or more fantastical than the other. The axes are also referred to as real and imaginary on the complex plane, despite the fact that they are both real enough that the only way to tell them apart is through rotation: the rotation from the real to the imaginary axis is counterclockwise. Complex numbers with no real portion, i.e. numbers in the form yi for some real y, are referred to be totally imaginary.
We connect another complex number (x - yi) with every complex number (x + yi), which is known as its conjugate. The conjugate of the number z is most commonly represented by a bar above it, occasionally by an asterisk to the right of it, rarely by an apostrophe, and even less frequently by the simple symbol Conj as in
Conj(z) = z* = z' = z.
For technical reasons, I prefer using the least common notations, z' or Conj(z):
Conj(x + yi) = (x + yi)' = x - yi.
The importance of the conjugate stems from the following fact:
(x + yi)(x + yi)' = (x + yi)(x - yi) = x2 + y2,
Which is a non-negative real number for every complex number z = x + yi. The modulus or absolute value of the complex number z is the non-negative square root of this number:
(m) |x + yi| = √x² + y²
The distance between the point represented by z (or the point with complex coordinate z and real coordinates (x, y)) and the origin 0, according to the Pythagorean theorem, is |z|. The distance between points z and u is defined as |z - u| in general.
The identity operator is the square of the operator Conj, which is an involution:
Conj(Conj(z)) = z'' = z
And therefore
|z|2 = z·z' = |z'|2.
Also
(zw)' = z'·w',
It is easily verifiable by direct means. The concept of modulus is the same as the definition of absolute value in real numbers:
|(x, 0)| = |x|.
In addition, it has several important properties:
(m1) |z| ≥ 0, |z| = 0 iff z = 0.
(m2) |zw| = |z|·|w|.
(m3) |z + w| ≤ |z| + |w|.
The triangle inequality is the name for the latter. It's a Euclidean feature in terms of geometry. It may be found using the Argand diagram, which involves matching complex numbers to points in a plane using a triangle inequality valid in the Euclidean plane. It's also possible to deduce it algebraically. As a result of the definition, (m1) follows. (m2) is a result of the fundamental rules.
|zw|2 = (zw)·(zw)’
= z·w·z’·w’
= [z·z’]·[w·w’]
= |z|2·|w|2
= (|z|·|w|)2.
In particular, for a real r > 0, |rz| = r|z|, for any complex z.
The equation of the unit circle centred at the origin is |z| = 1 since |z| is the distance to the origin. Points on the unit circle are associated with an angle such that they and only those points have the form (cos, sin) for some angle that is not uniquely specified. The points on the unit circle have the form as a complex number.
z = cos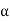
+ i·sin
.
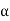For any z ≠ 0, |z/|z|| = 1 which means that z/|z| lies on the unit circle and therefore has the above form for some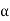 
. If we denote |z| = r, then z can be written as
(3) z = r(cos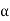
+ i·sin
),
Which is known as the trigonometric form of complex number, its polar representation.
If z ≠ 0 and 
1 and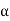 
2 satisfy (3), then they differ by a factor of 2
:
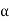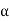1 -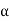 
2 = k·2
,
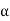Where k an integer. In other words,
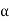1 = 
2 (mod 2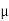
).
There is a unique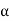 
[0, 2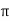
), which denotes a half-open interval from 0 to 2
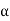in which 0 is included but 2
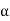is not. This 
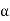is called the argument of z denoted arg(z):
z = |z|·(cos(arg(z)) + i·sin(arg(z))),
Where arg(z) [0, 2
). Zero is not assigned an argument. Thus the argument of a complex number is a real number in a limited interval. The extended argument Arg(z) of a number z is the set of all real numbers congruent to arg(z) modulo 2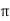
:
Arg(z) = {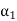
: 
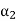= arg(z) (mod 2
))}
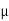= {arg(z) + k·2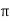
: kN}.
So that
z = |z|·(cos(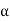
) + i·sin(
)), for any 
Arg(z).
Obviously, the number i = (0, 1) plays a special role in the theory of complex numbers. From the properties of sine and cosine, arg(i) = /2. Furthermore,
i·(x, y) = (0, 1)·(x, y)
= (0·x - 1·y, 0·y + 1·x)
= (-y, x).
Treated as two vectors, (x, y) and (-y, x) are immediately seen to be orthogonal, with the latter obtained from the former by a rotation through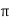 
/2 in the positive direction.
NUMERICALS:
1) Express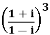 
in the form A + iB where A and B are real numbers.
Solution:
Given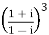 
Now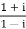 
= 
= 
= 
= 
= 
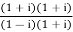
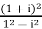
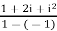
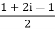
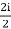
= i
Therefore,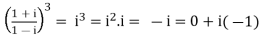
which is the required form A + iB where A = 0 and B = -1.
2) Find the modulus of the complex quantity (2 - 3i)(-1 + 7i).
Solution:
The given complex quantity is (2 - 3i)(-1 + 7i)
Let z1 = 2 - 3i and z2 = -1 + 7i
Therefore, |z1| =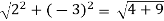 
= 
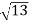
And |z2| =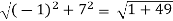 
= 
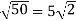
Therefore, the required modulus of the given complex quantity = |z1z1| = |z1| |z1| =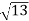 
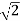. 5
= 5
1.1.2 The complex plane
The geometry of complex numbers
We can depict complex numbers as points in the xy-plane because the complex number z = x + iy is described by two quantities, x and y. The complicated plane is what we call it when we do this. The x-axis is referred to as the real axis since x is the real part of z. Similarly, the imaginary axis is the y-axis.
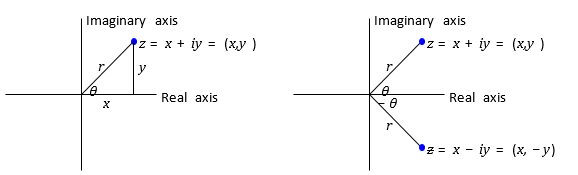
The triangle inequality
The triangle inequality states that the sum of any two legs' lengths is greater than the length of the third leg in a triangle.
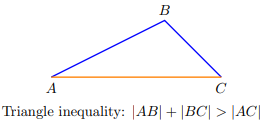
Triangle inequality: |AB| + |BC| > |AC|
The triangle inequality is a statement about complex magnitudes for complex numbers. Precisely: for complex numbers z1, z2
|z1| + |z2|≥|z1 + z2|
With equality only if one of them is 0 or if arg(z1) = arg(z2). This is illustrated in the following figure.
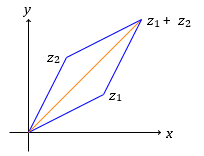
Triangle inequality: |z1| + |z2|≥|z1 + z2|
We get equality only if z1 and z2 are on the same ray from the origin, i.e. they have the same argument.
1.1.3 Radius of convergence in complex analysis:
By changing the argument of a power series with a positive radius of convergence to a complex variable, it can be transformed into a holomorphic function. The following theorem can be used to define the radius of convergence:
The distance from a to the nearest point where cannot be specified in a fashion that makes it holomorphic is equal to the radius of convergence of a power series centred on a point a.
The disc of convergence is the collection of all points whose distance from an is strictly less than the radius of convergence.
Even if the centre and all coefficients are real, the nearest point is in the complex plane, not necessarily on the real line. For instance, consider the function
f(z) =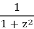 
Has no singularities on the real line, since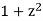 
has no real roots. Its Taylor series about 0 is given by
The root test shows that its radius of convergence is 1. In accordance with this, the function ƒ(z) has singularities at ±i, which are at a distance 1 from 0.
A simple example
The arctangent function of trigonometry can be expanded in a power series:
Arctan(z) = z - 
It is easy to apply the root test in this case to find that the radius of convergence is 1.
A more complicated example
Consider this power series:
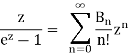
Where the numbers are reasonable The Bernoulli numbers are Bn. Using the ratio test to determine the radius of convergence of this series could be time consuming. However, the above-mentioned complex analysis theorem immediately solves the problem. Because the singularity is detachable, there is no singularity at z = 0. As a result, the only non-removable singularities are found at the sites where the denominator is zero. We find solutions to problems.
ez – 1 = 0
By recalling that if z = x + iy and e iy = cos(y) + i sin(y) then
ez = ex eiy = ex ( cos (y) + i sin(y)),
And then take x and y to be real. Since y is real, the absolute value of cos(y) + i sin(y) is necessarily 1. Therefore, the absolute value of e z can be 1 only if e x is 1; since x is real, that happens only if x = 0. Therefore z is pure imaginary and cos(y) + i sin(y) = 1. Since y is real, that happens only if cos(y) = 1 and sin(y) = 0, so that y is an integer multiple of 2π. Consequently the singular points of this function occur atz = a nonzero integer multiple of 2πi.
The singularities nearest 0, which is the center of the power series expansion, are at ±2πi. The distance from the center to either of those points is 2π, so the radius of convergence is 2π.
Numerical:
(i) Let un =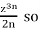 
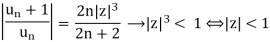
So R = 1
(ii) Let vn = (2n + i)(z – i)n so
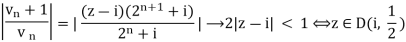
So R=1/2
(iii) Let ωn = zn! so
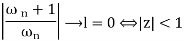
So R = 1
Key takeaways:
- A complex number is one that may be written as a+bi a + b I with a and b being real numbers and I being the imaginary unit.
- The real number an is known as the real portion of the complex number z=a+bi z = a + b I and it is written as Rea+bi=a Re a + b I = a.
1.2.1 Continuous functions
If there are no abrupt jumps in a function, it is said to be continuous. This is the gist of the definition that follows.
Definition.If the function f(z) is defined on an open disk around z0 and limf(z) = f(z0)z→z0then we say f is continuous at z0. If f is defined on an open region Athen the phrase ‘f is continuous on A’ means that f is continuous at every point in A.
As usual, we can rephrase this in terms of functions of (x,y):
Fact. f(z) = u(x,y) + iv(x,y) is continuous iffu(x,y) and v(x,y) are continuous as functions of two variables.
Example. (Some continuous functions)
(i) A polynomial
P(z) = a0 + a1z + a2z2 + ... + anzn
Is continuous on the entire plane. Reason: it is clear that each power (x+iy)kis continuous as a function of (x,y).
(ii) The exponential function is continuous on the entire plane. Reason:
ez= ex+iy= ex cos(y) + iexsin(y).
So the both the real and imaginary parts are clearly continuous as a function of (x,y).
(iii) The principal branch Arg(z) is continuous on the plane minus the non-positive real axis. Reason: this is clear and is the reason we defined branch cuts for arg. We have to remove the negative real axis because Arg(z) jumps by 2π when you cross it. We also have to remove z = 0 because Arg(z) is not even defined at 0.
(iv) The principal branch of the function log(z) is continuous on the plane minus the nonpositive real axis. Reason: the principal branch of log has
Log(z) = log(r) + iArg(z).
So the continuity of log(z) follows from the continuity of Arg(z).
Properties of continuous functions
We have the following qualities of continuous functions because continuity is defined in terms of limits.
Suppose f(z) and g(z) are continuous on a region A. Then
- f(z) + g(z) is continuous on A.
- f(z)g(z) is continuous on A.
- f(z)/g(z) is continuous on A except (possibly) at points where g(z) = 0.
- If h is continuous on f(A) then h(f(z)) is continuous on A.
Using these properties we can claim continuity for each of the following functions:
- Ez2
- Cos(z) = (eiz+ e−iz)/2
- If P(z) and Q(z) are polynomials then P(z)/Q(z) is continuous except at roots of Q(z).
1.2.2 Holomorphic Functions
Holomorphic Functions and Derivatives
DefinitionA function f:D →C defined on an open set D in the complex plane is said to be holomorphic on D if the limit
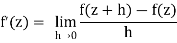
Is defined for all z ∈ D. The value of this limit is denoted by f0(z), or by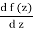 
, and is referred to as the derivative of the function f at z.
Note that if f:D →C is a holomorphic function defined on an open set C in the complex plane then f is continuous on D. For let z ∈ D. Then
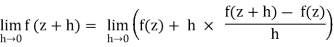
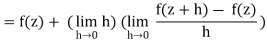
= f(z).
And thus the function f is continuous at z, as required.
Lemma: A function f:D →C, defined on an open set D in the complex plane, is holomorphic on D if and only if, given any complex number w belonging to D, and given any positive real number ε, there exists some real positive number δ such that |f(z)−f(w)−(z−w)f0(w)|≤ ε|z−w| whenever |z − w| <δ.
Proof: The function f has a well-defined derivative f0(w) at a point w of D if and only if
f’(ω) =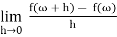 
= 
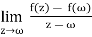
This limit exists if and only if, given any positive real number ε, there exists some positive real number δsuch that
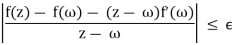
Whenever 0 < |z−w| <δ. The required result follows directly on rearranging the above inequality.
Proposition: Let f:D →C and g:D →C be holomorphic functions defined over an open set D in the complex plane. Then the sum f + g, difference f − g and product f · g of the functions f and g are holomorphic, where (f + g)(z) = f(z) + g(z), (f − g)(z) = f(z) − g(z) and (f · g)(z) = f(z)g(z) for all z ∈ D. Moreover (f + g)0(z) = f0(z) + g0(z), (f − g)0(z) = f0(z) − g0(z) and (f · g)0(z) = f0(z)g(z) + f(z)g0(z) for all z ∈ D.
Proof The results for f + g and f − g follow easily from the fact that the limit of a sum or difference of two complex-valued functions is the sum or difference of the limits of those functions (Proposition 1.11). The limit of a product of complex-valued functions is the product of the limits of those functions, and therefore
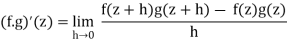
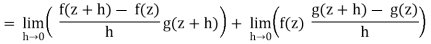
= f’(z) g(z) + f(z) g’(z)
As required.
The Chain Rule for Holomorphic Functions
Proposition: Let f:D →C and g:E→C be holomorphic functions defined over open sets D and E in the complex plane. Suppose that f(D) ⊂ E. Then the composition function g ◦ f:D →C is a holomorphic function on D, and (g ◦ f)0(z) = g0(f(z))f0(z) for all z ∈ D.
Proof: Let z0 be a point of D and let w0 = f(z0). Then
For all z ∈ D satisfying z 6= z0, where
G(ω) = 
if w 6= w 0; 0g0(w0) if w = w0,
Now limG(w) = G(w0), and therefore the function G is continuous at w0 w→w0
(Lemma 1.12). It follows that the composition function G ◦ f:D →C is continuous at atz0 (Lemma 1.14), and therefore limG((f(z)) = G(f(z0)) =
z→z0
G(w0) = g0(f(z0)). It follows from standard properties of limits of complexvalued functions (Proposition 1.11) that the limit defining the derivative
(g ◦ f)0(z0) of g ◦ f at z0 exists, and
(g o f)’ (z0) =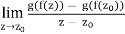 
= 
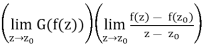
= g’ ( f(z0)) f’( z0).
As required.
Let γ:(a,b) →C be a complex-valued function defined on an open interval (a,b). Then there are real-valued functions αand βdefined on (a,b) such that γ(t) = α(t) + iβ(t). For all t ∈(a,b). We say that the function γisdifferentiable on (a,b) if the functions αand βare differentiable, in which case we define
Υ(t) =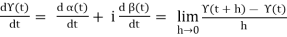 
Lemma Let f:D →C be a holomorphic function defined over a subset D of C and let γ:[a,b] → D be a continuously differentiable path in D. Then (f ◦γ)0(t) = f0(γ(t))γ0(t) for all t ∈[a,b].
Proof: The method of proof is the same at that used to prove Proposition 5.3. Given t0 ∈(a,b) let z0 = γ(t0), and let
F(z) = 
if z 6= z 0;
f0(z0)) if z = z0,
For all z ∈ D. Then the function F is continuous at z0, and therefore
(f o Υ)’(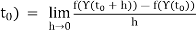
= 
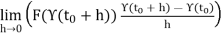
= F(Υ(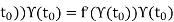
As required.
Lemma Let f:D →C be a holomorphic function defined over a subset D of C and let γ:[a,b] → D be a piecewise continuously differentiable path in D. Then
Z f0(z)dz= f(γ(b)) − f(γ(a))γ
Proof First suppose that the path γ:[a,b] → D is continuously differentiable. It follows from Lemma 5.4 and the definition of the path integral that
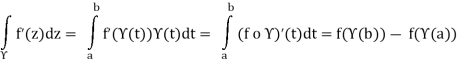
Now let γbe a piecewise continuously differentiable path. Then there exist real numbers s0,s1,...,smsatisfyinga = s0 < s1 <···<sm= b such that the restriction γi:[sj−1,sj] → D of γto the interval [sj−1,sj] is continuously differentiable for j = 1,2,...,n. Thenm
= f(γ(b)) − f(γ(a)),
As required.
NUMERICALS:
1) Find the multiplicative inverse of the complex number z = 4 - 5i.
Solution:
The given complex number is z = 4 - 5i.
We know that every non-zero complex number z = x +iy possesses multiplicative inverse given by
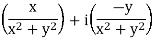
Therefore, using the above formula, we get
z-1 =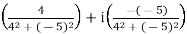 
= 
= 
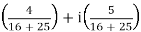
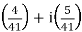
Therefore, the multiplicative inverse of the complex number z = 4 - 5i is
= 
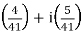
2) Factorize: x2 + y2
Solution:
X2 - (-1) y2 = x2 - I2y2 = (x + iy)(x - iy)
3) Find real values of the number a for which a.i is a solution of the polynomial equation
z4 - 2z3 + 7z2 - 4z + 10 = 0.
Then find all roots of this equation
Since a.i is a solution of the equation, we have
(a.i)4 - 2(a.i)3 + 7(a.i)2 - 4(a.i) + 10 = 0
<=>
a4 + 2.i.a3 - 7a2 - 4.i.a + 10 = 0
<=>
a4 - 7a2 + 10 = 0 and 2a3 - 4a = 0
<=>
a2 = 2
<=>
a = sqrt(2) or a = - sqrt(2)
Now, we know that sqrt(2).i and - sqrt(2).i are roots of z4 - 2z3 + 7z2 - 4z + 10 = 0 .
This means that z4 - 2z3 + 7z2 - 4z + 10 is divisible by (z - sqrt(2).i)(z + sqrt(2).i) = z2 - 2.
The quotient is (z2 - 2 z + 5) . The roots of this polynomial are 1 + 2 i and 1 - 2 i.
The four roots of the given equation are
Sqrt(2).i -sqrt(2).i 1 + 2 i 1 - 2 i.
Key takeaways:
A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of every point in its domain. An entire function is a holomorphic function whose domain is the entire complex plane.
1.3.1 Power series:
Remember that we were able to "simultaneously" evaluate all geometric series to discover that
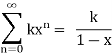
If |x|<1, and that the series diverges when |x|≥1. At the time, we thought of x as an unspecified constant, but we could just as well think of it as a variable, in which case the series
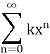
Is a function, namely, the function k/(1−x), as long as |x|<1. While k/(1−x) is a reasonably easy function to deal with, the more complicated ∑kxn does have its attractions: it appears to be an infinite version of one of the simplest function types—a polynomial.
The geometric series has a special feature that makes it unlike a typical polynomial—the coefficients of the powers of x are the same, namely k. We will need to allow more general coefficients if we are to get anything other than the geometric series.
Definition: A power series has the form
With the understanding that an may depend on n but not on x.
Convergence of a Power Series
Since the terms in a power series involve a variable x, the series may converge for certain values of x and diverge for other values of x. For a power series centered at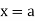 
the value of the series at 
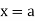is given by 
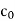Therefore, a power series always converges at its center. Some power series converge only at that value of x. Most power series, however, converge for more than one value of x. In that case, the power series either converges for all real numbers x or converges for all x in a finite interval. For example, the geometric series 
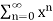converges for all x in the interval (-1, 1), but diverges for all x outside that interval. We now summarize these three possibilities for a general power series.
Convergence of a Power Series
Consider the power series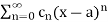 
The series satisfies exactly one of the following properties:
- The series converges at
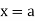and diverges for all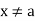 
- The series converges for all real numbers x.
- There exists a real number
such that the series converges if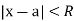 
and diverges if 
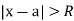At the values x where 
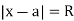the series may converge or diverge.
Properties of Power Series
Combining Power Series
If we have two power series with the same convergence interval, we can add or subtract them to make a new power series with the same convergence interval. To produce a new power series, we can multiply a power series by a power of x or evaluate a power series at xm given a positive integer m. We can use power series representations of other functions to find power series representations for particular functions. For example, since we know the power series representation for f(x) =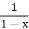 
, we can find power series representations for related functions, such as
y =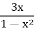 
and y =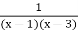 
We state findings for power series addition and subtraction, composition of apower series, and multiplication of a power series by a power of the variable in Combining Power Series. We express the theorem for power series centred at x=0 for clarity. Power series centred at x=a produce similar results.
Multiplication of Power Series
By multiplying power series, we can build new power series. Finding power series representations for functions is made easier by being able to multiply two power series.
We multiply them in the same manner we multiply polynomials. Let's say we wish to multiply something.
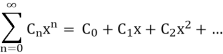
And
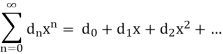
It appears that the product should satisfy
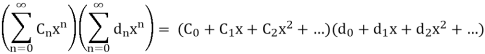
= c0d0 + (c1d0 + c0d1)x + (c2d0 + c1d1 + c0d2) x2 + ...
We state the basic result about multiplying power series in Multiplying Power Series, demonstrating that if
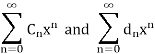
If the series converges on a common interval I, we can multiply it in this fashion, and the new series converges on the interval I as well.
The proof of this theorem is omitted since it is outside the scope of this text and is usually presented in a more advanced course. We will now use this theorem as an example by determining the power series representation for
f(x) =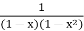 
Using the power series representations for
y =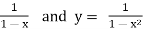 
Differentiating and Integrating Power Series
Consider a power series
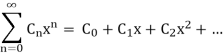
Let f be the function defined by this series that converges on some interval I. We'll answer two questions concerning f in this section.
• Is f differentiable, and how do we find the derivative f′ if it is?
• What is the formula for calculating the indefinite integral f(x)dx?
We know that we can evaluate the derivative of a polynomial with a finite number of terms by differentiating each component independently. Similarly, the indefinite integral can be evaluated by integrating each term independently. We illustrate how to achieve the same thing with convergent power series in this example. That is, assuming that
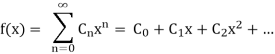
Converges on some interval I, then
f ‘ (x) = 
And
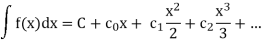
Converges on I.
1.3.2 Integration along the curve:
Finding the slope of the tangent line to a graph y=f(x) is easy -- just compute f′(x). Likewise, the areaunder the curve between x=a and x=b is just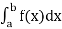 
. But how do we compute slopes and areas with parametrized curves?
The answer is to express everything in terms of the parameter t. By computing derivatives with respect to t and integrals with respect to t, we can compute everything we want.
For slopes, we are looking for dy/dx. This is a limit
= 
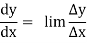
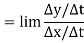
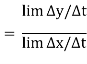
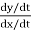
Where the limits are as Δt and Δx and Δy all go to zero. As long as we can take the derivatives of x and y, we can compute dy/dx.
Example: Find the slope of the tangent to the unit circle x=cos(t); y=sin(t) at time t=π/6, i.e. at the point (x,y)=(3√2,12).
Solution:
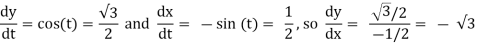
To find the area under a curve between x=a and x=b, we need to compute
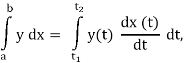
Where x(t1)=a and x(t2)=b. To find the area, we need to both compute a derivative as well as an integral.
Key takeaways:
A power series is a sort of series that has terms that involve a variable and is used to express common functions as well as define new functions.
Numericals:
1) For the following power series determine the interval and radius of convergence.
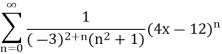
Solution:
Okay, let’s start off with the Ratio Test to get our hands on L.
=
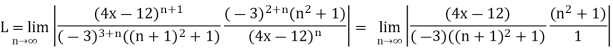
So, we know that the series will converge if,
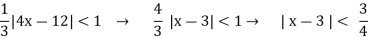
So, from the previous step we see that the radius of convergence is
R = 
Now, let’s start working on the interval of convergence. Let’s break up the inequality we got in Step 2.
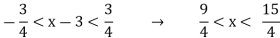
To finalize the interval of convergence we need to check the end points of the inequality from Step 4.
x =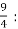 
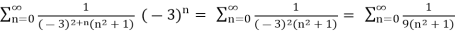
x =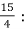 
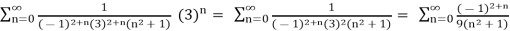
Now, we can do a quick Comparison Test on the first series to see that it converges and we can do a quick Alternating Series Test on the second series to see that is also converges.
We’ll leave it to you to verify both of these statements.
The interval of convergence is below and for summary purposes the radius of convergence is also shown.
Interval: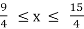 
R = 
2) For the following power series determine the interval and radius of convergence.
Solution:
Okay, let’s start off with the Ratio Test to get our hands on L.
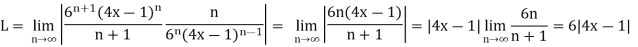
So, we know that the series will converge if,
6| 4x – 1| < 1 → 24| x – ¼ | < 1 → | x – ¼| < 1/24
So, from the previous step we see that the radius of convergence is
R = 1/24
Now, let’s start working on the interval of convergence. Let’s break up the inequality we got in Step 2.
-1/24 < x – ¼ < 1/24 → 5/24 < x < 7/24
To finalize the interval of convergence we need to check the end points of the inequality from Step 4.
x = 5/24 :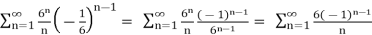 
x = 7/24 :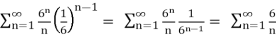 
Now, the first series is an alternating harmonic series which we know converges (or you could just do a quick Alternating Series Test to verify this) and the second series diverges by the p-series test.
The interval of convergence is below and for summary purposes the radius of convergence is also shown.
Interval: 5/24 ≤ x < 7/24 R = 1/24
3) Give a power series representation for the derivative of the following function.
g(x) =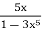 
Solution:
First let’s notice that we can quickly find a power series representation for this function. Here is that work.
g(x) = 
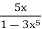= 5x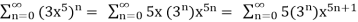 
Now, we know how to differentiate power series and we know that the derivative of the power series representation of a function is the power series representation of the derivative of the function.
Therefore,
g’ (x) =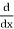 
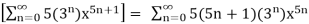
Remember that to differentiate a power series all we need to do is differentiate the term of the power series with respect to x.
Numerical Problems
Q.i2012 = ?
Solution:
i4 = 1 So 4n i = 1 (n is a positive integer) i2012 = 1
Q. Show that for each complex number z_z . z = a real number
Solution:
Say z = a+ib, then_z . z = (a+bi)(a-bi) = a2 + b2 = real number
Q. Find the polar representation of (i-sqrt(3))
Solution
The modulus of (i-sqrt(3)) is 2. (i-sqrt(3)) = 2.( -sqrt(3)/2 + (1/2)i ) Say, the argument is alpha. Cos(alpha) = -sqrt(3)/2 sin(alpha) = (1/2) Choose alpha = 5 pi/6 (i-sqrt(3)) = 2.(cos(5.pi/6) + i sin(5.pi/6))
Q. Find all z so that z4 = -8(i-sqrt(3))
Solution:
-8(i-sqrt(3)) = 16.(cos(-pi/6) + i sin(-pi/6))
The 4th roots are
z = 2.(cos(-pi/24 + k.pi/2) + i sin(-pi/24 + k.pi/2)) with k in Z
Q. Given: u = 1+i.sqrt(3) and v = sqrt(3) + i Calculate u3 / v4
Solution:
With the polar form u = 2 ( cos(pi/3) + i sin(pi/3) ) en v = 2 ( cos(pi/6) + i sin(pi/6))
Then u3 = 8(cos(pi) + i sin(pi)) = -8 and v4 = 16( cos(2 pi/3) + i sin(2 pi/3) )
u3 / v4 = -(1/2)( cos(2 pi/3) - i sin(2 pi/3) ) = (1/4) - i sqrt(3)/4
Q. Show that the equation has a real root. 4z3 - 6i sqrt(3) z2 - 3(3 + i sqrt(3)) z - 4 = 0
Solution:
If there exists a real root w then the imaginary part of the left hand side must be 0 for z = w.- 6i sqrt(3) w2 - 3.i sqrt(3) w = 0.This is equivalent to 2 w2 + w = 0. So, w = 0 or w = -1/2But w = 0 cannot be a Solution :- of the given equation.If there exists a real root w then it is -1/2.Now we check if -1/2 is a root of the given equation and we see that it is so.
Q. From this expression it is obvious that w is a pure imaginary number. Prove that in C, there are no divisors of zero. That is, z.z'=0 => (z=0 or z'=0)
Solution:
If z=0, the statement is proved. If z not 0, then there is a complex number z" (not zero) so that z".z=1.Then, z.z'=0 => z".z.z'=z".0 => 1.z'=0 => z'=0
Q. The image point of z = a + bi in the Gauss-plane is p. We rotate p about o and the angle of the rotation is pi/3. The new position of p is p'. Calculate the coordinates of p'.
Solution:
Say z has polar notation r(cos(t)+i sin(t)) p' is the image point of z.(cos(pi/3) + i sin(pi/3)) in the Gauss-plane Hence, p' is the image point of r(cos(t+pi/3) + i sin(t+pi/3)) The coordinates of p' are (r.cos(t+pi/3) ;r.sin(t+pi/3))
Q. a, b, c are real numbers in the polynomialp(z) = 2 z4 + a z3 + b z2 + c z + 3 .Find a such that the numbers 2 and i are roots of p(z) = 0.
Solution:
Since all the coefficients of p(z) are real, -i is a root of p(z) = 0. Let 2, i, -i, w be all the roots. The sum of the roots = 2 + w = -a/2.The product of the roots = 2w = 3/2. From this we find w = 3/4 and a = 11/2.
Q. Calculate the real values of x and y such that (x + iy)3 is real and |x + i y| is higher than 8.
Solution:
(x + iy)3 = x3 + 3 i x2 y - 3 x y2 - i y3 (x + iy)3 is real <=> 3 x2 y - y3 = 0 <=> y (3 x2 - y2 ) = 0 <=> y = 0 or 3 x2 - y2 = 0 <=> y = 0 or 3 x2 = y2 <=> y = 0 or y = sqrt(3) x or y = - sqrt(3) x
Conclusion: |x + iy| > 8 if and only if ( x> 2 and y = 0 ) y = sqrt(3) x and x2 + y2 > 64 <=> y = sqrt(3) x and 4x2 > 64 <=> y = sqrt(3) x and x2 > 16 <=> y = sqrt(3) x and |x| > 4 y = - sqrt(3) x and x2 + y2 > 64 <=> y = - sqrt(3) x and 4x2 > 64 <=> y = - sqrt(3) x and x2 > 16 <=> y = - sqrt(3) x and |x| > 4
Q. Calculate all Solution:-s of |z-1|.|z-1|=1
Solution:
Let z = x + iy |z - 1|2 = 1 <=>|x + iy - 1|2 = 1 <=> x - 1)2 + y2 = 1 We see that the Solution :-s are exactly the points (in the Gauss plane) of the circle with center (1,0) and radius 1.
Q. The equation z3 - (n + i) z + m + 2 i = 0 has three roots. n and m are real constants. a) Calculate m such that the modulus of the product of the roots is 5. b) Calculate the modulus of the sum of the roots.
Solution:
|z1 z2 z3 | = 5 <=> |-(m+2i)|= 5 <=> ...<=> m = 1 or -1 Since the sum of the roots is 0, the modulus of the sum is 0.
Q. Find the modulus and principal amplitude of -4.
Solution:
Let z = -4 + 0i.
Then, modulus of z = |z| = (−4)2+02−−−−−−−−−√(−4)2+02 = 16−−√16 = 4. Clearly, the point in the z-plane the point z = - 4 + 0i = (-4, 0) lies on the negative side of real axis. Therefore, the principal amplitude of z is π.
Q. Factorize: x22 + y22
Solution:
x22 - (-1) y22 = x22 - i22y22 = (x + iy)(x - iy)
Q. Perform the indicated operation and write your answer in standard form.(−3−i)−(6−7i)(−3−i)−(6−7i)
Solution:
We know how to subtract two polynomials and so we also know how to subtract two complex numbers.
(−3−i)−(6−7i)=−3−i−6+7i=−9+6i(−3−i)−(6−7i)=−3−i−6+7i=−9+6i
Q. Perform the indicated operation and write your answer in standard form.(1+4i)−(−16+9i)(1+4i)−(−16+9i)
Solution:
We know how to subtract two polynomials and so we also know how to subtract two complex numbers.
(1+4i)−(−16+9i)=1+4i+16−9i=17−5i(1+4i)−(−16+9i)=1+4i+16−9i=17−5i
Q. Perform the indicated operation and write your answer in standard form. 8i(10+2i)8i(10+2i)
Solution:
We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is distribute the 8ii to get, 8i(10+2i)=80i+16i28i(10+2i)=80i+16i2 All we need to do to finish the problem is to recall that i2=−1i2=−1. Upon using this fact, we can finish the problem. 8i(10+2i)=80i+16(−1)=−16+80i
Q. Perform the indicated operation and write your answer in standard form. (−3−9i)(1+10i)(−3−9i)(1+10i)
Solution:
We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is “foil” the two complex numbers to get,
(−3−9i)(1+10i)=−3−30i−9i−90i2(−3−9i)(1+10i)=−3−30i−9i−90i2 All we need to do to finish the problem is to recall that i2=−1i2=−1. Upon using this fact, we can finish the problem. (−3−9i)(1+10i)=−3−30i−9i−90(−1)=87−39i
Q. Evaluate the following expressions
a) (3 + 2i) - (8 - 5i)
b) (4 - 2i)*(1 - 5i)
c) (- 2 - 4i) / i
d) (- 3 + 2i) / (3 - 6i)
Solution:
a) -5 + 7i
b) -6 - 22i
c) -4 + 2i
d) -7/15 - 4i/15
Q. If (x + yi) / i = ( 7 + 9i ) , where x and y are real, what is the value of (x + yi)(x - yi)?
Solution:
(x + yi) / i = ( 7 + 9i )
(x + yi) = i(7 + 9i) = -9 + 7i
(x + yi)(x - yi) = (-9 + 7i)(-9 - 7i) = 81 + 49 = 130
Q. Determine all complex number z that satisfy the equation z + 3 z' = 5 - 6i where z' is the complex conjugate of z.
Solution:
Let z = a + bi , z' = a - bi ; a and b real numbers.
Substituting z and z' in the given equation obtain
a + bi + 3*(a - bi) = 5 - 6i
a + 3a + (b - 3b) i = 5 - 6i
4a = 5 and -2b = -6
a = 5/4 and b = 3
z = 5/4 + 3i
Q. Find all complex numbers of the form z = a + bi, where a and b are real numbers such that z z' = 25 and a + b = 7 where z' is the complex conjugate of z.
Solution:
z z' = (a + bi)(a - bi)
= a2 + b2 = 25
a + b = 7 gives b = 7 - a
Substitute above in the equation a2 + b2 = 25
a2 + (7 - a)2 = 25
Solution the above quadratic function for a and use b = 7 - a to find b.
a = 4 and b = 3 or a = 3 and b = 4
z = 4 + 3i and z = 3 + 4i have the property z z' = 25.
Q. The complex number 2 + 4i is one of the root to the quadratic equation x2 + bx + c = 0, where b and c are real numbers.
a) Find b and c
b) Write down the second root and check it.
Solution:
a) Substitute in equation: (2 + 4i)2 + b(2 + 4i) + c = 0
Expand terms in equation and rewrite as: (-12 + 2b + c) + (16 + 4b)i = 0
Real part and imaginary part equal zero.
-12 + 2b + c = 0 and 16 + 4b = 0
Solution for b: b = -4 , substitute and solution for c: c = 20
b) Since the given equation has real numbers, the second root is the complex conjugate of the given root: 2 - 4i is the second Solu.
Check: (2 - 4i)2 - 4 (2 - 4i) + 20
(Expand) = 4 - 16 - 16i - 8 + 16i + 20
= (4 - 16 - 8 + 20) + (-16 + 16)i = 0
Q. Find all complex numbers z such that z2 = -1 + 2 sqrt(6) i.
Solution:
Let z = a + bi
Substitute into given equation: (a + bi)2 = -1 + 2 sqrt(6) i
Expand: a2 - b2 + 2 ab i = - 1 + 2 sqrt(6) i
Real part and imaginary parts must be equal.
a2 - b2 = - 1 and 2 ab = 2 sqrt(6)
Equation 2 ab = 2 sqrt(6) gives: b = sqrt(6) / a
Substitute: a2 - ( sqrt(6) / a )2) = - 1
a4 - 6 = - a2
Solution above equation and select only real roots: a = sqrt(2) and a = - sqrt(2)
Substitute to find b and write the two complex numbers that satisfies the given equation.
z1 = sqrt(2) + sqrt(3) i , z2 = - sqrt(2) - sqrt(3) i
Q. Find all complex numbers z such that (4 + 2i)z + (8 - 2i)z' = -2 + 10i, where z' is the complex conjugate of z.
Solution:
Let z = a + bi where a and b are real numbers. The complex conjugate z' is written in terms of a and b as follows: z'= a - bi. Substitute z and z' in the given equation
(4 + 2i)(a + bi) + (8 - 2i)(a - bi) = -2 + 10i
Expand and separate real and imaginary parts.
(4a - 2b + 8a - 2b) + (4b + 2a - 8b - 2a )i = -2 + 10i
Two complex numbers are equal if their real parts and imaginary parts are equal. Group like terms.
12a - 4b = -2 and - 4b = 10
Solution the system of the unknown a and b to find:
b = -5/2 and a = -1
z = -1 - (5/2)i
References:
1. James Ward Brown and Ruel V. Churchill, Complex Variables and Applications (EighthEdition), McGraw - Hill International Edition, 2009.
2. G. F. Simmons, Introduction to Topology and Modern Analysis, Mcgraw-Hill, Edition 2004.
3. Joseph Bak and Donald 1. Newman, Complex analysis (2ndEdition), Undergraduate Texts inMathematics, Springer-Verlag New York, Inc., New York, 1997.
