Unit - 2
Cauchy’s Theorem and Its Applications
The Cauchy integral formula; this states that if f is holomorphic in an open set containing a circle C and its interior, then for all z inside C,
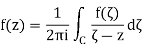
Differentiation of this identity yields other integral formulas, and in particular we obtain the regularity of holomorphic functions. This is remarkable, since holomorphicity assumed only the existence of the first derivative, and yet we obtain as a consequence the existence of derivatives of all orders.
Goursat’s theorem
If f has a primitive in an open set Ω, then
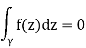
For any closed curve γin Ω. Conversely, if we can show that the above relation holds for some types of curves γ, then a primitive will exist.
Theorem:
If Ωis an open set in C, and T ⊂Ωa triangle whoseinterior is also contained in Ω, then
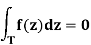
Whenever f is holomorphic in Ω.
Proof:
We call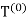 
our original triangle (with a fixed orientation
Which we choose to be positive), and let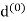 
and 
denote the diameterand perimeter of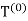 
, respectively. The first step in our constructionconsists of bisecting each side of the triangle and connecting the midpoints.
This creates four new smaller triangles, denoted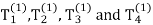 
that are similar to the original triangle. The construction andorientation of each triangle are illustrated in Figure 1. The orientation
Is chosen to be consistent with that of the original triangle, and so aftercancellations arising from integrating over the same side in two oppositedirections, we have
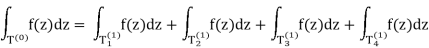
For some j we must have
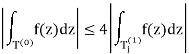
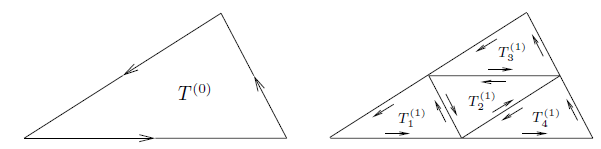
Fig: Bisection of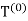 
For otherwise (2) would be contradicted. We choose a triangle thatsatisfies this inequality, and rename it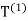 
. Observe that if 
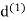and 
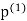denote the diameter and perimeter of 
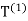respectively, then 
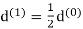and 
We now repeat this process for the triangle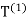
, bisecting it into four smaller triangles. Continuing this process,we obtain a sequence of triangles
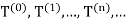
With the properties that
And
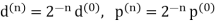
Where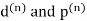 
denote the diameter and perimeter of 
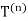respectively.
We also denote by 
the solid closed triangle with boundary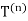
, and observe that our construction yields a sequence of nested compactsets
⊃
⊃···⊃
⊃···
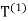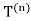Whose diameter goes to 0.
There existsa unique point z0 that belongs to all the solid triangles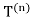 
Since f is
Holomorphic at z0 we can write
f(z) = f(z0) + f’ (z0)(z-z0) + ψ (z)(z – z0)
Where ψ(z) →0 as z →z0. Since the constant f(z0) and the linear function
f’(z0)(z −z0) have primitives, we can integrate the above equality
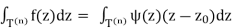……. (1)
Now z0 belongs to the closure of the solid triangle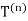 
and z to itsboundary, so we must have|z −z0| ≤
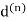and using (3) we get
The estimate
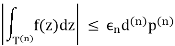
Where ϵn = sup z ∈ T(n) |ψ(z)| → 0 as n → ∞ , therefore
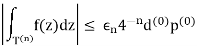
Which yields our final estimate
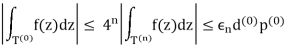
Letting n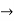
∞ concludes the proof since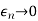 
Corollary: If f is holomorphic in an open set Ωthat contains arectangle R and its interior, then
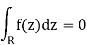
This is immediate since we first choose an orientation as in Figure and note that
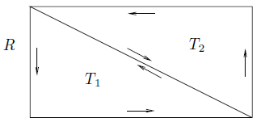
Fig: A rectangle as the union of two triangles
Theorem: A holomorphic function in an open disc has a primitive in that disc.
Proof:
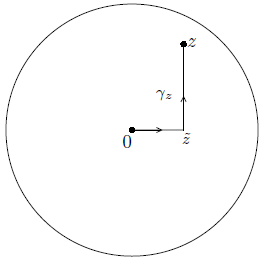
After a translation, we may assume without loss of generalitythat the disc, say D, is centered at the origin. Given a point z ∈D, consider the piecewise-smooth curve that joins 0 to z first by moving inthe horizontal direction from 0 to 
where
= Re(z), and then in thevertical direction from
to z. We choose the orientation from 0 to z, and denote this polygonal line (which consists of at most two segments)
By 
, see figure
Define
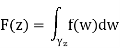
The choice of 
gives an unambiguous definition of the function F(z).
We contend that F is holomorphic in D and F’(z) = f(z). To prove this,fix z ∈D and let h ∈C be so small that z + h also belongs to the disc.
Now consider the difference
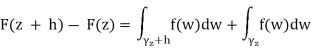
The function f is first integrated along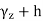 
with the original orientation,and then along 
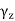with the reverse orientation (because of the minussign in front of the second integral). This corresponds to (a) in Figure 4.
Since we integrate f over the line segment starting at the origin in twoopposite directions, it cancels, leaving us with the contour in (b). Then,we complete the square and triangle as shown in (c), so that after anapplication of Goursat’s theorem for triangles and rectangles we are leftwith the line segment from z to z + h as given in (d).
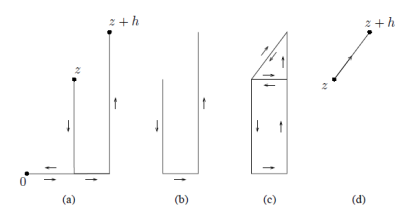
Fig: Relation between the polygonal lines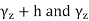 
Hence the above cancellations yield
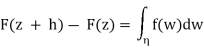
Where ηis the straight line segment from z to z + h. Since f is continuousat z we can write
f(w) = f(z) + ψ(w)
Where ψ(w) →0 as w →z. Therefore
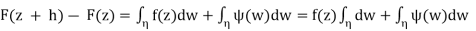…. (1)
On the one hand, the constant 1 has w as a primitive, so the first integralis simply hon other hand we have
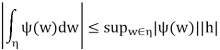
Since the supremum above goes to 0 as h tends to 0, we conclude fromequation (1) that
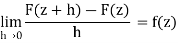
Thereby proving that F is a primitive for f on the disc
This theorem says that locally, every holomorphic function has a primitive.
Cauchy’s theorem for a disc:
If f is holomorphic in a disc, then
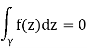
For any closed curve γin that disc.
Corollary:
Suppose f is holomorphic in an open set containing thecircle C and its interior. Then
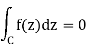
Proof:
Let D be the disc with boundary circle C. Then there existsa slightly larger disc D’ which contains D and so that f is holomorphicon D’. We may now apply Cauchy’s theorem in D’to conclude that
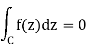
In fact, the proofs of the theorem and its corollary apply whenever wecan define without ambiguity the “interior” of a contour, and constructappropriate polygonal paths in an open neighborhood of that contour
And its interior. In the case of the circle, whose interior is the disc, therewas no problem since the geometry of the disc made it simple to travelhorizontally and vertically inside it.
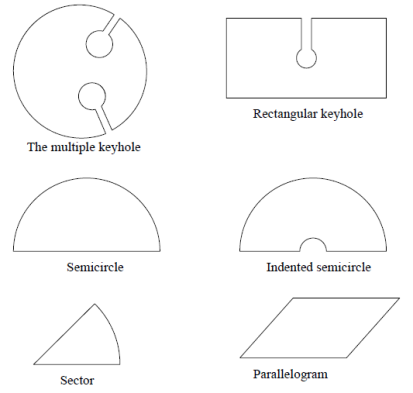
Its positive orientation is that for which the interior is to the leftas we travel along the toy contour. This is consistent with the definitionof the positive orientation of a circle. For example, circles, triangles,and rectangles are toy contours, since in each case we can modify (andactually copy) the argument given previously.
Another important example of a toy contour is the “keyhole” Γ (illustratedin Figure 1), which we shall put to use in the proof of the Cauchyintegral formula. It consists of two almost complete circles, one large
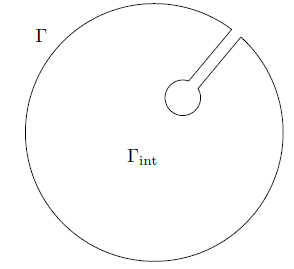
Fig: The keyhole contour
And one small, connected by a narrow corridor. The interior of Γ, whichwe denote by Γint, is clearly that region enclosed by the curve, and canbe given precise meaning with enough work. We fix a point z0 in thatinterior. If f is holomorphic in a neighborhood of Γ and its interior, then it is holomorphic in the inside of a slightly larger keyhole, say Λ,
Whose interior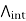 
contains ΓU
.
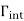If z ∈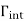
, let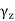 
denote any curvecontained inside Λintconnecting z0 to z, and which consists of finitelymany horizontal or vertical segments (as in Figure below). If 
is any othersuch curve, the rectangle version of Goursat’s theorem
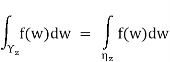
And we may therefore define F unambiguously in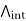 
.
Arguing as above allows us to show that F is a primitive of f in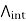 
and therefore
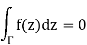
The important point is that for a toy contour γwe easily have that
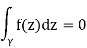
Whenever f is holomorphic in an open set that contains the contour γand its interior
While Cauchy’s theorem for toy contours is sufficient for most applicationswe deal with, the question still remains as to what happens for moregeneral curves. We take up this matter in Appendix B, where we proveJordan’s theorem for piecewise-smooth curves. This theorem states thata simple closed piecewise-smooth curve has a well defined interior thatis “simply connected.” As a consequence, we find that even in this moregeneral situation, Cauchy’s theorem holds.
Some examples of toy contours are-
Example: We show that if ξ∈R, then
…….(1)
This gives a new proof of the fact that 
is its own Fourier transform.
If ξ= 0, the formula is precisely the known integral
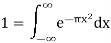
Now suppose that ξ>0, and consider the function f(z) =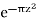 
Whichis entire, and in particular holomorphic in the interior of the toy contour
γR depicted in figure:
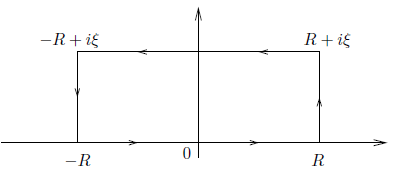
The contour γR consists of a rectangle with vertices R, R+ iξ,−R +
iξ,−R and the positive counterclockwise orientation. By Cauchy’s theorem,
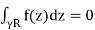……..(2)
The integral over the real segment is simply
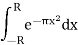
Which converges to 1 as R→∞. The integral on the vertical side on theright is
This integral goes to 0 as R→∞since ξis fixed and we may estimate it by
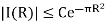
Similarly, the integral over the vertical segment on the left also goes to 0as R→∞for the same reasons. Finally, the integral over the horizontalsegment on top is
Therefore, we find in the limit as R→∞that (2) gives
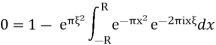
And our desired formula is established. In the caseξ<0, we then considerthe symmetric rectangle, in the lower half-plane.
The technique of shifting the contour of integration, which was usedin the previous example, has many other applications. Note that theoriginal integral (1) is taken over the real line, which by an applicationof Cauchy’s theorem is then shifted upwards or downwards (dependingon the sign of ξ) in the complex plane.
Example: Another example is
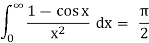
Here we consider the function f(z) = (1-eiz)/z2, and we integrate overthe indented semicircle in the upper half-plane positioned on the x-axis,as shown in Figure
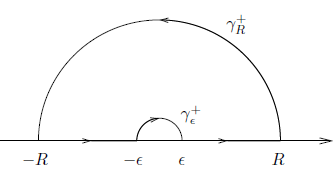
If we denote by Υϵ+ and ΥR+ the semicircles of radii 
and R with negativeand positive orientations respectively, Cauchy’s theorem gives
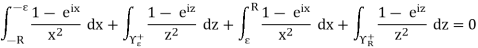
First we let R→∞and observe that
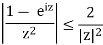
So the integral over ΥR+ goes to zero. Therefore
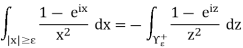
Now note that
f(z) =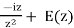 
Where E(z) is bounded as z →0, while on Υϵ+ we have z = εeiθ and dz = iεeiθ dθ .
Thus
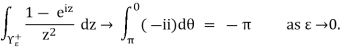
Taking real parts then yields
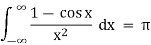
Since the integrand is even, the desired formula is proved.
Theorem: Suppose f is holomorphic in an open set that contains the closure of a disc D. If C denotes the boundary circle of this disc with the positive orientation, then
f(z) =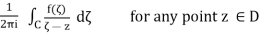 
Proof:
Fixz∈D and consider the “keyhole” Γδ,ε which omits thepoint z as shown in
Here δis the width of the corridor, and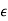 
the radius of the small circlecentered at z. Since the function F(ζ) = f(ζ)/(ζ−z) is holomorphicaway from the point ζ= z, we have
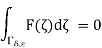
By Cauchy’s theorem for the chosen toy contour. Now we make thecorridor narrower by letting δtend to 0, and use the continuity of F tosee that in the limit, the integrals over the two sides of the corridor cancelout. The remaining part consists of two curves, the large boundary circle C with the positive orientation, and a small circle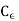 
centered at z ofradius 
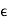and oriented negatively, that is, clockwise. To see what happensto the integral over the small circle we write
F(ζ) =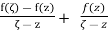 
……. (1)
And note that since f is holomorphic the first term on the right-handside of (1) is bounded so that its integral over Cε goes to 0 as 
→0.
To conclude the proof, it suffices to observe that
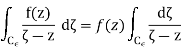
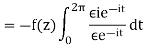
= - f(z) 2πi,
So that in the limit we find
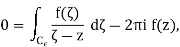
As was to be shown.
Corollary: If f is holomorphic in an open set Ω, then f has infinitelymany complex derivatives in Ω. Moreover, if C ⊂Ωis a circle whoseinterior is also contained in Ω, then
For all z in the interior of C.
We recall that, as in the above theorem, we take the circle C to have positive orientation.
Proof:
The proof is by induction on n, the case n = 0 being simplythe Cauchy integral formula. Suppose that f has up to n −1 complexderivatives and that
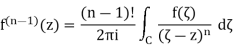
Now for h small, the difference quotient for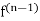 
takes the form
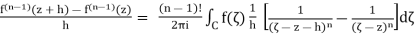…….. (2)
We now recall that
An – Bn = (A-B) [An-1 + An-2 B + … + ABn-2 + Bn-1]
With A = 1/ (ζ−z −h) and B = 1/(ζ−z), we see that the term inbrackets in equation (2) is equal to
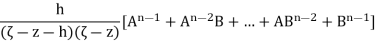
But observe that if h is small, then z + h and z stay at a finite distancefrom the boundary circle C, so in the limit as h tends to 0, we find thatthe quotient converges to
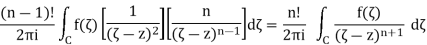
Which completes the induction argument and proves the theorem.
Note- above two formulas (theorem and corollary) are known as Cauchy integral formulas.
References:
1. Elias M. Stein & Rami Shakarchi, Complex Analysis, Princeton University press, Princeton and Oxford, 2003.
2. James Ward Brown and Ruel V. Churchill, Complex Variables and Applications (Eighth Edition), McGraw - Hill International Edition, 2009.
3. G. F. Simmons, Introduction to Topology and Modern Analysis, Mcgraw-Hill, Edition 2004.
4. Joseph Bak and Donald 1. Newman, Complex analysis (2ndEdition), Undergraduate Texts inMathematics, Springer-Verlag New York, Inc., New York, 1997.
5. COMPLEX ANALYSIS Elias M. Stein& Rami ShakarchiPRINCETON
