Unit - 4
Groups acting on themselves by conjugation
4.1.1 Conjugation
Two elements a and b of a group are conjugate in mathematics, especially group theory, if the group has an element g such that b = g-11ag. This is an equivalence relation with conjugacy classes as equivalence classes.
Because members of the same conjugacy class can't be identified only by their group structure, they share a lot of characteristics. The study of non-abelian groups' conjugacy classes is essential for understanding their structure. Each conjugacy class for an abelian group is a set of one element (singleton set).
Class functions are functions that are constant for members of the same conjugacy class.
Let G stand for a group. If there is an element g in G such that gag1 = b, two elements a and b of G are conjugate. Also, b is a conjugate of a, and an is a conjugate of b, according to some.
The conjugacy relation is known as matrix similarity in the case of the group GL(n) of invertible matrices.
Conjugacy can be simply demonstrated to be an equivalence relation, which divides G into equivalence classes. (This indicates that each group member belongs to only one conjugacy class, with Cl(a) and Cl(b) being same if and only if a and b are conjugate, and disjoint otherwise.) In G, the equivalence class containing the element an is
Cl(a) = { gag−1 | g ∈ G }
The conjugacy class of an is known as. The number of distinct (non-equivalent) conjugacy classes in G is the class number. The order of all items in the same conjugacy class is the same.
Conjugacy classes are denoted by acronyms such as "6A," which means "a certain conjugacy class of order 6 elements," and "6B," which means "a different conjugacy class of order 6 elements"; conjugacy class 1A is the conjugacy class of the identity. Conjugacy classes can be described uniformly in some circumstances; for example, cycle structure can be used to characterise them in the symmetric group.
4.1.2 Conjugacy as group action
If we define
g . x = gxg−1
We have a group action of G on G for any two elements g and x in G. The conjugacy classes are the orbits of this action, and the centralizer of a particular element is the stabiliser. [3]
Similarly, we can write "G group action on all subsets of G" to define a group action of G on the set of all subsets of G.
g . S = gSg−1,
Or on the set of the subgroups of G.
4.2.1 Class equation
Let G be a group and let AA be a G-set (given by a homomorphism G→homSet(A,A) of monoids, with which is associated an action α:G×A→ARecall that A is connected in the category of G-sets if A is inhabited and the action is transitive; in this case, choosing an element a∈A, there is a surjection of G-sets G→Asending 1↦a, and this induces an isomorphism G/Stab(a)≅Awhere Stab(a) is the stabilizer of a and G/Stab(a) is the G-set consisting of left cosets of Stab(a).
In general, each G-set A admits a canonical decomposition as a coproduct of its connected components, which are commonly referred to as the action's orbits. We have an isomorphism of G-sets if we choose a representative element axe in each orbit x.
A≅∑orbitsxG/Stab(ax).
By taking G and A to be finite and counting elements, we get an equation of the form
|A|=∑orbitsx|G||Stab(ax)|.
A class equation is an instance of this equation. Many beneficial consequences can be derived by carefully selecting groups G and G-sets A, typically in conjunction with number-theoretic reasons; some examples are provided below.
It's worth noting that viewing the class equation as
∑orbitsx1|Stab(ax)|=|A||G|
It expresses the groupoid cardinality of the action groupoid of G acting on A.
4.2.2 Consequences of class equation
- Centers of p-groups
Remember that a p-group is a finite group with an order that is a power of p. The following is a simple structural result.
- Proposition 3.1. A non-trivial p-group G has a nontrivial center Z(G)
Proof. Let G act on itself by the conjugation action G×G→Gto G, (g,h)↦ghg−1In this case an orbit Orb(h)is usually called the conjugacy class of h, and Orb(h)is trivial (consists of exactly one element h) iff h belongs to Z(G). In any case |Orb(h)|=|G||Stab(h)|= p^n, and therefore p divides |Orb(h) if h is noncentral. In this case the class equation takes the form
|G|=|Z(G)|+∑nontrivialorbitsx|G||Stab(ax)|
And now since pp divides |G| as well as each term in the sum over nontrivial orbits, it must also divide |Z(G)|. In particular, Z(G) has more than one element.
Because the centre is a normal subgroup and the quotient G/Z(G) is also a p-group, p-groups are solvable by induction. Because an abelian group formed by successive central extensions is nilpotent, p-groups are also nilpotent.
4.2.3 Number of fixed points
The number of fixed points of an involution on a finite set SS has the same parity as S, which is a basic observation that is frequently relevant. This is a statement about Z/(2)-sets; for general p-groups G, we generalise it to a statement about G-sets. (An element whose orbit is a singleton is a fixed point of a G-set.)
Proposition 3.2: If G is a p-group acting on a set A, it follows that
- |A|≡|Fix(A)|mod p
As special cases, if there is just one fixed point, then |A|≡1modp, and if p divides |A|, then p divides |Fix(A)|.
Proof. The class equation takes the form
|A|=|Fix(A)|+∑nontrivialorbitsx|G||Stab(ax)|
Where p divides each summand over nontrivial orbits on the right, since G is a p-group. Now reduce mod p.
Numericals:
1) Let G be a group of order |G|=pn for some n∈N (Such a group is called a p-group. Demonstrate that the group G's centre Z(G) is not trivial.
ANSWER
If G=Z(G), then the statement is true. So suppose that G≠Z(G).
Then by the class equation, we have
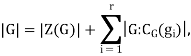
Where gi are representatives of the distinct conjugacy class not contained in the center Z(G), and CG(gi) is the centralizer of gi. (Since we are assuming that G≠Z(G) such gi exist.) Since gi∉Z(G), the groups CG(gi) are proper subgroups of G and hence p divides |G:CG(gi)|.Of course pp divides |G|, thus p should
Divide |Z(G)| as well.
Therefore the center Z(G) cannot be trivial.
2. Let G be any group. Let X be the set of all subgroups of G. Consider the conjugation action defined by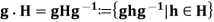 
For any g ∈ G and H ∈ X.
(i) Verify that this really is an action of G on X.
(2) Prove that a subgroup H of G is a fixed point of this action if and only if H is normal.
(3) in the special case where G=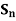
and H is the cycle group generated by (1,2,3,,…d) (where 
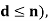compute the orbit of H.
ANSWER-
(1) we first need to show that 
is a subgroup of . It is non-empty since it contains 
Also it is closed, since for arbitrary elements 
and 
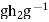in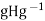 
, the product 
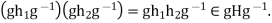Finally if 
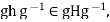then also 
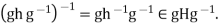Here we used that H is a subgroup. To see the axioms of an action are satisfied, we need to check that (1) e H=H; and (2) 
is obvious: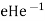 
=eHe=H. (2) is also easy: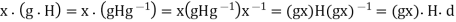 
(2) 
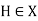is fixed by every 
if and only if 
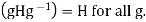This is the same as H being normal by theorem 8.11 in the book.
(3) we claim that eh orbit of H is the collection of all subgroups of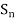 
that are generated by a d-cycle. First note that setting 
and H=
, we have 
, which is the group generated by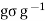 
. But also by we know that 
.
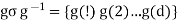Since we can find a 
that sends 1 ,2 ,3,… d to any list of d numbers between 1 and n, we conclude that the orbit of H is the collection of all subgroups of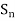 
generated by a d-cycle.
3. Let Zp be the field with p elements, p ≥ 3. Consider group U2(Zp) of invertible upper triangular matrices with coefficients in Zp (under multiplication).
Which of the following subgroups is normal?
(a) the subgroup 
of invertible diagonal matrices
(b) the subgroup of non-zero constant matrices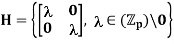 
(c) the subgroup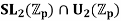 
of determinant one upper triangular matrices.
ANSWER-
(1) not normal: Norte that for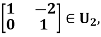 
the inverse is 
So
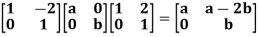
And this is not in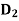 
if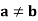 
(2) Yes normal. We know that the scalar matrices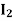 
commute with all matrices, so in particular 
(3) Yes! Normal. This the kernel of the map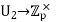 
sending A to det A. Since this is a group homomorphism, its kernel is a normal group.
4. Suppose that a group G acts on a set X. We define the action to be transitive if for every x, y ∈ X there exists g ∈ G such that g · x = y. In this case, we also say that G acts transitively on X. (i) Prove that if a finite group G acts transitivity on a set X, then the cardinality of X divides |G|
(2) Prove that 
cannot act transitively on any set with seven elements
(3) Prove that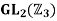 
can not act transitively on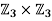 
ANSWER
(1) G acts transitively means that there is only one orbit all elements of X are in the same orbit. So by the orbit stabilizer theorem, 
So |X| divides |G|.
(2) from (1), if it did the n 7|6!. This is a contradiction.
(3) There of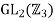 
is 
. The cardinally of 
is 9, which does not divide 48.
4.3.1 Conjugacy classes in the symmetric group Sn
We begin by proving that every permutation in Sn has a cycle decomposition, and we show that the cycle decomposition is fundamentally unique.
Theorem 1.
Up to the ordering of the cycles and a cyclic permutation of the elements within each cycle, every permutation in Sn has a cycle decomposition that is unique.
Proof.
We construct the cycle decomposition for σ∈Sn. Let X={1,…,n}, and regard σ as acting on X. Let G=⟨σ⟩ be the subgroup of Sn generated by σ. Then G acts on X, so by the orbit-stabilizer theorem, it partitions XX into a unique set of orbits. In addition, for any orbit Gx, we have that
σi x↔σi Gxx
Is a bijection, where Gx is the stabilizer of x in G.
Now, G=⟨σ⟩ is cyclic and thus G/Gxis cyclic as well; its order is the smallest power dd of σ such that σd∈Gx Note also that d=|Gx|=[G:Gx] Using the explicit bijection above, we see that the unique cosets of Gx in G are
Gx,σGx,…,σd−1GxGx,
And that the elements of Gx are
x,σx,…,σd−1xx,
Thus on any orbit of size d, σ is a d-cycle. This shows that a cycle decomposition exists.
Because the cycle specified by on an element of order d is uniquely determined by construction from the element, uniqueness follows simply. Instead, choosing a different element in the same orbit, such as jx, yields
σjx,σj+1x,…,σd−1x,x,σx,…,σj−1x
Which is the same cycle permuted left by j.
We can thus write
Definition 1.
If σ∈Sn and σ is written as the product of the disjoint cycles of lengths n1,…,nkn1,…,nk with ni≤ni+1ni≤ni+1 for each i<ki<k, then n1,…,nkn1,…,nk is the cycle type of σ.
The above theorem proves that the cycle type is well-defined.
Theorem 2.
Two permutations σ,τ∈Sn are conjugate if and only if they have the same cycle type.
Proof.
Assume first that σσ and ττ are conjugate; say τ=σ1σσ−11. Write σ as a product of disjoint cycles
(α1…αa)(β1…βb)(…)(α1…α)…)
To show that σσ and ττ have the same cycle type, it clearly suffices to show that if jj follows ii in the cycle decomposition of σσ, then σ1(j)σ1(j) follows σ1(i)σ1(i) in the cycle decomposition of ττ. But suppose σ(i)=jσ(i)=j. Then
τ(σ1(i))=σ1σσ−11(σ1(i))=σ1σ(i)=σ1(j)
And we are done.
Assume that and share the same cycle type. Write each permutation's cycle decomposition in such a way that the cycles are listed in nondescending order of length (including cycles of length 1). Then there's (for example)
(a1)(a2a3a4)(a5…an)=(a1)
=(b1)(b2b3b4)(b5…bn)=(b1)*(b2*b3*b4)*(b5*…*bn)
Define σ1σ1 to be the permutation that takes aiai to bi. Clearly σ∈Sn, since each of 1,…,n1,…,n appears exactly once among the aiai and once among the bi. But also, since the cycle types of σσ and ττ match, we see that
σ1σ−1(bi)=σ1σ(ai)
Where aj, bj are the ‘next’ elements in their respective cycles. Thus τ=σ1σ−1 and we are done.
Corollary 3.
The number of conjugacy classes in Sn is the number of partitions of n.
Proof.
Each cycle type in Sn corresponds to a different partition of nn, and each cycle type corresponds to a different conjugacy class. The end outcome is as follows. In Sn, we can express the size of each conjugacy class explicitly.
Theorem 4.
Suppose σ∈Sn, and let m1,m2,…mrbe the distinct integers (including 1 if applicable) in the cycle type of σ, and let there be ki cycles of order mi in σ. (Thus ∑kimi=n). Then the number of conjugates of σ is exactly
n!(k1!mk11)(k2!mk22)⋯(kr!mkrr)
Proof.
The number of cycles of a certain cycle type determines the size of a conjugacy class. Select a cycle type and arrange the cycles in a logical order. Consider the n!n! different ways to fill the ”‘holes”' in the cycles with integers ranging from 1 to n. If two similar arrangements describe the same permutation, they are said to be comparable. The fact that this is an equivalence relation and that it splits the configurations is obvious. The size of each equivalence class will be determined.
Consider a specific configuration (a permutation), and the ki cycles of order mimi in that configuration. Each cycle can be written in a variety of ways (by starting with a different element). The cycles can also appear in any of ki! possible orders while still indicating the same permutation. Thus if, for example, ki=2 and the first cycle contains a1,…al while the second contains b1,…,b1, that is the same permutation as if the first cycle contained b1,…,bl and the second contained a1,…,all. So there are ki!mkiiki!miki equivalent permutations considering the cycles of order mi. So the total number of permutations, considering each of the possible cycle orders, equivalent to the given permutation is
(k1!mk11)(k2!mk22)…(kr!mkrr)
And the result follows.
For example, let n=5 and let’s compute the size of the conjugacy class containing the permutation (23)(45). In this case,
m1=1, k1=1
m2=2=2, k2=2
And the skeleton for the permutation is
There are 5!=120 ways of placing 1,2,3,4,5 into this skeleton. However, given a particular choice, say (2)(13)(45), the first 2-cycle may be written as (13) or as (31), while the second may be written as either (45) or (54). In addition, either pair can appear first (k2=2). The number of choices for ways to represent the2-cycles is thus 2!⋅22=8. The formula in the theorem indeed predicts that there are 5!/(2!⋅22)=120/8=15 permutations with this cycle type; in fact, they are (omitting the trivial 1-cycles):
(1 2) (3 4) (1 2) (3 5) (1 2) (4 5) (1 3) (4 5) (2 3) (4 5)
(1 3) (2 4) (1 3) (2 5) (1 4) (2 5) (1 4) (3 5) (2 4) (3 5)
(1 4) (2 3) (1 5) (2 3) (1 5) (2 4) (1 5) (3 4) (2 5) (3 4)
4.3.2 Conjugacy classes in P-groups
The characters of finite p-groups with an abelian subgroup are defined by the well-known result [5, Theorem 26.9], which yields the characters of finite p-groups with an abelian subgroup of index p. To stress the number of conjugacy classes, we present this result in a slightly different approach. We can get very severe inequalities for such groups by using inequalities (6) and (7). The following lemma proves to be really helpful: G is a nonabelian p-group with an abelian subgroup H of index p, as shown in Lemma 6.1. Then there exists K C G such that K ⊆ H ∩ G0 ∩Z(G) and |K| = p.
Proof. We have 1 6= G0 C G thus G0 ∩Z(G) 6= 1. Let K be a subgroup of order p of G0 ∩Z(G). But then KH is an abelian subgroup of G; since H is maximal, it follows that KH = H, so K 6 H. Theorem 6.2. Let G be a group of order p n having an abelian subgroup H of index p. Let K be as in the lemma. Then (10) k(G) = k(G/H) + p n−2 − p n−3 . Proof. The irreducible characters of G/K lift to give exactly the characters of G that contain K in their kernel. The sum of the squares of their degrees is therefore |G/K| = p n−1 . We will construct another p n−2 − p n−3 irreducible characters of G, each of degree p; we will have then constructed all the irreducible characters of G since (11) p n−1 + (p n−2 − p n−3 )p 2 = p n = |G|. Let χ be a character of degree p of G. If χ is a sum of linear characters, then G0 6 Ker χ, thus K 6 Ker χ. Therefore if χ(1) = p and K Ker χ, then χ is irreducible. Now let Φ be the set of linear characters of H which do not have K in their kernel (that is, the lifts of the linear characters of G/K). Then |Φ| = p n−1 − p n−2 . Let ψ∈Φ. Since K 6 Z(G) we have (ψ↑ G)(k) = pψ(k), for all k ∈ K. We can conclude that ψ↑ G has degree p and can not contain K in its kernel, therefore is irreducible. Suppose now that ψ1 is a linear character of H such that ψ↑ G= ψ1 ↑ G. The Frobenius Reciprocity Theorem gives 1 = hψ↑ G, ψ1 ↑GiG = h(ψ↑ G) ↓H, ψ1iH. Since (ψ↑ G) ↓H has degree p, there are at most p elements ψ1 of Φ such that ψ1 ↑ G= ψ↑ G. It follows that the set {ψ↑ G | ψ∈Φ} gives at least |Φ|/p = p n−2 −p n−3 irreducible characters of G with degree p which do not have K in their kernel. But relation (11) assures us that this number is also the maximum, and the conclusion follows. Since in the above hypothesis G/K is a p-group, using the inequalities (6) and (7) we obtain the following estimations. Proposition 6.3. Let G be a group of order p n having an abelian subgroup of index p. Then a) k(G) > p n−2 − p n−3 + (m − 1)(p 2 − 1) + p, if n = 2m; b) k(G) > p n−2 − p n−3 + m(p 2 − 1) + 1, if n = 2m + 1. The equality (10) provides an upper bound for k(G). Proposition 6.4. Let G be a grop of order p n having an abelian subgroup of index p. Then k(G) 6 p n−1 + p n−2 − p n−3 , with equality if and only if |G0 | = p. Proof. In view of (10), the maximum of k(G) is reached when G/K is abelian, or, equivalently, G0 ⊆ K. But K ⊆ G0 ∩Z(G) and |K| = p, thus G0 ⊆ Z(G) and |G0 | = p. But the last equality implies the first one, and the conclusion follows.
Remark 6.5. a) The above inequalities are smooth (there is a group G for which the equality holds) if and only if the inequalities (6) and (7) used on G/K are smooth. We conclude, based on the remarks in the previous section, that the following estimations for groups G having abelian subgroups of index p are smooth: k(G) > p p−1 − p p−2 + 1 2 (p 3 − p 2 + p + 1), for |G| = p p+1; k(G) > 3 4 − 3 3 + 19 = 73 for |G| = 36 ; k(G) > 5 4 − 5 3 + 53 = 553 for |G| = 56 . b) The values of k(G) for groups of order p 3 and p 4 are known. We can also calculate them using the above inequalities. Clearly, a group of order p 3 contains an abelian subgroup of order p 2 . Let G be a group of order p 4 and |Z(G)| = p 2 . We can find a subgroup H of G of order p 3 such that Z(G) 6 H. But then, if H is not abelian, H/Z(H) is cyclic of order p, a contradiction. If |Z(G)| = p, taking into account the class equation (1), there is an element x of G with |x G| = p. Then H = CG(x) is of index p. Moreover, Z(G) and hxi are distinct subgroups of H, thus |Z(H)| > p 2 . As above, we conclude that H is abelian. Consequently, using Propositions 6.3 and 6.4 we obtain k(G) = p 2 + p − 1 for |G| = p 3 and 2p 2 − 1 6 k(G) 6 p 3 + p 2 − p for |G| = p 4 ; in view of relation (10), these are the only values that k(G) can take in this case.
4.4.1 Sylow's theorem
The Sylow theorems are a set of theorems in mathematics, specifically in the subject of finite group theory, named after the Norwegian mathematician Peter Ludwig Sylow[1]. They provide extensive information regarding the number of fixed order subgroups that a given finite group possesses. The Sylow theorems are significant in the categorization of finite simple groups and are a key aspect of finite group theory.
For a prime number P, a Sylow p-subgroup (sometimes p-Sylow subgroup) of a group G is a maximal P-subgroup of G, i.e., a subgroup of G that is a p-group (so that the order of every group element is a power of P) that is not a proper subgroup of any other P-subgroup of G. The set of all Sylow P-subgroups for a given prime P is sometimes written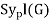 
The Sylow theorems state that Lagrange's theorem has a partial converse. The order (number of elements) of every subgroup of every finite group G divides the order of G, according to Lagrange's theorem. According to the Sylow theorems, there exists a Sylow P-subgroup of G of order P, the maximum power of P that divides the order of for any prime factor P of the order of a finite group G. Furthermore, every Sylow P-subgroup of P is a subgroup of order G, and the Sylow G-subgroups of a group (for a given prime P) are conjugate. Furthermore, for a given prime P, the number of Sylow P-subgroups of a group is equivalent to
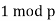
4.4.2 Consequences of Sylow's theorem
According to the Sylow theorems, for any prime number p, every Sylow p-subgroup has the same order, p. In contrast, if a subgroup has order p, it is a Sylow p-subgroup and is hence isomorphic to all other Sylow p subgroups. If h is any p-subgroup of G, then H is a subgroup of a p subgroup of order p due to the maximality criterion.
A very important consequence of Theorem 2 is that the condition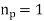 
is equivalent to saying that the Sylow p-subgroup of G is a normal subgroup. However, there are groups that have normal subgroups but no normal Sylow subgroups, such as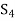 
Numericals:
1) Let G be a 57th-order group. Assume G is a non-cyclic group.
Then figure out how many elements there are in G of order 3.
Solution:
Take note of the prime factorization, which is 57=319
The number of Sylow 19-subgroups of G is n19.
We know this because of Sylow's theorem.
n191(mod19) and n193 (mod19)
As a result, n19=1.
Now notice that if gG, the order of g is either 1, 3, or 19. The order of g cannot be 57 since G is not a cyclic group.
Due to the fact that there is only one Sylow 19-subgroup P, any element not in P must have order 3.
As a result, the number of order 3 items is 5719=38.
2) Let G be a 12-order group. Demonstrate that G has a regular order 3 or 4 subgroup.
Solution:
Since 12=22⋅3, a Sylow 2-subgroup of G has order 4 and a Sylow 3-subgroup of G has order 3.
Let np denote the number of Sylow p-subgroups in G, where p=2,3 and np denotes the number of Sylow p-subgroups in G.
Remember that if np=1, the unique Sylow p-subgroup in G is normal.
We know that n2(3), therefore np=1,3 thanks to Sylow's theorem.
n31(mod3) and n34 are also defined by Sylow's theorem.
As a result, n3=1,4.
When n3=1, the unique Sylow 3-subgroup is a normal order 3 subgroup.
Assume that n3=4. After that, in G, there are four Sylow 3-subgroups.
Every non-identity element in a Sylow 3-subgroup has order 3, hence the intersection of two independent Sylow 3-subgroups intersects trivially (the intersection consists of the identity element).
As a result, each Sylow 3-subgroup has two components of order 3 that are not included in the other Sylow 3-subgroup.
In G, there are a total of 42=8 order 3 elements.
There are 128=4 elements of order not equal to 3 since |G|=12.
Because every Sylow 2-subgroup has four elements, these elements are used to fill up the gaps.
As a result, there is just one Sylow 2-subgroup, and it is a typical order 4 subgroup.
In each scenario, the G subgroup has an order 3 or 4 normal subgroup.
3. Consider the following Cayley table of a group G = {e, a, b, c}
V | e | a | b | c |
e | e | a | e | c |
a | a | e | c | b |
b | b | c | e | a |
c | c | b | a | e |
ANSWER-
We have
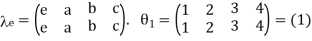
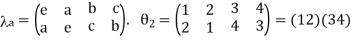
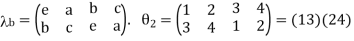
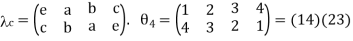
Hence G is isomorphic to the subgroup
{(1),(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)} = h(1 2)(3 4),(1 3)(2 4)i of S4.
Cauchy's integral theorem
In complex analysis, the Cauchy integral theorem (sometimes known as the Cauchy–Goursat theorem) is a key statement regarding line integrals for holomorphic functions in the complex plane, named after Augustin-Louis Cauchy (and ÉdouardGoursat). It states that if two separate pathways connect the same two points and a function is holomorphic everywhere in between the two paths, then the function's two path integrals will be the same.
Proof
If one assumes that the partial derivatives of a holomorphic function are continuous, the Cauchy integral theorem can be proved as a direct consequence of Green's theorem and the fact that the real and imaginary parts of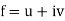 
must satisfy the Cauchy–Riemann equations in the region bounded by , and moreover in the open neighborhood U of this region. Cauchy provided this proof, but it was later proved by Goursat without requiring techniques from vector calculus, or the continuity of partial derivatives.
The integrand f, as well as the differential dz, can be broken down into real and imaginary components:
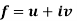
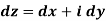
In this case we have
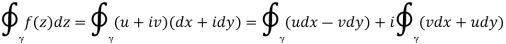
By Green's theorem, we may then replace the integrals around the closed contour with an area integral throughout the domain D that is enclosed by as follow
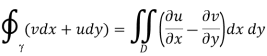
However, because u and v are the real and imaginary components of a holomorphic function in the domain D, they must fulfil the Cauchy–Riemann equations there:
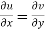
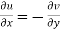
As a result, both integrands (and hence their integrals) are zero.
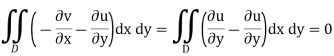
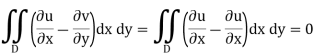
This gives the desired result
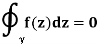
Numericals:
1) Evaluate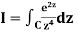 
where C:|z|=1.
Solution:
With Cauchy’s formula for derivatives this is easy. Let f(z)=e2z. Then,
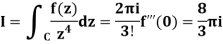
Let C represent the contour given below, and assess the same integral as before.
The integral is the same as the previous example, i.e. 
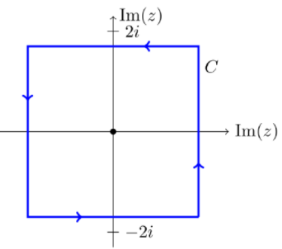
2) Compute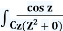 
dz over the contour shown.
Solution
Let f(z)=cos(z)/(z2+8). f(z) is analytic on and inside the curve C. That is, the roots of z2+8 are outside the curve. So, we rewrite the integral as
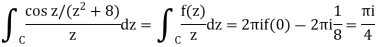
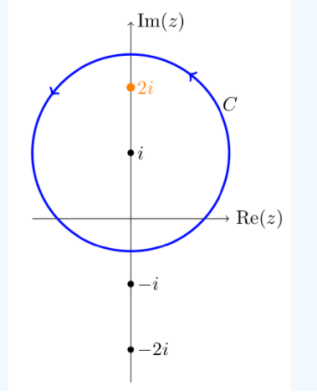
3) Compute 
dz over the contour shown.
Solution:
The denominator is factored as
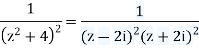
Let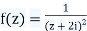 
Inside C, clear f(z) is analytic. So, according to Cauchy's derivatives formula:
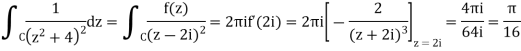
The fundamental concept is to use the commutator [g, h] := ghg1h 1 as a starting point. It's worth noting that we can think of this as g times a g1 conjugate or h times h1 conjugate. In our proof, we'll use both of these approaches to the commutator. The first stage is to identify a set of generators for An with limited support (moving only a few points): I assert that 3-cycles generate An, and that any two 3-cycles are conjugate if n 5. It suffices to note that a product of two separate transpositions is either a 3-cycle or a product of two 3-cycles for the first assumption. (1 2)(2 3) = (1 2 3) and (1 2)(3 4) = (1 4 3) are two common examples (1 2 3). For the second assumption, remember that in Sn, any two 3-cycles, say gg1 =, are conjugate. If g is an odd permutation, replace it with gh, where h is a centralising transposition. [This exists because n is more than 5.] Assume that 1 6= H E An Given the claim we just proved, if we can show that H contains a 3-cycle, the simplicity of An will follow. So, until we locate a 3-cycle in H, our goal will be to try to find an element h H with the simplest feasible cycle structure. Begin with a nontrivial h H, such as h(1) = 2. Consider the commutator [g, h] for any 3-cycle that does not involve 2, such as g = (1 3 4). We can see that the commutator is in H if we think of it as kh1 (where k is a conjugate of h). [g, h] can also be written as g(hg1h 1 ), indicating that it is the product of two 3-cycles, (1 3 4)(2 h(4) h(3)). The presence of 2 in only one location demonstrates that [g, h] 6= 1. When we replace h with this commutator, we get a nontrivial h H that is a product of two 3-cycles! Let's try to make it even simpler. Assume the two 3-cycles are disjoint, and h has a cycle decomposition of the kind h = (1 2 3). (4 5 6). Because (1 2 3)(4 5 6) is centred by the odd permutation (1 4)(2 5) in An, all permutations of this type are conjugate (3 6). As a result, H contains all of them. H contains k := (1 2 3)(4 5 6)1, and the product kh is a three-cycle in H, as required. Assume that the two 3-cycles are not disconnected at this point. Then h moves no more than 5 points, resulting in h being contained within an isomorphic duplicate of A5 within An. Thus H0 := H ∩A5 is a nontrivial normal subgroup of A5 and hence is all of A5, since we already know that the latter is simple. In particular, H0 contains a 3-cycle, and the proof is complete. What made this proof work, aside from some ad hoc arguments once we got down to A5? I see two general principles: (a) If H E G, then H is closed under the operation of forming commutators with arbitrary elements of G. (b) If g has “small support”, then [g, h] is often simpler than h [because it is the product of g and something that resembles g].
Sylow's test: Let n be a non-prime positive integer, and p be a prime divisor of n. There is no simple group of order n if 1 is the only divisor of n that is congruent to 1 modulo p.
Proof:
If n is a prime-power, then a group of order n has a nontrivial center[10] and, therefore, is not simple. If n is not a prime power, then every Sylow subgroup is proper, and, by
According to Sylow's Third Theorem, the number of Sylow p-subgroups of an order n group is equal to 1 modulo p and divides n. The Sylow p-subgroup is unique since 1 is the only such number, and hence it is normal. The group is not simple since it is a proper, non-identity subset.
Burnside: Order is divisible by at least three distinct primes in a non-Abelian finite simple group. This is the result of Burnside's theorem.
Let G be a group of Composite order such that p∣ o (G) where p is a prime number. If 1 is the only divisor of o (G) that is congruent to 1 mod p, then G is not simple. Proof: We have two cases Case I. o (G) = pn since o (G) = pn therefore Z (G) {e} Thus Z (G) is a proper normal subgroup of G. Hence G is not simple. Case II. O (G) = pn q By Sylow’s third theorem number of sylow p subgroups is 1+ kp where 1+ kp∣ o (G) Since 1 is the only divisor of that is congruent to 1 mod p therefore 1+ kp =1 Thus there is a unique sylow p subgroup which is normal is G. Hence G is not simple. Sylow Test for Non Simplicity serves an important tool for testing the simple groups up to order 200. After applying Sylow Test for Non Simplicity the only possible simple groups having composite order are of order 12, 24, 30, 36, 48, 56, 60, 72, 80, 90, 96, 105, 108, 112, 120, 132, 144, 150, 160, 168, 180, 192.
Theorem 2.7
If G is a group such that o (G) =pq where pq p,q are primes and p ∤ q-1. Then G is cyclic Proof: By Sylow’s First Theorem G has atleast on Sylow p-subgroup and one Sylow q-subgroup. By Sylow’s Second Theorem, the number of Sylow p-subgroup is 1+kp where 1+kp∣q Thus 1+kp = 1 or q
If 1+kp = 1 then sylow p-subgroup is unique hence normal in G hence G has a proper Normal subgroup thus G is not simple then we are through Again by Sylow’s Second Theorem, the number of Sylow q-subgroup is 1+kq where 1+k’q∣p Thus 1+k’q = 1 or p If 1+k’q = 1 then sylow q-subgroup is unique hence normal in G hence G has a proper Normal subgroup thus G is not simple again we are through If 1+k’q = p then k’q = p – 1 which means that q ∣p – 1 which is not true. Now o (H) = p, o (K) = q, and H ∩ K is a subgroup of both H and K. ∴o(H ∩ K) | p and o(H ∩ K) | q ⇒ o(H ∩ K) | (p,q ) ⇒o(H ∩ K) | 1 ⇒o(H ∩ K) | = 1 ⇒H ∩ K = {e}
We know if H and K are normal subgroups of G such that H ∩ K = {e}, Then hk = kh∀ h ∈ H and k ∈ K. Now H and K, being groups of prime orders, are cyclic. ∴ let H = , K = so that o (a) = o (H) =p, o (b) = o (K) = q Now ab=ba [because hk = kh∀ h ∈ H and k ∈ K]. And (o (a), o (b)) = (p, q) =1 Therefore o (ab) = o (a). o (b) = pq=o (G) Thus G has an element ab of order pq thus G is cyclic. After proving the result 2.7 the group satisfying the condition of 2.7 will always be cyclic group and as cyclic group is always abelian and by using 2.1 abelian group of composite order is not simple.
NUMERICALS
1) G is a group with the order 520=23513. We can see that np denotes the number of Sylow p-subgroups of G.
ANSWER
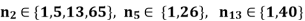
Assume that neither n2,n5 nor n13 equals 1 (otherwise, we're finished). Then n13=40, and there are 40(131)=480 order 13 elements. Similarly, n5=26, and order 5 has 26(51)=104 items. This implies that G has at least 480+104=584 elements, which is not conceivable. As a result, at least one of n2,n5, or n13 must equal 1, indicating that G is not simple.
References:
1. M. Artin, Abstract Algebra, 2nd Ed., Pearson, 2011.
2. David S. Dummit and Richard M. Foote, Abstract Algebra, 3rd Ed., John Wiley and Sons (Asia) Pvt. Ltd., Singapore, 2004.
3. J.R. Durbin, Modern Algebra, John Wiley & Sons, New York Inc., 2000.
