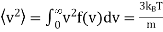Unit - 3
Kinetic Theory of Gases
3.1.1 Kinetic Theory of Gases
A gas has certain properties, such as temperature, pressure, energy, etc. which are characteristic of the gas as a whole rather than of its individual molecules.
In the kinetic theory of gases, we tend to relate the microscopic behaviour of the individual gas molecules to the macroscopic properties of the gas as a whole.
The kinetic theory is based on the following fundamental assumptions.
(i) A gas is composed for a large number of minute discrete particles called molecules. The molecules of a gas are considered rigid, perfectly elastic, solid spores, identical in all respects such as mass and size; but these properties differ from gas to gas.
(ii) The molecules within a container are in a state of ceaseless chaotic motion during which they move in all directions with all possible velocities.
(iii) The molecules in their motion collide with each other and with the walls of the container. Thus, their speeds and directions are changing continuously. It does not affect the molecular density of the gas as the molecules do not accumulate at any place.
(iv) The bombardment of the container walls by the molecules gives rise to the phenomenon called pressure which is the rate of change of momentum per unit surface area of the walls.
(v) All collisions between molecules and with the walls are perfectly elastic so that there is no loss of kinetic energy in the collisions.
(vi) The molecules exert no forces on each other except when they collide which means that the energy of the gas is wholly kinetic.
(vii) The molecules traverse straight paths between collisions. The distance between any two consecutive collisions in called free energy path and the average distance travelled by a molecule between successive collisions is called the mean free path.
(viii) The time of collision is negligible as compared with the time taken to traverse the free path.
(ix) Since the molecules are small as compared with the distance between them, their volume may be considered to be negligible compared with the total volume of the gas.
3.1.2 Maxwell-Boltzmann Law of Distribution of Velocities in an Ideal Gas
The law of distribution of velocities was first established by Clark Maxwell. The proof of which by direct methods was given by Boltzmann. The law is known as the Maxwell-Boltzmann's distribution law for the molecular velocities.
Maxwell and Boltzmann utilizing probability considerations, have in fact, shown that actual distribution of molecular velocities depends upon the temperature and molecular weight of a gas.
In order to derive the Maxwell-Boltzmann's law, let the gas molecules be assumed to obey the following conditions:
1. The number of gas molecules is large enough so that the number of molecules in any region in the same and that the molecules possess the same velocities in all directions.
2. The velocities along the three perpendicular co-ordinate axes-are independent of each other.
3. The probability that any molecule selected at random has velocities lying between certain limits is purely a function of the velocity and of the limits considered.
Let us now represent the molecules in a velocity diagram, with O as the origin and OX, OY, OZ as the coordinate axes. Then any given  and vx, vy, vz along X, Y and Z axes respectively. Thus, the relation velocity vector
and vx, vy, vz along X, Y and Z axes respectively. Thus, the relation velocity vector  can be decomposed into components vx, vy, vz.
can be decomposed into components vx, vy, vz.
Thus, the relation is given by
 ..... (1)
..... (1)
From assumption 3, it is obvious that the probability that a given molecule will have its velocity lying between vx and vx + d vx or is purely a function of the values of vx and dvx i.e., it may be written f (vx)dvx
Further, since the velocities are similar and equivalent in all directions the probability that the molecule will have velocity between vy and vy + dvy is f(vy)dvy and between vz and vz + d vz f (vz)dvz.
Since the probability of a composite event is equal to the product of the probabilities of individual events, provided that they are independent
By assumption 2, is given by
f (vx) f(vy) f (vz) dvx dvy dvz
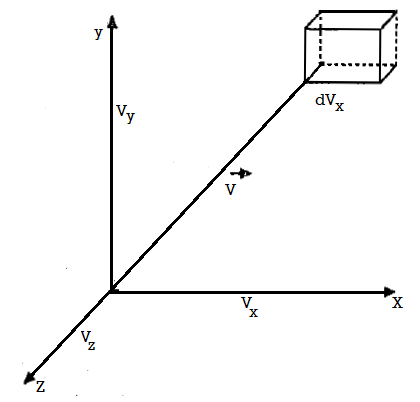
Figure 1: Maxwell-Boltzmann's distribution law
The resultant velocity of the molecules is given by a single 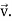 The probability of velocity
The probability of velocity  lies in the element of volume dvx dvy dvz is a function of v and of dvx dvy dvz, or more conveniently as φ(
lies in the element of volume dvx dvy dvz is a function of v and of dvx dvy dvz, or more conveniently as φ(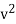 )dvx dvy dvz
)dvx dvy dvz where φ denotes some function.
where φ denotes some function.
On account of the isotropy of the gas, as regards the molecular velocity, we may write
f (vx) f(vy) f (vz) dvx dvy dvz = φ(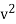 ) dvx dvy dvz
) dvx dvy dvz
Or using equation (1)
f (vx) f(vy) f (vz) = φ(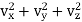 ) …..... (2)
) …..... (2)
In order to solve this equation, we note that for a particular value of v chosen; φ(v2) is a constant i.e., the differential of this quantity is equal W zero, hence
d [φ(v2)] = 0
d [f (vx) f(vy) f (vz)] =0
Differentiating it,
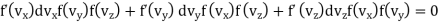
Dividing by f (vx) f(vy) f (vz)
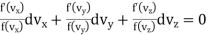 …..... (3)
…..... (3)
Now from eqn. (1), we have
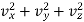
Which on differentiation for a fixed (constant) value of v gives
vxdvx + vydvy + vzdvz = 0
Multiplying eqn. (3) by an arbitrary constant  and adding the resultant to equation
and adding the resultant to equation
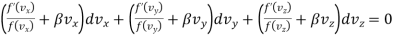 …..... (4)
…..... (4)
Now since by assumption 2 the velocity components are independent of each other, equation (4) can be satisfied only if each of the term is separately equal to zero.
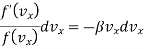
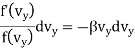
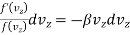 …..... (5)
…..... (5)
Therefore
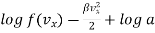 …..... (6)
…..... (6)

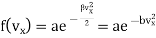 …..... (7)
…..... (7)
Where b = 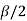
Similarly
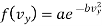
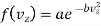 …..... (8)
…..... (8)
From eq (7) and (8)
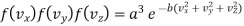 …..... (9)
…..... (9)
Thus f (vx) dvx, the probability that a molecule has velocity vx and vx + d vx
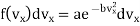 …..... (10)
…..... (10)
This distribution law expressed in eqn. (10) is represented graphically in figure where  is plotted against x. Thus b
is plotted against x. Thus b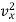 has been put equal to x2. The maximum ordinate of the Curve corresponds to vx = 0 and has the value a which has been put equal to 1 in figure.
has been put equal to x2. The maximum ordinate of the Curve corresponds to vx = 0 and has the value a which has been put equal to 1 in figure.
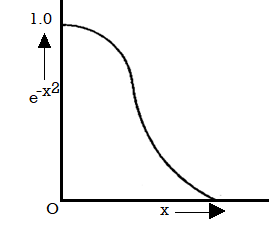
Figure 2: Distribution law
Evaluation of constants 'a' and 'b’
Let n be the number of molecules per unit volume of the gas with all possible velocities from -  to +
to +  . Then the number of molecules per unit volume with velocity components between vx and vx + dvx, vy and vy +dvy, vz and vz + dvz is nf (vx) f(vy) f (vz) dvx dvy dvz
. Then the number of molecules per unit volume with velocity components between vx and vx + dvx, vy and vy +dvy, vz and vz + dvz is nf (vx) f(vy) f (vz) dvx dvy dvz
Hence
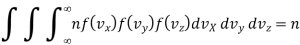
Substituting the values of the function from eqn. (9), we get
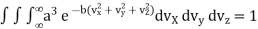 …..... (11)
…..... (11)
The value of the definite integral of
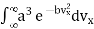 is
is 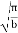
Substituting the values of such integrals in eqn, (11), we have
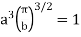
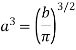
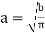 …..... (12)
…..... (12)
To determine b let us first calculate the pressure exerted by the gas on the walls of the enclosure. For it, let us consider a perfect gas enclosed in a vessel and take the X-axis to be perpendicular to one surface of the enclosure. Then a molecule moving with a velocity component vx will collide with this surface and will be reflected with a velocity — vx after collision.
Hence the change in momentum suffered by the molecule during collision is 2mvx. The other two components viz. vy and vz suffer no change, hence they contribute nothing to the pressure and can be neglected. Now pressure is equal to the change in momentum suffered by the molecule striking per unit area of the wall per second and hence it is equal to 2mvx multiplied by the number of collisions on the surface in-unit time.
If 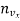 the number of molecules per unit volume having the velocity vx, the number of impacts on an area
the number of molecules per unit volume having the velocity vx, the number of impacts on an area  A in time
A in time 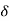 t must be equal to
t must be equal to 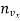 vx
vx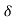 t
t A.
A.
Hence the pressure P on the wall, averaged through the time interval 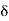 t is given by
t is given by
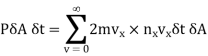
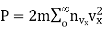 …..... (13)
…..... (13)
The sign of summation has been put because the pressure is caused by all molecules having a positive X-component of velocity which can have value ranging from 0 to 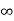 .
.
Now the number of molecules per unit volume having the velocity component lying between vx and vx +dvx, is given in accordance of eqn. (10) to be

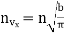
 …..... (14)
…..... (14)
Substituting this value of 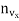 in eqn. (14) and replacing the sign of summation by the sign of integration we get
in eqn. (14) and replacing the sign of summation by the sign of integration we get
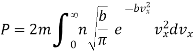
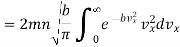
 …..... (15)
…..... (15)
Because
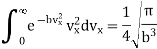
But P is equal to nkT, where k is Boltzmann constant. Therefore
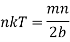
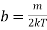 …..... (16)
…..... (16)
Substitution value of b in equation (12), we get
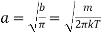 …..... (17)
…..... (17)
Thus, number dn of molecules having velocity component lying in the velocities vx and vx +dvx, vy and vx +dvy, vz and vz +dvz.
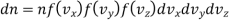
 …..... (18)
…..... (18)
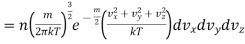 …..... (19)
…..... (19)
This is Maxwell’s Distribution Law.
Number of molecules having velocity within v and v + dv
Let all such molecules' lie between two concentric spheres of radii v and v + dv with O as the common centre, the starting point of all molecules.
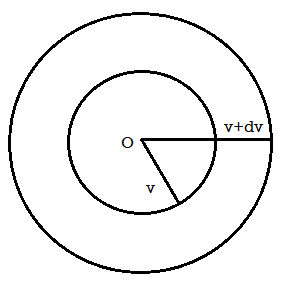
Figure 3: Number of molecules having velocity within v and v + dv
Then volume
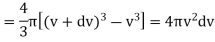
This is the same at the so called velocity volume dvx dvy dvz of equation (18).
Hence substituting 4πv2 for dvx dvy dvz and putting v2 =  in equation (18), we get
in equation (18), we get
 …..... (20)
…..... (20)
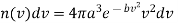 …..... (21)
…..... (21)
This is the required Maxwell-Boltzmann's distribution law for molecular velocities. In this expression n (v) dv is the number of molecules out of a total it having velocities lying between v and v + dv.
Graphical Representation
In equation (20) put bv2 =x2
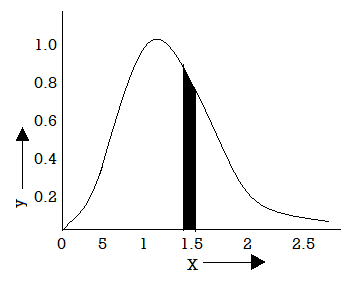
Figure 4: Graphical Representation
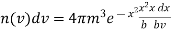
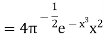
=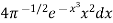 …..... (22)
…..... (22)
Which helps of represent the law graphically figure given the plot of the function
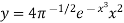 against x.
against x.
The number of molecules it (v) dv having velocities lying between x and x + dx is proportional to the shaded area. The total area between the curve and the x-axis gives the total number of molecules having velocities between zero and infinity. Thus, the molecular velocities range from zero to infinity.
From this plot it may be seen that the probability of a molecule being motionless an any instant is extremely small. It is zero when x =0 or x = 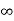 .
.
For velocities greater that zero, the probability increases which passes through the maximum and then falls away towards zero again for very high velocities.
Thus, both, very high and very low, velocities are highly improbable.
The probability corresponding to x = 1 is maximum while it is considerably small for x=2 or x= 1/2.
The velocity for which the curve is maximum is the most probable velocity. If we were to pick molecules at random, this velocity would be found most often.
3.1.3 Experimental Verification
Maxwell-Boltzmann law of distribution of molecular velocities was put to experimental test and found to be true.
From the finite width of spectral lines
The Maxwell-Boltzmann law can be verified by a study of the width of a spectral line. Theoretically every monochromatic beam of light should be represented by a line of no width (geometrical line) but the Doppler effect causes a broadening of otherwise narrow spectral lines. Thus, every spectral line has a finite width, because of the fact that no radiating atom is absolutely at rest but moving in all directions with all possible velocities.
The light emitted by an atom would be represented by a single line only if the atom is at rest but according to kinetic theory they are moving to and fro, the distribution of velocities being given by Maxwell's law.
Hence if the frequency of light emitted by an atom at rest is v0, that emitted by an atom approaching the observer with a velocity v would be changed by Doppler effect to vo(1 +v/c) where c is the velocity of light.
Since v varies from 0 to 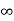 , the spectral line should theoretically have all frequencies or be of infinite width. But according to Maxwell's law very high velocities are extremely rare and hence their contribution to intensity is extremely small. We can now find the distribution of intensity in the line.
, the spectral line should theoretically have all frequencies or be of infinite width. But according to Maxwell's law very high velocities are extremely rare and hence their contribution to intensity is extremely small. We can now find the distribution of intensity in the line.
According to Maxwell's law the number of Molecule having their velocity lying between v and v + dv is given by
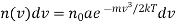
Where a is a constant.
These particles emit light of frequency ν 0 (1 +v/c) and the intensity of spectral line is proportional to the number of the particles.
Therefore,
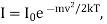
Where I0 is the intensity of the central line.
If λ0 = ν/c is the wave-length of the central line and an (λ0-x) of that corresponding to the frequency ν0 (1 +v/c).
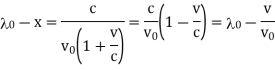
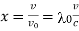
If Ix, is the intensity at a distance x (measured in wave-length units) from the
Central line, then
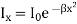
Where
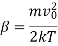
The distribution of intensity in the line about the centre is shown in Figure.
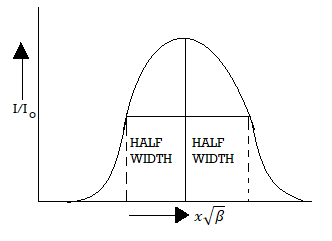
Figure 5: Distribution of intensity
The distance on the wavelength scale on either side, where Ix =  I0 is known as half width and is denoted by ω.
I0 is known as half width and is denoted by ω.

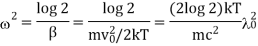
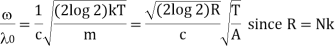
Where A is the atomic weight.
Thus, the half width is inversely proportional to atomic weight of the element i.e., it is more for lighter elements. It has actually been found to be so. Hydrogen lines are always found to be very much broad and diffuse. On the other hand, spectral lines due to heavy elements like Ag and Cd are found to be quite sharp thus, leading to an experiment verification of the Maxwell's law of distribution of velocities.
Key Takeaways
- A gas has certain properties, such as temperature, pressure, energy, etc. which are characteristic of the gas as a whole rather than of its individual molecules.
- In the kinetic theory of gases, we tend to relate the microscopic behaviour of the individual gas molecules to the macroscopic properties of the gas as a whole.
- The law of distribution of velocities was first established by Clark Maxwell. The proof of which by direct methods was given by Boltzmann. The law is known as the Maxwell-Boltzmann's distribution law for the molecular velocities.
- Maxwell and Boltzmann utilizing probability considerations, have in fact, shown that actual distribution of molecular velocities depends upon the temperature and molecular weight of a gas.
- The Maxwell-Boltzmann law can be verified by a study of the width of a spectral line.
The first direct experimental proof of Maxwell's law was given by Stem. Figure depicts the principle of his experiment, where L is a platinum wire coated with silver and represented perpendicular to the plane of the paper.
The wire is heated by an electric current and consequently it emits atomic silver in all-directions.
The slits S1 and S2 which are parallel to the platinum wire, define a stream of silver which condenses on the plates P and P'.
The whole apparatus is enclosed in a highly evacuated glass vessel so that the silver atoms may not suffer any collisions in space.

Figure 6: Stern's Experiment
The slits S1, S2 and the plates P, P' are rotated together as a rigid system about the wire L as axis in a clockwise direction as shown.
Had the plates been at rest, the stream would have traversed along LO forming a deposit at O but when the system is rotating at a high speed, as shown, the deposit is formed at a pea A above. Fast moving molecules or atoms will condense nearer to O, than the slower ones.
A velocity spectrum of silver will this be obtained. The relative intensity of the deposit can be measured by means of a microphotometer and then the ratio of number of molecules with different velocities can be deduced and Maxwell Boltzmann's law tested.
The results of Stem were however, not quite satisfactory because of the difficulty in retaining vacuum in the vessel as the spindle of the rotating system had to project outside the vessel for coupling it to the driving motor, as a result the Maxwellian law could be verified about 15%.
We want the fraction of molecules which are travelling with speeds between v = |v| and v +dv, and this corresponds to a spherical shell in velocity space of radius v and thickness dv. The volume of velocity space corresponding to speeds between v and v + dv is therefore equal to
4πv2dv
So that the fraction of molecules with speeds between v and v + dv can be defined as f(v) dv, where f(v) is given by
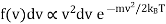 …..... (1)
…..... (1)
In this expression the 4π factor has been absorbed in the proportionality sign.
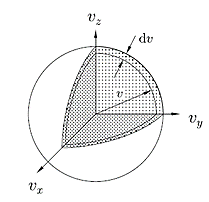
Figure 7: Molecules with speeds between v and v + dv occupy a volume of velocity space inside a spherical shell of radius v and thickness dv.
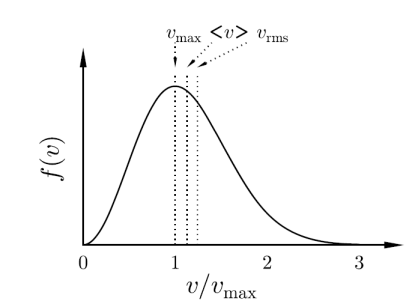
Figure 8: f(v), the distribution function for molecular speeds
To normalize this function, so that 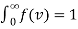 . We integrate between 0 and ∞, because the speed v = |v| is a positive quantity.
. We integrate between 0 and ∞, because the speed v = |v| is a positive quantity.
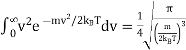 …..... (2)
…..... (2)
And
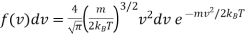 …..... (3)
…..... (3)
This speed distribution function is known as the Maxwell–Boltzmann speed distribution, or sometimes simply as a Maxwell distribution and is plotted in Figure.
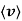 and
and 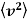
It is straight forward to find the following expected values of the Maxwell Boltzmann distribution using standard integrals
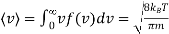 …..... (4)
…..... (4)
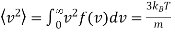 …..... (5)
…..... (5)
From (4) and (5)
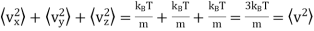 …..... (6)
…..... (6)
The root - mean squared speed of a molecule
 …..... (7)
…..... (7)
Is proportional to m−1/2.
The mean kinetic energy of a gas molecule is given by
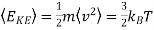 …..... (8)
…..... (8)
This is an important result, and we will later derive it again by a different route. It demonstrates that the average energy of a molecule in a gas depends only on temperature.
The maximum value of f(v) is found by setting
Df/dv = 0 ……….. (9)
And differentiation of eqn (9) yields
 ……….. (10)
……….. (10)
Since
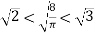 ……….. (11)
……….. (11)
We obtained
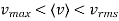 ……….. (12)
……….. (12)
And hence the points marked on Figure are in the order drawn. The mean speed of the Maxwell–Boltzmann distribution is higher than the value of the speed corresponding to the maximum in the distribution since the shape of f(v) is such that the tail to the right is very long.
Example: Mass of the oxygen molecule is 5.28 x10-26 Kg and its mean velocity at N.T.P. Is 4.25 x 102m/s. Calculate average kinetic energy of the molecule at 00C.
Solution
Average speed
r.m.s speed 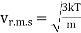
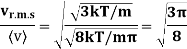
Average kinetic energy of oxygen molecule
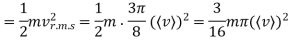
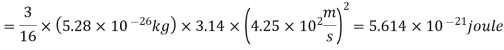
Example: Compute the most probable speed. The mean speed, end the root mean-square speed for helium at 0°C.
Solution:
Mass of a helium atom
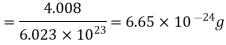
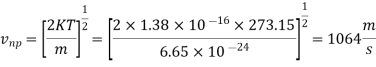
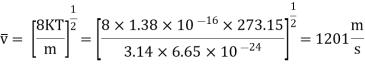
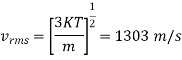
Key Takeaways
The number of degrees of freedom of a dynamical system is defined as the total number of co-ordinates or independent variables required to describe the position and configuration of the system.
For translatory motion
(a) A particle moving in a straight line along any one of the axes has one degree of freedom. For example: Bob of an oscillating simple pendulum.
(b) A particle moving in a plane (X and Y axes) has two degrees of freedom. For example: An ant that moves on a floor.
(c) A particle moving in space (X, Y and Z axes) has three degrees of freedom. For example: a bird that flies.
Monoatomic Molecule
Since a monoatomic molecule consists of only a single atom of point mass it has three degrees of freedom of translatory motion along the three co-ordinate axes as shown in figure.
Figure 9: Monoatomic Molecule
Examples: molecules of rare gases like helium, argon, etc.
Diatomic molecule

Figure 10: Diatomic Molecule
The diatomic molecule can rotate about any axis at right angles to its own axis. Hence it has two degrees of freedom of rotational motion in addition to three degrees of freedom of translational motion along the three axes. So, a diatomic molecule has five degrees of freedom as shown in figure.
Examples: molecules of O2, N2, CO, Cl2, etc.
Triatomic molecule (Linear type)
Figure 11: Triatomic Molecule
In the case of triatomic molecule of linear type, the centre of mass lies at the central atom. It, therefore, behaves like a diatomic molecule with three degrees of freedom of translation and two degrees of freedom of rotation, totally it has five degrees of freedom as shown in figure.
Examples: molecules of CO2, CS2, etc.
Triatomic molecule (Non-linear type)
A triatomic non-linear molecule may rotate, about the three mutually perpendicular axes, as shown in figure. Therefore, it possesses three degrees of freedom of rotation in addition to three degrees of freedom of translation along the three co-ordinate axes Hence it has six degrees of freedom Examples: molecules of H2O, SO2, etc.
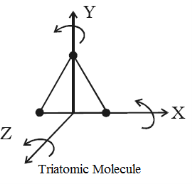
Figure 12: Triatomic Molecule
In all the above cases, only the translatory and rotatory motion of the molecules have been considered. The vibratory motion of the molecules has not been taken into consideration.
Key Takeaways
- The number of degrees of freedom of a dynamical system is defined as the total number of co-ordinates or independent variables required to describe the position and configuration of the system.
- In the case of triatomic molecule of linear type, the centre of mass lies at the central atom.
- It, therefore, behaves like a diatomic molecule with three degrees of freedom of translation and two degrees of freedom of rotation, totally it has five degrees of freedom
A point mass cannot undergo rotation, but only translatory motion. A rigid body with finite mass has both rotatory and translatory motion. The rotatory motion also can have three co-ordinates in space, like translatory motion; Therefore, a rigid body will have six degrees of freedom; three due to translatory motion and three due to rotatory motion.
Equipartition theorem very often in physics one is faced with an energy dependence that is quadratic in some variable.
The kinetic energy EK.E. of a particle with mass m and velocity v, which is given by
EKE = 1/2mv2 ……… (1)
The potential energy EPE of a mass suspended at one end of a spring with spring constant k and displaced by a distance x from its equilibrium point. This is given by
EPE = 1/2kx2 ……… (2)
In fact, the total energy E of a moving mass on the end of a spring is given by the sum of these two terms, so that
E = EKE + EPE = 1/2mv2 + 1/2kx2
And, as the mass undergoes simple harmonic motion, energy is exchanged between EKE and EPE, while the total energy remains fixed.
Let us suppose that a system whose energy has a quadratic dependence on some variable is allowed to interact with a heat bath. It is then able to borrow energy occasionally from its environment, or even give it back into the environment. Mean thermal energy it would have
The thermal energy would be stored as kinetic or potential energy, so if a mass on a spring is allowed to come into thermal equilibrium with its environment, one could in principle take a very big magnifying glass and see the mass on a spring jiggling around all by itself owing to such thermal vibrations.
The energy E of a system is
E = αx2
Let the energy E of a particular system be given by where α is some positive constant and x is some variable.
Let us also assume that x could in principle take any value with equal probability. The probability P(x) of the system having a particular energy αx2 is proportional to the Boltzmann factor  so that after normalizing, we have
so that after normalizing, we have
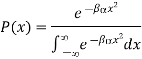
And mean energy is
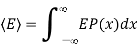
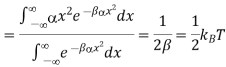
Each quadratic energy dependence of the system is called a mode of the system or degree of freedom of the system. The spring has two such modes.
The result of the example above shows that each mode of the system contributes an amount of energy equal to  kBT to the total mean energy of the system. This result is the basis of the equipartition theorem.
kBT to the total mean energy of the system. This result is the basis of the equipartition theorem.
Equipartition theorem
If the energy of a classical system is the sum of n quadratic modes, and that system is in contact with a heat reservoir at temperature T, the mean energy of the system is given by n ×  kBT.
kBT.
The equipartition theorem expresses the fact that energy is “equally partitioned” between all the separate modes of the system, each mode having a mean energy of precisely  kBT.
kBT.
Let us consider one mole of a monoatomic gas in thermal equilibrium at temperature T. Each molecule has 3 degrees of freedom due to translatory motion. According to kinetic theory of gases, the mean kinetic energy of a molecule is 3/2 kT.
½ mC2 = ½ mCx2 + ½ mCy2 + ½ mCz2
So, ½ mCx2 + ½ mCy2 + ½ mCz2 = 3/2 kT
Since molecules move at random, the average kinetic energy corresponding to each degree of freedom is the same.
½ mCx2 = ½ mCy2 = ½ mCz2
That is, ½ mCx2 = ½ mCy2 = ½ mCz2 = ½ kT
Thus, mean kinetic energy per molecule per degree of freedom is ½ kT.
Example: Hydrogen gas is heated in a vessel to a temperature of 1000 K. Let each molecule possess energy E1. A few molecules escape into atmosphere at 400 K. Due to collisions their energy changes to E2. Calculate E1/E2.
Solution:
At 1000 K, degree of freedom of hydrogen (diatomic gas), n = 7.
Thus, K.E. Per molecule, E1 = 7/2 kT = 7/2 k (1000) = 3500 k
At 400 K, degree of freedom of H2 = 5
K.E. Per molecule, E2 = 5/2 kT = 5/2 k (400) = 1000 k
Therefore,
E1/E2 = 3500 k/1000 k = 7/2
Key Takeaways
- Equipartition theorem very often in physics one is faced with an energy dependence that is quadratic in some variable.
- The equipartition theorem expresses the fact that energy is “equally partitioned” between all the separate modes of the system, each mode having a mean energy of precisely
 kBT.
kBT.
The specific heat capacity of a substance may be defined as the quantity of heat required to raise the temperature of unit mass of the substance by one degree. The unit of specific heat is J/kg-°C.
The quantity of heat required to raise the temperature of 1 kg of water by 1°C or 1 K is approximately 4.19 kJ. Hence, the specific heat capacity of water is 4.19 kJ/kg-°C or 4.19 kJ/kg-K.
The solids and liquids have only one value of specific heat but a gas is considered to have two distinct values of specific heat capacity.
- At constant pressure, Cp, and
- At constant volume, Cv.
The specific heat at constant pressure is greater than the specific heat at constant volume because heat supplied to a gas at constant pressure is utilized for two purposes for increasing the internal energy and also for doing the external work.
The ratio (specific heat of a gas at constant pressure/specific heat of a gas at constant volume) is denoted Greek letter γ ‘gamma’. It is also called the adiabatic index. This ratio of specific heats is of importance in perfect gas calculations.
Following the equipartition principle, the mean total energy of a molecule having f degrees of freedom is
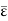 =
= 
And the total energy of N molecules is:
U = N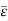 =
= 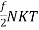 =
= 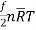
Or, molal internal energy, u = 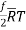
And molal specific heat at constant volume:
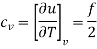
For an ideal gas
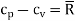
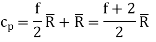

It is to be noted that cv, cp and 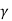 are all constants and independent of temperature.
are all constants and independent of temperature.
For a monoatomic gas which has only translational kinetic energy f = 3. Thus,

According to the classical kinetic theory of gases this ratio should have the values for monoatomic, diatomic and polyatomic gases are 5/3, 7/5 and 4/7 respectively.
Key Takeaways
- The specific heat capacity of a substance may be defined as the quantity of heat required to raise the temperature of unit mass of the substance by one degree. The unit of specific heat is J/kg-°C.
- The specific heat at constant pressure is greater than the specific heat at constant volume because heat supplied to a gas at constant pressure is utilized for two purposes for increasing the internal energy and also for doing the external work.
3.7.1 Mean Free Path
If molecules were truly geometrical points, no collision would take place between them. Actual molecules are, however, of finite size, rigid, perfectly elastic spheres free from mutual force action. They make frequent collisions with each other and change the magnitude and direction of their velocities.
As the molecules exert no force on one another except during collisions, they move in straight lines with uniform velocity between two successive collisions, this straight-line path being called the free path.
Thus, the path of the centre of mass of a small field molecules must be an irregular zig-zag having at each corner a collision with another molecule and consisting of straight free paths between them as shown in Figure.
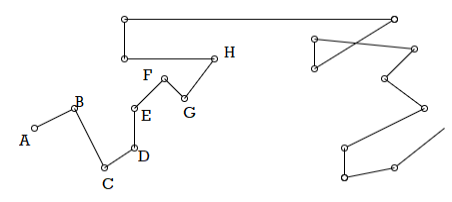
Figure 13: Mean Free Path
Thus, a molecule starting from A moves along AB, suffers a collision at B with another Molecule when the direction as well as magnitude of its velocity is changed and it moves along BC. After travelling a distance BC, it again suffers a collision at C A and moves, along CD and so on. AB, CD, DE etc., are all known as free paths and their individual lengths vary widely.
If we follow a molecule until it has traversed a great many free paths, the average of their lengths will have a definite value which is called the mean free path and is denoted by λ.
Thus, the mean free path is the average distance through with a molecule can travel through a gas without colliding with another molecule. It may be called the average free-run between-two collisions.
The distance traversed by a molecule between successive collisions is called the free path and the average length of these paths is called the mean free path.
It is a statistical quantity. However, if a reference is made to a group of molecules instead of a single one and a mean value of all the free paths that are executed in a given time by all the molecules in a given volume is taken we shall get a definite quantity provided the time and volume ate not too small.
Thus, if λ1, λ2, λ3, ………… λn are the successive free paths traversed in the total time t, then
λ1 +λ2 + λ3 + ………… + λn = 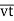
Where  , is the average speed of molecule and N the number of collisions suffered (i.e., the free path traversed) in time t. If λ is the mean free path, we must have
, is the average speed of molecule and N the number of collisions suffered (i.e., the free path traversed) in time t. If λ is the mean free path, we must have
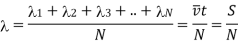
3.7.2 Expression for Mean Free Path
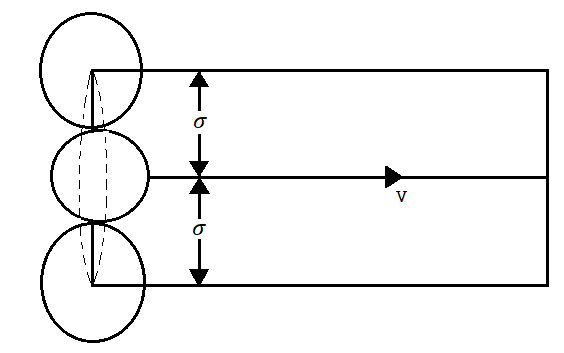
Figure 14: Mean Free Path
Let us consider a gas possessing n molecules per unit volume. Let us assume only a single molecule traversing the gas with velocity v and suppose other molecules are at rest.
The moving molecule will collide with all such molecules whose centres lie within a distance  from its centre, a being the molecular diameter as shown in figure.
from its centre, a being the molecular diameter as shown in figure.
The space thus traversed in a second is a cylinder of base = π 2
2
Height = v and
Thus Volume = π 2v
2v
The interior of the cylinder will enclose on the average molecules suffering impact =π 2vn
2vn
This expression also represents the number of collisions N made by the moving molecule per unit time i.e.
N= π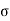 2vn ………… (1)
2vn ………… (1)
As the distance traversed by the molecule in one second is its velocity v, the mean free path is given by
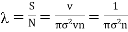 ………… (2)
………… (2)
This expression however, does not represent the actual state because it assumes that only one molecule under consideration is moving while all the other molecules are at rest.
Whereas the molecules possess all possible velocities, the distribution of velocities among them being given by Maxwell's distribution law.
Hence, if a molecule moves with absolute velocity v, in moving this distance v it will collide with π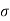 2rn other molecules where r represents the mean relative velocity of the molecules with respect to the others.
2rn other molecules where r represents the mean relative velocity of the molecules with respect to the others.
Therefore, the mean free path of that molecule is given by
 ………… (3)
………… (3)
But according to Maxwell's law, the particular molecule under consideration may have all possible velocities and hence if 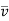 is the, average velocity of the molecule and r the mean relative velocity of all molecules with respect to all other, the mean free path averaged over molecules of all velocities is
is the, average velocity of the molecule and r the mean relative velocity of all molecules with respect to all other, the mean free path averaged over molecules of all velocities is
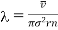 ………… (4)
………… (4)
Let us now suppose that the particular molecule under consideration moves with velocity v1. Its relative velocity with respect to another molecule of velocity v2 making an angle θ with it or the-relative velocity of approach between two molecules, is given by
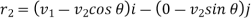
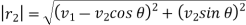
 ………… (5)
………… (5)
Now all the directions for velocity v2 are equally probable. The probability that it lies within the solid angle lying between θ and θ +dθ is  Sinθ dθ.
Sinθ dθ.
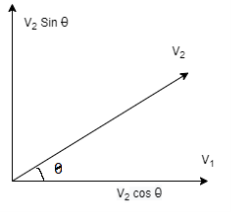
Figure 15: Velocity components
Average velocity is given by
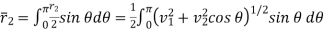 ………… (6)
………… (6)
Put
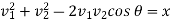
So that
 or
or 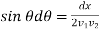
Again, substituting x in terms of θ
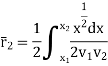
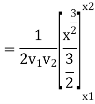
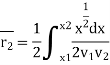
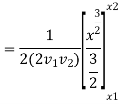
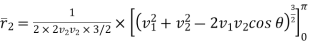 ………… (7)
………… (7)
The value of  depends whether v1>v2 or v2 >v1
depends whether v1>v2 or v2 >v1
For v1>v2 Solution give positive value and hence
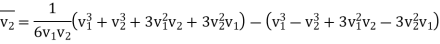

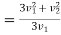 ………… (8)
………… (8)
For v2>v1 (v1 - v2) become negative value but relative velocity given by eq (5) give positive value. We will write (v2 – v1)3 as (v1 - v2)3
And hence For v2>v1
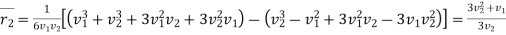 ………… (9)
………… (9)
Now the probability of exit molecule to lie in velocity range v2 and v2 + dv2
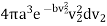 ………… (10)
………… (10)
Therefore, average relative velocity of molecule with velocity v1 with respect to all other molecule
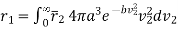 ………… (11)
………… (11)
But has two different values given by (7) and (9)
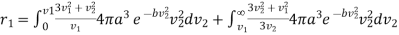 ………… (12)
………… (12)
The integration between 0 and v1 of the 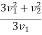 term applies to values of v2 < v1 and the integration from v1 to
term applies to values of v2 < v1 and the integration from v1 to  of the
of the  term applies to values of v2 > v1.
term applies to values of v2 > v1.
This value of r1 must next be multiplied by the probability of existence of molecules having the velocity v1 which is
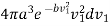 ………… (13)
………… (13)
And integrated from 0 to 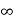 to take account of the variations in the velocity v2. Thus, the average velocity r of any molecule with respect to all others is space is
to take account of the variations in the velocity v2. Thus, the average velocity r of any molecule with respect to all others is space is


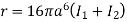
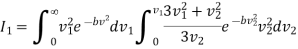
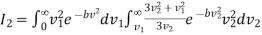 ………… (14)
………… (14)
On integration I2 is same as that of I1
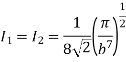
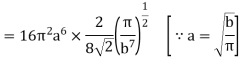

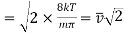 ………… (15)
………… (15)
Substituting the value of r in eq (4), we get expression of Mean free path
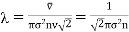 ………… (16)
………… (16)
Variation of λ
It may be noted from the expression for mean free path varies inversely with the square of the molecular diameter. Thus, smaller the size of the molecules, the larger will be the mean free path.
If in is the mass of molecule, then mn = p, the density of the gas. Thus, the expression for mean free path in terms of density becomes
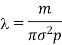
Thus, the mean free path is inversely proportional to the density of the gas.
Froth perfect gas equation
PV =nkT for V = 1
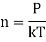
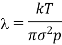
Obviously, the mean free path is inversely proportional to the pressure of the gas and directly proportional to the absolute temperature of the gas.
3.7.3 Collision Probability
Although a molecule suffers collisions quite irregularly but still there will be a certain average rate of collisions if considered over a long period of time. The average rate of collisions per second is called collision rate and is denoted by the P.
Thus, the number of collisions suffered by the molecule in time t is Pt.
Also, if the mean velocity of the molecule is v the total distance described by it in time t is vt.
Then the average distance travelled by the molecule between two successive - collisions, i.e., the mean free path λ is given by
λ = 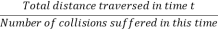 =
= 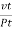 =
= 
We confine ourselves to those free paths only where the molecule possesses velocity v and denoted by λn.
If we confine ourselves to those free paths only where the molecule possesses velocity v and denoted by λn the mean free path and by Pn, the collision rate for the molecule of velocity v only, then above equation can be written as
λn = 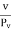
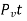 is the change or probability that the molecule of velocity v suffers collision in time t, we may now call the quantity Pv as collision probability.
is the change or probability that the molecule of velocity v suffers collision in time t, we may now call the quantity Pv as collision probability.
Example: The molecular diameter of a gas 3x 10-8 cm. Calculate the mean free path at temperature 270C and pressure 1 atmosphere.
Solution:
Mean free path
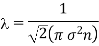
If m is mass of molecule mn=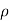 .
. 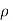 is the density of molecule.
is the density of molecule.
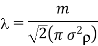
Pressure of the gas
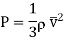
Where mean square velocity is given by
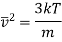
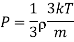
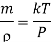
Hence Mean free path at T and P
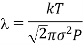
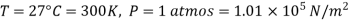
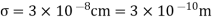 and
and 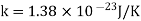
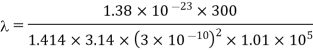
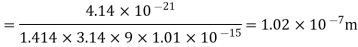
Example: Calculate the diameter of nitrogen molecule if mean free path is given as 0.80 x10-5 cm and n= 2.7 x1019 at normal T and P.
Solution:
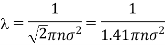
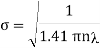
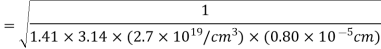
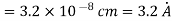
Key Takeaways
- As the molecules exert no force on one another except during collisions, they move in straight lines with uniform velocity between two successive collisions, this straight-line path being called the free path.
- The mean free path of that molecule is given by
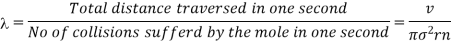
- Then the average distance travelled by the molecule between two successive - collisions, i.e., the mean free path λ is given by
λ = 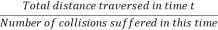 =
= 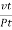 =
= 
Transport phenomenon in ideal gases
The equilibrium state of a gas is the most probable state; but if the gas is not in a state of equilibrium, we may have any of the following three cases:
1. The different parts of gas may have different velocities. If so, then there will be a relative motion of the layers of the gas with respect to one another. In such a case the layers moving faster impart momentum to the slower moving layers through a long chain of collisions to bring the equilibrium state. This gives rise to the phenomenon of viscosity.
2. The different parts of the gas may have different temperatures. If so, the molecules of the gas will carry kinetic energy from regions of higher temperature to the regions of lower temperature to bring the equilibrium state. This gives rise to the phenomenon of conduction.
3. The different parts of the gas may have different molecular concentrations, i.e., the number of molecules per unit volume. If so, the molecules of the gas will carry the mass from regions of higher concentrations to those of lower concentrations to bring the equilibrium state. This gives rise to the phenomenon of diffusions.
Thus, we see that viscosity, conduction and diffusion represent the transport of momentum, energy and mass respectively. These phenomena, i.e., viscosity conduction and diffusion are therefore called the transport phenomena.
1.Viscosity
The phenomenon of viscosity occurs in a gas when different layers of it move with different speeds.
Suppose a gas is moving in parallel layers between two horizontal planes AB and CD which are parallel to the XY-plane. Suppose that motion takes place parallel to the axis of X and that the velocity of the layer just in contact with the plane AB is zero and increases towards the plane CD. Thus, there is a relative motion between the layers and a velocity gradient in 'the z-direction.
Consider an imaginary intermediate plane MN. The layers of the gas above the plane MN are moving faster than those below it. The faster moving layers exert a tangential force on the plane MN tending to increase its velocity while the layers below MN exert an equal force in opposite direction.
Thus, the different A layers of the gas tend to destroy the relative motion between them. This property of the gas is called viscosity.
The molecules of the gas possess forward momentum in the X-direction due to the flow of gas. The layers of the gas above the plane MN have greater velocity and hence the greater momentum in a horizontal direction than the layers below MN.
Then, because of thermal motions, some of the molecules from a faster moving layer cross the plane MN downwards and drift into an adjacent layer where the forward velocity is less, transporting forward momentum to the slower moving layer.
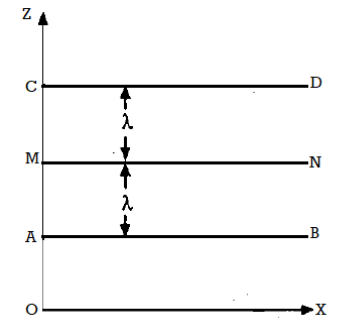
Figure 16: Viscosity
Conversely, some molecules of the slower moving layer cross the plane MN upwards and drift into, the faster moving layer decreasing the momentum of the latter.
This transfer of momentum, which is equivalent to internal friction, can be computed from kinetic theory consideration as follows:
Let G be the momentum of each molecule in the plane MN and (dG/dz) the momentum gradient (rate of change of momentum with distance) in an upward direction perpendicular to MN.
Let each of the planes AB and CD be at a distance λ from MN, where λ is the mean free path.
Then, The momentum of each molecule at the plane CD = G + λ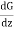 ……... (1)
……... (1)
And the momentum of each molecule at the plane AB = G - λ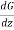 ……... (2)
……... (2)
Thus, a molecule crossing the plane MN in the downward direction, transports a momentum given by (1) and one going upwards transistor the momentum given by (2).
Hence the net transfer of momentum across the plane MN in the downward direction due the transfer of the above pair obtained by subtracting eqn. (2) from (1) which is
(G + λ ) - (G - λ
) - (G - λ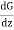 ) = 2λ
) = 2λ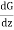 ……... (3)
……... (3)
The number of molecules crossing the plane MN in the downwards direction can now be calculated.
Let n be the number of molecules per unit volume and v their avenge speed. Then since molecules are moving due to thermal agitation in all possible direction, it may be supposed that one-third of these molecules are moving along each of-the-three directions X, Y and Z.
Therefore, on an-average, one-sixth of the molecules move parallel to any one axis in one particular direction.
Thus, the number of molecules crossing the plane MN upwards or downwards per unit area per second =  n
n ……... (4)
……... (4)
Making use of eqn. (3) we get for the total momentum transported downwards per unit area of the plane MN per second to be
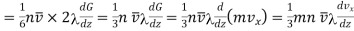 ……... (5)
……... (5)
Where momentum G=mvx, vx being the velocity of molecules at the plane MN.
But according to Newton's law, force is the rate of change of momentum. Hence expression (5) is a measure of force exerted on the plane MN by the upper layers. This force is same as tangential stress.
Now, the coefficient of viscosity is defined as the tangential force per unit area between two layers required to maintain a unit velocity gradient in it.
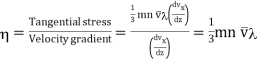 ……... (6)
……... (6)
But we know that mean free path
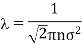
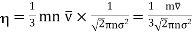 ……... (7)
……... (7)
2. Thermal Conductivity
The conduction of heat through a gas is molecular process, the molecules in the hotter regions of the gas having greater average energies than those in a colder part, and losing this excess of energy by impairing it to the colder molecules with which they collide.
Thus, thermal conductivity is the transport of energy resulting from molecular motions.
The total-transfer-of energy per unit area to be give
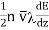 …... (1)
…... (1)
Consider two parallel plates P and P’ between which a steady temperature gradient is maintained keeping P at a higher temperature.
Let the plates be in XY-plane and space between them is filled with gas. Let us consider a plane z = z0 and let the mean energy (in joule) of a molecule in this plane be 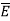 , so that E is a function of z.
, so that E is a function of z.
Consider now the molecules which cross a unit area of the plane z = z0. These molecules will, in general, come after traversing a distance λ from their last collision in a direction making an angle θ with the axis of Z.
Thus, these molecules on the average come from a plane whose z coordinate is
z0 + λ cosθ …... (2)
The mean energy of these molecules is therefore
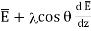 …... (3)
…... (3)
The number of molecules which in one second cross the unit area of this particular plane in a direction making an angle between θ and θ+ dθ with the axis of Z is
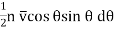 …... (4)
…... (4)
The amount of energy carried across the plane by them in the direction of Z increasing is
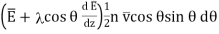 …... (5)
…... (5)
Total amount of energy in the direction of Z increasing.
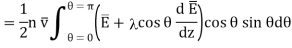
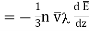 …... (6)
…... (6)
If K is thermal conductivity coefficient of the gas, the flow of heat across the unit area of the plane -K-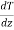 . Equating with eq (6)
. Equating with eq (6)
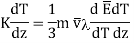
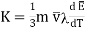 …... (7)
…... (7)
Specific Heat capacity at constant Volume is
 …... (8)
…... (8)
Thermal conductivity becomes
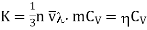 …... (9)
…... (9)
More correct form
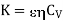 …... (10)
…... (10)
Where 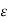 is a factor which depends on the atomicity of the gas and varies from 1 to 2.5. For monoatomic gases and obtained for molecules with translation energy only, and spherical symmetry, the value
is a factor which depends on the atomicity of the gas and varies from 1 to 2.5. For monoatomic gases and obtained for molecules with translation energy only, and spherical symmetry, the value
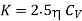 …... (11)
…... (11)
In which the coefficient 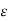 has the value 2.5. The value
has the value 2.5. The value 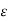 = 2.5 for all monoatomic gases is found fairly accurate and satisfactory.
= 2.5 for all monoatomic gases is found fairly accurate and satisfactory.
The evaluation of 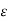 for polyatomic molecules presents a problem of great complexity since the molecules of this kind may rotate or have internal motions in addition to translational motions. Obviously, they will possess energy other than the translation energy.
for polyatomic molecules presents a problem of great complexity since the molecules of this kind may rotate or have internal motions in addition to translational motions. Obviously, they will possess energy other than the translation energy.
Let us suppose that on the average this energy (energy due to cause other than translation) is 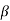 times the average translational energy. Then the average total energy of a molecule E now becomes
times the average translational energy. Then the average total energy of a molecule E now becomes
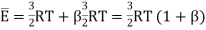 …... (12)
…... (12)
Is the kinetic energy of translational motion. Then Cv is
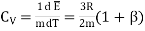 …... (13)
…... (13)
But since
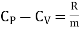 …... (14)
…... (14)
We have
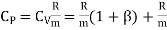 …... (15)
…... (15)
Hence
 …... (16)
…... (16)
Or
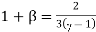 …... (17)
…... (17)
From eq (17), eq (9) becomes
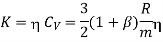
But, as we have seen, when energy is wholly translational ((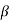 = 0), this value of K should be multiplied by
= 0), this value of K should be multiplied by  . Combining these two contributions to the transport of energy, we get
. Combining these two contributions to the transport of energy, we get
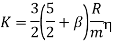
But
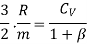
From eqn. (13)

Substituting the value of  and 1 +
and 1 +  from eqn. (17) we arrive at the formula
from eqn. (17) we arrive at the formula
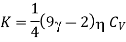
Hence

Thus, for monoatomic gases (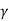 = 1.67),
= 1.67), 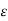 =2.5. For diatomic gases (
=2.5. For diatomic gases (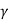 = 1.4),
= 1.4), 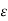 = 1.9; while for rigid triatomic molecules (
= 1.9; while for rigid triatomic molecules (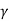 = 1.33;
= 1.33; 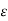 =1.75 becoming still smaller for polyatomic molecules.
=1.75 becoming still smaller for polyatomic molecules.
(3) Diffusion
In a gaseous mixture diffusion result from random molecular motion whenever there is a concentration gradient of any molecular species. Let us consider two different gases A and B at the same temperature and pressure on the two opposite sides of the partition in a vessel.
The number of molecules per unit volume (p/KT) is, therefore, the same on both sides. When the partition is removed, both the gases diffuse into each other, and after a lapse of time both the gases are uniformly distributed throughout the entire volume.
The diffusion process is often superposed by the hydrodynamic flow resulting from pressure differences, and the effects of molecules rebounding from the walls of the vessel.
If a gas contains two or more different kinds of molecules whose relative densities vary from point to point, a process known as diffusion takes place until the concentration is uniform throughout for it, consider a vessel containing two different gases G1 and G2 separated by a partition.
The gases are at the same pressure and temperature so that the number of molecules per unit volume is the same on both sides. When the partition is removed ice., the gases are made to communicate with each other, there is no mass motion of the gas in either direction but after some time both the gases are found to be distributed uniformly throughout the entire volume.
The phenomenon is known as inter diffusion of two gases and if we fix our attention only one gas, we can say that it diffuses into other gas. This phenomenon due to which each gas permeates the other is called diffusion.
The phenomenon of diffusion is not restricted to gases but occurs in liquids and solids also. It may be described as the transport of mass resulting from random molecular motion and takes place whenever there is a concentration gradient i.e., when the number of molecules per unit volume on one side of a surface differs from that on the other side.
In such a case a denser region will lose more molecules to regions of scarcity than it will gain. The density of a gas becomes uniform throughout volume when the gas reaches equilibrium state.
Coefficient of diffusion
Let us consider a horizontal plane. The number of molecules which cross unit area of the horizontal plane per unit area per second in the positive direction of the z-axis is given by
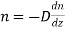 ………… (1)
………… (1)
Is called the coefficient of diffusion.
Imagine now two gases arranged in layers on above the other parallel to the axis of z diffusing through one another. Let at any instant n1 and n2 be the concentrations be the two gases which vary along the axis of z i.e., n1 and n2 are functions of z only.
As temperature and pressure must be constant throughout the gas, we must have from Avogadro's law for perfect gases
n1 + n2 = n = constant.
Differentiating with respect to z
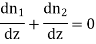
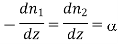
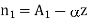
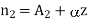 ………… (2)
………… (2)
Where A1, A2 and 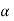 are constant referring to plane z=z0 across which we will consider molecular transfer.
are constant referring to plane z=z0 across which we will consider molecular transfer.
We will now calculate the number of molecules crossing the plane z = z0.
Let 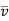 and λ1 denote respectively the mean molecular velocity and the mean free path for molecules of the first kind in the gas whereas of and λ2 denote corresponding quantities for the second kind.
and λ1 denote respectively the mean molecular velocity and the mean free path for molecules of the first kind in the gas whereas of and λ2 denote corresponding quantities for the second kind.
Those molecules which move making an angle θ with the axis of z might have suffered their last collision in a plane of which the z co-ordinate is zo - λ1cosθ and in this plane the concentration may be taken to be
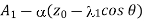 ………… (3)
………… (3)
Therefore, the number of molecules of the first kind which cross the plane z = z0 per unit area per unit time in the direction of z increasing, as in case of viscosity is given by
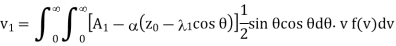
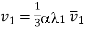 ………… (4)
………… (4)
Similarly, the number of molecules of the second kind in the direction of z increasing i.e., upwards is given by
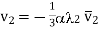 ………… (5)
………… (5)
Generally, v1 +v2 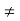 0 and hence a number of molecules v1 +v2 will tend to move in the upward direction tending to set a difference of pressure in the gas which should, however remain constant throughout.
0 and hence a number of molecules v1 +v2 will tend to move in the upward direction tending to set a difference of pressure in the gas which should, however remain constant throughout.
As a result, gas would adjust itself against this tendency by a slow mass motion with a velocity vz parallel to the-axis of z.
Obviously, the mass-velocity vz will be a function of z and will be such that there is no net transfer of volume in either direction. Thus, the rate of increase of the number of molecules of the first kind on the passive side of plane z = z0 per unit area actually becomes
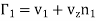 ………… (6)
………… (6)
Similarly, the rate of increase of molecules of the second kind
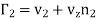 ………… (7)
………… (7)
As the flow is to be steady, the total flow of molecules over every plane must be zero
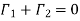
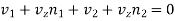
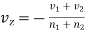 ………… (8)
………… (8)
Substituting this value of vz in equation (8), we have the true transfer of molecules of the first kind per unit area per unit time i.e., the diffusion current density given by
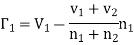
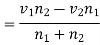
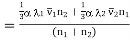 ………… (9)
………… (9)
As
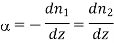
We have
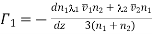 ………… (10)
………… (10)
But if D12 is the coefficient of diffusion of the two gases then according to definition the diffusion current density.
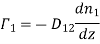
 ………… (11)
………… (11)
This is the well-known equation of diffusion and is symmetrical for the two gases,
D12 = D21
It is generally known as Mayer's formula for coefficient of diffusion.
Formula (11) becomes specially simple if the molecules of two gases, are approximately of equal size and mass. Then we may take λ and  to be the same for each gas and obtain
to be the same for each gas and obtain
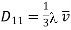 ………… (12)
………… (12)
Comparing it with the corresponding approximate formula for the coefficient of viscosity
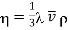 ………… (13)
………… (13)
We get
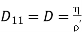 ………… (14)
………… (14)
Where D11 or D may be called the coefficient of self-diffusion or diffusivity of a single gas
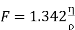 ………… (15)
………… (15)
We have
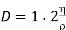 ………… (16)
………… (16)
While Maxwell's theory for molecules repelling each other according to inverse fifth power of the distance yields for coefficient of self-diffusion.
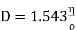 ………… (17)
………… (17)
Variation of diffusion
We shall now see how diffusivity should vary with temperature and pressure. It is anions from equation (13) that it should vary with temperature and pressure in the same way as do the relation (η/P) for the gases.
Since η varies as 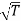 and not at all with P and also
and not at all with P and also  varies as P and T-1, it is obvious that the diffusivity should vary as P-1 and as T3/2.
varies as P and T-1, it is obvious that the diffusivity should vary as P-1 and as T3/2.
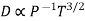
Experimental result show that D vanes inversely as the pressure but the power of T lies between 1.750 and 2.
Key Takeaways
- The different parts of gas may have different velocities. If so, then there will be a relative motion of the layers of the gas with respect to one another. In such a case the layers moving faster impart momentum to the slower moving layers through a long chain of collisions to bring the equilibrium state. This gives rise to the phenomenon of viscosity.
- The different parts of the gas may have different temperatures. If so, the molecules of the gas will carry kinetic energy from regions of higher temperature to the regions of lower temperature to bring the equilibrium state. This gives rise to the phenomenon of conduction.
- The different parts of the gas may have different molecular concentrations, i.e., the number of molecules per unit volume. If so, the molecules of the gas will carry the mass from regions of higher concentrations to those of lower concentrations to bring the equilibrium state. This gives rise to the phenomenon of diffusions.
- Since η varies as
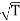 and not at all with P and also
and not at all with P and also 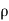 varies as P and T-1, it is obvious that the diffusivity should vary as P-1 and as T3/2.
varies as P and T-1, it is obvious that the diffusivity should vary as P-1 and as T3/2. 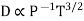
- Experimental result show that D vanes inversely as the pressure but the power of T lies between 1.750 and 2.
In 1827, a botanist Robert Brown observed that pollen grains suspended in water and viewed under a powerful microscope show an irregular continuous dancing motion. Extending his observations to suspensions of a large number of inorganic substances the so-called colloidal solutions, he found it to be a general phenomenon.
In fact, any kind of sufficiently small particles, no matter how non-vital suspended in a liquid performed similar perpetual dances. The suspended particles under a high-power microscope appear like stars of the light, dancing hither and-thither without apparent rhyme or reason.
Each particle spins, rises, sinks and rides again without ever corning to rest. The motion is perpetual and spontaneous and is one of the most interesting phenomenon in Physics.
This ceaseless random and swarming motion is called the Brownian motion.
The established facts regarding Brownian motion are as follows:
1. The motions are completely irregular and random. No two particles are found to execute some motion. Thus, it cannot be due to convection or eddy currents.
2. The motions are continuous and eternal i.e., the motions continue indefinitely without showing any signs of stopping.
3. The smaller the particles-the more-lively and noticeable are the motion.
4. It is independent of the nature of the suspended particles, -two particles of the same weight and size move equally fast at the same temperature.
5. The motion becomes more vigorous when the temperature is increased or the viscosity of the supporting fluid is decreased.
6. It is independent of the shaking of the vessel.
A large number of hypothesis as to the cause of Brownian motion have been put forward. It was at first attributed to surface tension irregularities in the temperature of the liquid vibrations, chemical or electrical action and so on.
All these explanations were found insufficient and a very little real progress was made in our knowledge of the subject until the modem view ascribing it to molecular agitation was put forward by Delsaux in 1877 and again by Gouy in 1888.
They showed that the particles were acting merely as indicators of the molecular motion of the liquid in which they were immersed. Thus, Brownian motion is due to bombardment of the dispersed particles by molecules of the medium. If the particles are sufficiently large, the forces due to molecule impact will almost completely balance and hence the Brownian motion cannot be observed with large sized particles.
But if the size of the particle is very small, it will be acted upon by a resultant unbalanced force and will consequently move this way or that in response to the force. Thus, the particles move to and fro in an entirely haphazard fashion corresponding to the haphazard movement of the molecules of the liquid.
French chemist Perrin made a thorough study of Brownian motion in colloidal suspension. He tested the hypothesis that the suspended particles which dance about in a stationary liquid in Brownian motion behave in the same way as a gas molecule. Although the molecules of a gas cannot be seen, it can be supposed that the gas molecules are in continuous motion in all directions frequently colliding against one another. Thus, from the point of view of thermal agitation there is no distinction between the molecules of an ordinary gas and the Brownian particles. We may indeed extend all the laws of kinetic theory of gases to a Suspension which is composed of a larger number of small particles suspended in liquid. The law holds good for light particle, heavy particle as well as visible particle known as Brownian particles.
Key Takeaways
- This ceaseless random and swarming motion is called the Brownian motion.
- French chemist Perrin made a thorough study of Brownian motion in colloidal suspension. He tested the hypothesis that the suspended particles which dance about in a stationary liquid in Brownian motion behave in the same way as a gas molecule.
References:
1. Theory and experiments on thermal Physics, P.K.Chakrabarty (New central book agency limited)-2017
2. Thermodynamics, Kinetic Theory and Statistical Thermodynamics- Sears and Salinger (Narosa)-1988
3. A Treatise on Heat- Meghnad Saha and B.N.Srivastava (The Indian Press) Heat, Thermodynamics and Statistical Physics, N.Subrahmanyam and Brij Lal (S.Chand Publishing)-2008
4. Thermal and Statistical Physics M.Das, P.K. Jena, S. Mishra, R.N.Mishra (Shri Krishna Publication)-2009