Unit - 2
Wave Packet
2.1.1 Superposition and Interference
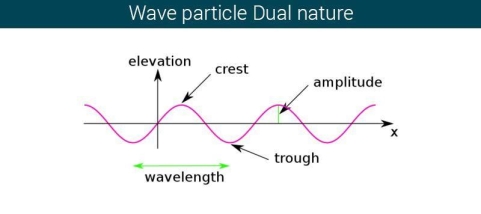
The majority of waves do not appear to be straightforward. They resemble the waves depicted in Figure rather than the ordinary water wave discussed in Waves. (Simple waves have a sinusoidal shape because they are formed by a simple harmonic oscillation.) Complex waves are more intriguing, even beautiful, but they appear to be intimidating. The majority of waves appear complex because they are made up of multiple simple waves that have been added together. Fortunately, the principles for adding waves are straightforward.

Figure 1.
When two or more waves arrive at the same location at the same time, they superimpose on each other. When waves collide, the disturbances of the waves are superimposed, a phenomenon known as superposition. Each disruption is associated with a force, which adds up. If the disturbances all follow the same path, the final wave is simply the sum of the individual waves' disturbances—that is, their amplitudes add. Figures 2 and 3 show superposition in two different situations, both of which yield straightforward results.
Figure 2 depicts two similar waves arriving at the same time and in phase. The crests and troughs of the two waves are perfectly aligned. The result of this superposition is pure constructive interference. Pure constructive interference generates a wave with double the amplitude of the component waves but the same wavelength since the disturbances add up.
Figure 3 illustrates two identical waves arriving out of phase—that is, with their crests and troughs precisely aligned—producing pure destructive interference. The resulting amplitude for pure destructive interference is 0 since the disturbances are in the opposite direction for this superposition—the waves entirely cancel.
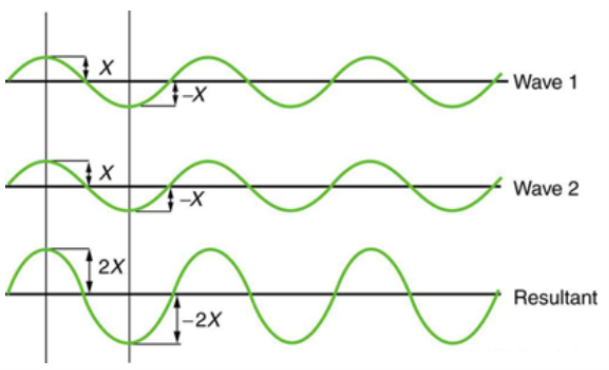
Figure 2: When two identical waves collide, the result is a wave with twice the amplitude but the same wavelength.
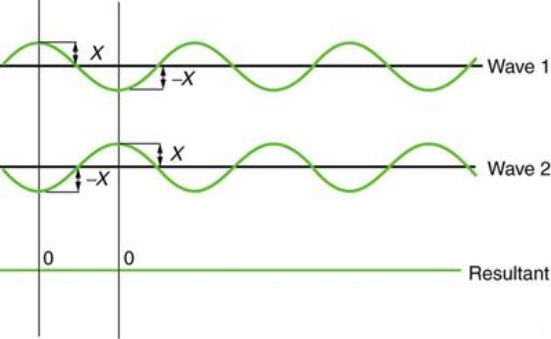
Figure 3: When two identical waves collide, the result is zero amplitude, or total cancellation.
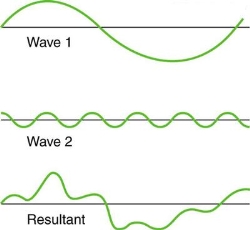
Figure 4. Superposition of non-identical waves exhibits both constructive and destructive interference.
While pure constructive and destructive interference do occur, they require identical waves to be exactly aligned. Most waves superpose, resulting in a mix of constructive and destructive interference that varies from location to place and time to time. A stereo's sound, for example, can be powerful in one place yet muted in another. Sound waves add partially constructively and partially destructively at different locations when their loudness varies. Sound waves are created by at least two speakers in a stereo, and sound waves can reflect off walls. All of these waves are stacked on top of each other. The combined whining of aeroplane jets perceived by a stationary passenger is an example of noises that change over time from constructive to detrimental. As the sound from the two engines changes in time from constructive to destructive, the total sound might fluctuate in amplitude. These are waves that are similar to each other. Figure 4 depicts an example of the superposition of two different waves. Again, the disturbances add and subtract, resulting in a wave that appears more intricate.
2.1.2 Principle of Superposition of Waves
Consider two waves travelling in opposite directions along the same stretched string, as shown in the diagram above. At any given time, we can see images of waveforms in the string. The algebraic total of the displacements owing to each wave is found to be the net displacement of every element of the string at any given time.
Let's imagine two waves are travelling alone, and any element of these two waves' displacements can be represented as y1(x, t) and y2(x, t) (x, t). The resultant displacement can be written as y when these two waves collide (x,t).
y (x, t) = y1(x, t) + y2(x, t) = y3(x, t) = y4(x, t) = y5(x, t) = y (x, t)
We can sum the overlapped waves algebraically to generate a consequent wave using the principle of superposition. Let us say that the wave functions of moving waves are as follows:
y1 = f1(x–vt),
y2 = f2(x–vt)
……….
yn = fn (x–vt)
Then the wave function describing the disturbance in the medium can be described as
y = f1(x – vt)+ f2(x – vt)+ …+ fn(x – vt)
Or, y=∑ i=1 to n = fi (x−vt)
Let us consider a wave travelling along a stretched string given by, y1(x, t) = A sin (kx – ωt) and another wave, shifted from the first by a phase φ, given as y2(x, t) = A sin (kx – ωt + φ)
From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A.
Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement y(x, t) = A sin (kx – ωt) + A sin (kx – ωt + φ)
The above equation can be written as,
y(x, t) = 2A cos (ϕ/2). Sin (kx −ωt + ϕ/2)
The resulting wave is a sinusoidal wave travelling in the positive X direction, with a phase angle half that of the component waves and an amplitude equal to [2cos/2] times the original waves' amplitudes.
2.1.3 Condition for Destructive Interference
Phase difference = (2n – 1)π
Path difference = (2n – 1)λ/2
I = Imin
Imin = I1 + I2 – 2 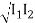

2.1.4 Standing Waves
Waves don't always appear to move; instead, they only vibrate in situ. Unmoving waves, for example, can be seen on the surface of a glass of milk in the refrigerator. The refrigerator motor's vibrations create waves on the milk that oscillate up and down but do not appear to travel over the surface. These waves are created by the superposition of two or more moving waves, such as the two identical waves flowing in opposite directions seen in Figure 5. The waves pass through each other, adding to the disruptions as they travel. When the amplitude and wavelength of two waves are the same, they alternate between constructive and destructive interference. The outcome is known as a standing wave because it resembles a wave that is stationary. Standing waves can be seen on the surface of a glass of milk. Other standing waves can be found in guitar strings and organ pipes. The two waves that generate standing waves in the glass of milk could be caused by reflections from the glass's side.
A detailed examination of earthquakes reveals evidence of resonance, standing waves, and constructive and destructive interference situations. A building may be vibrated for several seconds at a frequency that matches the natural frequency of vibration of the building, resulting in a resonance that causes one building to collapse while surrounding buildings remain intact. Buildings of a specific height are frequently destroyed, whereas taller structures remain standing. The height of the building corresponds to the conditions for creating a standing wave at that height. At specific spots along the Earth's surface, constructive interference occurs as seismic waves reflect off denser rocks. Areas near to the epicentre are frequently unaffected, whereas areas further away are.
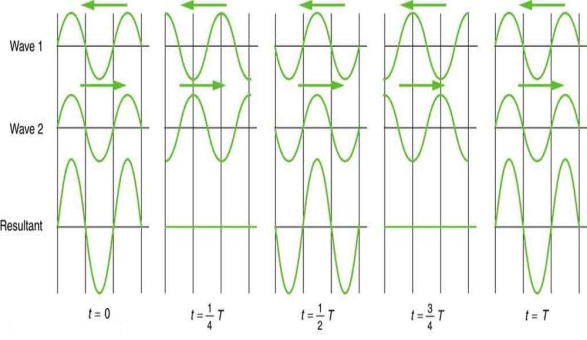
Figure 5: A standing wave is formed when two similar waves moving in opposite directions are superimposed. The oscillations occur at predetermined points in space and are caused by constructive and destructive interference.
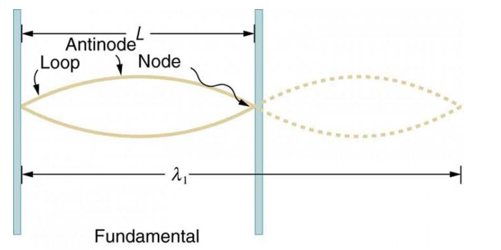
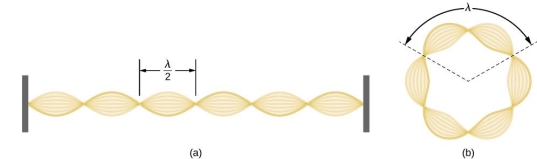
Standing waves can also be formed on musical instrument strings as a result of wave reflections from the ends of the string. Three standing waves can be formed on a string that is fastened at both ends, as seen in Figures 6 and 7. In a standing wave, nodes are the sites where the string does not move; more broadly, nodes are the sites where the wave disturbance is zero. Because the string cannot move, the fixed ends of strings must also be nodes. In standing waves, the term antinode refers to the place of maximum amplitude. Standing waves on strings have a frequency that is proportional to the disturbance's propagation speed vw. The distance between the spots where the string is fixed in place determines the wavelength.
The fundamental frequency, which is the lowest frequency, is so for the longest wavelength, which is 1 = 2L. f1=vw1=vw2f1=v The overtones or harmonics in this situation are multiples of the fundamental frequency. Because 2 = L, the first harmonic can be simply determined, as shown in Figure 7. As a result, f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1. In the same way, f3 = 3f1 and so on. The tension in the string can be adjusted to vary all of these frequencies. The higher the frequency, the higher the vw and the greater the stress. Anyone who has ever watched a string instrument being tuned would recognise this observation. Standing waves are critical to many resonance occurrences, such as sounding boxes on string instruments, as we will discover in later chapters.
f1 = 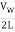

Figure 6. The figure shows a string oscillating at its fundamental frequency.

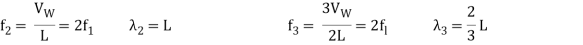
Figure 7. First and second harmonic frequencies are shown.
2.1.5 Beats
On a piano, striking two neighbouring keys generates a warbling sound that is normally considered unpleasant. The culprit is the superposition of two waves with comparable but not identical frequency. Another example can be seen during taxiing in jet aircraft, particularly the two-engine version. The combined sound of the engines increases and decreases in volume. Because the sound waves have comparable but not identical frequencies, the loudness varies. As the two waves travel in and out of phase, the discordant warbling of the piano and the varying loudness of the jet engine noise are both due to alternately constructive and destructive interference. This is visually depicted in Figure 8.

Figure 8 shows how beats are created by superimposing two waves with slightly different frequencies but identical amplitudes. The waves alternate between constructive and destructive interference over time, resulting in a wave with a variable amplitude.
The frequency of the wave that results from the superposition of two waves of comparable frequency is the average of the two. The amplitude of this wave swings in beats, at a frequency called the beat frequency. The beat frequency can be calculated by combining two waves together analytically. It's worth noting that at one point in space, a wave can be represented as
x = X cos (2πt/T) = X cos (2πft)
The frequency of the wave is f=1/T. When two waves with different frequencies but equal amplitudes are combined, the outcome is x = x1 + x2. x = Xcos(2 f1t) + Xcos(2 f2t), to be precise.
It can be demonstrated that x =2X cos(fBt)cos(2 favet) using a trigonometric identity, where fB = |f1 f2| is the beat frequency and fave is the average of f1 and f2. These findings indicate that the resultant wave has double the amplitude and average frequency of the two superimposed waves, but its overall amplitude changes at the beat frequency fB. The amplitude is effectively increased and decreased by the first cosine term in the formula. The wave with frequency fave is the second cosine term. This conclusion holds true for all forms of waves. If it's a sound wave, though, and the two frequencies are similar, we'll hear an average frequency that grows louder and softer (or warbles) as the beat frequency approaches.
While beats might be bothersome in auditory noises, we will see that they have a wide range of applications. Observing beats is a great technique to compare frequencies that are comparable. Ultrasonic imaging and radar speed traps are two seemingly unrelated applications of beats.
Key takeaway:
- The combination of two waves at the same spot is known as superposition.
- When two identical waves are superimposed in phase, constructive interference occurs.
- When two identical waves are overlaid perfectly out of phase, destructive interference results.
- A standing wave is created when two waves collide, resulting in a wave that changes in amplitude but does not propagate.
- In standing waves, nodes are sites where there is no motion.
- An antinode is the point at which a standing wave reaches its maximum amplitude.
- Waves on a string are resonant standing waves with a basic frequency that can have overtones or harmonics at higher multiples of the fundamental.
- When waves of similar frequency f1 and f2 are overlaid, beats occur. The oscillation frequency of the resulting amplitude is given by fB = |f1 f2|.
2.2.1 Harmonic Waves and Phase Velocity
The equation describes a one-dimensional harmonic wave (Figure 1).
u(x, t) = A0 sin (ωt – k x + φ)
Where A0 represents the wave amplitude, is the circular frequency, k represents the wave number, and is the starting, constant phase. The phase is the argument for the sine function, which is (x, t) = t - kx +. The spatial frequency or propagation constant are other names for the wave number.
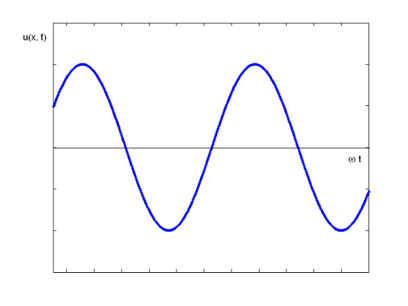
Figure 9: Harmonic Wave
This is a wave that is monochromatic (one frequency). In nature, there are no waves that are strictly monochromatic. For example, the wave's generating source could move significantly, resulting in spurious frequencies.
These waves propagate without warping in most cases. In other words, the phase (x, t) is constant:
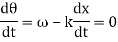
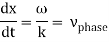
vphase is the phase velocity for a wave.
These waves are ineffective in terms of transmitting information. They remain the same in time and place. In order to transfer information, something must be modulated, such as frequency or amplitude. The resulting wave could be a wave packet, which is a disturbance that acts across a short distance. This wave packet can be thought of as a Fourier series or integral, which is a superposition of a number of harmonic waves.
2.2.2 Group Velocity
Something more than a basic harmonic wave is required to transmit information. The superposition of several such waves of differing frequencies, on the other hand, can produce a "envelope" wave and a carrier wave within the envelope. The envelope has the ability to convey data. The superposition of two harmonic waves with very near frequencies (1 2) and the same amplitude is a simple example. The motion's equations are as follows:
u(x, t) = A0 . Cos (ω1 t – k1 x) + A0 . Cos (ω2t – k2 x)
= 2 A0 . Cos ( 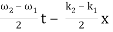 ) × cos (
) × cos ( 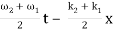 )
)
= u1 × u2
Figure depicts the plot of such a wave.
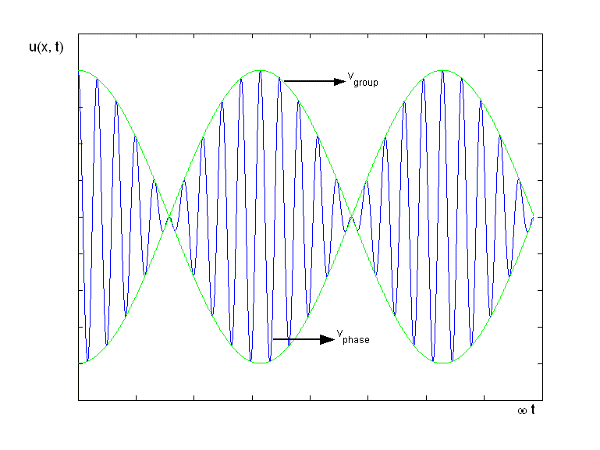
Figure 10: Group Velocity
u1 controls the envelope (the green line), which moves at the group velocity. The phase velocity of the carrier wave (the blue line) is provided by u2. The wave packet travels at the same speed as the rest of the group. It is the envelope that contains the data. The velocity of a group and the velocity of a phase are not always the same. The velocity of a group is given by,
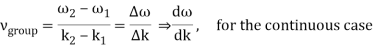
Rayleigh's formula links phase and group velocity together.
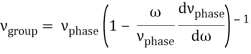
Group velocity equals phase velocity if the derivative term is zero. There is no dispersion in this scenario. When the different phase velocities of the envelope components cause the wave packet to "spread out" over time, this is called dispersion. The wave packet's (or envelope's) components separate to the point that they can no longer combine to complete the envelope.
2.3.1 Wave Packet Solution
Since the wave equation's travelling wave solution
y(x, t) = A sin (kx – ωt)
Is true for every value of the wave parameters, and since any superposition of solutions is likewise a solution, a wave packet solution can be constructed as a sum of travelling waves:
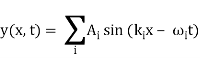
It is standard practise to express the amount 2/ by k, also known as the wave vector. The sum is replaced by an integral for a continuous range of wave vectors k:
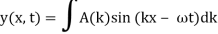
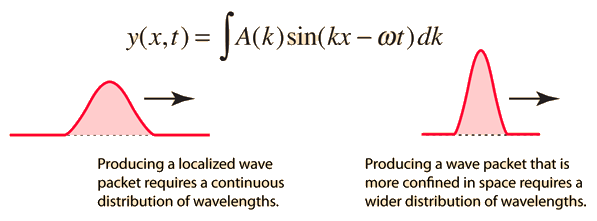
2.3.2 Wave Packet Details
Like a pulse on a string, a wave packet solution to the wave equation must have a variety of frequencies. The broader the range of frequency components necessary for quick transient behaviour, the shorter the pulse in time. For classical waves, this need can be expressed as a form of uncertainty principle:

The exact figures depend on how the pulse width is defined, however making brief pulses necessitates a large frequency bandwidth. The uncertainty principle in quantum mechanics is analogous to this.
2.3.3 Wave Packets from Discrete Waves
When discrete travelling wave solutions to the wave equation are concatenated, a wave packet that begins to localise the wave can be created. The quantum mechanical uncertainty principle mirrors this property of classical waves.

2.3.4 The Wave-Particle Puzzle
De Broglie's explanation of the Bohr atom quantization principles, together with Davisson and Germer's unintentional discovery of electron diffraction scattering, offer a compelling case for the electron's wave nature. Even so, the electron can act like a particle at times. An electron has a certain mass and charge, may move slowly, and can pass through a variety of devices, including a gun and a screen.
So, what's the connection between the wave and particle perspectives? Both were always present, according to De Broglie. He dubbed the wave a pilot wave, and he believed it steered the particle's motion. Unfortunately, the point of view leads to inconsistencies. The common current view is that the relative likelihood of detecting the particle at any position is determined by the strength of the wave (measured by the square of its amplitude).
The probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of the magnetic field vector. This interpretation, first proposed by Max Born in 1926, is analogous to the relationship between the electromagnetic field and quanta—the probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of The de Broglie wave function associated with the electron is written in standard notation as (x,t). The relative probability of finding the electron in a narrow period of length x near location x at time t is thus |(x,t)|2dx. (For the sake of simplicity, we limit the electron's movement to one dimension.) The generalisation is easy to understand.)
2.3.5 Keeping the Wave and the Particle Together?
Suppose following de Broglie we write down the relation between the "particle properties" of the electron and its "wave properties":
 mv2=E=hf, mv=p=h/λ.
mv2=E=hf, mv=p=h/λ.
It would seem that we can immediately figure out the speed of the wave, just using λf=c′, say.
We find:
λf=hmv⋅12mv2h=12v.
What? The speed of the wave is half the speed of the electron? How could they stay together? What's wrong with this calculation?
2.3.6 Localizing an Electron
To solve this question, consider the wave function corresponding to an electron moving in a vacuum tube, for example. The electron exits the cathode, travels through the vacuum, and collides with a grid's anode. It is travelling through the vacuum at a moment in this process, and the wave function must be nonzero across some volume, but zero in places the electron has not yet reached and zero in places it has definitely gone.
The electron, on the other hand, has a precise momentum if it possesses a precise energy, such as fifty electron volts. This necessitates the existence of a definite wavelength for the wave. However, the only wave with an exact wavelength is (x,t)=Asin(kxt).
Where k=2/ and =2f are constants. The issue is that this plane sine wave stretches to infinity in both spatial directions, therefore it can't represent a particle with a non-zero wave function in a finite region of space.
As a result, we must superpose waves of different wavelengths to represent a confined particle. Using the trigonometric addition formula, superpose two waves with somewhat varying wavelengths to demonstrate the principle:
Sin((kk)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((
Sin(kxt)cos((k)x()t sin(kxt)cos((k)x()t sin(k)x()t sin(k)x()t sin
The phenomena of beats between waves of similar frequency is represented by this formula. The first term, sin(kxt), oscillates at a frequency that is the average of the two. The slowly fluctuating second term, which oscillates once over a spatial range of order /k, modulates it. This is the distance at which waves that were in phase at the start turn fully out of phase. Of course, if the distance between the waves is increased by order /k, the waves will re-synchronize.
That is, combining two close frequencies creates a series of packets, or beats, from the continuous wave. A single packet is required to describe a single electron travelling through space. This can be accomplished by superposing waves with a continuous distribution of wavelengths, or wave numbers in the order of k, for example. The waves will be out of phase after a distance of order /k, but because they have so many distinct wavelengths, they will never be able to get back in phase. (All of this is adequately treated in Fourier transform theory.) We're just attempting to make it plausible right now.)
2.3.7 The Uncertainty Principle
It should be evident from the above argument that to construct a wave packet representing an electron localized in a small region of space, the component waves must get out of phase rapidly. This means that their wavelengths can't be too close. In reality, simply considering the two beating waves allows for a semi-quantitative approximation of the wavelength spread required.
A packet localized in a region of extent Δx can be constructed of waves having k 's spread over a range Δk, where Δx∼π/Δk.
Now, k=2π/λ, and p=h/λ, so k=2πp/h.
Therefore, Δk=2πΔp/h, and Δx∼π/Δk∼h/Δp, (dropping the factor of 2).
Thus:
Δx⋅Δp∼h.
This is Heisenberg's Uncertainty Principle, which we shall analyze in more detail in later lectures.
2.4.1 Gaussian wave packets:
We write a free wave packet as a linear combination of plane waves
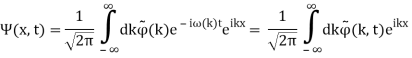
Where the momentum amplitudes absorb the time evolution of each plane wave, given by (k)=k2/2m (k,t). As a Gaussian, we chose the amplitude for the various plane waves.
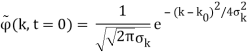
The momentum distribution |φ~(k,t)|2| is a Gaussian of width σk and mean k0 for all t.
At t=0, where the momentum amplitudes are real, the probability density of the resulting wave packet at is a Gaussian of width σx=1/2σk, i.e., it is as localized as is allowed by the Heisenberg principle (σx=1/2). The probability distribution stays Gaussian for all t. As the momentum amplitudes become complex, its width 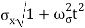 increases with a characteristic time 1/ωσ=2m
increases with a characteristic time 1/ωσ=2m /ℏ, and its center moves with the group velocity vg=ℏk0/m.
/ℏ, and its center moves with the group velocity vg=ℏk0/m.
The genuinely quantum mechanical aspect is the behaviour at t=0: We can't locate the particle any farther than the uncertainty principle allows. It is a direct result of the wave-description resulting directly from the Fourier transform's features. For long periods of time, the behaviour is consistent with that of an ensemble of classical particles with a Gaussian momentum distribution: A particle with momentum k will be at x(k,t)=kt/m at time tt. We get the probability density of discovering a classical particle by solving for k and inserting it into the momentum distribution.
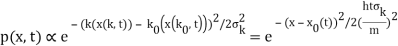
Which is a Gaussian of width σxωσt centered at
x0(t) = hk0t/m
The probability distribution for the wave packets has been plotted so far. We'll need a mechanism to visualise complex functions if we wish to draw the wave function. We could just plot the real and imagined parts of it. However, demonstrating its modulus (the square of which yields the probability density) and phase is more enlightening. It's simple to plot the modulus. We use colours to depict the phases, starting with red for phase zero, progressing through the rainbow colours as the phase progresses, and finally returning to red for phase two. The representation of a plane wave is shown below as an example. 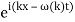
The propagating free Gaussian wave packet's wave function is given by
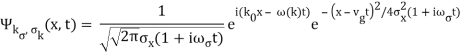
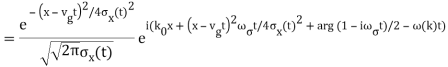
The phase of a Gaussian wave packet with a small momentum distribution is virtually identical to a plane wave with momentum k0.
The phase no longer has a well-defined wave length as the momentum dispersion widens. The phase has wave length 2/k0 around the maximum at x(t)=vgt.
2.4.2 Linear combination of wave packets (Schrödinger cat states)
Looking at linear combinations of Gaussian wave packets is equally fascinating. It's important to remember that we're still dealing with single-electron wave functions, which describe a single electron in a superposition state rather than two!
=GWP(k0,k,x0), What determines the interference pattern's wave length? Why is the amplitude of the wave packets in the middle always zero?
This is the same wave function as before, but with the probability density displayed. After the wave packets have travelled past each other, what happens to them? What would happen if their rate of broadening was slower than their velocity?
This wave packet flows slower and has a significantly larger momentum distribution. Why do the wave function's oscillations continue?
2.4.3 Reflection at hard wall

We can see how a Gaussian wave packet is reflected at a hard wall by looking at just one half of the above superpositions. Compare this approach to the electrostatics method of image charges.
Same thing, except this time for a wave packet with a significantly wider momentum dispersion.
2.5.1 Localization Of Waves; Relation To Uncertainty Principle
To grasp the uncertainty principle, one must first grasp a difficult but crucial concept concerning wave localizability: a wave can only be localised if distinct wavelengths are superposed. Consider a single-wavelength “pure” wave, as depicted below.

It's a perfect sine wave that repeats eternally with a perfectly defined fixed wavelength that's spread out in space. If it's an electron wave, it's a particle travelling at a constant speed with a well-defined momentum, as defined by the de Broglie equation: p = h/. What happened to the electron? It can be found anywhere—or is equally likely to be found anywhere (along the infinite dimension of the wave). 1 Its positional uncertainty is unlimited; its momentum (and wavelength) uncertainty is zero. This is a bizarre circumstance that, at the very least, adheres to the uncertainty principle. If the product of two uncertainties remains constant, one of them can only grow endlessly tiny if the other remains constant.
Consider the outcome of superposing many wavelengths. The superposition of two waves with wavelength differences of 10% is depicted below.
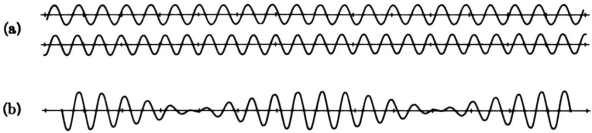
The waves interfere destructively five cycles after the point of maximum reinforcement. They reinforce again five cycles later. Partial localization of the wave is caused by the alternating of constructive and destructive interference, which causes the wave to bunch together into zones of around 10 wavelengths in length. This result contains an important indication concerning the uncertainty principle. The mixing of wavelengths required for partial localisation has resulted in momentum uncertainty.
By superposing a large number of distinct wavelengths, more localisation can be attained. The effect of mixing six separate pure waves, each with a wavelength difference of 2%, is shown in the diagram below.

The entire wavelength spread stays at 10%, with 5% on either side of the average wavelength. As a result, we can give a momentum uncertainty of around 5% of the dominant momentum:
Δp ≅ 0.05p.
Here, p denotes an average momentum, which is related to an average wavelength by the formula p = h/. The wave is better localised in the illustration because of the six-fold superposition. (The wave might be totally confined if all conceivable wavelengths within the provided span were superposed.) Its amplitude would sink to zero outside of a specified region of space, never to rise again.) The extent of the wave on either side of its center—roughly five wavelengths in the figure—represents the uncertainty of position:
Δx ≅ 5λ
In this case, the product of position and momentum uncertainty is
ΔxΔp ≅ 0.25λp.
Because the right-hand product p equals Planck's constant h, this equation can be written as
ΔxΔp ≅ 0.25h.
The numerical component 0.25 in this equation has no special relevance because we have made reasonable estimates of the uncertainty. The right side of the uncertainty equation, according to the technical definition of uncertainty employed in quantum mechanics, is exactly h/2, or, as stated in Essay Q6.
Since a 10% difference in momentum “crushed” the wave packet from infinite to just over 10 wavelengths, it's plausible to assume that momenta changing by almost 100% would be required to reduce the packet to a single cycle. This is correct. Maximum localization, x /2, necessitates superposition of wavelengths (and momenta) that differ by a factor of two. Then p p/2 p pppppppppp Because neither of these variables is clearly defined for a localised wave, p and refer to average values of momentum and wavelength in these equations. Again, the product xp is nearly identical to the product p, which is equal to Planck's constant.
The hydrogen atom contains an actual three-dimensional wave function, as opposed to the hypothetical one-dimensional waves outlined before. Its amplitude is depicted below along a radial line drawn across the atom's diameter.
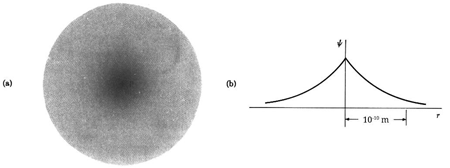
This electron wave function is highly confined, with only one oscillation cycle from one side of the atom to the other. This wave function's shape, with its central peak, is very different from that of a pure sine wave. With the appropriate mix of infinitely many wavelengths, any shape can be "fashioned."
The Heisenberg uncertainty principle is a result of the wave nature of particles, as demonstrated by this discussion of wave superposition. It is no more profound, and in this form, it says nothing more or less than the de Broglie equation for material particle wavelength. Measurement uncertainty stems mostly from the nonlocalizability of waves.
2.5.2 Two Examples of Localized Wave Packets
Lets now try two examples of a wave packet localized in k and properly normalized at t=0.
- A “square” packet: A(k) =
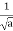 for k0 – a/2 < k < k0 + a/2 and 0 elsewhere.
for k0 – a/2 < k < k0 + a/2 and 0 elsewhere. - A Gaussian packet: A(k) = (2a/π)1/4 e-α (k – k0)2.
These are both localized in momentum about p= hk0.
Check the normalization of (1).
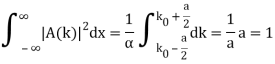
Check the normalization of (2) using the result for a definite integral of a Gaussian
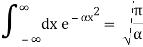

So now we take the Fourier Transform of (1) right here.

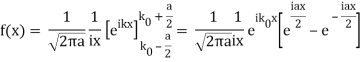
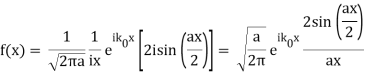
Note that 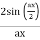 is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this
is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this 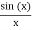 function.
function.
The Fourier Transform of a Gaussian wave packet
A(k) = 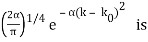
f(x) = 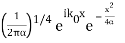
Also a Gaussian. We will show later that a Gaussian is the best one can do to localize a particle in position and momentum at the same time.
In both of these cases of f(x) (transformed from a normalized A(k) localized in momentum space) we see
- A coefficient which correctly normalizes the state to 1,
- eik0x - a wave corresponding to momentum hk0,
- And a packet function which is localized in x.
We've found states that represent a single free particle, which was our goal. We can have states that are localised in both position and momentum space, as we can see. We did this by creating wave packets, which are superpositions of definite-momentum states. While the wave packets are localised, they do have some width. x and in p.
2.6.1 Evolution of Wave Packets
We have

Where
ϕ(k) = kx – ω(k) t.
The function  is obtained by Fourier transforming the wavefunction at t = 0. Now,
is obtained by Fourier transforming the wavefunction at t = 0. Now, 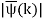 is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain
is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain

Where
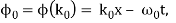
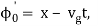
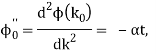
With
μ : ω (k0),
a : 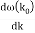
c : 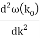
Rearranging, and then changing the variable of integration to y = (k – k0) / (2 ∆k), we get
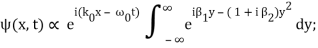
Where
2 ∆k ( x – x0 – vgt),
2 α (∆k)2t
Incidentally, ∆k = 1/ (2∆x) , where ∆x is the initial width of the wave packet. The above expression can be rearranged to give
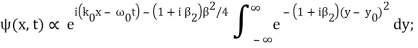
Where y0 = iβ/2 and β = β1 / (1+ iβ2). Again changing the variable of integration to z = (1+ iβ2)1/2 ( y – y0), we get
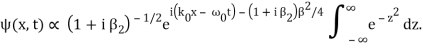
The integral now just reduces to a number. Hence, we obtain
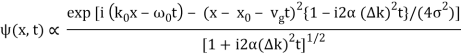
Where
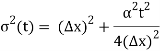
It's worth noting that the above wavefunction is the same as the one we started with at. This supports the estimate we produced before by extending the phase factor with Taylor. ϕ(k) about k = k0.
The probability density of our particle as a function of time is stated using Eq. (111).
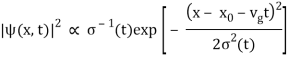
As a result, the probability distribution is Gaussian, with a characteristic width of and a maximum value of x = x0 + vgt. Our particle's most likely position now aligns with the distribution function's peak. As a result, the most likely position of the particle is provided by
x = x0 + vgt.
The particle essentially moves at a uniform velocity, as can be shown.
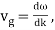
The particle essentially moves at a uniform velocity, as can be shown. vp = ω/k, whereas a wave packet travels at the group velocity,vg = d ω/dt. Now, it follows from the dispersion relation for particle waves that
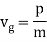
This, however, is the same as the classical particle velocity. As a result, once we learn that individual particles must be identified with wave packets rather than plane waves, the dispersion relation turns out to be consistent with classical physics. In reality, a continuous stream of particles moving in the same direction as the wave is commonly regarded as a plane wave.
The width of our wave packet grows as time passes, according to Eq. (112). Indeed, the characteristic time for a wave packet of original width to double in spatial extent is given by Eqs. (105).

For example, if an electron is initially isolated in an atomic scale region (i.e., ∆x ~ 10-10 m) then the doubling time is only about 10-16 s. Evidently, particle wave packets (for freely moving particles) spread very rapidly.
Note, from the previous analysis, that the rate of spreading of a wave packet is ultimately governed by the second derivative of ω(k) with respect to k. See Eqs. (105) and (112). This is why a functional relationship between and is sometimes referred to as a dispersion relation: it affects how wave packets spread over time. The second derivative of with respect to is 0 in the specific situation when is a linear function of, and hence there is no dispersion of wave packets: i.e. wave packets propagate without altering shape. In the case of light waves, the dispersion relation is now linear. Light pulses pass through a vacuum without spreading, as a result. Another feature of linear dispersion relationships is that the phase is preserved.
Velocity, vp = ω/k, and the group velocity, vg = dω/dk, are identical. Thus, both plane light waves and light pulses propagate through a vacuum at the characteristic speed c = 3 × 108 m/s. Of course, the dispersion relation for particle waves is not linear in k. Hence, particle plane waves and particle wave packets propagate at different velocities, and particle wave packets also gradually disperse as time progresses.
2.6.2 Time Development of a Gaussian Wave Packet
So far, we've just done our Fourier Transforms at and examined the results at t = 0. We'll now reintroduce time to the wave function and examine the wave packet at a later time. We'll see that photons and non-relativistic electrons behave very differently.
Assume we start with our Gaussian (minimum uncertainty) wave packet A(k) = 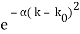 at t = 0. We can do the Fourier Transform to position space, including the time dependence.
at t = 0. We can do the Fourier Transform to position space, including the time dependence.
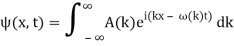
We state directly that is reliant on. This simply indicates that the energy of our free particle is determined by its motion. In the case of a photon, E = pc, so ℏ ω = ℏ kc, and hence ω = kc. For an non-relativistic electron, E = 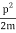 , so ℏ ω =
, so ℏ ω =  , and hence ω =
, and hence ω = 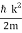 .
.
To cover the general case, lets expand ω(k) around the center of the wave packet in k-space.
ω(k) = ω(k0) + 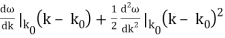
We make some educated guesses about the outcome and give the coefficients names.
ω(k) = ω0 + vg (k – k0) + β (k – k0)2
For the photon, vg = c and β=0. For the NR electron, vg = 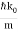 and β =
and β = 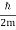 .
.
Performing the Fourier Transform, we get
ψ(x, t) = 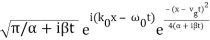
| ψ(x, t)|2 = 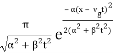
We can see that the photon will travel at the speed of light and that the wave will travel at the same speed.
Packet will not disperse, because β = 0.
The wave packet for the NR electron moves at the correct group velocity., vg = p/m, but the wave packet spreads with time. The RMS width is σ = 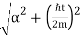
A wave packet naturally spreads because it contains waves of different momenta and hence different velocities. Wave packets that are very localized in space spread rapidly.
2.7.1 Wave-Particle Duality
The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.
Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
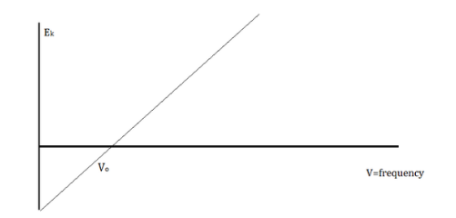
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.
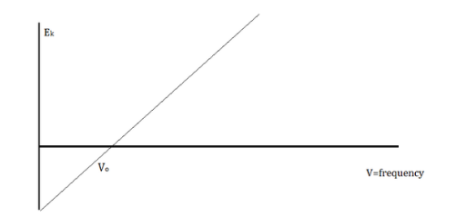
The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
We can say that light is a particle with the attribute of waves because the energy of waves and the energy of light do not correspond.
Einstein demonstrated that a photon's momentum equals
p = h/λ
This is readily demonstrated as follows. Assumption E = hv for a photon and λv = c for an electromagnetic wave, we obtain
E = hc/λ
We are now applying Einstein's relativity result. E = mc2 to find
λ = h/mc
Which is the same as equation (4). Because the rest mass of a photon is zero, this refers to the relativistic mass, not the rest mass. De Broglie reasoned in 1924 that matter can show this wave-particle duality because light can behave both as a wave (it may be diffracted and has a wavelength) and as a particle (it carries packets of energy). He went on to say that matter, like light, will obey the same equation (4). Davisson and Germer confirmed de Broglie's theory by observing diffraction patterns by hitting metals with electrons in 1927.
Bohr's assumption is justified according to de Broglie's equation (2). If we consider an electron to be a wave, the electron orbit must complete an integral number of wavelengths during its orbit to be stable. Otherwise, it would interfere with itself in a detrimental manner. This condition could be written as follows:
2πr = nλ
This can be expressed as using the de Broglie relation (4).
Mvr = nℏ
This is exactly the same as Bohr's equation (2).
While de Broglie's equation validates Bohr's quantization assumption, it also exposes a flaw in Bohr's model. The wave-particle duality, as demonstrated by Heisenberg, leads to the well-known uncertainty principle.
∆x∆p ≈ h
The uncertainty principle dictates that if the orbital radius of an electron in an atom is known precisely, the angular momentum must be unknown. The flaw in Bohr's model is that it stipulates both exactly and that the orbital angular momentum must be an integral multiple of. As a result, the stage was prepared for a new quantum theory that followed the uncertainty principle.
2.7.2 The duality of photons
“Light is a particle as well as a wave.” To have a better understanding of this concept, we conducted an experiment.
Young's Interference Experiment, often known as the Double-slit Interference Experiment, is a type of experiment. This experiment used technology to identify individual light particles to see if interference fringes appeared even when the light was severely attenuated to the point where there was just one particle. The experiment's findings confirmed that one photon had an interference fringe.
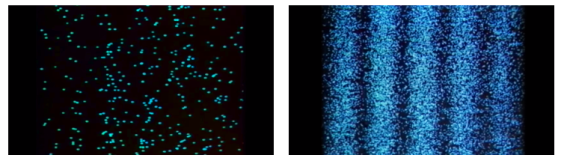
When light is detected that has been weakened to an extreme brightness limit and projected on a screen, it behaves like a particle, as shown on the left. When the number of particles detected rises, however, an interference fringe emerges, as shown on the right. As can be seen, light behaves similarly to a wave.
There was no interference fringe when one of the two slits in the experiment was closed, allowing only one photon particle to pass through the other slit. This proved that in the double-slit interference experiment, one photon particle travelled through both slits at the same time and interfered with itself.
These experiments show that while a photon was detected as having the properties of a particle, interference appeared like that of a wave while simultaneously passing through the double-slit, revealing that the photon has the dual properties of a particle and a wave.
Key takeaway:
- In quantum physics, wave–particle duality states that any particle or quantum phenomenon can be represented as either a particle or a wave. It expresses the difficulty of classical terminology like as "particle" and "wave" to completely characterise quantum-scale things' behaviour.
- He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
Complementarity is a concept in quantum mechanics that Niels Bohr considered to be a necessary property of the theory. According to the complementarity principle, objects have a set of complementary features that cannot all be viewed or measured at the same time. Position and momentum are an example of such a pair. One of quantum mechanics' foundational truths, according to Bohr, is that setting up an experiment to measure one of a pair of quantities, such as the position of an electron, excludes the possibility of measuring the other, despite the fact that understanding both experiments is required to characterise the object under study. The behaviour of atomic and subatomic things, according to Bohr, cannot be divorced from the measuring devices that form the framework in which they behave. As a result, there is no "one picture" that unifies the data gained in these various experimental situations, and only the "totality of the phenomena" as a whole can provide a complete description.
The failure of the operators that represent the observable quantities being measured to commute expresses complementarity mathematically:
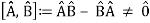
Incompatible observables are observables that correlate to non-commutative operators. There can't be a comprehensive set of shared eigenstates for incompatible observables. It's worth noting that there may be some simultaneous eigenstates of () A and () B, but not enough to form a complete basis. The canonical commutation relation is defined as follows:
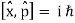
This suggests that this holds true for both position and momentum. Similarly, any two of the spin observables specified by the Pauli matrices have an equivalent relationship; measurements of spin along perpendicular axes are complimentary. Using mutually unbiased bases, which give complementary observables defined on finite-dimensional Hilbert spaces, this has been applied to discrete observables with more than two possible outcomes.
The principle of complementarity, or dialecticism, is a second key component of quantum physics. Is light a wave or a particle? Complementarity is defined as the recognition that though particle and wave behaviour are mutually exclusive, both are required for a complete explanation of all occurrences.
2.9.1 De Broglie’s Matter Waves:
When an electromagnetic wave interacts with matter, it can behave as a particle of light, according to Compton's formula. Louis de Broglie proposed a new speculative idea in 1924, claiming that electrons and other matter particles could behave like waves. De Broglie's hypothesis of matter waves is the name given to this concept today. De Broglie's hypothesis, combined with Bohr's early quantum theory, resulted in the development of a new wave quantum mechanics theory to describe the physics of atoms and subatomic particles in 1926. Quantum mechanics has made new technical inventions and technologies possible, such as the laser and magnetic resonance imaging (MRI). Other fields, such as biology and chemistry, benefit from this new technology.
According to de Broglie's hypothesis, both massless photons and heavy particles must satisfy a single set of relationships that link energy E to frequency f and linear momentum p to wavelength w. These photon-photon connections were previously studied in the context of Compton's effect. We're bringing them up now in a broader perspective. A de Broglie wave of frequency f and wavelength is any particle with energy and motion.
E = hf
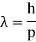
E and p denote a particle's relativistic energy and momentum, respectively. The wave vector is commonly used to express De Broglie's relations. 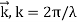 and the wave frequency ω = 2πf as we usually do for waves:
and the wave frequency ω = 2πf as we usually do for waves:
E = ℏω
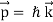
According to wave theory, a wave's energy is carried with the group velocity. This group velocity for matter waves is the particle's velocity u. De Broglie relations show that matter waves obey the following relation when the energy E and momentum p of a particle are identified with its relativistic energy mu and relativistic momentum mu, respectively.
λf = ω/k = 
Where β = u/c
When a particle is massless we have  and (Figure) becomes
and (Figure) becomes 
De Broglie gave an explanation for the quantization of the electron's angular momentum in the hydrogen atom, which was posited in Bohr's quantum theory, using the idea of the electron matter wave. When we suppose that an electron in a hydrogen atom behaves like a wave rather than a particle, the scientific explanation for the first Bohr quantization condition emerges easily. Imagine a stretched guitar string that is clamped at both ends and vibrates in one of its typical modes to see it clearly. The wavelengths of these vibrations cannot be random if the length of the string is l ((Figure)), but must be such that an integer k number of half-wavelengths /2 fits exactly on the distance l between the ends. A standing wave on a string has the constraint l=k/2. Let's pretend that instead of clamping the string to the walls, we bend it into a circle and tie the ends together. This results in a circular string that vibrates in normal modes and fulfils the same standing-wave requirement, but the number of half-wavelengths must now be an even number k,k=2n, and the length l is now tied to the circle's radius r n. This means that the radii cannot be chosen at random, but must meet the standing-wave condition:
2π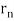 = 2n λ/2.
= 2n λ/2.
If an electron moves like a wave in the nth Bohr orbit, its wavelength must be equal to (Figure). λ = 2π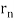 /n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
/n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
p = h/λ = nh/ (2 π = nh/
= nh/ . As a result, in a circular orbit, the electron's angular momentum must be
. As a result, in a circular orbit, the electron's angular momentum must be

The first of Bohr's quantization conditions, given by, is this equation (Figure). A plausible theoretical argument for the existence of matter waves is to provide a physical explanation for Bohr's quantization condition.
Standing-wave pattern: (a) a stretched string clamped against the walls; (b) an electron wave trapped in the hydrogen atom's third Bohr orbit.
In 1927, C. Davisson and L. Germer completed a series of electron-scattering tests that conclusively demonstrated that electrons behave like waves. Davisson and Germer's experiment were not designed to prove de Broglie's hypothesis: The proof came as a result of their usual experiments on metal surfaces bombarded by electrons.
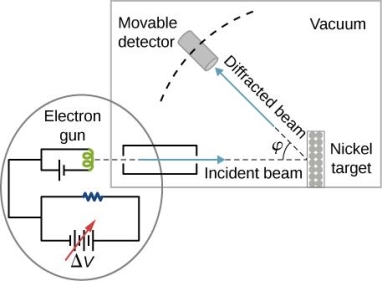
They analysed a nickel surface in the experiment that produced the first evidence of electron waves (now known as the Davisson–Germer experiment). Their nickel sample was treated in a high-temperature oven to transform it from its regular polycrystalline structure to one with massive single-crystal domains filling the volume. The experimental setup is depicted in (Figure). Thermal electrons are emitted from an electron gun's heated element (typically composed of tungsten) and accelerated through a potential difference V, resulting in a well-collimated stream of electrons. By adjusting the potential difference in the electron cannon, the kinetic energy K of the electrons can be modified. According to the law of conservation of energy, this results in a beam of electrons with a fixed linear momentum:
EV = K =  =
= 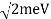
The electron beam strikes the nickel sample in a normal to its surface direction. It scatters in a variety of directions near the surface. A very sensitive detector measures the intensity of the beam scattered in a specific direction. The detector's angular location with relation to the incident beam's direction can range from to The entire setup is enclosed in a vacuum chamber to prevent electron collisions with air molecules, as such thermal collisions would change the electrons’ kinetic energy and are not desirable.
The Davisson–Germer diffraction experiment's experimental setup is shown schematically. The nickel target scatters a well-collimated beam of electrons. In the electron cannon, the kinetic energy of electrons in the incident beam is selected by setting a variable voltage, V. For a variety of scattering angles, the intensity of the scattered electron beam is measured, while the distance between the detector and the target remains constant.
The incident electrons scatter off the nickel target's surface in many random directions when it has a polycrystalline shape with many randomly aligned tiny crystals. As a result, the dispersed electron beam's intensity is nearly constant in all directions, simulating diffuse light reflection from a porous surface. When the nickel target has a regular crystalline structure, however, the intensity of the scattered electron beam reaches a definite maximum at a given angle, resulting in a distinct diffraction pattern (see Figure). William H. Bragg and William L. Bragg, father and son physicists, analysed similar diffraction patterns created by X-rays scattered by several crystalline substances in 1912. In X-ray crystallography, the Bragg law establishes a link between the wavelength of radiation impinge on a crystalline lattice, the lattice spacing, and the position of the diffracted radiation's interference maximum (see Diffraction).
The Davisson–Germer target's lattice spacing was measured using X-ray crystallography and found to be Unlike X-ray crystallography, in which X-rays penetrate the sample, only the surface atoms interact with the incident electron beam in the Davisson–Germer experiment. The highest intensity of the reflected electron beam is found for scattering angles that satisfy the requirement (see (Figure)) in surface diffraction. At a scattering angle of 50 at V54V, the first-order maximum (for n=1) is measured, yielding the wavelength of the incident light as λ = (2.15) sin 50 = 1.64. A 54-V potential, on the other hand, accelerates incident electrons to kinetic energies of K = 54 eV. Their momentum, calculated from (Figure), is p = 2.478 × 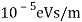 . When we substitute this result in (Figure), the de Broglie wavelength is obtained as
. When we substitute this result in (Figure), the de Broglie wavelength is obtained as
λ = h/p = 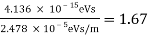
We get the same result when we utilise K = 54eV in (Figure). The theoretical result's closeness to the Davisson–Germer experimental value of 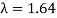 is a convincing argument for the existence of de Broglie matter waves.
is a convincing argument for the existence of de Broglie matter waves.
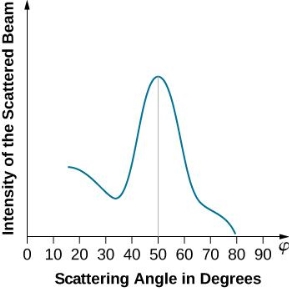
The experimental results of electron diffraction on a nickel target in an electron gun with an accelerating potential of around  At a scattering angle of around 45 degrees, the intensity maximum is recorded.
At a scattering angle of around 45 degrees, the intensity maximum is recorded.
The in-phase incident beams are reflected from atoms on the surface during surface diffraction of a monochromatic electromagnetic wave on a crystalline lattice structure. Where an is the lattice spacing, a ray reflected from the left atom travels an extra distance to the detector. When D is an integer multiple of the wavelength of the reflected beams, they remain in phase. For angles satisfactory, the strength of the reflected waves exhibits notable maxima.
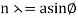

Because the incident electrons are dispersed only from the surface, diffraction lines recorded with low-energy electrons, such as those used in the Davisson–Germer experiment, are relatively broad (see (Figure)). When a higher-energy electron beam passes through a thin metal foil, the resolution of diffraction images improves dramatically. This happens because the diffraction image is made by scattering from a large number of crystallographic planes within the volume, and the maxima formed by scattering at Bragg angles are sharp (see Figure).
Diffraction patterns created by scattering X-rays and electrons on a crystalline material (a). The observed pattern represents the sample's crystalline structure's symmetry.

De Broglie's idea has been thoroughly examined using various experimental approaches since Davisson and Germer's work, and the presence of de Broglie waves has been proven for multiple elementary particles. Neutrons have been employed in scattering experiments to determine the crystalline structures of substances using neutron matter wave interference patterns. The mass of a neutron is comparable to that of a positively charged proton because it has no charge. Neutrons and protons can both be thought of as matter waves. As a result, being a matter wave is a property shared by all particles in motion, not only electrically charged ones. It has become possible to monitor matter waves of molecules as big as carbon C 60. As long as physical objects are in motion, they all have a matter wave associated with them. De Broglie matter waves have a universal character that has been established.
2.10.1 de Broglie Waves can be Experimentally Observed:
Electron diffraction studies conducted by G.P. Thomson in 1926 and C. Davisson and L. H. Germer in 1927 established the correctness of de Broglie's proposal. It was discovered in these investigations that electrons scattered from atoms in a crystal, and that these dispersed electrons generated an interference pattern. The interference pattern looked just like what happens when water waves flow through two holes in a barrier, generating independent wave fronts that merge and interfere. Both matter (e.g., electrons and neutrons) and electromagnetic radiation display these diffraction patterns, which are characteristic of wave-like behaviour. If the wavelength is equivalent to the spacing between scattering centres, diffraction patterns are generated.
We'll now look at the phenomena of electron diffraction as part of our analysis of experiments that led to the new quantum theory.
2.10.2 Light Diffraction (Young's Double Slit Experiment)
It is commonly known that light has the ability to diffract around things in its path, resulting in a pattern of interference that is unique to the object. In reality, this is how holography works (the interference pattern is created by allowing the diffracted light to interfere with the original beam so that the hologram can be viewed by shining the original beam on the image). The Young double slit experiment is a basic demonstration of light diffraction (Figure 1.7.1).

Figure 11: Experiment with a young double slit. A plane of light waves illuminates two apertures.
Water waves (shown as waves in a plane parallel to the double slit device) are used in this experiment to see what occurs when they hit the slits. Each slit then acts as a point source for spherical waves, which interfere with one another, resulting in the light and dark fringes seen on the right (Figure).
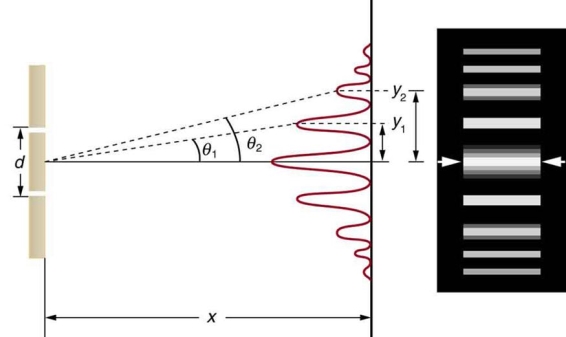
Figure 12: Interference through a double slit.
2.10.3 Electron Diffraction (Davisson–Germer Experiment)
Electrons, according to classical physics, should behave like particles, travelling in straight lines and not bending in flight until touched on by an external agent, such as a magnetic field. If we fire a beam of electrons through a double slit onto a detector in this scenario, we should obtain two bands of "hits," similar to what you'd get if you shot a machine gun through the side of a home with two windows - two regions of bullet-marked wall inside, while the remainder would be intact. Graph 1.7.3 (left).
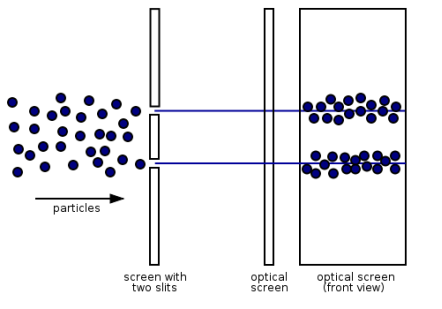
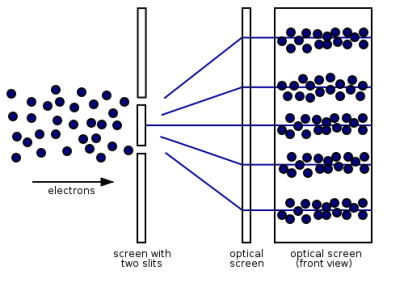
Figure 13: (left) classical model of electrons. (right) wave property of electrons.
However, if the slits are narrow and close enough together, we can see the electrons diffracting through the slits and interfering with one another, exactly like waves. This indicates that electrons, like photons, exhibit wave-particle duality, which is consistent with de Broglie's concept. They must have wavelength and frequency attributes in this scenario. The attributes can be deduced from the electrons' behaviour as they travel through our diffraction grating.
This was a watershed moment in the history of quantum physics. The Davisson–Germer experiment established the wave-nature of matter, completing the notion of wave-particle duality, much as the photoelectric effect had done for light. This concept was crucial to physicists since it suggested that not only could any particle display wave properties, but that wave equations could be used to describe processes in matter if the de Broglie wavelength was utilised.

2.10.4 Neutron Diffraction
Neutrons, like all quantum particles, can show wave behaviour, and atoms or their nuclei can behave as diffraction obstacles if the wavelength is short enough. When neutrons from a reactor are slowed and picked properly by their speed, their wavelength is near one angstrom (0.1 nm), which is the usual distance between atoms in a solid material. A diffraction experiment can then be carried out with such a beam. Neutrons interact directly with the nucleus of the atom, and each isotope contributes differently to the diffracted intensity; for example, ordinary hydrogen and deuterium contribute differently. Even in the presence of big Z atoms, light (low Z) atoms frequently contribute significantly to the diffracted intensity.
2.11.1 Davisson-Germer Experiment:
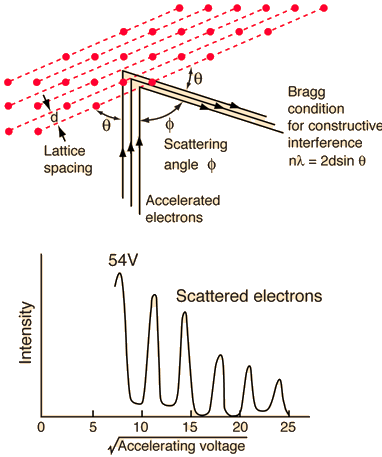
The Davisson-Germer experiment revealed the electron's wave character, validating deBroglie's earlier hypothesis. It was a big step forward in the development of quantum mechanics because it put wave-particle duality on a firm experimental footing. The Bragg diffraction law had previously been applied to x-ray diffraction, but this was the first time it had been applied to particle waves.
Davisson and Germer devised and constructed a vacuum apparatus for determining the energy of electrons scattered from a metal surface. A voltage was used to accelerate electrons from a hot filament and allow them to strike the surface of nickel metal.
The electron beam was focused on a nickel target that could be rotated to observe the dispersed electrons' angular dependency. Their electron detector (known as a Faraday box) was positioned on an arc and could be rotated to observe electrons from various angles. They were taken aback when they discovered that the intensity of the dispersed electron beam had a peak at some angles. The Bragg law could be used to calculate the lattice spacing in the nickel crystal based on this peak, which showed wave behaviour for the electrons.
With rising accelerating voltage, the experimental data above, replicated above Davisson's article, reveals recurrent maxima of scattered electron intensity. This information was gathered at a certain dispersion angle. The relationship is calculated using the Bragg law, the deBroglie wavelength expression, and the kinetic energy of the accelerated electrons.
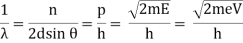
Electron Bragg deBroglie Acceleration wavelength law relationship through voltage V
An accelerating voltage of 54 volts produced a distinct peak at a scattering angle of 50° in the historical data. The Bragg law's angle theta for that scattering angle is 65°, and the computed lattice spacing for that angle is 0.092 nm. The wavelength as a function of voltage relationship is empirically determined for that lattice spacing and scattering angle.
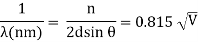
Trying this relationship for n=1,2,3 gives values for the square root of voltage 7.36, 14.7 and 22, which appear to agree with the first, third and fifth peaks above. What then accounts for the second, fourth, and sixth peaks? They could have come from a different set of crystal planes. Those peaks fall into the 2,3,4 sequence, implying that the series' first peak would have been around 5.85.
2.12.1 Deriving the de Broglie Wavelength
De Broglie arrived at his equation through a sequence of substitutions based on well-known theories:
De Broglie was the first to apply Einstein's famous equation for the relationship between matter and energy:
E = mc2 (1)
With
- E = energy,
- m = mass,
- c = speed of light
Using Planck's theory, each quantum in a wave has a discrete quantity of energy that can be calculated using Planck's equation:
E = hv
With
- E = energy,
- h = Plank's constant (6.62607 x 10-34 J s),
- ν= frequency
De Broglie hypothesised that the two energies would be equivalent because particles and waves share the same characteristics:
Mc2 = hv
De Broglie proposed velocity (v) for the speed of light since real particles do not travel at the speed of light (c).
Mv2 = hv
De Broglie replaced v/ for v in the equation and arrived at the final expression that connects wavelength and particle speed.
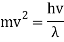
Hence
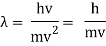
The majority of Wave-Particle Duality problems can be solved using Equation 6 and a few different cancelling out units.
De Broglie was given credit for his hypothesis, but he had no experimental proof to back it up. Clinton J. Davisson and Lester H. Germer fired electrons into a nickel crystal in 1927. They observed electron diffraction, which is analogous to wave diffraction against crystals (x-rays). In the same year, an English physicist, George P. Thomson fired electrons towards thin metal foil providing him with the same results as Davisson and Germer.
Key takeaway:
- De Broglie waves have a velocity. Beiser calls it "vp," and later shows that vp is the phase velocity of the waves. Vp=f is the formula for determining the velocity of a wave. De Broglie proposed the equation =h/mv for both particles and waves.
What is Wave-Particle Duality?
We've all heard about the nature of light and the various personalities it exhibits. Some of the features include interference, reflection, refraction, and diffraction. Particle-Wave The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.
Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.
The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
Since the energy of waves and energy of light does not coincide, we can say that light is a particle that has the property of waves.
The Uncertainty Principle
A particle's position and momentum cannot be measured with arbitrarily high precision at the same time. The product of the errors of these two measurements has a minimum. There is also a minimum for the product of the energy and time uncertainty.
∆x ∆p > ℏ/2
∆E ∆t > ℏ/2
This is not a remark about measuring equipment inaccuracy or the quality of experimental methods; it is a result of the wave qualities inherent in the quantum mechanical description of nature. The ambiguity is inherent in the nature of things, even with flawless instruments and skills.
The uncertainty principle, also known as the Heisenberg uncertainty principle or the indeterminacy principle, is a statement made by German physicist Werner Heisenberg in 1927. It states that an object's position and velocity cannot be measured precisely at the same time, even in theory. In fact, in nature, the concepts of absolute position and exact velocity have no relevance.
This principle is not obvious from everyday life. Because the uncertainties suggested by this concept for common objects are sufficiently small to be noticed, it is simple to measure both the position and velocity of, say, a car. The full rule states that the product of location and velocity uncertainties is equal to or larger than a small physical amount, or constant (h/(4), where h is Planck's constant, or approximately 6.6 1034 joule-second). Only for atoms and subatomic particles with extremely small masses can the product of uncertainty become important.
Any attempt to precisely measure the velocity of a subatomic particle, such as an electron, will cause it to move around in an unpredictable manner, rendering a simultaneous measurement of its position useless. This finding originates from the intimate relationship in nature between particles and waves in the world of subatomic dimensions, and has nothing to do with shortcomings in the measurement devices, procedure, or observer.
The wave-particle duality gives rise to the uncertainty principle. Every particle has a wave connected with it, and every particle behaves in a wavelike manner. The particle is most likely to be located where the wave's undulations are the most pronounced or powerful. However, the more powerful the associated wave's undulations get, the more ill-defined the wavelength becomes, which defines the particle's momentum. As a result, a strictly localised wave has an indeterminate wavelength, while its associated particle has a fixed position but no fixed velocity. A particle wave with a well-defined wavelength, on the other hand, is widely dispersed; the associated particle, albeit having a very accurate velocity, may be found practically anywhere. A very precise measurement of one observable entails a significant amount of uncertainty in the measurement of the other.
The uncertainty principle can also be represented in terms of the momentum and position of a particle. A particle's momentum is equal to the product of its mass and velocity. As a result, the product of a particle's momentum and position uncertainty equals h/(4+) or greater. The idea also holds true for other related (conjugate) pairings of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is taken equals h/(4+) or more. The uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it transitions to a more stable state are the same for an unstable atom or nucleus.
Are the uncertainty relations revealed by Heisenberg in 1927 simply the outcome of the equations utilised, or are they embedded in every measurement? Heisenberg used a thought experiment because he felt that all scientific concepts must be defined using actual or possible experimental observations.
Heisenberg imagined a microscope that achieves extremely fine resolution by illuminating with high-energy gamma rays. Although such a microscope does not exist at the moment, it may theoretically be built. Heisenberg envisaged seeing an electron and measuring its position using this microscope. He discovered that the electron's position and momentum obeyed the mathematically established uncertainty relation. The experiment had significant problems, which Bohr pointed out, but after they were fixed, the demonstration was completely compelling.
A free electron rests just beneath the centre of the microscope's lens in the revised version of the thought experiment (see the picture above). From the electron, the circular lens forms a cone with an angle of 2A. Gamma rays—high intensity light with the smallest wavelength—then illuminate the electron from the left. These have the maximum resolution because, according to a wave optics principle, the microscope can resolve (that is, "see" or distinguish) objects to a size of Dx, which is related to and to the gamma ray wavelength L by the expression:
Dx = L / (2sinA)
A gamma ray impacting an electron, on the other hand, provides it a kick in quantum mechanics, where a light wave can act like a particle. The electron is driven to the right when light is diffracted by the electron into the microscope lens. The gamma ray must be dispersed into any angle within the cone of angle 2A in order to be detected by the microscope. The gamma ray, like a particle, carries momentum in quantum physics. The wavelength is related to the total momentum p by the formula
p = h / L, where h is Planck's constant.
The total momentum in the x direction would be the sum of the electron's momentum p'x in the x direction and the gamma ray's momentum in the x direction in the extreme case of diffraction of the gamma ray to the right edge of the lens:
p'x + (h sinA ) / L', where L' is the wavelength of the deflected gamma ray.
In the other extreme, the observed gamma ray recoils backward, just hitting the left edge of the lens. The overall momentum in the x direction in this example is:
p''x - (h sinA ) / L''.
Because momentum is never lost, the final x momentum in each scenario must equal the beginning x momentum (it is conserved). As a result, the final x momenta are identical:
p'x + (h sinA ) / L' = p''x - (h sinA ) / L''
If A is tiny, the wavelengths are close to being the same, L' L" L. So there you have it.
p''x - p'x = Dpx ~ 2h sinA / L
We have a reciprocal link between the minimal uncertainty in the observed position, Dx, of the electron along the x axis and the uncertainty in its momentum, Dpx, in the x direction because Dx = L / (2 sinA ).
Dpx ~ h / Dx or Dpx Dx ~ h.
The "more than" indication can be used if there is more than the bare minimum of uncertainty.
This is Heisenberg's uncertainty relation for simultaneous measurement of an object's position and momentum, except for the factor of 4p and an equal sign.
Modern physicists warn that a careful examination of this image reveals an illusory classical mechanical interaction one step deeper, in the collision of the photon and the electron. In fact, despite its importance in the development and teaching of quantum theory, Heisenberg's microscope is not part of modern knowledge. Any depiction that resembles daily colliding items cannot represent the genuine quantum interaction and the genuine uncertainty associated with it. You must work through the formal mathematics that estimates probabilities for abstract quantum states to get the actual outcome. Experiments on these kind of interactions are still being carried out now. So far, the experiments have all confirmed Heisenberg's belief that no "genuine" microscopic classical collision occurs at the bottom.
The interpretation
So, how can we make sense of it all? Is this Heisenberg's own Principle being 'proven'? Yes and no, in my opinion. I'd say it's a combination of illustration and proof. The following are the key assumptions:
1. We can think of -ray photons, or any photon for that matter, as particles with momentum, and when they ‘collide,' or interact, with an electron, the photon will give that electron some momentum.
2. Because momentum is conserved, the total (linear) momentum before and after the collision must be the same for both particles–that is, (1) the incoming ray and the electron before the contact and (2) the released photon and the electron that receives the kick after the encounter.
3. We may connect (or associate, if you prefer) the wavelength of the -ray photon with its momentum p using the Planck relation or, equivalently for photons (since they have no mass), the de Broglie connection.
2.16.1 Single slit Experiment:
Interference, refraction, reflection, and diffraction are all examples of processes that occur as light travels through air. Diffraction of light occurs when it comes into contact with an obstruction.
The wavefront on the other side of the opening mimics the wave when light flows through a small opening that is comparable in size to the wavelength of the light. Please explain light diffraction and single slit diffraction, which occurs when light passes through a single slit.
When light passes through a single slit with a width (w) on the order of the wavelength of the light, we can witness single slit diffraction. The screen's diffraction pattern will be at a distance L >> w from the slit. The intensity is proportional to the angle.
We may examine the bending phenomena of light, or diffraction, in the single-slit diffraction experiment, which causes light from a coherent source to interfere with itself and generate a distinct pattern on the screen termed the diffraction pattern. When the sources are tiny enough to be comparable in size to the wavelength of light, diffraction occurs. This impact can be seen in the diagram below. The spreading out of huge apertures is minor and almost undetectable.

Single Slit Diffraction Formula
We shall assume the slit width a << D. xD is the separation between slit and source.
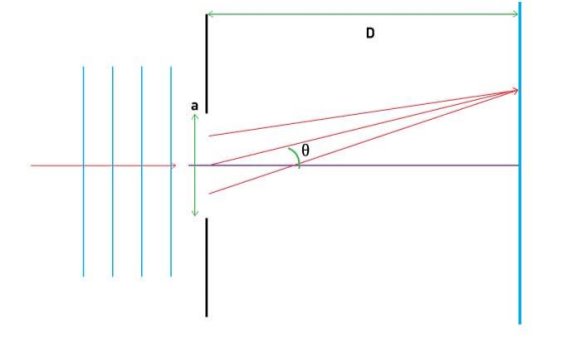
The angular position of any point on the screen will be determined by measuring from the slit centre, which divides the slit by lengths. To explain the pattern, we'll look at the condition of black fringes first. Let's also divide the split into equal-width zones.
lengths. To explain the pattern, we'll look at the condition of black fringes first. Let's also divide the split into equal-width zones. . Let's look at a pair of rays that come from a/2 distances apart, as indicated below.
. Let's look at a pair of rays that come from a/2 distances apart, as indicated below.
The path difference exhibited by the top two rays shown is:
∆L = a/2 sin θ
Remember that this is only a valid computation if D is really large. Check visit our article on Young's Double Slit experiment for more information on the approximation.
Any number of ray pairings that start at a distance of a2 from one another, such as the bottom two rays in the diagram, can be considered. Any arbitrary pair of rays separated by a2 can be taken into account. In a moment, we'll discover how important this trick is.
The path difference must induce destructive interference for a dark fringe; the path difference must be out of phase by 2. (represents the wavelength)
The first fringe is made up of
∆L = λ/2 = a/2 sin θ
λ = a sin θ
There is another ray at a distance a2 that can generate destructive interference for a ray emerging from any point in the slit.
As any ray emerging from a point has a counterpart that produces destructive interference, there is destructive interference at = sin1a. As a result, a dark fringe is created.
We can divide the slit into four equal sections of a/4 and use the same rationale for the next fringe. As a result, for the second minimum:
λ/2 = a/4 sin θ
2λ = a sin θ
Similarly, we can divide the slit into 2n sections for the nth fringe and utilise the following condition:
nλ = a sin θ
The Central Maximum
The maxima are located between the minima, and the width of the central maximum is equal to the distance between the first order minima on both sides of the screen.
The position of the minima determined by y (as measured from the screen's centre) is:
Tan θ ≈ θ ≈ y/D
For small ϑ,
Sin θ≈θ
⇒λ = a sin θ≈aθ
⇒θ = y/D = λa
⇒ y = λDa
The width of the central maximum is simply twice this value
⇒ Width of central maximum = 2λDa
⇒ Angular width of central maximum = 2θ = 2λa
The diffraction pattern and intensity graph is shown below.
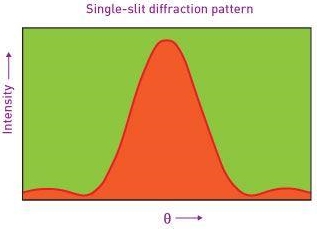
2.17.1 The Quantum Harmonic Oscillator:
One drawback of this traditional formulation is that it is not universal. We can't use it to represent diatomic molecular vibrations, for example, because quantum effects are important. Using the classical statement to limit discussion of a "spring" constant between the atoms is a first step toward a quantum formulation. The potential energy function can be stated in a more general sense this way.
U(x) = ½ m ω2 x2
When this expression is used with the time-independent Schrdinger equation, the result is

To solve (Figure), we need the wave functions to be symmetric around x=0 (the bottom of the potential well) and normalizable in order to discover the permitted energies E and their corresponding wave functions (x). When integrated throughout the complete range of x from to+, these requirements ensure that the probability density |(x)2 | must be finite. A more advanced course in quantum mechanics will cover how to solve (Figure); here, we will simply mention the results. The permitted energies are as follows:
En = ( n + ½ ) ℏω = 2n+1/2 ℏω, n = 0, 1, 2, 3, . . .
These energies (stationary states or states of defined energy) correlate to wave functions.
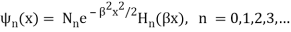
Where β =  ,
,  is the normalization constant, and Hn(y) is a polynomial of degree n called a Hermite polynomial. The first four Hermite polynomials are
is the normalization constant, and Hn(y) is a polynomial of degree n called a Hermite polynomial. The first four Hermite polynomials are
H0 (y) = 1
H1 (y) = 2y
H2 (y) = 4y2 – 2
H3 (y) = 8y3 – 12y
In this section, we'll look at a few sample wave functions (Figure). As the primary number grows larger, the solutions alternate between even and odd functions around the axis.
The quantum harmonic oscillator's first five wave functions. Vertical lines illustrate the classical limitations of the oscillator's motion, which correspond to the classical turning points at x=A of a classical particle with the same energy as a quantum oscillator in the state shown in the image.
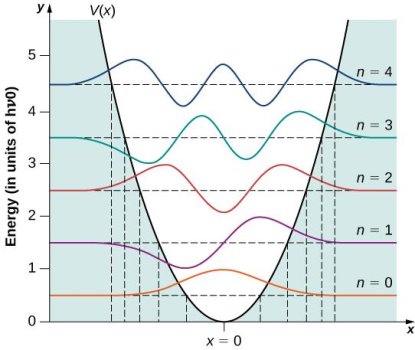
This solution has a number of intriguing properties. Unlike a classical oscillator, a quantum oscillator's observed energies can only have energy values given by (Figure). Furthermore, unlike a quantum particle trapped in a cage, the allowed energy levels are evenly distributed.
E = En+1 – En = 2(n+1)+1/2 ℏω – 2n+1/2 ℏω = ℏω = hf.
The smallest-energy quantum carried by the emitted photon must be hf when a particle coupled to such a system transition from a higher-energy state to a lower-energy state. Similarly, when a particle transitions from a lower-energy to a higher-energy state, the smallest-energy quantum that the particle may absorb is hf. Only multiples of this smallest-energy quantum can be absorbed or emitted by a quantum oscillator. In the blackbody radiation problem, this is consistent with Planck's notion for energy exchanges between radiation and cavity walls.
In three respects, the quantum oscillator varies from the traditional oscillator:
To begin with, a quantum oscillator's ground state is not zero. The lowest energy, according to conventional wisdom, is zero. Because of the omnipresent fluctuations that are a result of the Heisenberg uncertainty principle, all quantum-mechanical systems do not have a zero-energy state. The Heisenberg uncertainty principle would be violated if a quantum particle rested still at the bottom of the potential well, as both its momentum and position would have to be correct at the same time. As a result, the lowest-energy state must have errors in momentum and position, and a quantum particle's ground state must be above the bottom of the potential well.
Second, a particle in a quantum harmonic oscillator potential can be located outside the interval with a nonzero probability. A < x < +A. The particle would have no energy to be in this location under a traditional formulation of the problem. In the classically forbidden zone, the probability of finding a ground-state quantum particle is roughly 16 percent.
Third, the probability density distributions |ψn(x)|2 for a quantum oscillator in the ground low-energy state, ψ0(x), is largest at the middle of the well (x=0). For the particle to be found with greatest probability at the center of the well, we expect that the particle spends the most time there as it oscillates. This is opposite to the behavior of a classical oscillator, in which the particle spends most of its time moving with relative small speeds near the turning points.
For excited states, quantum probability density distributions vary in nature, becoming more like the classical distribution as the quantum number increases. Because the distribution of the first excited state of a quantum oscillator is different, we can see this change. |ψn(x)|2 As seen in, peaks near the turning points and vanishes at the equilibrium position (Figure). According to Bohr's correspondence principle, the quantum description of a harmonic oscillator converges to the classical description in the limit of large quantum numbers, as shown in (Figure). The quantum probability distribution for a quantum oscillator in this excited state is reasonably well approximated by the classical probability density distribution corresponding to the quantum energy of the n=12 state. For highly excited states, this agreement improves over time.
The probability density distribution for finding the n=12 quantum state of the quantum harmonic oscillator. The probability density distribution of a classical oscillator with the same energy is shown by the dashed curve.
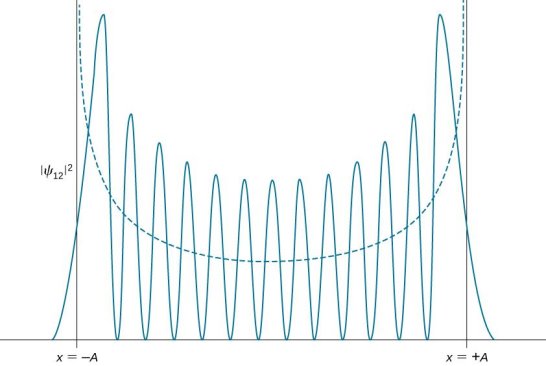
2.17.2 Estimate the Hydrogen Ground State Energy
The fundamentally uncertainty principle explains why the hydrogen atom (and other atoms) is so big. If the electron were to be contained in a smaller space,∆p would increase, causing p to increase on average. The energy would rise rather than fall.
The uncertainty principle can be used to calculate the minimal energy for hydrogen. This computation is not perfect, but it is more accurate than the Bohr model. The notion is that the radius must be greater than the positional spread, and the momentum must be greater than the momentum spread.
r ≥ ∆x
p ≥ ∆p = ℏ/2r
In terms of the dimensionless fine structure constant, this is our formula for potential energy. α.
V(r) = 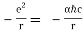
Let us calculate the energy.
E = 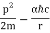
And include the uncertainty principle's influence.
Pr = ℏ
E = 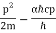
E = 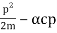
Differentiate in terms of p To get the minimum, set equal to zero.
DE/dp = p/m – 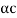 = 0
= 0
p = 

It's worth noting that potential energy is just (-2) times kinetic energy (as we expect from the Virial Theorem). The energy formula for the ground state is valid.
We can also make an educated guess at the radius.
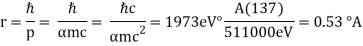
Hydrogen has no (orbital) angular momentum in its ground state. It is not travelling in a circular orbit as predicted by Bohr. The probability distribution of the electron is spread out over around 1. The energy would rise if it wasn't spread out.
The quantum physics-based Heisenberg uncertainty principle explains a number of things that classical physics could not explain. One of the applications is to demonstrate that an electron cannot exist within a nucleus. It goes like this:
Non-existence of electrons in the nucleus
Let us assume that electrons exist in the nucleus. As the radius of the nucleus in approximately 10-14 m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
∆x= 10-14 m
According to uncertainty principle,
∆x∆px =h/2∏
Thus ∆px=h/2∏∆x
Or ∆px =6.62 x10-34/2 x 3.14 x 10-14
∆px=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron, then the momentum of electron should be at least of this order, that is p=1.05*10-20 kg m/sec.
With such a large momentum, an electron's velocity must be similar to that of light. As a result, the following relativistic formula should be used to compute its energy.
E= √ m20 c4 + p2c2
E = √(9.1*10-31)2 (3*108)4 + (1.05*10-20)2(3*108)2
= √(6707.61*10-30) +(9.92*10-24)
=(0.006707*10-24) +(9.92*10-24)
= √9.9267*10-24
E= 3.15*10-12 J
Or E=3.15*10-12/1.6*10-19 eV
E= 19.6* 106 eV
Or E= 19.6 MeV
As a result, if the electron occurs in the nucleus, its energy should be in the range of 19.6 MeV. However, beta-particles (electrons) released from the nucleus during b-decay have energy of around 3 MeV, which differs significantly from the calculated value of 19.6 MeV. The second reason an electron cannot exist inside the nucleus is that no electron or particle in the atom has an energy greater than 4 MeV, according to experimental evidence.
Electrons have a negative charge, and if they can exist in the nucleus, the positive charges will neutralise them.
According to Heisenberg's uncertainty principle, the radius of atomic nuclei is 10-15 m, and if electrons exist in the nucleus, the maximum uncertainty in its position is 10-15 m.
Mass of the electron is 9.1 x 10-31 kg
No electron or particle in the atom possess energy greater than 4MeV
Hence the electrons do not exist inside the nucleus
2.19.1 Complementarity.
Complementarity is a concept in quantum mechanics that Niels Bohr considered to be a necessary property of the theory. According to the complementarity principle, objects have a set of complementary features that cannot all be viewed or measured at the same time. Position and momentum are an example of such a pair. One of quantum mechanics' foundational truths, according to Bohr, is that setting up an experiment to measure one of a pair of quantities, such as the position of an electron, excludes the possibility of measuring the other, despite the fact that understanding both experiments is required to characterise the object under study. The behaviour of atomic and subatomic things, according to Bohr, cannot be divorced from the measuring devices that form the framework in which they behave. As a result, there is no "one picture" that unifies the data gained in these various experimental situations, and only the "totality of the phenomena" as a whole can provide a complete description.
The failure of the operators that represent the observable quantities being measured to commute expresses complementarity mathematically:
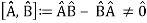
Incompatible observables are observables that correlate to non-commutative operators. There can't be a comprehensive set of shared eigenstates for incompatible observables. It's worth noting that there may be some simultaneous eigenstates of () A and () B, but not enough to form a complete basis. The canonical commutation relation is defined as follows:
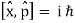
This suggests that this holds true for both position and momentum. Similarly, any two of the spin observables specified by the Pauli matrices have an equivalent relationship; measurements of spin along perpendicular axes are complimentary. Using mutually unbiased bases, which give complementary observables defined on finite-dimensional Hilbert spaces, this has been applied to discrete observables with more than two possible outcomes.
The principle of complementarity, or dialecticism, is a second key component of quantum physics. Is light a wave or a particle? Complementarity is defined as the recognition that though particle and wave behaviour are mutually exclusive, both are required for a complete explanation of all occurrences.
2.19.2 Uncertainty.
With difficulties of wave/particle duality, classical physics was on shaky ground, but the discovery of the uncertainty principle took them completely off surprise.
The uncertainty principle, also known as the Heisenberg Uncertainty Principle or Indeterminacy Principle, was proposed by German physicist Werner Heisenberg in 1927, and states that an object's position and velocity cannot be measured precisely at the same time, even in theory. In fact, in nature, the concepts of absolute position and exact velocity have no relevance.
This principle is not obvious from everyday life. Because the uncertainties suggested by this concept for common objects are sufficiently small to be noticed, it is simple to measure both the position and velocity of, say, a car. The full rule states that the product of position and velocity uncertainties is equal to or larger than a minuscule physical amount, or constant (about 10-34 joule-second, the value of the quantity h (where h is Planck's constant)). Only for atoms and subatomic particles with extremely small masses can the product of uncertainty become important.
Any attempt to precisely measure the velocity of a subatomic particle, such as an electron, will cause it to move around in an unpredictable manner, rendering a simultaneous measurement of its position useless. This finding originates from the intimate relationship in nature between particles and waves in the world of subatomic dimensions, and has nothing to do with shortcomings in the measurement devices, procedure, or observer.
Every particle has a wave connected with it, and every particle behaves in a wavelike manner. The particle is most likely to be located where the wave's undulations are the most pronounced or powerful. However, the more powerful the associated wave's undulations get, the more ill-defined the wavelength becomes, which defines the particle's momentum. As a result, a strictly localised wave has an indeterminate wavelength, while its associated particle has a fixed position but no fixed velocity. A particle wave with a well-defined wavelength, on the other hand, is widely dispersed; the associated particle, albeit having a very accurate velocity, may be found practically anywhere. A very precise measurement of one observable entails a significant amount of uncertainty in the measurement of the other.
The uncertainty principle can also be represented in terms of the momentum and position of a particle. A particle's momentum is equal to the product of its mass and velocity. As a result, the product of a particle's momentum and position uncertainty equals h/(2) or greater. The principle holds for other (conjugate) pairings of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is taken equals h/(2) or greater. The uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it transitions to a more stable state are the same for an unstable atom or nucleus.
W. Heisenberg discovered the uncertainty principle, which expresses the impact of wave-particle duality on the properties of subatomic things. Consider the concept of momentum in the microscopic world, which is similar to a wave. The wavelength of a wave determines its momentum. A wave packet, such as a photon or an electron, is made up of several waves. As a result, it must be made up of a variety of momentums. But how is it possible for one object to have several momentums?
Of course, once a particle's momentum is measured, a single momentum is observed. Momentum before the observation, like fuzzy position, is inherently ambiguous. The uncertainty principle states that certain quantities, such as position, energy, and time, are unknown save through probability. The uncertainty principle states that accurate knowledge of complementarity pairings is impossible in its purest form. You can measure an electron's location but not its momentum (energy) at the same time, for example.
The principle of complementarity, which "implies the impossibility of any clear separation between the behaviour of atomic objects and their interaction with the measuring devices that serve to specify the conditions under which the phenomena arise," is a defining element of quantum physics. As a result, "data gathered under various experimental conditions cannot be comprehended within a single picture, but must be treated as complimentary in the sense that only the entirety of the events exhausts the possible knowledge about the objects," according to the authors. During the 1930s, the majority of scientists increasingly adopted this interpretation of quantum physics, which indicated a different perspective of the significance of physical explanation.
The uncertainty principle can be expressed mathematically as follows, where x' denotes position and p' denotes momentum:
∆x∆p > h/2π
Next to E=mc2, this is possibly the most well-known equation in physics. It essentially states that the sum of the errors in position and momentum must always be bigger than Planck's constant. So, you can measure an electron's position to a certain degree of precision, but its momentum will fall within a very wide range of values. Similarly, you can precisely measure momentum, but its location is unknown.
Notice that this is not a different version of the measurement problem; for a quantum particle, the combination of position, energy (momentum), and time is really indeterminate until a measurement is done (then the wave function collapses).
Also, because Planck's constant, h, is so small, the uncertainty principle is irrelevant to macroscopic objects (10-34). A thrown baseball, for example, has a positional uncertainty of 10-30 millimetres.
When we raise the question, "Is our knowledge of reality unlimited?" we comprehend the depth of the uncertainty principle. No, because the uncertainty principle implies that Nature contains inherent uncertainty, indeterminacy, and unpredictability.
Key takeaway:
- In quantum physics, Heisenberg's uncertainty principle is a crucial concept. It goes something like this: if we know exactly where a particle is (the uncertainty of position is tiny), we know nothing about its momentum (the uncertainty of momentum is huge), and vice versa.
- According to the classical Uncertainty Principle, a function and its Fourier transform cannot be highly focused at the same time. This has the conceptual implication in quantum mechanics that determining a particle's position and momentum at the same time is impossible (Heisenberg Uncertainty Principle).
References:
1.Quantum Mechanics: Theory and Applications, A.K.Ghatakand S. Lokanathan,(Macmillan)-2004
2. Introduction to Quantum Theory, David Park (Dover Publications)-1974
3. Theory and Problems of Modern Physics, Schaum‘s outline,R.Gautreau and W.Savin- (Tata McGraw-Hill) 2nd Edition
4. Physics for scientists and engineer with Modern Physics-Jewell and Serway -(CENGAGE Learnings) 2010.
5. Modern Physics of Atoms and Molecules Bransden and Joachim (PearsonIndia)-2003
Unit - 2
Wave Packet
2.1.1 Superposition and Interference
The majority of waves do not appear to be straightforward. They resemble the waves depicted in Figure rather than the ordinary water wave discussed in Waves. (Simple waves have a sinusoidal shape because they are formed by a simple harmonic oscillation.) Complex waves are more intriguing, even beautiful, but they appear to be intimidating. The majority of waves appear complex because they are made up of multiple simple waves that have been added together. Fortunately, the principles for adding waves are straightforward.

Figure 1.
When two or more waves arrive at the same location at the same time, they superimpose on each other. When waves collide, the disturbances of the waves are superimposed, a phenomenon known as superposition. Each disruption is associated with a force, which adds up. If the disturbances all follow the same path, the final wave is simply the sum of the individual waves' disturbances—that is, their amplitudes add. Figures 2 and 3 show superposition in two different situations, both of which yield straightforward results.
Figure 2 depicts two similar waves arriving at the same time and in phase. The crests and troughs of the two waves are perfectly aligned. The result of this superposition is pure constructive interference. Pure constructive interference generates a wave with double the amplitude of the component waves but the same wavelength since the disturbances add up.
Figure 3 illustrates two identical waves arriving out of phase—that is, with their crests and troughs precisely aligned—producing pure destructive interference. The resulting amplitude for pure destructive interference is 0 since the disturbances are in the opposite direction for this superposition—the waves entirely cancel.
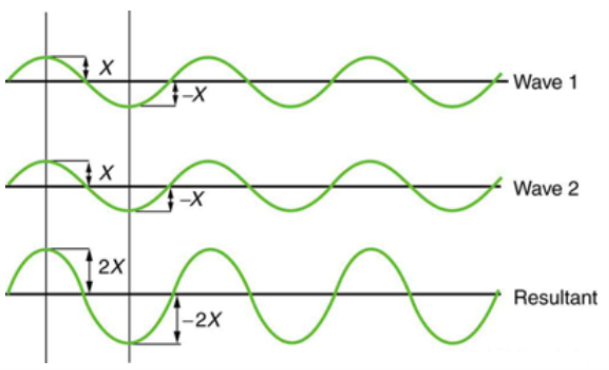
Figure 2: When two identical waves collide, the result is a wave with twice the amplitude but the same wavelength.

Figure 3: When two identical waves collide, the result is zero amplitude, or total cancellation.
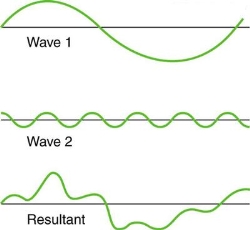
Figure 4. Superposition of non-identical waves exhibits both constructive and destructive interference.
While pure constructive and destructive interference do occur, they require identical waves to be exactly aligned. Most waves superpose, resulting in a mix of constructive and destructive interference that varies from location to place and time to time. A stereo's sound, for example, can be powerful in one place yet muted in another. Sound waves add partially constructively and partially destructively at different locations when their loudness varies. Sound waves are created by at least two speakers in a stereo, and sound waves can reflect off walls. All of these waves are stacked on top of each other. The combined whining of aeroplane jets perceived by a stationary passenger is an example of noises that change over time from constructive to detrimental. As the sound from the two engines changes in time from constructive to destructive, the total sound might fluctuate in amplitude. These are waves that are similar to each other. Figure 4 depicts an example of the superposition of two different waves. Again, the disturbances add and subtract, resulting in a wave that appears more intricate.
2.1.2 Principle of Superposition of Waves
Consider two waves travelling in opposite directions along the same stretched string, as shown in the diagram above. At any given time, we can see images of waveforms in the string. The algebraic total of the displacements owing to each wave is found to be the net displacement of every element of the string at any given time.
Let's imagine two waves are travelling alone, and any element of these two waves' displacements can be represented as y1(x, t) and y2(x, t) (x, t). The resultant displacement can be written as y when these two waves collide (x,t).
y (x, t) = y1(x, t) + y2(x, t) = y3(x, t) = y4(x, t) = y5(x, t) = y (x, t)
We can sum the overlapped waves algebraically to generate a consequent wave using the principle of superposition. Let us say that the wave functions of moving waves are as follows:
y1 = f1(x–vt),
y2 = f2(x–vt)
……….
yn = fn (x–vt)
Then the wave function describing the disturbance in the medium can be described as
y = f1(x – vt)+ f2(x – vt)+ …+ fn(x – vt)
Or, y=∑ i=1 to n = fi (x−vt)
Let us consider a wave travelling along a stretched string given by, y1(x, t) = A sin (kx – ωt) and another wave, shifted from the first by a phase φ, given as y2(x, t) = A sin (kx – ωt + φ)
From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A.
Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement y(x, t) = A sin (kx – ωt) + A sin (kx – ωt + φ)
The above equation can be written as,
y(x, t) = 2A cos (ϕ/2). Sin (kx −ωt + ϕ/2)
The resulting wave is a sinusoidal wave travelling in the positive X direction, with a phase angle half that of the component waves and an amplitude equal to [2cos/2] times the original waves' amplitudes.
2.1.3 Condition for Destructive Interference
Phase difference = (2n – 1)π
Path difference = (2n – 1)λ/2
I = Imin
Imin = I1 + I2 – 2 
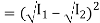
2.1.4 Standing Waves
Waves don't always appear to move; instead, they only vibrate in situ. Unmoving waves, for example, can be seen on the surface of a glass of milk in the refrigerator. The refrigerator motor's vibrations create waves on the milk that oscillate up and down but do not appear to travel over the surface. These waves are created by the superposition of two or more moving waves, such as the two identical waves flowing in opposite directions seen in Figure 5. The waves pass through each other, adding to the disruptions as they travel. When the amplitude and wavelength of two waves are the same, they alternate between constructive and destructive interference. The outcome is known as a standing wave because it resembles a wave that is stationary. Standing waves can be seen on the surface of a glass of milk. Other standing waves can be found in guitar strings and organ pipes. The two waves that generate standing waves in the glass of milk could be caused by reflections from the glass's side.
A detailed examination of earthquakes reveals evidence of resonance, standing waves, and constructive and destructive interference situations. A building may be vibrated for several seconds at a frequency that matches the natural frequency of vibration of the building, resulting in a resonance that causes one building to collapse while surrounding buildings remain intact. Buildings of a specific height are frequently destroyed, whereas taller structures remain standing. The height of the building corresponds to the conditions for creating a standing wave at that height. At specific spots along the Earth's surface, constructive interference occurs as seismic waves reflect off denser rocks. Areas near to the epicentre are frequently unaffected, whereas areas further away are.
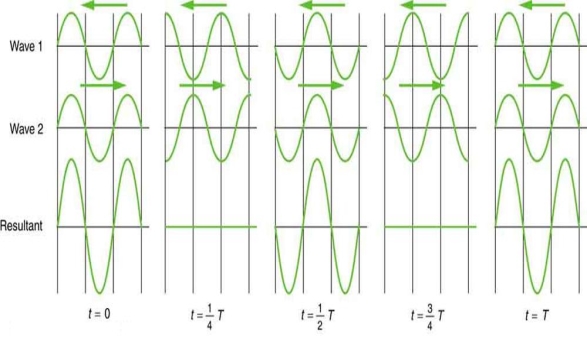
Figure 5: A standing wave is formed when two similar waves moving in opposite directions are superimposed. The oscillations occur at predetermined points in space and are caused by constructive and destructive interference.
Standing waves can also be formed on musical instrument strings as a result of wave reflections from the ends of the string. Three standing waves can be formed on a string that is fastened at both ends, as seen in Figures 6 and 7. In a standing wave, nodes are the sites where the string does not move; more broadly, nodes are the sites where the wave disturbance is zero. Because the string cannot move, the fixed ends of strings must also be nodes. In standing waves, the term antinode refers to the place of maximum amplitude. Standing waves on strings have a frequency that is proportional to the disturbance's propagation speed vw. The distance between the spots where the string is fixed in place determines the wavelength.
The fundamental frequency, which is the lowest frequency, is so for the longest wavelength, which is 1 = 2L. f1=vw1=vw2f1=v The overtones or harmonics in this situation are multiples of the fundamental frequency. Because 2 = L, the first harmonic can be simply determined, as shown in Figure 7. As a result, f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1. In the same way, f3 = 3f1 and so on. The tension in the string can be adjusted to vary all of these frequencies. The higher the frequency, the higher the vw and the greater the stress. Anyone who has ever watched a string instrument being tuned would recognise this observation. Standing waves are critical to many resonance occurrences, such as sounding boxes on string instruments, as we will discover in later chapters.
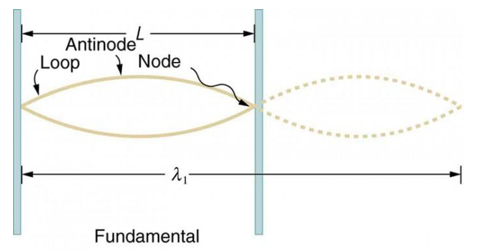
f1 = 

Figure 6. The figure shows a string oscillating at its fundamental frequency.
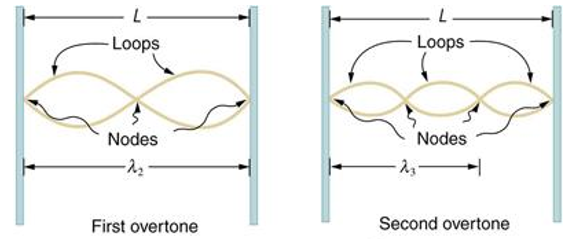
Figure 7. First and second harmonic frequencies are shown.
2.1.5 Beats
On a piano, striking two neighbouring keys generates a warbling sound that is normally considered unpleasant. The culprit is the superposition of two waves with comparable but not identical frequency. Another example can be seen during taxiing in jet aircraft, particularly the two-engine version. The combined sound of the engines increases and decreases in volume. Because the sound waves have comparable but not identical frequencies, the loudness varies. As the two waves travel in and out of phase, the discordant warbling of the piano and the varying loudness of the jet engine noise are both due to alternately constructive and destructive interference. This is visually depicted in Figure 8.
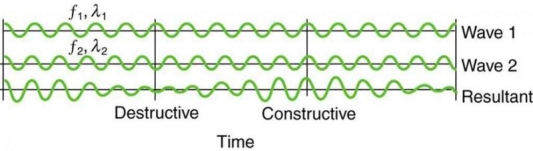
Figure 8 shows how beats are created by superimposing two waves with slightly different frequencies but identical amplitudes. The waves alternate between constructive and destructive interference over time, resulting in a wave with a variable amplitude.
The frequency of the wave that results from the superposition of two waves of comparable frequency is the average of the two. The amplitude of this wave swings in beats, at a frequency called the beat frequency. The beat frequency can be calculated by combining two waves together analytically. It's worth noting that at one point in space, a wave can be represented as
x = X cos (2πt/T) = X cos (2πft)
The frequency of the wave is f=1/T. When two waves with different frequencies but equal amplitudes are combined, the outcome is x = x1 + x2. x = Xcos(2 f1t) + Xcos(2 f2t), to be precise.
It can be demonstrated that x =2X cos(fBt)cos(2 favet) using a trigonometric identity, where fB = |f1 f2| is the beat frequency and fave is the average of f1 and f2. These findings indicate that the resultant wave has double the amplitude and average frequency of the two superimposed waves, but its overall amplitude changes at the beat frequency fB. The amplitude is effectively increased and decreased by the first cosine term in the formula. The wave with frequency fave is the second cosine term. This conclusion holds true for all forms of waves. If it's a sound wave, though, and the two frequencies are similar, we'll hear an average frequency that grows louder and softer (or warbles) as the beat frequency approaches.
While beats might be bothersome in auditory noises, we will see that they have a wide range of applications. Observing beats is a great technique to compare frequencies that are comparable. Ultrasonic imaging and radar speed traps are two seemingly unrelated applications of beats.
Key takeaway:
- The combination of two waves at the same spot is known as superposition.
- When two identical waves are superimposed in phase, constructive interference occurs.
- When two identical waves are overlaid perfectly out of phase, destructive interference results.
- A standing wave is created when two waves collide, resulting in a wave that changes in amplitude but does not propagate.
- In standing waves, nodes are sites where there is no motion.
- An antinode is the point at which a standing wave reaches its maximum amplitude.
- Waves on a string are resonant standing waves with a basic frequency that can have overtones or harmonics at higher multiples of the fundamental.
- When waves of similar frequency f1 and f2 are overlaid, beats occur. The oscillation frequency of the resulting amplitude is given by fB = |f1 f2|.
2.2.1 Harmonic Waves and Phase Velocity
The equation describes a one-dimensional harmonic wave (Figure 1).
u(x, t) = A0 sin (ωt – k x + φ)
Where A0 represents the wave amplitude, is the circular frequency, k represents the wave number, and is the starting, constant phase. The phase is the argument for the sine function, which is (x, t) = t - kx +. The spatial frequency or propagation constant are other names for the wave number.
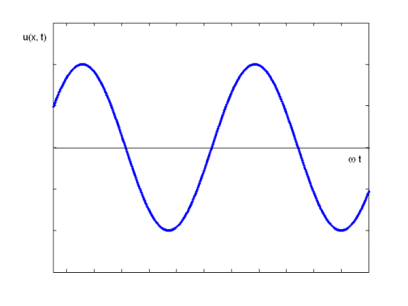
Figure 9: Harmonic Wave
This is a wave that is monochromatic (one frequency). In nature, there are no waves that are strictly monochromatic. For example, the wave's generating source could move significantly, resulting in spurious frequencies.
These waves propagate without warping in most cases. In other words, the phase (x, t) is constant:
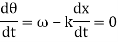
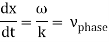
vphase is the phase velocity for a wave.
These waves are ineffective in terms of transmitting information. They remain the same in time and place. In order to transfer information, something must be modulated, such as frequency or amplitude. The resulting wave could be a wave packet, which is a disturbance that acts across a short distance. This wave packet can be thought of as a Fourier series or integral, which is a superposition of a number of harmonic waves.
2.2.2 Group Velocity
Something more than a basic harmonic wave is required to transmit information. The superposition of several such waves of differing frequencies, on the other hand, can produce a "envelope" wave and a carrier wave within the envelope. The envelope has the ability to convey data. The superposition of two harmonic waves with very near frequencies (1 2) and the same amplitude is a simple example. The motion's equations are as follows:
u(x, t) = A0 . Cos (ω1 t – k1 x) + A0 . Cos (ω2t – k2 x)
= 2 A0 . Cos ( 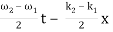 ) × cos (
) × cos ( 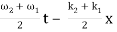 )
)
= u1 × u2
Figure depicts the plot of such a wave.
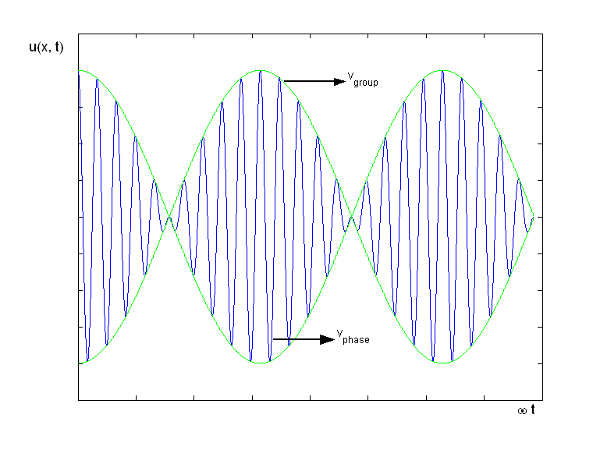
Figure 10: Group Velocity
u1 controls the envelope (the green line), which moves at the group velocity. The phase velocity of the carrier wave (the blue line) is provided by u2. The wave packet travels at the same speed as the rest of the group. It is the envelope that contains the data. The velocity of a group and the velocity of a phase are not always the same. The velocity of a group is given by,
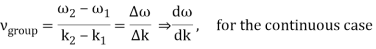
Rayleigh's formula links phase and group velocity together.
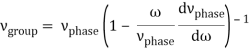
Group velocity equals phase velocity if the derivative term is zero. There is no dispersion in this scenario. When the different phase velocities of the envelope components cause the wave packet to "spread out" over time, this is called dispersion. The wave packet's (or envelope's) components separate to the point that they can no longer combine to complete the envelope.
2.3.1 Wave Packet Solution
Since the wave equation's travelling wave solution
y(x, t) = A sin (kx – ωt)
Is true for every value of the wave parameters, and since any superposition of solutions is likewise a solution, a wave packet solution can be constructed as a sum of travelling waves:
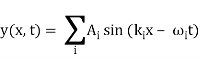
It is standard practise to express the amount 2/ by k, also known as the wave vector. The sum is replaced by an integral for a continuous range of wave vectors k:
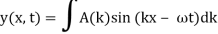
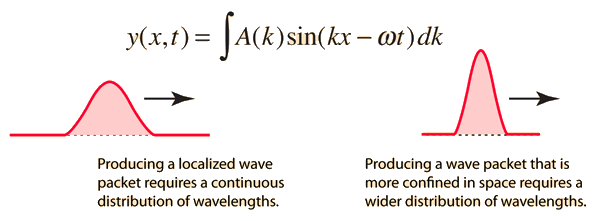
2.3.2 Wave Packet Details
Like a pulse on a string, a wave packet solution to the wave equation must have a variety of frequencies. The broader the range of frequency components necessary for quick transient behaviour, the shorter the pulse in time. For classical waves, this need can be expressed as a form of uncertainty principle:

The exact figures depend on how the pulse width is defined, however making brief pulses necessitates a large frequency bandwidth. The uncertainty principle in quantum mechanics is analogous to this.
2.3.3 Wave Packets from Discrete Waves
When discrete travelling wave solutions to the wave equation are concatenated, a wave packet that begins to localise the wave can be created. The quantum mechanical uncertainty principle mirrors this property of classical waves.
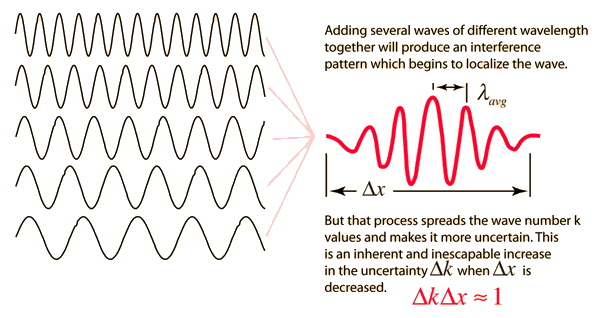
2.3.4 The Wave-Particle Puzzle
De Broglie's explanation of the Bohr atom quantization principles, together with Davisson and Germer's unintentional discovery of electron diffraction scattering, offer a compelling case for the electron's wave nature. Even so, the electron can act like a particle at times. An electron has a certain mass and charge, may move slowly, and can pass through a variety of devices, including a gun and a screen.
So, what's the connection between the wave and particle perspectives? Both were always present, according to De Broglie. He dubbed the wave a pilot wave, and he believed it steered the particle's motion. Unfortunately, the point of view leads to inconsistencies. The common current view is that the relative likelihood of detecting the particle at any position is determined by the strength of the wave (measured by the square of its amplitude).
The probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of the magnetic field vector. This interpretation, first proposed by Max Born in 1926, is analogous to the relationship between the electromagnetic field and quanta—the probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of The de Broglie wave function associated with the electron is written in standard notation as (x,t). The relative probability of finding the electron in a narrow period of length x near location x at time t is thus |(x,t)|2dx. (For the sake of simplicity, we limit the electron's movement to one dimension.) The generalisation is easy to understand.)
2.3.5 Keeping the Wave and the Particle Together?
Suppose following de Broglie we write down the relation between the "particle properties" of the electron and its "wave properties":
 mv2=E=hf, mv=p=h/λ.
mv2=E=hf, mv=p=h/λ.
It would seem that we can immediately figure out the speed of the wave, just using λf=c′, say.
We find:
λf=hmv⋅12mv2h=12v.
What? The speed of the wave is half the speed of the electron? How could they stay together? What's wrong with this calculation?
2.3.6 Localizing an Electron
To solve this question, consider the wave function corresponding to an electron moving in a vacuum tube, for example. The electron exits the cathode, travels through the vacuum, and collides with a grid's anode. It is travelling through the vacuum at a moment in this process, and the wave function must be nonzero across some volume, but zero in places the electron has not yet reached and zero in places it has definitely gone.
The electron, on the other hand, has a precise momentum if it possesses a precise energy, such as fifty electron volts. This necessitates the existence of a definite wavelength for the wave. However, the only wave with an exact wavelength is (x,t)=Asin(kxt).
Where k=2/ and =2f are constants. The issue is that this plane sine wave stretches to infinity in both spatial directions, therefore it can't represent a particle with a non-zero wave function in a finite region of space.
As a result, we must superpose waves of different wavelengths to represent a confined particle. Using the trigonometric addition formula, superpose two waves with somewhat varying wavelengths to demonstrate the principle:
Sin((kk)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((
Sin(kxt)cos((k)x()t sin(kxt)cos((k)x()t sin(k)x()t sin(k)x()t sin
The phenomena of beats between waves of similar frequency is represented by this formula. The first term, sin(kxt), oscillates at a frequency that is the average of the two. The slowly fluctuating second term, which oscillates once over a spatial range of order /k, modulates it. This is the distance at which waves that were in phase at the start turn fully out of phase. Of course, if the distance between the waves is increased by order /k, the waves will re-synchronize.
That is, combining two close frequencies creates a series of packets, or beats, from the continuous wave. A single packet is required to describe a single electron travelling through space. This can be accomplished by superposing waves with a continuous distribution of wavelengths, or wave numbers in the order of k, for example. The waves will be out of phase after a distance of order /k, but because they have so many distinct wavelengths, they will never be able to get back in phase. (All of this is adequately treated in Fourier transform theory.) We're just attempting to make it plausible right now.)
2.3.7 The Uncertainty Principle
It should be evident from the above argument that to construct a wave packet representing an electron localized in a small region of space, the component waves must get out of phase rapidly. This means that their wavelengths can't be too close. In reality, simply considering the two beating waves allows for a semi-quantitative approximation of the wavelength spread required.
A packet localized in a region of extent Δx can be constructed of waves having k 's spread over a range Δk, where Δx∼π/Δk.
Now, k=2π/λ, and p=h/λ, so k=2πp/h.
Therefore, Δk=2πΔp/h, and Δx∼π/Δk∼h/Δp, (dropping the factor of 2).
Thus:
Δx⋅Δp∼h.
This is Heisenberg's Uncertainty Principle, which we shall analyze in more detail in later lectures.
2.4.1 Gaussian wave packets:
We write a free wave packet as a linear combination of plane waves
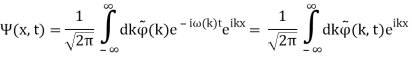
Where the momentum amplitudes absorb the time evolution of each plane wave, given by (k)=k2/2m (k,t). As a Gaussian, we chose the amplitude for the various plane waves.
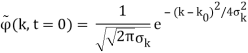
The momentum distribution |φ~(k,t)|2| is a Gaussian of width σk and mean k0 for all t.
At t=0, where the momentum amplitudes are real, the probability density of the resulting wave packet at is a Gaussian of width σx=1/2σk, i.e., it is as localized as is allowed by the Heisenberg principle (σx=1/2). The probability distribution stays Gaussian for all t. As the momentum amplitudes become complex, its width  increases with a characteristic time 1/ωσ=2m
increases with a characteristic time 1/ωσ=2m /ℏ, and its center moves with the group velocity vg=ℏk0/m.
/ℏ, and its center moves with the group velocity vg=ℏk0/m.
The genuinely quantum mechanical aspect is the behaviour at t=0: We can't locate the particle any farther than the uncertainty principle allows. It is a direct result of the wave-description resulting directly from the Fourier transform's features. For long periods of time, the behaviour is consistent with that of an ensemble of classical particles with a Gaussian momentum distribution: A particle with momentum k will be at x(k,t)=kt/m at time tt. We get the probability density of discovering a classical particle by solving for k and inserting it into the momentum distribution.
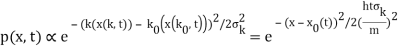
Which is a Gaussian of width σxωσt centered at
x0(t) = hk0t/m
The probability distribution for the wave packets has been plotted so far. We'll need a mechanism to visualise complex functions if we wish to draw the wave function. We could just plot the real and imagined parts of it. However, demonstrating its modulus (the square of which yields the probability density) and phase is more enlightening. It's simple to plot the modulus. We use colours to depict the phases, starting with red for phase zero, progressing through the rainbow colours as the phase progresses, and finally returning to red for phase two. The representation of a plane wave is shown below as an example. 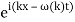
The propagating free Gaussian wave packet's wave function is given by
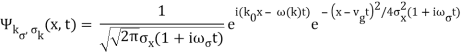
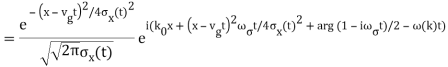
The phase of a Gaussian wave packet with a small momentum distribution is virtually identical to a plane wave with momentum k0.
The phase no longer has a well-defined wave length as the momentum dispersion widens. The phase has wave length 2/k0 around the maximum at x(t)=vgt.
2.4.2 Linear combination of wave packets (Schrödinger cat states)
Looking at linear combinations of Gaussian wave packets is equally fascinating. It's important to remember that we're still dealing with single-electron wave functions, which describe a single electron in a superposition state rather than two!
=GWP(k0,k,x0), What determines the interference pattern's wave length? Why is the amplitude of the wave packets in the middle always zero?
This is the same wave function as before, but with the probability density displayed. After the wave packets have travelled past each other, what happens to them? What would happen if their rate of broadening was slower than their velocity?
This wave packet flows slower and has a significantly larger momentum distribution. Why do the wave function's oscillations continue?
2.4.3 Reflection at hard wall
We can see how a Gaussian wave packet is reflected at a hard wall by looking at just one half of the above superpositions. Compare this approach to the electrostatics method of image charges.
Same thing, except this time for a wave packet with a significantly wider momentum dispersion.
2.5.1 Localization Of Waves; Relation To Uncertainty Principle
To grasp the uncertainty principle, one must first grasp a difficult but crucial concept concerning wave localizability: a wave can only be localised if distinct wavelengths are superposed. Consider a single-wavelength “pure” wave, as depicted below.

It's a perfect sine wave that repeats eternally with a perfectly defined fixed wavelength that's spread out in space. If it's an electron wave, it's a particle travelling at a constant speed with a well-defined momentum, as defined by the de Broglie equation: p = h/. What happened to the electron? It can be found anywhere—or is equally likely to be found anywhere (along the infinite dimension of the wave). 1 Its positional uncertainty is unlimited; its momentum (and wavelength) uncertainty is zero. This is a bizarre circumstance that, at the very least, adheres to the uncertainty principle. If the product of two uncertainties remains constant, one of them can only grow endlessly tiny if the other remains constant.
Consider the outcome of superposing many wavelengths. The superposition of two waves with wavelength differences of 10% is depicted below.
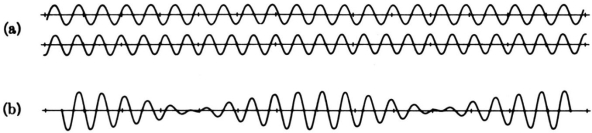
The waves interfere destructively five cycles after the point of maximum reinforcement. They reinforce again five cycles later. Partial localization of the wave is caused by the alternating of constructive and destructive interference, which causes the wave to bunch together into zones of around 10 wavelengths in length. This result contains an important indication concerning the uncertainty principle. The mixing of wavelengths required for partial localisation has resulted in momentum uncertainty.
By superposing a large number of distinct wavelengths, more localisation can be attained. The effect of mixing six separate pure waves, each with a wavelength difference of 2%, is shown in the diagram below.

The entire wavelength spread stays at 10%, with 5% on either side of the average wavelength. As a result, we can give a momentum uncertainty of around 5% of the dominant momentum:
Δp ≅ 0.05p.
Here, p denotes an average momentum, which is related to an average wavelength by the formula p = h/. The wave is better localised in the illustration because of the six-fold superposition. (The wave might be totally confined if all conceivable wavelengths within the provided span were superposed.) Its amplitude would sink to zero outside of a specified region of space, never to rise again.) The extent of the wave on either side of its center—roughly five wavelengths in the figure—represents the uncertainty of position:
Δx ≅ 5λ
In this case, the product of position and momentum uncertainty is
ΔxΔp ≅ 0.25λp.
Because the right-hand product p equals Planck's constant h, this equation can be written as
ΔxΔp ≅ 0.25h.
The numerical component 0.25 in this equation has no special relevance because we have made reasonable estimates of the uncertainty. The right side of the uncertainty equation, according to the technical definition of uncertainty employed in quantum mechanics, is exactly h/2, or, as stated in Essay Q6.
Since a 10% difference in momentum “crushed” the wave packet from infinite to just over 10 wavelengths, it's plausible to assume that momenta changing by almost 100% would be required to reduce the packet to a single cycle. This is correct. Maximum localization, x /2, necessitates superposition of wavelengths (and momenta) that differ by a factor of two. Then p p/2 p pppppppppp Because neither of these variables is clearly defined for a localised wave, p and refer to average values of momentum and wavelength in these equations. Again, the product xp is nearly identical to the product p, which is equal to Planck's constant.
The hydrogen atom contains an actual three-dimensional wave function, as opposed to the hypothetical one-dimensional waves outlined before. Its amplitude is depicted below along a radial line drawn across the atom's diameter.
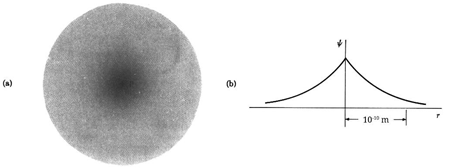
This electron wave function is highly confined, with only one oscillation cycle from one side of the atom to the other. This wave function's shape, with its central peak, is very different from that of a pure sine wave. With the appropriate mix of infinitely many wavelengths, any shape can be "fashioned."
The Heisenberg uncertainty principle is a result of the wave nature of particles, as demonstrated by this discussion of wave superposition. It is no more profound, and in this form, it says nothing more or less than the de Broglie equation for material particle wavelength. Measurement uncertainty stems mostly from the nonlocalizability of waves.
2.5.2 Two Examples of Localized Wave Packets
Lets now try two examples of a wave packet localized in k and properly normalized at t=0.
- A “square” packet: A(k) =
 for k0 – a/2 < k < k0 + a/2 and 0 elsewhere.
for k0 – a/2 < k < k0 + a/2 and 0 elsewhere. - A Gaussian packet: A(k) = (2a/π)1/4 e-α (k – k0)2.
These are both localized in momentum about p= hk0.
Check the normalization of (1).
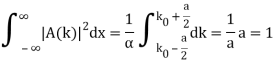
Check the normalization of (2) using the result for a definite integral of a Gaussian
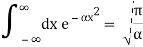
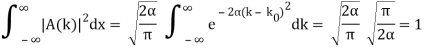
So now we take the Fourier Transform of (1) right here.
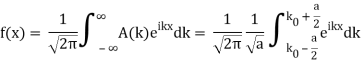
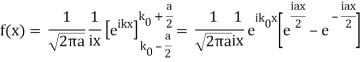
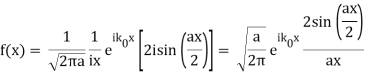
Note that 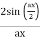 is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this
is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this 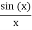 function.
function.
The Fourier Transform of a Gaussian wave packet
A(k) = 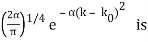
f(x) = 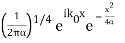
Also a Gaussian. We will show later that a Gaussian is the best one can do to localize a particle in position and momentum at the same time.
In both of these cases of f(x) (transformed from a normalized A(k) localized in momentum space) we see
- A coefficient which correctly normalizes the state to 1,
- eik0x - a wave corresponding to momentum hk0,
- And a packet function which is localized in x.
We've found states that represent a single free particle, which was our goal. We can have states that are localised in both position and momentum space, as we can see. We did this by creating wave packets, which are superpositions of definite-momentum states. While the wave packets are localised, they do have some width. x and in p.
2.6.1 Evolution of Wave Packets
We have

Where
ϕ(k) = kx – ω(k) t.
The function 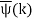 is obtained by Fourier transforming the wavefunction at t = 0. Now,
is obtained by Fourier transforming the wavefunction at t = 0. Now, 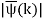 is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain
is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain
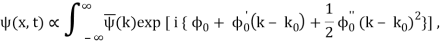
Where


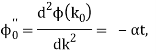
With
μ : ω (k0),
a : 
c : 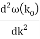
Rearranging, and then changing the variable of integration to y = (k – k0) / (2 ∆k), we get
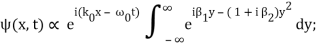
Where
2 ∆k ( x – x0 – vgt),
2 α (∆k)2t
Incidentally, ∆k = 1/ (2∆x) , where ∆x is the initial width of the wave packet. The above expression can be rearranged to give
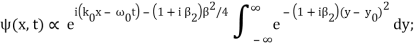
Where y0 = iβ/2 and β = β1 / (1+ iβ2). Again changing the variable of integration to z = (1+ iβ2)1/2 ( y – y0), we get
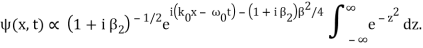
The integral now just reduces to a number. Hence, we obtain
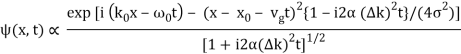
Where
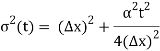
It's worth noting that the above wavefunction is the same as the one we started with at. This supports the estimate we produced before by extending the phase factor with Taylor. ϕ(k) about k = k0.
The probability density of our particle as a function of time is stated using Eq. (111).
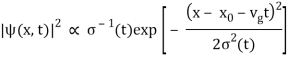
As a result, the probability distribution is Gaussian, with a characteristic width of and a maximum value of x = x0 + vgt. Our particle's most likely position now aligns with the distribution function's peak. As a result, the most likely position of the particle is provided by
x = x0 + vgt.
The particle essentially moves at a uniform velocity, as can be shown.
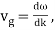
The particle essentially moves at a uniform velocity, as can be shown. vp = ω/k, whereas a wave packet travels at the group velocity,vg = d ω/dt. Now, it follows from the dispersion relation for particle waves that
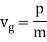
This, however, is the same as the classical particle velocity. As a result, once we learn that individual particles must be identified with wave packets rather than plane waves, the dispersion relation turns out to be consistent with classical physics. In reality, a continuous stream of particles moving in the same direction as the wave is commonly regarded as a plane wave.
The width of our wave packet grows as time passes, according to Eq. (112). Indeed, the characteristic time for a wave packet of original width to double in spatial extent is given by Eqs. (105).
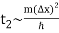
For example, if an electron is initially isolated in an atomic scale region (i.e., ∆x ~ 10-10 m) then the doubling time is only about 10-16 s. Evidently, particle wave packets (for freely moving particles) spread very rapidly.
Note, from the previous analysis, that the rate of spreading of a wave packet is ultimately governed by the second derivative of ω(k) with respect to k. See Eqs. (105) and (112). This is why a functional relationship between and is sometimes referred to as a dispersion relation: it affects how wave packets spread over time. The second derivative of with respect to is 0 in the specific situation when is a linear function of, and hence there is no dispersion of wave packets: i.e. wave packets propagate without altering shape. In the case of light waves, the dispersion relation is now linear. Light pulses pass through a vacuum without spreading, as a result. Another feature of linear dispersion relationships is that the phase is preserved.
Velocity, vp = ω/k, and the group velocity, vg = dω/dk, are identical. Thus, both plane light waves and light pulses propagate through a vacuum at the characteristic speed c = 3 × 108 m/s. Of course, the dispersion relation for particle waves is not linear in k. Hence, particle plane waves and particle wave packets propagate at different velocities, and particle wave packets also gradually disperse as time progresses.
2.6.2 Time Development of a Gaussian Wave Packet
So far, we've just done our Fourier Transforms at and examined the results at t = 0. We'll now reintroduce time to the wave function and examine the wave packet at a later time. We'll see that photons and non-relativistic electrons behave very differently.
Assume we start with our Gaussian (minimum uncertainty) wave packet A(k) = 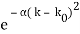 at t = 0. We can do the Fourier Transform to position space, including the time dependence.
at t = 0. We can do the Fourier Transform to position space, including the time dependence.
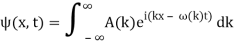
We state directly that is reliant on. This simply indicates that the energy of our free particle is determined by its motion. In the case of a photon, E = pc, so ℏ ω = ℏ kc, and hence ω = kc. For an non-relativistic electron, E = 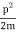 , so ℏ ω =
, so ℏ ω = 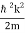 , and hence ω =
, and hence ω =  .
.
To cover the general case, lets expand ω(k) around the center of the wave packet in k-space.
ω(k) = ω(k0) + 
We make some educated guesses about the outcome and give the coefficients names.
ω(k) = ω0 + vg (k – k0) + β (k – k0)2
For the photon, vg = c and β=0. For the NR electron, vg = 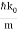 and β =
and β = 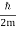 .
.
Performing the Fourier Transform, we get
ψ(x, t) = 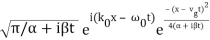
| ψ(x, t)|2 = 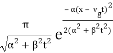
We can see that the photon will travel at the speed of light and that the wave will travel at the same speed.
Packet will not disperse, because β = 0.
The wave packet for the NR electron moves at the correct group velocity., vg = p/m, but the wave packet spreads with time. The RMS width is σ = 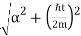
A wave packet naturally spreads because it contains waves of different momenta and hence different velocities. Wave packets that are very localized in space spread rapidly.
2.7.1 Wave-Particle Duality
The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.

Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.
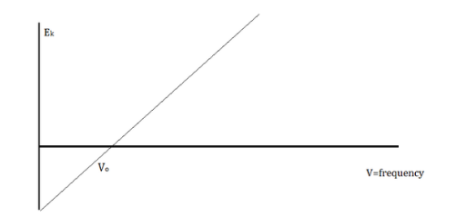
The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
We can say that light is a particle with the attribute of waves because the energy of waves and the energy of light do not correspond.
Einstein demonstrated that a photon's momentum equals
p = h/λ
This is readily demonstrated as follows. Assumption E = hv for a photon and λv = c for an electromagnetic wave, we obtain
E = hc/λ
We are now applying Einstein's relativity result. E = mc2 to find
λ = h/mc
Which is the same as equation (4). Because the rest mass of a photon is zero, this refers to the relativistic mass, not the rest mass. De Broglie reasoned in 1924 that matter can show this wave-particle duality because light can behave both as a wave (it may be diffracted and has a wavelength) and as a particle (it carries packets of energy). He went on to say that matter, like light, will obey the same equation (4). Davisson and Germer confirmed de Broglie's theory by observing diffraction patterns by hitting metals with electrons in 1927.
Bohr's assumption is justified according to de Broglie's equation (2). If we consider an electron to be a wave, the electron orbit must complete an integral number of wavelengths during its orbit to be stable. Otherwise, it would interfere with itself in a detrimental manner. This condition could be written as follows:
2πr = nλ
This can be expressed as using the de Broglie relation (4).
Mvr = nℏ
This is exactly the same as Bohr's equation (2).
While de Broglie's equation validates Bohr's quantization assumption, it also exposes a flaw in Bohr's model. The wave-particle duality, as demonstrated by Heisenberg, leads to the well-known uncertainty principle.
∆x∆p ≈ h
The uncertainty principle dictates that if the orbital radius of an electron in an atom is known precisely, the angular momentum must be unknown. The flaw in Bohr's model is that it stipulates both exactly and that the orbital angular momentum must be an integral multiple of. As a result, the stage was prepared for a new quantum theory that followed the uncertainty principle.
2.7.2 The duality of photons
“Light is a particle as well as a wave.” To have a better understanding of this concept, we conducted an experiment.
Young's Interference Experiment, often known as the Double-slit Interference Experiment, is a type of experiment. This experiment used technology to identify individual light particles to see if interference fringes appeared even when the light was severely attenuated to the point where there was just one particle. The experiment's findings confirmed that one photon had an interference fringe.
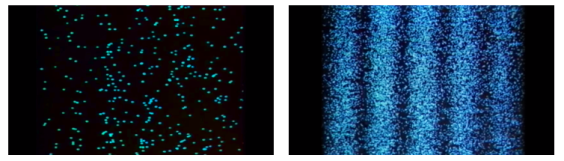
When light is detected that has been weakened to an extreme brightness limit and projected on a screen, it behaves like a particle, as shown on the left. When the number of particles detected rises, however, an interference fringe emerges, as shown on the right. As can be seen, light behaves similarly to a wave.
There was no interference fringe when one of the two slits in the experiment was closed, allowing only one photon particle to pass through the other slit. This proved that in the double-slit interference experiment, one photon particle travelled through both slits at the same time and interfered with itself.
These experiments show that while a photon was detected as having the properties of a particle, interference appeared like that of a wave while simultaneously passing through the double-slit, revealing that the photon has the dual properties of a particle and a wave.
Key takeaway:
- In quantum physics, wave–particle duality states that any particle or quantum phenomenon can be represented as either a particle or a wave. It expresses the difficulty of classical terminology like as "particle" and "wave" to completely characterise quantum-scale things' behaviour.
- He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
Complementarity is a concept in quantum mechanics that Niels Bohr considered to be a necessary property of the theory. According to the complementarity principle, objects have a set of complementary features that cannot all be viewed or measured at the same time. Position and momentum are an example of such a pair. One of quantum mechanics' foundational truths, according to Bohr, is that setting up an experiment to measure one of a pair of quantities, such as the position of an electron, excludes the possibility of measuring the other, despite the fact that understanding both experiments is required to characterise the object under study. The behaviour of atomic and subatomic things, according to Bohr, cannot be divorced from the measuring devices that form the framework in which they behave. As a result, there is no "one picture" that unifies the data gained in these various experimental situations, and only the "totality of the phenomena" as a whole can provide a complete description.
The failure of the operators that represent the observable quantities being measured to commute expresses complementarity mathematically:
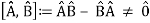
Incompatible observables are observables that correlate to non-commutative operators. There can't be a comprehensive set of shared eigenstates for incompatible observables. It's worth noting that there may be some simultaneous eigenstates of () A and () B, but not enough to form a complete basis. The canonical commutation relation is defined as follows:
This suggests that this holds true for both position and momentum. Similarly, any two of the spin observables specified by the Pauli matrices have an equivalent relationship; measurements of spin along perpendicular axes are complimentary. Using mutually unbiased bases, which give complementary observables defined on finite-dimensional Hilbert spaces, this has been applied to discrete observables with more than two possible outcomes.
The principle of complementarity, or dialecticism, is a second key component of quantum physics. Is light a wave or a particle? Complementarity is defined as the recognition that though particle and wave behaviour are mutually exclusive, both are required for a complete explanation of all occurrences.
2.9.1 De Broglie’s Matter Waves:
When an electromagnetic wave interacts with matter, it can behave as a particle of light, according to Compton's formula. Louis de Broglie proposed a new speculative idea in 1924, claiming that electrons and other matter particles could behave like waves. De Broglie's hypothesis of matter waves is the name given to this concept today. De Broglie's hypothesis, combined with Bohr's early quantum theory, resulted in the development of a new wave quantum mechanics theory to describe the physics of atoms and subatomic particles in 1926. Quantum mechanics has made new technical inventions and technologies possible, such as the laser and magnetic resonance imaging (MRI). Other fields, such as biology and chemistry, benefit from this new technology.
According to de Broglie's hypothesis, both massless photons and heavy particles must satisfy a single set of relationships that link energy E to frequency f and linear momentum p to wavelength w. These photon-photon connections were previously studied in the context of Compton's effect. We're bringing them up now in a broader perspective. A de Broglie wave of frequency f and wavelength is any particle with energy and motion.
E = hf
E and p denote a particle's relativistic energy and momentum, respectively. The wave vector is commonly used to express De Broglie's relations. 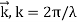 and the wave frequency ω = 2πf as we usually do for waves:
and the wave frequency ω = 2πf as we usually do for waves:
E = ℏω
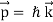
According to wave theory, a wave's energy is carried with the group velocity. This group velocity for matter waves is the particle's velocity u. De Broglie relations show that matter waves obey the following relation when the energy E and momentum p of a particle are identified with its relativistic energy mu and relativistic momentum mu, respectively.
λf = ω/k = 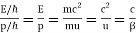
Where β = u/c
When a particle is massless we have 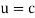 and (Figure) becomes
and (Figure) becomes 
De Broglie gave an explanation for the quantization of the electron's angular momentum in the hydrogen atom, which was posited in Bohr's quantum theory, using the idea of the electron matter wave. When we suppose that an electron in a hydrogen atom behaves like a wave rather than a particle, the scientific explanation for the first Bohr quantization condition emerges easily. Imagine a stretched guitar string that is clamped at both ends and vibrates in one of its typical modes to see it clearly. The wavelengths of these vibrations cannot be random if the length of the string is l ((Figure)), but must be such that an integer k number of half-wavelengths /2 fits exactly on the distance l between the ends. A standing wave on a string has the constraint l=k/2. Let's pretend that instead of clamping the string to the walls, we bend it into a circle and tie the ends together. This results in a circular string that vibrates in normal modes and fulfils the same standing-wave requirement, but the number of half-wavelengths must now be an even number k,k=2n, and the length l is now tied to the circle's radius r n. This means that the radii cannot be chosen at random, but must meet the standing-wave condition:
2π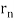 = 2n λ/2.
= 2n λ/2.
If an electron moves like a wave in the nth Bohr orbit, its wavelength must be equal to (Figure). λ = 2π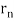 /n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
/n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
p = h/λ = nh/ (2 π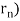 = nh/
= nh/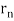 . As a result, in a circular orbit, the electron's angular momentum must be
. As a result, in a circular orbit, the electron's angular momentum must be
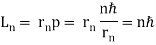
The first of Bohr's quantization conditions, given by, is this equation (Figure). A plausible theoretical argument for the existence of matter waves is to provide a physical explanation for Bohr's quantization condition.
Standing-wave pattern: (a) a stretched string clamped against the walls; (b) an electron wave trapped in the hydrogen atom's third Bohr orbit.
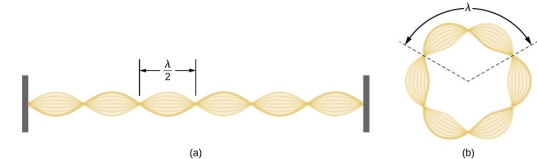
In 1927, C. Davisson and L. Germer completed a series of electron-scattering tests that conclusively demonstrated that electrons behave like waves. Davisson and Germer's experiment were not designed to prove de Broglie's hypothesis: The proof came as a result of their usual experiments on metal surfaces bombarded by electrons.
They analysed a nickel surface in the experiment that produced the first evidence of electron waves (now known as the Davisson–Germer experiment). Their nickel sample was treated in a high-temperature oven to transform it from its regular polycrystalline structure to one with massive single-crystal domains filling the volume. The experimental setup is depicted in (Figure). Thermal electrons are emitted from an electron gun's heated element (typically composed of tungsten) and accelerated through a potential difference V, resulting in a well-collimated stream of electrons. By adjusting the potential difference in the electron cannon, the kinetic energy K of the electrons can be modified. According to the law of conservation of energy, this results in a beam of electrons with a fixed linear momentum:
EV = K = 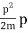 =
= 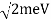
The electron beam strikes the nickel sample in a normal to its surface direction. It scatters in a variety of directions near the surface. A very sensitive detector measures the intensity of the beam scattered in a specific direction. The detector's angular location with relation to the incident beam's direction can range from to The entire setup is enclosed in a vacuum chamber to prevent electron collisions with air molecules, as such thermal collisions would change the electrons’ kinetic energy and are not desirable.
The Davisson–Germer diffraction experiment's experimental setup is shown schematically. The nickel target scatters a well-collimated beam of electrons. In the electron cannon, the kinetic energy of electrons in the incident beam is selected by setting a variable voltage, V. For a variety of scattering angles, the intensity of the scattered electron beam is measured, while the distance between the detector and the target remains constant.

The incident electrons scatter off the nickel target's surface in many random directions when it has a polycrystalline shape with many randomly aligned tiny crystals. As a result, the dispersed electron beam's intensity is nearly constant in all directions, simulating diffuse light reflection from a porous surface. When the nickel target has a regular crystalline structure, however, the intensity of the scattered electron beam reaches a definite maximum at a given angle, resulting in a distinct diffraction pattern (see Figure). William H. Bragg and William L. Bragg, father and son physicists, analysed similar diffraction patterns created by X-rays scattered by several crystalline substances in 1912. In X-ray crystallography, the Bragg law establishes a link between the wavelength of radiation impinge on a crystalline lattice, the lattice spacing, and the position of the diffracted radiation's interference maximum (see Diffraction).
The Davisson–Germer target's lattice spacing was measured using X-ray crystallography and found to be Unlike X-ray crystallography, in which X-rays penetrate the sample, only the surface atoms interact with the incident electron beam in the Davisson–Germer experiment. The highest intensity of the reflected electron beam is found for scattering angles that satisfy the requirement (see (Figure)) in surface diffraction. At a scattering angle of 50 at V54V, the first-order maximum (for n=1) is measured, yielding the wavelength of the incident light as λ = (2.15) sin 50 = 1.64. A 54-V potential, on the other hand, accelerates incident electrons to kinetic energies of K = 54 eV. Their momentum, calculated from (Figure), is p = 2.478 × 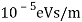 . When we substitute this result in (Figure), the de Broglie wavelength is obtained as
. When we substitute this result in (Figure), the de Broglie wavelength is obtained as
λ = h/p = 
We get the same result when we utilise K = 54eV in (Figure). The theoretical result's closeness to the Davisson–Germer experimental value of  is a convincing argument for the existence of de Broglie matter waves.
is a convincing argument for the existence of de Broglie matter waves.
The experimental results of electron diffraction on a nickel target in an electron gun with an accelerating potential of around 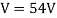 At a scattering angle of around 45 degrees, the intensity maximum is recorded.
At a scattering angle of around 45 degrees, the intensity maximum is recorded.
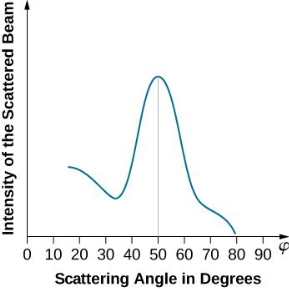
The in-phase incident beams are reflected from atoms on the surface during surface diffraction of a monochromatic electromagnetic wave on a crystalline lattice structure. Where an is the lattice spacing, a ray reflected from the left atom travels an extra distance to the detector. When D is an integer multiple of the wavelength of the reflected beams, they remain in phase. For angles satisfactory, the strength of the reflected waves exhibits notable maxima.
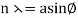
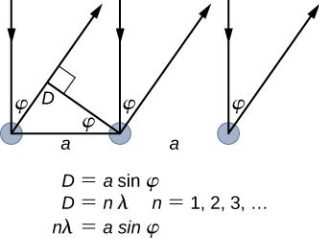
Because the incident electrons are dispersed only from the surface, diffraction lines recorded with low-energy electrons, such as those used in the Davisson–Germer experiment, are relatively broad (see (Figure)). When a higher-energy electron beam passes through a thin metal foil, the resolution of diffraction images improves dramatically. This happens because the diffraction image is made by scattering from a large number of crystallographic planes within the volume, and the maxima formed by scattering at Bragg angles are sharp (see Figure).
Diffraction patterns created by scattering X-rays and electrons on a crystalline material (a). The observed pattern represents the sample's crystalline structure's symmetry.

De Broglie's idea has been thoroughly examined using various experimental approaches since Davisson and Germer's work, and the presence of de Broglie waves has been proven for multiple elementary particles. Neutrons have been employed in scattering experiments to determine the crystalline structures of substances using neutron matter wave interference patterns. The mass of a neutron is comparable to that of a positively charged proton because it has no charge. Neutrons and protons can both be thought of as matter waves. As a result, being a matter wave is a property shared by all particles in motion, not only electrically charged ones. It has become possible to monitor matter waves of molecules as big as carbon C 60. As long as physical objects are in motion, they all have a matter wave associated with them. De Broglie matter waves have a universal character that has been established.
2.10.1 de Broglie Waves can be Experimentally Observed:
Electron diffraction studies conducted by G.P. Thomson in 1926 and C. Davisson and L. H. Germer in 1927 established the correctness of de Broglie's proposal. It was discovered in these investigations that electrons scattered from atoms in a crystal, and that these dispersed electrons generated an interference pattern. The interference pattern looked just like what happens when water waves flow through two holes in a barrier, generating independent wave fronts that merge and interfere. Both matter (e.g., electrons and neutrons) and electromagnetic radiation display these diffraction patterns, which are characteristic of wave-like behaviour. If the wavelength is equivalent to the spacing between scattering centres, diffraction patterns are generated.
We'll now look at the phenomena of electron diffraction as part of our analysis of experiments that led to the new quantum theory.
2.10.2 Light Diffraction (Young's Double Slit Experiment)
It is commonly known that light has the ability to diffract around things in its path, resulting in a pattern of interference that is unique to the object. In reality, this is how holography works (the interference pattern is created by allowing the diffracted light to interfere with the original beam so that the hologram can be viewed by shining the original beam on the image). The Young double slit experiment is a basic demonstration of light diffraction (Figure 1.7.1).

Figure 11: Experiment with a young double slit. A plane of light waves illuminates two apertures.
Water waves (shown as waves in a plane parallel to the double slit device) are used in this experiment to see what occurs when they hit the slits. Each slit then acts as a point source for spherical waves, which interfere with one another, resulting in the light and dark fringes seen on the right (Figure).
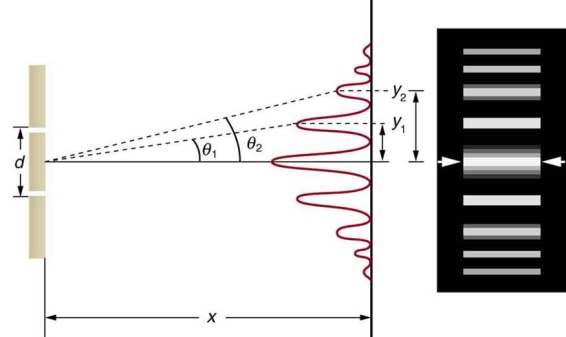
Figure 12: Interference through a double slit.
2.10.3 Electron Diffraction (Davisson–Germer Experiment)
Electrons, according to classical physics, should behave like particles, travelling in straight lines and not bending in flight until touched on by an external agent, such as a magnetic field. If we fire a beam of electrons through a double slit onto a detector in this scenario, we should obtain two bands of "hits," similar to what you'd get if you shot a machine gun through the side of a home with two windows - two regions of bullet-marked wall inside, while the remainder would be intact. Graph 1.7.3 (left).
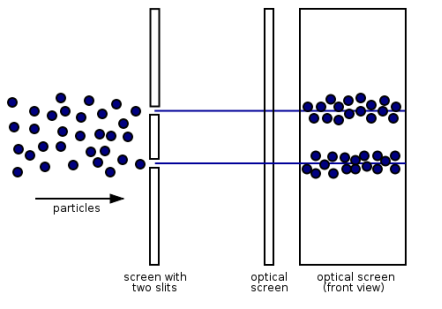
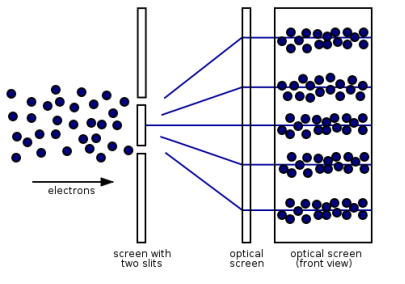
Figure 13: (left) classical model of electrons. (right) wave property of electrons.
However, if the slits are narrow and close enough together, we can see the electrons diffracting through the slits and interfering with one another, exactly like waves. This indicates that electrons, like photons, exhibit wave-particle duality, which is consistent with de Broglie's concept. They must have wavelength and frequency attributes in this scenario. The attributes can be deduced from the electrons' behaviour as they travel through our diffraction grating.
This was a watershed moment in the history of quantum physics. The Davisson–Germer experiment established the wave-nature of matter, completing the notion of wave-particle duality, much as the photoelectric effect had done for light. This concept was crucial to physicists since it suggested that not only could any particle display wave properties, but that wave equations could be used to describe processes in matter if the de Broglie wavelength was utilised.

2.10.4 Neutron Diffraction
Neutrons, like all quantum particles, can show wave behaviour, and atoms or their nuclei can behave as diffraction obstacles if the wavelength is short enough. When neutrons from a reactor are slowed and picked properly by their speed, their wavelength is near one angstrom (0.1 nm), which is the usual distance between atoms in a solid material. A diffraction experiment can then be carried out with such a beam. Neutrons interact directly with the nucleus of the atom, and each isotope contributes differently to the diffracted intensity; for example, ordinary hydrogen and deuterium contribute differently. Even in the presence of big Z atoms, light (low Z) atoms frequently contribute significantly to the diffracted intensity.
2.11.1 Davisson-Germer Experiment:

The Davisson-Germer experiment revealed the electron's wave character, validating deBroglie's earlier hypothesis. It was a big step forward in the development of quantum mechanics because it put wave-particle duality on a firm experimental footing. The Bragg diffraction law had previously been applied to x-ray diffraction, but this was the first time it had been applied to particle waves.
Davisson and Germer devised and constructed a vacuum apparatus for determining the energy of electrons scattered from a metal surface. A voltage was used to accelerate electrons from a hot filament and allow them to strike the surface of nickel metal.
The electron beam was focused on a nickel target that could be rotated to observe the dispersed electrons' angular dependency. Their electron detector (known as a Faraday box) was positioned on an arc and could be rotated to observe electrons from various angles. They were taken aback when they discovered that the intensity of the dispersed electron beam had a peak at some angles. The Bragg law could be used to calculate the lattice spacing in the nickel crystal based on this peak, which showed wave behaviour for the electrons.
With rising accelerating voltage, the experimental data above, replicated above Davisson's article, reveals recurrent maxima of scattered electron intensity. This information was gathered at a certain dispersion angle. The relationship is calculated using the Bragg law, the deBroglie wavelength expression, and the kinetic energy of the accelerated electrons.
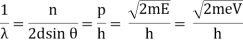
Electron Bragg deBroglie Acceleration wavelength law relationship through voltage V
An accelerating voltage of 54 volts produced a distinct peak at a scattering angle of 50° in the historical data. The Bragg law's angle theta for that scattering angle is 65°, and the computed lattice spacing for that angle is 0.092 nm. The wavelength as a function of voltage relationship is empirically determined for that lattice spacing and scattering angle.

Trying this relationship for n=1,2,3 gives values for the square root of voltage 7.36, 14.7 and 22, which appear to agree with the first, third and fifth peaks above. What then accounts for the second, fourth, and sixth peaks? They could have come from a different set of crystal planes. Those peaks fall into the 2,3,4 sequence, implying that the series' first peak would have been around 5.85.
2.12.1 Deriving the de Broglie Wavelength
De Broglie arrived at his equation through a sequence of substitutions based on well-known theories:
De Broglie was the first to apply Einstein's famous equation for the relationship between matter and energy:
E = mc2 (1)
With
- E = energy,
- m = mass,
- c = speed of light
Using Planck's theory, each quantum in a wave has a discrete quantity of energy that can be calculated using Planck's equation:
E = hv
With
- E = energy,
- h = Plank's constant (6.62607 x 10-34 J s),
- ν= frequency
De Broglie hypothesised that the two energies would be equivalent because particles and waves share the same characteristics:
Mc2 = hv
De Broglie proposed velocity (v) for the speed of light since real particles do not travel at the speed of light (c).
Mv2 = hv
De Broglie replaced v/ for v in the equation and arrived at the final expression that connects wavelength and particle speed.
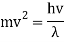
Hence
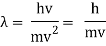
The majority of Wave-Particle Duality problems can be solved using Equation 6 and a few different cancelling out units.
De Broglie was given credit for his hypothesis, but he had no experimental proof to back it up. Clinton J. Davisson and Lester H. Germer fired electrons into a nickel crystal in 1927. They observed electron diffraction, which is analogous to wave diffraction against crystals (x-rays). In the same year, an English physicist, George P. Thomson fired electrons towards thin metal foil providing him with the same results as Davisson and Germer.
Key takeaway:
- De Broglie waves have a velocity. Beiser calls it "vp," and later shows that vp is the phase velocity of the waves. Vp=f is the formula for determining the velocity of a wave. De Broglie proposed the equation =h/mv for both particles and waves.
What is Wave-Particle Duality?
We've all heard about the nature of light and the various personalities it exhibits. Some of the features include interference, reflection, refraction, and diffraction. Particle-Wave The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.
Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.
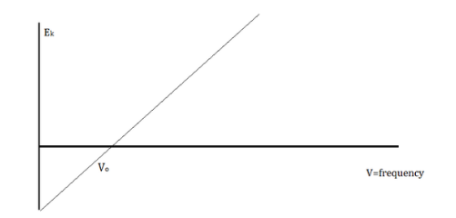
The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
Since the energy of waves and energy of light does not coincide, we can say that light is a particle that has the property of waves.
The Uncertainty Principle
A particle's position and momentum cannot be measured with arbitrarily high precision at the same time. The product of the errors of these two measurements has a minimum. There is also a minimum for the product of the energy and time uncertainty.
∆x ∆p > ℏ/2
∆E ∆t > ℏ/2
This is not a remark about measuring equipment inaccuracy or the quality of experimental methods; it is a result of the wave qualities inherent in the quantum mechanical description of nature. The ambiguity is inherent in the nature of things, even with flawless instruments and skills.
The uncertainty principle, also known as the Heisenberg uncertainty principle or the indeterminacy principle, is a statement made by German physicist Werner Heisenberg in 1927. It states that an object's position and velocity cannot be measured precisely at the same time, even in theory. In fact, in nature, the concepts of absolute position and exact velocity have no relevance.
This principle is not obvious from everyday life. Because the uncertainties suggested by this concept for common objects are sufficiently small to be noticed, it is simple to measure both the position and velocity of, say, a car. The full rule states that the product of location and velocity uncertainties is equal to or larger than a small physical amount, or constant (h/(4), where h is Planck's constant, or approximately 6.6 1034 joule-second). Only for atoms and subatomic particles with extremely small masses can the product of uncertainty become important.
Any attempt to precisely measure the velocity of a subatomic particle, such as an electron, will cause it to move around in an unpredictable manner, rendering a simultaneous measurement of its position useless. This finding originates from the intimate relationship in nature between particles and waves in the world of subatomic dimensions, and has nothing to do with shortcomings in the measurement devices, procedure, or observer.
The wave-particle duality gives rise to the uncertainty principle. Every particle has a wave connected with it, and every particle behaves in a wavelike manner. The particle is most likely to be located where the wave's undulations are the most pronounced or powerful. However, the more powerful the associated wave's undulations get, the more ill-defined the wavelength becomes, which defines the particle's momentum. As a result, a strictly localised wave has an indeterminate wavelength, while its associated particle has a fixed position but no fixed velocity. A particle wave with a well-defined wavelength, on the other hand, is widely dispersed; the associated particle, albeit having a very accurate velocity, may be found practically anywhere. A very precise measurement of one observable entails a significant amount of uncertainty in the measurement of the other.
The uncertainty principle can also be represented in terms of the momentum and position of a particle. A particle's momentum is equal to the product of its mass and velocity. As a result, the product of a particle's momentum and position uncertainty equals h/(4+) or greater. The idea also holds true for other related (conjugate) pairings of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is taken equals h/(4+) or more. The uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it transitions to a more stable state are the same for an unstable atom or nucleus.
Are the uncertainty relations revealed by Heisenberg in 1927 simply the outcome of the equations utilised, or are they embedded in every measurement? Heisenberg used a thought experiment because he felt that all scientific concepts must be defined using actual or possible experimental observations.
Heisenberg imagined a microscope that achieves extremely fine resolution by illuminating with high-energy gamma rays. Although such a microscope does not exist at the moment, it may theoretically be built. Heisenberg envisaged seeing an electron and measuring its position using this microscope. He discovered that the electron's position and momentum obeyed the mathematically established uncertainty relation. The experiment had significant problems, which Bohr pointed out, but after they were fixed, the demonstration was completely compelling.
A free electron rests just beneath the centre of the microscope's lens in the revised version of the thought experiment (see the picture above). From the electron, the circular lens forms a cone with an angle of 2A. Gamma rays—high intensity light with the smallest wavelength—then illuminate the electron from the left. These have the maximum resolution because, according to a wave optics principle, the microscope can resolve (that is, "see" or distinguish) objects to a size of Dx, which is related to and to the gamma ray wavelength L by the expression:
Dx = L / (2sinA)
A gamma ray impacting an electron, on the other hand, provides it a kick in quantum mechanics, where a light wave can act like a particle. The electron is driven to the right when light is diffracted by the electron into the microscope lens. The gamma ray must be dispersed into any angle within the cone of angle 2A in order to be detected by the microscope. The gamma ray, like a particle, carries momentum in quantum physics. The wavelength is related to the total momentum p by the formula
p = h / L, where h is Planck's constant.
The total momentum in the x direction would be the sum of the electron's momentum p'x in the x direction and the gamma ray's momentum in the x direction in the extreme case of diffraction of the gamma ray to the right edge of the lens:
p'x + (h sinA ) / L', where L' is the wavelength of the deflected gamma ray.
In the other extreme, the observed gamma ray recoils backward, just hitting the left edge of the lens. The overall momentum in the x direction in this example is:
p''x - (h sinA ) / L''.
Because momentum is never lost, the final x momentum in each scenario must equal the beginning x momentum (it is conserved). As a result, the final x momenta are identical:
p'x + (h sinA ) / L' = p''x - (h sinA ) / L''
If A is tiny, the wavelengths are close to being the same, L' L" L. So there you have it.
p''x - p'x = Dpx ~ 2h sinA / L
We have a reciprocal link between the minimal uncertainty in the observed position, Dx, of the electron along the x axis and the uncertainty in its momentum, Dpx, in the x direction because Dx = L / (2 sinA ).
Dpx ~ h / Dx or Dpx Dx ~ h.
The "more than" indication can be used if there is more than the bare minimum of uncertainty.
This is Heisenberg's uncertainty relation for simultaneous measurement of an object's position and momentum, except for the factor of 4p and an equal sign.
Modern physicists warn that a careful examination of this image reveals an illusory classical mechanical interaction one step deeper, in the collision of the photon and the electron. In fact, despite its importance in the development and teaching of quantum theory, Heisenberg's microscope is not part of modern knowledge. Any depiction that resembles daily colliding items cannot represent the genuine quantum interaction and the genuine uncertainty associated with it. You must work through the formal mathematics that estimates probabilities for abstract quantum states to get the actual outcome. Experiments on these kind of interactions are still being carried out now. So far, the experiments have all confirmed Heisenberg's belief that no "genuine" microscopic classical collision occurs at the bottom.
The interpretation
So, how can we make sense of it all? Is this Heisenberg's own Principle being 'proven'? Yes and no, in my opinion. I'd say it's a combination of illustration and proof. The following are the key assumptions:
1. We can think of -ray photons, or any photon for that matter, as particles with momentum, and when they ‘collide,' or interact, with an electron, the photon will give that electron some momentum.
2. Because momentum is conserved, the total (linear) momentum before and after the collision must be the same for both particles–that is, (1) the incoming ray and the electron before the contact and (2) the released photon and the electron that receives the kick after the encounter.
3. We may connect (or associate, if you prefer) the wavelength of the -ray photon with its momentum p using the Planck relation or, equivalently for photons (since they have no mass), the de Broglie connection.
Unit - 2
Wave Packet
2.1.1 Superposition and Interference
The majority of waves do not appear to be straightforward. They resemble the waves depicted in Figure rather than the ordinary water wave discussed in Waves. (Simple waves have a sinusoidal shape because they are formed by a simple harmonic oscillation.) Complex waves are more intriguing, even beautiful, but they appear to be intimidating. The majority of waves appear complex because they are made up of multiple simple waves that have been added together. Fortunately, the principles for adding waves are straightforward.

Figure 1.
When two or more waves arrive at the same location at the same time, they superimpose on each other. When waves collide, the disturbances of the waves are superimposed, a phenomenon known as superposition. Each disruption is associated with a force, which adds up. If the disturbances all follow the same path, the final wave is simply the sum of the individual waves' disturbances—that is, their amplitudes add. Figures 2 and 3 show superposition in two different situations, both of which yield straightforward results.
Figure 2 depicts two similar waves arriving at the same time and in phase. The crests and troughs of the two waves are perfectly aligned. The result of this superposition is pure constructive interference. Pure constructive interference generates a wave with double the amplitude of the component waves but the same wavelength since the disturbances add up.
Figure 3 illustrates two identical waves arriving out of phase—that is, with their crests and troughs precisely aligned—producing pure destructive interference. The resulting amplitude for pure destructive interference is 0 since the disturbances are in the opposite direction for this superposition—the waves entirely cancel.
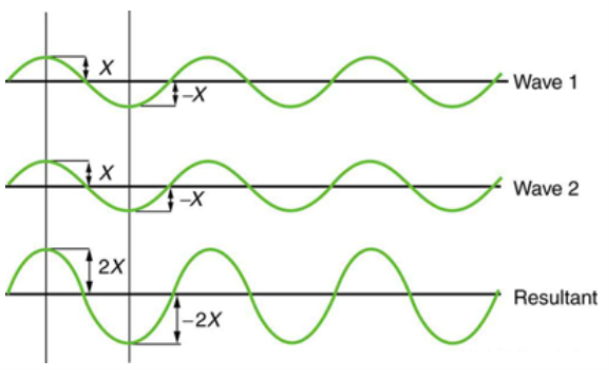
Figure 2: When two identical waves collide, the result is a wave with twice the amplitude but the same wavelength.
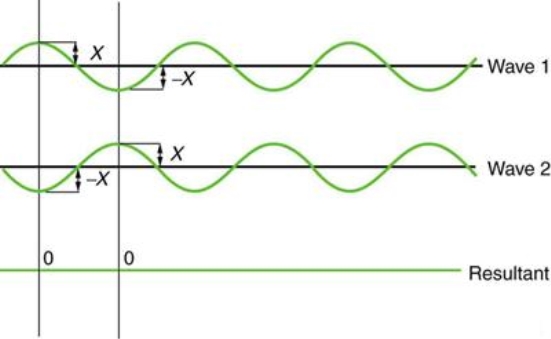
Figure 3: When two identical waves collide, the result is zero amplitude, or total cancellation.

Figure 4. Superposition of non-identical waves exhibits both constructive and destructive interference.
While pure constructive and destructive interference do occur, they require identical waves to be exactly aligned. Most waves superpose, resulting in a mix of constructive and destructive interference that varies from location to place and time to time. A stereo's sound, for example, can be powerful in one place yet muted in another. Sound waves add partially constructively and partially destructively at different locations when their loudness varies. Sound waves are created by at least two speakers in a stereo, and sound waves can reflect off walls. All of these waves are stacked on top of each other. The combined whining of aeroplane jets perceived by a stationary passenger is an example of noises that change over time from constructive to detrimental. As the sound from the two engines changes in time from constructive to destructive, the total sound might fluctuate in amplitude. These are waves that are similar to each other. Figure 4 depicts an example of the superposition of two different waves. Again, the disturbances add and subtract, resulting in a wave that appears more intricate.
2.1.2 Principle of Superposition of Waves
Consider two waves travelling in opposite directions along the same stretched string, as shown in the diagram above. At any given time, we can see images of waveforms in the string. The algebraic total of the displacements owing to each wave is found to be the net displacement of every element of the string at any given time.
Let's imagine two waves are travelling alone, and any element of these two waves' displacements can be represented as y1(x, t) and y2(x, t) (x, t). The resultant displacement can be written as y when these two waves collide (x,t).
y (x, t) = y1(x, t) + y2(x, t) = y3(x, t) = y4(x, t) = y5(x, t) = y (x, t)
We can sum the overlapped waves algebraically to generate a consequent wave using the principle of superposition. Let us say that the wave functions of moving waves are as follows:
y1 = f1(x–vt),
y2 = f2(x–vt)
……….
yn = fn (x–vt)
Then the wave function describing the disturbance in the medium can be described as
y = f1(x – vt)+ f2(x – vt)+ …+ fn(x – vt)
Or, y=∑ i=1 to n = fi (x−vt)
Let us consider a wave travelling along a stretched string given by, y1(x, t) = A sin (kx – ωt) and another wave, shifted from the first by a phase φ, given as y2(x, t) = A sin (kx – ωt + φ)
From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A.
Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement y(x, t) = A sin (kx – ωt) + A sin (kx – ωt + φ)
The above equation can be written as,
y(x, t) = 2A cos (ϕ/2). Sin (kx −ωt + ϕ/2)
The resulting wave is a sinusoidal wave travelling in the positive X direction, with a phase angle half that of the component waves and an amplitude equal to [2cos/2] times the original waves' amplitudes.
2.1.3 Condition for Destructive Interference
Phase difference = (2n – 1)π
Path difference = (2n – 1)λ/2
I = Imin
Imin = I1 + I2 – 2 
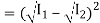
2.1.4 Standing Waves
Waves don't always appear to move; instead, they only vibrate in situ. Unmoving waves, for example, can be seen on the surface of a glass of milk in the refrigerator. The refrigerator motor's vibrations create waves on the milk that oscillate up and down but do not appear to travel over the surface. These waves are created by the superposition of two or more moving waves, such as the two identical waves flowing in opposite directions seen in Figure 5. The waves pass through each other, adding to the disruptions as they travel. When the amplitude and wavelength of two waves are the same, they alternate between constructive and destructive interference. The outcome is known as a standing wave because it resembles a wave that is stationary. Standing waves can be seen on the surface of a glass of milk. Other standing waves can be found in guitar strings and organ pipes. The two waves that generate standing waves in the glass of milk could be caused by reflections from the glass's side.
A detailed examination of earthquakes reveals evidence of resonance, standing waves, and constructive and destructive interference situations. A building may be vibrated for several seconds at a frequency that matches the natural frequency of vibration of the building, resulting in a resonance that causes one building to collapse while surrounding buildings remain intact. Buildings of a specific height are frequently destroyed, whereas taller structures remain standing. The height of the building corresponds to the conditions for creating a standing wave at that height. At specific spots along the Earth's surface, constructive interference occurs as seismic waves reflect off denser rocks. Areas near to the epicentre are frequently unaffected, whereas areas further away are.
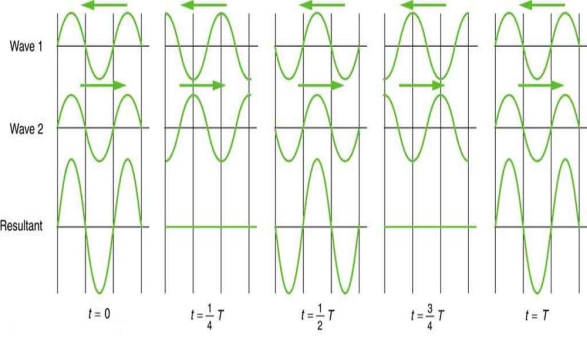
Figure 5: A standing wave is formed when two similar waves moving in opposite directions are superimposed. The oscillations occur at predetermined points in space and are caused by constructive and destructive interference.
Standing waves can also be formed on musical instrument strings as a result of wave reflections from the ends of the string. Three standing waves can be formed on a string that is fastened at both ends, as seen in Figures 6 and 7. In a standing wave, nodes are the sites where the string does not move; more broadly, nodes are the sites where the wave disturbance is zero. Because the string cannot move, the fixed ends of strings must also be nodes. In standing waves, the term antinode refers to the place of maximum amplitude. Standing waves on strings have a frequency that is proportional to the disturbance's propagation speed vw. The distance between the spots where the string is fixed in place determines the wavelength.
The fundamental frequency, which is the lowest frequency, is so for the longest wavelength, which is 1 = 2L. f1=vw1=vw2f1=v The overtones or harmonics in this situation are multiples of the fundamental frequency. Because 2 = L, the first harmonic can be simply determined, as shown in Figure 7. As a result, f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1. In the same way, f3 = 3f1 and so on. The tension in the string can be adjusted to vary all of these frequencies. The higher the frequency, the higher the vw and the greater the stress. Anyone who has ever watched a string instrument being tuned would recognise this observation. Standing waves are critical to many resonance occurrences, such as sounding boxes on string instruments, as we will discover in later chapters.
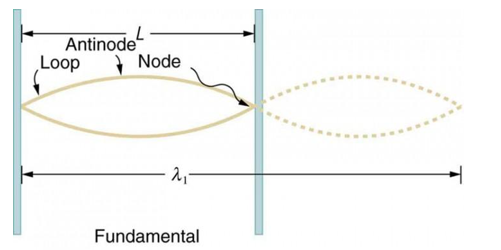
f1 = 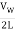

Figure 6. The figure shows a string oscillating at its fundamental frequency.
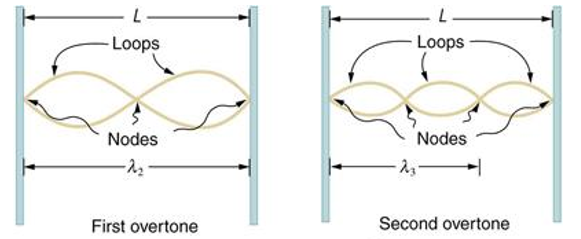
Figure 7. First and second harmonic frequencies are shown.
2.1.5 Beats
On a piano, striking two neighbouring keys generates a warbling sound that is normally considered unpleasant. The culprit is the superposition of two waves with comparable but not identical frequency. Another example can be seen during taxiing in jet aircraft, particularly the two-engine version. The combined sound of the engines increases and decreases in volume. Because the sound waves have comparable but not identical frequencies, the loudness varies. As the two waves travel in and out of phase, the discordant warbling of the piano and the varying loudness of the jet engine noise are both due to alternately constructive and destructive interference. This is visually depicted in Figure 8.
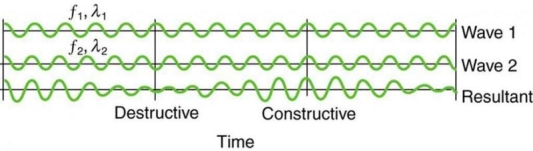
Figure 8 shows how beats are created by superimposing two waves with slightly different frequencies but identical amplitudes. The waves alternate between constructive and destructive interference over time, resulting in a wave with a variable amplitude.
The frequency of the wave that results from the superposition of two waves of comparable frequency is the average of the two. The amplitude of this wave swings in beats, at a frequency called the beat frequency. The beat frequency can be calculated by combining two waves together analytically. It's worth noting that at one point in space, a wave can be represented as
x = X cos (2πt/T) = X cos (2πft)
The frequency of the wave is f=1/T. When two waves with different frequencies but equal amplitudes are combined, the outcome is x = x1 + x2. x = Xcos(2 f1t) + Xcos(2 f2t), to be precise.
It can be demonstrated that x =2X cos(fBt)cos(2 favet) using a trigonometric identity, where fB = |f1 f2| is the beat frequency and fave is the average of f1 and f2. These findings indicate that the resultant wave has double the amplitude and average frequency of the two superimposed waves, but its overall amplitude changes at the beat frequency fB. The amplitude is effectively increased and decreased by the first cosine term in the formula. The wave with frequency fave is the second cosine term. This conclusion holds true for all forms of waves. If it's a sound wave, though, and the two frequencies are similar, we'll hear an average frequency that grows louder and softer (or warbles) as the beat frequency approaches.
While beats might be bothersome in auditory noises, we will see that they have a wide range of applications. Observing beats is a great technique to compare frequencies that are comparable. Ultrasonic imaging and radar speed traps are two seemingly unrelated applications of beats.
Key takeaway:
- The combination of two waves at the same spot is known as superposition.
- When two identical waves are superimposed in phase, constructive interference occurs.
- When two identical waves are overlaid perfectly out of phase, destructive interference results.
- A standing wave is created when two waves collide, resulting in a wave that changes in amplitude but does not propagate.
- In standing waves, nodes are sites where there is no motion.
- An antinode is the point at which a standing wave reaches its maximum amplitude.
- Waves on a string are resonant standing waves with a basic frequency that can have overtones or harmonics at higher multiples of the fundamental.
- When waves of similar frequency f1 and f2 are overlaid, beats occur. The oscillation frequency of the resulting amplitude is given by fB = |f1 f2|.
2.2.1 Harmonic Waves and Phase Velocity
The equation describes a one-dimensional harmonic wave (Figure 1).
u(x, t) = A0 sin (ωt – k x + φ)
Where A0 represents the wave amplitude, is the circular frequency, k represents the wave number, and is the starting, constant phase. The phase is the argument for the sine function, which is (x, t) = t - kx +. The spatial frequency or propagation constant are other names for the wave number.
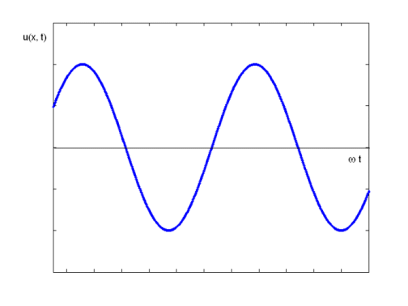
Figure 9: Harmonic Wave
This is a wave that is monochromatic (one frequency). In nature, there are no waves that are strictly monochromatic. For example, the wave's generating source could move significantly, resulting in spurious frequencies.
These waves propagate without warping in most cases. In other words, the phase (x, t) is constant:
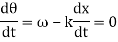
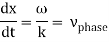
vphase is the phase velocity for a wave.
These waves are ineffective in terms of transmitting information. They remain the same in time and place. In order to transfer information, something must be modulated, such as frequency or amplitude. The resulting wave could be a wave packet, which is a disturbance that acts across a short distance. This wave packet can be thought of as a Fourier series or integral, which is a superposition of a number of harmonic waves.
2.2.2 Group Velocity
Something more than a basic harmonic wave is required to transmit information. The superposition of several such waves of differing frequencies, on the other hand, can produce a "envelope" wave and a carrier wave within the envelope. The envelope has the ability to convey data. The superposition of two harmonic waves with very near frequencies (1 2) and the same amplitude is a simple example. The motion's equations are as follows:
u(x, t) = A0 . Cos (ω1 t – k1 x) + A0 . Cos (ω2t – k2 x)
= 2 A0 . Cos (  ) × cos (
) × cos (  )
)
= u1 × u2
Figure depicts the plot of such a wave.
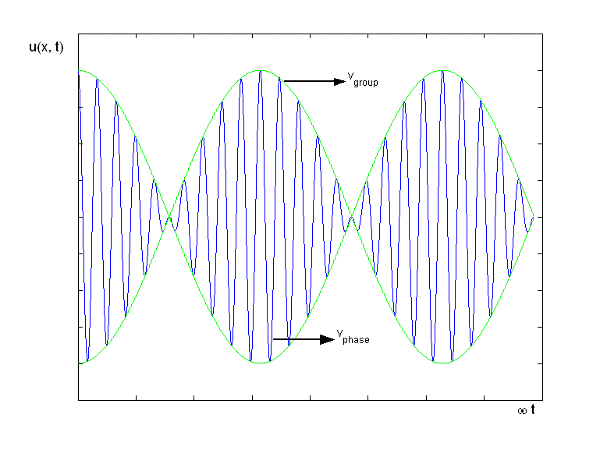
Figure 10: Group Velocity
u1 controls the envelope (the green line), which moves at the group velocity. The phase velocity of the carrier wave (the blue line) is provided by u2. The wave packet travels at the same speed as the rest of the group. It is the envelope that contains the data. The velocity of a group and the velocity of a phase are not always the same. The velocity of a group is given by,
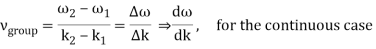
Rayleigh's formula links phase and group velocity together.
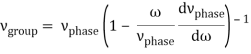
Group velocity equals phase velocity if the derivative term is zero. There is no dispersion in this scenario. When the different phase velocities of the envelope components cause the wave packet to "spread out" over time, this is called dispersion. The wave packet's (or envelope's) components separate to the point that they can no longer combine to complete the envelope.
2.3.1 Wave Packet Solution
Since the wave equation's travelling wave solution
y(x, t) = A sin (kx – ωt)
Is true for every value of the wave parameters, and since any superposition of solutions is likewise a solution, a wave packet solution can be constructed as a sum of travelling waves:
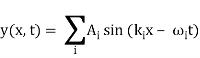
It is standard practise to express the amount 2/ by k, also known as the wave vector. The sum is replaced by an integral for a continuous range of wave vectors k:
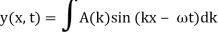
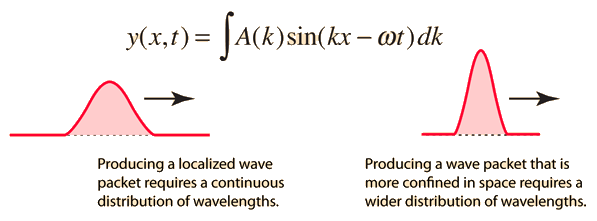
2.3.2 Wave Packet Details
Like a pulse on a string, a wave packet solution to the wave equation must have a variety of frequencies. The broader the range of frequency components necessary for quick transient behaviour, the shorter the pulse in time. For classical waves, this need can be expressed as a form of uncertainty principle:

The exact figures depend on how the pulse width is defined, however making brief pulses necessitates a large frequency bandwidth. The uncertainty principle in quantum mechanics is analogous to this.
2.3.3 Wave Packets from Discrete Waves
When discrete travelling wave solutions to the wave equation are concatenated, a wave packet that begins to localise the wave can be created. The quantum mechanical uncertainty principle mirrors this property of classical waves.
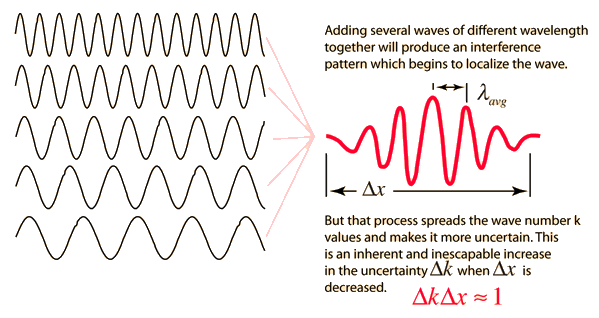
2.3.4 The Wave-Particle Puzzle
De Broglie's explanation of the Bohr atom quantization principles, together with Davisson and Germer's unintentional discovery of electron diffraction scattering, offer a compelling case for the electron's wave nature. Even so, the electron can act like a particle at times. An electron has a certain mass and charge, may move slowly, and can pass through a variety of devices, including a gun and a screen.
So, what's the connection between the wave and particle perspectives? Both were always present, according to De Broglie. He dubbed the wave a pilot wave, and he believed it steered the particle's motion. Unfortunately, the point of view leads to inconsistencies. The common current view is that the relative likelihood of detecting the particle at any position is determined by the strength of the wave (measured by the square of its amplitude).
The probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of the magnetic field vector. This interpretation, first proposed by Max Born in 1926, is analogous to the relationship between the electromagnetic field and quanta—the probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of The de Broglie wave function associated with the electron is written in standard notation as (x,t). The relative probability of finding the electron in a narrow period of length x near location x at time t is thus |(x,t)|2dx. (For the sake of simplicity, we limit the electron's movement to one dimension.) The generalisation is easy to understand.)
2.3.5 Keeping the Wave and the Particle Together?
Suppose following de Broglie we write down the relation between the "particle properties" of the electron and its "wave properties":
 mv2=E=hf, mv=p=h/λ.
mv2=E=hf, mv=p=h/λ.
It would seem that we can immediately figure out the speed of the wave, just using λf=c′, say.
We find:
λf=hmv⋅12mv2h=12v.
What? The speed of the wave is half the speed of the electron? How could they stay together? What's wrong with this calculation?
2.3.6 Localizing an Electron
To solve this question, consider the wave function corresponding to an electron moving in a vacuum tube, for example. The electron exits the cathode, travels through the vacuum, and collides with a grid's anode. It is travelling through the vacuum at a moment in this process, and the wave function must be nonzero across some volume, but zero in places the electron has not yet reached and zero in places it has definitely gone.
The electron, on the other hand, has a precise momentum if it possesses a precise energy, such as fifty electron volts. This necessitates the existence of a definite wavelength for the wave. However, the only wave with an exact wavelength is (x,t)=Asin(kxt).
Where k=2/ and =2f are constants. The issue is that this plane sine wave stretches to infinity in both spatial directions, therefore it can't represent a particle with a non-zero wave function in a finite region of space.
As a result, we must superpose waves of different wavelengths to represent a confined particle. Using the trigonometric addition formula, superpose two waves with somewhat varying wavelengths to demonstrate the principle:
Sin((kk)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((
Sin(kxt)cos((k)x()t sin(kxt)cos((k)x()t sin(k)x()t sin(k)x()t sin
The phenomena of beats between waves of similar frequency is represented by this formula. The first term, sin(kxt), oscillates at a frequency that is the average of the two. The slowly fluctuating second term, which oscillates once over a spatial range of order /k, modulates it. This is the distance at which waves that were in phase at the start turn fully out of phase. Of course, if the distance between the waves is increased by order /k, the waves will re-synchronize.
That is, combining two close frequencies creates a series of packets, or beats, from the continuous wave. A single packet is required to describe a single electron travelling through space. This can be accomplished by superposing waves with a continuous distribution of wavelengths, or wave numbers in the order of k, for example. The waves will be out of phase after a distance of order /k, but because they have so many distinct wavelengths, they will never be able to get back in phase. (All of this is adequately treated in Fourier transform theory.) We're just attempting to make it plausible right now.)
2.3.7 The Uncertainty Principle
It should be evident from the above argument that to construct a wave packet representing an electron localized in a small region of space, the component waves must get out of phase rapidly. This means that their wavelengths can't be too close. In reality, simply considering the two beating waves allows for a semi-quantitative approximation of the wavelength spread required.
A packet localized in a region of extent Δx can be constructed of waves having k 's spread over a range Δk, where Δx∼π/Δk.
Now, k=2π/λ, and p=h/λ, so k=2πp/h.
Therefore, Δk=2πΔp/h, and Δx∼π/Δk∼h/Δp, (dropping the factor of 2).
Thus:
Δx⋅Δp∼h.
This is Heisenberg's Uncertainty Principle, which we shall analyze in more detail in later lectures.
2.4.1 Gaussian wave packets:
We write a free wave packet as a linear combination of plane waves
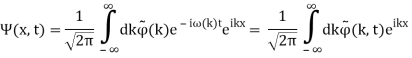
Where the momentum amplitudes absorb the time evolution of each plane wave, given by (k)=k2/2m (k,t). As a Gaussian, we chose the amplitude for the various plane waves.

The momentum distribution |φ~(k,t)|2| is a Gaussian of width σk and mean k0 for all t.
At t=0, where the momentum amplitudes are real, the probability density of the resulting wave packet at is a Gaussian of width σx=1/2σk, i.e., it is as localized as is allowed by the Heisenberg principle (σx=1/2). The probability distribution stays Gaussian for all t. As the momentum amplitudes become complex, its width 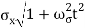 increases with a characteristic time 1/ωσ=2m
increases with a characteristic time 1/ωσ=2m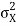 /ℏ, and its center moves with the group velocity vg=ℏk0/m.
/ℏ, and its center moves with the group velocity vg=ℏk0/m.
The genuinely quantum mechanical aspect is the behaviour at t=0: We can't locate the particle any farther than the uncertainty principle allows. It is a direct result of the wave-description resulting directly from the Fourier transform's features. For long periods of time, the behaviour is consistent with that of an ensemble of classical particles with a Gaussian momentum distribution: A particle with momentum k will be at x(k,t)=kt/m at time tt. We get the probability density of discovering a classical particle by solving for k and inserting it into the momentum distribution.
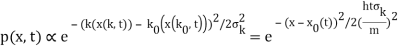
Which is a Gaussian of width σxωσt centered at
x0(t) = hk0t/m
The probability distribution for the wave packets has been plotted so far. We'll need a mechanism to visualise complex functions if we wish to draw the wave function. We could just plot the real and imagined parts of it. However, demonstrating its modulus (the square of which yields the probability density) and phase is more enlightening. It's simple to plot the modulus. We use colours to depict the phases, starting with red for phase zero, progressing through the rainbow colours as the phase progresses, and finally returning to red for phase two. The representation of a plane wave is shown below as an example. 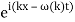
The propagating free Gaussian wave packet's wave function is given by
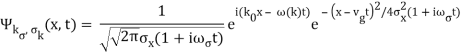

The phase of a Gaussian wave packet with a small momentum distribution is virtually identical to a plane wave with momentum k0.
The phase no longer has a well-defined wave length as the momentum dispersion widens. The phase has wave length 2/k0 around the maximum at x(t)=vgt.
2.4.2 Linear combination of wave packets (Schrödinger cat states)
Looking at linear combinations of Gaussian wave packets is equally fascinating. It's important to remember that we're still dealing with single-electron wave functions, which describe a single electron in a superposition state rather than two!
=GWP(k0,k,x0), What determines the interference pattern's wave length? Why is the amplitude of the wave packets in the middle always zero?
This is the same wave function as before, but with the probability density displayed. After the wave packets have travelled past each other, what happens to them? What would happen if their rate of broadening was slower than their velocity?
This wave packet flows slower and has a significantly larger momentum distribution. Why do the wave function's oscillations continue?
2.4.3 Reflection at hard wall
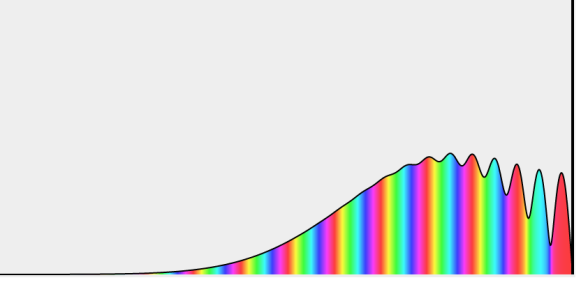
We can see how a Gaussian wave packet is reflected at a hard wall by looking at just one half of the above superpositions. Compare this approach to the electrostatics method of image charges.
Same thing, except this time for a wave packet with a significantly wider momentum dispersion.
2.5.1 Localization Of Waves; Relation To Uncertainty Principle
To grasp the uncertainty principle, one must first grasp a difficult but crucial concept concerning wave localizability: a wave can only be localised if distinct wavelengths are superposed. Consider a single-wavelength “pure” wave, as depicted below.

It's a perfect sine wave that repeats eternally with a perfectly defined fixed wavelength that's spread out in space. If it's an electron wave, it's a particle travelling at a constant speed with a well-defined momentum, as defined by the de Broglie equation: p = h/. What happened to the electron? It can be found anywhere—or is equally likely to be found anywhere (along the infinite dimension of the wave). 1 Its positional uncertainty is unlimited; its momentum (and wavelength) uncertainty is zero. This is a bizarre circumstance that, at the very least, adheres to the uncertainty principle. If the product of two uncertainties remains constant, one of them can only grow endlessly tiny if the other remains constant.
Consider the outcome of superposing many wavelengths. The superposition of two waves with wavelength differences of 10% is depicted below.
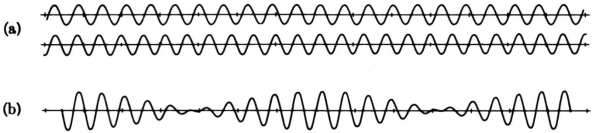
The waves interfere destructively five cycles after the point of maximum reinforcement. They reinforce again five cycles later. Partial localization of the wave is caused by the alternating of constructive and destructive interference, which causes the wave to bunch together into zones of around 10 wavelengths in length. This result contains an important indication concerning the uncertainty principle. The mixing of wavelengths required for partial localisation has resulted in momentum uncertainty.
By superposing a large number of distinct wavelengths, more localisation can be attained. The effect of mixing six separate pure waves, each with a wavelength difference of 2%, is shown in the diagram below.

The entire wavelength spread stays at 10%, with 5% on either side of the average wavelength. As a result, we can give a momentum uncertainty of around 5% of the dominant momentum:
Δp ≅ 0.05p.
Here, p denotes an average momentum, which is related to an average wavelength by the formula p = h/. The wave is better localised in the illustration because of the six-fold superposition. (The wave might be totally confined if all conceivable wavelengths within the provided span were superposed.) Its amplitude would sink to zero outside of a specified region of space, never to rise again.) The extent of the wave on either side of its center—roughly five wavelengths in the figure—represents the uncertainty of position:
Δx ≅ 5λ
In this case, the product of position and momentum uncertainty is
ΔxΔp ≅ 0.25λp.
Because the right-hand product p equals Planck's constant h, this equation can be written as
ΔxΔp ≅ 0.25h.
The numerical component 0.25 in this equation has no special relevance because we have made reasonable estimates of the uncertainty. The right side of the uncertainty equation, according to the technical definition of uncertainty employed in quantum mechanics, is exactly h/2, or, as stated in Essay Q6.
Since a 10% difference in momentum “crushed” the wave packet from infinite to just over 10 wavelengths, it's plausible to assume that momenta changing by almost 100% would be required to reduce the packet to a single cycle. This is correct. Maximum localization, x /2, necessitates superposition of wavelengths (and momenta) that differ by a factor of two. Then p p/2 p pppppppppp Because neither of these variables is clearly defined for a localised wave, p and refer to average values of momentum and wavelength in these equations. Again, the product xp is nearly identical to the product p, which is equal to Planck's constant.
The hydrogen atom contains an actual three-dimensional wave function, as opposed to the hypothetical one-dimensional waves outlined before. Its amplitude is depicted below along a radial line drawn across the atom's diameter.
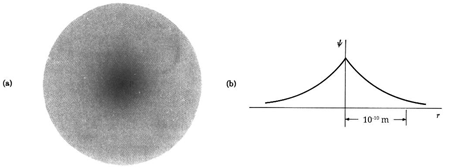
This electron wave function is highly confined, with only one oscillation cycle from one side of the atom to the other. This wave function's shape, with its central peak, is very different from that of a pure sine wave. With the appropriate mix of infinitely many wavelengths, any shape can be "fashioned."
The Heisenberg uncertainty principle is a result of the wave nature of particles, as demonstrated by this discussion of wave superposition. It is no more profound, and in this form, it says nothing more or less than the de Broglie equation for material particle wavelength. Measurement uncertainty stems mostly from the nonlocalizability of waves.
2.5.2 Two Examples of Localized Wave Packets
Lets now try two examples of a wave packet localized in k and properly normalized at t=0.
- A “square” packet: A(k) =
 for k0 – a/2 < k < k0 + a/2 and 0 elsewhere.
for k0 – a/2 < k < k0 + a/2 and 0 elsewhere. - A Gaussian packet: A(k) = (2a/π)1/4 e-α (k – k0)2.
These are both localized in momentum about p= hk0.
Check the normalization of (1).
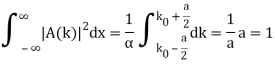
Check the normalization of (2) using the result for a definite integral of a Gaussian
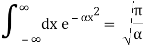
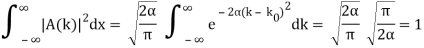
So now we take the Fourier Transform of (1) right here.
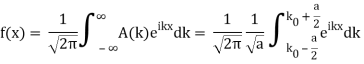
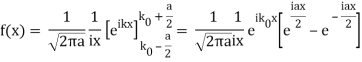
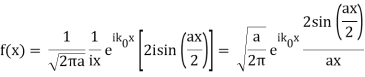
Note that 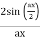 is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this
is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this  function.
function.
The Fourier Transform of a Gaussian wave packet
A(k) = 
f(x) = 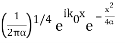
Also a Gaussian. We will show later that a Gaussian is the best one can do to localize a particle in position and momentum at the same time.
In both of these cases of f(x) (transformed from a normalized A(k) localized in momentum space) we see
- A coefficient which correctly normalizes the state to 1,
- eik0x - a wave corresponding to momentum hk0,
- And a packet function which is localized in x.
We've found states that represent a single free particle, which was our goal. We can have states that are localised in both position and momentum space, as we can see. We did this by creating wave packets, which are superpositions of definite-momentum states. While the wave packets are localised, they do have some width. x and in p.
2.6.1 Evolution of Wave Packets
We have
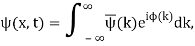
Where
ϕ(k) = kx – ω(k) t.
The function 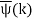 is obtained by Fourier transforming the wavefunction at t = 0. Now,
is obtained by Fourier transforming the wavefunction at t = 0. Now, 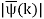 is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain
is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain
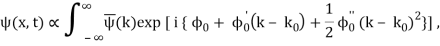
Where
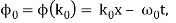
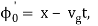
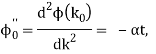
With
μ : ω (k0),
a : 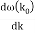
c : 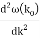
Rearranging, and then changing the variable of integration to y = (k – k0) / (2 ∆k), we get
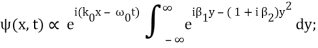
Where
2 ∆k ( x – x0 – vgt),
2 α (∆k)2t
Incidentally, ∆k = 1/ (2∆x) , where ∆x is the initial width of the wave packet. The above expression can be rearranged to give
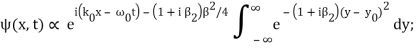
Where y0 = iβ/2 and β = β1 / (1+ iβ2). Again changing the variable of integration to z = (1+ iβ2)1/2 ( y – y0), we get
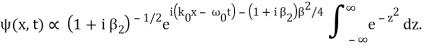
The integral now just reduces to a number. Hence, we obtain
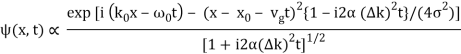
Where
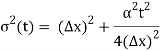
It's worth noting that the above wavefunction is the same as the one we started with at. This supports the estimate we produced before by extending the phase factor with Taylor. ϕ(k) about k = k0.
The probability density of our particle as a function of time is stated using Eq. (111).

As a result, the probability distribution is Gaussian, with a characteristic width of and a maximum value of x = x0 + vgt. Our particle's most likely position now aligns with the distribution function's peak. As a result, the most likely position of the particle is provided by
x = x0 + vgt.
The particle essentially moves at a uniform velocity, as can be shown.

The particle essentially moves at a uniform velocity, as can be shown. vp = ω/k, whereas a wave packet travels at the group velocity,vg = d ω/dt. Now, it follows from the dispersion relation for particle waves that
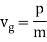
This, however, is the same as the classical particle velocity. As a result, once we learn that individual particles must be identified with wave packets rather than plane waves, the dispersion relation turns out to be consistent with classical physics. In reality, a continuous stream of particles moving in the same direction as the wave is commonly regarded as a plane wave.
The width of our wave packet grows as time passes, according to Eq. (112). Indeed, the characteristic time for a wave packet of original width to double in spatial extent is given by Eqs. (105).
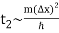
For example, if an electron is initially isolated in an atomic scale region (i.e., ∆x ~ 10-10 m) then the doubling time is only about 10-16 s. Evidently, particle wave packets (for freely moving particles) spread very rapidly.
Note, from the previous analysis, that the rate of spreading of a wave packet is ultimately governed by the second derivative of ω(k) with respect to k. See Eqs. (105) and (112). This is why a functional relationship between and is sometimes referred to as a dispersion relation: it affects how wave packets spread over time. The second derivative of with respect to is 0 in the specific situation when is a linear function of, and hence there is no dispersion of wave packets: i.e. wave packets propagate without altering shape. In the case of light waves, the dispersion relation is now linear. Light pulses pass through a vacuum without spreading, as a result. Another feature of linear dispersion relationships is that the phase is preserved.
Velocity, vp = ω/k, and the group velocity, vg = dω/dk, are identical. Thus, both plane light waves and light pulses propagate through a vacuum at the characteristic speed c = 3 × 108 m/s. Of course, the dispersion relation for particle waves is not linear in k. Hence, particle plane waves and particle wave packets propagate at different velocities, and particle wave packets also gradually disperse as time progresses.
2.6.2 Time Development of a Gaussian Wave Packet
So far, we've just done our Fourier Transforms at and examined the results at t = 0. We'll now reintroduce time to the wave function and examine the wave packet at a later time. We'll see that photons and non-relativistic electrons behave very differently.
Assume we start with our Gaussian (minimum uncertainty) wave packet A(k) = 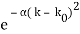 at t = 0. We can do the Fourier Transform to position space, including the time dependence.
at t = 0. We can do the Fourier Transform to position space, including the time dependence.
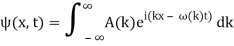
We state directly that is reliant on. This simply indicates that the energy of our free particle is determined by its motion. In the case of a photon, E = pc, so ℏ ω = ℏ kc, and hence ω = kc. For an non-relativistic electron, E =  , so ℏ ω =
, so ℏ ω =  , and hence ω =
, and hence ω = 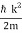 .
.
To cover the general case, lets expand ω(k) around the center of the wave packet in k-space.
ω(k) = ω(k0) + 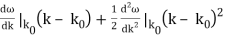
We make some educated guesses about the outcome and give the coefficients names.
ω(k) = ω0 + vg (k – k0) + β (k – k0)2
For the photon, vg = c and β=0. For the NR electron, vg = 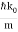 and β =
and β = 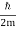 .
.
Performing the Fourier Transform, we get
ψ(x, t) = 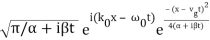
| ψ(x, t)|2 = 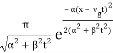
We can see that the photon will travel at the speed of light and that the wave will travel at the same speed.
Packet will not disperse, because β = 0.
The wave packet for the NR electron moves at the correct group velocity., vg = p/m, but the wave packet spreads with time. The RMS width is σ = 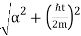
A wave packet naturally spreads because it contains waves of different momenta and hence different velocities. Wave packets that are very localized in space spread rapidly.
2.7.1 Wave-Particle Duality
The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.
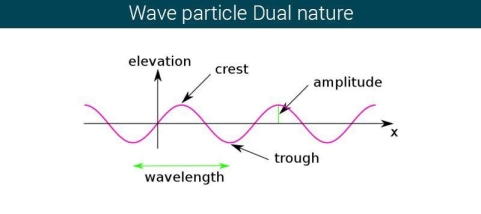
Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.

The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
We can say that light is a particle with the attribute of waves because the energy of waves and the energy of light do not correspond.
Einstein demonstrated that a photon's momentum equals
p = h/λ
This is readily demonstrated as follows. Assumption E = hv for a photon and λv = c for an electromagnetic wave, we obtain
E = hc/λ
We are now applying Einstein's relativity result. E = mc2 to find
λ = h/mc
Which is the same as equation (4). Because the rest mass of a photon is zero, this refers to the relativistic mass, not the rest mass. De Broglie reasoned in 1924 that matter can show this wave-particle duality because light can behave both as a wave (it may be diffracted and has a wavelength) and as a particle (it carries packets of energy). He went on to say that matter, like light, will obey the same equation (4). Davisson and Germer confirmed de Broglie's theory by observing diffraction patterns by hitting metals with electrons in 1927.
Bohr's assumption is justified according to de Broglie's equation (2). If we consider an electron to be a wave, the electron orbit must complete an integral number of wavelengths during its orbit to be stable. Otherwise, it would interfere with itself in a detrimental manner. This condition could be written as follows:
2πr = nλ
This can be expressed as using the de Broglie relation (4).
Mvr = nℏ
This is exactly the same as Bohr's equation (2).
While de Broglie's equation validates Bohr's quantization assumption, it also exposes a flaw in Bohr's model. The wave-particle duality, as demonstrated by Heisenberg, leads to the well-known uncertainty principle.
∆x∆p ≈ h
The uncertainty principle dictates that if the orbital radius of an electron in an atom is known precisely, the angular momentum must be unknown. The flaw in Bohr's model is that it stipulates both exactly and that the orbital angular momentum must be an integral multiple of. As a result, the stage was prepared for a new quantum theory that followed the uncertainty principle.
2.7.2 The duality of photons
“Light is a particle as well as a wave.” To have a better understanding of this concept, we conducted an experiment.
Young's Interference Experiment, often known as the Double-slit Interference Experiment, is a type of experiment. This experiment used technology to identify individual light particles to see if interference fringes appeared even when the light was severely attenuated to the point where there was just one particle. The experiment's findings confirmed that one photon had an interference fringe.
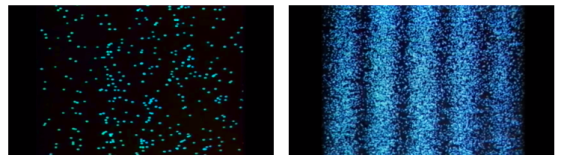
When light is detected that has been weakened to an extreme brightness limit and projected on a screen, it behaves like a particle, as shown on the left. When the number of particles detected rises, however, an interference fringe emerges, as shown on the right. As can be seen, light behaves similarly to a wave.
There was no interference fringe when one of the two slits in the experiment was closed, allowing only one photon particle to pass through the other slit. This proved that in the double-slit interference experiment, one photon particle travelled through both slits at the same time and interfered with itself.
These experiments show that while a photon was detected as having the properties of a particle, interference appeared like that of a wave while simultaneously passing through the double-slit, revealing that the photon has the dual properties of a particle and a wave.
Key takeaway:
- In quantum physics, wave–particle duality states that any particle or quantum phenomenon can be represented as either a particle or a wave. It expresses the difficulty of classical terminology like as "particle" and "wave" to completely characterise quantum-scale things' behaviour.
- He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
Complementarity is a concept in quantum mechanics that Niels Bohr considered to be a necessary property of the theory. According to the complementarity principle, objects have a set of complementary features that cannot all be viewed or measured at the same time. Position and momentum are an example of such a pair. One of quantum mechanics' foundational truths, according to Bohr, is that setting up an experiment to measure one of a pair of quantities, such as the position of an electron, excludes the possibility of measuring the other, despite the fact that understanding both experiments is required to characterise the object under study. The behaviour of atomic and subatomic things, according to Bohr, cannot be divorced from the measuring devices that form the framework in which they behave. As a result, there is no "one picture" that unifies the data gained in these various experimental situations, and only the "totality of the phenomena" as a whole can provide a complete description.
The failure of the operators that represent the observable quantities being measured to commute expresses complementarity mathematically:
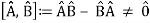
Incompatible observables are observables that correlate to non-commutative operators. There can't be a comprehensive set of shared eigenstates for incompatible observables. It's worth noting that there may be some simultaneous eigenstates of () A and () B, but not enough to form a complete basis. The canonical commutation relation is defined as follows:
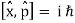
This suggests that this holds true for both position and momentum. Similarly, any two of the spin observables specified by the Pauli matrices have an equivalent relationship; measurements of spin along perpendicular axes are complimentary. Using mutually unbiased bases, which give complementary observables defined on finite-dimensional Hilbert spaces, this has been applied to discrete observables with more than two possible outcomes.
The principle of complementarity, or dialecticism, is a second key component of quantum physics. Is light a wave or a particle? Complementarity is defined as the recognition that though particle and wave behaviour are mutually exclusive, both are required for a complete explanation of all occurrences.
2.9.1 De Broglie’s Matter Waves:
When an electromagnetic wave interacts with matter, it can behave as a particle of light, according to Compton's formula. Louis de Broglie proposed a new speculative idea in 1924, claiming that electrons and other matter particles could behave like waves. De Broglie's hypothesis of matter waves is the name given to this concept today. De Broglie's hypothesis, combined with Bohr's early quantum theory, resulted in the development of a new wave quantum mechanics theory to describe the physics of atoms and subatomic particles in 1926. Quantum mechanics has made new technical inventions and technologies possible, such as the laser and magnetic resonance imaging (MRI). Other fields, such as biology and chemistry, benefit from this new technology.
According to de Broglie's hypothesis, both massless photons and heavy particles must satisfy a single set of relationships that link energy E to frequency f and linear momentum p to wavelength w. These photon-photon connections were previously studied in the context of Compton's effect. We're bringing them up now in a broader perspective. A de Broglie wave of frequency f and wavelength is any particle with energy and motion.
E = hf
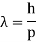
E and p denote a particle's relativistic energy and momentum, respectively. The wave vector is commonly used to express De Broglie's relations. 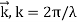 and the wave frequency ω = 2πf as we usually do for waves:
and the wave frequency ω = 2πf as we usually do for waves:
E = ℏω
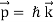
According to wave theory, a wave's energy is carried with the group velocity. This group velocity for matter waves is the particle's velocity u. De Broglie relations show that matter waves obey the following relation when the energy E and momentum p of a particle are identified with its relativistic energy mu and relativistic momentum mu, respectively.
λf = ω/k = 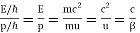
Where β = u/c
When a particle is massless we have 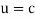 and (Figure) becomes
and (Figure) becomes 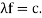
De Broglie gave an explanation for the quantization of the electron's angular momentum in the hydrogen atom, which was posited in Bohr's quantum theory, using the idea of the electron matter wave. When we suppose that an electron in a hydrogen atom behaves like a wave rather than a particle, the scientific explanation for the first Bohr quantization condition emerges easily. Imagine a stretched guitar string that is clamped at both ends and vibrates in one of its typical modes to see it clearly. The wavelengths of these vibrations cannot be random if the length of the string is l ((Figure)), but must be such that an integer k number of half-wavelengths /2 fits exactly on the distance l between the ends. A standing wave on a string has the constraint l=k/2. Let's pretend that instead of clamping the string to the walls, we bend it into a circle and tie the ends together. This results in a circular string that vibrates in normal modes and fulfils the same standing-wave requirement, but the number of half-wavelengths must now be an even number k,k=2n, and the length l is now tied to the circle's radius r n. This means that the radii cannot be chosen at random, but must meet the standing-wave condition:
2π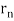 = 2n λ/2.
= 2n λ/2.
If an electron moves like a wave in the nth Bohr orbit, its wavelength must be equal to (Figure). λ = 2π /n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
/n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
p = h/λ = nh/ (2 π = nh/
= nh/ . As a result, in a circular orbit, the electron's angular momentum must be
. As a result, in a circular orbit, the electron's angular momentum must be
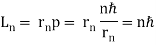
The first of Bohr's quantization conditions, given by, is this equation (Figure). A plausible theoretical argument for the existence of matter waves is to provide a physical explanation for Bohr's quantization condition.
Standing-wave pattern: (a) a stretched string clamped against the walls; (b) an electron wave trapped in the hydrogen atom's third Bohr orbit.

In 1927, C. Davisson and L. Germer completed a series of electron-scattering tests that conclusively demonstrated that electrons behave like waves. Davisson and Germer's experiment were not designed to prove de Broglie's hypothesis: The proof came as a result of their usual experiments on metal surfaces bombarded by electrons.
They analysed a nickel surface in the experiment that produced the first evidence of electron waves (now known as the Davisson–Germer experiment). Their nickel sample was treated in a high-temperature oven to transform it from its regular polycrystalline structure to one with massive single-crystal domains filling the volume. The experimental setup is depicted in (Figure). Thermal electrons are emitted from an electron gun's heated element (typically composed of tungsten) and accelerated through a potential difference V, resulting in a well-collimated stream of electrons. By adjusting the potential difference in the electron cannon, the kinetic energy K of the electrons can be modified. According to the law of conservation of energy, this results in a beam of electrons with a fixed linear momentum:
EV = K = 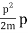 =
= 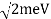
The electron beam strikes the nickel sample in a normal to its surface direction. It scatters in a variety of directions near the surface. A very sensitive detector measures the intensity of the beam scattered in a specific direction. The detector's angular location with relation to the incident beam's direction can range from to The entire setup is enclosed in a vacuum chamber to prevent electron collisions with air molecules, as such thermal collisions would change the electrons’ kinetic energy and are not desirable.
The Davisson–Germer diffraction experiment's experimental setup is shown schematically. The nickel target scatters a well-collimated beam of electrons. In the electron cannon, the kinetic energy of electrons in the incident beam is selected by setting a variable voltage, V. For a variety of scattering angles, the intensity of the scattered electron beam is measured, while the distance between the detector and the target remains constant.
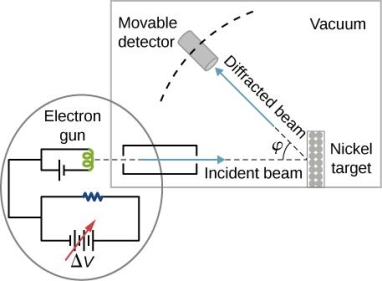
The incident electrons scatter off the nickel target's surface in many random directions when it has a polycrystalline shape with many randomly aligned tiny crystals. As a result, the dispersed electron beam's intensity is nearly constant in all directions, simulating diffuse light reflection from a porous surface. When the nickel target has a regular crystalline structure, however, the intensity of the scattered electron beam reaches a definite maximum at a given angle, resulting in a distinct diffraction pattern (see Figure). William H. Bragg and William L. Bragg, father and son physicists, analysed similar diffraction patterns created by X-rays scattered by several crystalline substances in 1912. In X-ray crystallography, the Bragg law establishes a link between the wavelength of radiation impinge on a crystalline lattice, the lattice spacing, and the position of the diffracted radiation's interference maximum (see Diffraction).
The Davisson–Germer target's lattice spacing was measured using X-ray crystallography and found to be Unlike X-ray crystallography, in which X-rays penetrate the sample, only the surface atoms interact with the incident electron beam in the Davisson–Germer experiment. The highest intensity of the reflected electron beam is found for scattering angles that satisfy the requirement (see (Figure)) in surface diffraction. At a scattering angle of 50 at V54V, the first-order maximum (for n=1) is measured, yielding the wavelength of the incident light as λ = (2.15) sin 50 = 1.64. A 54-V potential, on the other hand, accelerates incident electrons to kinetic energies of K = 54 eV. Their momentum, calculated from (Figure), is p = 2.478 × 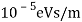 . When we substitute this result in (Figure), the de Broglie wavelength is obtained as
. When we substitute this result in (Figure), the de Broglie wavelength is obtained as
λ = h/p = 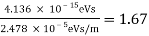
We get the same result when we utilise K = 54eV in (Figure). The theoretical result's closeness to the Davisson–Germer experimental value of 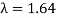 is a convincing argument for the existence of de Broglie matter waves.
is a convincing argument for the existence of de Broglie matter waves.
The experimental results of electron diffraction on a nickel target in an electron gun with an accelerating potential of around 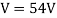 At a scattering angle of around 45 degrees, the intensity maximum is recorded.
At a scattering angle of around 45 degrees, the intensity maximum is recorded.
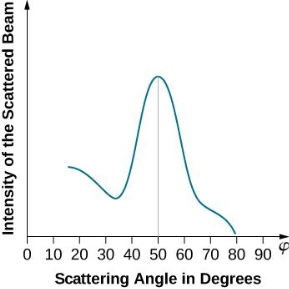
The in-phase incident beams are reflected from atoms on the surface during surface diffraction of a monochromatic electromagnetic wave on a crystalline lattice structure. Where an is the lattice spacing, a ray reflected from the left atom travels an extra distance to the detector. When D is an integer multiple of the wavelength of the reflected beams, they remain in phase. For angles satisfactory, the strength of the reflected waves exhibits notable maxima.

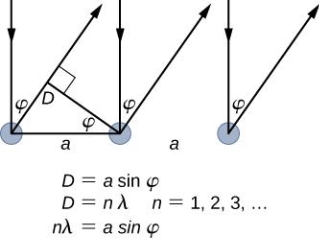
Because the incident electrons are dispersed only from the surface, diffraction lines recorded with low-energy electrons, such as those used in the Davisson–Germer experiment, are relatively broad (see (Figure)). When a higher-energy electron beam passes through a thin metal foil, the resolution of diffraction images improves dramatically. This happens because the diffraction image is made by scattering from a large number of crystallographic planes within the volume, and the maxima formed by scattering at Bragg angles are sharp (see Figure).
Diffraction patterns created by scattering X-rays and electrons on a crystalline material (a). The observed pattern represents the sample's crystalline structure's symmetry.

De Broglie's idea has been thoroughly examined using various experimental approaches since Davisson and Germer's work, and the presence of de Broglie waves has been proven for multiple elementary particles. Neutrons have been employed in scattering experiments to determine the crystalline structures of substances using neutron matter wave interference patterns. The mass of a neutron is comparable to that of a positively charged proton because it has no charge. Neutrons and protons can both be thought of as matter waves. As a result, being a matter wave is a property shared by all particles in motion, not only electrically charged ones. It has become possible to monitor matter waves of molecules as big as carbon C 60. As long as physical objects are in motion, they all have a matter wave associated with them. De Broglie matter waves have a universal character that has been established.
2.10.1 de Broglie Waves can be Experimentally Observed:
Electron diffraction studies conducted by G.P. Thomson in 1926 and C. Davisson and L. H. Germer in 1927 established the correctness of de Broglie's proposal. It was discovered in these investigations that electrons scattered from atoms in a crystal, and that these dispersed electrons generated an interference pattern. The interference pattern looked just like what happens when water waves flow through two holes in a barrier, generating independent wave fronts that merge and interfere. Both matter (e.g., electrons and neutrons) and electromagnetic radiation display these diffraction patterns, which are characteristic of wave-like behaviour. If the wavelength is equivalent to the spacing between scattering centres, diffraction patterns are generated.
We'll now look at the phenomena of electron diffraction as part of our analysis of experiments that led to the new quantum theory.
2.10.2 Light Diffraction (Young's Double Slit Experiment)
It is commonly known that light has the ability to diffract around things in its path, resulting in a pattern of interference that is unique to the object. In reality, this is how holography works (the interference pattern is created by allowing the diffracted light to interfere with the original beam so that the hologram can be viewed by shining the original beam on the image). The Young double slit experiment is a basic demonstration of light diffraction (Figure 1.7.1).

Figure 11: Experiment with a young double slit. A plane of light waves illuminates two apertures.
Water waves (shown as waves in a plane parallel to the double slit device) are used in this experiment to see what occurs when they hit the slits. Each slit then acts as a point source for spherical waves, which interfere with one another, resulting in the light and dark fringes seen on the right (Figure).
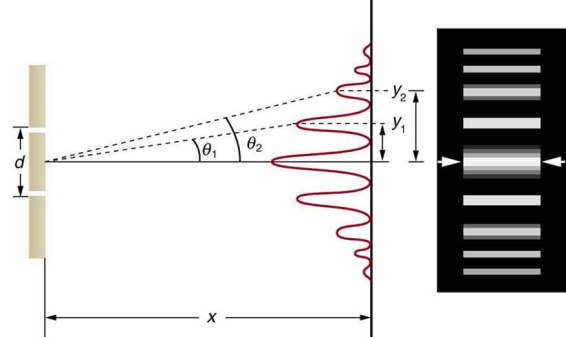
Figure 12: Interference through a double slit.
2.10.3 Electron Diffraction (Davisson–Germer Experiment)
Electrons, according to classical physics, should behave like particles, travelling in straight lines and not bending in flight until touched on by an external agent, such as a magnetic field. If we fire a beam of electrons through a double slit onto a detector in this scenario, we should obtain two bands of "hits," similar to what you'd get if you shot a machine gun through the side of a home with two windows - two regions of bullet-marked wall inside, while the remainder would be intact. Graph 1.7.3 (left).
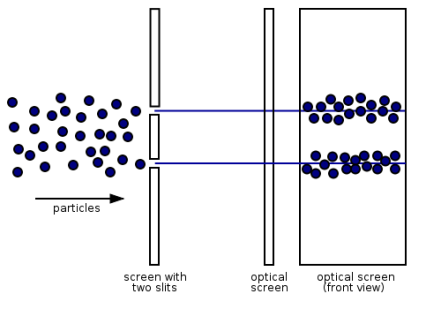
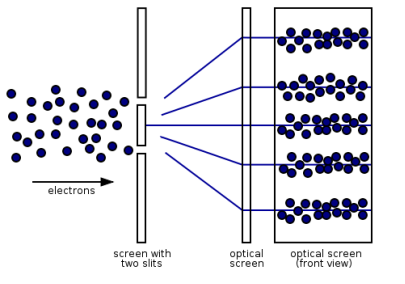
Figure 13: (left) classical model of electrons. (right) wave property of electrons.
However, if the slits are narrow and close enough together, we can see the electrons diffracting through the slits and interfering with one another, exactly like waves. This indicates that electrons, like photons, exhibit wave-particle duality, which is consistent with de Broglie's concept. They must have wavelength and frequency attributes in this scenario. The attributes can be deduced from the electrons' behaviour as they travel through our diffraction grating.
This was a watershed moment in the history of quantum physics. The Davisson–Germer experiment established the wave-nature of matter, completing the notion of wave-particle duality, much as the photoelectric effect had done for light. This concept was crucial to physicists since it suggested that not only could any particle display wave properties, but that wave equations could be used to describe processes in matter if the de Broglie wavelength was utilised.

2.10.4 Neutron Diffraction
Neutrons, like all quantum particles, can show wave behaviour, and atoms or their nuclei can behave as diffraction obstacles if the wavelength is short enough. When neutrons from a reactor are slowed and picked properly by their speed, their wavelength is near one angstrom (0.1 nm), which is the usual distance between atoms in a solid material. A diffraction experiment can then be carried out with such a beam. Neutrons interact directly with the nucleus of the atom, and each isotope contributes differently to the diffracted intensity; for example, ordinary hydrogen and deuterium contribute differently. Even in the presence of big Z atoms, light (low Z) atoms frequently contribute significantly to the diffracted intensity.
2.11.1 Davisson-Germer Experiment:
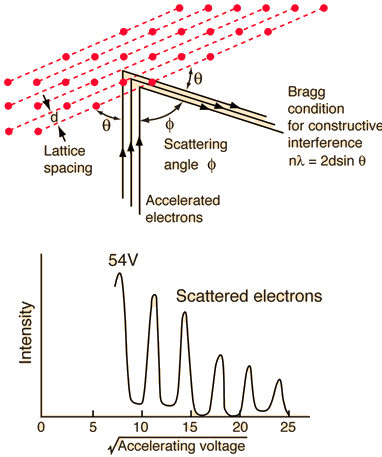
The Davisson-Germer experiment revealed the electron's wave character, validating deBroglie's earlier hypothesis. It was a big step forward in the development of quantum mechanics because it put wave-particle duality on a firm experimental footing. The Bragg diffraction law had previously been applied to x-ray diffraction, but this was the first time it had been applied to particle waves.
Davisson and Germer devised and constructed a vacuum apparatus for determining the energy of electrons scattered from a metal surface. A voltage was used to accelerate electrons from a hot filament and allow them to strike the surface of nickel metal.
The electron beam was focused on a nickel target that could be rotated to observe the dispersed electrons' angular dependency. Their electron detector (known as a Faraday box) was positioned on an arc and could be rotated to observe electrons from various angles. They were taken aback when they discovered that the intensity of the dispersed electron beam had a peak at some angles. The Bragg law could be used to calculate the lattice spacing in the nickel crystal based on this peak, which showed wave behaviour for the electrons.
With rising accelerating voltage, the experimental data above, replicated above Davisson's article, reveals recurrent maxima of scattered electron intensity. This information was gathered at a certain dispersion angle. The relationship is calculated using the Bragg law, the deBroglie wavelength expression, and the kinetic energy of the accelerated electrons.
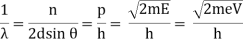
Electron Bragg deBroglie Acceleration wavelength law relationship through voltage V
An accelerating voltage of 54 volts produced a distinct peak at a scattering angle of 50° in the historical data. The Bragg law's angle theta for that scattering angle is 65°, and the computed lattice spacing for that angle is 0.092 nm. The wavelength as a function of voltage relationship is empirically determined for that lattice spacing and scattering angle.
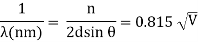
Trying this relationship for n=1,2,3 gives values for the square root of voltage 7.36, 14.7 and 22, which appear to agree with the first, third and fifth peaks above. What then accounts for the second, fourth, and sixth peaks? They could have come from a different set of crystal planes. Those peaks fall into the 2,3,4 sequence, implying that the series' first peak would have been around 5.85.
2.12.1 Deriving the de Broglie Wavelength
De Broglie arrived at his equation through a sequence of substitutions based on well-known theories:
De Broglie was the first to apply Einstein's famous equation for the relationship between matter and energy:
E = mc2 (1)
With
- E = energy,
- m = mass,
- c = speed of light
Using Planck's theory, each quantum in a wave has a discrete quantity of energy that can be calculated using Planck's equation:
E = hv
With
- E = energy,
- h = Plank's constant (6.62607 x 10-34 J s),
- ν= frequency
De Broglie hypothesised that the two energies would be equivalent because particles and waves share the same characteristics:
Mc2 = hv
De Broglie proposed velocity (v) for the speed of light since real particles do not travel at the speed of light (c).
Mv2 = hv
De Broglie replaced v/ for v in the equation and arrived at the final expression that connects wavelength and particle speed.
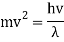
Hence
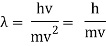
The majority of Wave-Particle Duality problems can be solved using Equation 6 and a few different cancelling out units.
De Broglie was given credit for his hypothesis, but he had no experimental proof to back it up. Clinton J. Davisson and Lester H. Germer fired electrons into a nickel crystal in 1927. They observed electron diffraction, which is analogous to wave diffraction against crystals (x-rays). In the same year, an English physicist, George P. Thomson fired electrons towards thin metal foil providing him with the same results as Davisson and Germer.
Key takeaway:
- De Broglie waves have a velocity. Beiser calls it "vp," and later shows that vp is the phase velocity of the waves. Vp=f is the formula for determining the velocity of a wave. De Broglie proposed the equation =h/mv for both particles and waves.
What is Wave-Particle Duality?
We've all heard about the nature of light and the various personalities it exhibits. Some of the features include interference, reflection, refraction, and diffraction. Particle-Wave The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.
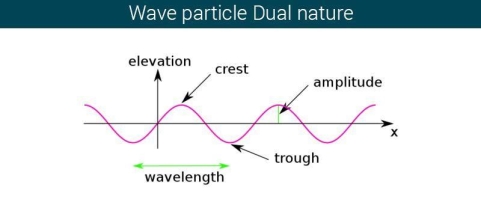
Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.
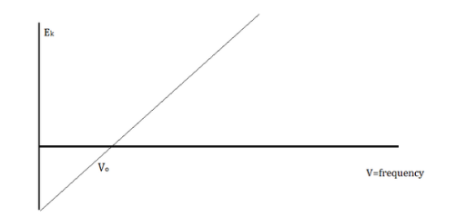
The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
Since the energy of waves and energy of light does not coincide, we can say that light is a particle that has the property of waves.
The Uncertainty Principle
A particle's position and momentum cannot be measured with arbitrarily high precision at the same time. The product of the errors of these two measurements has a minimum. There is also a minimum for the product of the energy and time uncertainty.
∆x ∆p > ℏ/2
∆E ∆t > ℏ/2
This is not a remark about measuring equipment inaccuracy or the quality of experimental methods; it is a result of the wave qualities inherent in the quantum mechanical description of nature. The ambiguity is inherent in the nature of things, even with flawless instruments and skills.
The uncertainty principle, also known as the Heisenberg uncertainty principle or the indeterminacy principle, is a statement made by German physicist Werner Heisenberg in 1927. It states that an object's position and velocity cannot be measured precisely at the same time, even in theory. In fact, in nature, the concepts of absolute position and exact velocity have no relevance.
This principle is not obvious from everyday life. Because the uncertainties suggested by this concept for common objects are sufficiently small to be noticed, it is simple to measure both the position and velocity of, say, a car. The full rule states that the product of location and velocity uncertainties is equal to or larger than a small physical amount, or constant (h/(4), where h is Planck's constant, or approximately 6.6 1034 joule-second). Only for atoms and subatomic particles with extremely small masses can the product of uncertainty become important.
Any attempt to precisely measure the velocity of a subatomic particle, such as an electron, will cause it to move around in an unpredictable manner, rendering a simultaneous measurement of its position useless. This finding originates from the intimate relationship in nature between particles and waves in the world of subatomic dimensions, and has nothing to do with shortcomings in the measurement devices, procedure, or observer.
The wave-particle duality gives rise to the uncertainty principle. Every particle has a wave connected with it, and every particle behaves in a wavelike manner. The particle is most likely to be located where the wave's undulations are the most pronounced or powerful. However, the more powerful the associated wave's undulations get, the more ill-defined the wavelength becomes, which defines the particle's momentum. As a result, a strictly localised wave has an indeterminate wavelength, while its associated particle has a fixed position but no fixed velocity. A particle wave with a well-defined wavelength, on the other hand, is widely dispersed; the associated particle, albeit having a very accurate velocity, may be found practically anywhere. A very precise measurement of one observable entails a significant amount of uncertainty in the measurement of the other.
The uncertainty principle can also be represented in terms of the momentum and position of a particle. A particle's momentum is equal to the product of its mass and velocity. As a result, the product of a particle's momentum and position uncertainty equals h/(4+) or greater. The idea also holds true for other related (conjugate) pairings of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is taken equals h/(4+) or more. The uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it transitions to a more stable state are the same for an unstable atom or nucleus.
Are the uncertainty relations revealed by Heisenberg in 1927 simply the outcome of the equations utilised, or are they embedded in every measurement? Heisenberg used a thought experiment because he felt that all scientific concepts must be defined using actual or possible experimental observations.
Heisenberg imagined a microscope that achieves extremely fine resolution by illuminating with high-energy gamma rays. Although such a microscope does not exist at the moment, it may theoretically be built. Heisenberg envisaged seeing an electron and measuring its position using this microscope. He discovered that the electron's position and momentum obeyed the mathematically established uncertainty relation. The experiment had significant problems, which Bohr pointed out, but after they were fixed, the demonstration was completely compelling.
A free electron rests just beneath the centre of the microscope's lens in the revised version of the thought experiment (see the picture above). From the electron, the circular lens forms a cone with an angle of 2A. Gamma rays—high intensity light with the smallest wavelength—then illuminate the electron from the left. These have the maximum resolution because, according to a wave optics principle, the microscope can resolve (that is, "see" or distinguish) objects to a size of Dx, which is related to and to the gamma ray wavelength L by the expression:
Dx = L / (2sinA)
A gamma ray impacting an electron, on the other hand, provides it a kick in quantum mechanics, where a light wave can act like a particle. The electron is driven to the right when light is diffracted by the electron into the microscope lens. The gamma ray must be dispersed into any angle within the cone of angle 2A in order to be detected by the microscope. The gamma ray, like a particle, carries momentum in quantum physics. The wavelength is related to the total momentum p by the formula
p = h / L, where h is Planck's constant.
The total momentum in the x direction would be the sum of the electron's momentum p'x in the x direction and the gamma ray's momentum in the x direction in the extreme case of diffraction of the gamma ray to the right edge of the lens:
p'x + (h sinA ) / L', where L' is the wavelength of the deflected gamma ray.
In the other extreme, the observed gamma ray recoils backward, just hitting the left edge of the lens. The overall momentum in the x direction in this example is:
p''x - (h sinA ) / L''.
Because momentum is never lost, the final x momentum in each scenario must equal the beginning x momentum (it is conserved). As a result, the final x momenta are identical:
p'x + (h sinA ) / L' = p''x - (h sinA ) / L''
If A is tiny, the wavelengths are close to being the same, L' L" L. So there you have it.
p''x - p'x = Dpx ~ 2h sinA / L
We have a reciprocal link between the minimal uncertainty in the observed position, Dx, of the electron along the x axis and the uncertainty in its momentum, Dpx, in the x direction because Dx = L / (2 sinA ).
Dpx ~ h / Dx or Dpx Dx ~ h.
The "more than" indication can be used if there is more than the bare minimum of uncertainty.
This is Heisenberg's uncertainty relation for simultaneous measurement of an object's position and momentum, except for the factor of 4p and an equal sign.
Modern physicists warn that a careful examination of this image reveals an illusory classical mechanical interaction one step deeper, in the collision of the photon and the electron. In fact, despite its importance in the development and teaching of quantum theory, Heisenberg's microscope is not part of modern knowledge. Any depiction that resembles daily colliding items cannot represent the genuine quantum interaction and the genuine uncertainty associated with it. You must work through the formal mathematics that estimates probabilities for abstract quantum states to get the actual outcome. Experiments on these kind of interactions are still being carried out now. So far, the experiments have all confirmed Heisenberg's belief that no "genuine" microscopic classical collision occurs at the bottom.
The interpretation
So, how can we make sense of it all? Is this Heisenberg's own Principle being 'proven'? Yes and no, in my opinion. I'd say it's a combination of illustration and proof. The following are the key assumptions:
1. We can think of -ray photons, or any photon for that matter, as particles with momentum, and when they ‘collide,' or interact, with an electron, the photon will give that electron some momentum.
2. Because momentum is conserved, the total (linear) momentum before and after the collision must be the same for both particles–that is, (1) the incoming ray and the electron before the contact and (2) the released photon and the electron that receives the kick after the encounter.
3. We may connect (or associate, if you prefer) the wavelength of the -ray photon with its momentum p using the Planck relation or, equivalently for photons (since they have no mass), the de Broglie connection.
2.16.1 Single slit Experiment:
Interference, refraction, reflection, and diffraction are all examples of processes that occur as light travels through air. Diffraction of light occurs when it comes into contact with an obstruction.
The wavefront on the other side of the opening mimics the wave when light flows through a small opening that is comparable in size to the wavelength of the light. Please explain light diffraction and single slit diffraction, which occurs when light passes through a single slit.
When light passes through a single slit with a width (w) on the order of the wavelength of the light, we can witness single slit diffraction. The screen's diffraction pattern will be at a distance L >> w from the slit. The intensity is proportional to the angle.
We may examine the bending phenomena of light, or diffraction, in the single-slit diffraction experiment, which causes light from a coherent source to interfere with itself and generate a distinct pattern on the screen termed the diffraction pattern. When the sources are tiny enough to be comparable in size to the wavelength of light, diffraction occurs. This impact can be seen in the diagram below. The spreading out of huge apertures is minor and almost undetectable.
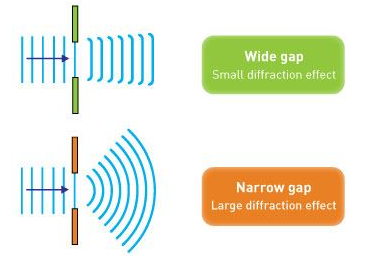
Single Slit Diffraction Formula
We shall assume the slit width a << D. xD is the separation between slit and source.
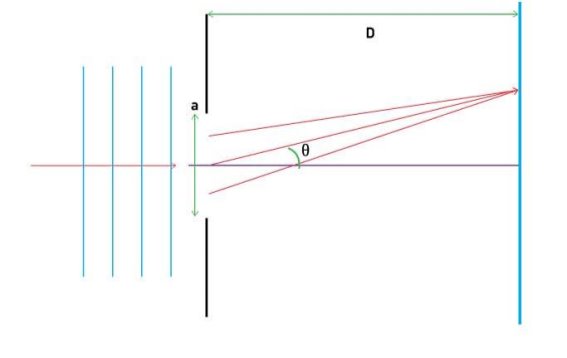
The angular position of any point on the screen will be determined by measuring from the slit centre, which divides the slit by lengths. To explain the pattern, we'll look at the condition of black fringes first. Let's also divide the split into equal-width zones.
lengths. To explain the pattern, we'll look at the condition of black fringes first. Let's also divide the split into equal-width zones. . Let's look at a pair of rays that come from a/2 distances apart, as indicated below.
. Let's look at a pair of rays that come from a/2 distances apart, as indicated below.

The path difference exhibited by the top two rays shown is:
∆L = a/2 sin θ
Remember that this is only a valid computation if D is really large. Check visit our article on Young's Double Slit experiment for more information on the approximation.
Any number of ray pairings that start at a distance of a2 from one another, such as the bottom two rays in the diagram, can be considered. Any arbitrary pair of rays separated by a2 can be taken into account. In a moment, we'll discover how important this trick is.
The path difference must induce destructive interference for a dark fringe; the path difference must be out of phase by 2. (represents the wavelength)
The first fringe is made up of
∆L = λ/2 = a/2 sin θ
λ = a sin θ
There is another ray at a distance a2 that can generate destructive interference for a ray emerging from any point in the slit.
As any ray emerging from a point has a counterpart that produces destructive interference, there is destructive interference at = sin1a. As a result, a dark fringe is created.
We can divide the slit into four equal sections of a/4 and use the same rationale for the next fringe. As a result, for the second minimum:
λ/2 = a/4 sin θ
2λ = a sin θ
Similarly, we can divide the slit into 2n sections for the nth fringe and utilise the following condition:
nλ = a sin θ
The Central Maximum
The maxima are located between the minima, and the width of the central maximum is equal to the distance between the first order minima on both sides of the screen.
The position of the minima determined by y (as measured from the screen's centre) is:
Tan θ ≈ θ ≈ y/D
For small ϑ,
Sin θ≈θ
⇒λ = a sin θ≈aθ
⇒θ = y/D = λa
⇒ y = λDa
The width of the central maximum is simply twice this value
⇒ Width of central maximum = 2λDa
⇒ Angular width of central maximum = 2θ = 2λa
The diffraction pattern and intensity graph is shown below.

2.17.1 The Quantum Harmonic Oscillator:
One drawback of this traditional formulation is that it is not universal. We can't use it to represent diatomic molecular vibrations, for example, because quantum effects are important. Using the classical statement to limit discussion of a "spring" constant between the atoms is a first step toward a quantum formulation. The potential energy function can be stated in a more general sense this way.
U(x) = ½ m ω2 x2
When this expression is used with the time-independent Schrdinger equation, the result is
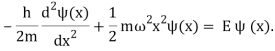
To solve (Figure), we need the wave functions to be symmetric around x=0 (the bottom of the potential well) and normalizable in order to discover the permitted energies E and their corresponding wave functions (x). When integrated throughout the complete range of x from to+, these requirements ensure that the probability density |(x)2 | must be finite. A more advanced course in quantum mechanics will cover how to solve (Figure); here, we will simply mention the results. The permitted energies are as follows:
En = ( n + ½ ) ℏω = 2n+1/2 ℏω, n = 0, 1, 2, 3, . . .
These energies (stationary states or states of defined energy) correlate to wave functions.
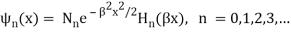
Where β = 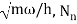 ,
,  is the normalization constant, and Hn(y) is a polynomial of degree n called a Hermite polynomial. The first four Hermite polynomials are
is the normalization constant, and Hn(y) is a polynomial of degree n called a Hermite polynomial. The first four Hermite polynomials are
H0 (y) = 1
H1 (y) = 2y
H2 (y) = 4y2 – 2
H3 (y) = 8y3 – 12y
In this section, we'll look at a few sample wave functions (Figure). As the primary number grows larger, the solutions alternate between even and odd functions around the axis.
The quantum harmonic oscillator's first five wave functions. Vertical lines illustrate the classical limitations of the oscillator's motion, which correspond to the classical turning points at x=A of a classical particle with the same energy as a quantum oscillator in the state shown in the image.
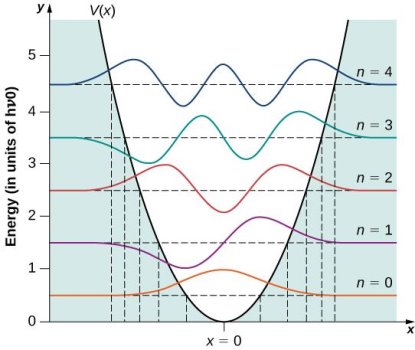
This solution has a number of intriguing properties. Unlike a classical oscillator, a quantum oscillator's observed energies can only have energy values given by (Figure). Furthermore, unlike a quantum particle trapped in a cage, the allowed energy levels are evenly distributed.
E = En+1 – En = 2(n+1)+1/2 ℏω – 2n+1/2 ℏω = ℏω = hf.
The smallest-energy quantum carried by the emitted photon must be hf when a particle coupled to such a system transition from a higher-energy state to a lower-energy state. Similarly, when a particle transitions from a lower-energy to a higher-energy state, the smallest-energy quantum that the particle may absorb is hf. Only multiples of this smallest-energy quantum can be absorbed or emitted by a quantum oscillator. In the blackbody radiation problem, this is consistent with Planck's notion for energy exchanges between radiation and cavity walls.
In three respects, the quantum oscillator varies from the traditional oscillator:
To begin with, a quantum oscillator's ground state is not zero. The lowest energy, according to conventional wisdom, is zero. Because of the omnipresent fluctuations that are a result of the Heisenberg uncertainty principle, all quantum-mechanical systems do not have a zero-energy state. The Heisenberg uncertainty principle would be violated if a quantum particle rested still at the bottom of the potential well, as both its momentum and position would have to be correct at the same time. As a result, the lowest-energy state must have errors in momentum and position, and a quantum particle's ground state must be above the bottom of the potential well.
Second, a particle in a quantum harmonic oscillator potential can be located outside the interval with a nonzero probability. A < x < +A. The particle would have no energy to be in this location under a traditional formulation of the problem. In the classically forbidden zone, the probability of finding a ground-state quantum particle is roughly 16 percent.
Third, the probability density distributions |ψn(x)|2 for a quantum oscillator in the ground low-energy state, ψ0(x), is largest at the middle of the well (x=0). For the particle to be found with greatest probability at the center of the well, we expect that the particle spends the most time there as it oscillates. This is opposite to the behavior of a classical oscillator, in which the particle spends most of its time moving with relative small speeds near the turning points.
For excited states, quantum probability density distributions vary in nature, becoming more like the classical distribution as the quantum number increases. Because the distribution of the first excited state of a quantum oscillator is different, we can see this change. |ψn(x)|2 As seen in, peaks near the turning points and vanishes at the equilibrium position (Figure). According to Bohr's correspondence principle, the quantum description of a harmonic oscillator converges to the classical description in the limit of large quantum numbers, as shown in (Figure). The quantum probability distribution for a quantum oscillator in this excited state is reasonably well approximated by the classical probability density distribution corresponding to the quantum energy of the n=12 state. For highly excited states, this agreement improves over time.
The probability density distribution for finding the n=12 quantum state of the quantum harmonic oscillator. The probability density distribution of a classical oscillator with the same energy is shown by the dashed curve.
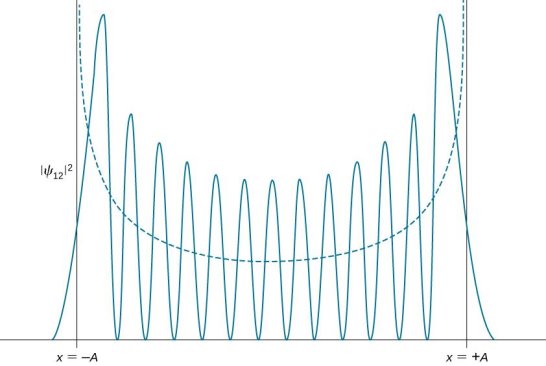
2.17.2 Estimate the Hydrogen Ground State Energy
The fundamentally uncertainty principle explains why the hydrogen atom (and other atoms) is so big. If the electron were to be contained in a smaller space,∆p would increase, causing p to increase on average. The energy would rise rather than fall.
The uncertainty principle can be used to calculate the minimal energy for hydrogen. This computation is not perfect, but it is more accurate than the Bohr model. The notion is that the radius must be greater than the positional spread, and the momentum must be greater than the momentum spread.
r ≥ ∆x
p ≥ ∆p = ℏ/2r
In terms of the dimensionless fine structure constant, this is our formula for potential energy. α.
V(r) = 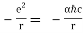
Let us calculate the energy.
E = 
And include the uncertainty principle's influence.
Pr = ℏ
E = 
E = 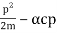
Differentiate in terms of p To get the minimum, set equal to zero.
DE/dp = p/m – 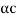 = 0
= 0
p = 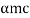

It's worth noting that potential energy is just (-2) times kinetic energy (as we expect from the Virial Theorem). The energy formula for the ground state is valid.
We can also make an educated guess at the radius.
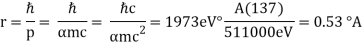
Hydrogen has no (orbital) angular momentum in its ground state. It is not travelling in a circular orbit as predicted by Bohr. The probability distribution of the electron is spread out over around 1. The energy would rise if it wasn't spread out.
The quantum physics-based Heisenberg uncertainty principle explains a number of things that classical physics could not explain. One of the applications is to demonstrate that an electron cannot exist within a nucleus. It goes like this:
Non-existence of electrons in the nucleus
Let us assume that electrons exist in the nucleus. As the radius of the nucleus in approximately 10-14 m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
∆x= 10-14 m
According to uncertainty principle,
∆x∆px =h/2∏
Thus ∆px=h/2∏∆x
Or ∆px =6.62 x10-34/2 x 3.14 x 10-14
∆px=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron, then the momentum of electron should be at least of this order, that is p=1.05*10-20 kg m/sec.
With such a large momentum, an electron's velocity must be similar to that of light. As a result, the following relativistic formula should be used to compute its energy.
E= √ m20 c4 + p2c2
E = √(9.1*10-31)2 (3*108)4 + (1.05*10-20)2(3*108)2
= √(6707.61*10-30) +(9.92*10-24)
=(0.006707*10-24) +(9.92*10-24)
= √9.9267*10-24
E= 3.15*10-12 J
Or E=3.15*10-12/1.6*10-19 eV
E= 19.6* 106 eV
Or E= 19.6 MeV
As a result, if the electron occurs in the nucleus, its energy should be in the range of 19.6 MeV. However, beta-particles (electrons) released from the nucleus during b-decay have energy of around 3 MeV, which differs significantly from the calculated value of 19.6 MeV. The second reason an electron cannot exist inside the nucleus is that no electron or particle in the atom has an energy greater than 4 MeV, according to experimental evidence.
Electrons have a negative charge, and if they can exist in the nucleus, the positive charges will neutralise them.
According to Heisenberg's uncertainty principle, the radius of atomic nuclei is 10-15 m, and if electrons exist in the nucleus, the maximum uncertainty in its position is 10-15 m.
Mass of the electron is 9.1 x 10-31 kg
No electron or particle in the atom possess energy greater than 4MeV
Hence the electrons do not exist inside the nucleus
2.19.1 Complementarity.
Complementarity is a concept in quantum mechanics that Niels Bohr considered to be a necessary property of the theory. According to the complementarity principle, objects have a set of complementary features that cannot all be viewed or measured at the same time. Position and momentum are an example of such a pair. One of quantum mechanics' foundational truths, according to Bohr, is that setting up an experiment to measure one of a pair of quantities, such as the position of an electron, excludes the possibility of measuring the other, despite the fact that understanding both experiments is required to characterise the object under study. The behaviour of atomic and subatomic things, according to Bohr, cannot be divorced from the measuring devices that form the framework in which they behave. As a result, there is no "one picture" that unifies the data gained in these various experimental situations, and only the "totality of the phenomena" as a whole can provide a complete description.
The failure of the operators that represent the observable quantities being measured to commute expresses complementarity mathematically:
Incompatible observables are observables that correlate to non-commutative operators. There can't be a comprehensive set of shared eigenstates for incompatible observables. It's worth noting that there may be some simultaneous eigenstates of () A and () B, but not enough to form a complete basis. The canonical commutation relation is defined as follows:
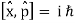
This suggests that this holds true for both position and momentum. Similarly, any two of the spin observables specified by the Pauli matrices have an equivalent relationship; measurements of spin along perpendicular axes are complimentary. Using mutually unbiased bases, which give complementary observables defined on finite-dimensional Hilbert spaces, this has been applied to discrete observables with more than two possible outcomes.
The principle of complementarity, or dialecticism, is a second key component of quantum physics. Is light a wave or a particle? Complementarity is defined as the recognition that though particle and wave behaviour are mutually exclusive, both are required for a complete explanation of all occurrences.
2.19.2 Uncertainty.
With difficulties of wave/particle duality, classical physics was on shaky ground, but the discovery of the uncertainty principle took them completely off surprise.
The uncertainty principle, also known as the Heisenberg Uncertainty Principle or Indeterminacy Principle, was proposed by German physicist Werner Heisenberg in 1927, and states that an object's position and velocity cannot be measured precisely at the same time, even in theory. In fact, in nature, the concepts of absolute position and exact velocity have no relevance.
This principle is not obvious from everyday life. Because the uncertainties suggested by this concept for common objects are sufficiently small to be noticed, it is simple to measure both the position and velocity of, say, a car. The full rule states that the product of position and velocity uncertainties is equal to or larger than a minuscule physical amount, or constant (about 10-34 joule-second, the value of the quantity h (where h is Planck's constant)). Only for atoms and subatomic particles with extremely small masses can the product of uncertainty become important.
Any attempt to precisely measure the velocity of a subatomic particle, such as an electron, will cause it to move around in an unpredictable manner, rendering a simultaneous measurement of its position useless. This finding originates from the intimate relationship in nature between particles and waves in the world of subatomic dimensions, and has nothing to do with shortcomings in the measurement devices, procedure, or observer.
Every particle has a wave connected with it, and every particle behaves in a wavelike manner. The particle is most likely to be located where the wave's undulations are the most pronounced or powerful. However, the more powerful the associated wave's undulations get, the more ill-defined the wavelength becomes, which defines the particle's momentum. As a result, a strictly localised wave has an indeterminate wavelength, while its associated particle has a fixed position but no fixed velocity. A particle wave with a well-defined wavelength, on the other hand, is widely dispersed; the associated particle, albeit having a very accurate velocity, may be found practically anywhere. A very precise measurement of one observable entails a significant amount of uncertainty in the measurement of the other.
The uncertainty principle can also be represented in terms of the momentum and position of a particle. A particle's momentum is equal to the product of its mass and velocity. As a result, the product of a particle's momentum and position uncertainty equals h/(2) or greater. The principle holds for other (conjugate) pairings of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is taken equals h/(2) or greater. The uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it transitions to a more stable state are the same for an unstable atom or nucleus.
W. Heisenberg discovered the uncertainty principle, which expresses the impact of wave-particle duality on the properties of subatomic things. Consider the concept of momentum in the microscopic world, which is similar to a wave. The wavelength of a wave determines its momentum. A wave packet, such as a photon or an electron, is made up of several waves. As a result, it must be made up of a variety of momentums. But how is it possible for one object to have several momentums?
Of course, once a particle's momentum is measured, a single momentum is observed. Momentum before the observation, like fuzzy position, is inherently ambiguous. The uncertainty principle states that certain quantities, such as position, energy, and time, are unknown save through probability. The uncertainty principle states that accurate knowledge of complementarity pairings is impossible in its purest form. You can measure an electron's location but not its momentum (energy) at the same time, for example.
The principle of complementarity, which "implies the impossibility of any clear separation between the behaviour of atomic objects and their interaction with the measuring devices that serve to specify the conditions under which the phenomena arise," is a defining element of quantum physics. As a result, "data gathered under various experimental conditions cannot be comprehended within a single picture, but must be treated as complimentary in the sense that only the entirety of the events exhausts the possible knowledge about the objects," according to the authors. During the 1930s, the majority of scientists increasingly adopted this interpretation of quantum physics, which indicated a different perspective of the significance of physical explanation.
The uncertainty principle can be expressed mathematically as follows, where x' denotes position and p' denotes momentum:
∆x∆p > h/2π
Next to E=mc2, this is possibly the most well-known equation in physics. It essentially states that the sum of the errors in position and momentum must always be bigger than Planck's constant. So, you can measure an electron's position to a certain degree of precision, but its momentum will fall within a very wide range of values. Similarly, you can precisely measure momentum, but its location is unknown.
Notice that this is not a different version of the measurement problem; for a quantum particle, the combination of position, energy (momentum), and time is really indeterminate until a measurement is done (then the wave function collapses).
Also, because Planck's constant, h, is so small, the uncertainty principle is irrelevant to macroscopic objects (10-34). A thrown baseball, for example, has a positional uncertainty of 10-30 millimetres.
When we raise the question, "Is our knowledge of reality unlimited?" we comprehend the depth of the uncertainty principle. No, because the uncertainty principle implies that Nature contains inherent uncertainty, indeterminacy, and unpredictability.
Key takeaway:
- In quantum physics, Heisenberg's uncertainty principle is a crucial concept. It goes something like this: if we know exactly where a particle is (the uncertainty of position is tiny), we know nothing about its momentum (the uncertainty of momentum is huge), and vice versa.
- According to the classical Uncertainty Principle, a function and its Fourier transform cannot be highly focused at the same time. This has the conceptual implication in quantum mechanics that determining a particle's position and momentum at the same time is impossible (Heisenberg Uncertainty Principle).
References:
1.Quantum Mechanics: Theory and Applications, A.K.Ghatakand S. Lokanathan,(Macmillan)-2004
2. Introduction to Quantum Theory, David Park (Dover Publications)-1974
3. Theory and Problems of Modern Physics, Schaum‘s outline,R.Gautreau and W.Savin- (Tata McGraw-Hill) 2nd Edition
4. Physics for scientists and engineer with Modern Physics-Jewell and Serway -(CENGAGE Learnings) 2010.
5. Modern Physics of Atoms and Molecules Bransden and Joachim (PearsonIndia)-2003
Unit - 2
Wave Packet
2.1.1 Superposition and Interference
The majority of waves do not appear to be straightforward. They resemble the waves depicted in Figure rather than the ordinary water wave discussed in Waves. (Simple waves have a sinusoidal shape because they are formed by a simple harmonic oscillation.) Complex waves are more intriguing, even beautiful, but they appear to be intimidating. The majority of waves appear complex because they are made up of multiple simple waves that have been added together. Fortunately, the principles for adding waves are straightforward.

Figure 1.
When two or more waves arrive at the same location at the same time, they superimpose on each other. When waves collide, the disturbances of the waves are superimposed, a phenomenon known as superposition. Each disruption is associated with a force, which adds up. If the disturbances all follow the same path, the final wave is simply the sum of the individual waves' disturbances—that is, their amplitudes add. Figures 2 and 3 show superposition in two different situations, both of which yield straightforward results.
Figure 2 depicts two similar waves arriving at the same time and in phase. The crests and troughs of the two waves are perfectly aligned. The result of this superposition is pure constructive interference. Pure constructive interference generates a wave with double the amplitude of the component waves but the same wavelength since the disturbances add up.
Figure 3 illustrates two identical waves arriving out of phase—that is, with their crests and troughs precisely aligned—producing pure destructive interference. The resulting amplitude for pure destructive interference is 0 since the disturbances are in the opposite direction for this superposition—the waves entirely cancel.
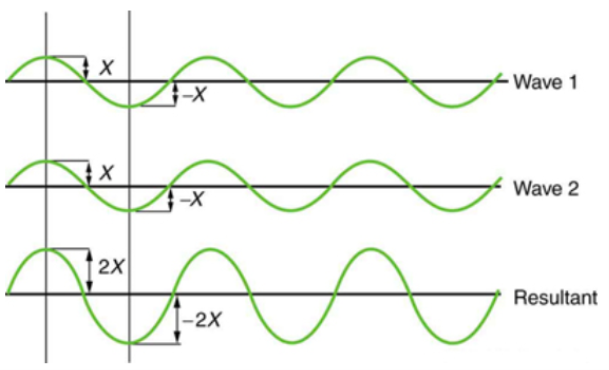
Figure 2: When two identical waves collide, the result is a wave with twice the amplitude but the same wavelength.
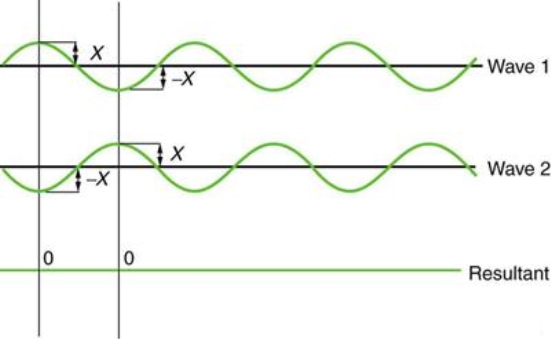
Figure 3: When two identical waves collide, the result is zero amplitude, or total cancellation.
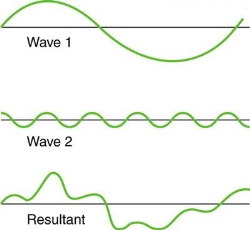
Figure 4. Superposition of non-identical waves exhibits both constructive and destructive interference.
While pure constructive and destructive interference do occur, they require identical waves to be exactly aligned. Most waves superpose, resulting in a mix of constructive and destructive interference that varies from location to place and time to time. A stereo's sound, for example, can be powerful in one place yet muted in another. Sound waves add partially constructively and partially destructively at different locations when their loudness varies. Sound waves are created by at least two speakers in a stereo, and sound waves can reflect off walls. All of these waves are stacked on top of each other. The combined whining of aeroplane jets perceived by a stationary passenger is an example of noises that change over time from constructive to detrimental. As the sound from the two engines changes in time from constructive to destructive, the total sound might fluctuate in amplitude. These are waves that are similar to each other. Figure 4 depicts an example of the superposition of two different waves. Again, the disturbances add and subtract, resulting in a wave that appears more intricate.
2.1.2 Principle of Superposition of Waves
Consider two waves travelling in opposite directions along the same stretched string, as shown in the diagram above. At any given time, we can see images of waveforms in the string. The algebraic total of the displacements owing to each wave is found to be the net displacement of every element of the string at any given time.
Let's imagine two waves are travelling alone, and any element of these two waves' displacements can be represented as y1(x, t) and y2(x, t) (x, t). The resultant displacement can be written as y when these two waves collide (x,t).
y (x, t) = y1(x, t) + y2(x, t) = y3(x, t) = y4(x, t) = y5(x, t) = y (x, t)
We can sum the overlapped waves algebraically to generate a consequent wave using the principle of superposition. Let us say that the wave functions of moving waves are as follows:
y1 = f1(x–vt),
y2 = f2(x–vt)
……….
yn = fn (x–vt)
Then the wave function describing the disturbance in the medium can be described as
y = f1(x – vt)+ f2(x – vt)+ …+ fn(x – vt)
Or, y=∑ i=1 to n = fi (x−vt)
Let us consider a wave travelling along a stretched string given by, y1(x, t) = A sin (kx – ωt) and another wave, shifted from the first by a phase φ, given as y2(x, t) = A sin (kx – ωt + φ)
From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A.
Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement y(x, t) = A sin (kx – ωt) + A sin (kx – ωt + φ)
The above equation can be written as,
y(x, t) = 2A cos (ϕ/2). Sin (kx −ωt + ϕ/2)
The resulting wave is a sinusoidal wave travelling in the positive X direction, with a phase angle half that of the component waves and an amplitude equal to [2cos/2] times the original waves' amplitudes.
2.1.3 Condition for Destructive Interference
Phase difference = (2n – 1)π
Path difference = (2n – 1)λ/2
I = Imin
Imin = I1 + I2 – 2 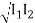
2.1.4 Standing Waves
Waves don't always appear to move; instead, they only vibrate in situ. Unmoving waves, for example, can be seen on the surface of a glass of milk in the refrigerator. The refrigerator motor's vibrations create waves on the milk that oscillate up and down but do not appear to travel over the surface. These waves are created by the superposition of two or more moving waves, such as the two identical waves flowing in opposite directions seen in Figure 5. The waves pass through each other, adding to the disruptions as they travel. When the amplitude and wavelength of two waves are the same, they alternate between constructive and destructive interference. The outcome is known as a standing wave because it resembles a wave that is stationary. Standing waves can be seen on the surface of a glass of milk. Other standing waves can be found in guitar strings and organ pipes. The two waves that generate standing waves in the glass of milk could be caused by reflections from the glass's side.
A detailed examination of earthquakes reveals evidence of resonance, standing waves, and constructive and destructive interference situations. A building may be vibrated for several seconds at a frequency that matches the natural frequency of vibration of the building, resulting in a resonance that causes one building to collapse while surrounding buildings remain intact. Buildings of a specific height are frequently destroyed, whereas taller structures remain standing. The height of the building corresponds to the conditions for creating a standing wave at that height. At specific spots along the Earth's surface, constructive interference occurs as seismic waves reflect off denser rocks. Areas near to the epicentre are frequently unaffected, whereas areas further away are.
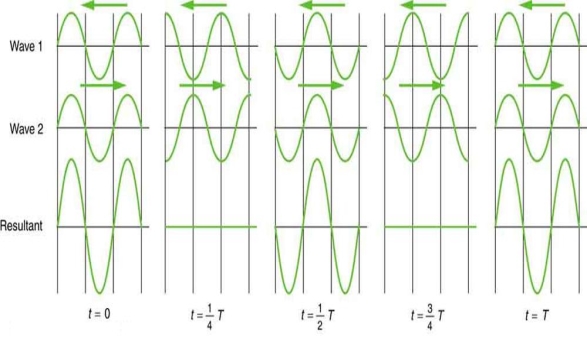
Figure 5: A standing wave is formed when two similar waves moving in opposite directions are superimposed. The oscillations occur at predetermined points in space and are caused by constructive and destructive interference.
Standing waves can also be formed on musical instrument strings as a result of wave reflections from the ends of the string. Three standing waves can be formed on a string that is fastened at both ends, as seen in Figures 6 and 7. In a standing wave, nodes are the sites where the string does not move; more broadly, nodes are the sites where the wave disturbance is zero. Because the string cannot move, the fixed ends of strings must also be nodes. In standing waves, the term antinode refers to the place of maximum amplitude. Standing waves on strings have a frequency that is proportional to the disturbance's propagation speed vw. The distance between the spots where the string is fixed in place determines the wavelength.
The fundamental frequency, which is the lowest frequency, is so for the longest wavelength, which is 1 = 2L. f1=vw1=vw2f1=v The overtones or harmonics in this situation are multiples of the fundamental frequency. Because 2 = L, the first harmonic can be simply determined, as shown in Figure 7. As a result, f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1f2=vw2=vw2L=2f1. In the same way, f3 = 3f1 and so on. The tension in the string can be adjusted to vary all of these frequencies. The higher the frequency, the higher the vw and the greater the stress. Anyone who has ever watched a string instrument being tuned would recognise this observation. Standing waves are critical to many resonance occurrences, such as sounding boxes on string instruments, as we will discover in later chapters.
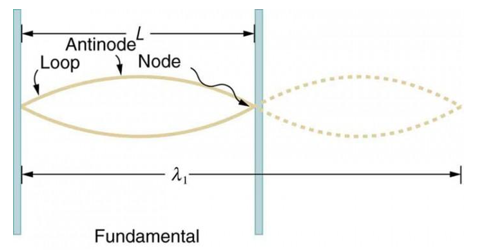
f1 = 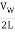

Figure 6. The figure shows a string oscillating at its fundamental frequency.
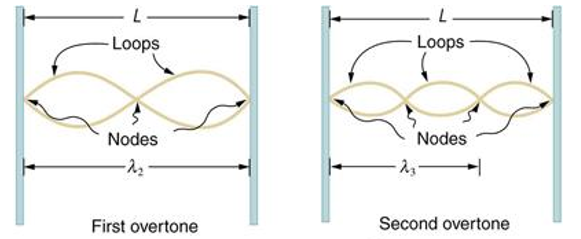
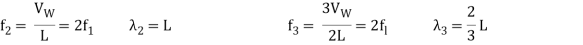
Figure 7. First and second harmonic frequencies are shown.
2.1.5 Beats
On a piano, striking two neighbouring keys generates a warbling sound that is normally considered unpleasant. The culprit is the superposition of two waves with comparable but not identical frequency. Another example can be seen during taxiing in jet aircraft, particularly the two-engine version. The combined sound of the engines increases and decreases in volume. Because the sound waves have comparable but not identical frequencies, the loudness varies. As the two waves travel in and out of phase, the discordant warbling of the piano and the varying loudness of the jet engine noise are both due to alternately constructive and destructive interference. This is visually depicted in Figure 8.
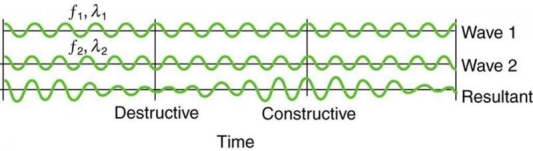
Figure 8 shows how beats are created by superimposing two waves with slightly different frequencies but identical amplitudes. The waves alternate between constructive and destructive interference over time, resulting in a wave with a variable amplitude.
The frequency of the wave that results from the superposition of two waves of comparable frequency is the average of the two. The amplitude of this wave swings in beats, at a frequency called the beat frequency. The beat frequency can be calculated by combining two waves together analytically. It's worth noting that at one point in space, a wave can be represented as
x = X cos (2πt/T) = X cos (2πft)
The frequency of the wave is f=1/T. When two waves with different frequencies but equal amplitudes are combined, the outcome is x = x1 + x2. x = Xcos(2 f1t) + Xcos(2 f2t), to be precise.
It can be demonstrated that x =2X cos(fBt)cos(2 favet) using a trigonometric identity, where fB = |f1 f2| is the beat frequency and fave is the average of f1 and f2. These findings indicate that the resultant wave has double the amplitude and average frequency of the two superimposed waves, but its overall amplitude changes at the beat frequency fB. The amplitude is effectively increased and decreased by the first cosine term in the formula. The wave with frequency fave is the second cosine term. This conclusion holds true for all forms of waves. If it's a sound wave, though, and the two frequencies are similar, we'll hear an average frequency that grows louder and softer (or warbles) as the beat frequency approaches.
While beats might be bothersome in auditory noises, we will see that they have a wide range of applications. Observing beats is a great technique to compare frequencies that are comparable. Ultrasonic imaging and radar speed traps are two seemingly unrelated applications of beats.
Key takeaway:
- The combination of two waves at the same spot is known as superposition.
- When two identical waves are superimposed in phase, constructive interference occurs.
- When two identical waves are overlaid perfectly out of phase, destructive interference results.
- A standing wave is created when two waves collide, resulting in a wave that changes in amplitude but does not propagate.
- In standing waves, nodes are sites where there is no motion.
- An antinode is the point at which a standing wave reaches its maximum amplitude.
- Waves on a string are resonant standing waves with a basic frequency that can have overtones or harmonics at higher multiples of the fundamental.
- When waves of similar frequency f1 and f2 are overlaid, beats occur. The oscillation frequency of the resulting amplitude is given by fB = |f1 f2|.
2.2.1 Harmonic Waves and Phase Velocity
The equation describes a one-dimensional harmonic wave (Figure 1).
u(x, t) = A0 sin (ωt – k x + φ)
Where A0 represents the wave amplitude, is the circular frequency, k represents the wave number, and is the starting, constant phase. The phase is the argument for the sine function, which is (x, t) = t - kx +. The spatial frequency or propagation constant are other names for the wave number.
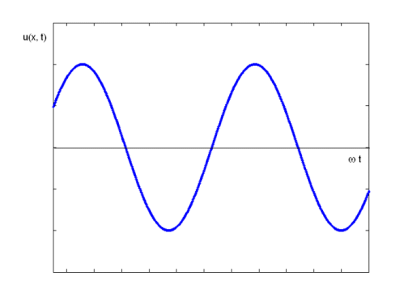
Figure 9: Harmonic Wave
This is a wave that is monochromatic (one frequency). In nature, there are no waves that are strictly monochromatic. For example, the wave's generating source could move significantly, resulting in spurious frequencies.
These waves propagate without warping in most cases. In other words, the phase (x, t) is constant:
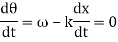
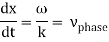
vphase is the phase velocity for a wave.
These waves are ineffective in terms of transmitting information. They remain the same in time and place. In order to transfer information, something must be modulated, such as frequency or amplitude. The resulting wave could be a wave packet, which is a disturbance that acts across a short distance. This wave packet can be thought of as a Fourier series or integral, which is a superposition of a number of harmonic waves.
2.2.2 Group Velocity
Something more than a basic harmonic wave is required to transmit information. The superposition of several such waves of differing frequencies, on the other hand, can produce a "envelope" wave and a carrier wave within the envelope. The envelope has the ability to convey data. The superposition of two harmonic waves with very near frequencies (1 2) and the same amplitude is a simple example. The motion's equations are as follows:
u(x, t) = A0 . Cos (ω1 t – k1 x) + A0 . Cos (ω2t – k2 x)
= 2 A0 . Cos ( 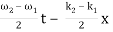 ) × cos (
) × cos ( 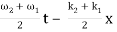 )
)
= u1 × u2
Figure depicts the plot of such a wave.
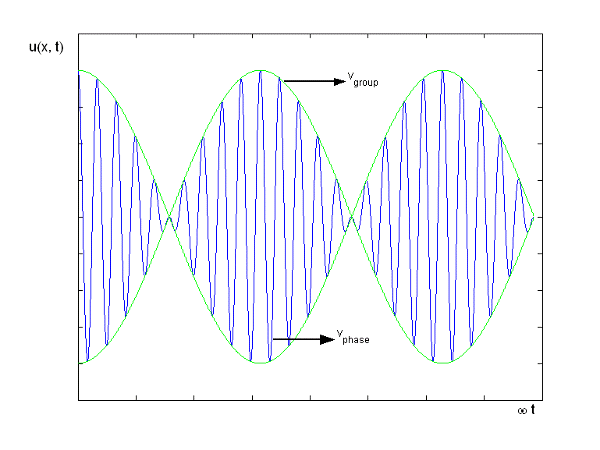
Figure 10: Group Velocity
u1 controls the envelope (the green line), which moves at the group velocity. The phase velocity of the carrier wave (the blue line) is provided by u2. The wave packet travels at the same speed as the rest of the group. It is the envelope that contains the data. The velocity of a group and the velocity of a phase are not always the same. The velocity of a group is given by,
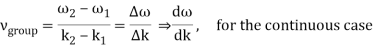
Rayleigh's formula links phase and group velocity together.
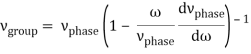
Group velocity equals phase velocity if the derivative term is zero. There is no dispersion in this scenario. When the different phase velocities of the envelope components cause the wave packet to "spread out" over time, this is called dispersion. The wave packet's (or envelope's) components separate to the point that they can no longer combine to complete the envelope.
2.3.1 Wave Packet Solution
Since the wave equation's travelling wave solution
y(x, t) = A sin (kx – ωt)
Is true for every value of the wave parameters, and since any superposition of solutions is likewise a solution, a wave packet solution can be constructed as a sum of travelling waves:
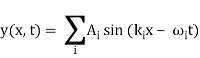
It is standard practise to express the amount 2/ by k, also known as the wave vector. The sum is replaced by an integral for a continuous range of wave vectors k:
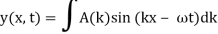

2.3.2 Wave Packet Details
Like a pulse on a string, a wave packet solution to the wave equation must have a variety of frequencies. The broader the range of frequency components necessary for quick transient behaviour, the shorter the pulse in time. For classical waves, this need can be expressed as a form of uncertainty principle:

The exact figures depend on how the pulse width is defined, however making brief pulses necessitates a large frequency bandwidth. The uncertainty principle in quantum mechanics is analogous to this.
2.3.3 Wave Packets from Discrete Waves
When discrete travelling wave solutions to the wave equation are concatenated, a wave packet that begins to localise the wave can be created. The quantum mechanical uncertainty principle mirrors this property of classical waves.

2.3.4 The Wave-Particle Puzzle
De Broglie's explanation of the Bohr atom quantization principles, together with Davisson and Germer's unintentional discovery of electron diffraction scattering, offer a compelling case for the electron's wave nature. Even so, the electron can act like a particle at times. An electron has a certain mass and charge, may move slowly, and can pass through a variety of devices, including a gun and a screen.
So, what's the connection between the wave and particle perspectives? Both were always present, according to De Broglie. He dubbed the wave a pilot wave, and he believed it steered the particle's motion. Unfortunately, the point of view leads to inconsistencies. The common current view is that the relative likelihood of detecting the particle at any position is determined by the strength of the wave (measured by the square of its amplitude).
The probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of the magnetic field vector. This interpretation, first proposed by Max Born in 1926, is analogous to the relationship between the electromagnetic field and quanta—the probability of finding a quantum (photon) at any point is proportional to the energy density of the field at that point, which is the square of the electric field vector plus the square of The de Broglie wave function associated with the electron is written in standard notation as (x,t). The relative probability of finding the electron in a narrow period of length x near location x at time t is thus |(x,t)|2dx. (For the sake of simplicity, we limit the electron's movement to one dimension.) The generalisation is easy to understand.)
2.3.5 Keeping the Wave and the Particle Together?
Suppose following de Broglie we write down the relation between the "particle properties" of the electron and its "wave properties":
 mv2=E=hf, mv=p=h/λ.
mv2=E=hf, mv=p=h/λ.
It would seem that we can immediately figure out the speed of the wave, just using λf=c′, say.
We find:
λf=hmv⋅12mv2h=12v.
What? The speed of the wave is half the speed of the electron? How could they stay together? What's wrong with this calculation?
2.3.6 Localizing an Electron
To solve this question, consider the wave function corresponding to an electron moving in a vacuum tube, for example. The electron exits the cathode, travels through the vacuum, and collides with a grid's anode. It is travelling through the vacuum at a moment in this process, and the wave function must be nonzero across some volume, but zero in places the electron has not yet reached and zero in places it has definitely gone.
The electron, on the other hand, has a precise momentum if it possesses a precise energy, such as fifty electron volts. This necessitates the existence of a definite wavelength for the wave. However, the only wave with an exact wavelength is (x,t)=Asin(kxt).
Where k=2/ and =2f are constants. The issue is that this plane sine wave stretches to infinity in both spatial directions, therefore it can't represent a particle with a non-zero wave function in a finite region of space.
As a result, we must superpose waves of different wavelengths to represent a confined particle. Using the trigonometric addition formula, superpose two waves with somewhat varying wavelengths to demonstrate the principle:
Sin((kk)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((k+k)x(+)t)=2 sin((
Sin(kxt)cos((k)x()t sin(kxt)cos((k)x()t sin(k)x()t sin(k)x()t sin
The phenomena of beats between waves of similar frequency is represented by this formula. The first term, sin(kxt), oscillates at a frequency that is the average of the two. The slowly fluctuating second term, which oscillates once over a spatial range of order /k, modulates it. This is the distance at which waves that were in phase at the start turn fully out of phase. Of course, if the distance between the waves is increased by order /k, the waves will re-synchronize.
That is, combining two close frequencies creates a series of packets, or beats, from the continuous wave. A single packet is required to describe a single electron travelling through space. This can be accomplished by superposing waves with a continuous distribution of wavelengths, or wave numbers in the order of k, for example. The waves will be out of phase after a distance of order /k, but because they have so many distinct wavelengths, they will never be able to get back in phase. (All of this is adequately treated in Fourier transform theory.) We're just attempting to make it plausible right now.)
2.3.7 The Uncertainty Principle
It should be evident from the above argument that to construct a wave packet representing an electron localized in a small region of space, the component waves must get out of phase rapidly. This means that their wavelengths can't be too close. In reality, simply considering the two beating waves allows for a semi-quantitative approximation of the wavelength spread required.
A packet localized in a region of extent Δx can be constructed of waves having k 's spread over a range Δk, where Δx∼π/Δk.
Now, k=2π/λ, and p=h/λ, so k=2πp/h.
Therefore, Δk=2πΔp/h, and Δx∼π/Δk∼h/Δp, (dropping the factor of 2).
Thus:
Δx⋅Δp∼h.
This is Heisenberg's Uncertainty Principle, which we shall analyze in more detail in later lectures.
2.4.1 Gaussian wave packets:
We write a free wave packet as a linear combination of plane waves

Where the momentum amplitudes absorb the time evolution of each plane wave, given by (k)=k2/2m (k,t). As a Gaussian, we chose the amplitude for the various plane waves.
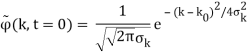
The momentum distribution |φ~(k,t)|2| is a Gaussian of width σk and mean k0 for all t.
At t=0, where the momentum amplitudes are real, the probability density of the resulting wave packet at is a Gaussian of width σx=1/2σk, i.e., it is as localized as is allowed by the Heisenberg principle (σx=1/2). The probability distribution stays Gaussian for all t. As the momentum amplitudes become complex, its width 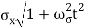 increases with a characteristic time 1/ωσ=2m
increases with a characteristic time 1/ωσ=2m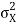 /ℏ, and its center moves with the group velocity vg=ℏk0/m.
/ℏ, and its center moves with the group velocity vg=ℏk0/m.
The genuinely quantum mechanical aspect is the behaviour at t=0: We can't locate the particle any farther than the uncertainty principle allows. It is a direct result of the wave-description resulting directly from the Fourier transform's features. For long periods of time, the behaviour is consistent with that of an ensemble of classical particles with a Gaussian momentum distribution: A particle with momentum k will be at x(k,t)=kt/m at time tt. We get the probability density of discovering a classical particle by solving for k and inserting it into the momentum distribution.
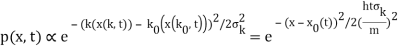
Which is a Gaussian of width σxωσt centered at
x0(t) = hk0t/m
The probability distribution for the wave packets has been plotted so far. We'll need a mechanism to visualise complex functions if we wish to draw the wave function. We could just plot the real and imagined parts of it. However, demonstrating its modulus (the square of which yields the probability density) and phase is more enlightening. It's simple to plot the modulus. We use colours to depict the phases, starting with red for phase zero, progressing through the rainbow colours as the phase progresses, and finally returning to red for phase two. The representation of a plane wave is shown below as an example. 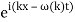
The propagating free Gaussian wave packet's wave function is given by
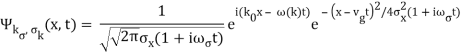
The phase of a Gaussian wave packet with a small momentum distribution is virtually identical to a plane wave with momentum k0.
The phase no longer has a well-defined wave length as the momentum dispersion widens. The phase has wave length 2/k0 around the maximum at x(t)=vgt.
2.4.2 Linear combination of wave packets (Schrödinger cat states)
Looking at linear combinations of Gaussian wave packets is equally fascinating. It's important to remember that we're still dealing with single-electron wave functions, which describe a single electron in a superposition state rather than two!
=GWP(k0,k,x0), What determines the interference pattern's wave length? Why is the amplitude of the wave packets in the middle always zero?
This is the same wave function as before, but with the probability density displayed. After the wave packets have travelled past each other, what happens to them? What would happen if their rate of broadening was slower than their velocity?
This wave packet flows slower and has a significantly larger momentum distribution. Why do the wave function's oscillations continue?
2.4.3 Reflection at hard wall
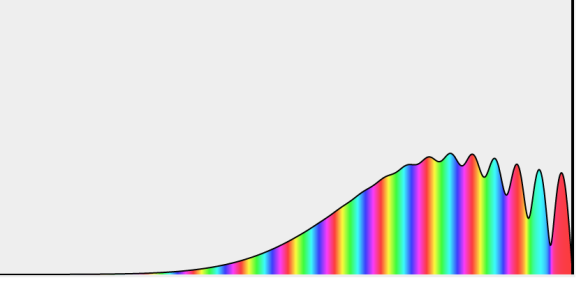
We can see how a Gaussian wave packet is reflected at a hard wall by looking at just one half of the above superpositions. Compare this approach to the electrostatics method of image charges.
Same thing, except this time for a wave packet with a significantly wider momentum dispersion.
2.5.1 Localization Of Waves; Relation To Uncertainty Principle
To grasp the uncertainty principle, one must first grasp a difficult but crucial concept concerning wave localizability: a wave can only be localised if distinct wavelengths are superposed. Consider a single-wavelength “pure” wave, as depicted below.

It's a perfect sine wave that repeats eternally with a perfectly defined fixed wavelength that's spread out in space. If it's an electron wave, it's a particle travelling at a constant speed with a well-defined momentum, as defined by the de Broglie equation: p = h/. What happened to the electron? It can be found anywhere—or is equally likely to be found anywhere (along the infinite dimension of the wave). 1 Its positional uncertainty is unlimited; its momentum (and wavelength) uncertainty is zero. This is a bizarre circumstance that, at the very least, adheres to the uncertainty principle. If the product of two uncertainties remains constant, one of them can only grow endlessly tiny if the other remains constant.
Consider the outcome of superposing many wavelengths. The superposition of two waves with wavelength differences of 10% is depicted below.
The waves interfere destructively five cycles after the point of maximum reinforcement. They reinforce again five cycles later. Partial localization of the wave is caused by the alternating of constructive and destructive interference, which causes the wave to bunch together into zones of around 10 wavelengths in length. This result contains an important indication concerning the uncertainty principle. The mixing of wavelengths required for partial localisation has resulted in momentum uncertainty.
By superposing a large number of distinct wavelengths, more localisation can be attained. The effect of mixing six separate pure waves, each with a wavelength difference of 2%, is shown in the diagram below.

The entire wavelength spread stays at 10%, with 5% on either side of the average wavelength. As a result, we can give a momentum uncertainty of around 5% of the dominant momentum:
Δp ≅ 0.05p.
Here, p denotes an average momentum, which is related to an average wavelength by the formula p = h/. The wave is better localised in the illustration because of the six-fold superposition. (The wave might be totally confined if all conceivable wavelengths within the provided span were superposed.) Its amplitude would sink to zero outside of a specified region of space, never to rise again.) The extent of the wave on either side of its center—roughly five wavelengths in the figure—represents the uncertainty of position:
Δx ≅ 5λ
In this case, the product of position and momentum uncertainty is
ΔxΔp ≅ 0.25λp.
Because the right-hand product p equals Planck's constant h, this equation can be written as
ΔxΔp ≅ 0.25h.
The numerical component 0.25 in this equation has no special relevance because we have made reasonable estimates of the uncertainty. The right side of the uncertainty equation, according to the technical definition of uncertainty employed in quantum mechanics, is exactly h/2, or, as stated in Essay Q6.
Since a 10% difference in momentum “crushed” the wave packet from infinite to just over 10 wavelengths, it's plausible to assume that momenta changing by almost 100% would be required to reduce the packet to a single cycle. This is correct. Maximum localization, x /2, necessitates superposition of wavelengths (and momenta) that differ by a factor of two. Then p p/2 p pppppppppp Because neither of these variables is clearly defined for a localised wave, p and refer to average values of momentum and wavelength in these equations. Again, the product xp is nearly identical to the product p, which is equal to Planck's constant.
The hydrogen atom contains an actual three-dimensional wave function, as opposed to the hypothetical one-dimensional waves outlined before. Its amplitude is depicted below along a radial line drawn across the atom's diameter.
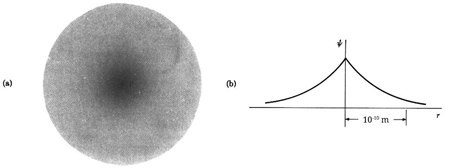
This electron wave function is highly confined, with only one oscillation cycle from one side of the atom to the other. This wave function's shape, with its central peak, is very different from that of a pure sine wave. With the appropriate mix of infinitely many wavelengths, any shape can be "fashioned."
The Heisenberg uncertainty principle is a result of the wave nature of particles, as demonstrated by this discussion of wave superposition. It is no more profound, and in this form, it says nothing more or less than the de Broglie equation for material particle wavelength. Measurement uncertainty stems mostly from the nonlocalizability of waves.
2.5.2 Two Examples of Localized Wave Packets
Lets now try two examples of a wave packet localized in k and properly normalized at t=0.
- A “square” packet: A(k) =
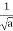 for k0 – a/2 < k < k0 + a/2 and 0 elsewhere.
for k0 – a/2 < k < k0 + a/2 and 0 elsewhere. - A Gaussian packet: A(k) = (2a/π)1/4 e-α (k – k0)2.
These are both localized in momentum about p= hk0.
Check the normalization of (1).
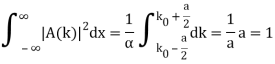
Check the normalization of (2) using the result for a definite integral of a Gaussian
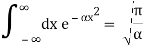
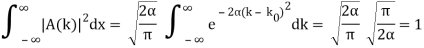
So now we take the Fourier Transform of (1) right here.
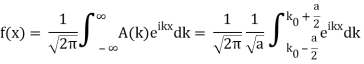
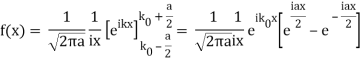

Note that 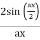 is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this
is equal to 1 at x = 0 and that it decreases from there. If you square this, it should remind you of a single slit diffraction pattern! In fact, the single slit gives us a square localization in position space and the F.T. Is this 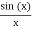 function.
function.
The Fourier Transform of a Gaussian wave packet
A(k) = 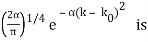
f(x) = 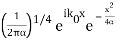
Also a Gaussian. We will show later that a Gaussian is the best one can do to localize a particle in position and momentum at the same time.
In both of these cases of f(x) (transformed from a normalized A(k) localized in momentum space) we see
- A coefficient which correctly normalizes the state to 1,
- eik0x - a wave corresponding to momentum hk0,
- And a packet function which is localized in x.
We've found states that represent a single free particle, which was our goal. We can have states that are localised in both position and momentum space, as we can see. We did this by creating wave packets, which are superpositions of definite-momentum states. While the wave packets are localised, they do have some width. x and in p.
2.6.1 Evolution of Wave Packets
We have
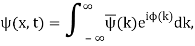
Where
ϕ(k) = kx – ω(k) t.
The function 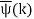 is obtained by Fourier transforming the wavefunction at t = 0. Now,
is obtained by Fourier transforming the wavefunction at t = 0. Now, 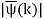 is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain
is strongly peaked around k = k0. Thus, it is a reasonable approximation to Taylor expand ϕ(k) about k0. Keeping terms up to second-order in k – k0, we obtain

Where
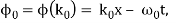
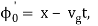
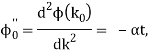
With
μ : ω (k0),
a : 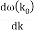
c : 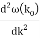
Rearranging, and then changing the variable of integration to y = (k – k0) / (2 ∆k), we get
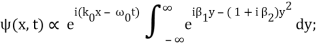
Where
2 ∆k ( x – x0 – vgt),
2 α (∆k)2t
Incidentally, ∆k = 1/ (2∆x) , where ∆x is the initial width of the wave packet. The above expression can be rearranged to give
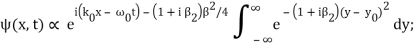
Where y0 = iβ/2 and β = β1 / (1+ iβ2). Again changing the variable of integration to z = (1+ iβ2)1/2 ( y – y0), we get
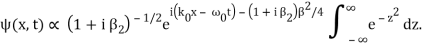
The integral now just reduces to a number. Hence, we obtain
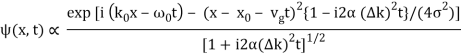
Where
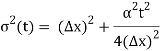
It's worth noting that the above wavefunction is the same as the one we started with at. This supports the estimate we produced before by extending the phase factor with Taylor. ϕ(k) about k = k0.
The probability density of our particle as a function of time is stated using Eq. (111).
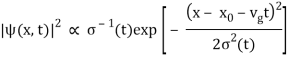
As a result, the probability distribution is Gaussian, with a characteristic width of and a maximum value of x = x0 + vgt. Our particle's most likely position now aligns with the distribution function's peak. As a result, the most likely position of the particle is provided by
x = x0 + vgt.
The particle essentially moves at a uniform velocity, as can be shown.
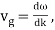
The particle essentially moves at a uniform velocity, as can be shown. vp = ω/k, whereas a wave packet travels at the group velocity,vg = d ω/dt. Now, it follows from the dispersion relation for particle waves that
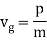
This, however, is the same as the classical particle velocity. As a result, once we learn that individual particles must be identified with wave packets rather than plane waves, the dispersion relation turns out to be consistent with classical physics. In reality, a continuous stream of particles moving in the same direction as the wave is commonly regarded as a plane wave.
The width of our wave packet grows as time passes, according to Eq. (112). Indeed, the characteristic time for a wave packet of original width to double in spatial extent is given by Eqs. (105).
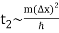
For example, if an electron is initially isolated in an atomic scale region (i.e., ∆x ~ 10-10 m) then the doubling time is only about 10-16 s. Evidently, particle wave packets (for freely moving particles) spread very rapidly.
Note, from the previous analysis, that the rate of spreading of a wave packet is ultimately governed by the second derivative of ω(k) with respect to k. See Eqs. (105) and (112). This is why a functional relationship between and is sometimes referred to as a dispersion relation: it affects how wave packets spread over time. The second derivative of with respect to is 0 in the specific situation when is a linear function of, and hence there is no dispersion of wave packets: i.e. wave packets propagate without altering shape. In the case of light waves, the dispersion relation is now linear. Light pulses pass through a vacuum without spreading, as a result. Another feature of linear dispersion relationships is that the phase is preserved.
Velocity, vp = ω/k, and the group velocity, vg = dω/dk, are identical. Thus, both plane light waves and light pulses propagate through a vacuum at the characteristic speed c = 3 × 108 m/s. Of course, the dispersion relation for particle waves is not linear in k. Hence, particle plane waves and particle wave packets propagate at different velocities, and particle wave packets also gradually disperse as time progresses.
2.6.2 Time Development of a Gaussian Wave Packet
So far, we've just done our Fourier Transforms at and examined the results at t = 0. We'll now reintroduce time to the wave function and examine the wave packet at a later time. We'll see that photons and non-relativistic electrons behave very differently.
Assume we start with our Gaussian (minimum uncertainty) wave packet A(k) = 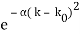 at t = 0. We can do the Fourier Transform to position space, including the time dependence.
at t = 0. We can do the Fourier Transform to position space, including the time dependence.
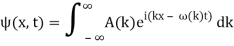
We state directly that is reliant on. This simply indicates that the energy of our free particle is determined by its motion. In the case of a photon, E = pc, so ℏ ω = ℏ kc, and hence ω = kc. For an non-relativistic electron, E =  , so ℏ ω =
, so ℏ ω = 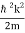 , and hence ω =
, and hence ω = 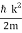 .
.
To cover the general case, lets expand ω(k) around the center of the wave packet in k-space.
ω(k) = ω(k0) + 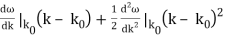
We make some educated guesses about the outcome and give the coefficients names.
ω(k) = ω0 + vg (k – k0) + β (k – k0)2
For the photon, vg = c and β=0. For the NR electron, vg = 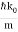 and β =
and β = 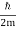 .
.
Performing the Fourier Transform, we get
ψ(x, t) = 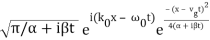
| ψ(x, t)|2 = 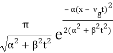
We can see that the photon will travel at the speed of light and that the wave will travel at the same speed.
Packet will not disperse, because β = 0.
The wave packet for the NR electron moves at the correct group velocity., vg = p/m, but the wave packet spreads with time. The RMS width is σ = 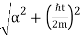
A wave packet naturally spreads because it contains waves of different momenta and hence different velocities. Wave packets that are very localized in space spread rapidly.
2.7.1 Wave-Particle Duality
The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.
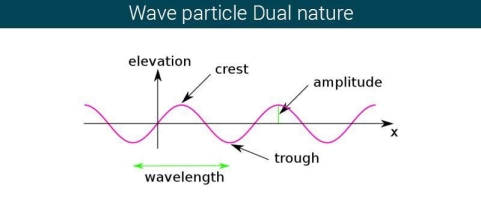
Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.
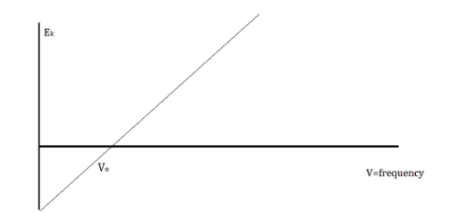
The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
We can say that light is a particle with the attribute of waves because the energy of waves and the energy of light do not correspond.
Einstein demonstrated that a photon's momentum equals
p = h/λ
This is readily demonstrated as follows. Assumption E = hv for a photon and λv = c for an electromagnetic wave, we obtain
E = hc/λ
We are now applying Einstein's relativity result. E = mc2 to find
λ = h/mc
Which is the same as equation (4). Because the rest mass of a photon is zero, this refers to the relativistic mass, not the rest mass. De Broglie reasoned in 1924 that matter can show this wave-particle duality because light can behave both as a wave (it may be diffracted and has a wavelength) and as a particle (it carries packets of energy). He went on to say that matter, like light, will obey the same equation (4). Davisson and Germer confirmed de Broglie's theory by observing diffraction patterns by hitting metals with electrons in 1927.
Bohr's assumption is justified according to de Broglie's equation (2). If we consider an electron to be a wave, the electron orbit must complete an integral number of wavelengths during its orbit to be stable. Otherwise, it would interfere with itself in a detrimental manner. This condition could be written as follows:
2πr = nλ
This can be expressed as using the de Broglie relation (4).
Mvr = nℏ
This is exactly the same as Bohr's equation (2).
While de Broglie's equation validates Bohr's quantization assumption, it also exposes a flaw in Bohr's model. The wave-particle duality, as demonstrated by Heisenberg, leads to the well-known uncertainty principle.
∆x∆p ≈ h
The uncertainty principle dictates that if the orbital radius of an electron in an atom is known precisely, the angular momentum must be unknown. The flaw in Bohr's model is that it stipulates both exactly and that the orbital angular momentum must be an integral multiple of. As a result, the stage was prepared for a new quantum theory that followed the uncertainty principle.
2.7.2 The duality of photons
“Light is a particle as well as a wave.” To have a better understanding of this concept, we conducted an experiment.
Young's Interference Experiment, often known as the Double-slit Interference Experiment, is a type of experiment. This experiment used technology to identify individual light particles to see if interference fringes appeared even when the light was severely attenuated to the point where there was just one particle. The experiment's findings confirmed that one photon had an interference fringe.
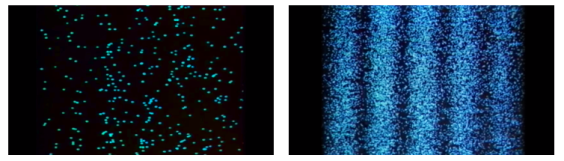
When light is detected that has been weakened to an extreme brightness limit and projected on a screen, it behaves like a particle, as shown on the left. When the number of particles detected rises, however, an interference fringe emerges, as shown on the right. As can be seen, light behaves similarly to a wave.
There was no interference fringe when one of the two slits in the experiment was closed, allowing only one photon particle to pass through the other slit. This proved that in the double-slit interference experiment, one photon particle travelled through both slits at the same time and interfered with itself.
These experiments show that while a photon was detected as having the properties of a particle, interference appeared like that of a wave while simultaneously passing through the double-slit, revealing that the photon has the dual properties of a particle and a wave.
Key takeaway:
- In quantum physics, wave–particle duality states that any particle or quantum phenomenon can be represented as either a particle or a wave. It expresses the difficulty of classical terminology like as "particle" and "wave" to completely characterise quantum-scale things' behaviour.
- He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
Complementarity is a concept in quantum mechanics that Niels Bohr considered to be a necessary property of the theory. According to the complementarity principle, objects have a set of complementary features that cannot all be viewed or measured at the same time. Position and momentum are an example of such a pair. One of quantum mechanics' foundational truths, according to Bohr, is that setting up an experiment to measure one of a pair of quantities, such as the position of an electron, excludes the possibility of measuring the other, despite the fact that understanding both experiments is required to characterise the object under study. The behaviour of atomic and subatomic things, according to Bohr, cannot be divorced from the measuring devices that form the framework in which they behave. As a result, there is no "one picture" that unifies the data gained in these various experimental situations, and only the "totality of the phenomena" as a whole can provide a complete description.
The failure of the operators that represent the observable quantities being measured to commute expresses complementarity mathematically:
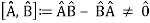
Incompatible observables are observables that correlate to non-commutative operators. There can't be a comprehensive set of shared eigenstates for incompatible observables. It's worth noting that there may be some simultaneous eigenstates of () A and () B, but not enough to form a complete basis. The canonical commutation relation is defined as follows:
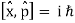
This suggests that this holds true for both position and momentum. Similarly, any two of the spin observables specified by the Pauli matrices have an equivalent relationship; measurements of spin along perpendicular axes are complimentary. Using mutually unbiased bases, which give complementary observables defined on finite-dimensional Hilbert spaces, this has been applied to discrete observables with more than two possible outcomes.
The principle of complementarity, or dialecticism, is a second key component of quantum physics. Is light a wave or a particle? Complementarity is defined as the recognition that though particle and wave behaviour are mutually exclusive, both are required for a complete explanation of all occurrences.
2.9.1 De Broglie’s Matter Waves:
When an electromagnetic wave interacts with matter, it can behave as a particle of light, according to Compton's formula. Louis de Broglie proposed a new speculative idea in 1924, claiming that electrons and other matter particles could behave like waves. De Broglie's hypothesis of matter waves is the name given to this concept today. De Broglie's hypothesis, combined with Bohr's early quantum theory, resulted in the development of a new wave quantum mechanics theory to describe the physics of atoms and subatomic particles in 1926. Quantum mechanics has made new technical inventions and technologies possible, such as the laser and magnetic resonance imaging (MRI). Other fields, such as biology and chemistry, benefit from this new technology.
According to de Broglie's hypothesis, both massless photons and heavy particles must satisfy a single set of relationships that link energy E to frequency f and linear momentum p to wavelength w. These photon-photon connections were previously studied in the context of Compton's effect. We're bringing them up now in a broader perspective. A de Broglie wave of frequency f and wavelength is any particle with energy and motion.
E = hf
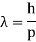
E and p denote a particle's relativistic energy and momentum, respectively. The wave vector is commonly used to express De Broglie's relations. 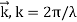 and the wave frequency ω = 2πf as we usually do for waves:
and the wave frequency ω = 2πf as we usually do for waves:
E = ℏω
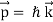
According to wave theory, a wave's energy is carried with the group velocity. This group velocity for matter waves is the particle's velocity u. De Broglie relations show that matter waves obey the following relation when the energy E and momentum p of a particle are identified with its relativistic energy mu and relativistic momentum mu, respectively.
λf = ω/k = 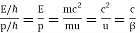
Where β = u/c
When a particle is massless we have 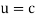 and (Figure) becomes
and (Figure) becomes 
De Broglie gave an explanation for the quantization of the electron's angular momentum in the hydrogen atom, which was posited in Bohr's quantum theory, using the idea of the electron matter wave. When we suppose that an electron in a hydrogen atom behaves like a wave rather than a particle, the scientific explanation for the first Bohr quantization condition emerges easily. Imagine a stretched guitar string that is clamped at both ends and vibrates in one of its typical modes to see it clearly. The wavelengths of these vibrations cannot be random if the length of the string is l ((Figure)), but must be such that an integer k number of half-wavelengths /2 fits exactly on the distance l between the ends. A standing wave on a string has the constraint l=k/2. Let's pretend that instead of clamping the string to the walls, we bend it into a circle and tie the ends together. This results in a circular string that vibrates in normal modes and fulfils the same standing-wave requirement, but the number of half-wavelengths must now be an even number k,k=2n, and the length l is now tied to the circle's radius r n. This means that the radii cannot be chosen at random, but must meet the standing-wave condition:
2π = 2n λ/2.
= 2n λ/2.
If an electron moves like a wave in the nth Bohr orbit, its wavelength must be equal to (Figure). λ = 2π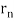 /n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
/n. If (Figure) is correct, the electron wave of this wavelength corresponds to the linear momentum of the electron.
p = h/λ = nh/ (2 π = nh/
= nh/ . As a result, in a circular orbit, the electron's angular momentum must be
. As a result, in a circular orbit, the electron's angular momentum must be

The first of Bohr's quantization conditions, given by, is this equation (Figure). A plausible theoretical argument for the existence of matter waves is to provide a physical explanation for Bohr's quantization condition.
Standing-wave pattern: (a) a stretched string clamped against the walls; (b) an electron wave trapped in the hydrogen atom's third Bohr orbit.
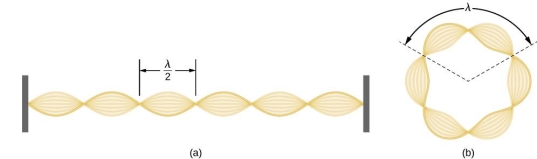
In 1927, C. Davisson and L. Germer completed a series of electron-scattering tests that conclusively demonstrated that electrons behave like waves. Davisson and Germer's experiment were not designed to prove de Broglie's hypothesis: The proof came as a result of their usual experiments on metal surfaces bombarded by electrons.
They analysed a nickel surface in the experiment that produced the first evidence of electron waves (now known as the Davisson–Germer experiment). Their nickel sample was treated in a high-temperature oven to transform it from its regular polycrystalline structure to one with massive single-crystal domains filling the volume. The experimental setup is depicted in (Figure). Thermal electrons are emitted from an electron gun's heated element (typically composed of tungsten) and accelerated through a potential difference V, resulting in a well-collimated stream of electrons. By adjusting the potential difference in the electron cannon, the kinetic energy K of the electrons can be modified. According to the law of conservation of energy, this results in a beam of electrons with a fixed linear momentum:
EV = K =  =
= 
The electron beam strikes the nickel sample in a normal to its surface direction. It scatters in a variety of directions near the surface. A very sensitive detector measures the intensity of the beam scattered in a specific direction. The detector's angular location with relation to the incident beam's direction can range from to The entire setup is enclosed in a vacuum chamber to prevent electron collisions with air molecules, as such thermal collisions would change the electrons’ kinetic energy and are not desirable.
The Davisson–Germer diffraction experiment's experimental setup is shown schematically. The nickel target scatters a well-collimated beam of electrons. In the electron cannon, the kinetic energy of electrons in the incident beam is selected by setting a variable voltage, V. For a variety of scattering angles, the intensity of the scattered electron beam is measured, while the distance between the detector and the target remains constant.

The incident electrons scatter off the nickel target's surface in many random directions when it has a polycrystalline shape with many randomly aligned tiny crystals. As a result, the dispersed electron beam's intensity is nearly constant in all directions, simulating diffuse light reflection from a porous surface. When the nickel target has a regular crystalline structure, however, the intensity of the scattered electron beam reaches a definite maximum at a given angle, resulting in a distinct diffraction pattern (see Figure). William H. Bragg and William L. Bragg, father and son physicists, analysed similar diffraction patterns created by X-rays scattered by several crystalline substances in 1912. In X-ray crystallography, the Bragg law establishes a link between the wavelength of radiation impinge on a crystalline lattice, the lattice spacing, and the position of the diffracted radiation's interference maximum (see Diffraction).
The Davisson–Germer target's lattice spacing was measured using X-ray crystallography and found to be Unlike X-ray crystallography, in which X-rays penetrate the sample, only the surface atoms interact with the incident electron beam in the Davisson–Germer experiment. The highest intensity of the reflected electron beam is found for scattering angles that satisfy the requirement (see (Figure)) in surface diffraction. At a scattering angle of 50 at V54V, the first-order maximum (for n=1) is measured, yielding the wavelength of the incident light as λ = (2.15) sin 50 = 1.64. A 54-V potential, on the other hand, accelerates incident electrons to kinetic energies of K = 54 eV. Their momentum, calculated from (Figure), is p = 2.478 ×  . When we substitute this result in (Figure), the de Broglie wavelength is obtained as
. When we substitute this result in (Figure), the de Broglie wavelength is obtained as
λ = h/p = 
We get the same result when we utilise K = 54eV in (Figure). The theoretical result's closeness to the Davisson–Germer experimental value of 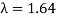 is a convincing argument for the existence of de Broglie matter waves.
is a convincing argument for the existence of de Broglie matter waves.
The experimental results of electron diffraction on a nickel target in an electron gun with an accelerating potential of around 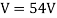 At a scattering angle of around 45 degrees, the intensity maximum is recorded.
At a scattering angle of around 45 degrees, the intensity maximum is recorded.
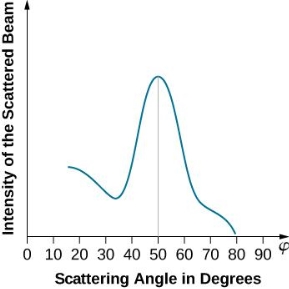
The in-phase incident beams are reflected from atoms on the surface during surface diffraction of a monochromatic electromagnetic wave on a crystalline lattice structure. Where an is the lattice spacing, a ray reflected from the left atom travels an extra distance to the detector. When D is an integer multiple of the wavelength of the reflected beams, they remain in phase. For angles satisfactory, the strength of the reflected waves exhibits notable maxima.
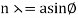
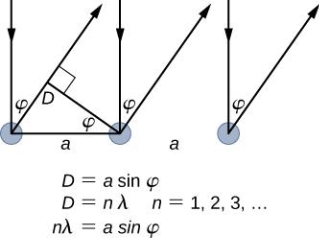
Because the incident electrons are dispersed only from the surface, diffraction lines recorded with low-energy electrons, such as those used in the Davisson–Germer experiment, are relatively broad (see (Figure)). When a higher-energy electron beam passes through a thin metal foil, the resolution of diffraction images improves dramatically. This happens because the diffraction image is made by scattering from a large number of crystallographic planes within the volume, and the maxima formed by scattering at Bragg angles are sharp (see Figure).
Diffraction patterns created by scattering X-rays and electrons on a crystalline material (a). The observed pattern represents the sample's crystalline structure's symmetry.

De Broglie's idea has been thoroughly examined using various experimental approaches since Davisson and Germer's work, and the presence of de Broglie waves has been proven for multiple elementary particles. Neutrons have been employed in scattering experiments to determine the crystalline structures of substances using neutron matter wave interference patterns. The mass of a neutron is comparable to that of a positively charged proton because it has no charge. Neutrons and protons can both be thought of as matter waves. As a result, being a matter wave is a property shared by all particles in motion, not only electrically charged ones. It has become possible to monitor matter waves of molecules as big as carbon C 60. As long as physical objects are in motion, they all have a matter wave associated with them. De Broglie matter waves have a universal character that has been established.
2.10.1 de Broglie Waves can be Experimentally Observed:
Electron diffraction studies conducted by G.P. Thomson in 1926 and C. Davisson and L. H. Germer in 1927 established the correctness of de Broglie's proposal. It was discovered in these investigations that electrons scattered from atoms in a crystal, and that these dispersed electrons generated an interference pattern. The interference pattern looked just like what happens when water waves flow through two holes in a barrier, generating independent wave fronts that merge and interfere. Both matter (e.g., electrons and neutrons) and electromagnetic radiation display these diffraction patterns, which are characteristic of wave-like behaviour. If the wavelength is equivalent to the spacing between scattering centres, diffraction patterns are generated.
We'll now look at the phenomena of electron diffraction as part of our analysis of experiments that led to the new quantum theory.
2.10.2 Light Diffraction (Young's Double Slit Experiment)
It is commonly known that light has the ability to diffract around things in its path, resulting in a pattern of interference that is unique to the object. In reality, this is how holography works (the interference pattern is created by allowing the diffracted light to interfere with the original beam so that the hologram can be viewed by shining the original beam on the image). The Young double slit experiment is a basic demonstration of light diffraction (Figure 1.7.1).

Figure 11: Experiment with a young double slit. A plane of light waves illuminates two apertures.
Water waves (shown as waves in a plane parallel to the double slit device) are used in this experiment to see what occurs when they hit the slits. Each slit then acts as a point source for spherical waves, which interfere with one another, resulting in the light and dark fringes seen on the right (Figure).
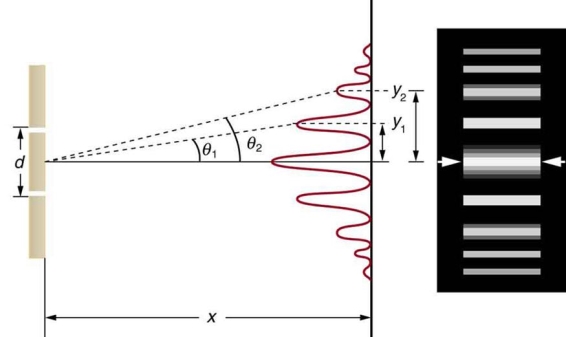
Figure 12: Interference through a double slit.
2.10.3 Electron Diffraction (Davisson–Germer Experiment)
Electrons, according to classical physics, should behave like particles, travelling in straight lines and not bending in flight until touched on by an external agent, such as a magnetic field. If we fire a beam of electrons through a double slit onto a detector in this scenario, we should obtain two bands of "hits," similar to what you'd get if you shot a machine gun through the side of a home with two windows - two regions of bullet-marked wall inside, while the remainder would be intact. Graph 1.7.3 (left).
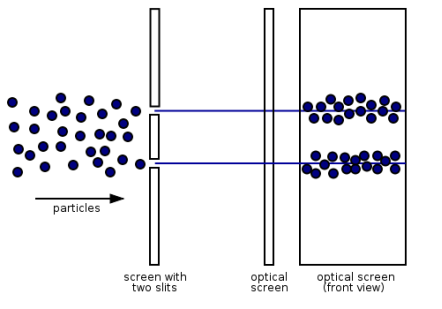
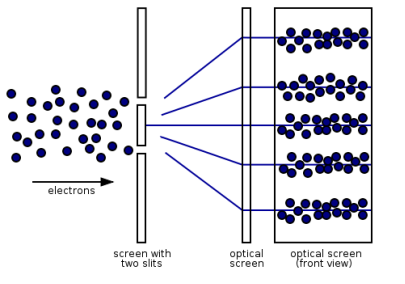
Figure 13: (left) classical model of electrons. (right) wave property of electrons.
However, if the slits are narrow and close enough together, we can see the electrons diffracting through the slits and interfering with one another, exactly like waves. This indicates that electrons, like photons, exhibit wave-particle duality, which is consistent with de Broglie's concept. They must have wavelength and frequency attributes in this scenario. The attributes can be deduced from the electrons' behaviour as they travel through our diffraction grating.
This was a watershed moment in the history of quantum physics. The Davisson–Germer experiment established the wave-nature of matter, completing the notion of wave-particle duality, much as the photoelectric effect had done for light. This concept was crucial to physicists since it suggested that not only could any particle display wave properties, but that wave equations could be used to describe processes in matter if the de Broglie wavelength was utilised.

2.10.4 Neutron Diffraction
Neutrons, like all quantum particles, can show wave behaviour, and atoms or their nuclei can behave as diffraction obstacles if the wavelength is short enough. When neutrons from a reactor are slowed and picked properly by their speed, their wavelength is near one angstrom (0.1 nm), which is the usual distance between atoms in a solid material. A diffraction experiment can then be carried out with such a beam. Neutrons interact directly with the nucleus of the atom, and each isotope contributes differently to the diffracted intensity; for example, ordinary hydrogen and deuterium contribute differently. Even in the presence of big Z atoms, light (low Z) atoms frequently contribute significantly to the diffracted intensity.
2.11.1 Davisson-Germer Experiment:
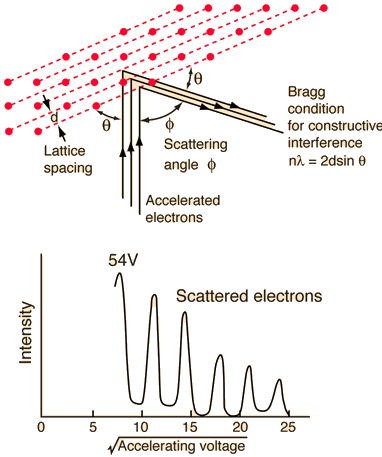
The Davisson-Germer experiment revealed the electron's wave character, validating deBroglie's earlier hypothesis. It was a big step forward in the development of quantum mechanics because it put wave-particle duality on a firm experimental footing. The Bragg diffraction law had previously been applied to x-ray diffraction, but this was the first time it had been applied to particle waves.
Davisson and Germer devised and constructed a vacuum apparatus for determining the energy of electrons scattered from a metal surface. A voltage was used to accelerate electrons from a hot filament and allow them to strike the surface of nickel metal.
The electron beam was focused on a nickel target that could be rotated to observe the dispersed electrons' angular dependency. Their electron detector (known as a Faraday box) was positioned on an arc and could be rotated to observe electrons from various angles. They were taken aback when they discovered that the intensity of the dispersed electron beam had a peak at some angles. The Bragg law could be used to calculate the lattice spacing in the nickel crystal based on this peak, which showed wave behaviour for the electrons.
With rising accelerating voltage, the experimental data above, replicated above Davisson's article, reveals recurrent maxima of scattered electron intensity. This information was gathered at a certain dispersion angle. The relationship is calculated using the Bragg law, the deBroglie wavelength expression, and the kinetic energy of the accelerated electrons.
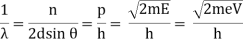
Electron Bragg deBroglie Acceleration wavelength law relationship through voltage V
An accelerating voltage of 54 volts produced a distinct peak at a scattering angle of 50° in the historical data. The Bragg law's angle theta for that scattering angle is 65°, and the computed lattice spacing for that angle is 0.092 nm. The wavelength as a function of voltage relationship is empirically determined for that lattice spacing and scattering angle.
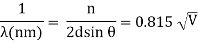
Trying this relationship for n=1,2,3 gives values for the square root of voltage 7.36, 14.7 and 22, which appear to agree with the first, third and fifth peaks above. What then accounts for the second, fourth, and sixth peaks? They could have come from a different set of crystal planes. Those peaks fall into the 2,3,4 sequence, implying that the series' first peak would have been around 5.85.
2.12.1 Deriving the de Broglie Wavelength
De Broglie arrived at his equation through a sequence of substitutions based on well-known theories:
De Broglie was the first to apply Einstein's famous equation for the relationship between matter and energy:
E = mc2 (1)
With
- E = energy,
- m = mass,
- c = speed of light
Using Planck's theory, each quantum in a wave has a discrete quantity of energy that can be calculated using Planck's equation:
E = hv
With
- E = energy,
- h = Plank's constant (6.62607 x 10-34 J s),
- ν= frequency
De Broglie hypothesised that the two energies would be equivalent because particles and waves share the same characteristics:
Mc2 = hv
De Broglie proposed velocity (v) for the speed of light since real particles do not travel at the speed of light (c).
Mv2 = hv
De Broglie replaced v/ for v in the equation and arrived at the final expression that connects wavelength and particle speed.
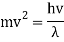
Hence
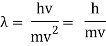
The majority of Wave-Particle Duality problems can be solved using Equation 6 and a few different cancelling out units.
De Broglie was given credit for his hypothesis, but he had no experimental proof to back it up. Clinton J. Davisson and Lester H. Germer fired electrons into a nickel crystal in 1927. They observed electron diffraction, which is analogous to wave diffraction against crystals (x-rays). In the same year, an English physicist, George P. Thomson fired electrons towards thin metal foil providing him with the same results as Davisson and Germer.
Key takeaway:
- De Broglie waves have a velocity. Beiser calls it "vp," and later shows that vp is the phase velocity of the waves. Vp=f is the formula for determining the velocity of a wave. De Broglie proposed the equation =h/mv for both particles and waves.
What is Wave-Particle Duality?
We've all heard about the nature of light and the various personalities it exhibits. Some of the features include interference, reflection, refraction, and diffraction. Particle-Wave The concept of duality aids us in comprehending the particle and wave aspects of light.
Based on the premise that light and all other electromagnetic radiation can be classified as either particles or waves, physicist Louis De Broglie proposed in 1923 that the same duality must apply to matter. Any particle of matter with momentum (p) has a corresponding wavelength (), according to him.
De Broglie Wavelength formula is given by λ= h/p
Where, h is the Planck constant
For a particle of momentum mv, the wavelength is given by λ=h/mv
This equation is true for photons as well.
De Broglie realised early in the twentieth century that both models describe the same phenomena. Particles can be described as waves, and waves can be described as particles. Light has a wave-like character as revealed by diffraction and interference events, but it also has a particle-like character as revealed by the photoelectric effect, absorption, and emission by atoms. Although electrons have mass, they may be diffracted in the same way that caverns can. Nature shows particle duality and ambiguity in ways that science does not. While the interpretation of this wave-particle duality is still debated, many physicists today embrace the Bohr complement-yarn principle. Both models are necessary for a thorough description of nature, yet they are mutually exclusive. e.

Energy is emitted as quanta, which are small packets of energy, according to Planck's Hypothesis of Quantum Theory. He claims that the energy emitted is proportional to the frequency of the emitted light, a concept known as Wave-Particle Duality. The quantum energy is connected to the frequency by the equation E = hv, according to Planck's hypothesis.
One of the simplest methods to demonstrate the duality between a particle and a wave is to see a light. Because light is akin to waves, it can diffract, refract, interface, and so on.
De Broglie's Theory benefited greatly from Albert Einstein's photoelectric effect theory, which proved that particles and waves may collide. Light can also be viewed as a photon, which is a small particle. Electrons are released when light is viewed on certain objects. To remove one electron from an object's surface, a specific amount of energy is required. When a photon with more energy than an electron collides with a material, an electron is emitted.
When electrons are emitted, kinetic energy is also released. The greater the intensity, the larger the energy, according to classical wave theory. Because a wave's energy is related to its amplitude, scientists had a difficult time finding high-intensity lights that did not alter the wave's overall kinetic energy.
The amount of kinetic energy might be adjusted by changing the frequency of light, according to researchers. A threshold value V0 is used because some things do not produce electrons at specific frequencies. The amount of kinetic energy necessary for a photon to expel an electron is described by this threshold. The scientists discovered a linear relationship between frequency and kinetic energy, which is depicted in the sketch below.
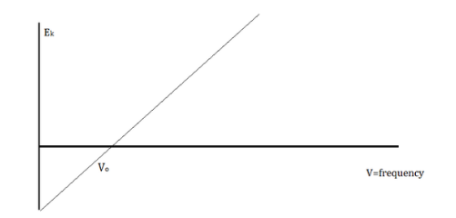
The slope of this line is known as Planck’s Constant, h = 6.63 x 10-34
Since the energy of waves and energy of light does not coincide, we can say that light is a particle that has the property of waves.
The Uncertainty Principle
A particle's position and momentum cannot be measured with arbitrarily high precision at the same time. The product of the errors of these two measurements has a minimum. There is also a minimum for the product of the energy and time uncertainty.
∆x ∆p > ℏ/2
∆E ∆t > ℏ/2
This is not a remark about measuring equipment inaccuracy or the quality of experimental methods; it is a result of the wave qualities inherent in the quantum mechanical description of nature. The ambiguity is inherent in the nature of things, even with flawless instruments and skills.
The uncertainty principle, also known as the Heisenberg uncertainty principle or the indeterminacy principle, is a statement made by German physicist Werner Heisenberg in 1927. It states that an object's position and velocity cannot be measured precisely at the same time, even in theory. In fact, in nature, the concepts of absolute position and exact velocity have no relevance.
This principle is not obvious from everyday life. Because the uncertainties suggested by this concept for common objects are sufficiently small to be noticed, it is simple to measure both the position and velocity of, say, a car. The full rule states that the product of location and velocity uncertainties is equal to or larger than a small physical amount, or constant (h/(4), where h is Planck's constant, or approximately 6.6 1034 joule-second). Only for atoms and subatomic particles with extremely small masses can the product of uncertainty become important.
Any attempt to precisely measure the velocity of a subatomic particle, such as an electron, will cause it to move around in an unpredictable manner, rendering a simultaneous measurement of its position useless. This finding originates from the intimate relationship in nature between particles and waves in the world of subatomic dimensions, and has nothing to do with shortcomings in the measurement devices, procedure, or observer.
The wave-particle duality gives rise to the uncertainty principle. Every particle has a wave connected with it, and every particle behaves in a wavelike manner. The particle is most likely to be located where the wave's undulations are the most pronounced or powerful. However, the more powerful the associated wave's undulations get, the more ill-defined the wavelength becomes, which defines the particle's momentum. As a result, a strictly localised wave has an indeterminate wavelength, while its associated particle has a fixed position but no fixed velocity. A particle wave with a well-defined wavelength, on the other hand, is widely dispersed; the associated particle, albeit having a very accurate velocity, may be found practically anywhere. A very precise measurement of one observable entails a significant amount of uncertainty in the measurement of the other.
The uncertainty principle can also be represented in terms of the momentum and position of a particle. A particle's momentum is equal to the product of its mass and velocity. As a result, the product of a particle's momentum and position uncertainty equals h/(4+) or greater. The idea also holds true for other related (conjugate) pairings of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is taken equals h/(4+) or more. The uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it transitions to a more stable state are the same for an unstable atom or nucleus.
Are the uncertainty relations revealed by Heisenberg in 1927 simply the outcome of the equations utilised, or are they embedded in every measurement? Heisenberg used a thought experiment because he felt that all scientific concepts must be defined using actual or possible experimental observations.
Heisenberg imagined a microscope that achieves extremely fine resolution by illuminating with high-energy gamma rays. Although such a microscope does not exist at the moment, it may theoretically be built. Heisenberg envisaged seeing an electron and measuring its position using this microscope. He discovered that the electron's position and momentum obeyed the mathematically established uncertainty relation. The experiment had significant problems, which Bohr pointed out, but after they were fixed, the demonstration was completely compelling.
A free electron rests just beneath the centre of the microscope's lens in the revised version of the thought experiment (see the picture above). From the electron, the circular lens forms a cone with an angle of 2A. Gamma rays—high intensity light with the smallest wavelength—then illuminate the electron from the left. These have the maximum resolution because, according to a wave optics principle, the microscope can resolve (that is, "see" or distinguish) objects to a size of Dx, which is related to and to the gamma ray wavelength L by the expression:
Dx = L / (2sinA)
A gamma ray impacting an electron, on the other hand, provides it a kick in quantum mechanics, where a light wave can act like a particle. The electron is driven to the right when light is diffracted by the electron into the microscope lens. The gamma ray must be dispersed into any angle within the cone of angle 2A in order to be detected by the microscope. The gamma ray, like a particle, carries momentum in quantum physics. The wavelength is related to the total momentum p by the formula
p = h / L, where h is Planck's constant.
The total momentum in the x direction would be the sum of the electron's momentum p'x in the x direction and the gamma ray's momentum in the x direction in the extreme case of diffraction of the gamma ray to the right edge of the lens:
p'x + (h sinA ) / L', where L' is the wavelength of the deflected gamma ray.
In the other extreme, the observed gamma ray recoils backward, just hitting the left edge of the lens. The overall momentum in the x direction in this example is:
p''x - (h sinA ) / L''.
Because momentum is never lost, the final x momentum in each scenario must equal the beginning x momentum (it is conserved). As a result, the final x momenta are identical:
p'x + (h sinA ) / L' = p''x - (h sinA ) / L''
If A is tiny, the wavelengths are close to being the same, L' L" L. So there you have it.
p''x - p'x = Dpx ~ 2h sinA / L
We have a reciprocal link between the minimal uncertainty in the observed position, Dx, of the electron along the x axis and the uncertainty in its momentum, Dpx, in the x direction because Dx = L / (2 sinA ).
Dpx ~ h / Dx or Dpx Dx ~ h.
The "more than" indication can be used if there is more than the bare minimum of uncertainty.
This is Heisenberg's uncertainty relation for simultaneous measurement of an object's position and momentum, except for the factor of 4p and an equal sign.
Modern physicists warn that a careful examination of this image reveals an illusory classical mechanical interaction one step deeper, in the collision of the photon and the electron. In fact, despite its importance in the development and teaching of quantum theory, Heisenberg's microscope is not part of modern knowledge. Any depiction that resembles daily colliding items cannot represent the genuine quantum interaction and the genuine uncertainty associated with it. You must work through the formal mathematics that estimates probabilities for abstract quantum states to get the actual outcome. Experiments on these kind of interactions are still being carried out now. So far, the experiments have all confirmed Heisenberg's belief that no "genuine" microscopic classical collision occurs at the bottom.
The interpretation
So, how can we make sense of it all? Is this Heisenberg's own Principle being 'proven'? Yes and no, in my opinion. I'd say it's a combination of illustration and proof. The following are the key assumptions:
1. We can think of -ray photons, or any photon for that matter, as particles with momentum, and when they ‘collide,' or interact, with an electron, the photon will give that electron some momentum.
2. Because momentum is conserved, the total (linear) momentum before and after the collision must be the same for both particles–that is, (1) the incoming ray and the electron before the contact and (2) the released photon and the electron that receives the kick after the encounter.
3. We may connect (or associate, if you prefer) the wavelength of the -ray photon with its momentum p using the Planck relation or, equivalently for photons (since they have no mass), the de Broglie connection.
2.16.1 Single slit Experiment:
Interference, refraction, reflection, and diffraction are all examples of processes that occur as light travels through air. Diffraction of light occurs when it comes into contact with an obstruction.
The wavefront on the other side of the opening mimics the wave when light flows through a small opening that is comparable in size to the wavelength of the light. Please explain light diffraction and single slit diffraction, which occurs when light passes through a single slit.
When light passes through a single slit with a width (w) on the order of the wavelength of the light, we can witness single slit diffraction. The screen's diffraction pattern will be at a distance L >> w from the slit. The intensity is proportional to the angle.
We may examine the bending phenomena of light, or diffraction, in the single-slit diffraction experiment, which causes light from a coherent source to interfere with itself and generate a distinct pattern on the screen termed the diffraction pattern. When the sources are tiny enough to be comparable in size to the wavelength of light, diffraction occurs. This impact can be seen in the diagram below. The spreading out of huge apertures is minor and almost undetectable.

Single Slit Diffraction Formula
We shall assume the slit width a << D. xD is the separation between slit and source.
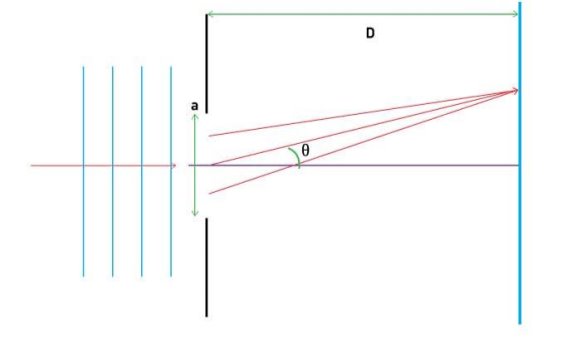
The angular position of any point on the screen will be determined by measuring from the slit centre, which divides the slit by lengths. To explain the pattern, we'll look at the condition of black fringes first. Let's also divide the split into equal-width zones.
lengths. To explain the pattern, we'll look at the condition of black fringes first. Let's also divide the split into equal-width zones. . Let's look at a pair of rays that come from a/2 distances apart, as indicated below.
. Let's look at a pair of rays that come from a/2 distances apart, as indicated below.
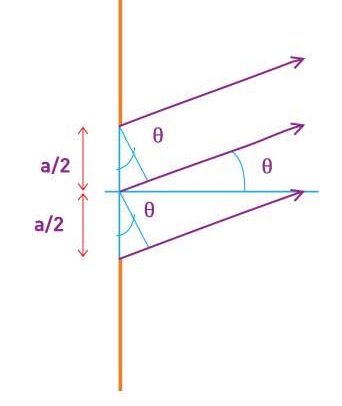
The path difference exhibited by the top two rays shown is:
∆L = a/2 sin θ
Remember that this is only a valid computation if D is really large. Check visit our article on Young's Double Slit experiment for more information on the approximation.
Any number of ray pairings that start at a distance of a2 from one another, such as the bottom two rays in the diagram, can be considered. Any arbitrary pair of rays separated by a2 can be taken into account. In a moment, we'll discover how important this trick is.
The path difference must induce destructive interference for a dark fringe; the path difference must be out of phase by 2. (represents the wavelength)
The first fringe is made up of
∆L = λ/2 = a/2 sin θ
λ = a sin θ
There is another ray at a distance a2 that can generate destructive interference for a ray emerging from any point in the slit.
As any ray emerging from a point has a counterpart that produces destructive interference, there is destructive interference at = sin1a. As a result, a dark fringe is created.
We can divide the slit into four equal sections of a/4 and use the same rationale for the next fringe. As a result, for the second minimum:
λ/2 = a/4 sin θ
2λ = a sin θ
Similarly, we can divide the slit into 2n sections for the nth fringe and utilise the following condition:
nλ = a sin θ
The Central Maximum
The maxima are located between the minima, and the width of the central maximum is equal to the distance between the first order minima on both sides of the screen.
The position of the minima determined by y (as measured from the screen's centre) is:
Tan θ ≈ θ ≈ y/D
For small ϑ,
Sin θ≈θ
⇒λ = a sin θ≈aθ
⇒θ = y/D = λa
⇒ y = λDa
The width of the central maximum is simply twice this value
⇒ Width of central maximum = 2λDa
⇒ Angular width of central maximum = 2θ = 2λa
The diffraction pattern and intensity graph is shown below.

2.17.1 The Quantum Harmonic Oscillator:
One drawback of this traditional formulation is that it is not universal. We can't use it to represent diatomic molecular vibrations, for example, because quantum effects are important. Using the classical statement to limit discussion of a "spring" constant between the atoms is a first step toward a quantum formulation. The potential energy function can be stated in a more general sense this way.
U(x) = ½ m ω2 x2
When this expression is used with the time-independent Schrdinger equation, the result is
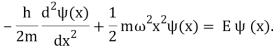
To solve (Figure), we need the wave functions to be symmetric around x=0 (the bottom of the potential well) and normalizable in order to discover the permitted energies E and their corresponding wave functions (x). When integrated throughout the complete range of x from to+, these requirements ensure that the probability density |(x)2 | must be finite. A more advanced course in quantum mechanics will cover how to solve (Figure); here, we will simply mention the results. The permitted energies are as follows:
En = ( n + ½ ) ℏω = 2n+1/2 ℏω, n = 0, 1, 2, 3, . . .
These energies (stationary states or states of defined energy) correlate to wave functions.

Where β =  ,
,  is the normalization constant, and Hn(y) is a polynomial of degree n called a Hermite polynomial. The first four Hermite polynomials are
is the normalization constant, and Hn(y) is a polynomial of degree n called a Hermite polynomial. The first four Hermite polynomials are
H0 (y) = 1
H1 (y) = 2y
H2 (y) = 4y2 – 2
H3 (y) = 8y3 – 12y
In this section, we'll look at a few sample wave functions (Figure). As the primary number grows larger, the solutions alternate between even and odd functions around the axis.
The quantum harmonic oscillator's first five wave functions. Vertical lines illustrate the classical limitations of the oscillator's motion, which correspond to the classical turning points at x=A of a classical particle with the same energy as a quantum oscillator in the state shown in the image.

This solution has a number of intriguing properties. Unlike a classical oscillator, a quantum oscillator's observed energies can only have energy values given by (Figure). Furthermore, unlike a quantum particle trapped in a cage, the allowed energy levels are evenly distributed.
E = En+1 – En = 2(n+1)+1/2 ℏω – 2n+1/2 ℏω = ℏω = hf.
The smallest-energy quantum carried by the emitted photon must be hf when a particle coupled to such a system transition from a higher-energy state to a lower-energy state. Similarly, when a particle transitions from a lower-energy to a higher-energy state, the smallest-energy quantum that the particle may absorb is hf. Only multiples of this smallest-energy quantum can be absorbed or emitted by a quantum oscillator. In the blackbody radiation problem, this is consistent with Planck's notion for energy exchanges between radiation and cavity walls.
In three respects, the quantum oscillator varies from the traditional oscillator:
To begin with, a quantum oscillator's ground state is not zero. The lowest energy, according to conventional wisdom, is zero. Because of the omnipresent fluctuations that are a result of the Heisenberg uncertainty principle, all quantum-mechanical systems do not have a zero-energy state. The Heisenberg uncertainty principle would be violated if a quantum particle rested still at the bottom of the potential well, as both its momentum and position would have to be correct at the same time. As a result, the lowest-energy state must have errors in momentum and position, and a quantum particle's ground state must be above the bottom of the potential well.
Second, a particle in a quantum harmonic oscillator potential can be located outside the interval with a nonzero probability. A < x < +A. The particle would have no energy to be in this location under a traditional formulation of the problem. In the classically forbidden zone, the probability of finding a ground-state quantum particle is roughly 16 percent.
Third, the probability density distributions |ψn(x)|2 for a quantum oscillator in the ground low-energy state, ψ0(x), is largest at the middle of the well (x=0). For the particle to be found with greatest probability at the center of the well, we expect that the particle spends the most time there as it oscillates. This is opposite to the behavior of a classical oscillator, in which the particle spends most of its time moving with relative small speeds near the turning points.
For excited states, quantum probability density distributions vary in nature, becoming more like the classical distribution as the quantum number increases. Because the distribution of the first excited state of a quantum oscillator is different, we can see this change. |ψn(x)|2 As seen in, peaks near the turning points and vanishes at the equilibrium position (Figure). According to Bohr's correspondence principle, the quantum description of a harmonic oscillator converges to the classical description in the limit of large quantum numbers, as shown in (Figure). The quantum probability distribution for a quantum oscillator in this excited state is reasonably well approximated by the classical probability density distribution corresponding to the quantum energy of the n=12 state. For highly excited states, this agreement improves over time.
The probability density distribution for finding the n=12 quantum state of the quantum harmonic oscillator. The probability density distribution of a classical oscillator with the same energy is shown by the dashed curve.
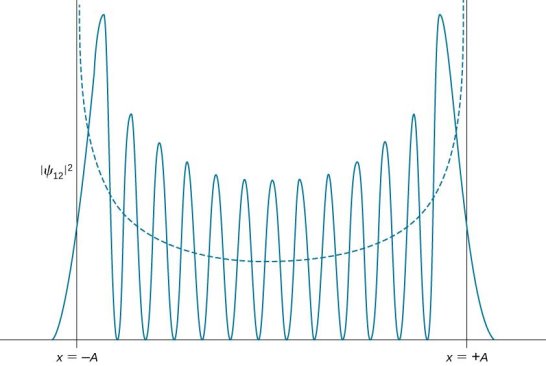
2.17.2 Estimate the Hydrogen Ground State Energy
The fundamentally uncertainty principle explains why the hydrogen atom (and other atoms) is so big. If the electron were to be contained in a smaller space,∆p would increase, causing p to increase on average. The energy would rise rather than fall.
The uncertainty principle can be used to calculate the minimal energy for hydrogen. This computation is not perfect, but it is more accurate than the Bohr model. The notion is that the radius must be greater than the positional spread, and the momentum must be greater than the momentum spread.
r ≥ ∆x
p ≥ ∆p = ℏ/2r
In terms of the dimensionless fine structure constant, this is our formula for potential energy. α.
V(r) = 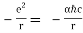
Let us calculate the energy.
E = 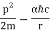
And include the uncertainty principle's influence.
Pr = ℏ
E = 
E = 
Differentiate in terms of p To get the minimum, set equal to zero.
DE/dp = p/m – 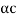 = 0
= 0
p = 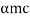

It's worth noting that potential energy is just (-2) times kinetic energy (as we expect from the Virial Theorem). The energy formula for the ground state is valid.
We can also make an educated guess at the radius.
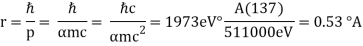
Hydrogen has no (orbital) angular momentum in its ground state. It is not travelling in a circular orbit as predicted by Bohr. The probability distribution of the electron is spread out over around 1. The energy would rise if it wasn't spread out.
The quantum physics-based Heisenberg uncertainty principle explains a number of things that classical physics could not explain. One of the applications is to demonstrate that an electron cannot exist within a nucleus. It goes like this:
Non-existence of electrons in the nucleus
Let us assume that electrons exist in the nucleus. As the radius of the nucleus in approximately 10-14 m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
∆x= 10-14 m
According to uncertainty principle,
∆x∆px =h/2∏
Thus ∆px=h/2∏∆x
Or ∆px =6.62 x10-34/2 x 3.14 x 10-14
∆px=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron, then the momentum of electron should be at least of this order, that is p=1.05*10-20 kg m/sec.
With such a large momentum, an electron's velocity must be similar to that of light. As a result, the following relativistic formula should be used to compute its energy.
E= √ m20 c4 + p2c2
E = √(9.1*10-31)2 (3*108)4 + (1.05*10-20)2(3*108)2
= √(6707.61*10-30) +(9.92*10-24)
=(0.006707*10-24) +(9.92*10-24)
= √9.9267*10-24
E= 3.15*10-12 J
Or E=3.15*10-12/1.6*10-19 eV
E= 19.6* 106 eV
Or E= 19.6 MeV
As a result, if the electron occurs in the nucleus, its energy should be in the range of 19.6 MeV. However, beta-particles (electrons) released from the nucleus during b-decay have energy of around 3 MeV, which differs significantly from the calculated value of 19.6 MeV. The second reason an electron cannot exist inside the nucleus is that no electron or particle in the atom has an energy greater than 4 MeV, according to experimental evidence.
Electrons have a negative charge, and if they can exist in the nucleus, the positive charges will neutralise them.
According to Heisenberg's uncertainty principle, the radius of atomic nuclei is 10-15 m, and if electrons exist in the nucleus, the maximum uncertainty in its position is 10-15 m.
Mass of the electron is 9.1 x 10-31 kg
No electron or particle in the atom possess energy greater than 4MeV
Hence the electrons do not exist inside the nucleus
2.19.1 Complementarity.
Complementarity is a concept in quantum mechanics that Niels Bohr considered to be a necessary property of the theory. According to the complementarity principle, objects have a set of complementary features that cannot all be viewed or measured at the same time. Position and momentum are an example of such a pair. One of quantum mechanics' foundational truths, according to Bohr, is that setting up an experiment to measure one of a pair of quantities, such as the position of an electron, excludes the possibility of measuring the other, despite the fact that understanding both experiments is required to characterise the object under study. The behaviour of atomic and subatomic things, according to Bohr, cannot be divorced from the measuring devices that form the framework in which they behave. As a result, there is no "one picture" that unifies the data gained in these various experimental situations, and only the "totality of the phenomena" as a whole can provide a complete description.
The failure of the operators that represent the observable quantities being measured to commute expresses complementarity mathematically:
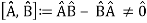
Incompatible observables are observables that correlate to non-commutative operators. There can't be a comprehensive set of shared eigenstates for incompatible observables. It's worth noting that there may be some simultaneous eigenstates of () A and () B, but not enough to form a complete basis. The canonical commutation relation is defined as follows:
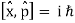
This suggests that this holds true for both position and momentum. Similarly, any two of the spin observables specified by the Pauli matrices have an equivalent relationship; measurements of spin along perpendicular axes are complimentary. Using mutually unbiased bases, which give complementary observables defined on finite-dimensional Hilbert spaces, this has been applied to discrete observables with more than two possible outcomes.
The principle of complementarity, or dialecticism, is a second key component of quantum physics. Is light a wave or a particle? Complementarity is defined as the recognition that though particle and wave behaviour are mutually exclusive, both are required for a complete explanation of all occurrences.
2.19.2 Uncertainty.
With difficulties of wave/particle duality, classical physics was on shaky ground, but the discovery of the uncertainty principle took them completely off surprise.
The uncertainty principle, also known as the Heisenberg Uncertainty Principle or Indeterminacy Principle, was proposed by German physicist Werner Heisenberg in 1927, and states that an object's position and velocity cannot be measured precisely at the same time, even in theory. In fact, in nature, the concepts of absolute position and exact velocity have no relevance.
This principle is not obvious from everyday life. Because the uncertainties suggested by this concept for common objects are sufficiently small to be noticed, it is simple to measure both the position and velocity of, say, a car. The full rule states that the product of position and velocity uncertainties is equal to or larger than a minuscule physical amount, or constant (about 10-34 joule-second, the value of the quantity h (where h is Planck's constant)). Only for atoms and subatomic particles with extremely small masses can the product of uncertainty become important.
Any attempt to precisely measure the velocity of a subatomic particle, such as an electron, will cause it to move around in an unpredictable manner, rendering a simultaneous measurement of its position useless. This finding originates from the intimate relationship in nature between particles and waves in the world of subatomic dimensions, and has nothing to do with shortcomings in the measurement devices, procedure, or observer.
Every particle has a wave connected with it, and every particle behaves in a wavelike manner. The particle is most likely to be located where the wave's undulations are the most pronounced or powerful. However, the more powerful the associated wave's undulations get, the more ill-defined the wavelength becomes, which defines the particle's momentum. As a result, a strictly localised wave has an indeterminate wavelength, while its associated particle has a fixed position but no fixed velocity. A particle wave with a well-defined wavelength, on the other hand, is widely dispersed; the associated particle, albeit having a very accurate velocity, may be found practically anywhere. A very precise measurement of one observable entails a significant amount of uncertainty in the measurement of the other.
The uncertainty principle can also be represented in terms of the momentum and position of a particle. A particle's momentum is equal to the product of its mass and velocity. As a result, the product of a particle's momentum and position uncertainty equals h/(2) or greater. The principle holds for other (conjugate) pairings of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is taken equals h/(2) or greater. The uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it transitions to a more stable state are the same for an unstable atom or nucleus.
W. Heisenberg discovered the uncertainty principle, which expresses the impact of wave-particle duality on the properties of subatomic things. Consider the concept of momentum in the microscopic world, which is similar to a wave. The wavelength of a wave determines its momentum. A wave packet, such as a photon or an electron, is made up of several waves. As a result, it must be made up of a variety of momentums. But how is it possible for one object to have several momentums?
Of course, once a particle's momentum is measured, a single momentum is observed. Momentum before the observation, like fuzzy position, is inherently ambiguous. The uncertainty principle states that certain quantities, such as position, energy, and time, are unknown save through probability. The uncertainty principle states that accurate knowledge of complementarity pairings is impossible in its purest form. You can measure an electron's location but not its momentum (energy) at the same time, for example.
The principle of complementarity, which "implies the impossibility of any clear separation between the behaviour of atomic objects and their interaction with the measuring devices that serve to specify the conditions under which the phenomena arise," is a defining element of quantum physics. As a result, "data gathered under various experimental conditions cannot be comprehended within a single picture, but must be treated as complimentary in the sense that only the entirety of the events exhausts the possible knowledge about the objects," according to the authors. During the 1930s, the majority of scientists increasingly adopted this interpretation of quantum physics, which indicated a different perspective of the significance of physical explanation.
The uncertainty principle can be expressed mathematically as follows, where x' denotes position and p' denotes momentum:
∆x∆p > h/2π
Next to E=mc2, this is possibly the most well-known equation in physics. It essentially states that the sum of the errors in position and momentum must always be bigger than Planck's constant. So, you can measure an electron's position to a certain degree of precision, but its momentum will fall within a very wide range of values. Similarly, you can precisely measure momentum, but its location is unknown.
Notice that this is not a different version of the measurement problem; for a quantum particle, the combination of position, energy (momentum), and time is really indeterminate until a measurement is done (then the wave function collapses).
Also, because Planck's constant, h, is so small, the uncertainty principle is irrelevant to macroscopic objects (10-34). A thrown baseball, for example, has a positional uncertainty of 10-30 millimetres.
When we raise the question, "Is our knowledge of reality unlimited?" we comprehend the depth of the uncertainty principle. No, because the uncertainty principle implies that Nature contains inherent uncertainty, indeterminacy, and unpredictability.
Key takeaway:
- In quantum physics, Heisenberg's uncertainty principle is a crucial concept. It goes something like this: if we know exactly where a particle is (the uncertainty of position is tiny), we know nothing about its momentum (the uncertainty of momentum is huge), and vice versa.
- According to the classical Uncertainty Principle, a function and its Fourier transform cannot be highly focused at the same time. This has the conceptual implication in quantum mechanics that determining a particle's position and momentum at the same time is impossible (Heisenberg Uncertainty Principle).
References:
1.Quantum Mechanics: Theory and Applications, A.K.Ghatakand S. Lokanathan,(Macmillan)-2004
2. Introduction to Quantum Theory, David Park (Dover Publications)-1974
3. Theory and Problems of Modern Physics, Schaum‘s outline,R.Gautreau and W.Savin- (Tata McGraw-Hill) 2nd Edition
4. Physics for scientists and engineer with Modern Physics-Jewell and Serway -(CENGAGE Learnings) 2010.
5. Modern Physics of Atoms and Molecules Bransden and Joachim (PearsonIndia)-2003