Unit - 3
Nuclear Physics- I
3.1.1 Atomic Nucleus: Definition, Structure & Size
The Nucleus
The atomic nucleus is the nucleus, which is the most central part of the atom. Protons and neutrons are the two types of subatomic particles that make up the nucleus.
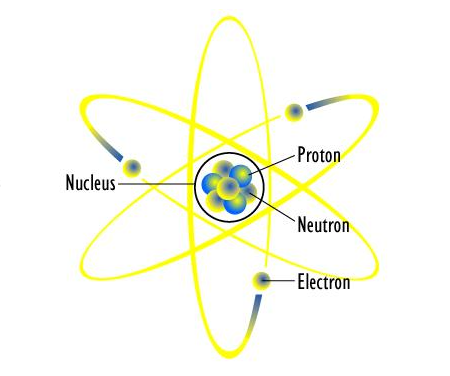
Atoms are the fundamental constituents of all substance. Atoms make up everything you can see, feel, and touch. Even things that you can't see, feel, hear, or touch are made up of atoms. Atoms are the building blocks of everything.
The Gold Foil Experiments were conducted by Ernest Rutherford and Hans Geiger and Ernest Marsden in 1909. They shot particles through exceedingly thin sheets of gold foil during the experiments. In 1911, Rutherford came to the conclusion that the atom had a dense nucleus because most of the particles shot straight through, but some of the particles were deflected due to the dense nucleus of the gold atoms. This notion would disprove the concept that the atom was more like plum pudding in structure. Until Rutherford's discoveries, the plum pudding model was the predominant model of atomic structure.
3.1.2 Atomic Numbers
The atomic nucleus is located in the atom's centre. The number of protons and neutrons in an atom determines the atom's type or element. A group of atoms with the same atomic structure is referred to as an element. Hydrogen, for example, is an element.
The atomic nucleus' composition reveals a great deal about the element it represents. The atomic number is determined by the number of protons inside the nucleus. Protons have a positive charge (+). The electrons (-) must balance the atom's negative charge in order for it to have a neutral charge. As a result, there are exactly as many protons as electrons in a neutral atom. So, if you know the atomic number and the charge of the atom, you can easily calculate the number of electrons. For example, because hydrogen has one proton, 1+, it must have a one-charge in order to be neutral. As a result, hydrogen only contains one electron.
What role do neutrons play in all of this? Neutrons, after all, are neutral. I use the first letters to keep everything straight: Neutrons are Neutral, and Protons are Positive. I then recall Electrons as a result of the Elimination Process.
Despite the fact that neutrons do not provide the atom any charge, they are nonetheless significant in the atomic structure. The neutron is the biggest particle in the subatomic world. The atomic mass is calculated by adding the neutrons and protons together. Because electrons are so tiny, their mass only accounts for.01 percent of the total mass. The electrons aren't inside the nucleus; instead, they're whizzing around on the nucleus's periphery.
We can find the number of neutrons by subtracting the atomic number from the atomic mass, because the atomic number tells us the number of protons in an atom and the atomic mass tells us the number of protons and neutrons.
The number of neutrons is equal to the atomic mass minus the atomic number.
3.1.3 Structure of the nucleus
Because the electron and proton were the only known particles at the time, the nucleus' structure was poorly understood. It had already been proven that nuclei are typically roughly twice as heavy than protons alone can account for. Until English scientist James Chadwick discovered the neutron in 1932, a consistent hypothesis was impossible. He discovered that when alpha particles collided with beryllium nuclei, neutral particles of roughly the same mass as protons were ejected. Almost all nuclear processes may be explained in terms of neutrons and protons in a nucleus. Surprisingly, the nucleus' neutrons and protons move in orbitals to a significant extent, as if their wave functions are independent of one another. A stationary wave pattern featuring peaks and nodes, as well as angular momentum quantum numbers, describes each neutron or proton orbital. The shell nuclear model is a nucleus theory that is based on these orbitals. It was independently introduced in 1948 by Maria Goeppert Mayer of the United States and Johannes Hans Daniel Jensen of West Germany, and it grew into a full theory of the nucleus during the following decades.
Enrico Fermi, an Italian-born American physicist, and others researched the interactions of neutrons with nuclei in the mid-1930s. Neutrons, unlike protons or alpha particles, are not repelled from the nucleus by a positive charge, hence they are easily captured. When a neutron is captured, the atomic mass of the new nucleus increases by one unit. If a more stable isotope of that atomic mass is close, the new nucleus will be radioactive, converting the neutron to a proton and taking on the more stable form.
In 1938, German chemists Otto Hahn and Fritz Strassmann discovered nuclear fission as a result of experiments initiated and explained by Austrian physicist Lise Meitner. In fission, a uranium nucleus captures a neutron and gains enough energy to cause the nucleus to split into two lighter nuclei of nearly equal size due to its inherent instability. More neutrons are released during the fission process, which can be exploited to induce more fissions. Under Fermi's leadership, the first nuclear reactor, a device designed to allow controlled fission chain reactions, was built at the University of Chicago, and the first self-sustaining chain reaction occurred in this reactor in 1942. In 1945, American scientists developed the first fission weapon, also known as an atomic weapon, which employed uncontrolled fission events in uranium or plutonium. In 1952, American scientists utilised a fission explosion to start a fusion reaction, in which hydrogen isotopes thermally fused to form heavier helium nuclei. This was the world's first thermonuclear bomb, commonly known as an H-bomb, a weapon capable of releasing hundreds or thousands of times the energy of a fission bomb.
3.1.4 Quantum field theory and the standard model
Dirac not only proposed the relativistic equation for the electron, but he also pioneered quantum field theory, a relativistic analysis of particle interactions. The theory allows for the creation and destruction of particles and just requires the presence of proper interactions with appropriate energy. Quantum field theory also states that interactions can only extend across a distance if the force is carried by a particle, or field quantum. The photon, or quantum of light, carries the electromagnetic force, which may act over large distances. Mathematical challenges occurred in applying the theory since it permits particles to interact with their own field quanta.
An experiment conducted by American physicist Willis Eugene Lamb, Jr. In 1946 and 1947 overcame the theoretical deadlock. He demonstrated that the hydrogen spectrum is around one-tenth of one percent different from Dirac's predicted picture using microwave techniques developed during WWII. Later, American physicist Polykarp Kusch, who was born in Germany, discovered a similar anomaly in the magnitude of the electron's magnetic moment. Lamb's findings were revealed at the well-known Shelter Island Conference in the United States in 1947. Hans Bethe, a German-born American physicist, and others concluded that the so-called Lamb shift was most likely caused by electrons and field quanta produced by the vacuum. Richard Feynman, Julian Schwinger, and Tomonaga Shin'ichir, who won the Nobel Prize for Physics in 1965, and Freeman Dyson, who demonstrated that their varied techniques were mathematically similar, overcame the earlier mathematical hurdles. Quantum electrodynamics, a novel theory, was discovered to explain all of the measurements with extreme precision. Quantum electrodynamics, it appears, provides a full account of how electrons behave in the presence of electromagnetism.
The weak force and electromagnetic were discovered to have parallels in the 1960s. The electroweak hypothesis, for which Sheldon Glashow, Abdus Salam, and Steven Weinberg received the Nobel Prize in Physics in 1979, integrated the two forces. Three field quanta—the W particle, the Z particle, and the Higgs boson—were predicted as extra force carriers in addition to the photon. The Higgs boson was the carrier of the Higgs field, while the W and Z particles were carriers of the weak force, resulting in the W and Z particles being heavy and the photon having a mass of zero. The discovery of the W and Z particles in 1983, which had masses that were exactly predicted, proved the electroweak theory's validity. In 2012, a particle that was most likely the Higgs boson was discovered.
Since the first unstable particle, the muon, was discovered in cosmic rays in the 1930s, hundreds more subatomic particles have been discovered. By the 1960s, patterns in the properties and connections of subatomic particles had emerged, leading to the development of the quark theory. The Standard Model was created by combining the electroweak theory and the quark theory to create a theoretical framework that encompasses all known particles and field quanta. The leptons and quarks are the two broad kinds of particles in the Standard Model. Electrons, muons, and neutrinos are all leptons, and they only interact with the electroweak force apart from gravity.
The strong force affects quarks, and they join in a variety of ways to form bound states. The neutron and proton are two of the bound quark states, known as hadrons. A proton, a neutron, or any of the heavy hadrons known as baryons are formed when three quarks unite. The pion is formed when a quark and an antiquark unite. Quarks have never been seen before, and physicists don't expect to see one anytime soon. Outside hadrons, the strong force is so strong that quarks cannot be separated from each other. However, the existence of quarks has been indirectly verified in numerous ways. Beginning in 1967, researchers observed that some electrons fired against proton targets were deflected at significant angles in tests using high-energy electron accelerators. The large-angle deflection, like Rutherford's gold-foil experiment, implies that hadrons have an interior structure comprising very small charged items. Quarks are thought to be the tiny things. Physicists developed quantum chromodynamics, a novel quantum field theory, in the mid-1970s to accommodate quarks and their unusual features. This hypothesis describes the confinement of quarks to hadrons qualitatively. The theory, according to physicists, should explain all features of hadrons. However, dealing with strong interactions in quantum chromodynamics presents more mathematical challenges than dealing with weak interactions in quantum electrodynamics, making comprehensive computations of hadron features impossible. Nonetheless, numerical computations utilising the most powerful computers seems to support the theory's veracity.
3.1.5 Properties of Nuclei
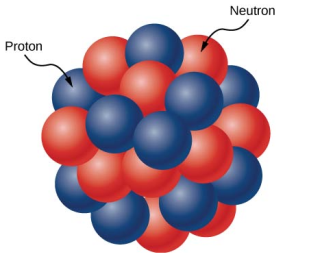
Protons and neutrons make up the atomic nucleus ((Figure)). Although protons and neutrons have about the same mass, protons have one unit of positive charge whereas neutrons have none. At the heart of an atom, these particles are crammed into a very small space. The nucleus is spherical or ellipsoidal in form, and about 1/100,000th the size of a hydrogen atom, according to scattering measurements. The nucleus of an atom would be around the size of a baseball if it were the size of a big league baseball stadium. Nucleons are protons and neutrons that make up the nucleus.
Protons and neutrons make up the atomic nucleus. Protons are depicted in blue, while neutrons are depicted in red.
Key takeaway:
- Protons, neutrons, and electrons make up the atoms themselves. The atomic number of each element is equal to the number of protons in its nucleus. The number of neutrons in an element's isotopes varies. An atomic symbol is used to symbolise elements.
- Nuclei with magic numbers of neutrons or protons, as well as those that are doubly magical, are particularly stable.
The atomic number, Z, determines the number of protons in the nucleus. The neutron number, N, is the number of neutrons in the nucleus. The mass number, A, is the total number of nucleons. These figures are connected by
A = Z + N.
A nucleus is represented symbolically by
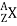
Where X is the chemical element, A denotes its mass, and Z denotes its atomic number. 612c, for example, is the carbon nucleus, which has six protons and six neutrons (or 12 nucleons).
For a variety of stable nuclei (nuclides), a graph of the number N of neutrons vs the number Z of protons is illustrated in (Figure). Multiple values of N (blue points) are feasible for a given value of Z. The number of neutrons equals the number of protons N=P for tiny values of Z, and the data fall on the red line. The number of neutrons is more than the number of protons N>P for large values of Z, and the data points are above the red line. For Z>15, the number of neutrons is usually more than the number of protons.
For stable atomic nuclei, this graph shows the number of neutrons N vs the number of protons Z. Neutrons outnumber protons in larger nuclei.

This graph is used to create a graphic that provides more specific information on each nucleus (Figure). This graph is known as a nuclide graph. A nucleus is represented by each cell or tile. The nuclei are organised in ascending Z (horizontal) and ascending N (vertical) order (along the vertical direction).
The nuclides are depicted in part on this graph. Cell values for stable nuclei (dark blue backgrounds) show the percentage of nuclei with the same atomic number found on Earth (percent abundance). The number represents the half-life of unstable nuclei.

Isotopes are atoms with nuclei that have the same number of protons (Z) but differing numbers of neutrons (N). Normal hydrogen (1 proton, no neutrons), deuterium (1 proton and one neutron), and tritium (1 proton and one neutron) are the three isotopes of hydrogen (one proton and two neutrons). Because chemical properties are dictated by interactions between the atom's outer electrons, rather than the nucleons, isotopes of the same atom have the same chemical properties. Water containing deuterium rather than hydrogen ("heavy water"), for example, looks and tastes like regular water. A list of common isotopes may be found in the table below.
Common Isotopes*No entry if less than 0.001 (trace amount). | |||||
Element | Symbol | Mass Number | Mass (Atomic Mass Units) | Percent Abundance* | Half-life** |
Hydrogen | H | 1 | 1.0078 | 99.99 | Stable |
2H or D | 2 | 2.0141 | 0.01 | Stable | |
3H  | 3 | 3.0160 | − | 12.32 y | |
Carbon | 12C | 12 | 12.0000 | 98.91 | Stable |
13C  | 13 | 13.0034 | 1.1 | Stable | |
14C  | 14 | 14.0032 | − | 5730 y | |
Nitrogen | 14N | 14 | 14.0031 | 99.6 | Stable |
15N | 15 | 15.0001 | 0.4 | Stable | |
16N | 16 | 16.0061 | − | 7.13 s | |
Oxygen | 16O | 16 | 15.9949 | 99.76 | Stable |
17O  | 17 | 16.9991 | 0.04 | Stable | |
18O | 18 | 17.9992 | 0.20 | Stable | |
19O  | 19 | 19.0035 | − | 26.46 s | |
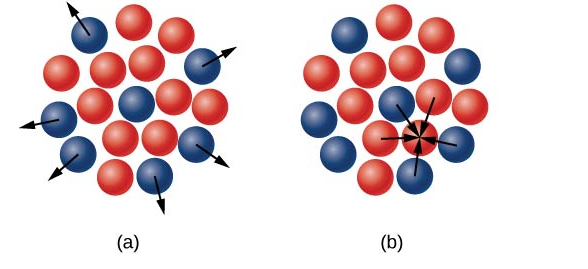
In heavier nuclei, why do neutrons outweigh protons ((Figure))? Understanding the forces inside the nucleus is required to address this question. There are two sorts of forces: (1) the long-range electrostatic (Coulomb) force, which repels positively charged protons, and (2) the short-range strong nuclear force, which attracts all nucleons in the nucleus. You may have also heard of a nuclear force that is “weak.” Although this force is responsible for some nuclear decays, it does not play a role in keeping the nucleus stable against the strong Coulomb repulsion it faces. In the next chapter, when we study particle physics, we will go over the strong nuclear force in greater depth. When the attractive interactions between nucleons balance out the repulsive, long-range electrostatic interactions between all protons in the nucleus, nuclear stability is achieved. Excess neutrons are required for heavy nuclei to prevent electrostatic interactions from tearing the nucleus apart, as seen in (Figure).
(a) The electrostatic force is repulsive and has a large range of application. The arrows show outward forces exerted by a proton (also in blue) at the centre on protons (in blue) at the nuclear surface. (a) The strong nuclear force acts on nucleons in close proximity. The arrows show the attractive forces that a neutron (in red) exerts on its closest neighbours.
Because stable isotopes exist, it's important to be cautious when mentioning an element's mass. Copper (Cu), for example, has two stable isotopes:
V(CPn) = 

3.2.1 Probability: The Heisenberg Uncertainty Principle
Probability Distribution
Matter and photons are waves, which means they are dispersed over a large area. What is a particle's location, such as an electron's? Is it right in the middle of the tidal wave? The solution lies in how an electron's location is measured. Unlike a wave, experiments reveal that the electron will be found at a specific point. But if you set up exactly the same situation and measure it again, you will find the electron in a different location, often far outside any experimental uncertainty in your measurement. Repeated measurements will reveal a wavelike statistical distribution of sites.
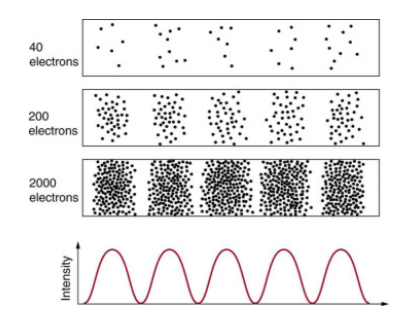
Many scientists, including Schrödinger and Heisenberg, investigated the repercussions after de Broglie postulated the wave nature of matter. Because of its wave nature, it was rapidly realised that a particle's route and destination could not be anticipated precisely for each particle separately. Each particle, on the other hand, has a specific destination.
You acquire a distribution connected to the particle's wavelength and diffraction pattern after collecting enough data. The likelihood of finding the particle at a given position is known as a probability distribution, and the overall pattern is known as a probability distribution. Quantum physicists discovered equations that predicted the probability distribution in a variety of situations.
It's a little unsettling to believe that you can't foresee where a single particle will go or even follow it to its final destination. Let's see what occurs when we try to track a particle. Figure 2 shows the double-slit patterns obtained for electrons and photons. First, we observe that these patterns are similar when using d sin = m, the double-slit constructive interference equation presented in Photon Energies and the Electromagnetic Spectrum, where d is the slit separation and m is the electron or photon wavelength.

As individual particles fall on the detector, both patterns accumulate statistically. This can be seen with photons or electrons, but for now, we'll focus on electrons. You may envisage the electrons interfering with one another in the same way that waves do. Reduce the intensity until there is never more than one electron between the slits and the screen to test this. The interference pattern repeats itself! This means that a particle's probability distribution spans both slits, and particles collide with one another. Does this imply that the electron passes through both slits as well? An electron is a non-divisible basic unit of matter. However, because it is a valid question, we should investigate whether the electron passes through one or both slits. Coils encircling the slits may detect charges passing through them, for example. An electron always passes through one slit or the other; it does not split to pass through both slits. However, there is a catch. When you determine that the electron passed through one of the slits, you obtain single slit interference instead of a double slit pattern. There is no way to determine which slit the electron passed through using another means. A single-slit pattern is forced because the particle only passed through one slit. You get a double-slit pattern if you don't pay attention to which slit the electron passes through.
3.2.2 Heisenberg Uncertainty
What difference does it make knowing which slit the electron passed through make to the pattern? The response is crucial: measurement has an impact on the system being studied. Information can be lost, and it is often impossible to precisely measure two physical things at the same time. For example, scattering light or other electrons off a moving electron can be used to determine its position. Those probes have momentum of their own, and scattering from the electron causes the electron's momentum to shift in a way that causes information to be lost. Even in principle, absolute knowledge has a limit.
As a result of his work on quantum mechanics and the wave properties of all particles, Werner Heisenberg initially declared this limit to knowledge in 1929. (See Fig. 3.) Consider measuring the position and momentum of an electron at the same time (it could be any particle). Position x has an uncertainty that is roughly equal to the wavelength of the particle. x
A wave does not exist in a single location in space, as previously stated. When the position of an electron is measured repeatedly, a spread in locations is seen, signalling that position x is uncertain. We must interact with the particle in order to detect its position, such as by causing it to collide with a detector. The particle will lose momentum as a result of the collision. This change in momentum could be somewhere between zero and the particle's whole momentum.
Somewhere between zero and the particle's entire momentum, p=hp=h Because it is impossible to predict how much momentum will be transferred to a detector, momentum p is also unpredictable. In fact, the uncertainty in momentum can be as big as the momentum itself, resulting in ph in equation form.
Since x, the position uncertainty can be decreased by utilising a shorter-wavelength electron. However, because p=hp=h, reducing the wavelength increases the uncertainty in momentum. Using a longer-wavelength electron, on the other hand, reduces the uncertainty in momentum while increasing the uncertainty in location. This trade-off can be expressed mathematically by increasing the uncertainties. Xp h is left after the wavelength cancels.
As a result, if one uncertainty is lowered, the other must be increased in order for the product to be acceptable.
Heisenberg demonstrated that using advanced mathematics, the best that can be done in a simultaneous measurement of position and momentum is xph4.
The Heisenberg uncertainty principle is the name for this. With uncertainties x and p that multiply to less than h4, measuring position x and momentum p at the same time is impossible. There can't be zero uncertainty in either case. Neither uncertainty can be reduced to a small size without the other increasing in size. A narrow wavelength allows for precise location measurement, but it also increases the probe's momentum, which disrupts the momentum of the system being monitored. For example, if an electron is scattered from an atom and its wavelength is narrow enough to detect the position of electrons in the atom, the momentum of the electrons can knock them out of their orbits, causing information about their original motion to be lost. As a result, following an electron in its orbit around an atom is difficult. The electron will be found in a certain location if its position is measured, but the atom will be disrupted. Repeated measurements on similar atoms will yield intriguing probability distributions for electrons in the atom's vicinity, but not motion information. Electron clouds or orbitals are terms used to describe probability distributions.
EXAMPLE 1. HEISENBERG UNCERTAINTY PRINCIPLE IN POSITION AND MOMENTUM FOR AN ATOM
1. What is the uncertainty in velocity of an electron in an atom whose position is measured to a precision of 0.0100 nm?
2. What is the electron's kinetic energy in eV if it has this velocity?
Strategy
The measurement's accuracy, or x = 0.0100 nm, is the uncertainty in position. Xph4xph4 can thus be used to find the smallest uncertainty in momentum p. Once the uncertainty in momentum p has been determined, p = mv can be used to determine the uncertainty in velocity.
Solution for Part 1
Using the equals sign in the uncertainty principle to express the minimum uncertainty, we have
ΔxΔp=h4π
Solving for Δp and substituting known values gives
Δp=h4πΔx=6.63×10−34 J⋅ s4π(1.00×10−11 m)=5.28×10−24 kg⋅ m/s
Thus, Δp = 5.28 × 10−24 kg · m/s = mΔv.
Solving for Δv and substituting the mass of an electron gives
Δv=Δpm=5.28×10−24 kg⋅ m/s9.11×10−31 kg=5.79×106 m/s
Solution for Part 2
Although large, this velocity is not highly relativistic, and so the electron’s kinetic energy is
KEe=12mv2 =12(9.11×10−31 kg)(5.79×106 m/s)2 =(1.53×10−17 J)(1 eV1.60×10−19 J)=95.5 eV
Discussion
Because atoms are about 0.1 nm in size, knowing an electron's position to 0.0100 nm accurately localises it within the atom. This would be the equivalent of being able to perceive details a tenth the size of an atom. However, the resulting velocity uncertainty is significant. You wouldn't be able to keep up with it if its speed was so unpredictable. To gain a better notion of how big the velocity uncertainty is, we assumed the electron's velocity was equal to its uncertainty, which resulted in a kinetic energy of 95.5 eV. This is far larger than the normal energy difference between levels in atoms (see Table 1 in Photon Energies and the Electromagnetic Spectrum), making it hard to calculate an energy for the electron even if we know its position reasonably well.
Why don't we perceive Heisenberg's principle of uncertainty in everyday life? Planck's constant is very small, as the solution implies. As a result, the uncertainty in estimating the location and momentum of massive objects is negligible at its lowest point. Jupiter's reflected sunlight may be detected, allowing us to track the planet's orbit around the Sun. The reflected sunlight changes Jupiter's momentum and causes uncertainty, but this is insignificant in comparison to Jupiter's massive momentum. For huge objects, the correspondence principle states that quantum mechanics predictions become indistinguishable from classical physics predictions, which is the situation here.
3.2.3 Heisenberg Uncertainty for Energy and Time
There is another form of Heisenberg’s uncertainty principle for simultaneous measurements of energy and time. In equation form, ΔEΔt≥h4πΔEΔt≥h4π, where ΔE is the uncertainty in energy and Δt is the uncertainty in time. This means that within a time interval Δt, it is not possible to measure energy precisely—there will be an uncertainty ΔE in the measurement. In order to measure energy more precisely (to make ΔE smaller), we must increase Δt. This time interval may be the amount of time we take to make the measurement, or it could be the amount of time a particular state exists, as in the next Example 2.
EXAMPLE 2. HEISENBERG UNCERTAINTY PRINCIPLE FOR ENERGY AND TIME FOR AN ATOM
An atom in an excited state stores energy for a short period of time. What is the minimal uncertainty in the energy of the state in eV if the duration of this excited state is measured to be 1.0 1010 s?
Strategy
The equals sign in Etth4Etth4 is used to find the least uncertainty in energy E, which corresponds to a suitable option for the uncertainty in time. The whole lifespan of the excited state, or t = 1.0 1010 s, has the greatest time uncertainty.
Solution
Solving the uncertainty principle for ΔE and substituting known values gives
ΔE=h4πΔt=6.63×10−34 J⋅ s4π(1.0×10−10 s)=5.3×10−25 J
Now converting to eV yields
ΔE=(5.3×10−25 J)(1 eV1.6×10−19 J)=3.3×10−6 eV
Discussion
Excited states in atoms have a lifetime of 1010 s, which means they swiftly release their accumulated energy on human time scales. The energy uncertainty is merely a few millionths of an eV. When compared to the normal excitation energy in atoms, which are on the order of 1 eV, this uncertainty is negligible. As a result, the uncertainty principle restricts the precision with which we can measure the lifetime and energy of such states, but only slightly.
If a system's lifespan is very short, the uncertainty principle for energy and time can be quite important. Then t is very tiny, and E is quite large as a result. Some nuclei and exotic particles have extremely short lifetimes (as little as 1025 s), resulting in energy uncertainty of many GeV. (109 eV). Because stored energy manifests as increased rest mass, the rest mass of short-lived particles is subject to considerable uncertainty. When masses or decay energies are measured repeatedly, a spread of masses or energies is obtained. E is the spread. You might wonder if this energy uncertainty may be prevented by not calculating lifetime. No, that is not the case. Nature is aware of the lifetime, and its shortness has an impact on the particle's energy. This is so well established empirically that the lifespan of short-lived states is calculated using the uncertainty in decay energy. It's difficult to measure the lifetime of some nuclei and particles since they are so short-lived. However, if their decay energy can be determined, the spread is E, which is employed in the uncertainty principle (Eth4) to compute the lifetime t.
The uncertainty principle has another implication for energy and time. If E is unclear about energy, then E can break energy conservation for a time t. If the breach is transitory and lower than the uncertainty in energy, neither physicists nor nature can detect if conservation of energy has been violated. While this may appear benign at first, as we will learn in later chapters, it allows for the temporary formation of matter from nothing and has ramifications for how nature transmits forces over extremely short distances.
Finally, we mentioned that individual measurements create exact or particle-like findings in our explanation of particles and waves. Each time we detect an electron, for example, a precise position is obtained. Repeated measurements, on the other hand, yield a range of values that is consistent with wave characteristics. “What there are, are particles,” said the brilliant theoretical physicist Richard Feynman (1918–1988). When you watch enough of them, they begin to disseminate themselves in the way that a wave would. We can't discern what they are while they go, though, since when we try to measure, we change the way they travel.
3.2.4 On the basis of Heisenberg's uncertainty principle, show that the electron can not exist within the nucleus.
Radius of the nucleus is of the order of 10-15 m and thus maximum uncertainity in the position of electron i.e. ∆x if it is within the nucleus will be 10-15 m.
Now, ∆x m∆V ≥ h/4π
Or, ∆V = 6.626 × 10-34 / 4 × 3.14 × 9.1 × 10-31 × 10-15 = 5.97 × 1010 m/s
As this level of uncertainty in velocity is impossible to be achieved hence electron can not exist in the nucleus.
Key takeaway:
In quantum physics, Heisenberg's uncertainty principle is a crucial concept. It goes something like this: if we know exactly where a particle is (the uncertainty of position is tiny), we know nothing about its momentum (the uncertainty of momentum is huge), and vice versa.
3.3.1 Nuclear Forces
The forces that act between two or more nucleons are known as nuclear forces (also known as nuclear interactions or strong forces). They form atomic nuclei by binding protons and neutrons ("nucleons"). The nuclear force is tens of millions of times more powerful than the chemical bonds that keep atoms in molecules together. This is why, when compared to chemical fuels like oil or coal, nuclear reactors produce around a million times more energy per kilogramme of fuel. However, the nuclear force has a limited range, only a few femtometers (1 fm =1015 m), after which it rapidly declines. That is why, despite its immense strength, we are unaware of its existence on an atomic scale or in everyday life. For seven decades, some of the world's greatest physicists have been working on a proper theory of nuclear forces, and it has been one of the most important areas of physics research in the twentieth century. The initial theory was that the force is created by the exchange of mesons, which are lighter than nucleons, and this theory spawned a new branch of modern physics known as (elementary) particle physics. The nuclear force is now thought to be a residual interaction (similar to the van der Waals force between neutral atoms) of a stronger force between quarks, which is mediated by gluon exchange and maintains quarks together inside a nucleon.
3.3.2 Historical perspective
It was obvious after Chadwick's discovery of the neutron in 1932 (Chadwick, 1932) that the atomic nucleus is made up of protons and neutrons. Electromagnetic forces cannot be the cause of the nucleus' elements adhering together in such a system. The nucleus should be blown apart by the repulsive electrical Coulomb interaction between the protons. As a result, the idea of a new strong nuclear force was proposed. Hideki Yukawa (Yukawa,1935), a Japanese scientist, proposed the original theory for this new force in 1935, claiming that nucleons would exchange particles between each other and this mechanism would create the force. Yukawa's theory is based on the electromagnetic interaction hypothesis, in which the force is caused by the exchange of a (massless) photon. In the case of the nuclear force, Yukawa postulated that the "force-makers" (later dubbed "mesons") have a mass that is a fraction of the mass of the nucleon. Because heavy particles may only travel a finite distance due to the uncertainty principle, the force's effect is limited to a finite range. Yukawa's predicted meson, the pion, was discovered in 1947 in cosmic ray and in 1948 in the laboratory. Yukawa won the Nobel Prize for Physics in 1949. More mesons were discovered in accelerator operations in the 1950s and 1960s, and the meson theory of nuclear forces was expanded to incorporate many more mesons. These models became known as one-boson-exchange models, which refers to the fact that the individual mesons in this model are traded separately. At low energies, the one-boson-exchange model is quite good in explaining almost all aspects of the nucleon-nucleon interaction. In the 1970s and 1980s, meson models that went beyond the conventional single-particle exchange mechanism were also devised. The explicit exchange of two pions, with all its complexities, was included in these models. The Paris (Lacombe et al., 1980) and Bonn potential models are well-known examples of the latter type (Machleidt et al., 1987).
These meson models appeared to be the solution to the nuclear force problem since they were numerically highly successful. When it was discovered (in the 1970s) that quantum chromodynamics (QCD) rather than meson theory is the fundamental theory of strong interactions, all "meson theories" had to be considered as models, and attempts to derive a real theory of the nuclear force had to start all over again.
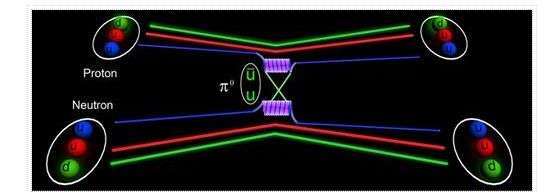
There are two issues in deriving nuclear forces from QCD. First, each nucleon is made up of three quarks, therefore a two-nucleon system is already a six-body problem. Second, the force between quarks, which is formed by the interchange of gluons, has the property of being extremely strong at the low energy scales found in nuclear physics. Finding “convergent” mathematical solutions is challenging due to this remarkable strength. As a result, the models offered in the initial round of fresh attempts were simply "QCD-inspired." These models have the advantage of attempting to explain both nucleon structure (three quarks) and nucleon-nucleon interactions (six-quark systems) on an equal footing. Such models successfully describe some of the gross properties of the two-nucleon force, such as the "hard core" (see below). However, it should be stressed that these quark-based approaches are just another set of models, not a theory, from a critical standpoint. Alternatively, by placing the six-quark system on a four-dimensional lattice of discrete points that symbolises three dimensions of space and one dimension of time, one can try to solve the six-quark issue with sheer computing power. Lattice QCD is the name given to this approach, which is making progress. Such computations, however, are computationally prohibitively expensive and so cannot be utilised as a conventional nuclear physics instrument.
When Nobel Laureate Steven Weinberg applied the concept of an Effective Field Theory (EFT) to low-energy QCD about 1990, he made a big breakthrough (Weinberg, 1979, 1991). He just typed down the most general theory that is consistent with all of the properties of low-energy QCD, as this theory would be identical to low-energy QCD. The so-called chiral symmetry, which is “spontaneously” violated, is a particularly essential characteristic. Chiral symmetry is observed by massless particles, which means that their spin and momentum are either parallel (“right-handed”) or anti-parallel (“left-handed”) and will remain thus indefinitely. Because the quarks that make up nucleons ("up" and "down") are virtually massless, near chiral symmetry is a given. This symmetry, naively, should lead to the discovery of mesons of the same mass in nature, but with positive and negative parity. This is not the case, and such failure is referred to as a "spontaneous" symmetry break. The spontaneous breaking of a symmetry creates a particle, which in this case is the pion, according to a theory first demonstrated by Jeffrey Goldstone. As a result, the pion becomes a key participant in the development of nuclear weapons. When compared to the interaction of gluons with quarks, the interaction of pions with nucleons is weak. As a result, pion-nucleon reactions may be estimated easily. Furthermore, this effective field theory can be extended in terms of powers of momentum over "scale," where scale refers to the "chiral symmetry breaking scale," which is around 1 GeV (= 109 eV). Chiral Perturbation Theory (ChPT) is a theory that allows you to compute the numerous terms that make up the nuclear force power by power, or order by order. Another benefit of the chiral EFT method is that it may generate forces between two nucleons as well as many-nucleon forces on the same basis. The chiral EFT technique is becoming increasingly popular in modern theoretical nuclear physics and is being used with considerable effectiveness.
3.3.3 Properties of the nuclear force
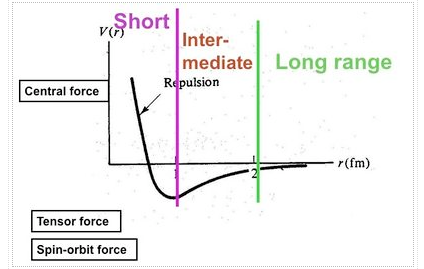
The properties of nuclei can be used to determine some properties of nuclear interactions. The volume of nuclei rises according to the quantity of nucleons, a phenomenon known as saturation. This feature implies that the nuclear (central) force has a short range (a few fm) and is extremely attracting at that range, explaining nuclear binding. The nuclear force, on the other hand, has a complex spin-dependence. The observation that the deuteron (the proton-neutron bound state, the lowest atomic nucleus) deviates somewhat from a spherical shape: it has a non-vanishing quadrupole moment was the first proof of this attribute. This proposes a force that is determined by the orientation of the nucleons' spins in relation to the vector connecting the two nucleons (a tensor force). A shell structure has been seen in heavier nuclei, which, according to M. G. Mayer and J. H. D. Jensen, can be explained by a strong force between the nucleon's spin and its orbital motion (the spin-orbit force). Scattering experiments, in which one nucleon is scattered off another nucleon with differing spin orientations, provide more direct evidence for spin dependence. The presence of the nuclear spin-orbit and tensor forces has been demonstrated in such tests. At higher energies (more than 200 MeV), scattering measurements show that the nucleon-nucleon interaction becomes repulsive at short inter-nucleon distances (smaller than 0.5 fm, the hard core).
There are three-nucleon forces (3NFs), four-nucleon forces (4NFs), and so on, in addition to the force between two nucleons (2NF). The 2NF, on the other hand, is far more powerful than the 3NF, which is far more powerful than the 4NF, and so on. The importance of 3NFs has been demonstrated in exact computations of the properties of light nuclei based on the "elementary" nuclear forces. Their contribution is tiny, yet it is critical. The necessity for 4NFs to explain nuclear properties hasn't been proven (yet).
When electromagnetic forces are neglected, nuclear forces are essentially charge-independent, meaning that the force between two protons, two neutrons, and a proton and a neutron is almost the same (in the same quantum mechanical state).
3.3.4 Phenomenological approaches
Traditionally, nuclear force research has been divided into two categories: phenomenology and theory. To begin, we'll look at phenomenology. At very low energies, nucleon-nucleon scattering can be represented by the so-called effective range expansion, which has just two parameters in its simplest form (Bethe, 1949); for a textbook exposition, see Brown and Jackson (1976). This expansion has been recovered in modern times from an EFT that does not include the pion ('pionless EFT'); for an introduction, see Bedaque and van Kolck (2002). The spin-dependence of the nuclear force becomes significant at intermediate energies. Okuba and Marshak (1958) imposed the following symmetries to derive a general equation for the NN potential (that incorporates spin and momentum dependences):
Invariance in translation
Invariance of Galileo
Invariance of rotation
Invariance of space reflection
Invariance of time reversal
Invariance when particle 1 and 2 are interchanged
3.3.5 The meson theory of nuclear forces
Yukawa's idea of 1935
In 1935, Yukawa (1935) introduced the concept of massive particle exchange to explain the nuclear force. He constructed an analogy to classical electrodynamics. In electrodynamics, the Coulomb potential
ϕ(r)=q4π1r
Is the solution of Poisson's equation
∇2ϕ(r⃗ )=−qδ(3)(r⃗ ).
When adding a mass term to this equation (and flipping the sign on the r.h.s. To adjust for scalar coupling),
(∇2−m2)φ(r⃗ )=gδ(3)(r⃗ ),
The solution becomes
φ(r)=−g4πe−mrr,
Which is the scalar field generated by one nucleon. A second nucleon, with also coupling g, at a distance r from the first one will be exposed to the interaction energy
V(r)=−g24πe−mrr,
Which is known as the Yukawa potential. The exponential in this expression, that is due to the mass m of the meson, restricts the potential to a finite range, which is the essential point. For m→0 we are back to the form of the Coulomb potential.
3.3.6 The one-boson-exchange model
The initial derivation by Yukawa was for scalar bosons. When a true meson was discovered in 1947/48, it was discovered to be pseudo-scalar with a mass of roughly 138 MeV, and it was named the -meson or pion. As a result, attempts to derive the nuclear force in the 1950s concentrated on ideas that solely incorporated pions. These 'pion theories' had numerous flaws and failed miserably—for reasons we now understand: pion dynamics is bound by chiral symmetry, a concept unknown in the 1950s. Heavier (non-strange) mesons, such as the vector (spin-1) mesons (770) and (770), were discovered in experiments in the early 1960s (782). Theoreticians were eager to extend meson theory by integrating more and diverse species of mesons because of the challenges with pion theories. This led to the development of one-boson-exchange (OBE) models in the 1960s, which proved to be quite successful for the two-nucleon interaction.
Let's start with the question of which mesons to think about. When calculating the nuclear force, the forecasts for the longer flung sections are often more reliable. Because the range of a meson's force, R, is inversely proportional to the mass of the meson, m,

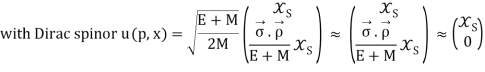
Where E = 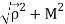 and
and  is a two-component Pauli spinor.
is a two-component Pauli spinor.
Lagrangian: 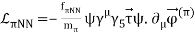
Vertex: I times the Lagrangian stripped off the fields ( for an incoming pion)
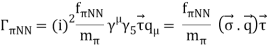
Potential: I times the amplitude ( Pπ = I, q2 = - 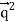 )
)
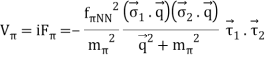
Using the operator identity
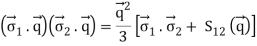
With 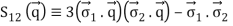 (“Tensor operator”)
(“Tensor operator”)
The one-pion exchange potential (OPEP) can be written as
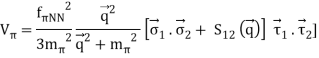
Lagrangian: 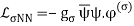
Vertex: 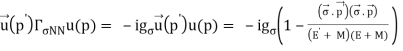
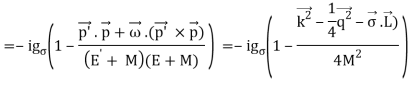
Potental: keeping all terms up to Q2/ M2 [ Pσ = i, 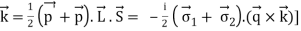
Vσ =  =
= 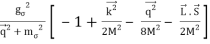
Lagrangian: 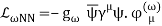
Vertex:
μ = 0: 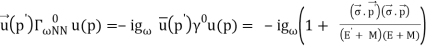

Potential, including also the 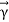 terms : [ Pω
terms : [ Pω 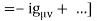
Vω 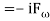 =
= 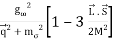
Starting with the lightest mesons, one progresses to mesons with masses in the order of the mass of the nucleon. This fundamentally comprises six mesons (PDG, 2012), namely (138), (548), (500), (770), (782), and a0(980), where the masses in MeV are indicated by the numbers in parenthesis. As it turns out, and a0 aren't particularly essential (Machleidt, 1989), so we'll concentrate on the pseudo-scalar isovector pion (0,1), the scalar isoscalar sigma (0+,0), and the scalar isoscalar sigma (0+,0).
The isoscalar vector omega (1,0),
Rho (1,1), the vector isovector
The parenthetical information (JP,I) summarises each particle's spin J, parity P, and isospin I.
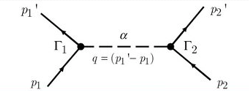
Yukawa's initial calculations were based on classical field theory. A more proper derivation, as we will employ here, should be based on quantum field theory. The mesons are exchanged single in the one-boson-exchange (OBE) model, as depicted in Figure 4's Feynman diagram. The contributions of the various mesons to the NN potential are calculated in Figures 5 to 8. We always begin with an acceptable interaction Lagrangian for meson-nucleon coupling, which is built using symmetry principles as a guide (the Lagrangian must be a Lorentz scalar). We should notice that the Lagrangians for the vector mesons and (Figures 7 and 8) can have both a vector and a tensor coupling (with coupling constants gv and fv, respectively):
LvNN=gv (v)fv4M (v)
The interaction of a photon with a nucleon is analogous to these two couplings. The first relates to the Dirac current's coupling to the electromagnetic vector potential, while the second corresponds to the anomalous magnetic moment's Pauli coupling. The close resemblance is not coincidental; the vector-meson dominance model (VDM) for the nucleon's electromagnetic form factor explains it. The VDM assumes that the photon links to the nucleon through a vector boson, which explains the nucleon electromagnetic form factor's extended shape. The coupling constants ratio, f/g, should be 3.7 under a strict interpretation of this model, and dispersion analysis yields even f/g6. In any event, the tensor coupling of the is substantially more than its vector coupling, which is why the vector coupling was removed in Figure 8. It's the other way around for the meson: the vector dominance model predicts a coupling constants ratio of f/g=0.12 for the meson. In most meson models, the is given no tensor coupling because it is close to zero (cf. Figure 7).
The vector boson propagator in its entirety is
Pv=ig+qq/m2vq2m2v, Pv=ig+qq/m2vq2m2v (7)
Where the qq/m2v-term was removed in Figures 7 and 8. This term vanishes on-shell, but not off-shell, due to nuclear current conservation. Holinde and Machleidt (1975) investigated the off-shell effect of this word and found it to be insignificant.
To ensure that the scattering equation converges, it is common practise to multiply the vertices with cutoffs that suppress high-momentum components. For these cutoffs, a simple form is
(m2+q 2)n, (m2+q)n, (m2+q)n, (m2+q)n, (m2+q)n
The cutoff mass is usually set anywhere between 1.3 and 2.0 GeV. Our derivations do not explicitly show the multiplication by these form factors. The computation is carried out in momentum space and in the center-of-mass (CMS) system of the two interacting nucleons, with p1=(E,p ) and p2=(E,p ) in the initial states and p′1=(E′,p′) and p′2=(E′,p′) in the final states, respectively. Furthermore,
q k L S12(q) q k L S12(q) q k L S12(q) q k L
12(p ′+p )=p ′+p )=p ′+p )=p ′+p )=p ′+p )=p ′+p )=p
i(q k )=i(p ′p )=i(q k )=i(q k )=i(q k )=i(q k )=i(q k )
1 q 2 q 1 q 1 q 1 q 1 q 1 q 1 q 1 q 1 q 1 2 is the tensor operator in momentum space, the average momentum, the total orbital angular momentum in momentum space, and the momentum transfer. (eight)
Table 1 summarizes the characteristic qualities of the contributions from the various mesons derived in Figures 5 to 8.
The OBE NN potential (OBEP) is defined as the sum of the contributions from the four mesons mentioned above, plus a few others, such as,
Lagrangian: 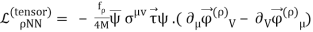
Vertex 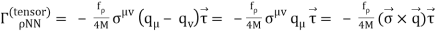
(incoming meson)
Potential: [ Pρ = - igμv + . . . ]

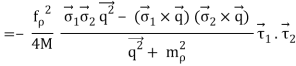
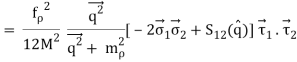
VOBE=∑α=π,σ,ω,ρ,η,a0Vα.(9)
Meson | Central | Spin-Spin | Tensor | Spin-Orbit |
π(138) | --- | Weak, long-ranged | Strong, long-ranged | --- |
σ(500) | Strong, attractive, intermediate-ranged | --- | --- | Moderate, intermediate-ranged |
ω(782) | Strong, repulsive, short-ranged | --- | --- | Strong, short-ranged, coherent with σ |
ρ(770) | --- | Weak, short-ranged, coherent with π | Moderate, short-ranged, opposite to π | --- |
Table: The four most important mesons and the main characteristics of their contributions to components of the nuclear force. | ||||
3.3.7 Relativistic OBEPs
The first OBEPs were created along the lines described above: starting with an OBE's Feynman amplitude, one executes a Q/M expansion up to terms of order (Q/M)2. This procedure was motivated by two factors: First, one wanted to see how the interchange of different mesons produced distinct force components (e.g., central, spin-spin, tensor, spin-orbit, etc.). Second, early researchers favoured a local potential in position space, i.e., an analytic formulation for the potential based on the relative distance between the two nucleons, r. This necessitates the ability to do the Fourier transform of the momentum space equations analytically.
Calculations in position space, on the other hand, are not required. Calculations of NN scattering and nuclear bound states can be done in momentum space just as effectively, and often more elegantly. In momentum space, locality is not a concern and offers no benefits. The original relativistic Feynman amplitudes of OBE are functions of p′ and p, and VrelOBE(p′,p)=iF(p′,p) is the relativistic OBEP.
Figure shows F(p′,p) being evaluated in full beauty and without approximations. The Bethe-Salpeter equation (Salpeter and Bethe, 1951) describes two-nucleon scattering in a covariant way, and VrelOBE is used to solve it. Due to the difficulty of solving the four-dimensional Bethe-Salpeter (BS) equation (Fleischer and Tjon, 1975), relativistic three-dimensional (3D) versions of the BS problem are widely utilised, which are easier to solve numerically. The time component of the relative momentum is set in some covariant fashion in the derivation of all relativistic three-dimensional equations, so it no longer exists as a separate variable. As a result
Vrel3DOBE(p′,p)VrelOBE(p′,p)Vrel3DOBE(p′,p).
3.3.8 Beyond the OBE approximation
The OBE model simplifies the difficult scenario of a meson theory for the NN interaction significantly. Consequently, despite the quantitative effectiveness of the OBEPs, we should be cautious about the model's approximations. The scalar isoscalar'meson' of around 500 MeV, as well as the omission of any non-iterative diagrams, are major considerations.
The significance of meson-nucleon resonances
When two pions are 'in the air,' they can have a lot of interaction. They form a correct resonance, the meson, when in a relative P-wave (L=1). They can also interact in the form of a relative S-wave (L=0), resulting in the boson. Even though the Particle Data Group identifies a f0(500) or (500) meson with a width of 400-700 MeV, it is debatable if the is a legitimate resonance. What is certain is that two pions exhibit correlations, and if one does not believe in the existence of a two-pion resonance, one must account for these correlations. Dispersion theory and field theory are the two main methodologies for dealing with the two-pion exchange contribution to the NN interaction (which provides the intermediate range attraction).
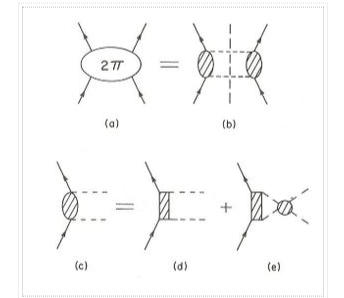
Figure depicts the dispersion-theoretic image schematically. This method requires that the whole diagram (a) may be broken down into two 'halves' (b). All potential processes that two pions and a nucleon can go through are represented by the hatched ovals. This is made clearer in (d) and (e) (e). All conceivable baryon intermediate states, including the nucleon, are represented by the hatched boxes. (It's worth noting that there are some exchanges that aren't represented.) Scattering is shown by the shaded circle. These processes are taken into account quantitatively by using empirical data from N and scattering (e.g. Phase shifts) as the input for such a calculation. Dispersion relations then produce an on-shell NN amplitude, which is represented as a potential with some form of realistic prescription. The Paris potential (Lacombe et al., 1980) is built along these lines, with one-pion-exchange and -exchange added for good measure. We direct interested readers to an educational paper authored by Vinh Mau for further information (1979).
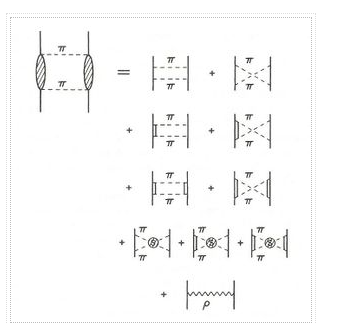
Figure depicts a field-theoretic model for the 2-exchange contribution. Isobar and correlation contributions are also included in the model. This can be regarded in the same way as the picture of dispersion relations. Only the lowest-lying N resonance, the so-called isobar (spin 3/2, isospin 3/2, mass 1232 MeV), is taken into consideration in general. Other resonance contributions have been shown to be minor for the low-energy NN processes under study. The isobar is treated as an elementary (Rarita-Schwinger) particle in a field-theoretic model. Figure 11's six upper diagrams depict uncorrelated 2 exchange. The two-particle exchanges that are crossed (non-iterative) (second diagram in each row) are crucial. Due to characteristic cancellations in the isospin dependent regions of box and crossed box diagrams, they ensure correct (very weak) isospin dependence. Furthermore, their contribution is comparable to that of the related box diagrams (iterative diagrams), therefore they are not insignificant. In addition to the procedures mentioned, linked 2 exchange must be taken into account (lower two rows of Figure 11). In terms of magnitude, these contributions are comparable to those from uncorrelated activities.
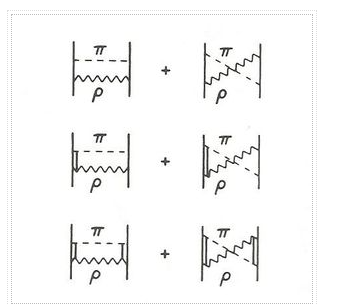
There are contributions from a mix of different mesons in addition to the contributions from two pions. The combination of and is especially crucial, as shown in Figure. This contribution is repulsive, and it is necessary to dampen the 2 exchange contribution at high momenta (or short distances), which is too powerful on its own.
The Bonn Full Model (Machleidt et al., 1987), which incorporates all of the diagrams seen in Figures 11 and 12, as well as single and exchange, is the most developed meson-theoretic model for the NN interaction. Apart from that, the Bonn Full Model includes non-iterative graphs of and andandand exchanges. The aggregate contribution of the latter two sets of diagrams, on the other hand, is minimal and insignificant.
Highly sophisticated models, such as the Paris and Bonn potentials, can be used to check the approximations made in the simple OBE model. The enormously intricate 2 exchange contributions to the NN interaction regulated by the diagrams can, as it turns out, be well represented by the single scalar isoscalar boson, the, with a mass of roughly 550 MeV. This fact serves as retroactive support for the simple OBE model.
Noteworthy examples
- Bryan and Scott (1964, 1967, 1969), position-space OBEPs, are among the first examples of meson-theoretic NN potentials.
- Early Bonn potentials (Erkelenz, 1974), relativistic momentum-space OBEPs (Holinde and Machleidt, 1975).
- Position-space OBEP of the early Nijmegen potential (Nagels et al., 1978).
- Position-space potential, 2 from dispersion theory plus and (Lacombe et al., 1980), Paris potential (Lacombe et al., 1980).
- The most thorough meson-theoretic model for the NN interaction ever constructed is the Bonn Full Model (Machleidt et al, 1987).
- 2/datum1 for fit of NN data, high-precision Nijmegen potential (Stoks et al., 1994), charge-dependent position-space OBEP
- 2/datum1 for fit of NN data, charge-dependent momentum-space OBEP (Machleidt, 2001), high-precision Bonn potential (CD-Bonn) (Machleidt, 2001).
- Gross and Stadler (2008), relativistic OBEP with the Gross equation and reliable np data fit.
This may have been the joyful ending for nuclear forces hypothesis. However, since QCD has risen to the top of the authoritative theory of strong interactions, meson theory has been demoted to a lower level of a model (though a beautiful one), and we must start over—-in the next part.
3.3.9 QCD and the nuclear force
The theory of strong interactions is known as quantum chromodynamics (QCD). It is part of the Standard Model of Particle Physics and deals with quarks, gluons, and their interactions. Color SU(3) is the underlying gauge group of QCD, which is a non-Abelian gauge field theory. The theory's non-Abelian character has far-reaching implications. While the interaction between coloured particles is weak at short distances or with high momentum transfer (asymptotic freedom), it is strong over long distances (1fm) or with low energies, resulting in the confinement of quarks into colourless hadrons. As a result, at high energies, QCD allows for perturbative analysis, whereas at low energies, it is highly non-perturbative. The force between nucleons is a residual colour interaction, analogous to the van der Waals force between neutral molecules, and it exists at low energies. As a result, the nuclear force is an extremely difficult issue in terms of quarks and gluons that can be tackled with brute computer power on a discretized, Euclidean space-time lattice (known as lattice QCD). The neutron-proton scattering lengths in the singlet and triplet S-waves in completely dynamical lattice QCD with a lowest pion mass of 354 MeV were found in a recent study (Beane et al., 2006). Using chiral perturbation theory, this conclusion is then extended to the physical pion mass. The 354 MeV pion mass is still too huge for meaningful extrapolations, but the feasibility has been established, and additional work is expected in the near future. The nucleon-nucleon (NN) potential was examined in a different form of lattice calculation (Hatsuda, 2012). The centre component of the potential has a repulsive core with a medium-range attraction. This is a really promising outcome, although it should be remembered that enormous pion masses are still being used in this study. In any case, advanced lattice QCD calculations are in the works and becoming better all the time. However, because these computations take a long time and are costly, they can only be used to check a few sample significant issues. A more efficient methodology is required for everyday nuclear structural physics.
3.3.10 The chiral effective field theory approach to nuclear forces
An effective field theory is the most efficient technique (EFT). It is critical to determine a scale separation when developing an EFT. A considerable difference between the masses of the pions and the masses of the vector mesons, such as (770) and (782), may be seen in the hadron spectrum. As a result, it is reasonable to believe that the pion mass determines the "soft scale," Qm, while the rho mass determines the "hard scale," m, also known as the chiral-symmetry breaking scale. This suggests that an expansion in terms of the soft scale over the hard scale, Q/, should be considered. In terms of relevant degrees of freedom, we've already established that quarks and gluons are ineffectual degrees of freedom for the ground state and low-energy excitation spectrum of an atomic nucleus, as well as for ordinary nuclear processes, whereas nucleons and pions are (this may include also low-lying nucleon resonances, s. Below). To ensure that this EFT is more than a phenomenology, it must have a strong connection to QCD. The relationship is formed by having the EFT witness all of the underlying theory's relevant symmetries. Weinberg's "folk theorem" (Weinberg, 1979) is the basis for this requirement:
The result will simply be the most general possible S-matrix consistent with analyticity, perturbative unitarity, cluster decomposition, and the assumed symmetry principles if one writes down the most general possible Lagrangian, including all terms consistent with assumed symmetry principles, and then calculates matrix elements with this Lagrangian to any given order of perturbation theory.
The EFT programme, in brief, consists of the following steps:
1. Determine the proper soft and hard scales, as well as degrees of freedom, for (low-energy) nuclear physics.
2. Identify the relevant low-energy QCD symmetries and analyse whether and how they are broken.
3. Construct the most general Lagrangian that is consistent with those symmetry breakings and symmetries.
4. Create an organisational structure that can differentiate between important and little contributions: a low-momentum growth.
5. Using the expansion as a guide, calculate Feynman diagrams for the situation at hand to the appropriate accuracy.
(Weinberg, 1991), (Ordonez et al., 1994), (Kaiser et al., 1997) are important publications on the issue (Epelbaum et al., 2009). There is a review with a fairly educational start in (Machleidt and Entem, 2011).
The chiral EFT, which scales with the -mass and contains pion degrees of freedom, is presented here. However, the -mass is not the only (hard) scale available. Other scales may be more suited depending on the energy we're interested in. If we want to focus on a nuclear situation at very low energy (m), for example, we should use the pion-mass, m, as a scale. Because such EFT can no longer have pion degrees of freedom, it is referred to as pionless EFT. It contains solely of contact phrases. As a result, though this pionless EFT may appear frighteningly simple at first glance, it turns out to have some rather exciting properties, particularly in terms of renormalization and power counting (s. Below). Because it is beyond the scope of this essay to go into detail about pionless EFT, we would like to direct interested readers to Bedaque and van Kolck (2002) and van Kolck (2002) good review studies (2007).
We'll go through each of the actions described above in detail in the subsections that follow. Since we've previously covered the first step, we'll go on to step two.
Symmetries of low-energy QCD and their breakings
The QCD Lagrangian reads LQCD=q¯(iγμDμ−M)q−14Gμν,aGμνa(10) with the gauge-covariant derivative
Dμ=∂μ−igλa2Aμ,a(11)
And the gluon field strength tensor (note that for SU(N) group indices, we use Latin letters, …,a,b,c,…,i,j,k,…, and, in general, do not distinguish between subscripts and superscripts)
Gμν,a=∂μAν,a−∂νAμ,a+gfabcAμ,bAν,c.(12)
In the above, q denotes the quark fields and M the quark mass matrix. Further, g is the strong coupling constant and Aμ,a are the gluon fields. The λa are the Gell-Mann matrices and the fabc the structure constants of the SU(3)color Lie algebra (a,b,c=1,…,8); summation over repeated indices is always implied. The gluon-gluon term in the last equation arises from the non-Abelian nature of the gauge theory and is the reason for the peculiar features of the color force.
The masses of the up (u), down (d), and strange (s) quarks are (PDG, 2012):
Mumdms===2.3±0.7 MeV,4.8±0.7 MeV,95±5 MeV.(13)(14)(15)
These masses are small as compared to a typical hadronic scale, i.e., a scale of low-mass hadrons which are not Goldstone bosons, e.g., mρ=0.78 GeV≈1 GeV.
It is therefore of interest to discuss the QCD Lagrangian in the limit of vanishing quark masses:
L0QCD=q¯iγμDμq−14Gμν,aGμνa.
Defining right- and left-handed quark fields,
QR=PRq,qL=PLq,
With
PR=12(1+γ5),PL=12(1−γ5),
We can rewrite the Lagrangian as follows:
L0QCD=q¯RiγμDμqR+q¯LiγμDμqL−14Gμν,aGμνa.
This equation reveals that the right- and left-handed components of massless quarks do not mix in the QCD Lagrangian. For the two-flavor case, this is SU(2)R×SU(2)L symmetry, also known as chiral symmetry. However, this symmetry is broken in two ways: explicitly and spontaneously.
3.3.11 Spontaneous symmetry breaking
A (continuous) symmetry is said to be spontaneously broken if the Lagrangian symmetry is not realised in the system's ground state. There is evidence that the QCD Lagrangian's (approximate) chiral symmetry is spontaneously broken—-for nonperturbative dynamical causes that are not fully understood at this time. The hadron spectrum provides the most convincing evidence.
The existence of degenerate hadron multiplets of opposite parity is naively expected from chiral symmetry, i.e., for each hadron of positive parity, one would expect a degenerate hadron state of negative parity, and vice versa. These 'parity doublets', however, do not exist in nature. Consider the -meson, which is a negative parity (JP=1) vector meson with a mass of 776 MeV. A 1+ meson, the a1, does exist, however it has a mass of 1230 MeV and so cannot be considered degenerate with the. The meson, on the other hand, has three charge states (corresponding to three isospin states), the, and the 0, each with a mass difference of only a few MeV. Thus, SU(2)V (isospin) symmetry is well seen in the hadron spectrum, whereas axial symmetry is destroyed: SU(2)RSU(2)L is broken down to SU(2)V.
The presence of (massless) Goldstone bosons is implied by a spontaneously violated global symmetry. The isospin triplet of (pseudoscalar) pions is associated with the Goldstone bosons, which explains why pions are so light. The masses of the pions aren't quite zero since the masses of the up and down quarks aren't quite zero either (explicit symmetry breaking). As a result, pions are a truly unusual species: they exhibit both implicit and explicit symmetry violation. At low energies, Goldstone bosons have a weak interaction. Because they are degenerate in comparison to the vacuum, interactions between them must vanish at zero momentum and at the chiral limit (m0).
3.3.12 Chiral effective Lagrangians
Building the most general Lagrangian consistent with the (broken) symmetries outlined above is the next phase in the EFT programme. Callan et al. (1969), who figured out the group-theoretical underpinnings of non-linear realisations of chiral symmetry, devised an elegant framework for the creation of such Lagrangians. When functions of the Goldstone bosons appear in the Lagrangian, they are always accompanied by at least one space-time derivative, which is characteristic of these non-linear realisations. The following Lagrangians are based on the Callan et al. (1969) formalism.
The relevant degrees of freedom are pions (Goldstone bosons) and nucleons, as previously stated. Because Goldstone boson interactions must vanish at zero momentum transfer and in the chiral limit (m0), the Lagrangian's low-energy expansion is organised in powers of derivatives and pion masses. The chiral-symmetry breaking scale, 1 GeV, is the hard scale. As a result, the expansion is measured in powers of Q/, where Q denotes a (small) momentum or pion mass. The essence of chiral perturbation theory is this (ChPT).
The effective Lagrangian can be stated in formal terms as,
LNN contains two-nucleon contact interactions that consist of four nucleon-fields (four nucleon legs) and no meson fields, whereas L explains the interaction between pions and a nucleon. The ellipsis denotes phrases involving two nucleons plus pions and three or more nucleons with or without pions, which are relevant for nuclear many-body forces (see Eq. (20, below). Individual Lagrangians are arranged in the following order:
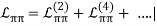
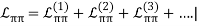

(17)
The number of derivatives or pion mass insertions (chiral dimension) is denoted by the superscript, while the ellipsis denotes terms of greater dimensions.
The Lagrangians have been sorted by the number of derivatives or pion-mass insertions. This is the typical method, which is particularly useful when considering - and -N scattering. It turns out that for nucleon interactions, it's sometimes more beneficial to consider the so-called index of the interaction, which is defined as the number of nucleons involved in the contact.
∆ ≡ d + n/2 – 2, (18)
Where n is the number of nucleon field operators and d is the number of derivatives or pion-mass insertions (nucleon legs). We'll now write down the Lagrangian in terms of increasing parameter values, using the so-called Heavy-Baryon (HB) formalism, which we'll denote with a "hat."
The Lagrangian reads with the lowest index,
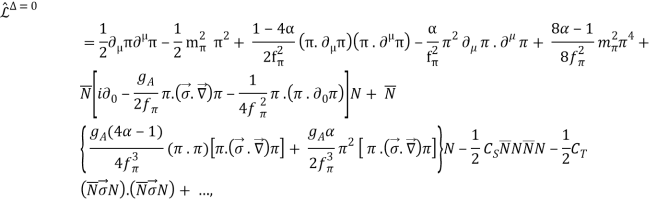
(19)
And higher-index Lagrangians are,
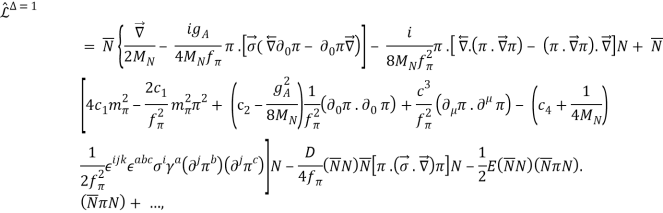

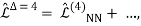 (22)
(22)
The ellipses reflect terms that aren't significant for deriving nuclear forces up to fourth order. (Fettes et al., 2000) has the LagrangianL(3)N, and the NN contact Lagrangians are given below. The heavy baryon nucleon field is denoted by N (N=N), while the pion fields are indicated by. Furthermore, the axial-vector coupling constant, pion decay constant, pion mass, and nucleon mass are represented by gA, f, m, and MN, respectively. These quantities' numerical values will be provided later. The ci are Low-Energy Constants (LECs) from the dimension two N Lagrangian, and is a parameter that arises in the pion field expansion; for further information, see (Machleidt and Entem, 2011). The results are unaffected by. The NN coupling constant, fNN, is related to the foregoing numbers by in the derivation of the one-pion-exchange potential in Figure 5.
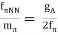 (23)
(23)
Cf. Eq. (33) below.
The lowest order (or leading order) NN Lagrangian has no derivatives and reads
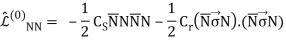
Where CS and CT are unknown constants which are determined by a fit to the NN data.
The second order NN Lagrangian can be stated as follows,
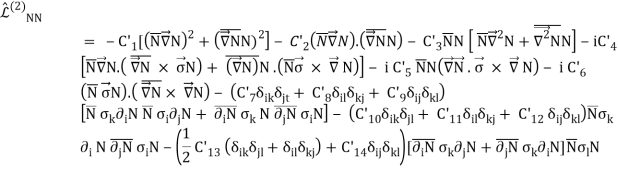
The C′i of Eq. (25) are unknown constants that are fixed via a fit to the NN data, similar to the CS and CT of Eq. (24). With higher order, these contact Lagrangians obviously blow up a lot, which is why we don't offer L(4)NN directly here. Below are the NN contact potentials that come from these Lagrangians.
3.3.13 Power counting
Effective Lagrangians have an infinite number of terms, allowing for the calculation of an endless number of Feynman graphs. As a result, we require a system that allows us to handle and calculate the theory. Chiral perturbation theory is a scheme that shows us how to discern between large (important) and minor (unimportant) contributions (ChPT).
In ChPT, graphs are evaluated in terms of powers of small external momenta on a large scale: (Q/)v, where Q stands for a momentum (nucleon three-momentum or pion four-momentum) or a pion mass, and 1 GeV stands for the chiral symmetry breaking scale (hadronic scale, hard scale). Power counting is the process of determining a person's power.
Irreducible graphs are used to construct the nuclear potential. An irreducible graph, by definition, is one that cannot be divided into two by cutting just nucleon lines. A nucleon propagator is Q1, a pion propagator is Q2, each derivative in any interaction is Q, and each four-momentum integration is Q4, according to Feynman's laws of covariant perturbation theory. Naive dimensional analysis is another name for this. The power of an irreducible diagram involving A nucleons can then be calculated using some topological identities.
v = - 2 + 2A – 2C + 2L + 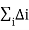
(28)
With
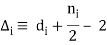
(27)
Where C is the number of separately connected pieces in the diagram and L is the number of loops; di is the number of derivatives or pion-mass insertions involved in vertex I and ni is the number of nucleon fields (nucleon legs); and the sum runs over all vertices I in the diagram under consideration. It's worth noting that i0 is true for all chiral symmetry-enabled interactions. Purely pionic interactions have at least two derivatives (di2,ni=0), pion-nucleon interactions have at least one (di1,ni=2), and nucleon-nucleon contact terms (ni=4) contain di0. This explains how chiral symmetry ensures that the expansion is low-energy.
The leading orders of connected multi-nucleon forces can be predicted using the power expression Eq. (26) Consider an A-nucleon system (mA) with an irreducibly connected m-nucleon diagram (m-nucleon force). C=Am+1 is the number of parts that are joined individually. v=2m4 is obtained by plugging this into Eq. (26) with L=0 and ii=0. Two-nucleon forces (m=2) begin at =0, three-nucleon forces (m=3) begin at =2 (but cancel in that order), and four-nucleon forces begin at =4 (they do not cancel). More on this in the following section.
For later purposes, we note that for an irreducible NN diagram (A=2, C=1), the power formula collapses to the very simple expression
v = 2L + 
(28)
In summary, the chief point of the ChPT expansion is that, at a given order ν, there exists only a finite number of graphs. This is what makes the theory calculable. The expression (Q/Λχ)ν+1 provides a rough estimate of the relative size of the contributions left out and, thus, of the accuracy at order ν. In this sense, the theory can be calculated to any desired accuracy and has predictive power.
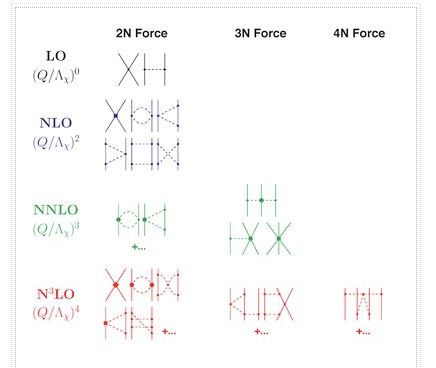
The hierarchy of nuclear forces: Overview
Nuclear forces develop as a hierarchy governed by the power v, according to chiral perturbation theory and power counting (Figure).
The NN potential is made up of two momentum-independent contact terms (Q0) in lowest order, also known as leading order (LO,=0), as depicted by the four-nucleon-leg graph with a little dot in the first row of Figure 13. In addition, the static one-pion exchange (1PE) is depicted in the second schematic in the first row of the picture. Of course, this is a crude approximation of the two-nucleon force (2NF), but it accounts for certain key properties. The 1PE describes NN scattering in peripheral partial waves with very high orbital angular momentum and gives the tensor force required to characterise the deuteron. The two contacts, which only participate in S-waves, offer the primitive short- and intermediate-range interaction at this order.
Due to parity and time-reversal invariance, all contributions vanish in the next order, v=1.
As a result, the next-to-leading order (NLO) is equal to 2. For the first time, two-pion exchange (2PE) happens ("leading 2PE"), and therefore the development of a more detailed description of the intermediate-range interaction begins (Ordonez et al., 1996). The vertices must have i=0 because the loop in each 2PE-diagram already implies =2 [cf. Eq. (28)]. As a result, only the lowest order NN and NN vertices are allowed at this order, which is why the leading 2PE is quite weak. In addition, there are seven new O(Q2) contact terms that participate in S and P waves, as indicated in the figure by the four-nucleon-leg graph with a solid square. A spin-orbit term, in addition to central, spin-spin, and tensor terms, is included in the operator structure of these connections. As a result, virtually all spin-isospin structures required to phenomenologically explain the two-nucleon force have been created. At this stage of growth, the fundamental flaw is a lack of intermediate-range attractiveness.
Finally, the problem is solved at order three (=3), the next-to-next-to-leading order (NNLO). The two-derivative NN seagull vertices (proportional to the ci LECs) are now included in the 2PE, as seen by a huge solid dot in Figure 13. These vertices exhibit intermediate (1232)-isobar contributions as well as associated 2PE contributions. These two contributions are critical for a realistic and quantitative 2PE model, as is well known from the meson phenomenology of nuclear forces. As a result, the 2PE now assumes a more realistic scale and roughly describes the nuclear force's intermediate-range attraction (Ordonez et al., 1996). Furthermore, at this order, the first relativistic adjustments are applied. Because contacts only appear in even numbers, there are no new contacts.
The reason we talk about a nuclear force hierarchy is that two-nucleon and many-nucleon forces are formed on an equal basis and appear in increasing numbers as we go up in order. The first set of nonvanishing three-nucleon forces (3NFs) occurs at NNLO, as seen in Figure 13's column '3N Force' (van Kolck, 1994). In truth, NLO, irreducible 3N graphs exist in the preceding order; nevertheless, it can be proved that these diagrams all cancel. When contrast to the 2NF, which starts at order (Q/)0, nonvanishing 3NF contributions happen initially at order (Q/)3.
At =4, the next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to For the first time, two-loop 2PE graphs appear (Kaiser, 2001), as does three-pion exchange (3PE), which requires two loops (Kaiser, 2000). At this level, the 3PE is insignificant. Most crucially, 15 new contact terms dubbed Q4 appear, which are represented by a solid diamond on a four-nucleon-leg graph. They contribute up to D-waves and include a quadratic spin-orbit term.
Tlab bin (MeV) | Number of np data | N3LO | NNLO | NLO |
0--100 | 1058 | 1.05 | 1.7 | 4.5 |
100--190 | 501 | 1.08 | 22 | 100 |
190--290 | 843 | 1.15 | 47 | 180 |
0--290 | 2402 | 1.10 | 20 | 86 |
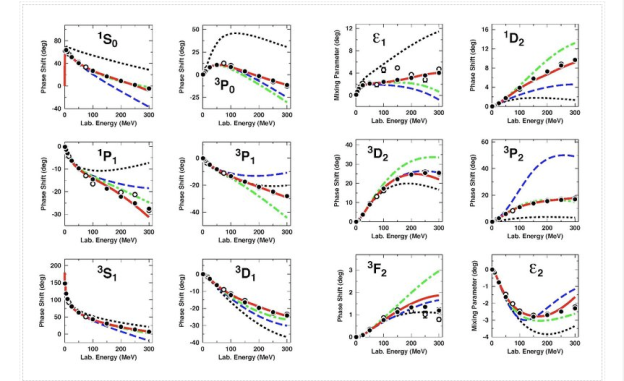
Table: 2/datum for chiral NN potentials at NLO, NNLO (Epelbaum et al., 2005), and N3LO in reproducing np data below 290 MeV. (Entem and Machleidt, 2003). The kinetic energy of the incident nucleon in the laboratory system is denoted by Tlab.
Furthermore, at N3LO, there are more 3NF contributions, and four-nucleon forces (4NFs) begin at this level. 4NFs are weaker than 3NFs because the leading 4NFs emerge one order higher than the leading 3NFs. As a result, ChPT provides a simple explanation for the empirically established fact that 2NF 3NF 4NF..
3.3.14 Comparison with conventional meson theory
We now have two ways that can both quantitatively explain the NN interaction, which is a non-trivial finding. It's only natural to wonder how the two techniques vary. There is a straightforward and revealing response.
The nuclear potential is enlarged in chiral EFT by raising the powers of tiny momenta, (Q/)v (Figure 13). In meson theory, the expansion is expressed in terms of Yukawas, Y(mr), which correspond to decreasing ranges 1/m for rising masses m. (cf. Figure 9).
Both approaches should be numerically equal to a significant extent because they describe the same difficult item. Figure 15 illustrates this point. First, both situations have a 1PE, which is insignificant. The 2PE may appear to be extremely dissimilar diagrammatically, however the figure depicts the relationship between the contributions. The fundamental distinction is that the 2PE in chiral EFT is built up order by order, whereas it comes as a single set in traditional meson theory. Finally, with heavy boson exchange (like -exchange) in meson theory and contacts in chiral EFT, the short-range contributions appear graphically very different. However, since Qm, a heavy-meson propagator can be stretched into a power series creating increasing-order contacts, as seen in Figure 16.
Although the two procedures are comparable, there are some reasons to believe that chiral EFT is preferable. Chiral EFT is more closely related to QCD due to chiral symmetry; it has an organisational scheme (power counting) that allows one to estimate the accuracy of the predictions (in a given order); and it has an organizational scheme (power counting) that allows one to estimate the accuracy of the predictions (in a given order).
On an equal footing, generates two- and many-body forces.
3.3.15 Two-nucleon forces: Doing the math
We'll fill in the mathematical subtleties we left out when providing the chiral hierarchy overview in this section. The many irreducible diagrams, depicted in Figure 13 and defining the chiral NN potential order by order, are as follows:
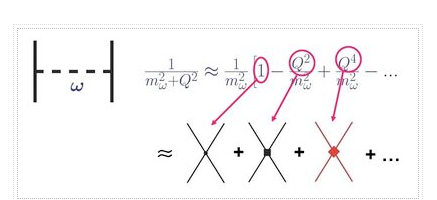
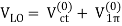
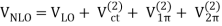

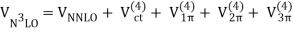
The order v of the low-momentum expansion is denoted by the superscript. The subscript "ct" denotes contact potentials, while an evident subscript denotes pion-exchange potentials.
The charge-independent 1PE potential reads
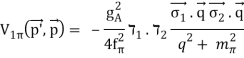
(33)
The constants' numerical values are f=92.4 MeV, gA=1.29, and m=138 MeV for the average pion mass (see Figure 5 and Eq. (23)). Because higher order corrections only affect mass and coupling constant renormalizations and there are no relativistic corrections on the shell, the on-shell 1PE has the same form as Eq. (33) at all orders.
The two zero-order contact terms at LO are
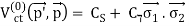
(34)
To state the mathematical expressions for 2PE contributions, we use the following scheme:
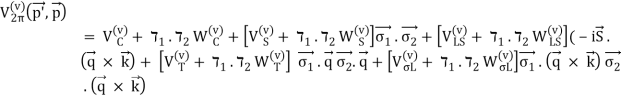
(35)
Where p⃗ ′ and p⃗ denote the final and initial nucleon momenta in the CMS, respectively; moreover,
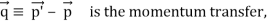

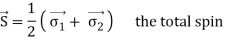
(36)
And σ⃗ 1,2 and τ1,2 are the spin and isospin operators, respectively, of nucleon 1 and 2. For on-energy-shell scattering, Vi and Wi (i=C,S,LS,T,σL) can be expressed as functions of q and k, only (with q≡|q⃗ | and k≡|k⃗ |).
Using the above scheme, the contribution from the five NLO 2PE diagrams can be stated in an amazingly compact form, namely,
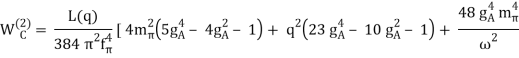
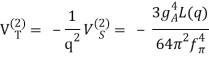
(38)
Where
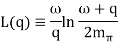
And
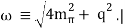
For the typical pion mass, the constants' numerical values are f=92.4 MeV, gA=1.29, and m=138 MeV (see Figure 5 and Eq. (23)). The on-shell 1PE has the same form as Eq. (33) at all orders since higher order corrections only influence mass and coupling constant renormalizations and there are no relativistic corrections on the shell.
The seven NLO contact terms are:
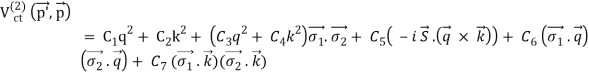
(39)
Of course, the coefficients Ci in the contact potential are related to the coefficients C′i in the LagrangianL(2)NN, Eq. (25), but the precise relationship is immaterial.
The following formulations (Kaiser et al., 1997) indicate the NNLO 2PE:
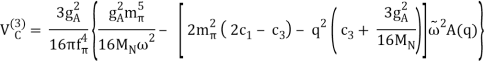
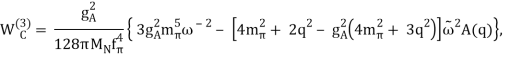
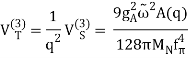
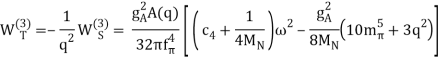
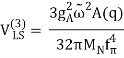
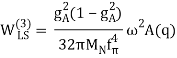
(42)
With
A(q) = 1/2q arctan q/2mπ |
And
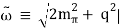
This is the most important contributor to the 2PE because it generates a strong intermediate-range attraction. Because the LEC c3 is negative and of great magnitude, the iso-scalar central potential, V(3)C, is powerful and appealing. c3 is linked to - correlations ('mesons') and virtual -isobar excitations via resonance saturation, which are the most important contributions to 2PE in the framework of conventional meson theory (Machleidt et al., 1987). At this order, first relativistic 1/MN adjustments enter the equation; they are incorporated in the potential expressions above.
The contacts at N3LO are:

(43)
The 2PE potential at N3LO, V(4)2, is quite complicated, which is why its expressions will not be given here. It is located in (Machleidt and Entem, 2011). The contributions of N3LO 3PE, V(4)3, are insignificant.
Large scattering lengths and shallow bound states (the deuteron) characterise the two-nucleon system, which cannot be computed using perturbation theory. To derive the N amplitude, the NN potential must be entered into a Schrödinger or Lippmann-Schwinger (LS) equation.
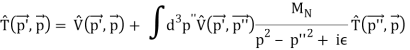
(44)
Where the definitions

(45)
And
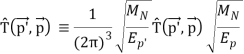
(46)
Are used, with 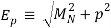 . Iteration of Vˆ in the LS equation, Eq. (44), requires cutting Vˆ off for high momenta to avoid infinities. This is consistent with the fact that ChPT is a low-momentum expansion which is valid only for momenta Q<Λχ≈1 GeV. Therefore, the potential Vˆ is multiplied with a regulator function f(p′,p),
. Iteration of Vˆ in the LS equation, Eq. (44), requires cutting Vˆ off for high momenta to avoid infinities. This is consistent with the fact that ChPT is a low-momentum expansion which is valid only for momenta Q<Λχ≈1 GeV. Therefore, the potential Vˆ is multiplied with a regulator function f(p′,p),
Vˆ(p⃗ ′,p⃗ )⟼Vˆ(p⃗ ′,p⃗ )f(p′,p)
With, for example,
f(p’ , p) = exp[ - (p’/Λ)2n - (p/Λ)2n ] .(47)
Typical choices for the cutoff parameter Λ that appears in the regulator are Λ≈0.5 GeV<Λχ≈1 GeV.
It is self-evident that the T-matrix results will be sensitive to the regulator and its cutoff parameter, which is undesirable. Renormalization is the process of removing regulator reliance. It's worth noting that renormalizability is critical for an EFT's validity. Entem and Machleidt (2003) use two regularisation strategies in their quantitative chiral NN potentials: Dimensional regularisation is employed in the potential derivation (where the cutoff is taken to infinity), whereas the regulator Eq. (47) is employed with a finite cutoff in the LS equation, Eq. (44). Although this method has yielded useful NN potentials, the way regularisation and renormalization are handled is debatable. Despite nearly two decades of effort by a diverse group of theoretical physicists, the community has yet to reach an agreement on how to successfully renormalize chiral EFT-based nuclear forces. The pionless EFT has proven to be enlightening in this situation, since it allows for a more transparent renormalization procedure (because it consists of contacts only and does not include pion loops).
The accurate counting of the powers of the low-energy expansion is a similar unresolved topic. It's worth noting that the power in Eq. (26) is the perturbatively determined potential's power. The T-matrix, on the other hand, is a physical quantity that is obtained by iterating the potential in the LS equation, Eq. (44), which may vary the power. The pionless theory has also proved useful in this case since, due to its simplicity, it allows for analytic solutions of the LS equation that directly indicate the power.
3.3.16 Three-nucleon forces
The 2NF, of course, contributes the most to microscopic computations of nuclear structure and reactions. However, it is widely known from ab-initio investigations that 3NFs are required for precise microscopic explanation of certain few-nucleon reactions and nuclear structural difficulties. In a nutshell, 3NFs are required. As previously stated, one of the major advantages of the EFT approach to nuclear forces is that it equalises two- and many-nucleon forces (cf. Figure 13).
For a 3NF, we have A=3 and C=1 and, thus, Eq. (26) implies
ν=2+2L+∑iΔi.(48)
We will use this equation to analyze 3NF contributions order by order.
The lowest possible power is obviously ν=2 (NLO), which is obtained for no loops (L=0) and only leading vertices (∑iΔi=0). As it turns out, this contribution vanishes.
The first non-vanishing 3NF appears at NNLO (ν=3). The power ν=3 is obtained when there are no loops (L=0) and ∑iΔi=1, i.e., Δi=1 for one vertex while Δi=0 for all other vertices. There are three topologies which fulfill this condition, known as the 2PE, 1PE, and contact graphs, Figure 17 (van Kolck, 1994), (Epelbaum et al., 2002).
The 2PE 3N-potential is derived to be
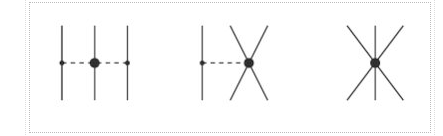

(49)
With q⃗ i≡pi→′−p⃗ i, where p⃗ i and pi→′ are the initial and final momenta of nucleon i, respectively, and
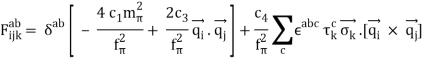
(50)
The derivations of 2PE 3NFs from conventional meson theory are very similar to this force (Fujita and Miyazawa, 1957; Coon et al., 1979).
Taking the remaining two terms of the =1 Lagrangian, Eq. (20), into account yields the other two 3NF contributions. The contribution of 1PE is

(51)
And the 3N contact potential reads
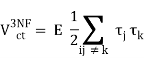
(52)
The two new parameters D and E, which do not occur in the 2N problem, are used in these 3NF words. There are numerous methods for determining these two factors. One method is to use the triton binding energy and the nd doublet scattering length 2 and. The binding energies of 3H and 4He, as well as an optimal overall match of the properties of light nuclei, can be chosen. The findings for other 3N, 4N, and so on observables are forecasts once D and E are fixed.
The 3NF at NNLO has had a lot of success in computations of few-nucleon processes, light- and medium-mass nuclei structure, and nuclear and neutron matter. However, the 'Ay puzzle,' which involves the underprediction of the analysing power of nucleon-deuteron and p-3He scattering, is not answered by this 3NF. Furthermore, there is room for improvement in the spectra of light nuclei. As a result, higher-order 3NFs are required for at least two reasons: to address unsolved difficulties in microscopic structure and reactions, and to maintain consistency with the 2NF (recall that a precise 2NF is of order N3LO).
The following order is N3LO (v=4), which presents us with a huge number of loop diagrams (Figure 18). Because L is one in those loops, all I must be zero to ensure that =4. As a result, these one-loop 3NF diagrams can only contain leading order vertices, whose parameters are determined via N and NN analysis. There are five loop topologies to choose from. For each topology, we display one sample diagram in Figure. However, each topology is made up of a large number of diagrams, with the overall number of diagrams ranging from 50 to 100, depending on how the diagrams are represented (Bernard et al., 2011). The N3LO 3NF is fairly weak, according to preliminary applications of the 3N potentials produced from these diagrams, and does not answer the Ay conundrum (Witala et al., 2013).
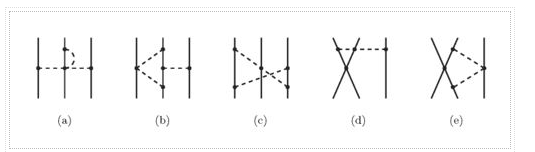
Because we're dealing with a perturbation theory, it's only reasonable to look for advances in the next order. As a result, we place an order for N4LO (v=5). These loop contributions (Figure) are produced by replacing one vertex in the N3LO loops with an i=1 vertex (with LEC ci), which is why these loops may be larger than the N3LO loops. There are five loop topologies in all, each with numerous diagrams. In addition, three 'tree' topologies (Figure 20) with a novel set of 3N contact interactions [graph (c)] are available. In comparison to loop diagrams, contact terms are often simple, and their coefficients are unbounded (except for naturalness). All potential spin-isospin-momentum configurations that a 3NF can have are included in the N4LO 3NF words. As a result, there's a chance that the 3NF at N4LO will fill in the gaps in the 3NF jigsaw. The burst of 3NF contributions that arise at N3LO and N4LO, however, poses a challenge.
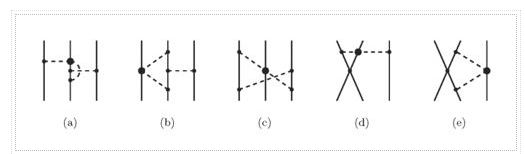
3.3.17 Four-nucleon forces
For connected (C=1) A=4 diagrams, Eq. (26) yields

v = 4 + 2L +  (53)
(53)
As a result, at v=4 (N3LO), a linked 4NF occurs for the first time, with no loops and just leading vertices, Figure. There are no new parameters in this 4NF, and it does not disappear. Figure shows some graphs that appear to be reducible (iterative). However, keep in mind that they are Feynman diagrams, which are best understood using time-ordered perturbation theory. Some irreducible topologies are included in the various time-orderings (which are, by definition, 4NFs). Or, to put it another way, the Feynman diagram minus the reducible part yields the 4NF's (irreducible) contribution.
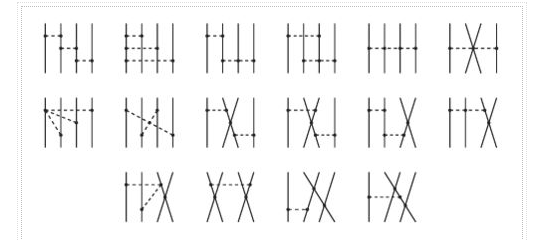
A contribution of order (Q/)4 is expected to be negligible assuming a good rate of convergence. As a result, ChPT forecasts that 4NF will be virtually inconsequential, which is consistent with previous experience. Even still, nothing in physics is entirely established unless detailed calculations are conducted. The leading 4NF was used to calculate the 4He binding energy, and it was discovered to contribute roughly 0.1 MeV. When compared to the whole 4He binding energy of 28.3 MeV, this is a minor difference.
3.3.18 Introducing Δ-isobar degrees of freedom
The (1232) resonance or isobar (a -N P-wave resonance with both spin and isospin 3/2) has an excitation energy of M=MMN=293 MeV and is the nucleon's lowest excited state. It is an important component of models of pion-nucleon scattering in the -region and pion production from the two-nucleon system at intermediate energies, where particle production is dominated by the formation of isobars, due to its strong coupling to the -N system and low excitation energy. The virtual excitation of's, which accounts for about half of the nuclear force's intermediate-range attraction in these models at low energies—-as demonstrated by the Bonn potential—-is included in the more sophisticated conventional models for the 2-exchange contribution to the NN interaction at low energies (Machleidt et al., 1987).
Because of its tiny excitation energy, it is unclear whether the should be explicitly taken into account in an EFT or integrated out as a heavy degree of freedom. Mm, in addition to the pion mass and small external momenta, is regarded additional tiny expansion parameter if it is included. Small-scale expansion is the name given to this strategy (SSE). However, because M does not vanish in the chiral limit, this extension is phenomenological in nature.
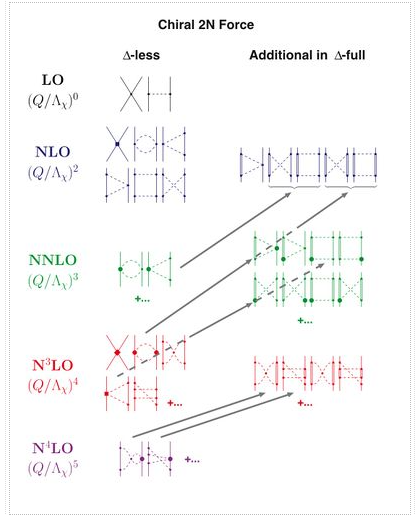
The effects of isobars are implicitly taken into consideration in the chiral EFT outlined so far (also known as the -less theory). It's worth noting that the dimension-two LECs, ci, have abnormally high values. The reason for this is that the -isobar (as well as various meson resonances) play a significant role in the ci—-a phenomenon known as resonance saturation. As a result, the explicit inclusion of the [so-called -full theory (Ordonez et al., 1996), (Kaiser et al., 1998)] detracts from the power of these LECs and shifts it to a lower order. As a result, the expansion's convergence improves, which is another reason for providing explicit -degrees of freedom. The subleading 2PE and 3PE contributions to the 2NF are bigger than the leading ones in the -less theory. The -full theory solves this problem by promoting large contributions by one order (Ordonez et al., 1996).
The N coupling is proportional to hA/2f and contains one derivative, similar to the NN coupling, which is proportional to gA/2f and contains one derivative. The LECs of the N Lagrangian are often recovered during the study of -N scattering data, and they obviously differ in the -full theory from the -less theory. While the LECs c3 and c4 have a magnitude of roughly 3-5 GeV1 in the -less theory, they have a magnitude of roughly 1 GeV1 in the -full theory.
The virtual excitation of -isobars in the 2NF necessitates at least one loop, therefore the contribution occurs initially at v=2 (NLO), as seen in Figure 22. The coherence of the -full and -less theories has been demonstrated by demonstrating that contributions from intermediate -excitations, enlarged in powers of 1/M, may be absorbed into a redefinition of the -less theory's LECs. The LECs c3,c4's equivalent shift is determined by

c3=−2c4=−h2A9ΔM.(54)
Using hA=3gA/2 (huge Nc value), the resonance explains practically all of c3 and a significant portion of c4.
With the explicit insertion of the -isobar, a considerable portion of the 2NF's intermediate-range attraction is switched from NNLO to NLO, according to several studies. The NNLO 2PE potential of the -less theory, on the other hand, is found to be a very excellent approximation to the NNLO potential in the -full theory.
Figure shows how the isobar affects the 3NF scenario. The 2PE 3NF in the lead gets promoted to NLO. This term has the same mathematical form in the -full theory as the analogous term in the -less theory, Eqs. (49) and (50), assuming c1=0 and c3, c4 according to Eq (54). As a result of the antisymmetrisation of the 3N states, the other two NLO 3NF terms involving's vanish. Because the subleading N vertex has a time-derivative, which demotes the contributions by one order, the contributions to the 3NF at NNLO vanish at this order. However, one-loop diagrams with one, two, or three intermediate -excitations, which correspond to diagrams of order N4LO, N5LO, and N6LO, respectively, in the -less theory, are projected to make significant 3NF contributions at N3LO.
To summarise, the inclusion of explicit degrees of freedom improves chiral expansion convergence by moving significant contributions from NNLO to NLO. The results for the -full and -less theories, on the other hand, are essentially the same at NNLO. The -full theory includes all diagrams involving's as well as all diagrams from the -less theory. As a result, the -full theory is substantially more complicated. Furthermore, 1/MN 2NF corrections arise at NNLO (not shown in Figure 22) in the -full theory, which were found to be uncomfortably big (Kaiser et al., 1998). As a result, it appears that the -less theory is more workable up to NNLO.
However, when possibly big donations join the scene at N3LO, the scenario may alter. Because these terms are spread out over N3LO, N4LO, and, in part, N5LO in the -less theory, it may be more efficient to compute them in the -full theory. These higher-order contributions are an important test for the convergence of the chiral expansion of nuclear forces and a difficult area for future investigation.
3.3.19 Baryon-baryon interactions
All baryons have a significant interaction with one another. As a result, in addition to the nucleon-nucleon interactions discussed in this article, there are many additional strong baryon-baryon interactions. The forces between nucleons and hyperons (strange baryons) and hyperons and hyperons have traditionally been a focus. In addition, the contact between a baryon and an anti-baryon has piqued curiosity, with the nucleon-antinucleon contact being the most investigated. Phenomenology, meson theory, quark models, lattice QCD, and effective field theory have all been used to try to explain the baryon-(anti)baryon interactions, much as they have for the nucleon-nucleon interaction. Although it is not the goal of this article to discuss those other baryon-baryon interactions, it is worth noting that all baryon-baryon interactions are connected due to the quark sub-structure of hadrons. As a result, the nucleon-nucleon interaction covered in this paper should be viewed in the context of all baryonic interactions. Achieving a description of all baryon-baryon interactions that is consistent with all relevant underlying symmetries is a difficult task in today's study. We want to recommend interested readers to the literature for more information on this issue. Rijken et al. (2013) review hyperon-nucleon interactions in the meson image, while Haidenbauer et al. (2013) review chiral EFT. See Klempt et al. (2005) for a nucleon-antinucleon approach, and Kang et al. (2013) for a chiral EFT technique.
Key takeaway:
- The residual strong force is the force that acts between nucleons and binds protons and neutrons into atomic nuclei.
- The force between two nucleons does not act along the line connecting their centres, hence nuclear forces are non-central forces. This demonstrates that nucleons are not spherically symmetric in the nucleus. Whether the nucleons are neutrons or protons has no effect on the nuclear force. Charge independence is the name for this characteristic. Because it has a non-central or tensor component, the force is dependent on whether the nucleons' spins are parallel or antiparallel.
3.4.1Stability: the N-Z curve
The N-Z curve | Decay process | Decay chains |
The N-Z curve

The N-Z curve is a plot of the number of neutrons(N) against the number of protons(Z).
Lines:
i) the'stability' line, which is a gentle curve that begins at the origin and gradually increases in gradient.
Ii) the line N = Z - a gradient '1' straight line through the origin
Regions
i) emitters of beta minus (electron) particles
Ii)positron particle emitters (beta plus)
Iii) top of the curve alpha particle emitters (not shown)
Description:
N=Z is a straight line for proton numbers (Z) up to 20.
The line slopes upwards for all nuclei with Z>20 because stable nuclei contain more neutrons than protons.
3.4.2 The Decay Process
By losing neutrons, unstable neutron-rich nuclei can become more stable. This is accomplished by a process known as 'beta decay.'
The effect of this for a single nucleus is to raise its the proton number (Z) by 1 and decrease its neutron number(N) by 1, bringing the N-Z plot of the nucleus closer to the stability curve.
The point moves one unit to the right and one unit to the left.
Beta decay: Z + 1 N – 1
Unstable neutron-poor nuclei can become more stable by gaining neutrons. They do this by 'positron decay'.
For a single nucleus, this has the effect of lowering its proton number (Z) and increasing its neutron number (N), putting the nucleus' N-Z plot closer to the stability curve.
The point moves one unit to the left and one unit to the right.
Positron decay: Z - 1 N + 1

- The position of a nucleus in relation to the stability curve is unaffected by alpha decay. This is because the loss of an alpha particle (two protons and two neutrons) does not significantly alter the N-Z ratio.
- Z - 2 and N - 2 are the coordinates of a nucleus. Alpha decay involves only big nuclei. As a result, the influence is limited to the curve's very top part.
Alpha decay: Z - 2 N – 2
3.4.3 Decay Chains
A decay chain (or radioactive series) depicts the various types of radioactive decay that a nucleus goes through until it reaches a stable isotope.
The actinium series, thorium series, and uranium series are the only three naturally occurring decay chains.
Plus the neptunium series, which involves a trans-uranium element.
A graph of nucleon number (A) versus proton number (B) appropriately describes a decay chain (Z).
The diagram depicts the entire Thorium-232 decay chain.
Important observations are:
Alpha decay ...........2 units to the left, 4 units down
beta- decay ...........1 unit to the right
Bismuth ...............2 possible decay outcomes
Equations describing the Thorium Series:
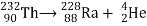

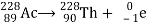
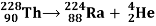
3.4.4 Nuclear Magic Numbers
Introduction
When compared to the periodic table, an isotope is an element with the same atomic number but a different atomic mass. Protons, neutrons, and electrons are found in every element. Unless it's an ion, the number of protons equals the atomic number, and the number of electrons equals the number of protons. The number of neutrons in an element is calculated by subtracting the atomic number from the atomic mass. Atomic mass is denoted by (AA), atomic number is denoted by (ZZ), and neutrons are denoted by (N) (NN).
A=N+Z(1)A=N+Z(1)A=N+Z(1)A=N+Z(1)A=N+Z(1)A
The neutron to proton ratio is the most important factor in determining whether a nucleus is stable. The nuclei of elements with (Z20Z20) are lighter, and their nuclei have a ratio of 1:1, preferring to have the same number of protons and neutrons.
Isotope Stability
The Band (or Belt) of Stability is a graph of stable elements that is often used. A y-axis labelled neutrons, an x-axis labelled protons, and a nucleus make up the graph. The radionuclides that decay by alpha decay are at the upper end (top right) of the band of stability; below is positron emission or electron capture; above is beta emissions; and elements beyond the atomic number of 83 are solely unstable radioactive elements. The neutron:proton ratio in stable nuclei with atomic numbers up to roughly 20 is roughly 1:1. (solid line).
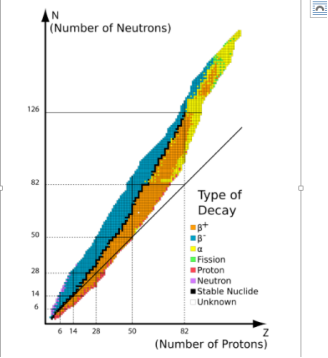 .
.
The deviation from the N:Z=1N:Z=1 line on the stability belt is due to a non-unity N:ZN:Z ratio required for total nuclei stability. To put it another way, more neutrons are needed to stabilise the repulsive forces generated by a smaller number of protons within a nucleus (i.e., N>ZN>Z).
It's simple to figure out where alpha decay, beta decay, and positron emission or electron capture happen because to the belt of stability.
Alpha Decay: Alpha decay is near the top of the plotted line because it reduces the mass number of the element, which helps to maintain the isotope stable. This is done by emitting an alpha particle, which is nothing more than a helium (HeHe) nucleus. The unstable isotope's proton number PP is reduced by two and its neutron number (NN) is reduced by two in this decay pathway. The nucleon number AA lowers by 4 as a result of this (Equation 11).
Beta decay receives protons, resulting in a change in the number of protons and neutrons. The number of protons rises by one, whereas the number of neutrons falls by one. This pathway arises in unstable nuclides with an excess of neutrons over the stability band (blue isotopes in Figure 11).
Positron ++ Decay occurs when an isotope gets additional neutrons by positron ++ emission and electron capture. Because the isotope ratio has more protons than neutrons, positron emission and electron capture are below the band of stability. Think of it this way: there are too few protons for the quantity of neutrons, hence it's below the band of stability (yellow isotopes in Figure 11).
If the daughter nuclei are not on the Belt, as with other decay pathways, subsequent decay paths will proceed until the daughter nuclei are on the Belt.
3.4.5 Magic Numbers
The Octet Rule was developed as a result of the discovery that atoms containing eight valence electrons were particularly stable (and common). Nuclei have a similar scenario in terms of the number of neutrons and proton quantities that produce stable (non-radioactive) isotopes. These "magic numbers" are natural occurrences in especially stable isotopes. Numbers of protons and neutrons are listed in Table 1; isotopes with these numbers in either the proton or neutron are stable. In some situations, isotopes can have magic numbers for both protons and neutrons, which are referred to as double magic numbers. Because of the repulsion of the interactions between the protons, double numbers only appear for heavier isotopes. The magic numbers are as follows:
- 2, 8, 20, 28, 50, 82, 114 proton
- 2, 8, 20, 28, 50, 82, 126, 184 neutron
There's also the idea that isotopes with a mix of even-even, even-odd, odd-even, and odd-odd isotopes are all stable. Even-even nuclides exist in greater numbers than odd-odd nuclides. Many isotopes with no magic number of nucleons are stable, just as there are exceptions to the octet rule.
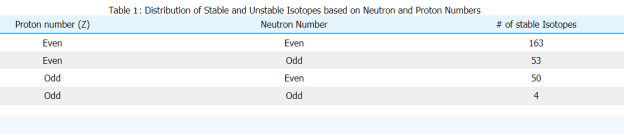
Unstable or Stable
Here's a basic chart that can help you determine whether or not an element is likely to remain steady.
- Calculate the nuclide's total number of nucleons (protons and neutrons). There's a strong likelihood it's stable if the number of nucleons is even.
- Is there a certain amount of protons or neutrons that must be present? In nuclei, the numbers 2,8,20,28,50,82,114 (protons), 126 (neutrons), and 184 (neutrons) are extremely stable.
- Determine the optimal route to travel from an unstable nucleus to a stable nucleus by calculating the N/Z ratio and using the belt of stability.
3.4.6 Stable nuclides
Hundreds of nuclides have been identified; in this episode, an N-Z plot is used to examine the pattern of stability and evaluate the necessity for an additional, attractive force to hold the nucleus together.
Which stable nuclides exist
Rehearse and expand on what your students already know. The nucleus is made up of N neutrons and Z protons, hence A = N + Z nucleons. Explain (or update) nuclide nomenclature with the following example:
Bismuth-83 (20983Bi) is the heaviest stable element.
In this nucleus, how many protons and neutrons are there? (83 and 126)
Between hydrogen (Z is 1) and uranium (U), there are 90 naturally occurring elements ( Z is 92). Is there anything out of the ordinary about this? (Two are missing; 9943Tc (technitium) and 6361Pm are both artificial and man-made) (promethium). On a geological time span, both are radioactive and would have decayed long ago.)
All elements with a Z greater than 92 have been created by humans. The current record (as of February 2004) is Z of 116.
Create a visualisation of N vs Z for stable nuclides using a spreadsheet. Prepare an Excel spreadsheet with the data below already recorded (columns for the element name, A, Z, and, anticipating future work, the nucleus mass in atomic mass units u – see below) to save time (and transcription errors!).
Representative stable nuclides:
3.4.7 Interpreting the graph
Explain the graph. (It's linear (N Z) up to Z 20, then gradually N > Z: there's a neutron excess.) The neutron excess is critical for understanding nuclear stability and setting up a chain reaction in nuclear reaction exploitation.
Consider the Coulomb repulsion that exists between protons. What exactly are the neutrons doing inside? ( Neutrons must assist in overcoming the strong repulsion between protons, partly by diluting them and, more importantly, by supplying an attractive force to counteract the electric repulsion. As a result, the term "strong nuclear force" was coined.
3.4.8 Calculating the force between protons
If Coulomb’s law has been covered, calculate the repulsive force between two protons that just touch, so the separation of their centres r is the diameter of a proton 1.4 × 10-15 m).
Fe = 14 π ε0 q1 q2r 2
Where q1 and q2 both have the same value, +e = 1.6 × 10-19 C. So:
Fe ~ 100 N
3.4.9 The nature of the strong nuclear force
Explain the need for the strong nuclear force to balance the Coulomb repulsion. This force must be attractive – it overcomes the coulomb repulsion; independent of electric charge – it acts between nn, pp and np; and very short range ~ 1 fm = 1 × 10-15 m.
3.4.10 Calculating nuclear densities
Calculate the density of a nucleon:
Nucleon mass ~1.7 × 10-27 kg; radius ~1.4 × 10-15 m; density r ~1.4 × 1017 kg m-3
This is enormous compared to the density of everyday matter. Ask your students to repeat the calculation for He-4 (or give data for other nuclides):
Nuclide mass ~6.6 × 10-27 kg; radius ~2 × 10-15 m; density ~1.6 × 1017 kg-3
So the density is roughly the same for all nuclei. This is summed up in the relationship:
r = r0 × A ⅓
With r0 = 1.4 fm
3.5.1 The liquid drop model

In the liquid drop model of the atomic nucleus, the terms of the semi-empirical mass formula are illustrated.
George Gamow proposed the liquid drop model, which was further developed by Niels Bohr and John Archibald Wheeler. It treats the nucleus as an incompressible fluid drop with a very high density that is held together by the nuclear force (a residual effect of the strong force), with a structure that resembles that of a spherical liquid drop. The liquid drop model, albeit primitive, accounts for most nuclei's spherical shape and offers a rough forecast of binding energy.
The mass formula is solely specified in terms of the number of protons and neutrons it contains. Five terms are defined in the original Weizsäcker formula:
When an assembly of nucleons of the same size is packed together into the smallest volume, each inside nucleon comes into contact with a particular number of other nucleons. As a result, the amount of nuclear energy produced is proportional to the volume.
The assumption that each nucleon interacts with the same number of other nucleons is corrected by surface energy. Because this term is negative and proportionate to surface area, it is nearly similar to liquid surface tension.
The potential energy of each pair of protons is known as Coulomb energy. The binding energy is lowered because this is a repulsive force.
The Pauli exclusion principle is explained by asymmetry energy (also known as Pauli Energy). Uneven quantities of neutrons and protons mean that one type of particle will fill higher energy levels while the other will leave lower energy levels empty.
The likelihood for proton and neutron pairs to form is explained by pairing energy. Due to spin coupling, an even number of particles is more stable than an odd number.
3.5.2 Binding energy and Semi-empirical mass formula
Binding Energy
The nuclear binding energy and the mass of nuclides are two significant nuclear parameters that we want to investigate. You might suppose that since we know the masses of the proton and neutron, we can simply use the formula mN = Zmp + Nmn to get the masses of all nuclides.
However, experimental evidence suggests that this is not the case. We know from special relativity theory that each mass corresponds to a certain amount of energy, E=mc2E=mc2. Then we may calculate how much energy they represent by adding the masses of all the elements of a nucleus. The intrinsic energy of a nucleus is likewise proportional to its mass. It's only natural that this isn't just the sum of its constituent energies, because we expect some additional energy to be expended to hold the nucleus together. If the energy levels were equal, bound nuclei would be undesirable, and all nuclei would be unstable, continually shifting from their bound state to a sum of protons and neutrons.
The difference in mass energy between the nucleus and its parts is then used to calculate the nucleus' binding energy. The binding energy B of a nucleus is given by
B=[Zmp+Nmn−mN(AX)]c2B=[Zmp+Nmn−mN(AX)]c2
However, we want to express this quantity in terms of experimentally accessible quantities. Thus we write the nuclear mass in terms of the atomic mass, that we can measure,
MN(AX)c2=[mA(AX)−Zme]c2+Be(1.2.2)(1.2.2)mN(AX)c2=[mA(AX)−Zme]c2+Be
Where mA(AX)mA(AX) is the atomic mass of the nucleus. We further neglect the electronic binding energy BeBe by setting
MN(AX)c2=[mA(AX)−Zme]c2.(1.2.3)(1.2.3)mN(AX)c2=[mA(AX)−Zme]c2.
We finally obtain the expression for the nuclear binding energy:
B={Zmp+Nmn−[mA(AX)−Zme]}c2B={Zmp+Nmn−[mA(AX)−Zme]}c2
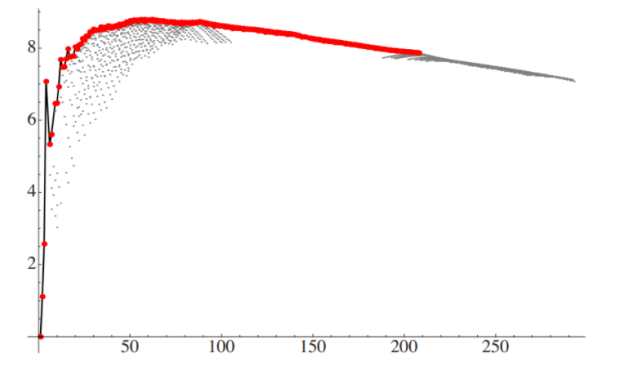
Quantities of interest are also the neutron and proton separation energies:
SnSp=B(AZXN)−B(A−1ZXN−1)=B(AZXN)−B(A−1Z−1XN)Sn=B(ZAXN)−B(ZA−1XN−1)Sp=B(ZAXN)−B(Z−1A−1XN)
Which are the analogous of the ionization energies in atomic physics, reflecting the energies of the valence nucleons. We will see that these energies show signatures of the shell structure of nuclei.
Semi-empirical mass formula
B/A, or binding energy per nucleon, is a common representation of binding energy. Because B/A is largely constant, the binding energy is simply proportional to A in general.
However, there are reversals in this pattern. The semi-empirical mass formula captures B/reliance A's on A (and Z). This formula is based on first-principles considerations (a nuclear force model) as well as experimental evidence to determine the specific parameters that define it. All nucleons are uniformly distributed inside a nucleus in this model, known as the liquid-drop model, and are linked together by the nuclear force, whereas the Coulomb interaction causes protons to repel one another. Part of the semi-empirical mass formula is explained by nuclear force (short range) and Coulomb interaction characteristics. Other (smaller) corrections, on the other hand, have been proposed to account for changes in the binding energy that arise due to its quantum-mechanical character (and that give rise to the nuclear shell model).
The semi-empirical mass formula (SEMF) is
M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2
Where the binding energy B(Z, A) is given by the following formula:

3.5.3 Volume term
The first term is avA, which describes how the binding energy is primarily proportional to A. Why is it the case?
Keep in mind that the binding energy is a measure of nucleon interaction. Because nucleons are packed so tightly in the nucleus and the nuclear force has such a short range, each nucleon only interacts with a few neighbours. This indicates that regardless of the overall number of nucleons, each one makes the same contribution. As a result, the force is proportional to A(A 1)/2 A2 (the total number of nucleons with which one nucleon can interact), rather than A(A 1)/2 A2. The constant of proportionality (av = 15.5MeV) is a fitting parameter that has been determined empirically.
This is less than the nucleons' binding energy to their neighbours, which is governed by the strength of the nuclear (strong) interaction. The energy binding one nucleon to the other nucleons is discovered to be on the order of 50 MeV (which we will look at further). Instead, the total binding energy is the difference between a nucleon's interaction with its neighbour and the nucleon's kinetic energy. The nucleons in an atom are fermions, therefore they can't all be in the same state with zero kinetic energy, but according to Pauli's exclusion principle, they'll fill up all the kinetic energy levels. This model, which accounts for nuclear binding energy as well as kinetic energy owing to shell filling, provides an accurate estimate of av.
3.5.4 Surface term
The surface component, asA2/3asA2/3, is a correction to the volume term. It is likewise based on the strong force. The volume term, we said, arises from the fact that each nucleon interacts with a fixed number of nucleons, regardless of A. While this is true for nucleons deep inside the nucleus, nucleons at the nucleus' surface have fewer nearest neighbours. Surface forces, which occur in droplets of liquids, for example, are a mechanism that causes surface tension in liquids.
We estimate a surface force of (BV)2/3(BV)2/3 (because the surface SV2/3SV2/3) since the volume force is proportional to BV A. In addition, the term must be deducted from the volume term, and the coefficient should be of equal value to av. As a matter of fact, as = 13 18MeV.
3.5.5 Coulomb term
AcZ(Z1)A1/3acZ(Z1) is the third term. The Coulomb interaction between protons gives rise to A1/3, which is proportional to Z. Because the Coulomb repulsion makes a nucleus with numerous protons less favourable, this term is removed from the volume term (more energetic).
The nucleus is treated as a uniformly charged sphere to motivate the form of the term and estimate the coefficient ac. Such a charge distribution's potential energy equals
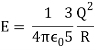
Since from the uniform distribution inside the sphere we have the charge
q(r) = 4/3 πr3 ρ = Q (r/R)3
And the potential energy is then:
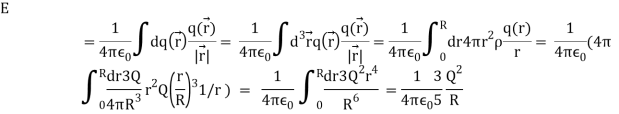
Using the empirical radius formula
R = R0A1/3
And the total charge
Q2 = e2 Z (Z – 1)
(reflecting the fact that this term will appear only if Z > 1, i.e. if there are at least two protons) we have:
Q2/R = e2 Z (Z – 1)/R0A1/3
Which gives the shape of the Coulomb term. Then the constant ac can be estimated from
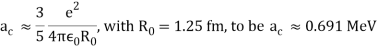
With R0 = 1.25 fm, to be ac ≈ 0.691 MeV, not far from the experimental value.
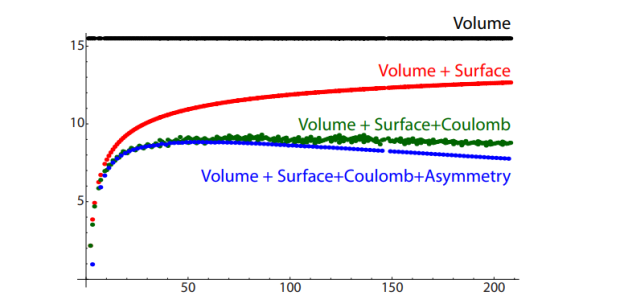
3.5.6 Symmetry term
The Coulomb phrase appears to indicate that having fewer protons and more neutrons in a nucleus is preferable. However, this is not the case, and we must use a model other than the liquid-drop model to explain why stable nuclei contain nearly the same amount of neutrons and protons. As a result, there is a correction component in the SEMF that attempts to account for the symmetry in protons and neutrons. This (and subsequent) corrections can only be explained by a more sophisticated nucleus model, the shell model, in conjunction with the quantum-mechanical exclusion principle, which we shall discuss later in the class. If we add more neutrons, they will have to be more energetic, which will increase the nucleus' total energy. This increases the Coulomb repulsion more than offsets it, making it preferable to have roughly equal numbers of protons and neutrons. The symmetry term has the shape (A2Z)2A. It's easier to understand if you realise that this term is zero for A = 2Z and has a smaller influence for bigger A. (while for smaller nuclei the symmetry effect is more important). Asym=23 MeV is the coefficient.
3.5.7 Pairing term
The last word refers to physical proof that like-nucleons tend to group together. If we have an even-even nucleus, where all of the neutrons and protons are paired-off, then the binding energy is bigger (> 0). It is therefore preferable to turn one of the protons into a neutron or vice versa if we have a nucleus with an odd number of neutrons and protons (of course, taking into account the other constraints above). As a result, for odd-odd configurations, we must deduct ( 0) a term from the binding energy with all other factors constant. Finally, we do not expect this pairing energy (= 0) to have any effect on even-odd configurations. The term for pairing is then

With ap ≈ 34MeV. [Sometimes the form ∝ A−1/2 is also found].
3.5.8 Line of Stability in the Chart of nuclides
We can compute the optimal Z such that the mass is minimal by taking the first derivative wrt Z. We get the following results:
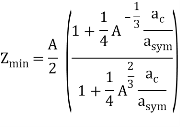

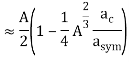
ZA2 is obtained for tiny A, but there is a correction for bigger A, resulting in Z 0.41A for heavy nuclei.
The nuclides lie between 1/2 and 0.41 on a plot of Z/AZ/A vs. A. Following the stable isotopes, there is a line of stability (red in Figure 1.2.4 and black in Figure). The isotopes are then identified in various ways, such as here by their lifetime.
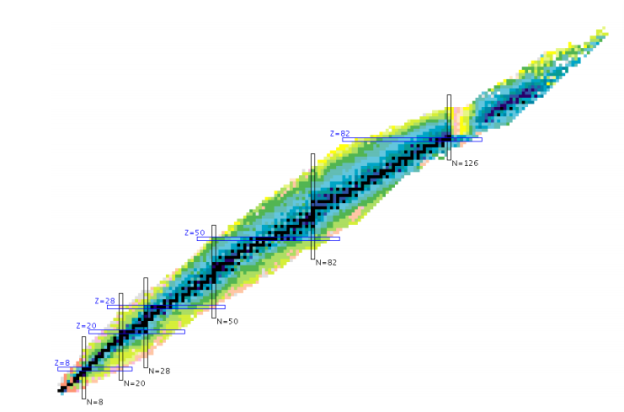
Figure: Chart of nuclides
Key takeaway:
- The nuclear binding energy is used to assess whether fission or fusion is the better option. The mass defect of a nucleus is the difference between the mass of a nucleus and the sum of the masses of the nucleons that make it up, and it represents the mass of the energy binding the nucleus.
- BE divided by A gives the binding energy per nucleon (BEN) (Equation 10.3. 3). BE=[2mp+2mn]m(4He)c2.
3.6.1 The Shell Model
The Shell Model, for example, accounts for a number of aspects of nuclear energy levels. According to this paradigm, the average attractive force of all the other nucleons governs the mobility of each nucleon. The orbits that arise form "shells," much like the orbits of electrons in atoms. As more nucleons are introduced to the nucleus, they fall into the lowest-energy shells allowed by the Pauli Principle, which stipulates that each nucleon must have its own set of quantum numbers to describe its motion.
.
A nucleus of remarkable stability arises when a shell is full (that is, when the nucleons have used up all of the feasible sets of quantum number assignments). This is comparable to the idea found in an atom, where a filled set of electron quantum numbers produces an atom with extraordinary stability–an inert gas. The number of protons or neutrons in a nucleus is dubbed a "magic number" when all of them are in filled shells. 2, 8, 20, 28, 50, 82, and 126 are some of the magical numbers. The magic number of protons in 116Sn is 50, and the magic number of neutrons in 54Fe is 54. (28). Some nuclei, such as 40Ca and 208Pb, have magical numbers of protons and neutrons; these nuclei are referred to as "doubly magical" because of their unusual stability. On the nuclide chart, magic numbers are indicated.
The total angular momentum, J, of filled shells is zero. The J of the new ground state is determined by the next additional nucleon (a valence nucleon). When nucleons (individually or in pairs) are aroused out of the ground state, their angular momentum, as well as their parity and isospin projection quantum numbers, are altered. The shell model explains how much energy it takes to transfer nucleons from one orbit to the next, as well as how quantum numbers fluctuate. The energy diagram of the two filled shells of the 12C ground state is shown in the diagram above. When a nucleon or a pair of nucleons are promoted to an empty shell, the nucleus enters one of the excited states.
Excited nuclear states decay to more stable states, i.e. nucleon orbitals that are more stable. To precisely calculate the energy and half-life of the decay, specialised alpha, beta, and gamma detectors and related electronic circuitry are used to measure transition rates between nuclear energy levels. Nuclear scientists can calculate the transition probability (rate of decay) between nuclear states using quantum mechanics and shell-model theory. The Shell Model calculations accord very well with measured values of spin and parity assignments and transition probabilities for nuclei whose structure can be explained by a small number of valence nucleons outside filled shells.
Above is an illustration of transitions between the energy levels of a nucleus. The 12B (5 protons, 7 neutrons) and 12N (7 protons, 5 neutrons) ground states are connected to each other as well as the 15.1 MeV state in 12C. Each possesses a nucleon in the third energy level, the quantum number 1+, 1, and decays to carbon's ground state. The beta decay of boron and nitrogen produces an e- and an e+, respectively. Carbon's 15.1 MeV state decays via gamma emission. Even though different decay mechanisms are at action in each example, the shell model calculations of these transition probabilities accord pretty well with the measured rates. The shell model is being refined by nuclear theorists in order to better understand the complexities of nuclear structure and to apply that knowledge to nuclear technologies.
3.6.2 Nuclear Shell Model
It illustrates how energy levels are distributed among distinct atom shells and nucleus atom shells. The energy level where particles with the same energy exist is referred to as a shell. All nuclear particles in this model are coupled one-to-one, neutron with neutron and proton with proton. When the number of neutrons or protons in a nuclear energy level equals 2, 8,20,28,50,82, or 126, the paired neutrons and protons are filled. These are the magic numbers that show which nuclei are the most stable.

The unpaired ones are in charge of a nucleus' qualities, whereas valence electrons are in charge of an element's chemical qualities. We can reliably anticipate the properties of nuclei, such as angular momentum, using the shell model. However, for highly unstable nuclei, other models such as the collective model, liquid-drop model, and compound nucleus model must be adjusted or replaced with the shell model.
3.6.3 Shell Model of the Atom
It explains how different electrons are arranged around the nucleus of an atom according to their energy levels.
Fig. Shell Model of the Atom
Atomic Number = number of electrons in an atom
The atomic shell model explains how atoms are structured. The electrons, which are negatively charged fundamental particles, are thought to occupy diffuse shells in the region surrounding the positively charged nucleus. The initial shell is the one that is closest to the nucleus.
The shells are labelled as follows:
K | First shell |
L | Second shell |
M | Third shell and so on |
The electrons inhabit the shell in the following order: 2, 8, 18, 32, 50, 72, 98.
The atomic shell model also aids in the comprehension of atomic chemical characteristics.
The following formula is used to calculate the maximum number of electrons that can occupy an atom's energy level:
Electron capacity = 2n2
The principal quantum number is n in this case.
The shell layers and their electron capacity are listed in the table below:
Energy Level | Shell Designation | Maximum no.of electrons |
1 | K | 2 |
2 | L | 8 |
3 | M | 18 |
4 | N | 32 |
5 | O | 50 |
6 | P | 72 |
3.6.4 Difference Between Shell Structure of Nuclei and Shell Structure of Atom
Shell Structure of Nuclei | Shell Structure of Atom |
The energy level starts at zero. | The initial state is where the energy level begins. |
Z=2,8,20,28,50,82,126, and so on are Magic Numbers. | Z = 2,10,18,36,54,86, and so on are all magical numbers. |
The average potential of nuclei differs from the average potential of an atom. | Potential differs from one to another. |
Neutrons and protons are particles that make up the shell structure of nuclei. | Electrons are particles that make up an atom's shell structure. |
3.6.5 Magic number
A magic number in nuclear physics is the number of nucleons (either protons or neutrons) that may be organised into full shells within the atomic nucleus. As a result, atomic nuclei with a'magic' number of protons or neutrons are far more stable than nuclei with a different number of protons or neutrons. As of 2019, the seven most well-known magic numbers are 2, 8, 20, 28, 50, 82, and 126. (sequence A018226 in the OEIS). Although 126 is only known to be a magical number for neutrons, it correlates to the elements helium, oxygen, calcium, nickel, tin, lead, and the speculative unbihexium for protons. Atomic nuclei with such a large number of nucleons have a greater average binding energy per nucleon than one might expect based on predictions like the semi-empirical mass formula, and hence are more resistant to nuclear decay.
Transuranium elements might possibly be formed with exceptionally large nuclei and not be susceptible to the highly rapid radioactive decay generally associated with high atomic numbers due to the exceptional stability of isotopes with magic numbers. In an island of stability, large isotopes with magical quantities of nucleons are supposed to exist. Theoretical calculations predict that nuclei in the island of stability are distorted, unlike the magic numbers 2–126, which are realised in spherical nuclei. Higher magic numbers, such as 184, 258, 350, and 462 (OEIS sequence A033547), were previously predicted based on basic calculations assuming spherical shapes: these are generated using the formula (see binomial coefficient). The sequence of spherical magic numbers is now thought to be unextendable in this fashion. Protons are anticipated to have magic numbers of 114, 122, 124, and 164, whereas neutrons will have magic numbers of 184, 196, 236, and 318. More recent studies, however, suggest that neutrons will have a mass of 228 and 308, in addition to 184 and 196.
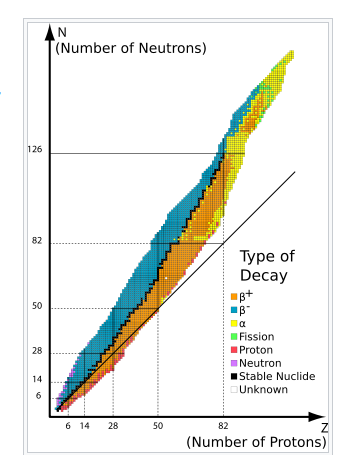
3.6.6 History and origin of the term
Maria Goeppert Mayer, a German scientist, became interested in the features of nuclear fission products, such as decay energies and half-lives, while working on the Manhattan Project. She published a body of experimental evidence supporting closed nuclear shells in nuclei with 50 or 82 protons or 50, 82, and 126 neutrons in 1948. (It was already known that nuclei with 20 protons or neutrons were stable; calculations by Hungarian-American physicist Eugene Wigner, one of her Manhattan Project colleagues, demonstrated this.) Two years later, in 1950, she published a second paper in which she blamed spin-orbit coupling for the shell closures at the magic numbers.
According to Maria Goeppert Mayer's student Steven Moszkowski, the word "Wigner coined the phrase "magic number": "Wigner, too, believed in the liquid drop model, but he recognised the very strong evidence for the closed shells from Maria Mayer's work." It appeared to him to be a little like magic, and hence the term 'Magic Numbers' was coined."
These magic numbers formed the foundation of Mayer's nuclear shell model, which he developed with Hans Jensen over the next few years and resulted in their joint Nobel Prize in Physics in 1963.
3.6.7 Doubly magic
Nuclei with neutron and proton (atomic) numbers both equal to one of the magic numbers are referred to as "doubly magical," and they are particularly resistant to disintegration. Helium-4, helium-10, oxygen-16, calcium-40, calcium-48, nickel-48, nickel-56, nickel-78, tin-100, tin-132, and lead-208 are the known doubly magical isotopes. However, only the first, third, fourth, and fifth of these doubly magical nuclides are totally stable, despite the fact that calcium-48 is extraordinarily long-lived and so naturally occurring, decomposing only by a slow double beta minus decay process.
Doubly-magic effects may allow stable isotopes to exist that would not have been predicted otherwise. Calcium-40, which has 20 neutrons and 20 protons and is the heaviest stable isotope with the same amount of protons and neutrons, is an example. Because calcium-48 has 20 protons and 28 neutrons, while nickel-48 has 28 protons and 20 neutrons, both are doubly magical. Calcium-48 has a lot of neutrons for such a light element, yet it's stabilised by being doubly magical, just like calcium-40.
Ordinary abundances of elements show magic number shell effects: helium-4 is one of the most numerous (and stable) nuclei in the universe[12], whereas lead-208 is the heaviest stable nuclide.
Magical influences can prevent unstable nuclides from disintegrating as quickly as they should. The nuclides tin-100 and tin-132, for example, are unstable doubly magic isotopes of tin that designate endpoints beyond which stability rapidly declines. Nickel-48 is the most proton-rich doubly magic nuclide known, having been found in 1999. Apart from tritium, which has one proton and two neutrons, nickel-78 is doubly magical, with 28 protons and 50 neutrons, a ratio seen only in far heavier atoms (78Ni: 28/50 = 0.56; 238U: 92/146 = 0.63).
An multinational team of scientists led by the Technical University of Munich found hassium-270 in December 2006, with 108 protons and 162 neutrons with a half-life of 9 seconds. Hassium-270 appears to be part of a stable island, and its distorted (American football- or rugby ball-like) shape suggests it may be doubly magical.
Despite the fact that Z = 92 and N = 164 are not magical numbers, the undiscovered neutron-rich nucleus uranium-256 could be doubly magical and spherical due to the size difference between low- and high-angular momentum orbitals, which changes the form of the nuclear potential.
3.6.8 Derivation
Empirical investigations are commonly used to derive magic numbers; if the nature of the nuclear potential is known, the Schrödinger equation for nucleon mobility can be solved, and energy levels can be derived. When the separation between energy levels is much greater than the local mean separation, nuclear shells are said to form.
Magic numbers are the numbers of nucleons at which a shell is filled in the shell model for the nucleus. Because there is a big energy gap between the 1p1/2 and the next highest 1d5/2 energy levels, the magic number 8 occurs when the 1s1/2, 1p3/2, and 1p1/2 energy levels are filled.
The atomic equivalent of nuclear magic numbers are the numbers of electrons that cause ionisation energy discontinuities. Helium, neon, argon, krypton, xenon, radon, and oganesson are examples of noble gases. As a result, 2, 10, 18, 36, 54, 86, and 118 are the "atomic magic numbers." As with nuclear magic numbers, spin–orbit coupling phenomena impacting subshell energy levels are likely to change them in the superheavy zone. As a result, copernicium (112) and flerovium (114) should be more inert than oganesson (118), and the next noble gas should appear at element 172 rather than 168. (which would continue the pattern).
In 2010, symmetry considerations were proposed as an alternate explanation for magic numbers. The ground state parameters (including the magic numbers) for metallic clusters and nuclei were simultaneously derived analytically based on the fractional extension of the standard rotation group. In this paradigm, a precise potential term is not required.
Key takeaway:
1. The magic numbers in stable nuclei are 2, 8, 20, 28, 50, 82, and 126, which have similar numbers of protons and neutrons and do not decay radioactively.
2. Nuclei with neutron and proton (atomic) numbers both equal to one of the magic numbers are referred to as "double magic" and are particularly resistant to disintegration. Helium-4, oxygen-16, calcium-40, calcium-48, nickel-48, nickel-78, and lead-208 are examples of double magic isotopes.
3. Nuclei with totally filled proton and neutron shells are referred to as doubly magical by physicists. Lead-208 is the most enormous doubly magical nucleus in this group, making it stand out.
References:
1.Quantum Mechanics: Theory and Applications, A.K. Ghatak and S. Lokanathan,(Macmillan)-2004
2. Introduction to Quantum Theory, David Park (Dover Publications)-1974
3. Theory and Problems of Modern Physics, Schaum‘s outline, R.Gautreau and W.Savin- (Tata McGraw-Hill) 2nd Edition
4. Physics for scientists and engineer with Modern Physics-Jewell and Serway -(CENGAGE Learnings) 2010.
5. Modern Physics of Atoms and Molecules Bransden and Joachim (PearsonIndia)-2003
Unit - 3
Nuclear Physics- I
3.1.1 Atomic Nucleus: Definition, Structure & Size
The Nucleus
The atomic nucleus is the nucleus, which is the most central part of the atom. Protons and neutrons are the two types of subatomic particles that make up the nucleus.
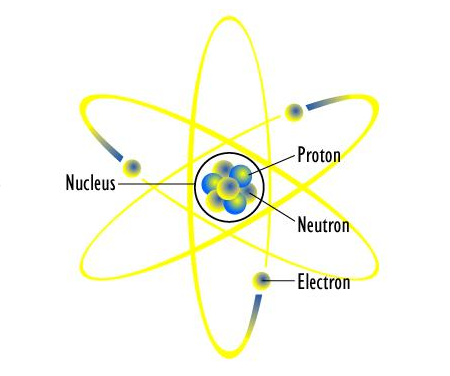
Atoms are the fundamental constituents of all substance. Atoms make up everything you can see, feel, and touch. Even things that you can't see, feel, hear, or touch are made up of atoms. Atoms are the building blocks of everything.
The Gold Foil Experiments were conducted by Ernest Rutherford and Hans Geiger and Ernest Marsden in 1909. They shot particles through exceedingly thin sheets of gold foil during the experiments. In 1911, Rutherford came to the conclusion that the atom had a dense nucleus because most of the particles shot straight through, but some of the particles were deflected due to the dense nucleus of the gold atoms. This notion would disprove the concept that the atom was more like plum pudding in structure. Until Rutherford's discoveries, the plum pudding model was the predominant model of atomic structure.
3.1.2 Atomic Numbers
The atomic nucleus is located in the atom's centre. The number of protons and neutrons in an atom determines the atom's type or element. A group of atoms with the same atomic structure is referred to as an element. Hydrogen, for example, is an element.
The atomic nucleus' composition reveals a great deal about the element it represents. The atomic number is determined by the number of protons inside the nucleus. Protons have a positive charge (+). The electrons (-) must balance the atom's negative charge in order for it to have a neutral charge. As a result, there are exactly as many protons as electrons in a neutral atom. So, if you know the atomic number and the charge of the atom, you can easily calculate the number of electrons. For example, because hydrogen has one proton, 1+, it must have a one-charge in order to be neutral. As a result, hydrogen only contains one electron.
What role do neutrons play in all of this? Neutrons, after all, are neutral. I use the first letters to keep everything straight: Neutrons are Neutral, and Protons are Positive. I then recall Electrons as a result of the Elimination Process.
Despite the fact that neutrons do not provide the atom any charge, they are nonetheless significant in the atomic structure. The neutron is the biggest particle in the subatomic world. The atomic mass is calculated by adding the neutrons and protons together. Because electrons are so tiny, their mass only accounts for.01 percent of the total mass. The electrons aren't inside the nucleus; instead, they're whizzing around on the nucleus's periphery.
We can find the number of neutrons by subtracting the atomic number from the atomic mass, because the atomic number tells us the number of protons in an atom and the atomic mass tells us the number of protons and neutrons.
The number of neutrons is equal to the atomic mass minus the atomic number.
3.1.3 Structure of the nucleus
Because the electron and proton were the only known particles at the time, the nucleus' structure was poorly understood. It had already been proven that nuclei are typically roughly twice as heavy than protons alone can account for. Until English scientist James Chadwick discovered the neutron in 1932, a consistent hypothesis was impossible. He discovered that when alpha particles collided with beryllium nuclei, neutral particles of roughly the same mass as protons were ejected. Almost all nuclear processes may be explained in terms of neutrons and protons in a nucleus. Surprisingly, the nucleus' neutrons and protons move in orbitals to a significant extent, as if their wave functions are independent of one another. A stationary wave pattern featuring peaks and nodes, as well as angular momentum quantum numbers, describes each neutron or proton orbital. The shell nuclear model is a nucleus theory that is based on these orbitals. It was independently introduced in 1948 by Maria Goeppert Mayer of the United States and Johannes Hans Daniel Jensen of West Germany, and it grew into a full theory of the nucleus during the following decades.
Enrico Fermi, an Italian-born American physicist, and others researched the interactions of neutrons with nuclei in the mid-1930s. Neutrons, unlike protons or alpha particles, are not repelled from the nucleus by a positive charge, hence they are easily captured. When a neutron is captured, the atomic mass of the new nucleus increases by one unit. If a more stable isotope of that atomic mass is close, the new nucleus will be radioactive, converting the neutron to a proton and taking on the more stable form.
In 1938, German chemists Otto Hahn and Fritz Strassmann discovered nuclear fission as a result of experiments initiated and explained by Austrian physicist Lise Meitner. In fission, a uranium nucleus captures a neutron and gains enough energy to cause the nucleus to split into two lighter nuclei of nearly equal size due to its inherent instability. More neutrons are released during the fission process, which can be exploited to induce more fissions. Under Fermi's leadership, the first nuclear reactor, a device designed to allow controlled fission chain reactions, was built at the University of Chicago, and the first self-sustaining chain reaction occurred in this reactor in 1942. In 1945, American scientists developed the first fission weapon, also known as an atomic weapon, which employed uncontrolled fission events in uranium or plutonium. In 1952, American scientists utilised a fission explosion to start a fusion reaction, in which hydrogen isotopes thermally fused to form heavier helium nuclei. This was the world's first thermonuclear bomb, commonly known as an H-bomb, a weapon capable of releasing hundreds or thousands of times the energy of a fission bomb.
3.1.4 Quantum field theory and the standard model
Dirac not only proposed the relativistic equation for the electron, but he also pioneered quantum field theory, a relativistic analysis of particle interactions. The theory allows for the creation and destruction of particles and just requires the presence of proper interactions with appropriate energy. Quantum field theory also states that interactions can only extend across a distance if the force is carried by a particle, or field quantum. The photon, or quantum of light, carries the electromagnetic force, which may act over large distances. Mathematical challenges occurred in applying the theory since it permits particles to interact with their own field quanta.
An experiment conducted by American physicist Willis Eugene Lamb, Jr. In 1946 and 1947 overcame the theoretical deadlock. He demonstrated that the hydrogen spectrum is around one-tenth of one percent different from Dirac's predicted picture using microwave techniques developed during WWII. Later, American physicist Polykarp Kusch, who was born in Germany, discovered a similar anomaly in the magnitude of the electron's magnetic moment. Lamb's findings were revealed at the well-known Shelter Island Conference in the United States in 1947. Hans Bethe, a German-born American physicist, and others concluded that the so-called Lamb shift was most likely caused by electrons and field quanta produced by the vacuum. Richard Feynman, Julian Schwinger, and Tomonaga Shin'ichir, who won the Nobel Prize for Physics in 1965, and Freeman Dyson, who demonstrated that their varied techniques were mathematically similar, overcame the earlier mathematical hurdles. Quantum electrodynamics, a novel theory, was discovered to explain all of the measurements with extreme precision. Quantum electrodynamics, it appears, provides a full account of how electrons behave in the presence of electromagnetism.
The weak force and electromagnetic were discovered to have parallels in the 1960s. The electroweak hypothesis, for which Sheldon Glashow, Abdus Salam, and Steven Weinberg received the Nobel Prize in Physics in 1979, integrated the two forces. Three field quanta—the W particle, the Z particle, and the Higgs boson—were predicted as extra force carriers in addition to the photon. The Higgs boson was the carrier of the Higgs field, while the W and Z particles were carriers of the weak force, resulting in the W and Z particles being heavy and the photon having a mass of zero. The discovery of the W and Z particles in 1983, which had masses that were exactly predicted, proved the electroweak theory's validity. In 2012, a particle that was most likely the Higgs boson was discovered.
Since the first unstable particle, the muon, was discovered in cosmic rays in the 1930s, hundreds more subatomic particles have been discovered. By the 1960s, patterns in the properties and connections of subatomic particles had emerged, leading to the development of the quark theory. The Standard Model was created by combining the electroweak theory and the quark theory to create a theoretical framework that encompasses all known particles and field quanta. The leptons and quarks are the two broad kinds of particles in the Standard Model. Electrons, muons, and neutrinos are all leptons, and they only interact with the electroweak force apart from gravity.
The strong force affects quarks, and they join in a variety of ways to form bound states. The neutron and proton are two of the bound quark states, known as hadrons. A proton, a neutron, or any of the heavy hadrons known as baryons are formed when three quarks unite. The pion is formed when a quark and an antiquark unite. Quarks have never been seen before, and physicists don't expect to see one anytime soon. Outside hadrons, the strong force is so strong that quarks cannot be separated from each other. However, the existence of quarks has been indirectly verified in numerous ways. Beginning in 1967, researchers observed that some electrons fired against proton targets were deflected at significant angles in tests using high-energy electron accelerators. The large-angle deflection, like Rutherford's gold-foil experiment, implies that hadrons have an interior structure comprising very small charged items. Quarks are thought to be the tiny things. Physicists developed quantum chromodynamics, a novel quantum field theory, in the mid-1970s to accommodate quarks and their unusual features. This hypothesis describes the confinement of quarks to hadrons qualitatively. The theory, according to physicists, should explain all features of hadrons. However, dealing with strong interactions in quantum chromodynamics presents more mathematical challenges than dealing with weak interactions in quantum electrodynamics, making comprehensive computations of hadron features impossible. Nonetheless, numerical computations utilising the most powerful computers seems to support the theory's veracity.
3.1.5 Properties of Nuclei
Protons and neutrons make up the atomic nucleus ((Figure)). Although protons and neutrons have about the same mass, protons have one unit of positive charge whereas neutrons have none. At the heart of an atom, these particles are crammed into a very small space. The nucleus is spherical or ellipsoidal in form, and about 1/100,000th the size of a hydrogen atom, according to scattering measurements. The nucleus of an atom would be around the size of a baseball if it were the size of a big league baseball stadium. Nucleons are protons and neutrons that make up the nucleus.
Protons and neutrons make up the atomic nucleus. Protons are depicted in blue, while neutrons are depicted in red.
Key takeaway:
- Protons, neutrons, and electrons make up the atoms themselves. The atomic number of each element is equal to the number of protons in its nucleus. The number of neutrons in an element's isotopes varies. An atomic symbol is used to symbolise elements.
- Nuclei with magic numbers of neutrons or protons, as well as those that are doubly magical, are particularly stable.
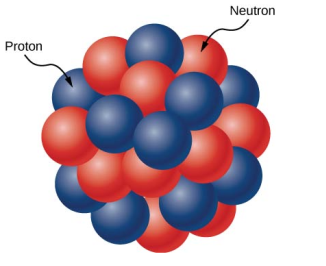
The atomic number, Z, determines the number of protons in the nucleus. The neutron number, N, is the number of neutrons in the nucleus. The mass number, A, is the total number of nucleons. These figures are connected by
A = Z + N.
A nucleus is represented symbolically by
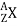
Where X is the chemical element, A denotes its mass, and Z denotes its atomic number. 612c, for example, is the carbon nucleus, which has six protons and six neutrons (or 12 nucleons).
For a variety of stable nuclei (nuclides), a graph of the number N of neutrons vs the number Z of protons is illustrated in (Figure). Multiple values of N (blue points) are feasible for a given value of Z. The number of neutrons equals the number of protons N=P for tiny values of Z, and the data fall on the red line. The number of neutrons is more than the number of protons N>P for large values of Z, and the data points are above the red line. For Z>15, the number of neutrons is usually more than the number of protons.
For stable atomic nuclei, this graph shows the number of neutrons N vs the number of protons Z. Neutrons outnumber protons in larger nuclei.
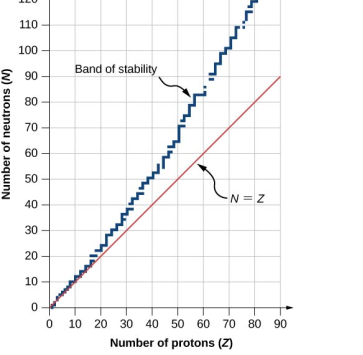
This graph is used to create a graphic that provides more specific information on each nucleus (Figure). This graph is known as a nuclide graph. A nucleus is represented by each cell or tile. The nuclei are organised in ascending Z (horizontal) and ascending N (vertical) order (along the vertical direction).
The nuclides are depicted in part on this graph. Cell values for stable nuclei (dark blue backgrounds) show the percentage of nuclei with the same atomic number found on Earth (percent abundance). The number represents the half-life of unstable nuclei.

Isotopes are atoms with nuclei that have the same number of protons (Z) but differing numbers of neutrons (N). Normal hydrogen (1 proton, no neutrons), deuterium (1 proton and one neutron), and tritium (1 proton and one neutron) are the three isotopes of hydrogen (one proton and two neutrons). Because chemical properties are dictated by interactions between the atom's outer electrons, rather than the nucleons, isotopes of the same atom have the same chemical properties. Water containing deuterium rather than hydrogen ("heavy water"), for example, looks and tastes like regular water. A list of common isotopes may be found in the table below.
Common Isotopes*No entry if less than 0.001 (trace amount). | |||||
Element | Symbol | Mass Number | Mass (Atomic Mass Units) | Percent Abundance* | Half-life** |
Hydrogen | H | 1 | 1.0078 | 99.99 | Stable |
2H or D | 2 | 2.0141 | 0.01 | Stable | |
3H  | 3 | 3.0160 | − | 12.32 y | |
Carbon | 12C | 12 | 12.0000 | 98.91 | Stable |
13C  | 13 | 13.0034 | 1.1 | Stable | |
14C  | 14 | 14.0032 | − | 5730 y | |
Nitrogen | 14N | 14 | 14.0031 | 99.6 | Stable |
15N | 15 | 15.0001 | 0.4 | Stable | |
16N | 16 | 16.0061 | − | 7.13 s | |
Oxygen | 16O | 16 | 15.9949 | 99.76 | Stable |
17O  | 17 | 16.9991 | 0.04 | Stable | |
18O | 18 | 17.9992 | 0.20 | Stable | |
19O  | 19 | 19.0035 | − | 26.46 s | |
In heavier nuclei, why do neutrons outweigh protons ((Figure))? Understanding the forces inside the nucleus is required to address this question. There are two sorts of forces: (1) the long-range electrostatic (Coulomb) force, which repels positively charged protons, and (2) the short-range strong nuclear force, which attracts all nucleons in the nucleus. You may have also heard of a nuclear force that is “weak.” Although this force is responsible for some nuclear decays, it does not play a role in keeping the nucleus stable against the strong Coulomb repulsion it faces. In the next chapter, when we study particle physics, we will go over the strong nuclear force in greater depth. When the attractive interactions between nucleons balance out the repulsive, long-range electrostatic interactions between all protons in the nucleus, nuclear stability is achieved. Excess neutrons are required for heavy nuclei to prevent electrostatic interactions from tearing the nucleus apart, as seen in (Figure).
(a) The electrostatic force is repulsive and has a large range of application. The arrows show outward forces exerted by a proton (also in blue) at the centre on protons (in blue) at the nuclear surface. (a) The strong nuclear force acts on nucleons in close proximity. The arrows show the attractive forces that a neutron (in red) exerts on its closest neighbours.
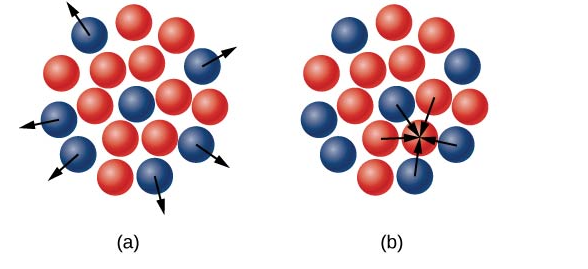
Because stable isotopes exist, it's important to be cautious when mentioning an element's mass. Copper (Cu), for example, has two stable isotopes:
V(CPn) = 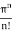
3.2.1 Probability: The Heisenberg Uncertainty Principle
Probability Distribution
Matter and photons are waves, which means they are dispersed over a large area. What is a particle's location, such as an electron's? Is it right in the middle of the tidal wave? The solution lies in how an electron's location is measured. Unlike a wave, experiments reveal that the electron will be found at a specific point. But if you set up exactly the same situation and measure it again, you will find the electron in a different location, often far outside any experimental uncertainty in your measurement. Repeated measurements will reveal a wavelike statistical distribution of sites.
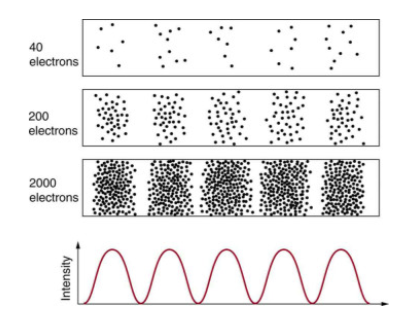
Many scientists, including Schrödinger and Heisenberg, investigated the repercussions after de Broglie postulated the wave nature of matter. Because of its wave nature, it was rapidly realised that a particle's route and destination could not be anticipated precisely for each particle separately. Each particle, on the other hand, has a specific destination.
You acquire a distribution connected to the particle's wavelength and diffraction pattern after collecting enough data. The likelihood of finding the particle at a given position is known as a probability distribution, and the overall pattern is known as a probability distribution. Quantum physicists discovered equations that predicted the probability distribution in a variety of situations.
It's a little unsettling to believe that you can't foresee where a single particle will go or even follow it to its final destination. Let's see what occurs when we try to track a particle. Figure 2 shows the double-slit patterns obtained for electrons and photons. First, we observe that these patterns are similar when using d sin = m, the double-slit constructive interference equation presented in Photon Energies and the Electromagnetic Spectrum, where d is the slit separation and m is the electron or photon wavelength.

As individual particles fall on the detector, both patterns accumulate statistically. This can be seen with photons or electrons, but for now, we'll focus on electrons. You may envisage the electrons interfering with one another in the same way that waves do. Reduce the intensity until there is never more than one electron between the slits and the screen to test this. The interference pattern repeats itself! This means that a particle's probability distribution spans both slits, and particles collide with one another. Does this imply that the electron passes through both slits as well? An electron is a non-divisible basic unit of matter. However, because it is a valid question, we should investigate whether the electron passes through one or both slits. Coils encircling the slits may detect charges passing through them, for example. An electron always passes through one slit or the other; it does not split to pass through both slits. However, there is a catch. When you determine that the electron passed through one of the slits, you obtain single slit interference instead of a double slit pattern. There is no way to determine which slit the electron passed through using another means. A single-slit pattern is forced because the particle only passed through one slit. You get a double-slit pattern if you don't pay attention to which slit the electron passes through.
3.2.2 Heisenberg Uncertainty
What difference does it make knowing which slit the electron passed through make to the pattern? The response is crucial: measurement has an impact on the system being studied. Information can be lost, and it is often impossible to precisely measure two physical things at the same time. For example, scattering light or other electrons off a moving electron can be used to determine its position. Those probes have momentum of their own, and scattering from the electron causes the electron's momentum to shift in a way that causes information to be lost. Even in principle, absolute knowledge has a limit.
As a result of his work on quantum mechanics and the wave properties of all particles, Werner Heisenberg initially declared this limit to knowledge in 1929. (See Fig. 3.) Consider measuring the position and momentum of an electron at the same time (it could be any particle). Position x has an uncertainty that is roughly equal to the wavelength of the particle. x
A wave does not exist in a single location in space, as previously stated. When the position of an electron is measured repeatedly, a spread in locations is seen, signalling that position x is uncertain. We must interact with the particle in order to detect its position, such as by causing it to collide with a detector. The particle will lose momentum as a result of the collision. This change in momentum could be somewhere between zero and the particle's whole momentum.
Somewhere between zero and the particle's entire momentum, p=hp=h Because it is impossible to predict how much momentum will be transferred to a detector, momentum p is also unpredictable. In fact, the uncertainty in momentum can be as big as the momentum itself, resulting in ph in equation form.
Since x, the position uncertainty can be decreased by utilising a shorter-wavelength electron. However, because p=hp=h, reducing the wavelength increases the uncertainty in momentum. Using a longer-wavelength electron, on the other hand, reduces the uncertainty in momentum while increasing the uncertainty in location. This trade-off can be expressed mathematically by increasing the uncertainties. Xp h is left after the wavelength cancels.
As a result, if one uncertainty is lowered, the other must be increased in order for the product to be acceptable.
Heisenberg demonstrated that using advanced mathematics, the best that can be done in a simultaneous measurement of position and momentum is xph4.
The Heisenberg uncertainty principle is the name for this. With uncertainties x and p that multiply to less than h4, measuring position x and momentum p at the same time is impossible. There can't be zero uncertainty in either case. Neither uncertainty can be reduced to a small size without the other increasing in size. A narrow wavelength allows for precise location measurement, but it also increases the probe's momentum, which disrupts the momentum of the system being monitored. For example, if an electron is scattered from an atom and its wavelength is narrow enough to detect the position of electrons in the atom, the momentum of the electrons can knock them out of their orbits, causing information about their original motion to be lost. As a result, following an electron in its orbit around an atom is difficult. The electron will be found in a certain location if its position is measured, but the atom will be disrupted. Repeated measurements on similar atoms will yield intriguing probability distributions for electrons in the atom's vicinity, but not motion information. Electron clouds or orbitals are terms used to describe probability distributions.
EXAMPLE 1. HEISENBERG UNCERTAINTY PRINCIPLE IN POSITION AND MOMENTUM FOR AN ATOM
1. What is the uncertainty in velocity of an electron in an atom whose position is measured to a precision of 0.0100 nm?
2. What is the electron's kinetic energy in eV if it has this velocity?
Strategy
The measurement's accuracy, or x = 0.0100 nm, is the uncertainty in position. Xph4xph4 can thus be used to find the smallest uncertainty in momentum p. Once the uncertainty in momentum p has been determined, p = mv can be used to determine the uncertainty in velocity.
Solution for Part 1
Using the equals sign in the uncertainty principle to express the minimum uncertainty, we have
ΔxΔp=h4π
Solving for Δp and substituting known values gives
Δp=h4πΔx=6.63×10−34 J⋅ s4π(1.00×10−11 m)=5.28×10−24 kg⋅ m/s
Thus, Δp = 5.28 × 10−24 kg · m/s = mΔv.
Solving for Δv and substituting the mass of an electron gives
Δv=Δpm=5.28×10−24 kg⋅ m/s9.11×10−31 kg=5.79×106 m/s
Solution for Part 2
Although large, this velocity is not highly relativistic, and so the electron’s kinetic energy is
KEe=12mv2 =12(9.11×10−31 kg)(5.79×106 m/s)2 =(1.53×10−17 J)(1 eV1.60×10−19 J)=95.5 eV
Discussion
Because atoms are about 0.1 nm in size, knowing an electron's position to 0.0100 nm accurately localises it within the atom. This would be the equivalent of being able to perceive details a tenth the size of an atom. However, the resulting velocity uncertainty is significant. You wouldn't be able to keep up with it if its speed was so unpredictable. To gain a better notion of how big the velocity uncertainty is, we assumed the electron's velocity was equal to its uncertainty, which resulted in a kinetic energy of 95.5 eV. This is far larger than the normal energy difference between levels in atoms (see Table 1 in Photon Energies and the Electromagnetic Spectrum), making it hard to calculate an energy for the electron even if we know its position reasonably well.
Why don't we perceive Heisenberg's principle of uncertainty in everyday life? Planck's constant is very small, as the solution implies. As a result, the uncertainty in estimating the location and momentum of massive objects is negligible at its lowest point. Jupiter's reflected sunlight may be detected, allowing us to track the planet's orbit around the Sun. The reflected sunlight changes Jupiter's momentum and causes uncertainty, but this is insignificant in comparison to Jupiter's massive momentum. For huge objects, the correspondence principle states that quantum mechanics predictions become indistinguishable from classical physics predictions, which is the situation here.
3.2.3 Heisenberg Uncertainty for Energy and Time
There is another form of Heisenberg’s uncertainty principle for simultaneous measurements of energy and time. In equation form, ΔEΔt≥h4πΔEΔt≥h4π, where ΔE is the uncertainty in energy and Δt is the uncertainty in time. This means that within a time interval Δt, it is not possible to measure energy precisely—there will be an uncertainty ΔE in the measurement. In order to measure energy more precisely (to make ΔE smaller), we must increase Δt. This time interval may be the amount of time we take to make the measurement, or it could be the amount of time a particular state exists, as in the next Example 2.
EXAMPLE 2. HEISENBERG UNCERTAINTY PRINCIPLE FOR ENERGY AND TIME FOR AN ATOM
An atom in an excited state stores energy for a short period of time. What is the minimal uncertainty in the energy of the state in eV if the duration of this excited state is measured to be 1.0 1010 s?
Strategy
The equals sign in Etth4Etth4 is used to find the least uncertainty in energy E, which corresponds to a suitable option for the uncertainty in time. The whole lifespan of the excited state, or t = 1.0 1010 s, has the greatest time uncertainty.
Solution
Solving the uncertainty principle for ΔE and substituting known values gives
ΔE=h4πΔt=6.63×10−34 J⋅ s4π(1.0×10−10 s)=5.3×10−25 J
Now converting to eV yields
ΔE=(5.3×10−25 J)(1 eV1.6×10−19 J)=3.3×10−6 eV
Discussion
Excited states in atoms have a lifetime of 1010 s, which means they swiftly release their accumulated energy on human time scales. The energy uncertainty is merely a few millionths of an eV. When compared to the normal excitation energy in atoms, which are on the order of 1 eV, this uncertainty is negligible. As a result, the uncertainty principle restricts the precision with which we can measure the lifetime and energy of such states, but only slightly.
If a system's lifespan is very short, the uncertainty principle for energy and time can be quite important. Then t is very tiny, and E is quite large as a result. Some nuclei and exotic particles have extremely short lifetimes (as little as 1025 s), resulting in energy uncertainty of many GeV. (109 eV). Because stored energy manifests as increased rest mass, the rest mass of short-lived particles is subject to considerable uncertainty. When masses or decay energies are measured repeatedly, a spread of masses or energies is obtained. E is the spread. You might wonder if this energy uncertainty may be prevented by not calculating lifetime. No, that is not the case. Nature is aware of the lifetime, and its shortness has an impact on the particle's energy. This is so well established empirically that the lifespan of short-lived states is calculated using the uncertainty in decay energy. It's difficult to measure the lifetime of some nuclei and particles since they are so short-lived. However, if their decay energy can be determined, the spread is E, which is employed in the uncertainty principle (Eth4) to compute the lifetime t.
The uncertainty principle has another implication for energy and time. If E is unclear about energy, then E can break energy conservation for a time t. If the breach is transitory and lower than the uncertainty in energy, neither physicists nor nature can detect if conservation of energy has been violated. While this may appear benign at first, as we will learn in later chapters, it allows for the temporary formation of matter from nothing and has ramifications for how nature transmits forces over extremely short distances.
Finally, we mentioned that individual measurements create exact or particle-like findings in our explanation of particles and waves. Each time we detect an electron, for example, a precise position is obtained. Repeated measurements, on the other hand, yield a range of values that is consistent with wave characteristics. “What there are, are particles,” said the brilliant theoretical physicist Richard Feynman (1918–1988). When you watch enough of them, they begin to disseminate themselves in the way that a wave would. We can't discern what they are while they go, though, since when we try to measure, we change the way they travel.
3.2.4 On the basis of Heisenberg's uncertainty principle, show that the electron can not exist within the nucleus.
Radius of the nucleus is of the order of 10-15 m and thus maximum uncertainity in the position of electron i.e. ∆x if it is within the nucleus will be 10-15 m.
Now, ∆x m∆V ≥ h/4π
Or, ∆V = 6.626 × 10-34 / 4 × 3.14 × 9.1 × 10-31 × 10-15 = 5.97 × 1010 m/s
As this level of uncertainty in velocity is impossible to be achieved hence electron can not exist in the nucleus.
Key takeaway:
In quantum physics, Heisenberg's uncertainty principle is a crucial concept. It goes something like this: if we know exactly where a particle is (the uncertainty of position is tiny), we know nothing about its momentum (the uncertainty of momentum is huge), and vice versa.
3.3.1 Nuclear Forces
The forces that act between two or more nucleons are known as nuclear forces (also known as nuclear interactions or strong forces). They form atomic nuclei by binding protons and neutrons ("nucleons"). The nuclear force is tens of millions of times more powerful than the chemical bonds that keep atoms in molecules together. This is why, when compared to chemical fuels like oil or coal, nuclear reactors produce around a million times more energy per kilogramme of fuel. However, the nuclear force has a limited range, only a few femtometers (1 fm =1015 m), after which it rapidly declines. That is why, despite its immense strength, we are unaware of its existence on an atomic scale or in everyday life. For seven decades, some of the world's greatest physicists have been working on a proper theory of nuclear forces, and it has been one of the most important areas of physics research in the twentieth century. The initial theory was that the force is created by the exchange of mesons, which are lighter than nucleons, and this theory spawned a new branch of modern physics known as (elementary) particle physics. The nuclear force is now thought to be a residual interaction (similar to the van der Waals force between neutral atoms) of a stronger force between quarks, which is mediated by gluon exchange and maintains quarks together inside a nucleon.
3.3.2 Historical perspective
It was obvious after Chadwick's discovery of the neutron in 1932 (Chadwick, 1932) that the atomic nucleus is made up of protons and neutrons. Electromagnetic forces cannot be the cause of the nucleus' elements adhering together in such a system. The nucleus should be blown apart by the repulsive electrical Coulomb interaction between the protons. As a result, the idea of a new strong nuclear force was proposed. Hideki Yukawa (Yukawa,1935), a Japanese scientist, proposed the original theory for this new force in 1935, claiming that nucleons would exchange particles between each other and this mechanism would create the force. Yukawa's theory is based on the electromagnetic interaction hypothesis, in which the force is caused by the exchange of a (massless) photon. In the case of the nuclear force, Yukawa postulated that the "force-makers" (later dubbed "mesons") have a mass that is a fraction of the mass of the nucleon. Because heavy particles may only travel a finite distance due to the uncertainty principle, the force's effect is limited to a finite range. Yukawa's predicted meson, the pion, was discovered in 1947 in cosmic ray and in 1948 in the laboratory. Yukawa won the Nobel Prize for Physics in 1949. More mesons were discovered in accelerator operations in the 1950s and 1960s, and the meson theory of nuclear forces was expanded to incorporate many more mesons. These models became known as one-boson-exchange models, which refers to the fact that the individual mesons in this model are traded separately. At low energies, the one-boson-exchange model is quite good in explaining almost all aspects of the nucleon-nucleon interaction. In the 1970s and 1980s, meson models that went beyond the conventional single-particle exchange mechanism were also devised. The explicit exchange of two pions, with all its complexities, was included in these models. The Paris (Lacombe et al., 1980) and Bonn potential models are well-known examples of the latter type (Machleidt et al., 1987).
These meson models appeared to be the solution to the nuclear force problem since they were numerically highly successful. When it was discovered (in the 1970s) that quantum chromodynamics (QCD) rather than meson theory is the fundamental theory of strong interactions, all "meson theories" had to be considered as models, and attempts to derive a real theory of the nuclear force had to start all over again.
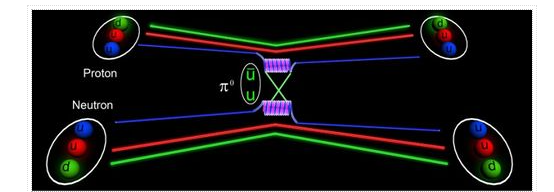
There are two issues in deriving nuclear forces from QCD. First, each nucleon is made up of three quarks, therefore a two-nucleon system is already a six-body problem. Second, the force between quarks, which is formed by the interchange of gluons, has the property of being extremely strong at the low energy scales found in nuclear physics. Finding “convergent” mathematical solutions is challenging due to this remarkable strength. As a result, the models offered in the initial round of fresh attempts were simply "QCD-inspired." These models have the advantage of attempting to explain both nucleon structure (three quarks) and nucleon-nucleon interactions (six-quark systems) on an equal footing. Such models successfully describe some of the gross properties of the two-nucleon force, such as the "hard core" (see below). However, it should be stressed that these quark-based approaches are just another set of models, not a theory, from a critical standpoint. Alternatively, by placing the six-quark system on a four-dimensional lattice of discrete points that symbolises three dimensions of space and one dimension of time, one can try to solve the six-quark issue with sheer computing power. Lattice QCD is the name given to this approach, which is making progress. Such computations, however, are computationally prohibitively expensive and so cannot be utilised as a conventional nuclear physics instrument.
When Nobel Laureate Steven Weinberg applied the concept of an Effective Field Theory (EFT) to low-energy QCD about 1990, he made a big breakthrough (Weinberg, 1979, 1991). He just typed down the most general theory that is consistent with all of the properties of low-energy QCD, as this theory would be identical to low-energy QCD. The so-called chiral symmetry, which is “spontaneously” violated, is a particularly essential characteristic. Chiral symmetry is observed by massless particles, which means that their spin and momentum are either parallel (“right-handed”) or anti-parallel (“left-handed”) and will remain thus indefinitely. Because the quarks that make up nucleons ("up" and "down") are virtually massless, near chiral symmetry is a given. This symmetry, naively, should lead to the discovery of mesons of the same mass in nature, but with positive and negative parity. This is not the case, and such failure is referred to as a "spontaneous" symmetry break. The spontaneous breaking of a symmetry creates a particle, which in this case is the pion, according to a theory first demonstrated by Jeffrey Goldstone. As a result, the pion becomes a key participant in the development of nuclear weapons. When compared to the interaction of gluons with quarks, the interaction of pions with nucleons is weak. As a result, pion-nucleon reactions may be estimated easily. Furthermore, this effective field theory can be extended in terms of powers of momentum over "scale," where scale refers to the "chiral symmetry breaking scale," which is around 1 GeV (= 109 eV). Chiral Perturbation Theory (ChPT) is a theory that allows you to compute the numerous terms that make up the nuclear force power by power, or order by order. Another benefit of the chiral EFT method is that it may generate forces between two nucleons as well as many-nucleon forces on the same basis. The chiral EFT technique is becoming increasingly popular in modern theoretical nuclear physics and is being used with considerable effectiveness.
3.3.3 Properties of the nuclear force

The properties of nuclei can be used to determine some properties of nuclear interactions. The volume of nuclei rises according to the quantity of nucleons, a phenomenon known as saturation. This feature implies that the nuclear (central) force has a short range (a few fm) and is extremely attracting at that range, explaining nuclear binding. The nuclear force, on the other hand, has a complex spin-dependence. The observation that the deuteron (the proton-neutron bound state, the lowest atomic nucleus) deviates somewhat from a spherical shape: it has a non-vanishing quadrupole moment was the first proof of this attribute. This proposes a force that is determined by the orientation of the nucleons' spins in relation to the vector connecting the two nucleons (a tensor force). A shell structure has been seen in heavier nuclei, which, according to M. G. Mayer and J. H. D. Jensen, can be explained by a strong force between the nucleon's spin and its orbital motion (the spin-orbit force). Scattering experiments, in which one nucleon is scattered off another nucleon with differing spin orientations, provide more direct evidence for spin dependence. The presence of the nuclear spin-orbit and tensor forces has been demonstrated in such tests. At higher energies (more than 200 MeV), scattering measurements show that the nucleon-nucleon interaction becomes repulsive at short inter-nucleon distances (smaller than 0.5 fm, the hard core).
There are three-nucleon forces (3NFs), four-nucleon forces (4NFs), and so on, in addition to the force between two nucleons (2NF). The 2NF, on the other hand, is far more powerful than the 3NF, which is far more powerful than the 4NF, and so on. The importance of 3NFs has been demonstrated in exact computations of the properties of light nuclei based on the "elementary" nuclear forces. Their contribution is tiny, yet it is critical. The necessity for 4NFs to explain nuclear properties hasn't been proven (yet).
When electromagnetic forces are neglected, nuclear forces are essentially charge-independent, meaning that the force between two protons, two neutrons, and a proton and a neutron is almost the same (in the same quantum mechanical state).
3.3.4 Phenomenological approaches
Traditionally, nuclear force research has been divided into two categories: phenomenology and theory. To begin, we'll look at phenomenology. At very low energies, nucleon-nucleon scattering can be represented by the so-called effective range expansion, which has just two parameters in its simplest form (Bethe, 1949); for a textbook exposition, see Brown and Jackson (1976). This expansion has been recovered in modern times from an EFT that does not include the pion ('pionless EFT'); for an introduction, see Bedaque and van Kolck (2002). The spin-dependence of the nuclear force becomes significant at intermediate energies. Okuba and Marshak (1958) imposed the following symmetries to derive a general equation for the NN potential (that incorporates spin and momentum dependences):
Invariance in translation
Invariance of Galileo
Invariance of rotation
Invariance of space reflection
Invariance of time reversal
Invariance when particle 1 and 2 are interchanged
3.3.5 The meson theory of nuclear forces
Yukawa's idea of 1935
In 1935, Yukawa (1935) introduced the concept of massive particle exchange to explain the nuclear force. He constructed an analogy to classical electrodynamics. In electrodynamics, the Coulomb potential
ϕ(r)=q4π1r
Is the solution of Poisson's equation
∇2ϕ(r⃗ )=−qδ(3)(r⃗ ).
When adding a mass term to this equation (and flipping the sign on the r.h.s. To adjust for scalar coupling),
(∇2−m2)φ(r⃗ )=gδ(3)(r⃗ ),
The solution becomes
φ(r)=−g4πe−mrr,
Which is the scalar field generated by one nucleon. A second nucleon, with also coupling g, at a distance r from the first one will be exposed to the interaction energy
V(r)=−g24πe−mrr,
Which is known as the Yukawa potential. The exponential in this expression, that is due to the mass m of the meson, restricts the potential to a finite range, which is the essential point. For m→0 we are back to the form of the Coulomb potential.
3.3.6 The one-boson-exchange model
The initial derivation by Yukawa was for scalar bosons. When a true meson was discovered in 1947/48, it was discovered to be pseudo-scalar with a mass of roughly 138 MeV, and it was named the -meson or pion. As a result, attempts to derive the nuclear force in the 1950s concentrated on ideas that solely incorporated pions. These 'pion theories' had numerous flaws and failed miserably—for reasons we now understand: pion dynamics is bound by chiral symmetry, a concept unknown in the 1950s. Heavier (non-strange) mesons, such as the vector (spin-1) mesons (770) and (770), were discovered in experiments in the early 1960s (782). Theoreticians were eager to extend meson theory by integrating more and diverse species of mesons because of the challenges with pion theories. This led to the development of one-boson-exchange (OBE) models in the 1960s, which proved to be quite successful for the two-nucleon interaction.
Let's start with the question of which mesons to think about. When calculating the nuclear force, the forecasts for the longer flung sections are often more reliable. Because the range of a meson's force, R, is inversely proportional to the mass of the meson, m,
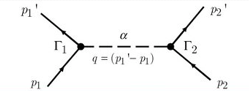

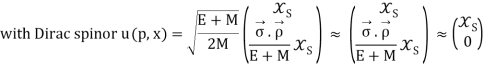
Where E = 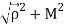 and
and 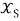 is a two-component Pauli spinor.
is a two-component Pauli spinor.
Lagrangian: 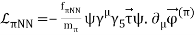
Vertex: I times the Lagrangian stripped off the fields ( for an incoming pion)

Potential: I times the amplitude ( Pπ = I, q2 = - 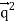 )
)
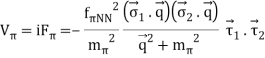
Using the operator identity
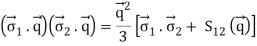
With 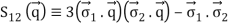 (“Tensor operator”)
(“Tensor operator”)
The one-pion exchange potential (OPEP) can be written as
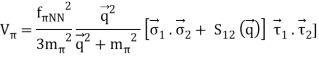
Lagrangian: 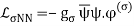
Vertex: 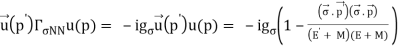
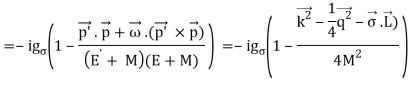
Potental: keeping all terms up to Q2/ M2 [ Pσ = i, 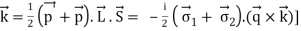
Vσ = 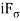 =
= 
Lagrangian: 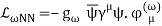
Vertex:
μ = 0: 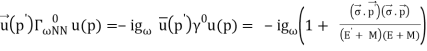

Potential, including also the  terms : [ Pω
terms : [ Pω 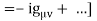
Vω  =
= 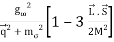
Starting with the lightest mesons, one progresses to mesons with masses in the order of the mass of the nucleon. This fundamentally comprises six mesons (PDG, 2012), namely (138), (548), (500), (770), (782), and a0(980), where the masses in MeV are indicated by the numbers in parenthesis. As it turns out, and a0 aren't particularly essential (Machleidt, 1989), so we'll concentrate on the pseudo-scalar isovector pion (0,1), the scalar isoscalar sigma (0+,0), and the scalar isoscalar sigma (0+,0).
The isoscalar vector omega (1,0),
Rho (1,1), the vector isovector
The parenthetical information (JP,I) summarises each particle's spin J, parity P, and isospin I.
Yukawa's initial calculations were based on classical field theory. A more proper derivation, as we will employ here, should be based on quantum field theory. The mesons are exchanged single in the one-boson-exchange (OBE) model, as depicted in Figure 4's Feynman diagram. The contributions of the various mesons to the NN potential are calculated in Figures 5 to 8. We always begin with an acceptable interaction Lagrangian for meson-nucleon coupling, which is built using symmetry principles as a guide (the Lagrangian must be a Lorentz scalar). We should notice that the Lagrangians for the vector mesons and (Figures 7 and 8) can have both a vector and a tensor coupling (with coupling constants gv and fv, respectively):
LvNN=gv (v)fv4M (v)
The interaction of a photon with a nucleon is analogous to these two couplings. The first relates to the Dirac current's coupling to the electromagnetic vector potential, while the second corresponds to the anomalous magnetic moment's Pauli coupling. The close resemblance is not coincidental; the vector-meson dominance model (VDM) for the nucleon's electromagnetic form factor explains it. The VDM assumes that the photon links to the nucleon through a vector boson, which explains the nucleon electromagnetic form factor's extended shape. The coupling constants ratio, f/g, should be 3.7 under a strict interpretation of this model, and dispersion analysis yields even f/g6. In any event, the tensor coupling of the is substantially more than its vector coupling, which is why the vector coupling was removed in Figure 8. It's the other way around for the meson: the vector dominance model predicts a coupling constants ratio of f/g=0.12 for the meson. In most meson models, the is given no tensor coupling because it is close to zero (cf. Figure 7).
The vector boson propagator in its entirety is
Pv=ig+qq/m2vq2m2v, Pv=ig+qq/m2vq2m2v (7)
Where the qq/m2v-term was removed in Figures 7 and 8. This term vanishes on-shell, but not off-shell, due to nuclear current conservation. Holinde and Machleidt (1975) investigated the off-shell effect of this word and found it to be insignificant.
To ensure that the scattering equation converges, it is common practise to multiply the vertices with cutoffs that suppress high-momentum components. For these cutoffs, a simple form is
(m2+q 2)n, (m2+q)n, (m2+q)n, (m2+q)n, (m2+q)n
The cutoff mass is usually set anywhere between 1.3 and 2.0 GeV. Our derivations do not explicitly show the multiplication by these form factors. The computation is carried out in momentum space and in the center-of-mass (CMS) system of the two interacting nucleons, with p1=(E,p ) and p2=(E,p ) in the initial states and p′1=(E′,p′) and p′2=(E′,p′) in the final states, respectively. Furthermore,
q k L S12(q) q k L S12(q) q k L S12(q) q k L
12(p ′+p )=p ′+p )=p ′+p )=p ′+p )=p ′+p )=p ′+p )=p
i(q k )=i(p ′p )=i(q k )=i(q k )=i(q k )=i(q k )=i(q k )
1 q 2 q 1 q 1 q 1 q 1 q 1 q 1 q 1 q 1 q 1 2 is the tensor operator in momentum space, the average momentum, the total orbital angular momentum in momentum space, and the momentum transfer. (eight)
Table 1 summarizes the characteristic qualities of the contributions from the various mesons derived in Figures 5 to 8.
The OBE NN potential (OBEP) is defined as the sum of the contributions from the four mesons mentioned above, plus a few others, such as,
Lagrangian: 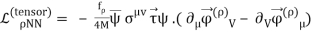
Vertex 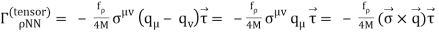
(incoming meson)
Potential: [ Pρ = - igμv + . . . ]
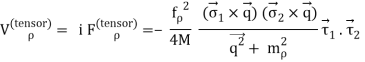
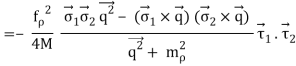
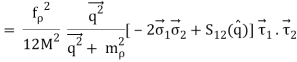
VOBE=∑α=π,σ,ω,ρ,η,a0Vα.(9)
Meson | Central | Spin-Spin | Tensor | Spin-Orbit |
π(138) | --- | Weak, long-ranged | Strong, long-ranged | --- |
σ(500) | Strong, attractive, intermediate-ranged | --- | --- | Moderate, intermediate-ranged |
ω(782) | Strong, repulsive, short-ranged | --- | --- | Strong, short-ranged, coherent with σ |
ρ(770) | --- | Weak, short-ranged, coherent with π | Moderate, short-ranged, opposite to π | --- |
Table: The four most important mesons and the main characteristics of their contributions to components of the nuclear force. | ||||
3.3.7 Relativistic OBEPs
The first OBEPs were created along the lines described above: starting with an OBE's Feynman amplitude, one executes a Q/M expansion up to terms of order (Q/M)2. This procedure was motivated by two factors: First, one wanted to see how the interchange of different mesons produced distinct force components (e.g., central, spin-spin, tensor, spin-orbit, etc.). Second, early researchers favoured a local potential in position space, i.e., an analytic formulation for the potential based on the relative distance between the two nucleons, r. This necessitates the ability to do the Fourier transform of the momentum space equations analytically.
Calculations in position space, on the other hand, are not required. Calculations of NN scattering and nuclear bound states can be done in momentum space just as effectively, and often more elegantly. In momentum space, locality is not a concern and offers no benefits. The original relativistic Feynman amplitudes of OBE are functions of p′ and p, and VrelOBE(p′,p)=iF(p′,p) is the relativistic OBEP.
Figure shows F(p′,p) being evaluated in full beauty and without approximations. The Bethe-Salpeter equation (Salpeter and Bethe, 1951) describes two-nucleon scattering in a covariant way, and VrelOBE is used to solve it. Due to the difficulty of solving the four-dimensional Bethe-Salpeter (BS) equation (Fleischer and Tjon, 1975), relativistic three-dimensional (3D) versions of the BS problem are widely utilised, which are easier to solve numerically. The time component of the relative momentum is set in some covariant fashion in the derivation of all relativistic three-dimensional equations, so it no longer exists as a separate variable. As a result
Vrel3DOBE(p′,p)VrelOBE(p′,p)Vrel3DOBE(p′,p).
3.3.8 Beyond the OBE approximation
The OBE model simplifies the difficult scenario of a meson theory for the NN interaction significantly. Consequently, despite the quantitative effectiveness of the OBEPs, we should be cautious about the model's approximations. The scalar isoscalar'meson' of around 500 MeV, as well as the omission of any non-iterative diagrams, are major considerations.
The significance of meson-nucleon resonances
When two pions are 'in the air,' they can have a lot of interaction. They form a correct resonance, the meson, when in a relative P-wave (L=1). They can also interact in the form of a relative S-wave (L=0), resulting in the boson. Even though the Particle Data Group identifies a f0(500) or (500) meson with a width of 400-700 MeV, it is debatable if the is a legitimate resonance. What is certain is that two pions exhibit correlations, and if one does not believe in the existence of a two-pion resonance, one must account for these correlations. Dispersion theory and field theory are the two main methodologies for dealing with the two-pion exchange contribution to the NN interaction (which provides the intermediate range attraction).

Figure depicts the dispersion-theoretic image schematically. This method requires that the whole diagram (a) may be broken down into two 'halves' (b). All potential processes that two pions and a nucleon can go through are represented by the hatched ovals. This is made clearer in (d) and (e) (e). All conceivable baryon intermediate states, including the nucleon, are represented by the hatched boxes. (It's worth noting that there are some exchanges that aren't represented.) Scattering is shown by the shaded circle. These processes are taken into account quantitatively by using empirical data from N and scattering (e.g. Phase shifts) as the input for such a calculation. Dispersion relations then produce an on-shell NN amplitude, which is represented as a potential with some form of realistic prescription. The Paris potential (Lacombe et al., 1980) is built along these lines, with one-pion-exchange and -exchange added for good measure. We direct interested readers to an educational paper authored by Vinh Mau for further information (1979).
Figure depicts a field-theoretic model for the 2-exchange contribution. Isobar and correlation contributions are also included in the model. This can be regarded in the same way as the picture of dispersion relations. Only the lowest-lying N resonance, the so-called isobar (spin 3/2, isospin 3/2, mass 1232 MeV), is taken into consideration in general. Other resonance contributions have been shown to be minor for the low-energy NN processes under study. The isobar is treated as an elementary (Rarita-Schwinger) particle in a field-theoretic model. Figure 11's six upper diagrams depict uncorrelated 2 exchange. The two-particle exchanges that are crossed (non-iterative) (second diagram in each row) are crucial. Due to characteristic cancellations in the isospin dependent regions of box and crossed box diagrams, they ensure correct (very weak) isospin dependence. Furthermore, their contribution is comparable to that of the related box diagrams (iterative diagrams), therefore they are not insignificant. In addition to the procedures mentioned, linked 2 exchange must be taken into account (lower two rows of Figure 11). In terms of magnitude, these contributions are comparable to those from uncorrelated activities.
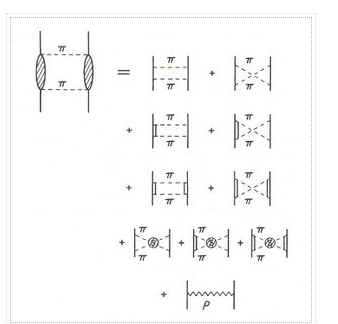
There are contributions from a mix of different mesons in addition to the contributions from two pions. The combination of and is especially crucial, as shown in Figure. This contribution is repulsive, and it is necessary to dampen the 2 exchange contribution at high momenta (or short distances), which is too powerful on its own.
The Bonn Full Model (Machleidt et al., 1987), which incorporates all of the diagrams seen in Figures 11 and 12, as well as single and exchange, is the most developed meson-theoretic model for the NN interaction. Apart from that, the Bonn Full Model includes non-iterative graphs of and andandand exchanges. The aggregate contribution of the latter two sets of diagrams, on the other hand, is minimal and insignificant.
Highly sophisticated models, such as the Paris and Bonn potentials, can be used to check the approximations made in the simple OBE model. The enormously intricate 2 exchange contributions to the NN interaction regulated by the diagrams can, as it turns out, be well represented by the single scalar isoscalar boson, the, with a mass of roughly 550 MeV. This fact serves as retroactive support for the simple OBE model.
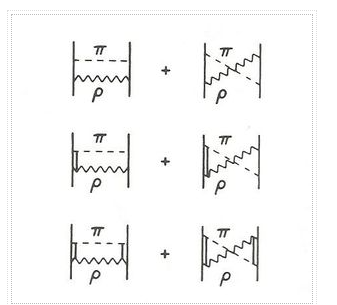
Noteworthy examples
- Bryan and Scott (1964, 1967, 1969), position-space OBEPs, are among the first examples of meson-theoretic NN potentials.
- Early Bonn potentials (Erkelenz, 1974), relativistic momentum-space OBEPs (Holinde and Machleidt, 1975).
- Position-space OBEP of the early Nijmegen potential (Nagels et al., 1978).
- Position-space potential, 2 from dispersion theory plus and (Lacombe et al., 1980), Paris potential (Lacombe et al., 1980).
- The most thorough meson-theoretic model for the NN interaction ever constructed is the Bonn Full Model (Machleidt et al, 1987).
- 2/datum1 for fit of NN data, high-precision Nijmegen potential (Stoks et al., 1994), charge-dependent position-space OBEP
- 2/datum1 for fit of NN data, charge-dependent momentum-space OBEP (Machleidt, 2001), high-precision Bonn potential (CD-Bonn) (Machleidt, 2001).
- Gross and Stadler (2008), relativistic OBEP with the Gross equation and reliable np data fit.
This may have been the joyful ending for nuclear forces hypothesis. However, since QCD has risen to the top of the authoritative theory of strong interactions, meson theory has been demoted to a lower level of a model (though a beautiful one), and we must start over—-in the next part.
3.3.9 QCD and the nuclear force
The theory of strong interactions is known as quantum chromodynamics (QCD). It is part of the Standard Model of Particle Physics and deals with quarks, gluons, and their interactions. Color SU(3) is the underlying gauge group of QCD, which is a non-Abelian gauge field theory. The theory's non-Abelian character has far-reaching implications. While the interaction between coloured particles is weak at short distances or with high momentum transfer (asymptotic freedom), it is strong over long distances (1fm) or with low energies, resulting in the confinement of quarks into colourless hadrons. As a result, at high energies, QCD allows for perturbative analysis, whereas at low energies, it is highly non-perturbative. The force between nucleons is a residual colour interaction, analogous to the van der Waals force between neutral molecules, and it exists at low energies. As a result, the nuclear force is an extremely difficult issue in terms of quarks and gluons that can be tackled with brute computer power on a discretized, Euclidean space-time lattice (known as lattice QCD). The neutron-proton scattering lengths in the singlet and triplet S-waves in completely dynamical lattice QCD with a lowest pion mass of 354 MeV were found in a recent study (Beane et al., 2006). Using chiral perturbation theory, this conclusion is then extended to the physical pion mass. The 354 MeV pion mass is still too huge for meaningful extrapolations, but the feasibility has been established, and additional work is expected in the near future. The nucleon-nucleon (NN) potential was examined in a different form of lattice calculation (Hatsuda, 2012). The centre component of the potential has a repulsive core with a medium-range attraction. This is a really promising outcome, although it should be remembered that enormous pion masses are still being used in this study. In any case, advanced lattice QCD calculations are in the works and becoming better all the time. However, because these computations take a long time and are costly, they can only be used to check a few sample significant issues. A more efficient methodology is required for everyday nuclear structural physics.
3.3.10 The chiral effective field theory approach to nuclear forces
An effective field theory is the most efficient technique (EFT). It is critical to determine a scale separation when developing an EFT. A considerable difference between the masses of the pions and the masses of the vector mesons, such as (770) and (782), may be seen in the hadron spectrum. As a result, it is reasonable to believe that the pion mass determines the "soft scale," Qm, while the rho mass determines the "hard scale," m, also known as the chiral-symmetry breaking scale. This suggests that an expansion in terms of the soft scale over the hard scale, Q/, should be considered. In terms of relevant degrees of freedom, we've already established that quarks and gluons are ineffectual degrees of freedom for the ground state and low-energy excitation spectrum of an atomic nucleus, as well as for ordinary nuclear processes, whereas nucleons and pions are (this may include also low-lying nucleon resonances, s. Below). To ensure that this EFT is more than a phenomenology, it must have a strong connection to QCD. The relationship is formed by having the EFT witness all of the underlying theory's relevant symmetries. Weinberg's "folk theorem" (Weinberg, 1979) is the basis for this requirement:
The result will simply be the most general possible S-matrix consistent with analyticity, perturbative unitarity, cluster decomposition, and the assumed symmetry principles if one writes down the most general possible Lagrangian, including all terms consistent with assumed symmetry principles, and then calculates matrix elements with this Lagrangian to any given order of perturbation theory.
The EFT programme, in brief, consists of the following steps:
1. Determine the proper soft and hard scales, as well as degrees of freedom, for (low-energy) nuclear physics.
2. Identify the relevant low-energy QCD symmetries and analyse whether and how they are broken.
3. Construct the most general Lagrangian that is consistent with those symmetry breakings and symmetries.
4. Create an organisational structure that can differentiate between important and little contributions: a low-momentum growth.
5. Using the expansion as a guide, calculate Feynman diagrams for the situation at hand to the appropriate accuracy.
(Weinberg, 1991), (Ordonez et al., 1994), (Kaiser et al., 1997) are important publications on the issue (Epelbaum et al., 2009). There is a review with a fairly educational start in (Machleidt and Entem, 2011).
The chiral EFT, which scales with the -mass and contains pion degrees of freedom, is presented here. However, the -mass is not the only (hard) scale available. Other scales may be more suited depending on the energy we're interested in. If we want to focus on a nuclear situation at very low energy (m), for example, we should use the pion-mass, m, as a scale. Because such EFT can no longer have pion degrees of freedom, it is referred to as pionless EFT. It contains solely of contact phrases. As a result, though this pionless EFT may appear frighteningly simple at first glance, it turns out to have some rather exciting properties, particularly in terms of renormalization and power counting (s. Below). Because it is beyond the scope of this essay to go into detail about pionless EFT, we would like to direct interested readers to Bedaque and van Kolck (2002) and van Kolck (2002) good review studies (2007).
We'll go through each of the actions described above in detail in the subsections that follow. Since we've previously covered the first step, we'll go on to step two.
Symmetries of low-energy QCD and their breakings
The QCD Lagrangian reads LQCD=q¯(iγμDμ−M)q−14Gμν,aGμνa(10) with the gauge-covariant derivative
Dμ=∂μ−igλa2Aμ,a(11)
And the gluon field strength tensor (note that for SU(N) group indices, we use Latin letters, …,a,b,c,…,i,j,k,…, and, in general, do not distinguish between subscripts and superscripts)
Gμν,a=∂μAν,a−∂νAμ,a+gfabcAμ,bAν,c.(12)
In the above, q denotes the quark fields and M the quark mass matrix. Further, g is the strong coupling constant and Aμ,a are the gluon fields. The λa are the Gell-Mann matrices and the fabc the structure constants of the SU(3)color Lie algebra (a,b,c=1,…,8); summation over repeated indices is always implied. The gluon-gluon term in the last equation arises from the non-Abelian nature of the gauge theory and is the reason for the peculiar features of the color force.
The masses of the up (u), down (d), and strange (s) quarks are (PDG, 2012):
Mumdms===2.3±0.7 MeV,4.8±0.7 MeV,95±5 MeV.(13)(14)(15)
These masses are small as compared to a typical hadronic scale, i.e., a scale of low-mass hadrons which are not Goldstone bosons, e.g., mρ=0.78 GeV≈1 GeV.
It is therefore of interest to discuss the QCD Lagrangian in the limit of vanishing quark masses:
L0QCD=q¯iγμDμq−14Gμν,aGμνa.
Defining right- and left-handed quark fields,
QR=PRq,qL=PLq,
With
PR=12(1+γ5),PL=12(1−γ5),
We can rewrite the Lagrangian as follows:
L0QCD=q¯RiγμDμqR+q¯LiγμDμqL−14Gμν,aGμνa.
This equation reveals that the right- and left-handed components of massless quarks do not mix in the QCD Lagrangian. For the two-flavor case, this is SU(2)R×SU(2)L symmetry, also known as chiral symmetry. However, this symmetry is broken in two ways: explicitly and spontaneously.
3.3.11 Spontaneous symmetry breaking
A (continuous) symmetry is said to be spontaneously broken if the Lagrangian symmetry is not realised in the system's ground state. There is evidence that the QCD Lagrangian's (approximate) chiral symmetry is spontaneously broken—-for nonperturbative dynamical causes that are not fully understood at this time. The hadron spectrum provides the most convincing evidence.
The existence of degenerate hadron multiplets of opposite parity is naively expected from chiral symmetry, i.e., for each hadron of positive parity, one would expect a degenerate hadron state of negative parity, and vice versa. These 'parity doublets', however, do not exist in nature. Consider the -meson, which is a negative parity (JP=1) vector meson with a mass of 776 MeV. A 1+ meson, the a1, does exist, however it has a mass of 1230 MeV and so cannot be considered degenerate with the. The meson, on the other hand, has three charge states (corresponding to three isospin states), the, and the 0, each with a mass difference of only a few MeV. Thus, SU(2)V (isospin) symmetry is well seen in the hadron spectrum, whereas axial symmetry is destroyed: SU(2)RSU(2)L is broken down to SU(2)V.
The presence of (massless) Goldstone bosons is implied by a spontaneously violated global symmetry. The isospin triplet of (pseudoscalar) pions is associated with the Goldstone bosons, which explains why pions are so light. The masses of the pions aren't quite zero since the masses of the up and down quarks aren't quite zero either (explicit symmetry breaking). As a result, pions are a truly unusual species: they exhibit both implicit and explicit symmetry violation. At low energies, Goldstone bosons have a weak interaction. Because they are degenerate in comparison to the vacuum, interactions between them must vanish at zero momentum and at the chiral limit (m0).
3.3.12 Chiral effective Lagrangians
Building the most general Lagrangian consistent with the (broken) symmetries outlined above is the next phase in the EFT programme. Callan et al. (1969), who figured out the group-theoretical underpinnings of non-linear realisations of chiral symmetry, devised an elegant framework for the creation of such Lagrangians. When functions of the Goldstone bosons appear in the Lagrangian, they are always accompanied by at least one space-time derivative, which is characteristic of these non-linear realisations. The following Lagrangians are based on the Callan et al. (1969) formalism.
The relevant degrees of freedom are pions (Goldstone bosons) and nucleons, as previously stated. Because Goldstone boson interactions must vanish at zero momentum transfer and in the chiral limit (m0), the Lagrangian's low-energy expansion is organised in powers of derivatives and pion masses. The chiral-symmetry breaking scale, 1 GeV, is the hard scale. As a result, the expansion is measured in powers of Q/, where Q denotes a (small) momentum or pion mass. The essence of chiral perturbation theory is this (ChPT).
The effective Lagrangian can be stated in formal terms as,
LNN contains two-nucleon contact interactions that consist of four nucleon-fields (four nucleon legs) and no meson fields, whereas L explains the interaction between pions and a nucleon. The ellipsis denotes phrases involving two nucleons plus pions and three or more nucleons with or without pions, which are relevant for nuclear many-body forces (see Eq. (20, below). Individual Lagrangians are arranged in the following order:
(17)
The number of derivatives or pion mass insertions (chiral dimension) is denoted by the superscript, while the ellipsis denotes terms of greater dimensions.
The Lagrangians have been sorted by the number of derivatives or pion-mass insertions. This is the typical method, which is particularly useful when considering - and -N scattering. It turns out that for nucleon interactions, it's sometimes more beneficial to consider the so-called index of the interaction, which is defined as the number of nucleons involved in the contact.
∆ ≡ d + n/2 – 2, (18)
Where n is the number of nucleon field operators and d is the number of derivatives or pion-mass insertions (nucleon legs). We'll now write down the Lagrangian in terms of increasing parameter values, using the so-called Heavy-Baryon (HB) formalism, which we'll denote with a "hat."
The Lagrangian reads with the lowest index,
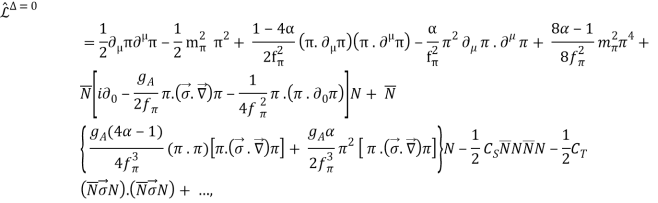
(19)
And higher-index Lagrangians are,
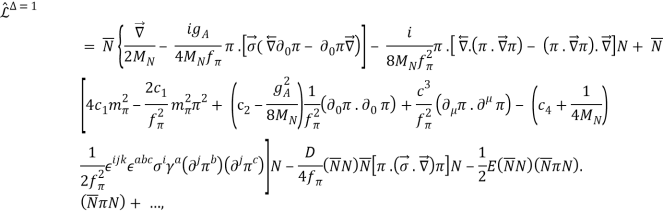
 (22)
(22)
The ellipses reflect terms that aren't significant for deriving nuclear forces up to fourth order. (Fettes et al., 2000) has the LagrangianL(3)N, and the NN contact Lagrangians are given below. The heavy baryon nucleon field is denoted by N (N=N), while the pion fields are indicated by. Furthermore, the axial-vector coupling constant, pion decay constant, pion mass, and nucleon mass are represented by gA, f, m, and MN, respectively. These quantities' numerical values will be provided later. The ci are Low-Energy Constants (LECs) from the dimension two N Lagrangian, and is a parameter that arises in the pion field expansion; for further information, see (Machleidt and Entem, 2011). The results are unaffected by. The NN coupling constant, fNN, is related to the foregoing numbers by in the derivation of the one-pion-exchange potential in Figure 5.
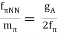 (23)
(23)
Cf. Eq. (33) below.
The lowest order (or leading order) NN Lagrangian has no derivatives and reads
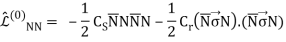
Where CS and CT are unknown constants which are determined by a fit to the NN data.
The second order NN Lagrangian can be stated as follows,
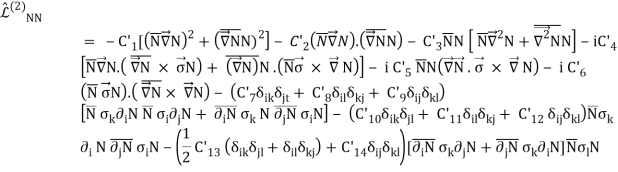
The C′i of Eq. (25) are unknown constants that are fixed via a fit to the NN data, similar to the CS and CT of Eq. (24). With higher order, these contact Lagrangians obviously blow up a lot, which is why we don't offer L(4)NN directly here. Below are the NN contact potentials that come from these Lagrangians.
3.3.13 Power counting
Effective Lagrangians have an infinite number of terms, allowing for the calculation of an endless number of Feynman graphs. As a result, we require a system that allows us to handle and calculate the theory. Chiral perturbation theory is a scheme that shows us how to discern between large (important) and minor (unimportant) contributions (ChPT).
In ChPT, graphs are evaluated in terms of powers of small external momenta on a large scale: (Q/)v, where Q stands for a momentum (nucleon three-momentum or pion four-momentum) or a pion mass, and 1 GeV stands for the chiral symmetry breaking scale (hadronic scale, hard scale). Power counting is the process of determining a person's power.
Irreducible graphs are used to construct the nuclear potential. An irreducible graph, by definition, is one that cannot be divided into two by cutting just nucleon lines. A nucleon propagator is Q1, a pion propagator is Q2, each derivative in any interaction is Q, and each four-momentum integration is Q4, according to Feynman's laws of covariant perturbation theory. Naive dimensional analysis is another name for this. The power of an irreducible diagram involving A nucleons can then be calculated using some topological identities.
v = - 2 + 2A – 2C + 2L + 
(28)
With
(27)
Where C is the number of separately connected pieces in the diagram and L is the number of loops; di is the number of derivatives or pion-mass insertions involved in vertex I and ni is the number of nucleon fields (nucleon legs); and the sum runs over all vertices I in the diagram under consideration. It's worth noting that i0 is true for all chiral symmetry-enabled interactions. Purely pionic interactions have at least two derivatives (di2,ni=0), pion-nucleon interactions have at least one (di1,ni=2), and nucleon-nucleon contact terms (ni=4) contain di0. This explains how chiral symmetry ensures that the expansion is low-energy.
The leading orders of connected multi-nucleon forces can be predicted using the power expression Eq. (26) Consider an A-nucleon system (mA) with an irreducibly connected m-nucleon diagram (m-nucleon force). C=Am+1 is the number of parts that are joined individually. v=2m4 is obtained by plugging this into Eq. (26) with L=0 and ii=0. Two-nucleon forces (m=2) begin at =0, three-nucleon forces (m=3) begin at =2 (but cancel in that order), and four-nucleon forces begin at =4 (they do not cancel). More on this in the following section.
For later purposes, we note that for an irreducible NN diagram (A=2, C=1), the power formula collapses to the very simple expression
v = 2L + 
(28)
In summary, the chief point of the ChPT expansion is that, at a given order ν, there exists only a finite number of graphs. This is what makes the theory calculable. The expression (Q/Λχ)ν+1 provides a rough estimate of the relative size of the contributions left out and, thus, of the accuracy at order ν. In this sense, the theory can be calculated to any desired accuracy and has predictive power.
The hierarchy of nuclear forces: Overview
Nuclear forces develop as a hierarchy governed by the power v, according to chiral perturbation theory and power counting (Figure).
The NN potential is made up of two momentum-independent contact terms (Q0) in lowest order, also known as leading order (LO,=0), as depicted by the four-nucleon-leg graph with a little dot in the first row of Figure 13. In addition, the static one-pion exchange (1PE) is depicted in the second schematic in the first row of the picture. Of course, this is a crude approximation of the two-nucleon force (2NF), but it accounts for certain key properties. The 1PE describes NN scattering in peripheral partial waves with very high orbital angular momentum and gives the tensor force required to characterise the deuteron. The two contacts, which only participate in S-waves, offer the primitive short- and intermediate-range interaction at this order.
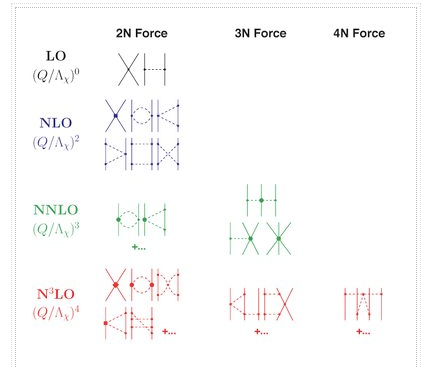
Due to parity and time-reversal invariance, all contributions vanish in the next order, v=1.
As a result, the next-to-leading order (NLO) is equal to 2. For the first time, two-pion exchange (2PE) happens ("leading 2PE"), and therefore the development of a more detailed description of the intermediate-range interaction begins (Ordonez et al., 1996). The vertices must have i=0 because the loop in each 2PE-diagram already implies =2 [cf. Eq. (28)]. As a result, only the lowest order NN and NN vertices are allowed at this order, which is why the leading 2PE is quite weak. In addition, there are seven new O(Q2) contact terms that participate in S and P waves, as indicated in the figure by the four-nucleon-leg graph with a solid square. A spin-orbit term, in addition to central, spin-spin, and tensor terms, is included in the operator structure of these connections. As a result, virtually all spin-isospin structures required to phenomenologically explain the two-nucleon force have been created. At this stage of growth, the fundamental flaw is a lack of intermediate-range attractiveness.
Finally, the problem is solved at order three (=3), the next-to-next-to-leading order (NNLO). The two-derivative NN seagull vertices (proportional to the ci LECs) are now included in the 2PE, as seen by a huge solid dot in Figure 13. These vertices exhibit intermediate (1232)-isobar contributions as well as associated 2PE contributions. These two contributions are critical for a realistic and quantitative 2PE model, as is well known from the meson phenomenology of nuclear forces. As a result, the 2PE now assumes a more realistic scale and roughly describes the nuclear force's intermediate-range attraction (Ordonez et al., 1996). Furthermore, at this order, the first relativistic adjustments are applied. Because contacts only appear in even numbers, there are no new contacts.
The reason we talk about a nuclear force hierarchy is that two-nucleon and many-nucleon forces are formed on an equal basis and appear in increasing numbers as we go up in order. The first set of nonvanishing three-nucleon forces (3NFs) occurs at NNLO, as seen in Figure 13's column '3N Force' (van Kolck, 1994). In truth, NLO, irreducible 3N graphs exist in the preceding order; nevertheless, it can be proved that these diagrams all cancel. When contrast to the 2NF, which starts at order (Q/)0, nonvanishing 3NF contributions happen initially at order (Q/)3.
At =4, the next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to-next-to For the first time, two-loop 2PE graphs appear (Kaiser, 2001), as does three-pion exchange (3PE), which requires two loops (Kaiser, 2000). At this level, the 3PE is insignificant. Most crucially, 15 new contact terms dubbed Q4 appear, which are represented by a solid diamond on a four-nucleon-leg graph. They contribute up to D-waves and include a quadratic spin-orbit term.
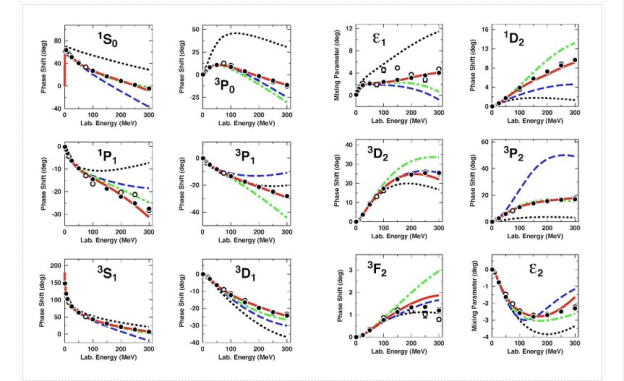
Tlab bin (MeV) | Number of np data | N3LO | NNLO | NLO |
0--100 | 1058 | 1.05 | 1.7 | 4.5 |
100--190 | 501 | 1.08 | 22 | 100 |
190--290 | 843 | 1.15 | 47 | 180 |
0--290 | 2402 | 1.10 | 20 | 86 |
Table: 2/datum for chiral NN potentials at NLO, NNLO (Epelbaum et al., 2005), and N3LO in reproducing np data below 290 MeV. (Entem and Machleidt, 2003). The kinetic energy of the incident nucleon in the laboratory system is denoted by Tlab.
Furthermore, at N3LO, there are more 3NF contributions, and four-nucleon forces (4NFs) begin at this level. 4NFs are weaker than 3NFs because the leading 4NFs emerge one order higher than the leading 3NFs. As a result, ChPT provides a simple explanation for the empirically established fact that 2NF 3NF 4NF..
3.3.14 Comparison with conventional meson theory
We now have two ways that can both quantitatively explain the NN interaction, which is a non-trivial finding. It's only natural to wonder how the two techniques vary. There is a straightforward and revealing response.
The nuclear potential is enlarged in chiral EFT by raising the powers of tiny momenta, (Q/)v (Figure 13). In meson theory, the expansion is expressed in terms of Yukawas, Y(mr), which correspond to decreasing ranges 1/m for rising masses m. (cf. Figure 9).
Both approaches should be numerically equal to a significant extent because they describe the same difficult item. Figure 15 illustrates this point. First, both situations have a 1PE, which is insignificant. The 2PE may appear to be extremely dissimilar diagrammatically, however the figure depicts the relationship between the contributions. The fundamental distinction is that the 2PE in chiral EFT is built up order by order, whereas it comes as a single set in traditional meson theory. Finally, with heavy boson exchange (like -exchange) in meson theory and contacts in chiral EFT, the short-range contributions appear graphically very different. However, since Qm, a heavy-meson propagator can be stretched into a power series creating increasing-order contacts, as seen in Figure 16.
Although the two procedures are comparable, there are some reasons to believe that chiral EFT is preferable. Chiral EFT is more closely related to QCD due to chiral symmetry; it has an organisational scheme (power counting) that allows one to estimate the accuracy of the predictions (in a given order); and it has an organizational scheme (power counting) that allows one to estimate the accuracy of the predictions (in a given order).
On an equal footing, generates two- and many-body forces.
3.3.15 Two-nucleon forces: Doing the math
We'll fill in the mathematical subtleties we left out when providing the chiral hierarchy overview in this section. The many irreducible diagrams, depicted in Figure 13 and defining the chiral NN potential order by order, are as follows:
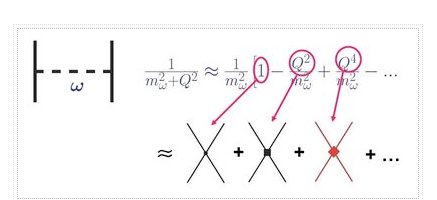
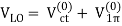
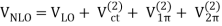

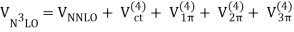
The order v of the low-momentum expansion is denoted by the superscript. The subscript "ct" denotes contact potentials, while an evident subscript denotes pion-exchange potentials.
The charge-independent 1PE potential reads
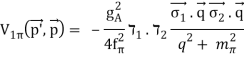
(33)
The constants' numerical values are f=92.4 MeV, gA=1.29, and m=138 MeV for the average pion mass (see Figure 5 and Eq. (23)). Because higher order corrections only affect mass and coupling constant renormalizations and there are no relativistic corrections on the shell, the on-shell 1PE has the same form as Eq. (33) at all orders.
The two zero-order contact terms at LO are
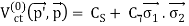
(34)
To state the mathematical expressions for 2PE contributions, we use the following scheme:
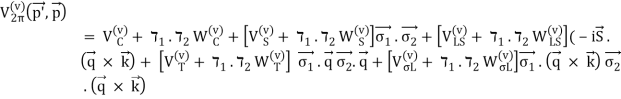
(35)
Where p⃗ ′ and p⃗ denote the final and initial nucleon momenta in the CMS, respectively; moreover,
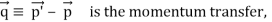

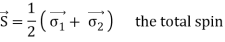
(36)
And σ⃗ 1,2 and τ1,2 are the spin and isospin operators, respectively, of nucleon 1 and 2. For on-energy-shell scattering, Vi and Wi (i=C,S,LS,T,σL) can be expressed as functions of q and k, only (with q≡|q⃗ | and k≡|k⃗ |).
Using the above scheme, the contribution from the five NLO 2PE diagrams can be stated in an amazingly compact form, namely,
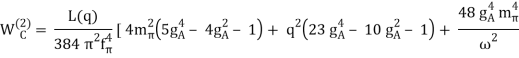

(38)
Where
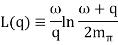
And
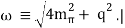
For the typical pion mass, the constants' numerical values are f=92.4 MeV, gA=1.29, and m=138 MeV (see Figure 5 and Eq. (23)). The on-shell 1PE has the same form as Eq. (33) at all orders since higher order corrections only influence mass and coupling constant renormalizations and there are no relativistic corrections on the shell.
The seven NLO contact terms are:
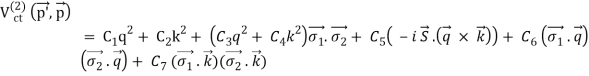
(39)
Of course, the coefficients Ci in the contact potential are related to the coefficients C′i in the LagrangianL(2)NN, Eq. (25), but the precise relationship is immaterial.
The following formulations (Kaiser et al., 1997) indicate the NNLO 2PE:
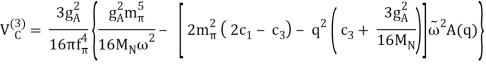
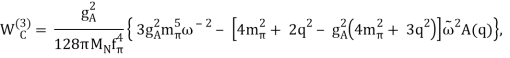
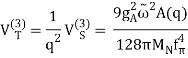
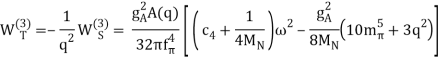
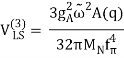

(42)
With
A(q) = 1/2q arctan q/2mπ |
And
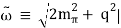
This is the most important contributor to the 2PE because it generates a strong intermediate-range attraction. Because the LEC c3 is negative and of great magnitude, the iso-scalar central potential, V(3)C, is powerful and appealing. c3 is linked to - correlations ('mesons') and virtual -isobar excitations via resonance saturation, which are the most important contributions to 2PE in the framework of conventional meson theory (Machleidt et al., 1987). At this order, first relativistic 1/MN adjustments enter the equation; they are incorporated in the potential expressions above.
The contacts at N3LO are:
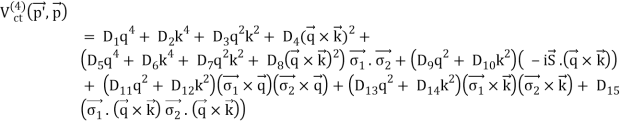
(43)
The 2PE potential at N3LO, V(4)2, is quite complicated, which is why its expressions will not be given here. It is located in (Machleidt and Entem, 2011). The contributions of N3LO 3PE, V(4)3, are insignificant.
Large scattering lengths and shallow bound states (the deuteron) characterise the two-nucleon system, which cannot be computed using perturbation theory. To derive the N amplitude, the NN potential must be entered into a Schrödinger or Lippmann-Schwinger (LS) equation.
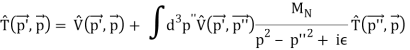
(44)
Where the definitions
(45)
And
(46)
Are used, with 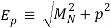 . Iteration of Vˆ in the LS equation, Eq. (44), requires cutting Vˆ off for high momenta to avoid infinities. This is consistent with the fact that ChPT is a low-momentum expansion which is valid only for momenta Q<Λχ≈1 GeV. Therefore, the potential Vˆ is multiplied with a regulator function f(p′,p),
. Iteration of Vˆ in the LS equation, Eq. (44), requires cutting Vˆ off for high momenta to avoid infinities. This is consistent with the fact that ChPT is a low-momentum expansion which is valid only for momenta Q<Λχ≈1 GeV. Therefore, the potential Vˆ is multiplied with a regulator function f(p′,p),
Vˆ(p⃗ ′,p⃗ )⟼Vˆ(p⃗ ′,p⃗ )f(p′,p)
With, for example,
f(p’ , p) = exp[ - (p’/Λ)2n - (p/Λ)2n ] .(47)
Typical choices for the cutoff parameter Λ that appears in the regulator are Λ≈0.5 GeV<Λχ≈1 GeV.
It is self-evident that the T-matrix results will be sensitive to the regulator and its cutoff parameter, which is undesirable. Renormalization is the process of removing regulator reliance. It's worth noting that renormalizability is critical for an EFT's validity. Entem and Machleidt (2003) use two regularisation strategies in their quantitative chiral NN potentials: Dimensional regularisation is employed in the potential derivation (where the cutoff is taken to infinity), whereas the regulator Eq. (47) is employed with a finite cutoff in the LS equation, Eq. (44). Although this method has yielded useful NN potentials, the way regularisation and renormalization are handled is debatable. Despite nearly two decades of effort by a diverse group of theoretical physicists, the community has yet to reach an agreement on how to successfully renormalize chiral EFT-based nuclear forces. The pionless EFT has proven to be enlightening in this situation, since it allows for a more transparent renormalization procedure (because it consists of contacts only and does not include pion loops).
The accurate counting of the powers of the low-energy expansion is a similar unresolved topic. It's worth noting that the power in Eq. (26) is the perturbatively determined potential's power. The T-matrix, on the other hand, is a physical quantity that is obtained by iterating the potential in the LS equation, Eq. (44), which may vary the power. The pionless theory has also proved useful in this case since, due to its simplicity, it allows for analytic solutions of the LS equation that directly indicate the power.
3.3.16 Three-nucleon forces
The 2NF, of course, contributes the most to microscopic computations of nuclear structure and reactions. However, it is widely known from ab-initio investigations that 3NFs are required for precise microscopic explanation of certain few-nucleon reactions and nuclear structural difficulties. In a nutshell, 3NFs are required. As previously stated, one of the major advantages of the EFT approach to nuclear forces is that it equalises two- and many-nucleon forces (cf. Figure 13).
For a 3NF, we have A=3 and C=1 and, thus, Eq. (26) implies
ν=2+2L+∑iΔi.(48)
We will use this equation to analyze 3NF contributions order by order.
The lowest possible power is obviously ν=2 (NLO), which is obtained for no loops (L=0) and only leading vertices (∑iΔi=0). As it turns out, this contribution vanishes.
The first non-vanishing 3NF appears at NNLO (ν=3). The power ν=3 is obtained when there are no loops (L=0) and ∑iΔi=1, i.e., Δi=1 for one vertex while Δi=0 for all other vertices. There are three topologies which fulfill this condition, known as the 2PE, 1PE, and contact graphs, Figure 17 (van Kolck, 1994), (Epelbaum et al., 2002).
The 2PE 3N-potential is derived to be
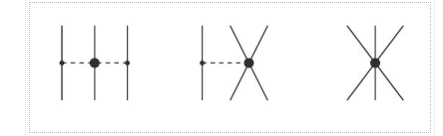
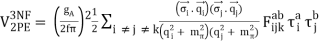
(49)
With q⃗ i≡pi→′−p⃗ i, where p⃗ i and pi→′ are the initial and final momenta of nucleon i, respectively, and
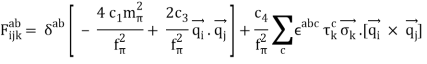
(50)
The derivations of 2PE 3NFs from conventional meson theory are very similar to this force (Fujita and Miyazawa, 1957; Coon et al., 1979).
Taking the remaining two terms of the =1 Lagrangian, Eq. (20), into account yields the other two 3NF contributions. The contribution of 1PE is
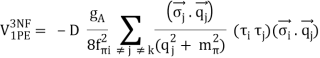
(51)
And the 3N contact potential reads
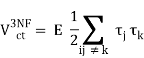
(52)
The two new parameters D and E, which do not occur in the 2N problem, are used in these 3NF words. There are numerous methods for determining these two factors. One method is to use the triton binding energy and the nd doublet scattering length 2 and. The binding energies of 3H and 4He, as well as an optimal overall match of the properties of light nuclei, can be chosen. The findings for other 3N, 4N, and so on observables are forecasts once D and E are fixed.
The 3NF at NNLO has had a lot of success in computations of few-nucleon processes, light- and medium-mass nuclei structure, and nuclear and neutron matter. However, the 'Ay puzzle,' which involves the underprediction of the analysing power of nucleon-deuteron and p-3He scattering, is not answered by this 3NF. Furthermore, there is room for improvement in the spectra of light nuclei. As a result, higher-order 3NFs are required for at least two reasons: to address unsolved difficulties in microscopic structure and reactions, and to maintain consistency with the 2NF (recall that a precise 2NF is of order N3LO).
The following order is N3LO (v=4), which presents us with a huge number of loop diagrams (Figure 18). Because L is one in those loops, all I must be zero to ensure that =4. As a result, these one-loop 3NF diagrams can only contain leading order vertices, whose parameters are determined via N and NN analysis. There are five loop topologies to choose from. For each topology, we display one sample diagram in Figure. However, each topology is made up of a large number of diagrams, with the overall number of diagrams ranging from 50 to 100, depending on how the diagrams are represented (Bernard et al., 2011). The N3LO 3NF is fairly weak, according to preliminary applications of the 3N potentials produced from these diagrams, and does not answer the Ay conundrum (Witala et al., 2013).
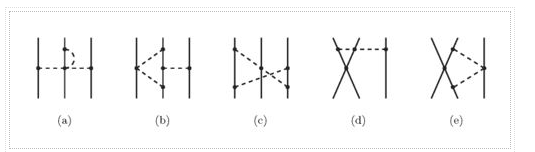
Because we're dealing with a perturbation theory, it's only reasonable to look for advances in the next order. As a result, we place an order for N4LO (v=5). These loop contributions (Figure) are produced by replacing one vertex in the N3LO loops with an i=1 vertex (with LEC ci), which is why these loops may be larger than the N3LO loops. There are five loop topologies in all, each with numerous diagrams. In addition, three 'tree' topologies (Figure 20) with a novel set of 3N contact interactions [graph (c)] are available. In comparison to loop diagrams, contact terms are often simple, and their coefficients are unbounded (except for naturalness). All potential spin-isospin-momentum configurations that a 3NF can have are included in the N4LO 3NF words. As a result, there's a chance that the 3NF at N4LO will fill in the gaps in the 3NF jigsaw. The burst of 3NF contributions that arise at N3LO and N4LO, however, poses a challenge.
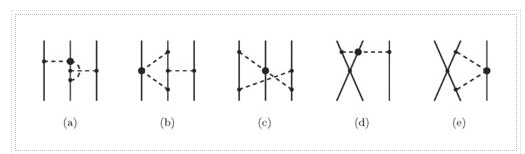
3.3.17 Four-nucleon forces
For connected (C=1) A=4 diagrams, Eq. (26) yields
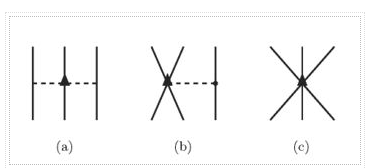
v = 4 + 2L +  (53)
(53)
As a result, at v=4 (N3LO), a linked 4NF occurs for the first time, with no loops and just leading vertices, Figure. There are no new parameters in this 4NF, and it does not disappear. Figure shows some graphs that appear to be reducible (iterative). However, keep in mind that they are Feynman diagrams, which are best understood using time-ordered perturbation theory. Some irreducible topologies are included in the various time-orderings (which are, by definition, 4NFs). Or, to put it another way, the Feynman diagram minus the reducible part yields the 4NF's (irreducible) contribution.
A contribution of order (Q/)4 is expected to be negligible assuming a good rate of convergence. As a result, ChPT forecasts that 4NF will be virtually inconsequential, which is consistent with previous experience. Even still, nothing in physics is entirely established unless detailed calculations are conducted. The leading 4NF was used to calculate the 4He binding energy, and it was discovered to contribute roughly 0.1 MeV. When compared to the whole 4He binding energy of 28.3 MeV, this is a minor difference.
3.3.18 Introducing Δ-isobar degrees of freedom
The (1232) resonance or isobar (a -N P-wave resonance with both spin and isospin 3/2) has an excitation energy of M=MMN=293 MeV and is the nucleon's lowest excited state. It is an important component of models of pion-nucleon scattering in the -region and pion production from the two-nucleon system at intermediate energies, where particle production is dominated by the formation of isobars, due to its strong coupling to the -N system and low excitation energy. The virtual excitation of's, which accounts for about half of the nuclear force's intermediate-range attraction in these models at low energies—-as demonstrated by the Bonn potential—-is included in the more sophisticated conventional models for the 2-exchange contribution to the NN interaction at low energies (Machleidt et al., 1987).
Because of its tiny excitation energy, it is unclear whether the should be explicitly taken into account in an EFT or integrated out as a heavy degree of freedom. Mm, in addition to the pion mass and small external momenta, is regarded additional tiny expansion parameter if it is included. Small-scale expansion is the name given to this strategy (SSE). However, because M does not vanish in the chiral limit, this extension is phenomenological in nature.
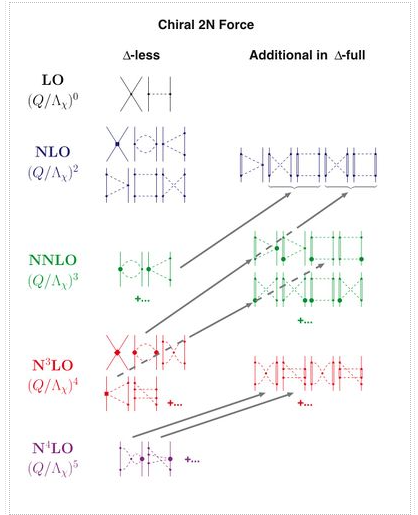
The effects of isobars are implicitly taken into consideration in the chiral EFT outlined so far (also known as the -less theory). It's worth noting that the dimension-two LECs, ci, have abnormally high values. The reason for this is that the -isobar (as well as various meson resonances) play a significant role in the ci—-a phenomenon known as resonance saturation. As a result, the explicit inclusion of the [so-called -full theory (Ordonez et al., 1996), (Kaiser et al., 1998)] detracts from the power of these LECs and shifts it to a lower order. As a result, the expansion's convergence improves, which is another reason for providing explicit -degrees of freedom. The subleading 2PE and 3PE contributions to the 2NF are bigger than the leading ones in the -less theory. The -full theory solves this problem by promoting large contributions by one order (Ordonez et al., 1996).
The N coupling is proportional to hA/2f and contains one derivative, similar to the NN coupling, which is proportional to gA/2f and contains one derivative. The LECs of the N Lagrangian are often recovered during the study of -N scattering data, and they obviously differ in the -full theory from the -less theory. While the LECs c3 and c4 have a magnitude of roughly 3-5 GeV1 in the -less theory, they have a magnitude of roughly 1 GeV1 in the -full theory.
The virtual excitation of -isobars in the 2NF necessitates at least one loop, therefore the contribution occurs initially at v=2 (NLO), as seen in Figure 22. The coherence of the -full and -less theories has been demonstrated by demonstrating that contributions from intermediate -excitations, enlarged in powers of 1/M, may be absorbed into a redefinition of the -less theory's LECs. The LECs c3,c4's equivalent shift is determined by
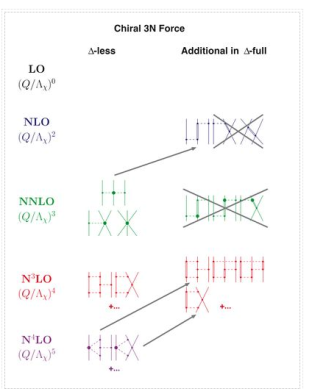
c3=−2c4=−h2A9ΔM.(54)
Using hA=3gA/2 (huge Nc value), the resonance explains practically all of c3 and a significant portion of c4.
With the explicit insertion of the -isobar, a considerable portion of the 2NF's intermediate-range attraction is switched from NNLO to NLO, according to several studies. The NNLO 2PE potential of the -less theory, on the other hand, is found to be a very excellent approximation to the NNLO potential in the -full theory.
Figure shows how the isobar affects the 3NF scenario. The 2PE 3NF in the lead gets promoted to NLO. This term has the same mathematical form in the -full theory as the analogous term in the -less theory, Eqs. (49) and (50), assuming c1=0 and c3, c4 according to Eq (54). As a result of the antisymmetrisation of the 3N states, the other two NLO 3NF terms involving's vanish. Because the subleading N vertex has a time-derivative, which demotes the contributions by one order, the contributions to the 3NF at NNLO vanish at this order. However, one-loop diagrams with one, two, or three intermediate -excitations, which correspond to diagrams of order N4LO, N5LO, and N6LO, respectively, in the -less theory, are projected to make significant 3NF contributions at N3LO.
To summarise, the inclusion of explicit degrees of freedom improves chiral expansion convergence by moving significant contributions from NNLO to NLO. The results for the -full and -less theories, on the other hand, are essentially the same at NNLO. The -full theory includes all diagrams involving's as well as all diagrams from the -less theory. As a result, the -full theory is substantially more complicated. Furthermore, 1/MN 2NF corrections arise at NNLO (not shown in Figure 22) in the -full theory, which were found to be uncomfortably big (Kaiser et al., 1998). As a result, it appears that the -less theory is more workable up to NNLO.
However, when possibly big donations join the scene at N3LO, the scenario may alter. Because these terms are spread out over N3LO, N4LO, and, in part, N5LO in the -less theory, it may be more efficient to compute them in the -full theory. These higher-order contributions are an important test for the convergence of the chiral expansion of nuclear forces and a difficult area for future investigation.
3.3.19 Baryon-baryon interactions
All baryons have a significant interaction with one another. As a result, in addition to the nucleon-nucleon interactions discussed in this article, there are many additional strong baryon-baryon interactions. The forces between nucleons and hyperons (strange baryons) and hyperons and hyperons have traditionally been a focus. In addition, the contact between a baryon and an anti-baryon has piqued curiosity, with the nucleon-antinucleon contact being the most investigated. Phenomenology, meson theory, quark models, lattice QCD, and effective field theory have all been used to try to explain the baryon-(anti)baryon interactions, much as they have for the nucleon-nucleon interaction. Although it is not the goal of this article to discuss those other baryon-baryon interactions, it is worth noting that all baryon-baryon interactions are connected due to the quark sub-structure of hadrons. As a result, the nucleon-nucleon interaction covered in this paper should be viewed in the context of all baryonic interactions. Achieving a description of all baryon-baryon interactions that is consistent with all relevant underlying symmetries is a difficult task in today's study. We want to recommend interested readers to the literature for more information on this issue. Rijken et al. (2013) review hyperon-nucleon interactions in the meson image, while Haidenbauer et al. (2013) review chiral EFT. See Klempt et al. (2005) for a nucleon-antinucleon approach, and Kang et al. (2013) for a chiral EFT technique.
Key takeaway:
- The residual strong force is the force that acts between nucleons and binds protons and neutrons into atomic nuclei.
- The force between two nucleons does not act along the line connecting their centres, hence nuclear forces are non-central forces. This demonstrates that nucleons are not spherically symmetric in the nucleus. Whether the nucleons are neutrons or protons has no effect on the nuclear force. Charge independence is the name for this characteristic. Because it has a non-central or tensor component, the force is dependent on whether the nucleons' spins are parallel or antiparallel.
3.4.1Stability: the N-Z curve
The N-Z curve | Decay process | Decay chains |
The N-Z curve
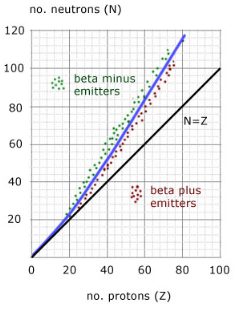
The N-Z curve is a plot of the number of neutrons(N) against the number of protons(Z).
Lines:
i) the'stability' line, which is a gentle curve that begins at the origin and gradually increases in gradient.
Ii) the line N = Z - a gradient '1' straight line through the origin
Regions
i) emitters of beta minus (electron) particles
Ii)positron particle emitters (beta plus)
Iii) top of the curve alpha particle emitters (not shown)
Description:
N=Z is a straight line for proton numbers (Z) up to 20.
The line slopes upwards for all nuclei with Z>20 because stable nuclei contain more neutrons than protons.
3.4.2 The Decay Process
By losing neutrons, unstable neutron-rich nuclei can become more stable. This is accomplished by a process known as 'beta decay.'
The effect of this for a single nucleus is to raise its the proton number (Z) by 1 and decrease its neutron number(N) by 1, bringing the N-Z plot of the nucleus closer to the stability curve.
The point moves one unit to the right and one unit to the left.
Beta decay: Z + 1 N – 1
Unstable neutron-poor nuclei can become more stable by gaining neutrons. They do this by 'positron decay'.
For a single nucleus, this has the effect of lowering its proton number (Z) and increasing its neutron number (N), putting the nucleus' N-Z plot closer to the stability curve.
The point moves one unit to the left and one unit to the right.
Positron decay: Z - 1 N + 1
- The position of a nucleus in relation to the stability curve is unaffected by alpha decay. This is because the loss of an alpha particle (two protons and two neutrons) does not significantly alter the N-Z ratio.
- Z - 2 and N - 2 are the coordinates of a nucleus. Alpha decay involves only big nuclei. As a result, the influence is limited to the curve's very top part.
Alpha decay: Z - 2 N – 2
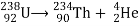
3.4.3 Decay Chains
A decay chain (or radioactive series) depicts the various types of radioactive decay that a nucleus goes through until it reaches a stable isotope.
The actinium series, thorium series, and uranium series are the only three naturally occurring decay chains.
Plus the neptunium series, which involves a trans-uranium element.
A graph of nucleon number (A) versus proton number (B) appropriately describes a decay chain (Z).
The diagram depicts the entire Thorium-232 decay chain.
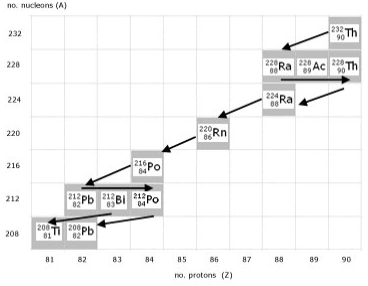
Important observations are:
Alpha decay ...........2 units to the left, 4 units down
beta- decay ...........1 unit to the right
Bismuth ...............2 possible decay outcomes
Equations describing the Thorium Series:
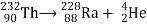

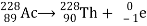
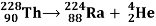
3.4.4 Nuclear Magic Numbers
Introduction
When compared to the periodic table, an isotope is an element with the same atomic number but a different atomic mass. Protons, neutrons, and electrons are found in every element. Unless it's an ion, the number of protons equals the atomic number, and the number of electrons equals the number of protons. The number of neutrons in an element is calculated by subtracting the atomic number from the atomic mass. Atomic mass is denoted by (AA), atomic number is denoted by (ZZ), and neutrons are denoted by (N) (NN).
A=N+Z(1)A=N+Z(1)A=N+Z(1)A=N+Z(1)A=N+Z(1)A
The neutron to proton ratio is the most important factor in determining whether a nucleus is stable. The nuclei of elements with (Z20Z20) are lighter, and their nuclei have a ratio of 1:1, preferring to have the same number of protons and neutrons.
Isotope Stability
The Band (or Belt) of Stability is a graph of stable elements that is often used. A y-axis labelled neutrons, an x-axis labelled protons, and a nucleus make up the graph. The radionuclides that decay by alpha decay are at the upper end (top right) of the band of stability; below is positron emission or electron capture; above is beta emissions; and elements beyond the atomic number of 83 are solely unstable radioactive elements. The neutron:proton ratio in stable nuclei with atomic numbers up to roughly 20 is roughly 1:1. (solid line).
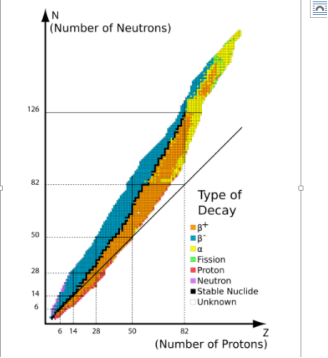 .
.
The deviation from the N:Z=1N:Z=1 line on the stability belt is due to a non-unity N:ZN:Z ratio required for total nuclei stability. To put it another way, more neutrons are needed to stabilise the repulsive forces generated by a smaller number of protons within a nucleus (i.e., N>ZN>Z).
It's simple to figure out where alpha decay, beta decay, and positron emission or electron capture happen because to the belt of stability.
Alpha Decay: Alpha decay is near the top of the plotted line because it reduces the mass number of the element, which helps to maintain the isotope stable. This is done by emitting an alpha particle, which is nothing more than a helium (HeHe) nucleus. The unstable isotope's proton number PP is reduced by two and its neutron number (NN) is reduced by two in this decay pathway. The nucleon number AA lowers by 4 as a result of this (Equation 11).
Beta decay receives protons, resulting in a change in the number of protons and neutrons. The number of protons rises by one, whereas the number of neutrons falls by one. This pathway arises in unstable nuclides with an excess of neutrons over the stability band (blue isotopes in Figure 11).
Positron ++ Decay occurs when an isotope gets additional neutrons by positron ++ emission and electron capture. Because the isotope ratio has more protons than neutrons, positron emission and electron capture are below the band of stability. Think of it this way: there are too few protons for the quantity of neutrons, hence it's below the band of stability (yellow isotopes in Figure 11).
If the daughter nuclei are not on the Belt, as with other decay pathways, subsequent decay paths will proceed until the daughter nuclei are on the Belt.
3.4.5 Magic Numbers
The Octet Rule was developed as a result of the discovery that atoms containing eight valence electrons were particularly stable (and common). Nuclei have a similar scenario in terms of the number of neutrons and proton quantities that produce stable (non-radioactive) isotopes. These "magic numbers" are natural occurrences in especially stable isotopes. Numbers of protons and neutrons are listed in Table 1; isotopes with these numbers in either the proton or neutron are stable. In some situations, isotopes can have magic numbers for both protons and neutrons, which are referred to as double magic numbers. Because of the repulsion of the interactions between the protons, double numbers only appear for heavier isotopes. The magic numbers are as follows:
- 2, 8, 20, 28, 50, 82, 114 proton
- 2, 8, 20, 28, 50, 82, 126, 184 neutron
There's also the idea that isotopes with a mix of even-even, even-odd, odd-even, and odd-odd isotopes are all stable. Even-even nuclides exist in greater numbers than odd-odd nuclides. Many isotopes with no magic number of nucleons are stable, just as there are exceptions to the octet rule.
Unstable or Stable
Here's a basic chart that can help you determine whether or not an element is likely to remain steady.
- Calculate the nuclide's total number of nucleons (protons and neutrons). There's a strong likelihood it's stable if the number of nucleons is even.
- Is there a certain amount of protons or neutrons that must be present? In nuclei, the numbers 2,8,20,28,50,82,114 (protons), 126 (neutrons), and 184 (neutrons) are extremely stable.
- Determine the optimal route to travel from an unstable nucleus to a stable nucleus by calculating the N/Z ratio and using the belt of stability.
3.4.6 Stable nuclides
Hundreds of nuclides have been identified; in this episode, an N-Z plot is used to examine the pattern of stability and evaluate the necessity for an additional, attractive force to hold the nucleus together.
Which stable nuclides exist
Rehearse and expand on what your students already know. The nucleus is made up of N neutrons and Z protons, hence A = N + Z nucleons. Explain (or update) nuclide nomenclature with the following example:
Bismuth-83 (20983Bi) is the heaviest stable element.
In this nucleus, how many protons and neutrons are there? (83 and 126)
Between hydrogen (Z is 1) and uranium (U), there are 90 naturally occurring elements ( Z is 92). Is there anything out of the ordinary about this? (Two are missing; 9943Tc (technitium) and 6361Pm are both artificial and man-made) (promethium). On a geological time span, both are radioactive and would have decayed long ago.)
All elements with a Z greater than 92 have been created by humans. The current record (as of February 2004) is Z of 116.
Create a visualisation of N vs Z for stable nuclides using a spreadsheet. Prepare an Excel spreadsheet with the data below already recorded (columns for the element name, A, Z, and, anticipating future work, the nucleus mass in atomic mass units u – see below) to save time (and transcription errors!).
Representative stable nuclides:
3.4.7 Interpreting the graph
Explain the graph. (It's linear (N Z) up to Z 20, then gradually N > Z: there's a neutron excess.) The neutron excess is critical for understanding nuclear stability and setting up a chain reaction in nuclear reaction exploitation.
Consider the Coulomb repulsion that exists between protons. What exactly are the neutrons doing inside? ( Neutrons must assist in overcoming the strong repulsion between protons, partly by diluting them and, more importantly, by supplying an attractive force to counteract the electric repulsion. As a result, the term "strong nuclear force" was coined.
3.4.8 Calculating the force between protons
If Coulomb’s law has been covered, calculate the repulsive force between two protons that just touch, so the separation of their centres r is the diameter of a proton 1.4 × 10-15 m).
Fe = 14 π ε0 q1 q2r 2
Where q1 and q2 both have the same value, +e = 1.6 × 10-19 C. So:
Fe ~ 100 N
3.4.9 The nature of the strong nuclear force
Explain the need for the strong nuclear force to balance the Coulomb repulsion. This force must be attractive – it overcomes the coulomb repulsion; independent of electric charge – it acts between nn, pp and np; and very short range ~ 1 fm = 1 × 10-15 m.
3.4.10 Calculating nuclear densities
Calculate the density of a nucleon:
Nucleon mass ~1.7 × 10-27 kg; radius ~1.4 × 10-15 m; density r ~1.4 × 1017 kg m-3
This is enormous compared to the density of everyday matter. Ask your students to repeat the calculation for He-4 (or give data for other nuclides):
Nuclide mass ~6.6 × 10-27 kg; radius ~2 × 10-15 m; density ~1.6 × 1017 kg-3
So the density is roughly the same for all nuclei. This is summed up in the relationship:
r = r0 × A ⅓
With r0 = 1.4 fm
3.5.1 The liquid drop model

In the liquid drop model of the atomic nucleus, the terms of the semi-empirical mass formula are illustrated.
George Gamow proposed the liquid drop model, which was further developed by Niels Bohr and John Archibald Wheeler. It treats the nucleus as an incompressible fluid drop with a very high density that is held together by the nuclear force (a residual effect of the strong force), with a structure that resembles that of a spherical liquid drop. The liquid drop model, albeit primitive, accounts for most nuclei's spherical shape and offers a rough forecast of binding energy.
The mass formula is solely specified in terms of the number of protons and neutrons it contains. Five terms are defined in the original Weizsäcker formula:
When an assembly of nucleons of the same size is packed together into the smallest volume, each inside nucleon comes into contact with a particular number of other nucleons. As a result, the amount of nuclear energy produced is proportional to the volume.
The assumption that each nucleon interacts with the same number of other nucleons is corrected by surface energy. Because this term is negative and proportionate to surface area, it is nearly similar to liquid surface tension.
The potential energy of each pair of protons is known as Coulomb energy. The binding energy is lowered because this is a repulsive force.
The Pauli exclusion principle is explained by asymmetry energy (also known as Pauli Energy). Uneven quantities of neutrons and protons mean that one type of particle will fill higher energy levels while the other will leave lower energy levels empty.
The likelihood for proton and neutron pairs to form is explained by pairing energy. Due to spin coupling, an even number of particles is more stable than an odd number.
3.5.2 Binding energy and Semi-empirical mass formula
Binding Energy
The nuclear binding energy and the mass of nuclides are two significant nuclear parameters that we want to investigate. You might suppose that since we know the masses of the proton and neutron, we can simply use the formula mN = Zmp + Nmn to get the masses of all nuclides.
However, experimental evidence suggests that this is not the case. We know from special relativity theory that each mass corresponds to a certain amount of energy, E=mc2E=mc2. Then we may calculate how much energy they represent by adding the masses of all the elements of a nucleus. The intrinsic energy of a nucleus is likewise proportional to its mass. It's only natural that this isn't just the sum of its constituent energies, because we expect some additional energy to be expended to hold the nucleus together. If the energy levels were equal, bound nuclei would be undesirable, and all nuclei would be unstable, continually shifting from their bound state to a sum of protons and neutrons.
The difference in mass energy between the nucleus and its parts is then used to calculate the nucleus' binding energy. The binding energy B of a nucleus is given by
B=[Zmp+Nmn−mN(AX)]c2B=[Zmp+Nmn−mN(AX)]c2
However, we want to express this quantity in terms of experimentally accessible quantities. Thus we write the nuclear mass in terms of the atomic mass, that we can measure,
MN(AX)c2=[mA(AX)−Zme]c2+Be(1.2.2)(1.2.2)mN(AX)c2=[mA(AX)−Zme]c2+Be
Where mA(AX)mA(AX) is the atomic mass of the nucleus. We further neglect the electronic binding energy BeBe by setting
MN(AX)c2=[mA(AX)−Zme]c2.(1.2.3)(1.2.3)mN(AX)c2=[mA(AX)−Zme]c2.
We finally obtain the expression for the nuclear binding energy:
B={Zmp+Nmn−[mA(AX)−Zme]}c2B={Zmp+Nmn−[mA(AX)−Zme]}c2
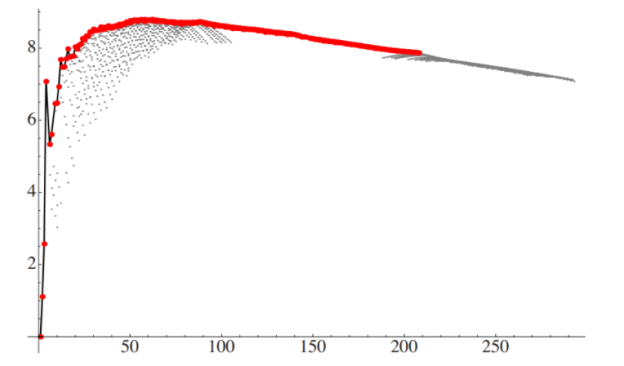
Quantities of interest are also the neutron and proton separation energies:
SnSp=B(AZXN)−B(A−1ZXN−1)=B(AZXN)−B(A−1Z−1XN)Sn=B(ZAXN)−B(ZA−1XN−1)Sp=B(ZAXN)−B(Z−1A−1XN)
Which are the analogous of the ionization energies in atomic physics, reflecting the energies of the valence nucleons. We will see that these energies show signatures of the shell structure of nuclei.
Semi-empirical mass formula
B/A, or binding energy per nucleon, is a common representation of binding energy. Because B/A is largely constant, the binding energy is simply proportional to A in general.
However, there are reversals in this pattern. The semi-empirical mass formula captures B/reliance A's on A (and Z). This formula is based on first-principles considerations (a nuclear force model) as well as experimental evidence to determine the specific parameters that define it. All nucleons are uniformly distributed inside a nucleus in this model, known as the liquid-drop model, and are linked together by the nuclear force, whereas the Coulomb interaction causes protons to repel one another. Part of the semi-empirical mass formula is explained by nuclear force (short range) and Coulomb interaction characteristics. Other (smaller) corrections, on the other hand, have been proposed to account for changes in the binding energy that arise due to its quantum-mechanical character (and that give rise to the nuclear shell model).
The semi-empirical mass formula (SEMF) is
M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2M(Z,A)=Zm(1H)+Nmn−B(Z,A)/c2
Where the binding energy B(Z, A) is given by the following formula:

3.5.3 Volume term
The first term is avA, which describes how the binding energy is primarily proportional to A. Why is it the case?
Keep in mind that the binding energy is a measure of nucleon interaction. Because nucleons are packed so tightly in the nucleus and the nuclear force has such a short range, each nucleon only interacts with a few neighbours. This indicates that regardless of the overall number of nucleons, each one makes the same contribution. As a result, the force is proportional to A(A 1)/2 A2 (the total number of nucleons with which one nucleon can interact), rather than A(A 1)/2 A2. The constant of proportionality (av = 15.5MeV) is a fitting parameter that has been determined empirically.
This is less than the nucleons' binding energy to their neighbours, which is governed by the strength of the nuclear (strong) interaction. The energy binding one nucleon to the other nucleons is discovered to be on the order of 50 MeV (which we will look at further). Instead, the total binding energy is the difference between a nucleon's interaction with its neighbour and the nucleon's kinetic energy. The nucleons in an atom are fermions, therefore they can't all be in the same state with zero kinetic energy, but according to Pauli's exclusion principle, they'll fill up all the kinetic energy levels. This model, which accounts for nuclear binding energy as well as kinetic energy owing to shell filling, provides an accurate estimate of av.
3.5.4 Surface term
The surface component, asA2/3asA2/3, is a correction to the volume term. It is likewise based on the strong force. The volume term, we said, arises from the fact that each nucleon interacts with a fixed number of nucleons, regardless of A. While this is true for nucleons deep inside the nucleus, nucleons at the nucleus' surface have fewer nearest neighbours. Surface forces, which occur in droplets of liquids, for example, are a mechanism that causes surface tension in liquids.
We estimate a surface force of (BV)2/3(BV)2/3 (because the surface SV2/3SV2/3) since the volume force is proportional to BV A. In addition, the term must be deducted from the volume term, and the coefficient should be of equal value to av. As a matter of fact, as = 13 18MeV.
3.5.5 Coulomb term
AcZ(Z1)A1/3acZ(Z1) is the third term. The Coulomb interaction between protons gives rise to A1/3, which is proportional to Z. Because the Coulomb repulsion makes a nucleus with numerous protons less favourable, this term is removed from the volume term (more energetic).
The nucleus is treated as a uniformly charged sphere to motivate the form of the term and estimate the coefficient ac. Such a charge distribution's potential energy equals
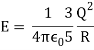
Since from the uniform distribution inside the sphere we have the charge
q(r) = 4/3 πr3 ρ = Q (r/R)3
And the potential energy is then:
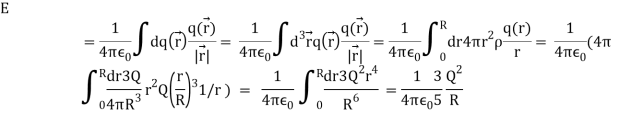
Using the empirical radius formula
R = R0A1/3
And the total charge
Q2 = e2 Z (Z – 1)
(reflecting the fact that this term will appear only if Z > 1, i.e. if there are at least two protons) we have:
Q2/R = e2 Z (Z – 1)/R0A1/3
Which gives the shape of the Coulomb term. Then the constant ac can be estimated from
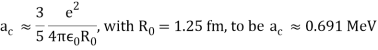
With R0 = 1.25 fm, to be ac ≈ 0.691 MeV, not far from the experimental value.
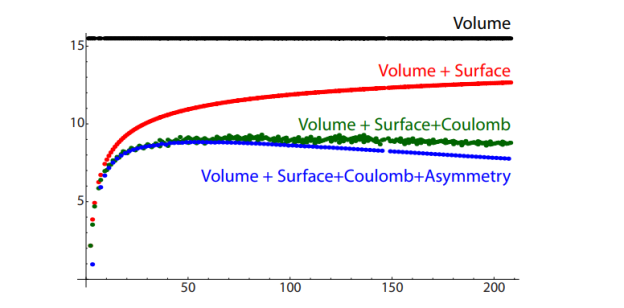
3.5.6 Symmetry term
The Coulomb phrase appears to indicate that having fewer protons and more neutrons in a nucleus is preferable. However, this is not the case, and we must use a model other than the liquid-drop model to explain why stable nuclei contain nearly the same amount of neutrons and protons. As a result, there is a correction component in the SEMF that attempts to account for the symmetry in protons and neutrons. This (and subsequent) corrections can only be explained by a more sophisticated nucleus model, the shell model, in conjunction with the quantum-mechanical exclusion principle, which we shall discuss later in the class. If we add more neutrons, they will have to be more energetic, which will increase the nucleus' total energy. This increases the Coulomb repulsion more than offsets it, making it preferable to have roughly equal numbers of protons and neutrons. The symmetry term has the shape (A2Z)2A. It's easier to understand if you realise that this term is zero for A = 2Z and has a smaller influence for bigger A. (while for smaller nuclei the symmetry effect is more important). Asym=23 MeV is the coefficient.
3.5.7 Pairing term
The last word refers to physical proof that like-nucleons tend to group together. If we have an even-even nucleus, where all of the neutrons and protons are paired-off, then the binding energy is bigger (> 0). It is therefore preferable to turn one of the protons into a neutron or vice versa if we have a nucleus with an odd number of neutrons and protons (of course, taking into account the other constraints above). As a result, for odd-odd configurations, we must deduct ( 0) a term from the binding energy with all other factors constant. Finally, we do not expect this pairing energy (= 0) to have any effect on even-odd configurations. The term for pairing is then
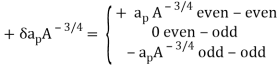
With ap ≈ 34MeV. [Sometimes the form ∝ A−1/2 is also found].
3.5.8 Line of Stability in the Chart of nuclides
We can compute the optimal Z such that the mass is minimal by taking the first derivative wrt Z. We get the following results:
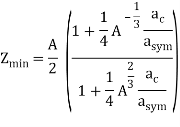
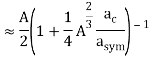
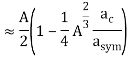
ZA2 is obtained for tiny A, but there is a correction for bigger A, resulting in Z 0.41A for heavy nuclei.
The nuclides lie between 1/2 and 0.41 on a plot of Z/AZ/A vs. A. Following the stable isotopes, there is a line of stability (red in Figure 1.2.4 and black in Figure). The isotopes are then identified in various ways, such as here by their lifetime.

Figure: Chart of nuclides
Key takeaway:
- The nuclear binding energy is used to assess whether fission or fusion is the better option. The mass defect of a nucleus is the difference between the mass of a nucleus and the sum of the masses of the nucleons that make it up, and it represents the mass of the energy binding the nucleus.
- BE divided by A gives the binding energy per nucleon (BEN) (Equation 10.3. 3). BE=[2mp+2mn]m(4He)c2.
3.6.1 The Shell Model
The Shell Model, for example, accounts for a number of aspects of nuclear energy levels. According to this paradigm, the average attractive force of all the other nucleons governs the mobility of each nucleon. The orbits that arise form "shells," much like the orbits of electrons in atoms. As more nucleons are introduced to the nucleus, they fall into the lowest-energy shells allowed by the Pauli Principle, which stipulates that each nucleon must have its own set of quantum numbers to describe its motion.
.
A nucleus of remarkable stability arises when a shell is full (that is, when the nucleons have used up all of the feasible sets of quantum number assignments). This is comparable to the idea found in an atom, where a filled set of electron quantum numbers produces an atom with extraordinary stability–an inert gas. The number of protons or neutrons in a nucleus is dubbed a "magic number" when all of them are in filled shells. 2, 8, 20, 28, 50, 82, and 126 are some of the magical numbers. The magic number of protons in 116Sn is 50, and the magic number of neutrons in 54Fe is 54. (28). Some nuclei, such as 40Ca and 208Pb, have magical numbers of protons and neutrons; these nuclei are referred to as "doubly magical" because of their unusual stability. On the nuclide chart, magic numbers are indicated.
The total angular momentum, J, of filled shells is zero. The J of the new ground state is determined by the next additional nucleon (a valence nucleon). When nucleons (individually or in pairs) are aroused out of the ground state, their angular momentum, as well as their parity and isospin projection quantum numbers, are altered. The shell model explains how much energy it takes to transfer nucleons from one orbit to the next, as well as how quantum numbers fluctuate. The energy diagram of the two filled shells of the 12C ground state is shown in the diagram above. When a nucleon or a pair of nucleons are promoted to an empty shell, the nucleus enters one of the excited states.
Excited nuclear states decay to more stable states, i.e. nucleon orbitals that are more stable. To precisely calculate the energy and half-life of the decay, specialised alpha, beta, and gamma detectors and related electronic circuitry are used to measure transition rates between nuclear energy levels. Nuclear scientists can calculate the transition probability (rate of decay) between nuclear states using quantum mechanics and shell-model theory. The Shell Model calculations accord very well with measured values of spin and parity assignments and transition probabilities for nuclei whose structure can be explained by a small number of valence nucleons outside filled shells.
Above is an illustration of transitions between the energy levels of a nucleus. The 12B (5 protons, 7 neutrons) and 12N (7 protons, 5 neutrons) ground states are connected to each other as well as the 15.1 MeV state in 12C. Each possesses a nucleon in the third energy level, the quantum number 1+, 1, and decays to carbon's ground state. The beta decay of boron and nitrogen produces an e- and an e+, respectively. Carbon's 15.1 MeV state decays via gamma emission. Even though different decay mechanisms are at action in each example, the shell model calculations of these transition probabilities accord pretty well with the measured rates. The shell model is being refined by nuclear theorists in order to better understand the complexities of nuclear structure and to apply that knowledge to nuclear technologies.
3.6.2 Nuclear Shell Model
It illustrates how energy levels are distributed among distinct atom shells and nucleus atom shells. The energy level where particles with the same energy exist is referred to as a shell. All nuclear particles in this model are coupled one-to-one, neutron with neutron and proton with proton. When the number of neutrons or protons in a nuclear energy level equals 2, 8,20,28,50,82, or 126, the paired neutrons and protons are filled. These are the magic numbers that show which nuclei are the most stable.
The unpaired ones are in charge of a nucleus' qualities, whereas valence electrons are in charge of an element's chemical qualities. We can reliably anticipate the properties of nuclei, such as angular momentum, using the shell model. However, for highly unstable nuclei, other models such as the collective model, liquid-drop model, and compound nucleus model must be adjusted or replaced with the shell model.
3.6.3 Shell Model of the Atom
It explains how different electrons are arranged around the nucleus of an atom according to their energy levels.
Fig. Shell Model of the Atom
Atomic Number = number of electrons in an atom
The atomic shell model explains how atoms are structured. The electrons, which are negatively charged fundamental particles, are thought to occupy diffuse shells in the region surrounding the positively charged nucleus. The initial shell is the one that is closest to the nucleus.
The shells are labelled as follows:
K | First shell |
L | Second shell |
M | Third shell and so on |
The electrons inhabit the shell in the following order: 2, 8, 18, 32, 50, 72, 98.
The atomic shell model also aids in the comprehension of atomic chemical characteristics.
The following formula is used to calculate the maximum number of electrons that can occupy an atom's energy level:
Electron capacity = 2n2
The principal quantum number is n in this case.
The shell layers and their electron capacity are listed in the table below:
Energy Level | Shell Designation | Maximum no.of electrons |
1 | K | 2 |
2 | L | 8 |
3 | M | 18 |
4 | N | 32 |
5 | O | 50 |
6 | P | 72 |
3.6.4 Difference Between Shell Structure of Nuclei and Shell Structure of Atom
Shell Structure of Nuclei | Shell Structure of Atom |
The energy level starts at zero. | The initial state is where the energy level begins. |
Z=2,8,20,28,50,82,126, and so on are Magic Numbers. | Z = 2,10,18,36,54,86, and so on are all magical numbers. |
The average potential of nuclei differs from the average potential of an atom. | Potential differs from one to another. |
Neutrons and protons are particles that make up the shell structure of nuclei. | Electrons are particles that make up an atom's shell structure. |
3.6.5 Magic number
A magic number in nuclear physics is the number of nucleons (either protons or neutrons) that may be organised into full shells within the atomic nucleus. As a result, atomic nuclei with a'magic' number of protons or neutrons are far more stable than nuclei with a different number of protons or neutrons. As of 2019, the seven most well-known magic numbers are 2, 8, 20, 28, 50, 82, and 126. (sequence A018226 in the OEIS). Although 126 is only known to be a magical number for neutrons, it correlates to the elements helium, oxygen, calcium, nickel, tin, lead, and the speculative unbihexium for protons. Atomic nuclei with such a large number of nucleons have a greater average binding energy per nucleon than one might expect based on predictions like the semi-empirical mass formula, and hence are more resistant to nuclear decay.
Transuranium elements might possibly be formed with exceptionally large nuclei and not be susceptible to the highly rapid radioactive decay generally associated with high atomic numbers due to the exceptional stability of isotopes with magic numbers. In an island of stability, large isotopes with magical quantities of nucleons are supposed to exist. Theoretical calculations predict that nuclei in the island of stability are distorted, unlike the magic numbers 2–126, which are realised in spherical nuclei. Higher magic numbers, such as 184, 258, 350, and 462 (OEIS sequence A033547), were previously predicted based on basic calculations assuming spherical shapes: these are generated using the formula (see binomial coefficient). The sequence of spherical magic numbers is now thought to be unextendable in this fashion. Protons are anticipated to have magic numbers of 114, 122, 124, and 164, whereas neutrons will have magic numbers of 184, 196, 236, and 318. More recent studies, however, suggest that neutrons will have a mass of 228 and 308, in addition to 184 and 196.
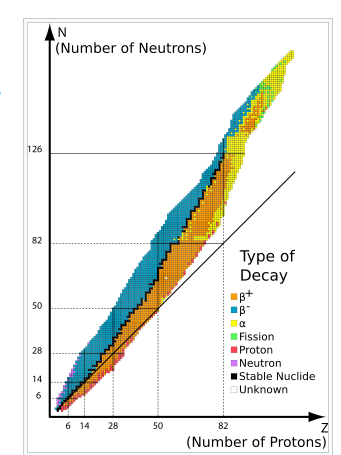
3.6.6 History and origin of the term
Maria Goeppert Mayer, a German scientist, became interested in the features of nuclear fission products, such as decay energies and half-lives, while working on the Manhattan Project. She published a body of experimental evidence supporting closed nuclear shells in nuclei with 50 or 82 protons or 50, 82, and 126 neutrons in 1948. (It was already known that nuclei with 20 protons or neutrons were stable; calculations by Hungarian-American physicist Eugene Wigner, one of her Manhattan Project colleagues, demonstrated this.) Two years later, in 1950, she published a second paper in which she blamed spin-orbit coupling for the shell closures at the magic numbers.
According to Maria Goeppert Mayer's student Steven Moszkowski, the word "Wigner coined the phrase "magic number": "Wigner, too, believed in the liquid drop model, but he recognised the very strong evidence for the closed shells from Maria Mayer's work." It appeared to him to be a little like magic, and hence the term 'Magic Numbers' was coined."
These magic numbers formed the foundation of Mayer's nuclear shell model, which he developed with Hans Jensen over the next few years and resulted in their joint Nobel Prize in Physics in 1963.
3.6.7 Doubly magic
Nuclei with neutron and proton (atomic) numbers both equal to one of the magic numbers are referred to as "doubly magical," and they are particularly resistant to disintegration. Helium-4, helium-10, oxygen-16, calcium-40, calcium-48, nickel-48, nickel-56, nickel-78, tin-100, tin-132, and lead-208 are the known doubly magical isotopes. However, only the first, third, fourth, and fifth of these doubly magical nuclides are totally stable, despite the fact that calcium-48 is extraordinarily long-lived and so naturally occurring, decomposing only by a slow double beta minus decay process.
Doubly-magic effects may allow stable isotopes to exist that would not have been predicted otherwise. Calcium-40, which has 20 neutrons and 20 protons and is the heaviest stable isotope with the same amount of protons and neutrons, is an example. Because calcium-48 has 20 protons and 28 neutrons, while nickel-48 has 28 protons and 20 neutrons, both are doubly magical. Calcium-48 has a lot of neutrons for such a light element, yet it's stabilised by being doubly magical, just like calcium-40.
Ordinary abundances of elements show magic number shell effects: helium-4 is one of the most numerous (and stable) nuclei in the universe[12], whereas lead-208 is the heaviest stable nuclide.
Magical influences can prevent unstable nuclides from disintegrating as quickly as they should. The nuclides tin-100 and tin-132, for example, are unstable doubly magic isotopes of tin that designate endpoints beyond which stability rapidly declines. Nickel-48 is the most proton-rich doubly magic nuclide known, having been found in 1999. Apart from tritium, which has one proton and two neutrons, nickel-78 is doubly magical, with 28 protons and 50 neutrons, a ratio seen only in far heavier atoms (78Ni: 28/50 = 0.56; 238U: 92/146 = 0.63).
An multinational team of scientists led by the Technical University of Munich found hassium-270 in December 2006, with 108 protons and 162 neutrons with a half-life of 9 seconds. Hassium-270 appears to be part of a stable island, and its distorted (American football- or rugby ball-like) shape suggests it may be doubly magical.
Despite the fact that Z = 92 and N = 164 are not magical numbers, the undiscovered neutron-rich nucleus uranium-256 could be doubly magical and spherical due to the size difference between low- and high-angular momentum orbitals, which changes the form of the nuclear potential.
3.6.8 Derivation
Empirical investigations are commonly used to derive magic numbers; if the nature of the nuclear potential is known, the Schrödinger equation for nucleon mobility can be solved, and energy levels can be derived. When the separation between energy levels is much greater than the local mean separation, nuclear shells are said to form.
Magic numbers are the numbers of nucleons at which a shell is filled in the shell model for the nucleus. Because there is a big energy gap between the 1p1/2 and the next highest 1d5/2 energy levels, the magic number 8 occurs when the 1s1/2, 1p3/2, and 1p1/2 energy levels are filled.
The atomic equivalent of nuclear magic numbers are the numbers of electrons that cause ionisation energy discontinuities. Helium, neon, argon, krypton, xenon, radon, and oganesson are examples of noble gases. As a result, 2, 10, 18, 36, 54, 86, and 118 are the "atomic magic numbers." As with nuclear magic numbers, spin–orbit coupling phenomena impacting subshell energy levels are likely to change them in the superheavy zone. As a result, copernicium (112) and flerovium (114) should be more inert than oganesson (118), and the next noble gas should appear at element 172 rather than 168. (which would continue the pattern).
In 2010, symmetry considerations were proposed as an alternate explanation for magic numbers. The ground state parameters (including the magic numbers) for metallic clusters and nuclei were simultaneously derived analytically based on the fractional extension of the standard rotation group. In this paradigm, a precise potential term is not required.
Key takeaway:
1. The magic numbers in stable nuclei are 2, 8, 20, 28, 50, 82, and 126, which have similar numbers of protons and neutrons and do not decay radioactively.
2. Nuclei with neutron and proton (atomic) numbers both equal to one of the magic numbers are referred to as "double magic" and are particularly resistant to disintegration. Helium-4, oxygen-16, calcium-40, calcium-48, nickel-48, nickel-78, and lead-208 are examples of double magic isotopes.
3. Nuclei with totally filled proton and neutron shells are referred to as doubly magical by physicists. Lead-208 is the most enormous doubly magical nucleus in this group, making it stand out.
References:
1.Quantum Mechanics: Theory and Applications, A.K. Ghatak and S. Lokanathan,(Macmillan)-2004
2. Introduction to Quantum Theory, David Park (Dover Publications)-1974
3. Theory and Problems of Modern Physics, Schaum‘s outline, R.Gautreau and W.Savin- (Tata McGraw-Hill) 2nd Edition
4. Physics for scientists and engineer with Modern Physics-Jewell and Serway -(CENGAGE Learnings) 2010.
5. Modern Physics of Atoms and Molecules Bransden and Joachim (PearsonIndia)-2003