Unit - 3
Integral Transforms-II
Let f(t) and g(t) be arbitrary functions of time 
with Fourier transforms. Take
f(t) = F-1v [F(v)](t) =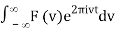 
g(t) = F-1v [G(v)](t) =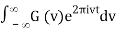 
Where F-1v (t) denotes the inverse Fourier transform (where the transform pair is defined to have constants A = 1 and B = - 2π). Then the convolution is
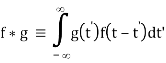
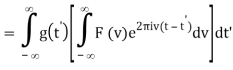
Interchange the order of integration,
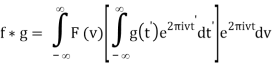
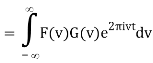
= Fv-1 [F(v) G(v)] (t)
So, applying a Fourier transform to each side, we have
F[f * g] = F[f] F[g]
The convolution theorem also takes the alternate forms
F[fg] = F[f] * F[g]
F-1 (F[f] F[g]) = f * g
F-1(F[f] * F[g]) = f g
NUMERICALS:
1) f(t) = eat and g(t) = ebt (a ≠ b)
Verify that L(f∗g)=L(f)L(g), as implied by the convolution theorem.
ANS:
We first compute
(f * g) = 
= 
= 
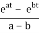
Since
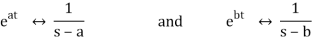
It follows that
ℒ(f * g) =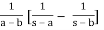 
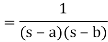
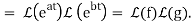
2) Find a formula for the solution of the initial value problem
y’’ – 2y’ + y = f(t), y(0) = k0, y’(0) = k1
Solution
Taking Laplace transforms in ABOVE Equation yields
(s2 – 2s + 1)Y(s)= F(s) + (k1 + k0s) – 2k0
Therefore
Y(s) = 1/(s – 1)2 F(s) + k1 + k0s – 2k0 / (s-1)2
= 1/(s – 1)2 F(s) +k0/s - 1+( k1 - k0 )/ (s-1)2
From the table of Laplace transforms,
ℒ-1 (k0/s - 1+( k1 - k0 )/ (s-1)2) = et (k0 + (k1 – k0)t)
Since
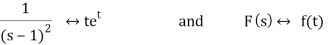
The convolution theorem implies that
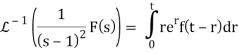
Therefore the solution
y(t) = et (k0 + (k1 – k0) t) +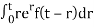 
The z-transform has features that are similar to those of the Fourier transform (and Laplace transform). The only distinction is that the ROCs require extra attention. Assumptions are made in the following sections.
Z [ x[n]] = X(z) ROC = Rx
And
Z [ y[n]] = Y(z) ROC = Ry
Linearity
Z [ ax[n] + by[n]] = a X(z) + bY(z), ROC ⊇ (Rx ∩ Ry)
While it is obvious that the ROC of the linear combination of x[n] and y[n] should be the intersection of the their individual ROCs Rx ∩ Ry in which both X(z) and Y(z) exist, note that in some cases the ROC of the linear combination could be larger than Rx ∩ Ry. For example, for both x[n] = anu[n] and y[n] = anu[n-1] , the ROC is |z| > |a| , but the ROC of their difference an u[n] – anu[n – 1] = δ[n] is the entire z-plane.
Time Shifting
Z[x[n – n0]] = Z-n0 X(z), ROC = Rx
Proof:
Z[x[n – n0]] =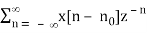 
Define m = n – n0, we have n = m + n0 and
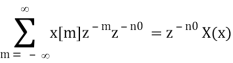
The new ROC is identical to the previous one, with the exception of the possibility of adding or removing the origin or infinity, as the shift may affect the signal's duration.
Time Expansion (Scaling)
Z[x[n/k]] = X(zk), ROC = R1/kx
The discrete signal x[n] cannot be continuously scaled in time as n has to be an integer (for a non-integer n x[n] is zero). Therefore x[n/k] is defined as
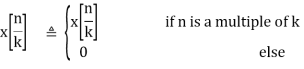
Example: If x[n] is ramp
n | 1 | 2 | 3 | 4 | 5 | 6 |
x[n] | 1 | 2 | 3 | 4 | 5 | 6 |
Then the expanded version x[n/2] is
n | 1 | 2 | 3 | 4 | 5 | 6 |
n/2 | 0.5 | 1 | 1.5 | 2 | 2.5
| 3 |
m |
| 1 |
| 2 |
| 3 |
x[n/2] | 0
| 1
| 0 | 2 | 0 | 3 |
Where m is the integer part of n/k.
Proof: The z-transform of a signal like this is
Z[x[n/k]] =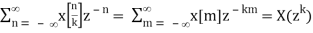 
Note that the change of the summation index from n to m has no effect as the terms skipped are all zeros.
Convolution
Z[x[n] * y[n]] = X(z) Y(z), ROC ⊇ (Rx ∩ Ry)
The ROC of the convolution could be larger than the intersection of Rx and Ry, due to the possible pole-zero cancellation caused by the convolution.
Time Difference
Z[x[n] – x[n – 1]] = (1 – z-1)X(z), ROC = Rx
Proof:
Z[x[n] – x[n – 1]] = X(z) – z-1 X(z) = (1 – z-1) X(z) = z – 1/z X(z)
Note that due to the additional zero z = 1 and pole z = 0, the resulting ROC is the same as Rx except the possible deletion of z = 0 caused by the added pole and/or addition of z = 1 caused by the added zero which may cancel an existing pole.
Time Accumulation
Z[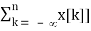 
= 
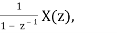ROC ⊇ [Rx ∩ (|z| > 1)]
Proof: The accumulation of x[n] can be written as its convolution with u[n]:
u[n] * x[n] =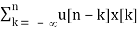 
= 
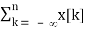
Applying the convolution property, we get
Z[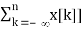 
= Z[u[n] * x[n]] =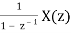 
As Z[u[n]] =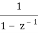 
.
Time Reversal
Z[x[-n]] = X(1/z) ROC = 1/Rx
Proof:
Z[x[-n]] =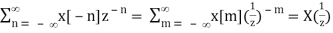 
Where m = -n.
Scaling in Z-domain
Z[an x[n]] = X(z/a), ROC = |a| Rx
Proof:
Z[an x[n]] =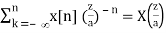 
In particular, if a = ej0 , the above becomes
Z[ejn0 x[n]] = X(e-j0 z) ROC = Rx
The multiplication by e-j0 to z corresponds to a rotation by angle 0 in the z-plane, i.e., a frequency shift by 0. The rotation is either clockwise (0 > 0) or counter clockwise (0 < 0) corresponding to, respectively, either a left-shift or a right shift in frequency domain. The property is essentially the same as the frequency shifting property of discrete Fourier transform.
Conjugation
Z[x* [n]] = X*(z*), ROC = Rx
Proof: Complex conjugate of the z-transform of x[n] is
X*(z) = [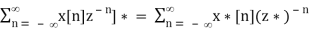 
Replacing z by z*, we get the desired result.
Differentiation in z-Domain
Z[nx[n]] = -z d/dz X(z), ROC = Rx
Proof:
d/dz X(z) =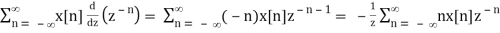 
i.e.,
Z[nx[n]] = - z d/dz X(z)
Example: Taking derivative with respect to z of the right side of
Z[an u[n]] = 
We get
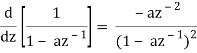
We have this feature of differentiation in the z-domain because of the property of differentiation in the z-domain.
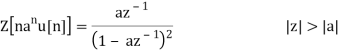
Note that for a different ROC |z| < |a|, we have
Z[ - nanu [ -n – 1]] =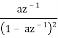 
|z| < |a|
3.3.1 The 3D Fourier Transform
The Fourier pairs are naturally extended to three-dimensional functions as well.
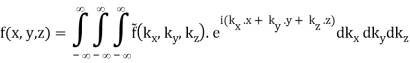
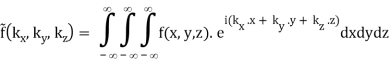
(B.39)
The 3D Fourier transform in cylindrical and spherical coordinates is then discussed.
3.3.2 Cylindrical Coordinates
In this case,
f(x, y, z) = g(r, θ,z)
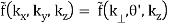
(B.40)
Where,
x + iy = r . eiθ
kx + iky =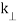 
. eiθ
(B.41)
The functions g and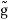 
are related by
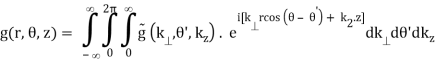
(B.42a)
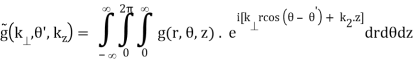
(B.42b)
Under circular symmetry, i.e., f independent of θ, and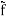 
, thus, independent of 
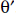, we have
f(x, y, z) = h(r, z)
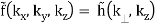
(B.43)
As a result, Eq. (B.42a-b) is formed (using the properties of the Hankel transform)
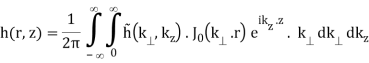
(B.44a)
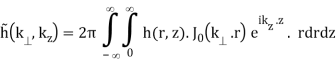
(B.44b)
The integral in Eq. (B.44a) can be seen to represent a 1D Fourier transform of the Hankel transform with respect to r along z.
We have cylindrical symmetry if the problem has it, which means that f is independent of both and z.
f(x, y, z) = p(r)
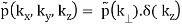
(B.45)
The Fourier transform can be reduced to
p(r) = 1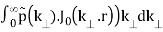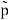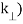/2π 
(
= 2π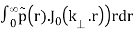 
(B.46)
3.3.3 Spherical Coordinates
In spherical coordinates,
f(x, y, z) = g(r, θ, )
= 
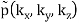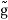(k, θ’, ’)
(B.47)
The coordinates are changed in the following way:
x = r sin θ cos , y = r sin θ sin , z = r cos θ
kx = k sin θ’ cos ’, ky = k sin θ’ sin ’, kz = k cos θ’
(B.48)
Where, again, k =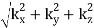 
.
The Fourier integrals are transformed into
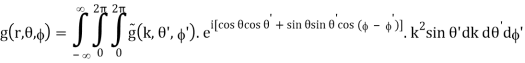
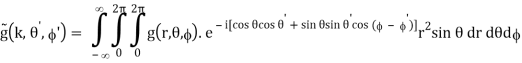
(B.49)
Under circular symmetry, i.e., f(x, y, z) is independent of , we have
f(x, y, z) = g(r, θ)
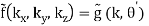
(B.50)
For circular symmetry, the Fourier transforms are
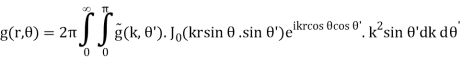
(B.51)
The function is independent of both angles for spherical symmetry, so we have
f(x, y, z) = h(r)
= 
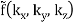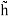(k)
(B.52)
The integrals are reduced to in this case.
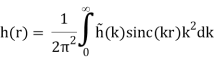
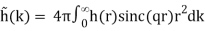(B.53)
The table below shows a few examples of 3D Fourier pairs that are relevant to scattering problems.
f(x, y, z) |  |
δ(x –a, y-b, z-c) | ei(Kx . a + Ky . b+Kz . c) |
π(x, y, z)(cube) |  |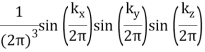
π(x, y) (bar) |  |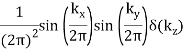
π(x) (slab) |  |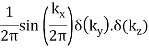
π(r/2) (ball) | Sin k – k . Cos k/2k3 |
π(x)π(  |  |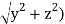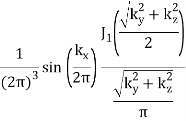
e-αr/4πr | 1/α2 + k2 |
 |  |
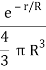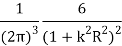e-αr2/2 | e-k2/2α |
3.4.1 Application of Fourier transform to differential equation
The solution of differential equations can also be done using Fourier Transforms. To demonstrate this concept, we'll go over an Ordinary Differential Equation (ODE) and see how the Fourier Transform can be used to solve a differential equation.
Take a look at the ODE in Equation [1]:
d2y(t)/dt2 – y(t) = - g(t) [Equation 1]
The function y(t) that satisfies Equation [1] is what we're looking for. Why not take the Fourier Transform of an equation? We can take the Fourier Transform of a function, so why not an equation? It turns out there's no reason why we shouldn't be able to. Because the Fourier Transform is a linear operation, the time domain produces an equation in which each term corresponds to a frequency domain term. Equation [2] is obtained by applying the Fourier Transform to Equation [1]:
F{d2y(t)/dt2 } – F{ y(t)} = F{- g(t)} [Equation 2]
F{d2y(t)/dt2 } – Y(f) = - G(f)
If you recall the Fourier Transform's differentiation property, we can see that derivatives in the time domain become simple multiplication in the frequency domain:
F{dy(t)/dt} = (2πif)Y(f)
F{d2y(t)/dt2} = (2πif)2 Y(f) . . . [Equation 3]
F{dny(t)/dtn} = (2πif)n Y(f)
Hence, Equation [2] becomes:
(2πif)2 Y(f) – Y(f) = - G(f) [Equation 4]
For Y(f), equation [4] is a simple algebraic equation! This is a simple problem to solve. The following is an example of how Fourier Transforms can be used to solve differential equations: They can solve algebraic equations by converting differential equations.
For Y(f), equation [4] can be easily solved:
Y(f) = -G(f)/(2πif)2 – 1 = G(f)/ 1+ 4π2f2 [Equation 5]
The solution is, in general, the inverse Fourier Transform of the result in Equation [5.] However, in this case, we can go a step further with the solution. Remember that the convolution in the Fourier domain is produced by multiplying two functions in the time domain, and the convolution in the time domain is produced by multiplying two functions in the Fourier (frequency) domain. Equation [5] thus becomes:
y(t) = F-1 {Y(f)} = F-1 { 1/ 1 + 4π2f2 . G(f) }
= F-1 { 1/ 1+4π2f2} * F-1 {G(f)} [Equation 6]
The inverse Fourier Transform for the left-most inverse Fourier transform in the second line of [6] is already known: it's one half of the two-sided decaying exponential function. As a result, we can start simplifying equation [6]:
y(t) = F-1 { 1/ 1+4π2f2} * F-1 {G(f)}
= e-|t|/2 * g(t) [Equation 7]
= ½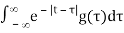 
And we've just found the answer to differential equation [1]. Give yourselves a standing ovation.
Here's where the fine print comes in. We assumed the Fourier Transform for y(t) existed when we moved from Step 1 to Step 2. This is a significant assumption. When g(t)=0, you may recall from differential equations class that the solution must also include the so-called homogeneous solution:
d2yh(t)/dt2 – yh(t) = 0
yh(t) = c1et + c2e-t [Equation 8]
The sum of the solution obtained in equation [7] and the homogeneous solution y h obtained in equation [8] is the "total" solution. So, why doesn't our method produce a homogeneous solution?
The answer is simple: there are no Fourier Transforms for the non-decaying exponentials in equation [8]. That is, if you try to take the Fourier Transform of exp(t) or exp(-t), the integral diverges, and thus no Fourier Transform exists. This is an extremely important caveat to remember.
We'll look at using Fourier Transforms to solve partial differential equations in the next section (PDEs).
3.4.2 1D wave equation
Consider problem
utt = c2uxx, - < x < , (32)
u|t=0 = g(x), (33)
ut|t=0 = h(x). (34)
We arrive at by performing a partial Fourier transform with respect to x.
Then characteristic equation for ODE (3535) is α2 = - c2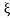
2 and α1,2 = ± ic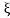
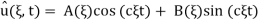
With initial conditions implying A(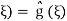
, 
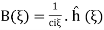and
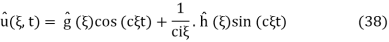
Rewriting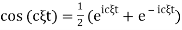 
and recalling that multiplication of FT by 
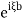is equivalen to to shifting original to the left by b we conclude that 
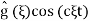is a Fourier transform of ½ (g(x+ct) + g(x – ct))
If we denote H as a primitive of hh then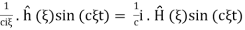 
which in virtue of the same arguments is FT of
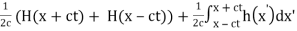
Therefore
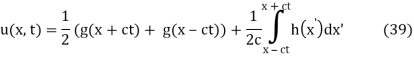
We've returned to the d'Alembert formula.
3.4.3 Heat Equation
Consider problem
ut = kuxx, t > 0, - < x < , (1)
u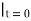
= g(x) (2)
Making partial Fourier transform with respect to x↦ξ (so u(x,t)↦u^(ξ,t)) we arrive to
Indeed, ∂x↦iξ and therefore ∂2 x↦−ξ2
Note that (3) is an ODE and solving it we arrive to
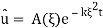; plugging into (4) we find that A(ξ) = 
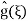and therefore
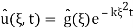
The right-hand expression is a product of two Fourier transforms, one is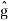 
(ξ) and another is Fourier transform of IFT of e−kξ2te
If we had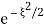 
we would have IFT equal to 
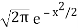but we can get from 
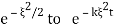by scaling 
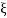↦ (2kt)-1/2
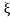and therefore x ↦ (2kt)-1/2x (and we need to multiply the result by (2kt)-1/2 ; therefore 
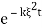is a Fourier transform of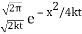 
Again: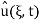 
is a product of FT of g and of 
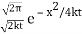and therefore uu is the convolution of these functions (multiplied by 1/(2π)):
u(x, t) = g * 1/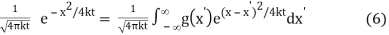
We recovered formula which we had already.
Key takeaway:
The convolution theorem states that the pointwise product of the Fourier transforms of two functions (or signals) is the Fourier transform of a convolution of two functions (or signals) under suitable conditions. The convolution theorem is useful because it allows us to simplify a variety of calculations. Convolutions are often much easier to calculate using Fourier transforms and multiplication than they are to calculate directly. The convolution theorem is a fundamental concept in linear systems theory. It means that, as shown in the next section, any stable causal LTI filter (recursive or nonrecursive) can be implemented by convolving the input signal with the filter's impulse response.
A fundamental property of the Fourier transform is the convolution theorem. It is frequently stated in this manner. "Multiplication in the frequency domain equals convolution in the time domain," or vice versa. "Time multiplication equals frequency domain convolution"
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014
Unit - 3
Integral Transforms-II
Let f(t) and g(t) be arbitrary functions of time 
with Fourier transforms. Take
f(t) = F-1v [F(v)](t) =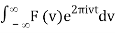 
g(t) = F-1v [G(v)](t) =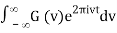 
Where F-1v (t) denotes the inverse Fourier transform (where the transform pair is defined to have constants A = 1 and B = - 2π). Then the convolution is
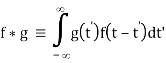
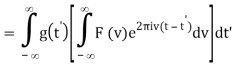
Interchange the order of integration,
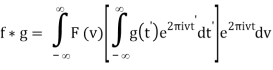
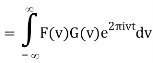
= Fv-1 [F(v) G(v)] (t)
So, applying a Fourier transform to each side, we have
F[f * g] = F[f] F[g]
The convolution theorem also takes the alternate forms
F[fg] = F[f] * F[g]
F-1 (F[f] F[g]) = f * g
F-1(F[f] * F[g]) = f g
NUMERICALS:
1) f(t) = eat and g(t) = ebt (a ≠ b)
Verify that L(f∗g)=L(f)L(g), as implied by the convolution theorem.
ANS:
We first compute
(f * g) = 
= 
= 
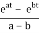
Since
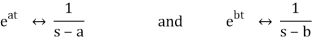
It follows that
ℒ(f * g) =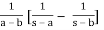 
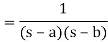
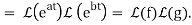
2) Find a formula for the solution of the initial value problem
y’’ – 2y’ + y = f(t), y(0) = k0, y’(0) = k1
Solution
Taking Laplace transforms in ABOVE Equation yields
(s2 – 2s + 1)Y(s)= F(s) + (k1 + k0s) – 2k0
Therefore
Y(s) = 1/(s – 1)2 F(s) + k1 + k0s – 2k0 / (s-1)2
= 1/(s – 1)2 F(s) +k0/s - 1+( k1 - k0 )/ (s-1)2
From the table of Laplace transforms,
ℒ-1 (k0/s - 1+( k1 - k0 )/ (s-1)2) = et (k0 + (k1 – k0)t)
Since
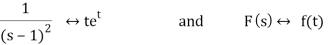
The convolution theorem implies that
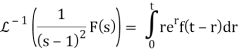
Therefore the solution
y(t) = et (k0 + (k1 – k0) t) +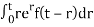 
The z-transform has features that are similar to those of the Fourier transform (and Laplace transform). The only distinction is that the ROCs require extra attention. Assumptions are made in the following sections.
Z [ x[n]] = X(z) ROC = Rx
And
Z [ y[n]] = Y(z) ROC = Ry
Linearity
Z [ ax[n] + by[n]] = a X(z) + bY(z), ROC ⊇ (Rx ∩ Ry)
While it is obvious that the ROC of the linear combination of x[n] and y[n] should be the intersection of the their individual ROCs Rx ∩ Ry in which both X(z) and Y(z) exist, note that in some cases the ROC of the linear combination could be larger than Rx ∩ Ry. For example, for both x[n] = anu[n] and y[n] = anu[n-1] , the ROC is |z| > |a| , but the ROC of their difference an u[n] – anu[n – 1] = δ[n] is the entire z-plane.
Time Shifting
Z[x[n – n0]] = Z-n0 X(z), ROC = Rx
Proof:
Z[x[n – n0]] =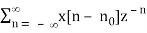 
Define m = n – n0, we have n = m + n0 and
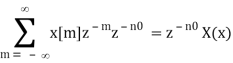
The new ROC is identical to the previous one, with the exception of the possibility of adding or removing the origin or infinity, as the shift may affect the signal's duration.
Time Expansion (Scaling)
Z[x[n/k]] = X(zk), ROC = R1/kx
The discrete signal x[n] cannot be continuously scaled in time as n has to be an integer (for a non-integer n x[n] is zero). Therefore x[n/k] is defined as
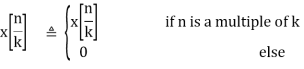
Example: If x[n] is ramp
n | 1 | 2 | 3 | 4 | 5 | 6 |
x[n] | 1 | 2 | 3 | 4 | 5 | 6 |
Then the expanded version x[n/2] is
n | 1 | 2 | 3 | 4 | 5 | 6 |
n/2 | 0.5 | 1 | 1.5 | 2 | 2.5
| 3 |
m |
| 1 |
| 2 |
| 3 |
x[n/2] | 0
| 1
| 0 | 2 | 0 | 3 |
Where m is the integer part of n/k.
Proof: The z-transform of a signal like this is
Z[x[n/k]] =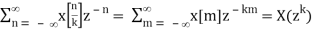 
Note that the change of the summation index from n to m has no effect as the terms skipped are all zeros.
Convolution
Z[x[n] * y[n]] = X(z) Y(z), ROC ⊇ (Rx ∩ Ry)
The ROC of the convolution could be larger than the intersection of Rx and Ry, due to the possible pole-zero cancellation caused by the convolution.
Time Difference
Z[x[n] – x[n – 1]] = (1 – z-1)X(z), ROC = Rx
Proof:
Z[x[n] – x[n – 1]] = X(z) – z-1 X(z) = (1 – z-1) X(z) = z – 1/z X(z)
Note that due to the additional zero z = 1 and pole z = 0, the resulting ROC is the same as Rx except the possible deletion of z = 0 caused by the added pole and/or addition of z = 1 caused by the added zero which may cancel an existing pole.
Time Accumulation
Z[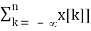 
= 
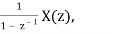ROC ⊇ [Rx ∩ (|z| > 1)]
Proof: The accumulation of x[n] can be written as its convolution with u[n]:
u[n] * x[n] =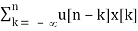 
= 
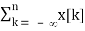
Applying the convolution property, we get
Z[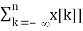 
= Z[u[n] * x[n]] =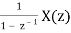 
As Z[u[n]] =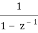 
.
Time Reversal
Z[x[-n]] = X(1/z) ROC = 1/Rx
Proof:
Z[x[-n]] =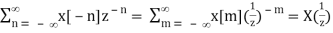 
Where m = -n.
Scaling in Z-domain
Z[an x[n]] = X(z/a), ROC = |a| Rx
Proof:
Z[an x[n]] =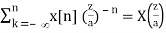 
In particular, if a = ej0 , the above becomes
Z[ejn0 x[n]] = X(e-j0 z) ROC = Rx
The multiplication by e-j0 to z corresponds to a rotation by angle 0 in the z-plane, i.e., a frequency shift by 0. The rotation is either clockwise (0 > 0) or counter clockwise (0 < 0) corresponding to, respectively, either a left-shift or a right shift in frequency domain. The property is essentially the same as the frequency shifting property of discrete Fourier transform.
Conjugation
Z[x* [n]] = X*(z*), ROC = Rx
Proof: Complex conjugate of the z-transform of x[n] is
X*(z) = [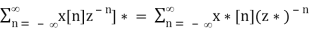 
Replacing z by z*, we get the desired result.
Differentiation in z-Domain
Z[nx[n]] = -z d/dz X(z), ROC = Rx
Proof:
d/dz X(z) =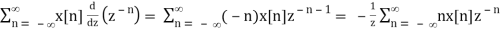 
i.e.,
Z[nx[n]] = - z d/dz X(z)
Example: Taking derivative with respect to z of the right side of
Z[an u[n]] = 
We get
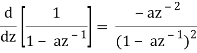
We have this feature of differentiation in the z-domain because of the property of differentiation in the z-domain.
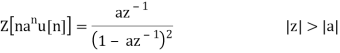
Note that for a different ROC |z| < |a|, we have
Z[ - nanu [ -n – 1]] =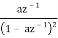 
|z| < |a|
3.3.1 The 3D Fourier Transform
The Fourier pairs are naturally extended to three-dimensional functions as well.
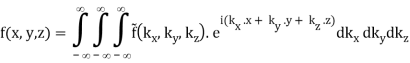
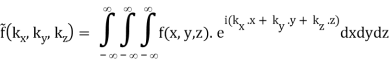
(B.39)
The 3D Fourier transform in cylindrical and spherical coordinates is then discussed.
3.3.2 Cylindrical Coordinates
In this case,
f(x, y, z) = g(r, θ,z)
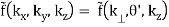
(B.40)
Where,
x + iy = r . eiθ
kx + iky =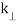 
. eiθ
(B.41)
The functions g and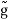 
are related by
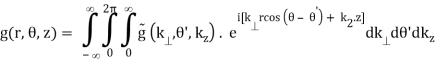
(B.42a)
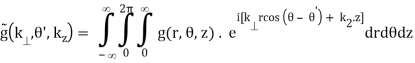
(B.42b)
Under circular symmetry, i.e., f independent of θ, and 
, thus, independent of 
, we have
f(x, y, z) = h(r, z)
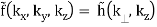
(B.43)
As a result, Eq. (B.42a-b) is formed (using the properties of the Hankel transform)
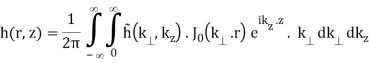
(B.44a)
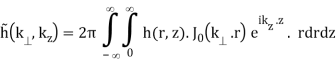
(B.44b)
The integral in Eq. (B.44a) can be seen to represent a 1D Fourier transform of the Hankel transform with respect to r along z.
We have cylindrical symmetry if the problem has it, which means that f is independent of both and z.
f(x, y, z) = p(r)
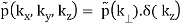
(B.45)
The Fourier transform can be reduced to
p(r) = 1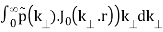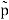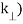/2π 
(
= 2π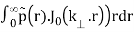 
(B.46)
3.3.3 Spherical Coordinates
In spherical coordinates,
f(x, y, z) = g(r, θ, )
= 
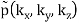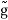(k, θ’, ’)
(B.47)
The coordinates are changed in the following way:
x = r sin θ cos , y = r sin θ sin , z = r cos θ
kx = k sin θ’ cos ’, ky = k sin θ’ sin ’, kz = k cos θ’
(B.48)
Where, again, k =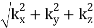 
.
The Fourier integrals are transformed into
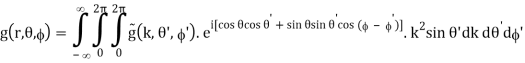
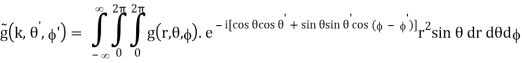
(B.49)
Under circular symmetry, i.e., f(x, y, z) is independent of , we have
f(x, y, z) = g(r, θ)
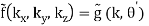
(B.50)
For circular symmetry, the Fourier transforms are
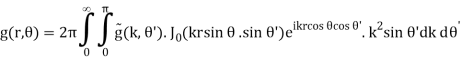
(B.51)
The function is independent of both angles for spherical symmetry, so we have
f(x, y, z) = h(r)
= 
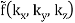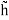(k)
(B.52)
The integrals are reduced to in this case.
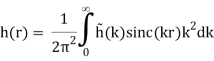
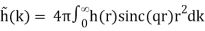(B.53)
The table below shows a few examples of 3D Fourier pairs that are relevant to scattering problems.
f(x, y, z) |  |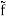
δ(x –a, y-b, z-c) | ei(Kx . a + Ky . b+Kz . c) |
π(x, y, z)(cube) |  |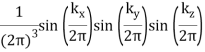
π(x, y) (bar) |  |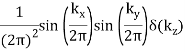
π(x) (slab) |  |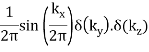
π(r/2) (ball) | Sin k – k . Cos k/2k3 |
π(x)π(  |  |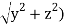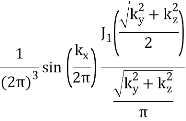
e-αr/4πr | 1/α2 + k2 |
 |  |
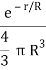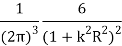e-αr2/2 | e-k2/2α |
3.4.1 Application of Fourier transform to differential equation
The solution of differential equations can also be done using Fourier Transforms. To demonstrate this concept, we'll go over an Ordinary Differential Equation (ODE) and see how the Fourier Transform can be used to solve a differential equation.
Take a look at the ODE in Equation [1]:
d2y(t)/dt2 – y(t) = - g(t) [Equation 1]
The function y(t) that satisfies Equation [1] is what we're looking for. Why not take the Fourier Transform of an equation? We can take the Fourier Transform of a function, so why not an equation? It turns out there's no reason why we shouldn't be able to. Because the Fourier Transform is a linear operation, the time domain produces an equation in which each term corresponds to a frequency domain term. Equation [2] is obtained by applying the Fourier Transform to Equation [1]:
F{d2y(t)/dt2 } – F{ y(t)} = F{- g(t)} [Equation 2]
F{d2y(t)/dt2 } – Y(f) = - G(f)
If you recall the Fourier Transform's differentiation property, we can see that derivatives in the time domain become simple multiplication in the frequency domain:
F{dy(t)/dt} = (2πif)Y(f)
F{d2y(t)/dt2} = (2πif)2 Y(f) . . . [Equation 3]
F{dny(t)/dtn} = (2πif)n Y(f)
Hence, Equation [2] becomes:
(2πif)2 Y(f) – Y(f) = - G(f) [Equation 4]
For Y(f), equation [4] is a simple algebraic equation! This is a simple problem to solve. The following is an example of how Fourier Transforms can be used to solve differential equations: They can solve algebraic equations by converting differential equations.
For Y(f), equation [4] can be easily solved:
Y(f) = -G(f)/(2πif)2 – 1 = G(f)/ 1+ 4π2f2 [Equation 5]
The solution is, in general, the inverse Fourier Transform of the result in Equation [5.] However, in this case, we can go a step further with the solution. Remember that the convolution in the Fourier domain is produced by multiplying two functions in the time domain, and the convolution in the time domain is produced by multiplying two functions in the Fourier (frequency) domain. Equation [5] thus becomes:
y(t) = F-1 {Y(f)} = F-1 { 1/ 1 + 4π2f2 . G(f) }
= F-1 { 1/ 1+4π2f2} * F-1 {G(f)} [Equation 6]
The inverse Fourier Transform for the left-most inverse Fourier transform in the second line of [6] is already known: it's one half of the two-sided decaying exponential function. As a result, we can start simplifying equation [6]:
y(t) = F-1 { 1/ 1+4π2f2} * F-1 {G(f)}
= e-|t|/2 * g(t) [Equation 7]
= ½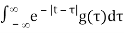 
And we've just found the answer to differential equation [1]. Give yourselves a standing ovation.
Here's where the fine print comes in. We assumed the Fourier Transform for y(t) existed when we moved from Step 1 to Step 2. This is a significant assumption. When g(t)=0, you may recall from differential equations class that the solution must also include the so-called homogeneous solution:
d2yh(t)/dt2 – yh(t) = 0
yh(t) = c1et + c2e-t [Equation 8]
The sum of the solution obtained in equation [7] and the homogeneous solution y h obtained in equation [8] is the "total" solution. So, why doesn't our method produce a homogeneous solution?
The answer is simple: there are no Fourier Transforms for the non-decaying exponentials in equation [8]. That is, if you try to take the Fourier Transform of exp(t) or exp(-t), the integral diverges, and thus no Fourier Transform exists. This is an extremely important caveat to remember.
We'll look at using Fourier Transforms to solve partial differential equations in the next section (PDEs).
3.4.2 1D wave equation
Consider problem
utt = c2uxx, - < x < , (32)
u|t=0 = g(x), (33)
ut|t=0 = h(x). (34)
We arrive at by performing a partial Fourier transform with respect to x.
Then characteristic equation for ODE (3535) is α2 = - c2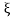
2 and α1,2 = ± ic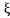
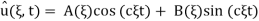
With initial conditions implying A(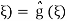
, 
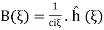and
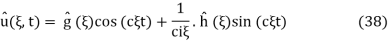
Rewriting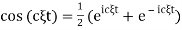 
and recalling that multiplication of FT by 
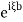is equivalen to to shifting original to the left by b we conclude that 
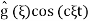is a Fourier transform of ½ (g(x+ct) + g(x – ct))
If we denote H as a primitive of hh then 
which in virtue of the same arguments is FT of
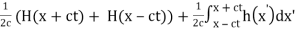
Therefore
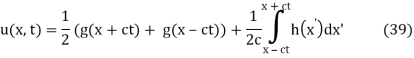
We've returned to the d'Alembert formula.
3.4.3 Heat Equation
Consider problem
ut = kuxx, t > 0, - < x < , (1)
u
= g(x) (2)
Making partial Fourier transform with respect to x↦ξ (so u(x,t)↦u^(ξ,t)) we arrive to
Indeed, ∂x↦iξ and therefore ∂2 x↦−ξ2
Note that (3) is an ODE and solving it we arrive to
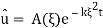; plugging into (4) we find that A(ξ) = 
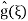and therefore
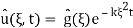
The right-hand expression is a product of two Fourier transforms, one is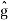 
(ξ) and another is Fourier transform of IFT of e−kξ2te
If we had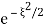 
we would have IFT equal to 
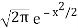but we can get from 
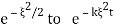by scaling 
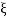↦ (2kt)-1/2
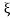and therefore x ↦ (2kt)-1/2x (and we need to multiply the result by (2kt)-1/2 ; therefore 
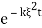is a Fourier transform of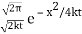 
Again: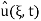 
is a product of FT of g and of 
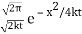and therefore uu is the convolution of these functions (multiplied by 1/(2π)):
u(x, t) = g * 1/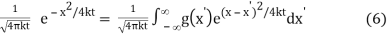
We recovered formula which we had already.
Key takeaway:
The convolution theorem states that the pointwise product of the Fourier transforms of two functions (or signals) is the Fourier transform of a convolution of two functions (or signals) under suitable conditions. The convolution theorem is useful because it allows us to simplify a variety of calculations. Convolutions are often much easier to calculate using Fourier transforms and multiplication than they are to calculate directly. The convolution theorem is a fundamental concept in linear systems theory. It means that, as shown in the next section, any stable causal LTI filter (recursive or nonrecursive) can be implemented by convolving the input signal with the filter's impulse response.
A fundamental property of the Fourier transform is the convolution theorem. It is frequently stated in this manner. "Multiplication in the frequency domain equals convolution in the time domain," or vice versa. "Time multiplication equals frequency domain convolution"
References:
1. Mathematical Physics and Special Relativity–M.Das, P.K. Jena and B.K. Dash (Srikrishna Prakashan)-2009
2. Mathematical Physics–H. K. Das, Dr. Rama Verma (S. Chand Publishing) 2011
3. Complex Variable: Schaum’s Outlines Series M. Spiegel (2nd Edition, Mc- Graw Hill Education)-2004
4. Complex variables and applications J.W.Brown and R.V.Churchill 7th Edition 2003
5. Mathematical Physics, Satya Prakash (Sultan Chand)-2014
