Unit - 4
Radiation
4.1.1 Definition:
Any matter with a temperature greater than absolute zero generates thermal radiation, which is transmitted as electromagnetic wave energy.
4.1.2 Characteristics of thermal radiation depend on the following properties of the emitting object or body:
- Surface temperature
- Smoothness or roughness of the surface
- Spectral absorptivity
- Spectral emissive power
Thermal radiation is made up of a continuous dispersion of photon energies with a spectrum of frequencies or wavelengths, just as electromagnetic waves. The distribution of the spectrum, the peak value of the wavelength, and the overall emitted amount of all wavelengths vary depending on the emitting body's surface temperature. The emitting body's absorptivity, reflectivity, and emissivity are all dependent on the wavelength of the radiation at a particular surface temperature.
4.1.3 Properties
The thermal radiation emitted by a body at any temperature has a wide frequency range. Planck's law of black-body radiation, as shown in the diagram at the top, gives the frequency distribution for an idealised emitter.
As the temperature of the emitter rises, the primary frequency (or colour) range of the emitted radiation moves to higher frequencies. A red hot item, for example, radiates primarily in the visible band's long wavelengths (red and orange). It begins to produce perceptible amounts of green and blue light as it heats up further, and the dispersion of frequencies over the visible range causes it to seem white to the human eye; it is white hot. Even at a white-hot temperature of 2000 K, 99 percent of the radiation's energy is still infrared. Wien's displacement law determines this. As the temperature rises, the peak value for each curve shifts to the left in the diagram.
As the temperature rises, the total amount of radiation of all frequencies increases sharply; it climbs as T4, where T is the absolute temperature of the body. On the absolute temperature scale, an object at the temperature of a cooking oven (600 K vs. 300 K) radiates 16 times as much power per unit area as one at ambient temperature (300 K). An object heated to the temperature of an incandescent light bulb filament—roughly 3000 K, or 10 times ambient temperature—radiates 10,000 times the amount of energy per unit area. According to the Stefan–Boltzmann law, the total radiative intensity of a dark body rises as the fourth power of the absolute temperature. As the temperature rises, the area under each curve climbs fast in the plot.
Reciprocity describes how the rate of electromagnetic radiation released at a particular frequency is related to the quantity of absorption experienced by the source. As a result, a surface that absorbs more red light emits more red light thermally. This principle holds true for all wave qualities, including wavelength (colour), direction, polarisation, and even coherence, making it conceivable to have polarised, coherent, and directional thermal radiation, albeit polarised and coherent forms are rather rare in nature far from sources (in terms of wavelength). For further information about this certification, see the section below.
Thermal light follows Super-Poissonian statistics in terms of photon statistics.
4.1.4 Near-field and far-field:
The general properties of thermal radiation as described by the Planck's law apply if the linear dimension of all parts considered, as well as radii of curvature of all surfaces are large compared with the wavelength of the ray considered' (typically from 8-25 micrometres for the emitter at 300 K). Thermal radiation, as described above, solely considers radiating waves (far-field, or electromagnetic radiation). For lesser distances from the thermal source or surface, a more complicated framework involving electromagnetic theory must be applied (near-field thermal radiation). While far-field thermal radiation over distances of more than one wavelength is often not coherent, near-field thermal radiation (i.e., radiation at distances of a fraction of various radiation wavelengths) may have some temporal and spatial coherence.
Predictions and effective demonstrations of radiative heat transmission between objects separated by nanoscale gaps that depart greatly from the law's predictions have challenged Planck's law of thermal radiation in recent decades. When the emitter and absorber support surface polariton modes that can couple through the gap between cold and hot objects, this divergence is very high (up to many orders of magnitude). The two objects must, however, be separated by ultra-narrow gaps on the order of microns or even nanometers to benefit from surface-polariton-mediated near-field radiative heat transfer. This constraint makes it difficult to create viable devices.
Another technique to change the object's thermal emission spectrum is to reduce the emitter's dimensionality. This method improves on the idea of confining electrons in quantum wells, wires, and dots by constructing confined photon states in two- and three-dimensional potential traps, such as wells, wires, and dots. At certain frequencies, such spatial confinement concentrates photon states and boosts thermal emission. The diameters of the radiating objects should be on the order of or below the thermal wavelength predicted by Planck's law to achieve the appropriate level of photon confinement. Most notably, the emission spectra of thermal wells, wires, and dots deviates from Planck's law predictions not only in the near field, but also in the far field, extending the range of their applications dramatically.
4.1.5 Subjective color to the eye of a black body thermal radiator:
°C (°F) | Subjective color |
480 °C (896 °F) | Faint red glow |
580 °C (1,076 °F) | Dark red |
730 °C (1,350 °F) | Bright red, slightly orange |
930 °C (1,710 °F) | Bright orange |
1,100 °C (2,010 °F) | Pale yellowish orange |
1,300 °C (2,370 °F) | Yellowish white |
> 1,400 °C (2,550 °F) | White (yellowish if seen from a distance through atmosphere) |
4.1.6 Selected radiant heat fluxes:
The time it takes for a person to be damaged by radiant heat is proportional to the pace at which the heat is delivered. Heat flux and consequences from radiation:(1 W/cm2 = 10 kW/m2)
KW/m2 | Effect |
170 | In a post-flashover compartment, the maximum flux was measured. |
80 | Personal Protective Equipment Thermal Protective Performance Test |
52 | Fiberboard catches fire after 5 seconds. |
29 | Given enough time, wood will ignite. |
20 | At the floor level of a residential room, a typical flashover begins. |
16 | After 5 seconds, human skin experiences sudden discomfort and second-degree burn blisters. |
12.5 | Pyrolysis produces flammable volatiles in wood. |
10.4 | Human skin: 3 seconds of pain, 9 seconds of second-degree burn blisters |
6.4 | After 18 seconds, second-degree burn blisters appear on human skin. |
4.5 | Human skin: second-degree burn blisters after 30 seconds |
2.5 | Human skin: long-term exposure causes burns, and radiant flux exposure is common in firefighting. |
1.4 | Sunlight can cause sunburn in as little as 30 minutes. A sunburn is not the same as a thermal burn. It is caused by UV radiation-induced cellular damage. |
Key takeaway:
Heat radiation travels at a speed of 3108 m/sec, and infrared radiation released by a standard household radiator or electric heater is an example of thermal radiation. Sunshine, or solar radiation, is thermal radiation from the sun's extremely hot gases, and this radiation heats the planet.
4.2.1 Blackbody Radiation
"Blackbody radiation" or "cavity radiation" refers to an object or system that absorbs all incident radiation and re-radiates energy that is unique to this radiating system and is unaffected by the type of radiation it receives. Standing wave or resonant modes of the radiating cavity are thought to be the source of the radiated energy.

In a particular frequency range, the amount of radiation emitted should be proportional to the number of modes in that range. All modes had an equal chance of being formed, according to classical physics, and the number of modes increased proportionally to the square of the frequency.
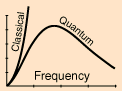
However, the projected frequency-dependent rise in radiated energy (called the "ultraviolet catastrophe") did not occur. Nature has a superior idea.
All items with a temperature greater than zero degrees Celsius (0 K, -273.15 oC) emit energy in the form of electromagnetic radiation.
A blackbody is a hypothetical or model body that absorbs all incident radiation and does not reflect or emit any. It is a hypothetical object that is a "perfect" radiation absorber and emitter across all wavelengths.
A blackbody's spectral distribution of thermal energy radiated (i.e., the pattern of the intensity of the radiation over a range of wavelengths or frequencies) is solely determined by its temperature.
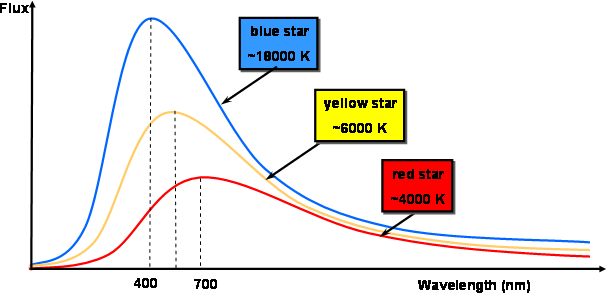
Fig 1. Curves of blackbody radiation at various temperatures.
Several laws can be used to describe the properties of blackbody radiation:
- Planck's Law of Blackbody Radiation, which is a formula for calculating the spectral energy density of emission at each wavelength (E) for a given absolute temperature (T).
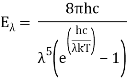
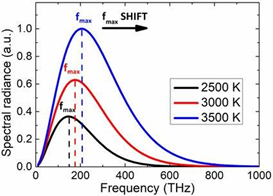
2. Wien's Displacement Law, according to which the frequency of the emission peak (fmax) increases linearly with absolute temperature (T). In contrast, as the body's temperature rises, the wavelength at the emission peak drops.
fmax ∝ T
3. The Stefan–Boltzmann Law, which connects total energy emitted (E) to absolute temperature (T).
E ∝ T4
Notice how the blackbody radiation curves have a complex structure (as described by Planck's Law) in the graphic above.
At a given temperature, the spectral profile (or curve) corresponds to a given peak wavelength, and vice versa.
The max wavelength of a blackbody decreases as its temperature rises (Wien's Law).
As the temperature of the blackbody rises, the intensity (or flux) at all wavelengths rises as well.
As the temperature rises, the total energy radiated (the area under the curve) increases rapidly (Stefan–Boltzmann Law).
Although the intensity may be very low at extremely short or long wavelengths, energy is theoretically emitted at all wavelengths at any temperature above absolute zero (the blackbody radiation curves never reach zero).
Stars are frequently modelled as blackbodies in astronomy, though this is not necessarily a reasonable approximation. The wavelength of the peak of a star's radiation curve can be used to calculate its temperature.
Penzias and Wilson, who eventually earned the Nobel Prize for their work, discovered the cosmic microwave background radiation (CMBR) in 1965. The COBE spacecraft measured the radiation spectrum, which was found to be a remarkable fit to a blackbody curve with a temperature of 2.725 K, implying that the cosmos has been expanding and cooling for 13.7 billion years. WMAP, a more recent mission, has studied spectral features to a far higher precision, uncovering minuscule temperature changes in the early Universe that eventually led to the large-scale structures we observe today.
4.2.2 Heated Bodies Radiate
Now we'll look at another conundrum that physicists faced at the turn of the century (1900): how do hot bodies radiate? Heat was known to cause the molecules and atoms of a solid to vibrate, and the molecules and atoms were themselves intricate patterns of electrical charges, so the mechanism was well understood. (As usual, Newton was right on the money.) Maxwell's predictions that oscillating charges create electromagnetic radiation were confirmed, at least for basic antennas, by Hertz and others' experiments. The fact that this radiation travelled at the speed of light was discovered thanks to Maxwell's equations, and it was realised that light and the closely related infrared heat radiation were both electromagnetic waves. When a substance was heated, the resulting vibrations on a molecular and atomic scale unavoidably caused charge oscillations, according to the picture. Assuming that Maxwell's electromagnetic radiation theory, which worked so well in the macroscopic world, was also valid at the molecular level, these oscillating charges would radiate, presumably emitting the heat and light observed.
4.2.3 How is Radiation Absorbed?
What exactly does "black body" radiation imply? The argument is that the radiation emitted by a heated body is influenced by the body being heated to some amount. Let's take a step back for a moment and analyse how different materials absorb radiation. Some, such as glass, appear to absorb very little light and let it pass right through. A gleaming metallic surface does not absorb light; instead, it reflects it. Light and heat are almost fully absorbed by a black material like soot, and the material becomes warm. How can we explain these diverse behaviours in terms of light interacting with charges in the material, causing these charges to oscillate and absorb energy from the radiation? In the case of glass, this clearly does not occur, at least not frequently. What's to stop you? Quantum mechanics is required to fully comprehend why, but the fundamental notion is that there are charges—electrons—in glass that can oscillate in response to an applied external oscillating electric field, but these charges are strongly linked to atoms and can only oscillate at particular frequencies. (These charge oscillations occur as an electron jumps from one orbit to another, according to quantum experts.) Of course, in the 1890s, when the first precision work on black body radiation was being done, this was not understood.) Because none of these frequencies correlate to visible light in regular glass, there is no resonance with a light wave, and thus minimal energy is absorbed. As a result, glass is ideal for windows! That's a given. Glass, on the other hand, is opaque at frequencies outside the visual range (in general, both in the infrared and the ultraviolet). These are the natural oscillation frequencies of the electrical charge distributions in atoms or bonds.
How can we comprehend how a metal surface reflects light? Electrons in a piece of metal are free to move across the entire solid. This is what distinguishes a metal from other materials: it easily transmits both electricity and heat, which are conveyed by currents of freely moving electrons. (Well, vibrations do carry a small amount of heat.) Metals, on the other hand, are easily identifiable due to their lustrous appearance—why is that? Again, it's those free electrons: the electrical field of the incoming light wave drives them into enormous (compared to the atoms) oscillations, and this generated oscillating current radiates electromagnetically, exactly like a current in a transmitting antenna. The reflected light is the source of this radiation. Little of the incoming radiant energy is absorbed as heat by a polished metal surface; instead, it is reradiated, or reflected.
Consider a substance that absorbs light and does not transmit or reflect it. With soot, we're quite near to perfect absorption. It will conduct an electric current like a metal, but not nearly as effectively. Unattached electrons can flow across the entire solid, but they constantly collide with objects because they have a short mean free path. They create vibration when they bump, similar to balls hitting bumpers in a pinball machine, and hence release kinetic energy as heat. Although the electrons in soot have a shorter mean free path than those in a good metal, they travel far more freely than electrons attached to atoms (as in glass), allowing them to accelerate and absorb energy from the light wave's electric field. As a result, they are extremely efficient at converting energy from light waves to heat.
4.2.4 The “Black Body” Spectrum: a Hole in the Oven
Any body that is above absolute zero will radiate to some extent, with the intensity and frequency distribution of the radiation varying depending on the body's detailed structure. To begin analysing heat radiation, we must first define the body that is radiating: the simplest feasible situation is an idealised entity that is a perfect absorber, and hence also a perfect emitter (based on the above logic). This is referred to as a "black body" for obvious reasons.
But we need to test our theories in the lab: how can we build a perfect absorber? OK, nothing is perfect, but Kirchhoff had a nice notion in 1859: any radiation that passes through a little hole in the side of a huge box bounces around inside, absorbing a lot of it on each bounce, and has little chance of ever getting out again. So, we can do it backwards: make an oven with a tiny hole on the side, and the radiation that comes out of the hole should be as close to a perfect emitter as we can get. Kirchhoff challenged theorists and experimentalists to calculate and measure the energy/frequency curve for this "cavity radiation," as he dubbed it (in German, of course: hohlraumstrahlung, where hohlraum means hollow room or cavity, strahlung is radiation). Kirchhoff's challenge in 1859, in fact, was the catalyst for quantum theory forty years later!
4.2.5 Understanding the Black Body Curve
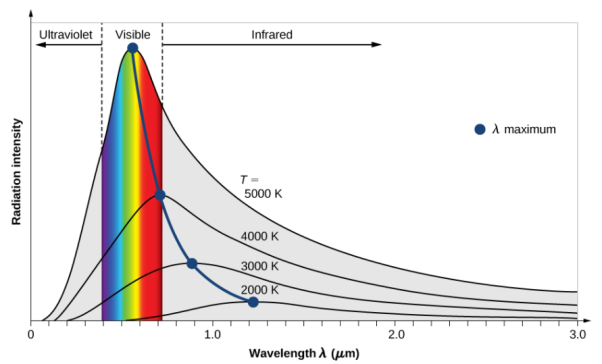
The key to a revolution was these exquisitely precise experimental data. Max Planck performed the first successful theoretical analysis of data in 1900. He focused on simulating the oscillating charges that must exist in the oven walls, radiating heat inwards while being driven by the radiation field in thermodynamic equilibrium.
The basic line is that he discovered he could account for the observed curve if he required these oscillators to lose or acquire energy in chunks, called quanta, of size hf for an oscillator of frequency f, rather than continuously, as the classical theory would require. Planck's constant is the name given to the constant h.h=6.626×10−34 joule⋅sec.
Planck computed the following formula for the radiation energy density within the oven based on this assumption:
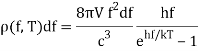
The perfect agreement of this formula with exact observations, and the resulting need for energy quantization, was the most significant advancement in physics of the century.
But no one noticed for a long time! His black body curve was universally acknowledged as correct: more and more precise experiments proved it time and time again, but the quantum assumption's radical nature remained a mystery. Planck wasn't too bothered; he didn't believe it either, and he considered it as a technological remedy that would (he hoped) someday be obsolete.
Part of the problem was Planck's long, complex, and improbable path to the formula—he even made contradicting assumptions at certain points, as Einstein later pointed out. But the result was right in any case, which is why we'll take a different, easier approach, which was started (but never completed) by Lord Rayleigh in England.
Key takeaway:
- A blackbody absorbs all incident radiation and enables all incident radiation to flow through it (no reflected energy) (no energy transmitted through the body). This is true for radiation of all wavelengths and incidence angles. As a result, the blackbody absorbs all incident radiation perfectly.
- The blackbodies are used in applications such as lighting, heating, security, thermal imaging, and testing and measuring. The Planck Law of Radiation can be used to determine the intensity of energy at any temperature and wavelength.
4.3.1 Temperature Dependence of the pH of pure Water:
It is an endothermic process to produce hydrogen ions (hydroxonium ions) and hydroxide ions from water. Using the less complicated equilibrium:
H2 O(l) ⇌ H(aq)+ + OH(aq)- (1)
As a result, the forward reaction "absorbs heat," as indicated.
If you change the conditions of a reaction in dynamic equilibrium, the location of equilibrium moves to counteract the change, according to Le Chatelier's Principle. As a result, if you raise the temperature of the water, the equilibrium will shift back to a lower temperature. It will accomplish this by absorbing the additional heat. This means that the forward reaction will be favoured, resulting in the formation of more hydrogen ions and hydroxide ions. As a result, as the temperature rises, the value of KwKw rises as well.
The influence of temperature on KwKw is shown in the table below. A new pH has been determined for each value of KwKw. It could be beneficial if you checked the pH levels yourself.
T (°C) | Kw (mol2 dm-6) | PH | POH |
0 | 0.114 x 10-14 | 7.47 | 7.47 |
10 | 0.293 x 10-14 | 7.27 | 7.27 |
20 | 0.681 x 10-14 | 7.08 | 7.08 |
25 | 1.008 x 10-14 | 7.00 | 7.00 |
30 | 1.471 x 10-14 | 6.92 | 6.92 |
40 | 2.916 x 10-14 | 6.77 | 6.77 |
50 | 5.476 x 10-14 | 6.63 | 6.63 |
100 | 51.3 x 10-14 | 6.14 | 6.14 |
The pH of pure water drops as the temperature rises, as can be shown. In the same way, the pOH decreases.

Temperature dependence of the resistivity of pure In and of In–Cd alloys; the curves were obtained during single thermocycling at an average rate of 0.25 K/min. The temperature interval of the measurement of the time dependence of is indicated in the lower part of panel ͑ a ͒; a 6-hour hold was made at 200 K during cooling of the alloy In– 4.3 at. %Cd ͑ b ͒.
4.4.1 What are Kirchhoff’s Law?
Gustav Kirchhoff, a German physicist, proposed a pair of rules in 1845 that deal with current and energy conservation in electrical circuits. Kirchhoff's Voltage and Current Law are the names for these two laws. These principles aid in determining the electrical resistance of a complex network, or impedance in the case of AC, as well as the current flow in the network's many streams. Let's have a look at what these laws say in the next part.
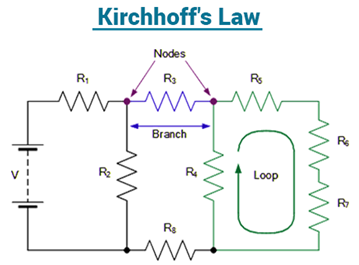
What do Kirchhoff’s laws state?
Kirchhoff's First Law and Kirchhoff's Junction Rule are two names for Kirchhoff's Current Law. In a circuit, the amount of currents in a junction equals the sum of currents outside the junction, according to the Junction rule.
Kirchhoff's Second Law and Kirchhoff's Loop Rule are two names for Kirchhoff's Voltage Law. The total of the voltages around a closed loop is null, according to the loop rule.
4.4.2 Kirchhoff’s First Law
The total current entering a junction or a node is equal to the charge exiting the node, according to Kirchhoff's Current Law, because no charge is lost.
To put it another way, the algebraic sum of all currents entering and exiting the node must be zero. Conservation of charge is the name given to this characteristic of Kirchhoff law.I(exit) + I(enter) = 0.
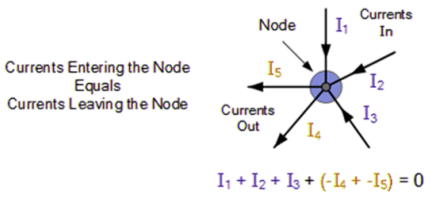
The currents I1, I2, and I3 entering the node are deemed positive in value, whereas the currents I4 and I5 exiting the nodes are regarded negative. This can be stated mathematically as follows:
I1 + I2 + I3 – I4 – I5 = 0
A junction or connection of two or more current-carrying routes, such as cables and other components, is referred to as a node. Parallel circuits can also be analysed using Kirchhoff's current law.
4.4.3 Kirchhoff’s Second Law
The voltage around a loop equals the sum of all voltage drops in the same loop for any closed network and also equals zero, according to Kirchhoff's Voltage Law.
To put it another way, the algebraic total of all the voltages in the loop must equal zero, and this property of Kirchhoff's law is known as energy conservation.
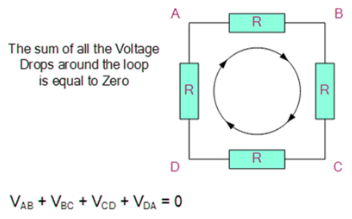
When you start at any position in the loop and keep going in the same direction, you'll see that the voltage declines in all directions, whether negative or positive, and you'll come back to the same spot. It is critical to maintain either a counterclockwise or a clockwise rotation; otherwise, the final voltage value will not be zero. The voltage law can also be used to analyse series circuits.
When analysing AC or DC circuits using Kirchhoff's circuit rules, you must be familiar with all of the terminologies and concepts used to define circuit components such as routes, nodes, meshes, and loops.
4.4.4 Kirchhoff’s Law Solved Example
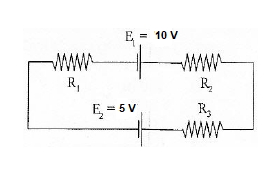
If R1 = 2Ω, R2 = 4Ω, R3 = 6Ω, determine the electric current that flows in the circuit below.
Solution:
The following are some considerations to make as you approach the problem:
You must decide on the current's direction. Let us choose the clockwise direction in this dilemma.
There is a potential drop when current travels over the resistor. As a result, V = IR has a negative sign.
Because of the charging of energy at the emf source, the source of emf (E) signs positive as the current moves from low to high. Similarly, if the current changes from high to low voltage (+ to -), the source of emf (E) signs negative due to the emf source's energy being depleted.
In this solution, the current flows in the same direction as the clockwise rotation.
– IR1 + E1 – IR2 – IR3 – E2 = 0
Substituting the values in the equation, we get
–2I + 10 – 4I – 6I – 5 = 0
-12I + 5 = 0
I = -5/-12
I = 0.416 AThe circuit has a current of 0.416 A flowing through it. The electric current is signed positive, which indicates that it rotates in the same direction as the clock. If the electric current is negative, it will flow in an anti-clockwise direction.
4.5.1 What is Stefan Boltzmann Law?
The amount of radiation emitted per unit time from an area A of a black body at absolute temperature T is exactly proportional to the fourth power of the temperature, according to Stefan Boltzmann's law.
u/A = σ T4 .. . . . (1)
Where σ is Stefan’s constant = 5.67 × 10-8 W/m2 k4
A non-black body absorbs and so emits less radiation, as shown by equation (1)
For such a body, u = e σ AT4 . . . . . . . (2)
Where e = emissivity (which is equal to absorptive power) which lies between 0 to 1.
Net energy emitted by an area A per unit time in the presence of temperature T0.
Δu = u – uo = eσA [T4 – T04] . . . . . . (3)
“Total energy emitted/radiated per unit surface” is a term used to describe how much energy is emitted or radiated per The temperature of a blackbody is proportional to the amount of power it emits per unit area, according to the Stefan Boltzmann Law. The area of a blackbody over all wavelengths per unit time is precisely proportional to the fourth power of the blackbody's thermodynamic temperature, according to this law.
4.5.2 Derivation of Stefan Boltzmann Law
Integrating Plank's radiation formula yields the total power radiated per unit area over all wavelengths of a dark body. As a function of wavelength, the radiated power per unit area is:
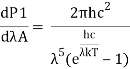
Where,
- P stands for radiated power.
- A is the blackbody's surface area, and is the wavelength of emitted radiation.
- Planck's constant is h.
- The speed of light is denoted by c.
- Boltzmann's constant is k.
- T stands for temperature.
When the Stefan Boltzmann equation is simplified, we get:
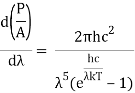
On integrating both sides in terms of and applying the restrictions that we obtain;
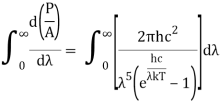
After removing the constants, the integrated power is:
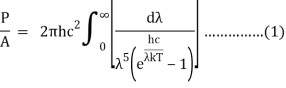
Analytically, this can be solved by substituting:
x = 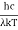
Therefore, dx = - 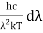
⟹ h = 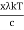
⟹ c = 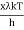
⟹ d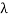 =
= 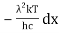
As a result of substituting them in equation (1)

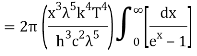
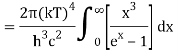
The following equation is equivalent to the conventional form of integral:
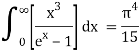
As a result of replacing the above result, we obtain
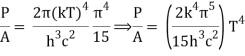
We get, when we simplify it even more,
⇒ P/A = σ T4
As a result, we arrive at a mathematical representation of Stephen Boltzmann's law:
⇒ε = σT4
Where,
ε = P/A
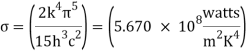
The behaviour of gases at low temperatures could be effectively expressed using this quantum mechanical result.
4.5.3 Relationship between energy density and pressure
Kinetic theory of gases with classical particles
The following relationship between the pressure of a gas p and the speed v of the particles contained inside was derived using the kinetic theory of gases in the article Pressure and temperature:

The number of gas particles in a volume V is denoted by N, and the mass of one particle (not the entire gas mass!) is denoted by m. The root mean square speed is referred to as the speed.
The mean kinetic energy of the particles can be given in very good approximation with in a classical perspective of perfect gases, in which the particle speeds are substantially below the speed of light.½⋅m⋅v² (Keep in mind that this formula only works in non-relativistic mechanics!) The following relationship between pressure and a particle's mean energy becomes clear:
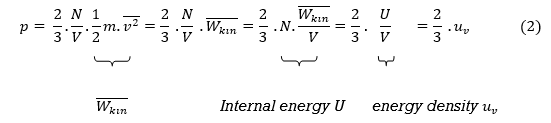
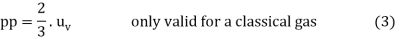
The product of the number of particles N and the mean kinetic energy of a particle was utilised in the foregoing derivation to correspond to the total energy contained in the gas, i.e. the so-called internal energy U. The quotient of internal energy U and volume V can thus be understood as (volumetric) energy density uv (a “v” is added to the energy density in the index to avoid ambiguities with the specific internal energy u as a mass-related variable).
Because the derivation was based on classical mechanics, the validity of the assumption was assumed.Wkin=½⋅m⋅v2, Only classical perfect gases have the obtained relationship between pressure and energy density.
4.5.4 First law of thermodynamics
The first law of thermodynamics can be applied at this moment since the photon gas is equivalent to a classical ideal gas. It is written in differential form as follows (where S is the entropy):
DU = T . DS – p . dV First law of thermodynamics (14)
At constant temperature, dividing this equation by dV yields the following relationship:

Without going into the details of how the so-called Maxwell thermodynamic connections are derived, they reveal another crucial relationship at this point: At constant temperature, a change in entropy and a change in volume have the same connection as a change in pressure and a change in temperature. This is stated mathematically as follows:
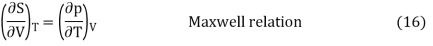
Equation (15) can now be written using this Maxwell relation:

The quantity (U/V)T in equation (13) can be substituted by the energy density uv. Furthermore, according to equation (8), the pressure p corresponds to only one-third of the energy density:



The partial derivative with regard to temperature can be represented as an ordinary derivative because the energy density is solely a function of temperature. We get the following results after separating the variables (Fourier method):



Both sides of the equation can now be integrated, and while computing the primitive function, constants of integration must be taken into account, which are summarised in the constant a (in this context, a generally stands for a constant, not a particular value!):

ln uv = 4 . Ln T + a (25)



uv = a . T4 (29)
As a result, the energy density uv is proportional to the absolute temperature T to the fourth power. The total energy U of a volume V filled with photons (e.g., the volume of the considered cavity) emitted by a blackbody at temperature T is as follows:
U = uv . V = a . T4 . V (30)
U = a . T4 . V (31)
Experimentally, the constant a could now be calculated. Usually, though, it is the power with which the body emits photons that is of importance, not the energy of the photon stream.
4.6.1 Introduction:
Charged particles make up material objects. According to the Lorentz force, an electromagnetic wave incident on the object exerts forces on the charged particles. As stated in the preceding section, these forces act on the object's particles, increasing its energy. Every warm sunny day brings with it the energy that sunlight carries. The extremely mild pressure that electromagnetic radiation produces by applying a force in the direction of the wave is a far less well-known aspect of electromagnetic radiation. Electromagnetic waves contain and transport momentum, resulting in this force.
Consider a plane electromagnetic wave incident on a metal in which electron motion as part of a current is damped by the metal's resistance, resulting in average electron motion in phase with the force creating it. This is analogous to an object moving against friction and coming to a halt as soon as the force pushing it ceases to exist (Figure 16.5.116.5.1). When the electric field is in the positive y-axis direction, electrons flow in the negative y-direction, while the magnetic field is in the positive z-axis direction. We can see that the force on the electron from the magnetic field is in the direction of the positive x-axis, which is the direction of wave propagation, by using the right-hand rule and accounting for the electron's negative charge. When the E E field reverses, the B B field reverses as well, and the force returns to its original direction. However, Maxwell's equations and the Lorentz force equation suggest the presence of radiation pressure in a much broader sense than this specific example.
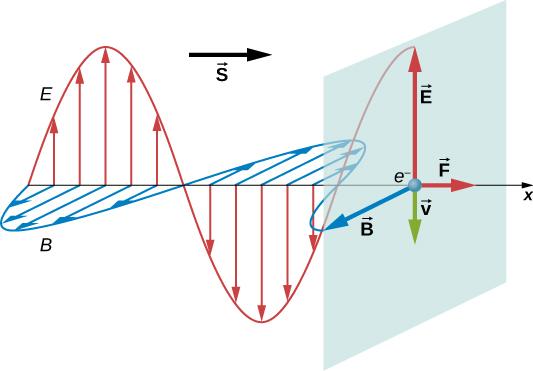
Figure 2: An electromagnetic wave's electric and magnetic fields can combine to produce a force in the propagation direction, as shown for the exceptional case of electrons whose speed is greatly slowed by a metal's resistance.
An electromagnetic wave, according to Maxwell, carries momentum. An object that absorbs an electromagnetic wave will feel a force in the wave's propagation direction. The force is equal to the wave's radiation pressure on the item. If the radiation was reflected instead of absorbed, the force would be twice as strong.
Nichols and Hull proved Maxwell's prediction in 1903 by using a torsion balance to precisely measure radiation pressures. Figure 16.5.2 depicts the schematic arrangement. Inside a glass container, the mirrors were suspended from a fibre. By placing light on one of the mirrors, Nichols and Hull were able to produce a little quantifiable deflection. They were able to compute the imbalanced force on the mirror using the measured deflection and find agreement with the projected value of the force.
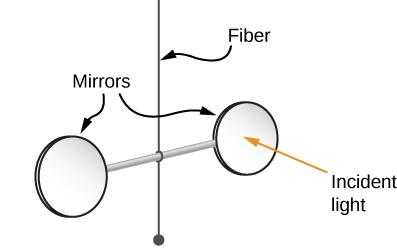
Figure 3: A simplified depiction of the central section of Nichols and Hull's setup for precisely measuring radiation pressure and confirming Maxwell's prediction.
An electromagnetic wave's radiation pressure prad on a fully absorbing surface turns out to be equal to the wave's energy density:

Because the momentum direction reverses upon reflection, the pressure produced is twice as great if the material is perfectly reflecting, such as a metal surface, and the incidence is along the normal to the surface:

We can vouch for the accuracy of the units:

Because the energy density oscillates rapidly, we are usually interested in the time-averaged radiation pressure, which can be written in terms of intensity: Equations 16.5.1 and 16.5.2 give the instantaneous pressure, but because the energy density oscillates rapidly, we are usually interested in the time-averaged radiation pressure, which can be written in terms of intensity:

Many observable celestial events, including the appearance of comets, are explained by radiation pressure. Comets are chunks of cold material with frozen gases, rock, and dust imbedded in them. When a comet gets close to the Sun, it warms up and starts to evaporate. The comet's coma is the hazy region around it caused by gases and dust. When gases and dust depart the comet, some of them form tails. A comet has two tails, as shown in Figure 16.5.31. Ionized gases make up the majority of the ion tail (or gas tail). The solar wind, which is a continuous stream of charged particles generated by the Sun, interacts electromagnetically with these ions. The solar wind exerts such a tremendous force on the ionised gases that the ion tail almost always points directly away from the Sun. The dust particles make up the second tail. The dust tail does not interact with the solar wind because it is electrically neutral. However, the radiation pressure created by the Sun's light has an effect on this tail. This pressure is strong enough to cause the dust tail to be pushed from the comet's path, despite its diminutive size.
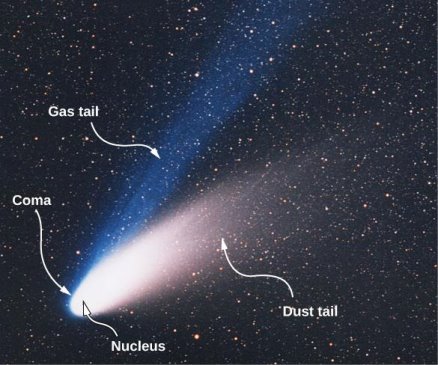
Figure 4: In this view of Comet Ison, evaporation of material warmed by the Sun generates two tails.
After Maxwell demonstrated that light carries both momentum and energy, a revolutionary idea arose, at first merely as science fiction. Radiation pressure could be used to propel a spacecraft with a big reflecting light sail. A vehicle like this would not need to carry any gasoline. Instead of the short bursts of rocket propulsion, it would be subjected to a constant yet tiny force from solar radiation. It would accelerate slowly at first, but with continued acceleration, it would eventually reach enormous speeds. To achieve a usable acceleration, a spaceship with a tiny total mass and a huge sail area would be required.
When NASA began its space programme in the 1960s, the idea began to receive serious consideration. The Planetary Society, a citizen-funded organisation, has made the most current advancement in light-propelled spacecraft. It is currently experimenting with the use of light sails to move a small vehicle made up of CubeSats, which are tiny satellites that NASA deploys in orbit for various research projects during space missions meant for other objectives.
The LightSail spacecraft (Figure 16.5.4) is made up of three CubeSats that have been packed together. It weighs roughly 5 kilogrammes and is about the size of a loaf of bread. Its sails are composed of very thin Mylar and open to a surface area of 32m2 after launch.

Figure 5: In May 2016, two miniature CubeSat spacecraft were launched from the International Space Station. When the CubeSats are far enough away from the Station, the solar sails open up.
Electromagnetic radiation exerts a minor force on everything it comes into contact with. This is referred to as radiation pressure, and it is defined as the transfer of momentum from photons as they impact the object's surface.
This pressure is insignificant in ordinary life, but it can become significant in the vicinity of stars due to the massive amounts of photons emitted. Radiation pressure is proportional to the fourth power of temperature under the virtually blackbody conditions that exist inside a star, as shown by the equation:

T is the temperature, c is the speed of light, and is the Stefan-Boltzmann constant. This means that even a modest increase in temperature causes a significant rise in radiation pressure.
The majority of stars in the main sequence have core temperatures in the millions of degrees and rely on gas pressure to resist gravity. Radiation pressure makes up a little part of the equation, but gas pressure takes the lead. Massive stars, on the other hand, have hundreds of times higher core temperatures, and radiation pressure takes over at these extremes. In the most massive stars, the mass of the star is supported against gravity primarily by radiation pressure, a situation which ultimately sets the upper limit for how massive a star can become.
Radiation pressure has an impact on other astronomical objects as well. The development of dust tails in comets in our Solar System is due to the pressure exerted by solar radiation. The creation of planetary nebulae is also influenced by radiation pressure. As the dying star shrinks down to a white dwarf, massive amounts of heat are released. The star's outer layers are pushed outwards, forming the surrounding gaseous nebula, due to the high radiation pressure.
The notion of solar sails is similarly based on the principle of radiation pressure. If the sail has a large enough reflective surface area and is made of sufficiently light material, the photons from the Sun should be able to exert enough pressure to move the spacecraft.
The force per unit area exerted by electromagnetic radiation is known as radiation pressure.
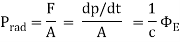
Where p is the momentum, c is the speed of light, and 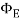 is then energy flux.
is then energy flux.
For relativistic particles, the radiation pressure P is related to the radiation density u by
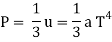
T is the temperature, while an is the radiation constant.
In the solar system, radiation pressure pushes particles of size ≈ 0.1 μm outward.s
Key takeaway:
- When photons are absorbed or reflected on a surface, momentum is transferred to the surface. Radiation pressure is the result of this momentum transfer. Radiation pressure is applied by electromagnetic radiation when the intensity (of a light beam) is divided by c. (speed of light).
- An electromagnetic wave's radiation pressure prad applied to a fully absorbing surface turns out to be equal to the wave's energy density: prad=u Perfect absorber
4.7.1 Wien's displacement law
Wien's displacement law describes one of the relationships between a black body's emission spectrum and temperature. It states that the lower the wavelength, the higher the temperature.λmax where the radiation curve achieves its pinnacle Photons with higher energy are associated with shorter wavelengths. To put it another way,λmax
Temperature and (peak wavelength) are inversely proportional.
The Stefan-Boltzmann law, like the Wien's law, takes into consideration the total power radiated by a body at any temperature. They both come from the Planck's distribution.
4.7.2 Wien's law formula
The equation describing Wien's law is very simple:
λmax = b / T,
Where:
- λmax is the aforementioned peak wavelength of light
- T is an absolute temperature of a black body
- b = 2.8977719 mm*K is the Wien's displacement constant
Although the relation between wavelength and frequency of electromagnetic waves is fairly simple (λ * f = c), we can't work out the peak frequency fmax by this analogy. The reason is that the spectral radiance is a sort of energy density function, so its shape and maximum depend on the argument (wavelength or frequency in our case). Knowing that the formula for the peak frequency is:
fmax = k * T,
Where k = 5.8789232 * 10¹⁰ Hz/K is a numerical constant.
The formula for Wien's law cannot be deduced from classical physics. Among the experiments that contributed to the establishment of quantum mechanics are several observations that validate this law (e.g., the photoelectric effect).
4.7.3 How to estimate the temperature of the Sun's surface? - example of use
Do you know how scientists can determine the temperature of items that are far away? Typically, they observe spectroscopically, fit the Planck function to the measurement, and acquire a temperature parameter as a result.
However, we can acquire a good estimate by using the Wien's displacement method.law to the results. Let's try to calculate the temperature of the Sun's surface:
- Find the peak wavelength of a solar spectrum. It's approximately λmax = 501.7 nm (or 5.017 * 10⁻⁷ m in the scientific notation).
- Transform the Wien's law formula to obtain the temperature: T = b / λmax = 2.8977719 mm * K / 501.7 nm = 5776 K.
The Wien's law is universal and can be a fairly good approximation for real objects, despite the fact that the black body is only an idealised model. You may also use this Wien's law calculator to calculate the temperature of any body, such as hot metal or lava, based on the hue of light it emits - see if the result surprises you!
4.8.1 Introduction:
Wien discovered a relationship between the monochromatic emittance of an ideal blackbody and its temperature based only on thermodynamic logic.
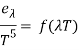
Where e is a blackbody's monochromatic emittance (emissive power) at wavelength and absolute temperature T, and f(T) is a function that cannot be derived only on thermodynamic grounds. Planck's formulation of f(T) in 1901 marked the start of modern quantum theory.
Take a look at Wien's law.
4.8.2 Wien’s distribution law (1896):
The energy of a black body in the wavelength interval, according to Wien, is given by
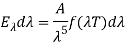
Wien discovered that the form of the function depends on the Maxwell-Boltzmann distribution law for the speed of atoms (or molecules) in a gas. 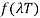 was
was
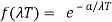
And so
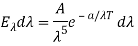
Where A and a were constants to be determined.
If we want to represent this in terms of frequency rather than wavelength, we must remember that, according to the wave equation., c = v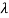 and so
and so 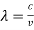 . But, we also need to rewrite d
. But, we also need to rewrite d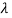 in terms of dv and to do this we write
in terms of dv and to do this we write
v = c/ → d
→ d = -c/ v2 dv
= -c/ v2 dv
The minus sign can be ignored because it just indicates that as the frequency increases, the wavelength decreases, and therefore substituting for 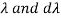 we can write that the energy in the frequency interval dv is given by
we can write that the energy in the frequency interval dv is given by
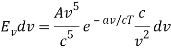
 where A’ and a’ are also just constants to be determined.
where A’ and a’ are also just constants to be determined.
4.8.3 Wien’s ‘law’ breaks down
On the short-wavelength side of the peak (what we now call the "Wien-side"), Wien's distribution rule showed good (but not perfect) agreement with the blackbody curve, as I'll illustrate next week. However, as long-wavelength experimental findings began to emerge from the PTR, it became evident that his "rule" did not apply there; it broke down on the long-wavelength side and exhibited very poor agreement with the actual observed curve.
Next week, in part 3 of this series, I'll explain how and why Planck became interested in the problem, as well as the solution he devised: the formula that would accurately define the blackbody spectrum and usher in the quantum era.
4.9.1 Saha’s Equation:
The mathematical relationship between the measured spectra of stars and their temperatures is known as the Saha equation. Meghnad N. Saha, an Indian astrophysicist, initially proposed the equation in 1920. It describes how the ionisation state of any given element in a star changes as temperature and pressure change. Because each atom or ion can absorb or emit radiation of a certain range of wavelengths, the spectrum of a star is directly related to the relative amount of atoms and ions it contains.
The Saha formula is
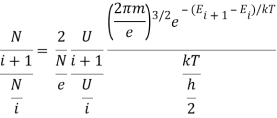
Where Ni + 1 and Ni are the number of atoms in the (i + 1)th and ith ionization states, respectively; Ui + 1 and Ui describe how energy is partitioned among the (i + 1)th and ith ionization states; Ei + 1 and Ei are the energies of the ionization states; Ne is the number of electrons; and T is the temperature. The other terms in the equation are physical constants: me stands for electron mass, k for Boltzmann constant, and h for Planck constant.
4.9.2 Derivation:
The thermal collisions of the atoms in a gas at a high enough temperature (here measured in energy units, i.e. keV or J) and/or density will ionise part of the atoms, resulting in an ionised gas. When several or more electrons in orbits around the atomic nucleus are released, they form an independent electron gas cloud that coexists with the surrounding gas of atomic ions and neutral atoms. As a result, an electric field is created, in which the motion of charges generates currents, creating a localised magnetic field, and resulting in the state of matter known as plasma.
As a function of temperature, density, and ionisation energies of the atoms, the Saha equation characterises the degree of ionisation for any gas in thermal equilibrium. The Saha equation is only valid for weakly ionised plasmas with a large Debye length. This means that other ions and electrons have little effect on the Coulomb interaction of ions and electrons. As a result, the following reduction in ionisation potentials and the "cutoff" of the partition function is minimal.
The Saha equation is expressed as follows for a gas made up of a single atomic species:
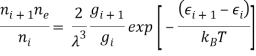
Where:
● 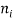 is the density of atoms in the i-th state of ionization, that is with i electrons removed.
is the density of atoms in the i-th state of ionization, that is with i electrons removed.
● 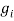 is the degeneracy of states for the i-ions
is the degeneracy of states for the i-ions
● 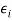 is the energy required to remove i electrons from a neutral atom, creating an i-level ion.
is the energy required to remove i electrons from a neutral atom, creating an i-level ion.
● 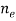 is the electron density
is the electron density
● λ is the thermal de Broglie wavelength of an electron
● 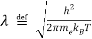
● 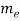 is the mass of an electron
is the mass of an electron
● T is the temperature of the gas
● h is Planck's constant
The expression (ϵi + 1 - ϵi) is the energy required to remove the (i + 1)th electron. In the case where only one level of ionization is important, we have n1 = ne and defining the total density n as n = n0 + n1 , the Saha equation simplifies to:
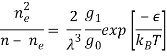
Where ϵ is the energy of ionization.
The Rayleigh-Jeans Radiation Law was an attempt to determine the functional form of thermal radiation spectra that was useful but not entirely successful. According to The Rayleigh-Jeans Radiation, the energy density uv per unit frequency interval at a frequency is

Where k is Boltzmann's constant, T is the radiating body's absolute temperature, and c is the speed of light in vacuum.
For low frequencies, this formula works well, but as the frequency gets higher, it starts to fail. The ultraviolet catastrophe was named after the formula's failure to match the new data. This faulty so-called law is significant because it establishes an asymptotic condition that other proposed formulas, such as Planck's, must meet. In Planck's thermal radiation formula, it lends a value to an otherwise arbitrary constant.
4.10.1 The Derivation
Consider a cube with an edge length L that reflects and re-reflects radiation off its walls. Standing waves form when an integral number of half-wave cycles fits inside a cube interval for radiation of a wavelength. This is required for radiation parallel to a cube's edge.

Where m is an integer or, equivalently
λ = 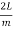 (3)
(3)
Consider an L-edged cube that reflects and re-reflects radiation off its walls. When an integral number of half-wave cycles fits inside a cube interval for wavelength radiation, standing waves arise. Radiation parallel to a cube's edge requires this.

Working with the quantity q, often known as the wavenumber, which is defined as

And hence

In terms of the cube's relationship,


And hence

The radian frequency (=2v) is another useful word. It follows from this that q=ω/c.
The requirement for a standing wave in the cube is that mX, mY, and mZ signify the integers for the three different directions in the cube.
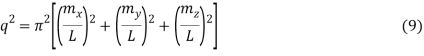
Which reduces to
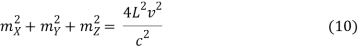
The goal now is to determine the number of nonnegative (mX, mY, mZ) combinations that fit between a sphere of radius R and one of radius R+dR. To begin, determine the number of combinations that do not violate the non-negativity criteria.
The volume of a spherical shell with inner radius R and outer radius R+dR can be calculated using the formula
DV = 4π R2dR (11)
If
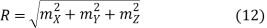
Then
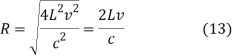
And hence

This means that
DV = 4π(2Lv/c)2(2L/c)dv = 32π(L3v2/c3)dv (15)
The non-negativity requirement for the combinations (mX, mY, and mZ) must now be considered. The nonnegative options in the two-dimensional example are roughly those in one circle quadrant. The matter of the combinations on the nonnegative quadrant's bounds gives rise to the approximation. Nonnegative combinations account for about one octant of the total in the three-dimensional example.Thus the number dN for the nonnegative combinations of (mX, mY, mZ) in this volume is equal to (1/8)dV and hence
DN = 4πv2dv (16)
Per degree of freedom, the average kinetic energy is½kT, The Boltzmann constant is k. Because kinetic and potential energy are identical in harmonic oscillators, the average energy per degree of freedom is kT. This means that the average radiation energy E per unit frequency can be calculated as follows:

Where the average energy density, uv, is calculated as follows:

The prior merely took into account one polarisation orientation for the radiation. If the two polarisation orientations are considered, a factor of 2 must be added to the above calculation; i.e.,

As the frequency approaches 0, the Raleigh-Jeans Law of Radiation holds empirically.
Key takeaway:
- Only for small v—that is, for long wavelengths—does the Rayleigh-Jeans law of radiation agree well with experiment. At long wavelengths (low frequencies), the Rayleigh–Jeans law coincides with experimental observations, but at short wavelengths, it significantly disagrees (high frequencies). The ultraviolet disaster is the name given to the discrepancy between observations and classical physics predictions.
4.11.1 Introduction:
Prior to Planck's idea, scientists attempted to use classical physics to describe the spectral brightness of electromagnetic radiation. The Rayleigh-Jeans law is an approximation based on classical physics.
The Rayleigh-Jeans law, like Planck's law, calculates a body's spectral brightness as a function of frequency v at absolute temperature T:
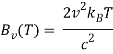
Where
- Bv(v,T) is the spectrum radiance density of frequency radiation per unit frequency at thermal equilibrium at temperature T (power per unit solid angle and per unit of area normal to propagation).
- The speed of light in a vacuum is c.
- The Boltzmann constant is kB.
- Is the electromagnetic radiation's frequency.
- T is the body's absolute temperature.
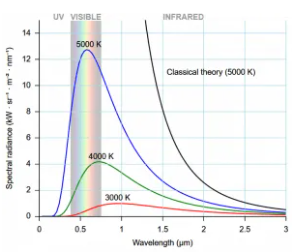
The ultraviolet catastrophe is the mistake in the Rayleigh–Jeans law (shown in the graph as “classical theory”) for the energy radiated by an ideal black-body at short wavelengths. The difference between the black curve (as anticipated by the Rayleigh–Jeans law) and the blue curve (as predicted by Planck's law) is the error, which is significantly more pronounced for short wavelengths.
At low frequencies (big wavelengths), the electromagnetic spectrum predicted by this formula fits with experimental observations, but at high frequencies, it substantially disagrees (short wavelengths). The ultraviolet catastrophe, also known as the Rayleigh–Jeans catastrophe, is a discrepancy between observations and classical physics predictions. Calculating the total amount of radiant energy (i.e., the sum of emissions in all frequency ranges) reveals that a blackbody would discharge an endless amount of energy, contradicting the law of conservation of energy.
The study of blackbody rules and the failure of classical physics to characterise them aided in the development of quantum mechanics' underpinnings. Max Planck, a German theoretical physicist, proposed a solution to this difficulty by introducing the rather unusual (at the time) concept that energy is radiated and absorbed in discrete “quanta” (or energy packets). The correct shape of the spectral distribution functions was determined by Planck's assumptions:
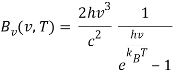
Where
- The spectral radiance Bv(v,T) (the power per unit solid angle and per unit of area normal to the propagation) At temperature T, the density of frequency radiation per unit frequency is at thermal equilibrium.
- The Planck constant is h.
- The speed of light in a vacuum is c.
- The Boltzmann constant is kB.
- Is the electromagnetic radiation's frequency.
- T is the body's absolute temperature.
Planck's quanta, which we now call photons, were real physical particles, not merely a mathematical fiction, according to Albert Einstein.
Synchrotron radiation is now widely used in a variety of scientific fields. Many research groups, particularly in the fields of physics, chemistry, and biology, rely heavily on the utilisation of this sort of radiation. A growing number of scientists are discovering that a few days of work at a synchrotron radiation source can give critical data to supplement their main laboratory-based study. The employment of X-ray diffraction and X-ray absorption fine-structure techniques in protein structure and materials characterisation are two of the best examples of this.
The expanding number of new synchrotron sources that have lately been established or are being planned or constructed — in many cases in nations where no such facilities previously existed, such as Brazil, Taiwan, Korea, India, and Switzerland – reflects synchrotron radiation's global applicability. Other countries, including as Japan, the United States, Italy, Germany, and Sweden, have recently established or are about to establish facilities, while the United Kingdom is contemplating whether to create a new DIAMOND source
The light emitted when very high-energy electrons or positrons are bent in magnetic fields is known as synchrotron radiation. The radiation has a broad spectrum range, ranging from infrared to “hard” X-rays with energy above 20 keV. The light is emitted in a narrow cone, allowing for the delivery of high quantities of photons to an experiment.
The light was collected “parasitically” from electron accelerators created and utilised for high-energy physics in the early days of synchrotron radiation research in the 1970s. The electrons were contained in a circular channel while being accelerated in these "first-generation" machines by bending magnets. The synchrotron radiation created by the electrons passing through these magnets could be retrieved without harming the particle scientists who were working on the equipment.
The “second-generation” sources from the 1980s are purpose-built electron storage rings in which the electrons are made to orbit the ring at a set kinetic energy once they have been accelerated. These storage rings feature beams with half-lives of up to 48 hours, making them a far more stable source of synchrotron radiation than previous machines. These, on the other hand, are still designed to take use of the radiation emitted by the bending magnets.
4.11.2 Third-generation sources
The most recent facilities, known as "third-generation" sources, make use of insertion devices. These are special magnetic structures that are put between the bending magnets on a storage ring's straight parts. They enable each beamline to have its unique set of spectral properties. Undulators and multipole wigglers are the two main types of insertion devices. They both use a linear array of alternating magnetic dipoles to cause the electron beam to undulate or wiggle along the supposedly straight track. Electromagnetic radiation is emitted by oscillating electrons.
A multipole wiggler emits radiation comparable to a standard bending magnet, but if the device has N pairs of magnetic dipoles, the total amount of light emitted is N times larger than a single bend. Another advantage of multipole wigglers is that their magnetic fields are typically stronger than those of bending magnets. This forces electrons to make tighter bends, resulting in more radiation being delivered at greater energy.
Undulators, on the other hand, have a smaller local field than wigglers. The radiation emitted at each equivalent point along the periodic oscillation trajectory, on the other hand, is temporally coherent, resulting in constructive interference. The emitted radiation has a pronounced peak at one photon energy – and higher harmonics of this energy – and is emitted in a cone that is even narrower than that of ordinary bending magnets.
Undulators, in particular, are particularly appealing radiation sources. Because of the narrow cone angle, the "spectral brilliance" – the number of photons per unit area per unit solid angle – is quite high, while the radiation's harmonic character means that a significant quantity of radiation power is concentrated at the wavelength of interest. The photon energy at which this peak power is created, on the other hand, is directly tied to the magnetic array's spatial period, and while this energy may be modified by adjusting the magnetic-field strength, the range is very restricted. An undulator can often deliver high-brilliance radiation with a photon-energy range of no more than 20-40. The tuning range accessible from the bending-magnet synchrotron radiation continuum is substantially narrower. In other words, because machine energy is so well matched to the photon energies of interest, it is critical for third-generation sources.
4.11.3 Missing spectral regions
The scientific community requires synchrotron radiation sources with a wide range of characteristic machine energies because undulators produce only a restricted band of photon energy. The issue is that all of the new synchrotron sources are grouped around only two different energy values. The 6 GeV European Synchrotron Radiation Facility in Grenoble, France, the 7 GeV Advanced Photon Source at the Argonne National Laboratory in the United States, and the 8 GeV Super Photon Ring in Harima Science Garden City, Japan are among the new sources optimised to produce X-rays with energies of 2-50 keV. Then there are sources with machine energies ranging from 1.2 to 2 GeV that produce undulator radiation in the 50-2000 eV range. Two more planned machines (DIAMOND in the UK and SOLEIL in France) will have energies in the middle, while multipole wigglers at all of these sites will provide access to even higher photon energies.
The absence of any efforts to create third-generation sources specialised for lower-energy vacuum ultraviolet (VUV) radiation, particularly in the 5-50 eV range, is notable. The machine energy of these sources would be around 0.5 GeV. To make matters worse, numerous existing second-generation machines that are heavily used in this photon-energy range are expected to be shut down as the new facilities come online, primarily due to operating expenses.
The problem is especially apparent in Europe, where one may expect national scientific policy to be properly coordinated in this area. However, four third-generation devices with energies ranging from 1.2 to 2.0 GeV are either operational or under construction. The ELETTRA source in Trieste, Italy, the MAX II source in Lund, Sweden, the BESSY II source in Berlin, Germany, and the Swiss Light Source in Villingen are among them. Meanwhile, the BESSY lab has stated that its second-generation source, BESSY I, will be shut down in 2000, with the process beginning later this year. SUPER-ACO in Orsay, France, is likewise rumoured to be shutting down shortly after SOLIEL development is set to begin.
4.11.4 Beamline closures
As a result, it appears that in the next five years or so, there will be a significant rise in the quantity and quality of synchrotron radiation facilities that produce photons with energies more than around 50 eV, but a significant decrease in lower-energy beamlines. It's perhaps ironic that the Birgeneau committee in the United States recently concluded – in connection with the Advanced Light Source, a new 1.5-1.9 GeV third-generation facility in Berkeley – that the number of important scientific issues requiring "soft X-ray" sources (photons with energies of 500-2000 eV) has decreased in recent years compared to those requiring higher-energy hard X-ray sources (Physics World November 1997).
At the absolute least, we believe that the loss of vacuum-ultraviolet facilities and the failure to fully use the potential of third-generation sources in this energy range is exceedingly foolish. After all, there is essential science to be done. Angle-resolved photoemission in this energy range has provided some of the clearest evidence on the nature of high-temperature superconductivity, a technique that allows the occupied electronic bands to be mapped directly. For example, German researchers led by Jörg Fink recently identified two Zhang-Rice singlet states associated with different cuprate sublattices of Ba2Cu3O4Cl2 using the BESSY source (1997 Phys. Rev. Lett . 78 4107). Such tests necessitate the high flux and spectrum resolution that undulator sources provide. VUV radiation is also an excellent source of photons for molecular photochemistry and a better knowledge of atomic physics. For example, a group of British and German scientists led by Hans Kleinpoppen and Uwe Becker recently investigated the magnetic dichroism in atomic oxygen photoemission (1996 Phys. Rev. Lett. 77 2642).
One popular misconception is that synchrotron radiation in this energy range is unnecessary since lasers can now – or will soon – provide far better sources for these studies. It's a misconception since synchrotron radiation and lasers have essentially different, though complementary, features. Synchrotron radiation provides a high average power and a time structure that is effectively continuous for most experiments, and it can be controlled over a wide range of energies. Lasers, on the other hand, have far higher immediate power and spectral resolution, but their tunability is limited or slow. Without severe restrictions, only a few tests could be transmitted between these two sorts of sources.
Planck's radiation law is a mathematical formula proposed by German scientist Max Planck in 1900 to describe the spectral-energy distribution of radiation emitted by a blackbody (a hypothetical body that completely absorbs all radiant energy falling upon it, reaches some equilibrium temperature, and then reemits that energy as quickly as it absorbs it). Planck hypothesised that the sources of radiation are oscillating atoms, and that each oscillator's vibrational energy can take any of a number of discrete values, but never any value in between. Planck also assumed that when an oscillator switches from one state of energy E1 to another of lower energy E2, the discrete amount of energy E1 E2, or quantum of radiation, is equal to the product of the frequency of the radiation, symbolised by the Greek letter v, and a constant h, now known as Planck's constant, which he calculated from blackbody radiation data.i.e., E1 − E2 = hν.
Planck’s law for the energy Eλ radiated per unit volume by a cavity of a blackbody in the wavelength interval λ to λ + Δλ (Δλ denotes an increment of wavelength) can be written in terms of Planck’s constant (h), the speed of light (c), the Boltzmann constant (k), and the absolute temperature (T):
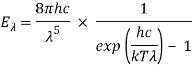
The emitted radiation's wavelength is inversely proportional to its frequency, orλ = c/ν. The value of Planck’s constant is defined as 6.62607015 × 10−34 joule∙second.
The majority of the radiation emitted by a blackbody at temperatures up to several hundred degrees is in the infrared region of the electromagnetic spectrum. At higher temperatures, the total radiated energy rises, and the intensity peak of the emitted spectrum moves to shorter wavelengths, resulting in visible light being released in greater amounts.
1. Wien’s Distribution law:
The energy of a black body in the wavelength interval, according to Wien, is given by
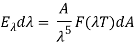
Wien discovered that the form of the function depends on the Maxwell-Boltzmann distribution law for the speed of atoms (or molecules) in a gas.  was
was
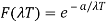
And so
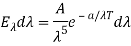
Where A and a were constants to be determined.
If we want to describe this in terms of frequency rather than wavelength, we must recall that, according to the wave equation, c = V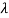 and so
and so 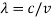 . But, we also need to rewrite d
. But, we also need to rewrite d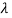 in terms of dv and to do this we write
in terms of dv and to do this we write
v= c/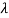 → d
→ d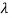 = -c/v2 dv
= -c/v2 dv
The minus sign can be ignored because it just indicates that as the frequency increases, the wavelength decreases, and therefore substituting for λ and dλ we can write that the energy in the frequency interval dv is given by
Ev dv = 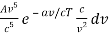
Ev dv = A’v3e-a’v/T dv
Where A’ and a’ are also just constants to be determined.
2. Rayleigh Jeans Law:
The Derivation
Consider a cube with an edge length L that reflects and re-reflects radiation off its walls. Standing waves form when an integral number of half-wave cycles fits inside a cube interval for radiation of a wavelength. This is required for radiation parallel to a cube's edge.

Where m is an integer or, equivalently
λ =  (3)
(3)
Consider an L-edged cube that reflects and re-reflects radiation off its walls. When an integral number of half-wave cycles fits inside a cube interval for wavelength radiation, standing waves arise. Radiation parallel to a cube's edge requires this.

Working with the quantity q, often known as the wavenumber, which is defined as

And hence

In terms of the cube's relationship,


And hence

The radian frequency (=2v) is another useful word. It follows from this that q=ω/c.
The requirement for a standing wave in the cube is that mX, mY, and mZ signify the integers for the three different directions in the cube.

Which reduces to

The goal now is to determine the number of nonnegative (mX, mY, mZ) combinations that fit between a sphere of radius R and one of radius R+dR. To begin, determine the number of combinations that do not violate the non-negativity criteria.
The volume of a spherical shell with inner radius R and outer radius R+dR can be calculated using the formula
DV = 4π R2dR (11)
If
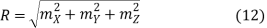
Then
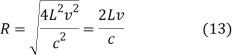
And hence

This means that
DV = 4π(2Lv/c)2(2L/c)dv = 32π(L3v2/c3)dv (15)
The non-negativity requirement for the combinations (mX, mY, and mZ) must now be considered. The nonnegative options in the two-dimensional example are roughly those in one circle quadrant. The matter of the combinations on the nonnegative quadrant's bounds gives rise to the approximation. Nonnegative combinations account for about one octant of the total in the three-dimensional example.Thus the number dN for the nonnegative combinations of (mX, mY, mZ) in this volume is equal to (1/8)dV and hence
DN = 4πv2dv (16)
Per degree of freedom, the average kinetic energy is½kT, The Boltzmann constant is k. Because kinetic and potential energy are identical in harmonic oscillators, the average energy per degree of freedom is kT. This means that the average radiation energy E per unit frequency can be calculated as follows:
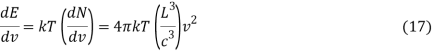
Where the average energy density, uv, is calculated as follows:

The prior merely took into account one polarisation orientation for the radiation. If the two polarisation orientations are considered, a factor of 2 must be added to the above calculation; i.e.,

As the frequency approaches 0, the Raleigh-Jeans Law of Radiation holds empirically.
3. Stefan Boltzmann Law
Integrating Plank's radiation formula yields the total power radiated per unit area over all wavelengths of a dark body. As a function of wavelength, the radiated power per unit area is:
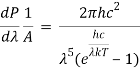
Where,
- P stands for radiated power.
- A is the blackbody's surface area, and is the wavelength of emitted radiation.
- Planck's constant is h.
- The speed of light is denoted by c.
- Boltzmann's constant is k.
- T stands for temperature.
When the Stefan Boltzmann equation is simplified, we get:

On integrating both sides in terms of and applying the restrictions that we obtain;
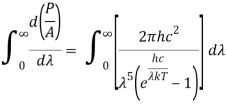
After removing the constants, the integrated power is:
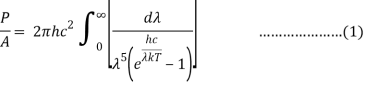
Analytically, this can be solved by substituting:
x = 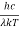
Therefore, dx = - 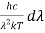
⇒ h = 
⇒ c = 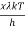
⇒ dλ = - 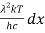
As a result of substituting them in equation (1)
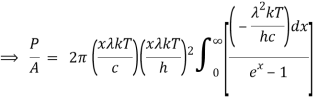
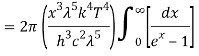
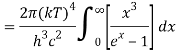
The following equation is equivalent to the conventional form of integral:
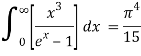
As a result of replacing the above result, we obtain
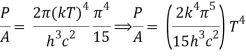
We get, when we simplify it even more,
⇒ P/A = σ T4
As a result, we arrive at a mathematical representation of Stephen Boltzmann's law:
⇒ε = σT4
Where,
ε = P/A
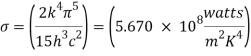
The behaviour of gases at low temperatures could be effectively expressed using this quantum mechanical result.
4. Wien’s Displacement Law from Planck’s Law:
The blackbody radiation curve at different temperatures peaks at a wavelength that is inversely proportional to the temperature, according to Wien's displacement law. The Planck radiation law, which specifies the spectrum brightness of black body radiation as a function of wavelength at any given temperature, causes that peak to shift. Wilhelm Wien had discovered it some years before Max Planck produced the more general equation, and it describes the full change of the spectrum of black body radiation toward shorter wavelengths as temperature rises.
Planck's law is used to derive Wien's displacement law. Follow these steps:
ρ(v, T) = 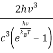 (1)
(1)
To get the peak wavelength, we must evaluate the derivative of Equation 1 with respect to v and set it to zero.
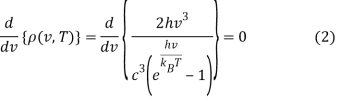
This can be solved via the quotient rule or product rule for differentiation. If you choose the latter, you'll need to rewrite Equation 2 as a product:
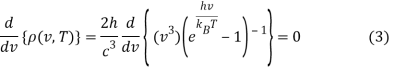
The application of the product rule (and power rule and chain rule)

As a result, when this expression is zero,

Or when simplified
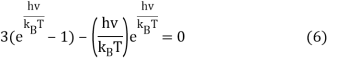
We can do a substitution u=hνkBT and Equation 6 becomes
3(eu – 1) – ueu = 0 (7)
Using Lambert's W-functions to find the solutions to this equation yields numerical data in
u = 3 + W(-3e-3 ) ≈ 2.8214 (8)
So unsubstituting the u variable
u = 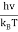 ≈ 2.8214 (9)
≈ 2.8214 (9)
Or
v ≈ 2.8214 kBT/h (10)
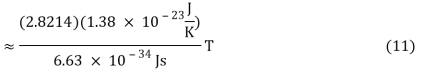
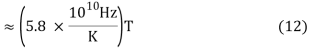
As a result, the shape of the blackbody radiation function would shift in frequency proportionately to temperature. Wien's constant was not explicitly included in Max Planck's later formulation of the accurate blackbody radiation function. Planck's constant h, on the other hand, was invented and incorporated into his new formula. Wien's constant (Equation 9) can be calculated using Planck's constant h and the Boltzmann constant k.
References:
1. Statistical Mechanics, B.K.Agarwal and Melvin Eisner (New Age Inter-national)-2013
2. Thermodynamics, Kinetic Theory and Statistical Thermodynamics: Francis W.Sears and Gerhard L. Salinger (Narosa) 1998
3. Statistical Mechanics: R.K.Pathria and Paul D. Beale (Academic Press)- 2011