Unit - 1
Chemical thermodynamics
Thermodynamic properties can be divided into 2 (two) general classes such as intensive and extensive properties.
An intensive property, is the system’s physical property that does not depend on the size or the amount of material in the system. In contrast the extensive property of a system is not dependent on the system size or the amount of the material. According to the definitions, density, pressure and temperature are intensive properties and volume, internal energy are extensive properties.
Symbols for representing properties: Extensive properties are symbolized by upper case (capital) letter such as V (volume), KE (kinetic energy), PE (potential energy), etc. Intensive properties are symbolized by lower case letters such as v (specific volume), ke (specific kinetic energy), e, u (specific internal energy), h (specific enthalpy), etc. Mole based properties are symbolized by lower case letters with overbars. For example, kinetic energy and molar specific potential energy respectively.
State and Path functions
In thermodynamics it is very important to differentiate between exact and inexact differentials. The common terms in thermodynamics variables such as the internal energy (UU), volume, pressure, and temperature, and entropy (SS) and free energy (GG).
All these variables are used to specify the state of a system. These properties are not dependent on the way the system works but is used to specify the properties of the current state of the system. For example, if a system consists of 1 mol of Heat 298 K and 1 atm, the system regardless of its history will have variable such as internal energy, entropy, free energy. If the system is compressed at 2atm or is heated in gas from 273K, all this becomes irrelevant to specify the pressure, entropy, etc, because all these variables are called state functions. State functions depend only on the state of the system.
Other quantities such as work (ww) and heat (qq), on the other hand, are not state functions. There is nothing like the work done or the heat in a system.in a process the amount of heat and work that is flowing in the system that connects specified initial and final states depend on how the process is carried out. Quantities that depend on the path followed between states are called path functions.
How is all this connected to differentials? Quantities whose values are independent of path are called state functions, and their differentials are exact (dPdP, dVdV, dGdG, dTdT...). Quantities that depend on the path followed between states are called path functions, and their differentials are inexact (dwdw, dqdq). When we integrate an exact differential, the result depends only on the final and initial points, but not on the path chosen. However, when we integrate an inexact differential, the path will have a huge influence in the result, even if we start and end at the same points.
Knowing that a differential is exact will help you derive equations and prove relationships when you study thermodynamics in your advanced physical chemistry courses. For example, you will learn that all the state functions we mentioned above are related through these equations:
DU=TdS−PdV
DH=TdS+VdP
DA=−SdT−PdV
DG=−SdT+VdP
Here, we introduced two new state functions: the enthalpy (HH), and the Helmholtz free energy (AA). They are state functions, just as the entropy and the free energy. Explicitly, T, P, VT, P, V and SS are not constants. When discussed about gases, we learned that P, VP, V and TT are not independent functions. If two of these variables are changed the third, or in other words, we cannot independently vary the pressure, volume and temperature. The equation of state tells you how the three variables depend on each other.
For one mole of gas, the equation of state as a function can be written as
P=P (V, T) P=P (V, T), or as a function V=V (T, P) V=V (T, P), or as a function T=T (P, V) T=T (P, V).
In the same way, you cannot independently change the pressure, volume, temperature and entropy of a system. If you modify the pressure and temperature, the volume and entropy will change as well. To make this clear, we can re-write the equations above as:
DU=T (S, V) dS−P (S, V) dV
DH=T (S, P) dS+V (S, P) dP
DA=−S (T, V) dT−P (T, V) dV
DG=−S (T, P) dT+V (T, P) dP
H, AU, H, A and GG are all state functions, their differentials are exact. We can derive a few relationships just from this fact.
For example, we see that G=G (T, P) G=G (T, P), and because it’s total differential, by definition, is:
DG=(∂G∂T) PdT+(∂G∂P) TdP
We rapidly conclude that
(∂G∂T) P=−S(∂G∂T) P=−S
And
(∂G∂P) T=V(∂G∂P) T=V
With minimal math, we concluded that if we change the pressure of a system at constant temperature, the rate of change of the free energy equals the volume. At this point this does not mean so much, but can hopefully appreciate how knowing that GG is a state function is enough for you to derive a thermodynamic relationship!
−(∂S∂P) T=(∂V∂T) P
We derived this equation from the knowledge that GG is a state function. Why are these equations useful? Let’s see an example We can integrate this expression with TT constant to get:
∫P2P1dS=ΔS=−∫P2P1(∂V∂T) PdP (constantT)
This equation tells you that the change in entropy in a system can be calculated by integrating (∂V∂T) P(∂V∂T) P data. This is extremely powerful, as we can easily measure temperature, pressure and volume in the lab, but we don’t have an instrument that directly measures entropy!
There are three types of systems in thermodynamics: open, closed, and isolated.
- An open system is a system where the heat and matter are exchanged with the surrounding. The stovetop example would be an open system, because heat and water vapor can be lost to the air.
- A closed system, on the contrary, this system will exchange only energy with its surroundings, not matter, if the pot is tightly fitted with a lid would be a good example for closed system.
- An isolated system is one that cannot exchange either matter or energy with its surroundings. A perfect isolated system is hard to come by, but an insulated drink cooler with a lid is conceptually similar to a true isolated system. The items inside can exchange energy with each other, which is why the drinks get cold and the ice melts a little, but they exchange very little energy (heat) with the outside environment.
- The system that doesn’t exchange energy, or matter with the surroundings is called an isolated system. The Zeroth law of thermodynamics states that thermodynamic processes have no effect on the energy of the system.
Example: Reactants present in a thermos flask or an insulated vessel, where neither energy nor the matter is exchanged with the environment.
Internal energy
Heat (q)
Thermal energy refers to the energy that is produced from heat, this heat is generated by the tiny particle movement present within an object. The faster the movement of particles, the heat generated will be more.
Internal Energy(U)
An energy form inherent in every system is the internal energy, which arises from the molecular state of motion of matter. The symbol U is used for the internal energy and the unit of measurement is the joules (J).
Internal energy U of a body or a system, that has well defined boundaries, refers to the total kinetic energy formed by the motion of molecules and the potential energy associated with the vibrational motion and electric energy of atoms within molecules. Internal energy also takes into account all the chemical bonds. From a microscopic point of view, the internal energy may be found in many different forms. For any material or repulsion between the individual molecules.
Internal energy is a state function of a system and is an extensive quantity.
Work (w)
In thermodynamics, work performed by a system is the energy transferred by the system to its surroundings. Work is a form of energy; however, the energy is in transit. Here the work includes the process that is completed by the system or on a system. In general, work is defined for mechanical systems as the action of a force on an object through a distance.
W = F.d
Where:
W = work (J)
F = force (N)
d = displacement (m)
A thermodynamic system in an equilibrium state possesses a state variable known as the internal energy(E). Between two systems the change in the internal energy is equal to the difference of the heat transfer into the system and the work done by the system.
The first law of thermodynamics states that the energy of the universe remains the same. Though it may be exchanged between the system and the surroundings, it can’t be created or destroyed. The law basically relates to the changes in energy states due to work and heat transfer. It redefines the conservation of energy concept.
First Law of Thermodynamics
The First Law of Thermodynamics states that heat is a form of energy, and thermodynamic processes are therefore subject to the principle of conservation of energy. This means that heat energy cannot be created or destroyed. It can, however, be transferred from one location to another and converted to and from other forms of energy.
First Law of Thermodynamics Equation
The equation for the first law of thermodynamics is given as;
ΔU = q + W
Where,
ΔU = change in internal energy of the system.
q = algebraic sum of heat transfer between system and surroundings.
W = work interaction of the system with its surroundings.
Enthalpy
Enthalpy is the measurement of energy in a thermodynamic system. The quantity of enthalpy equals the total content of heat of a system, equivalent to the system’s internal energy plus the product of volume and pressure.
In thermodynamics, the enthalpy is the measure of energy in a thermodynamic system. It is the thermodynamic quantity equivalent to the total heat content of a system
The Heat of Reaction (also known and Enthalpy of Reaction), occurs in the constant pressure, it is the change in the enthalpy of a chemical reaction.
Enthalpy is a state function and a thermodynamic unit for measurement. The enthalpy is used to calculate the amount of energy per mole that is either produced or released in the reaction. Since enthalpy is derived from pressure, volume, and internal energy, all of which are state functions.
When a process begins at constant pressure, the evolved heat (either absorbed or released) equals the change in enthalpy.
Enthalpy change is the sum of internal energy denoted by U and product of volume and Pressure, denoted by PV, expressed in the following manner.
H=U+PV
Enthalpy is also described as a state function completely based on state functions P, T and U. It is normally shown by the change in enthalpy (ΔH) of a process between the beginning and final states.
ΔH=ΔU+ΔV
If the pressure and temperature don’t change throughout the process and the task is limited to pressure and volume, the change in enthalpy is given by,
ΔH=ΔU+PΔV
The flow of heat (q) at constant pressure in a process equals the change in enthalpy based on the following equation,
ΔH=q
Any Enthalpy of a reaction is dependent on its physical conditions of the surroundings such as pressure, temperature etc. In order to specify the standard enthalpy of any reaction, the standard enthalpy of a reaction is calculated when the components that participate in the reaction are in standard form, the components include reactants and products.
Heat capacities
The heat capacity of a substance can be defined as the amount of heat required to change its temperature by one degree.
Thermodynamics in mainly concerned with heat, earlier heat was considered as a measure of an invisible fluid, caloric and present in any matter. The ability of a substance to hold this fluid was earlier referred to as the heat capacity of the system, the meaning however of today is that heat capacity is energy in transit. The development in thermodynamics and dependence of heat transfer on temperature changed the definition of heat.
Modern thermodynamics defines heat as the measure of the total internal energy of a system. In order to quantify the heat energy associated with matter and its dependence on temperature, two properties were defined. These properties were named as specific heat capacity and heat capacity of the system.
Heat Capacity Formula
- Heat energy is the measure of the total internal energy of a system. Which includes the potential energy of the molecules and the total kinetic energy of the system and the potential energy of the molecules.
- It has been seen that the internal energy of a system can be changed by either supplying heat energy to it, or doing work on it.
- The internal energy of a system is found to increase with the increase in temperature. The increase in the internal energy depends on the amount of matter and the temperature differences. Etc.
- Therefore, heat capacity is defined as the amount of heat energy required to raise the temperature of a given quantity of matter by one degree Celsius.
- Heat capacity for a given matter depends on its size or quantity and hence it is an extensive property. The unit of heat capacity is joule per Kelvin or joule per degree Celsius.
Mathematically,
Q=CΔT
Where Q is the heat energy required to bring about a temperature change of ΔT and C is the heat capacity of the system under study.
Specific Heat Capacity
For thermodynamic studies the scientists wanted a quantity that did not depend on the quantity or size of matter, this led to Specific heat capacity. The Heat capacity is an intensive property, as it depends on the size and quantity of matter. Specific heat capacity for any substance or matter can be defined as the amount of heat energy required to raise the temperature of a unit mass of that substance by one degree Celsius. Mathematically it is given as:
Q=msΔT
Here Q is the amount of heat energy required to change the temperature of m (kg) of a substance by ΔT, s is the specific heat capacity of the system.
Thermodynamics continues to play a vital role in our lives directly or indirectly. Scientists and engineers use the laws of thermodynamics to design new processes for reactions that would have high efficiency and product yield. Chemical and mechanical engineers apply the concepts of thermodynamics for designing heat engines with high efficiency and better outputs.
Relation between Cp and Cv
As the body absorbs heat the temperature of the body rises, but when heat is withdrawn from the body it cools down, so the heat of the body decreases. The temperature of any body is the measure of its molecule’s kinetic energy. Heat capacity is the ratio of heat absorbed by a material to the temperature change. Therefore, the temperature change in a body is directly proportional to the heat transferred to the given body.
Definition of Molar heat capacity
The total amount of energy in the form of heat needed to increase the temperature of 1 mole of any substance by 1 unit is called molar heat capacity(C) of that substance. It also depends greatly on the nature, size and composition of a substance in a system.
q=n C ΔT
q is the heat supplied or needed to bring about a change in temperature(ΔT) in 1 mole of any given substance.
n is the amount of moles; the constant C is known as the molar heat capacity of the body of the given substance.
Cp: in a system, Cp is the amount of heat energy released or absorbed by a unit mass of the substance with the change in temperature at a constant pressure.in other words, under constant pressure it is the heat energy transfer between a system and the surroundings. So, Cp represents the molar heat capacity, C when pressure is constant. The change in temperature will always cause a change in the enthalpy of the system.
Enthalpy (ΔH) is the heat energy absorbed or released by the system, furthermore enthalpy change occurs during the change of phase or state of a substance.
For example, when a solid change to its liquid form (i.e., the change from ice to water) enthalpy change is called the heat of fusion. When a liquid change to its gaseous form (i.e., the change from water-to-water vapour) the enthalpy change is called the heat of vaporisation.
The system absorbs or releases heat without the change in pressure in that substance, then its specific heat at constant pressure, Cp can be written as:
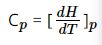……………………….1
Where Cp represents the specific heat at constant pressure; dH is the change in enthalpy; dT is the change in temperature.
Cv: During a small change in the temperature of a substance, Cv is the amount of heat energy absorbed/released per unit mass of a substance, where volume does not change, in other words Cv is the heat energy transfer between a system and its surroundings, without any change in the volume of the system.
Cv represents the molar heat capacity C when the volume is constant. Under a constant volume, the volume of a substance does not change, so the change in volume is zero.
As the term is related to the internal energy of a system, which is total of both potential energy and kinetic energy of that system. The system absorbs or releases heat without change in volume of that substance, then its specific heat at constant volume Cv can be
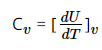………………………………….2
Where Cv represents the specific heat at constant volume, dU is the small change in the internal energy of the system; dT is the change in temperature of the systems.
Relationship between Cp and Cv
According to the first law of thermodynamics:
ΔQ= ΔU+ΔW where ΔQ is the amount of heat that is given to the system, ΔU is the internal energy and ΔW is the work done.
Therefore, we write
ΔQ=ΔU+PΔV as ΔW= PΔV……………………………3
Since ΔQ= nCpΔT and ΔU = nvCΔT
Therefore nCpΔT = nCpΔT + PΔV
We know that PV=nRT)
At T1 kelvin PV1=nRT1………………(a)
The following relationship can be given considering the ideal gas behaviour of a Gas.
Cp-Cv = R
Where R is the universal gas constant.
Calculations of q, w, U and H for reversible, irreversible and free expansion of gases (ideal and van der Waals) under isothermal and adiabatic conditions
The ideal gas law is the equation of state of a hypothetical gas, as illustrated in the figure, for an ideal gas there is no molecule-molecule interaction is present and only elastic collisions are allowed, although there are several limitations, it has a good approximation to the behaviour of various gases under different conditions. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle’s law and Charles’ law.
Atoms and Molecules in a Gas, are typically and widely separated as shown in the diagram, because the forces between them are quite weak at these distances, they are often described by the ideal gas law.
Empirical Derivation
Boyle’s law states that pressure P and volume V of a given mass of confined gas are inversely proportional:
While Charles’ law states that volume of a gas is proportional to the absolute temperature T of the gas at constant pressure
V∝T.
By combining the two laws, we get
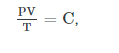
Where C is a constant which is directly proportional to the amount of gas, n (representing the number of moles).
The proportionality factor is the universal gas constant, R, i.e., C = nR.
Hence the ideal gas law
PV=nRT.
Equivalently, it can be written as PV=NkT,
Where k is Boltzmann’s constant and N is the number of molecules.
(Since N = nNA, and see that R=NAk, where NA is Avogadro’s number.)
The microscopic details are not considered by the empirical derivation However, the equation is therefore derived from the first principles of thermodynamics. (which goes beyond the scope of this Atom).
Microscopic version
We have seen in the Atom on “Origin of Pressure” that
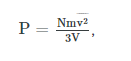where P is the pressure, N is the number of molecules, m is the mass of the molecule, v is the speed of molecules, and V is the volume of the gas. Therefore, we derive a microscopic version of the ideal gas law
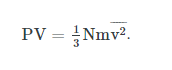
Isotherms
An isothermal process is a change of a system in which the temperature remains constant: ΔT = 0.
An isothermal process is a change in the system in which the temperature remains constant: ΔT=0. This occurs typically when a system is in contact with an outside thermal system such as heat bath, and the change occurs slowly enough to allow the system to adjust continually to the temperature of the reservoir through heat exchange.
In contrast, an adiabatic process occurs when a system exchanges no heat with its surroundings (Q=0), in ither words in an isothermal process, the value ΔT=0 but Q=0, while in an adiabatic process ΔT = 0 but Q = 0
For an ideal gas, the product PV (P: pressure, V: volume) is a constant if the gas is kept at isothermal conditions (Boyle’s law). According to the ideal gas law, the value of the constant is NkT, where N is the number of molecules of gas and k is Boltzmann’s constant.
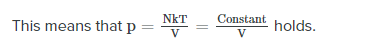
The family of curves generated by this equation is shown in the graph presented in. Each curve is called an isotherm. Such graphs are termed indicator diagrams first used by James Watt and others to monitor the efficiency of engines. The temperature corresponding to each curve in the figure increases from the lower left to the upper right.
Isotherm of an ideal gas: several isotherms of an ideal gas on a PV diagram.
Calculation of Work
In thermodynamics, the work involved when a gas changes from state A to state B is simply:
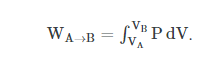
(This equation is derived in our Atom on “Constant Pressure” under kinetic theory. Note that P = F/A. This definition is consistent with our definition of work being force times distance.)
For an isothermal, reversible process, this integral equal the area under the relevant pressure-volume isotherm, and is indicated in blue in for an ideal gas. Again, P = nRT / V applies and with T being constant (as this is an isothermal process), we have:
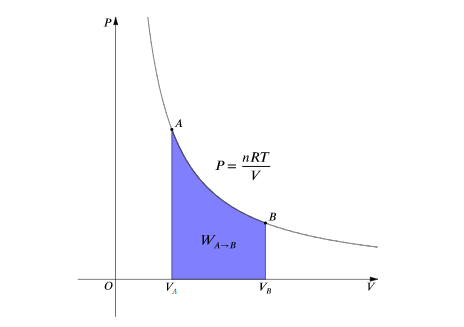
Work done by gas during expansion: The blue area represents ‘work’ done by the gas during expansion for this isothermal change.
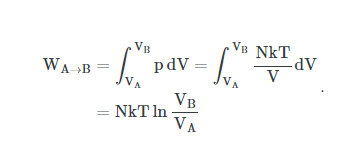
By convention, work is defined as the work the system does on its environment. If, for example, the system expands by a piston moving in the direction of force applied by the internal pressure of a gas, then the work is counted as positive. As this work is done by using internal energy of the system, the result is that the internal energy decreases. Conversely, if the environment does work on the system so that its internal energy increases, the work is counted as negative.
Difference Between Isothermal and Adiabatic Process
Following is the table explaining the isothermal vs adiabatic process:
Isothermal process | Adiabatic process |
An isothermal process is defined as one of the thermodynamic processes which occur at a constant temperature | An adiabatic process is defined as one of the thermodynamic processes which occur without any heat transfer between the system and the surrounding |
Work done is due to the change in the net heat content in the system | Work done is due to the change in its internal energy |
The temperature cannot be varied | The temperature can be varied |
There is a transfer of heat | There is no transfer of heat |
Relation between P-V, V-T and P-T for ideal gas
We will be deriving the relation between P, V and T using first the law of thermodynamics which states that heat supplied to the system is capable of doing work when heat absorbed by the system is equal to the sum of the increase in internal energy and the external work done on the surrounding by the system.
An essential condition is that
The system and surrounding must not be exchanging heat for which the walls should be insulated.
The process of expansion and compression so that the system should not be able to exchange heat with surroundings.
Relation between P and V
According to First law of thermodynamics
DQ = dU+ dW
For 1 mole of gas
DU= CvdT
DW = PdV
For adiabatic process dQ = 0
DQ =dU+dW
0=Cv dT+P dV
According to ideal Gas equation
PV= RT, differentiating on both sides we get
P dV+ V dP= R dT
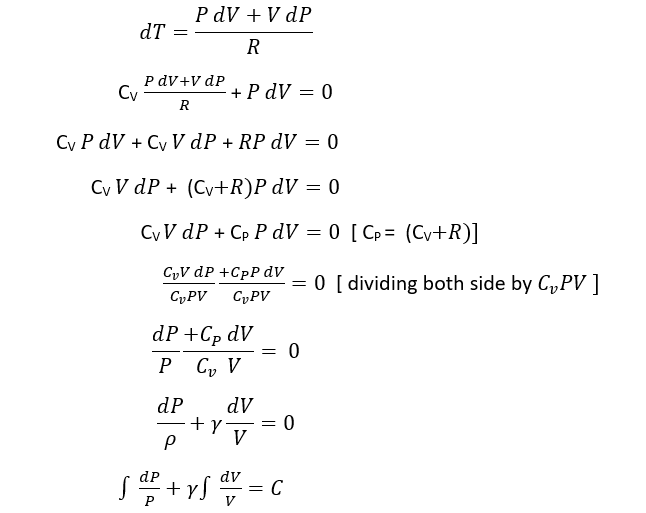
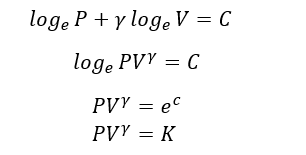
K is constant
This Equation gives the relationship between P and V of an ideal gas
Relation between P and T
We know that PV= RT for 1 mole of a gas
This equation gives the equation for P and T
Relation between V and T
We know that PV= RT for 1 mole of a gas
This equation gives the relation for V and T
Adiabatic processes for ideal gas
Adiabatically when an ideal gas is compressed, (Q=0) its temperature generally increases: when we consider an adiabatic expansion process, the ideal gas does not work and the temperature decreases, a few adiabatic compressions examples include compression occur in the cylinder of a car, where the gas-air mixture take place so quickly that there is no time for the mixture to exchange heat with its environment.
The figure below shows the adiabatic process in the free expansion of a gas, that is confined by a membrane to one side of a two-compartment that is thermally insulated container. When the membrane is punctured, the gases rushes to the other side of the container and therefore expand freely, Because the gas expands “against a vacuum” (p=0), it does no work, and because the vessel is thermally insulated, the expansion is adiabatic.
With Q=0 and W=0W=0 in the first law, ΔEint=0, ΔEint=0, so
Eint i = Eint f for free gas expansion.
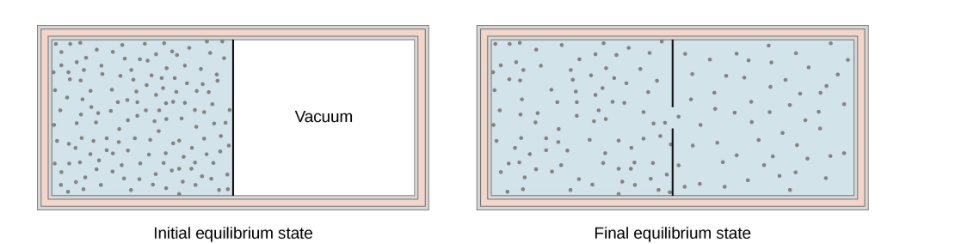
The gas in the left chamber expands freely into the right chamber when the membrane is punctured.
If the gas is ideal, the internal energy depends only on the temperature. Therefore, when an ideal gas expands freely, its temperature does not change.
Adiabatic reversible expansion of ideal gas
In an Adiabatic process no heat enters or leaves the system, therefore, for a reversible adiabatic process the first law takes the form
DU = − PdV
CV = (∂U/∂T)V (when the, molar heat capacity is taken into account)
But the internal energy of an ideal gas depends only on the temperature and is independent of the volume (because there are no intermolecular forces), and so, for an ideal gas,
CV = dU/dT, and so we have dU = CVdT.
Thus, for a reversible adiabatic process and an ideal gas,
CVdT = −PdV. (The minus sign shows that as V increases, T decreases, as expected.) But for a mole of an ideal gas,
PV = RT = (CP − CV) T, or P = (CP − CV) T/V.
Therefore
CvdT=−(CP−CV) TdV/V
Separate the variables and write γ for CP/CV:
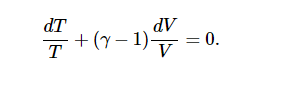
Integrate:
TVγ−1= constant.
This shows how temperature and volume of an ideal gas vary during a reversible adiabatic expansion or compression. If the gas expands, the temperature goes down. If the gas is compressed, it becomes hot. Of course, the pressure varies also, and the ideal gas conforms to the equation
PV/T = constant. On elimination of T, we obtain
PVγ= constant
On elimination of V, we obtain
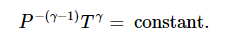
Dissociation energy and resonance energy from thermochemical data, effect of temperature (Kirchhoff’s equations) and pressure on enthalpy of reactions
Heat of reactions:
The Heat of Reaction (also known and Enthalpy of Reaction), occurs in the constant pressure, it is the change in the enthalpy of a chemical reaction.
Enthalpy is a state function and a thermodynamic unit for measurement. The enthalpy is used to calculate the amount of energy per mole that is either produced or released in the reaction. Since enthalpy is derived from pressure, volume, and internal energy, all of which are state functions.
As a process starts at a constant pressure, the heat (either absorbed or released) that is evolved is equal to the change in enthalpy.
Enthalpy change is denoted by U, which refers to the sum of internal energy and also the product of volume and Pressure, denoted by PV, expressed in the following manner.
H=U+PV
Enthalpy is also described as a state function completely based on state functions P, T and U. It is normally shown by the change in enthalpy (ΔH) of a process between the beginning and final states.
ΔH=ΔU+ΔV
If the pressure and temperature don’t change throughout the process and the task is limited to pressure and volume, the change in enthalpy is given by,
ΔH=ΔU+PΔV
The flow of heat (q) at constant pressure in a process equals the change in enthalpy based on the following equation,
ΔH=q
Any Enthalpy of a reaction is dependent on its physical conditions of the surroundings such as pressure, temperature etc. In order to specify the standard enthalpy of any reaction, the standard enthalpy of a reaction is calculated when the components that participate in the reaction are in standard form, the components include reactants and products.
Standard States
In chemistry, the standard states refer to the state of a material, whether substance is pure or a mixture or is present in solution form. The standard state is a reference point that is used to calculate, the properties of the material under different conditions. In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry (IUPAC) recommends a conventional set of standard states for general use. A standard pressure of 1 bar (101.3 kilopascals) has been accepted.
In strict terms, the parameter temperature is not a part of the definition of the standard state, the standard state of a gas is conventionally chosen to be 1 bar for an ideal gas, regardless of the temperature. However, most of the reactions in thermodynamic quantities are compiled at specific temperatures, most commonly 298.15 K (exactly 25°C) or, somewhat less commonly, 273.15 K (exactly 0°C).
The Standard states, where the atomic elements are considered, the allotrope that is stable for each element is counted, for example, white tin and graphite are the most stable allotropes of tin and carbon, respectively. Therefore, they are referred for reference point of standard states, that involves calculations for different thermodynamic properties of these elements.
Enthalpy of formation of molecules and ions
The enthalpy change with respect to a solution is the enthalpy change where 1 mole of an ionic substance dissolves in water to form a solution of indefinite dilution. The enthalpy of a solution is either negative or positive, in other words, some ionic substances dissolved endothermically (for example, NaCl); others dissolve exothermically (for example NaOH).
An infinitely solution that is dilute in one where there is an infinitely dilute solution is one where there is an adequately excess amount of water such that adding any further does not involve any heat to be absorbed or evolved. Therefore when 1 mole of sodium chloride crystals are dissolved in an excess of water, the enthalpy change of solution is found to be +3.9 kJ mol-1. The change is slightly endothermic, and so the temperature of the solution will be slightly lower than that of the original water.
When a substance dissolve why is it that heat is sometimes dissolved or absorbed. An imaginary process can be put forward the crystal lattice is first broken up into its separate gaseous ions and then those ions have water molecules wrapped around them. That is how they exist in the final solution.
- The heat energy needed to break up 1 mole of the crystal lattice is called the Lattice dissociation enthalpy
- The heat that is released when new bonds are formed between the ions and water molecules is called hydration enthalpy of the ion. The hydration enthalpy is the enthalpy change when 1 mole of gaseous ions dissolve in sufficient water to give an infinitely dilute solution. Hydration enthalpies are always negative.
Factors affecting the size of hydration enthalpy
Hydration enthalpy is a measure of the energy released when attractions are set up between positive or negative ions and water molecules.
- When ions are positive the attractions are loosened between the slightly negative oxygen atoms in the water molecules and the positive ions, or they may be covalent bond formation.
- When ions are negative the hydrogen bonds are formed between the lone pair of electrons on the negative ions and the slightly positive hydrogens in water molecules.
The size of the hydration enthalpy is governed by the amount of attraction between the ions and the water molecules.
- As we go down the periodic table the smallest lithium ion has the highest hydration enthalpy in group 1, the attractions are stronger when the ions are smaller, and the smallest fluoride ion has the highest hydration in group 7 The attractions are stronger the smaller the ion. In both groups, hydration enthalpy falls as the ions get bigger.
- The more highly charged the ion, the stronger is the attraction. For example, the hydration enthalpies of Group 2 ions (like Mg2+) are much higher than those of Group 1 ions (like Na+).
Estimating enthalpies of solution from lattice enthalpies and hydration enthalpies
The hydration enthalpies for calcium and chloride ions are given by the equations:
The following cycle is for calcium chloride, and includes a lattice dissociation enthalpy of +2258 kJ mol-1. We have to use double the hydration enthalpy of the chloride ion because we are hydrating 2 moles of chloride ions. Make sure you understand exactly how the cycle works.
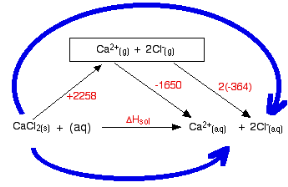
So
ΔHsol = +2258 - 1650 + 2(-364)
ΔHsol = -120 kJ mol-1
As the case above the negative hydration enthalpies are found to be more than the positive lattice dissociation enthalpy, depending on the size of the lattice enthalpy and the hydration enthalpy the enthalpy of solution corresponds to being positive or negative.
Standard Enthalpy of Combustion
Standard enthalpy of combustion is defined as the enthalpy change when one mole of a compound is completely burnt in oxygen with all the reactants and products in their standard state under standard conditions (298K and 1 bar pressure). For example:
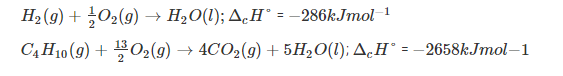
Applications
1) Calculation of heat of formation:
With respect to organic compounds, the heat of combustion is estimated easily, they are used to calculate the heat of formation of other compounds.
2) Calculation of calorific value of food and fuels:
The enthalpy of combustion is useful in calculating, the calorific value the calorific value is defined as the amount of heat produced in calories (or joules) when one gram of the substance is completely burnt. The SI unit of calorific value is J kg−1. However, it is usually expressed in cal g-1
Bond Energy
It is a measure of a chemical bond strength, which means that it tells the possibility of a pair of atoms to remain bonded in the midst of energy perturbations. Alternatively, it can also be thought as the stability that is obtained when two atoms bond to each other as opposed to their unbounded states.
Bond energy and its determination
The Bond energy is determined by calculating the heat that is required to break one mole of molecules into their individual atoms, it denotes the average energy that is associated with breaking the individual bonds of a molecule. The higher the bond energy, the ‘stronger’ we say the bond is between the two atoms, and the distance between them (bond length) is smaller.
For instance, the HO-H bond in a molecule of water involves 493kJ/mol to break and generate the hydroxide ion (OH–). Further the breaking of the O-H bond in the hydroxide ion needs an additional of 424 kJ/mol. Therefore, the bond energy of the covalent O-H bonds in water is determined to be the average of the both the values, or 458.9 kJ/mol. These energy values (493 and 424 kJ/mol) are required to break successive O-H bonds in a water molecule and are generally called as ‘bond dissociation energies,’ and they are different from the bond energy. Therefore, the bond energy is the average of the bond dissociation energies in a molecule.
The exact properties of a specific kind of bond are determined in part by the nature of the other bonds in the molecule; for example, the energy and length of the C–H bond will vary depending on what other atoms are bonded to the carbon atom. Similarly, the C-H bond length can vary by as much as 4% between different molecules. For this reason, the values of bond energy and bond length are usually averages taken over a variety of compounds that contain a specific atom pair.
We can apply bond energy values to determine the enthalpy of a compound’s formation.
Bond dissociation energy
Bond dissociation energy refers to the amount of energy that is needed to break a chemical bond homolytic ally. A homolytic process results in formation of a radical species. Shorthand notation for this energy is BDE, D0, or DH°. Bond dissociation energy often useful in measuring the strength present in chemical bond and also compare different bonds. Note the enthalpy change is temperature dependent. Typical units of bond dissociation energy are kJ/mol or kcal/mol. Bond dissociation energy may be measured experimentally using spectrometry, calorimetry, and electrochemical methods.
Bond Dissociation Energy
- Bond dissociation energy is the energy required to break a chemical bond.
- The energy is a means of quantifying the strength of a chemical bond.
- Bond dissociation energy equals bond energy only for diatomic molecules.
- The strongest bond dissociation energy is for the Si-F bond. The weakest energy is for a covalent bond and is comparable to the strength of intermolecular forces.
Bond Dissociation Energy Versus Bond Energy
Bond dissociation energy is only equal to bond energy for diatomic molecules. This is because the bond dissociation energy is the energy of a single chemical bond, while bond energy is the average value for all the bond dissociation energies of all bonds of a certain type within a molecule.
For example, consider removing successive hydrogen atoms from a methane molecule. The first bond dissociation energy is 105 kcal/mol, second is 110 kcal/mol, third is 101 kcal/mol, and final is 81 kcal/mol. So, the bond energy is the average of the bond dissociation energies, or 99 kcal/mol. In fact, the bond energy doesn't equal the bond dissociation energy for any of the C-H bonds in the methane molecule!
Resonance energy
The difference in energy between the actual molecule and the canonical form of the lowest energy is called the resonance energy, the resonance energy of a molecule is expressed in Kcal/mole or kJ/mole
The resonance energy is directly proportional to the stability of a molecule, so the stability of a molecule increases with increasing its resonance energy. For example, the resonance energy of benzene is 36kcal/mole and the resonance energy of pyridine is 28kcal/mole, this indicates that benzene is more stable than pyridine.
Effect of Temperature (Kirchhoff’s equations) and pressure on enthalpy of reactions.
In a chemical and physical process, the heat change depends on the temperature at which it takes place. This dependence on temperature is mathematically expressed in the form of what is known as Kirchhoff equation after G. R. Kirchhoff (1858) who first developed this equation. The equation may easily be derived with the help of the first law of thermodynamics.
Kirchhoff’s Equation is equality, it expresses the dependence of temperature of the thermal quantities that are linked with a chemical reaction, through the difference in heat capacities between the products and reactants. The same reaction, when carried at dissimilar temperatures, the enthalpies of reaction are also different.
Kirchhoff equation relates the heat of reaction with the definite heats of a structure before and after the reaction. Kirchhoff equation is represented as dQ/dt = C – C’
Where, Q is the heat energy evolved throughout the procedure at temperature ‘t’ without modifying in volume and C is the specific heats of the reactants and C’ is the specific heats of products.
A temperature transform occurs when the temperature is increased or decreased by the flow of heat. This shifts the chemical equilibrium toward the products or reactants, which can be resolute by studying the reaction and deciding whether it is endothermic or exothermic. The equation which indicates Effect of temperature on the heat of reaction is known as Kirchhoff’s equation.
Enthalpy a process or activity takes place at constant pressure, the heat released or absorbed is equal to the Enthalpy change. Enthalpy is occasionally called or known as “heat content”, “enthalpy” is derived from the Greek word which means “warming”. Enthalpy(H) is the sum of the internal energy(U) and the result of pressure(P) and volume(V).
Enthalpy H is written as,
H = U + PVm
Where, H = is the Enthalpy of the system
U = is the Internal energy of the system and is entirely dependent on the state functions T, p and U.
When a process occurs at constant pressure, the heat evolved (either released or absorbed) is equal to the change in enthalpy.
When a process occurs at constant pressure, the heat evolved (either released or absorbed) is equal to the change in enthalpy. Enthalpy is a state function which depends entirely on the state functions T, P and U.
Enthalpy is usually expressed as the change in enthalpy (ΔH) for a process between initial and final states:
ΔH=ΔU+ΔPV
If temperature and pressure remain constant through the process and the work is limited to pressure-volume work, then the enthalpy change is given by the equation:
ΔH=ΔU+PΔV
Enthalpy can also be written as
ΔH=ΔU+ΔPV.
P = is the Pressure of the system
V = Volume of the system Enthalpy is not directly measured, but the change in enthalpy (ΔH) is measured, which is the heat lost or added by the system,
Also, at constant pressure the heat flow (q)for the process is equal to the change in enthalpy defined by the equation:
ΔH=q
By looking at whether q is exothermic or endothermic we can determine a relationship between ΔH and q.
Key takeaway
The chemistry that deals with energy exchange, entropy, and the spontaneity of a chemical process
When energy is exchanged between thermodynamic systems by thermal interaction, the transfer of energy is called heat. Work is the transfer of energy by any process other than heat. Heat and work are related: work can be completely converted into heat, but the reverse is not true: heat cannot be completely converted to work
Enthalpy is a state function, and the change in enthalpy of a system is equal to the sum of the change in the internal energy of the system and the PV work done.
References:
1. Engel T. & Reid P., Physical Chemistry 3rd Ed. Pearson (2013).
2. McQuarrie, D. A. & Simon, J. D. Molecular Thermodynamics Viva Books Pvt. Ltd.: New Delhi (2004).
3. Kheterpal S.C., Pradeep’s Physical Chemistry, Vol. I & II, Pradeep Publications.
