Unit - 2
Carnot cycle
This concept was proposed by the French physicist Carnot 1824 and was later expanded by others in the year 1830-1840, the cycle deals with the theoretical idea of thermodynamic cycle.it highlights the higher levels of efficiency that any classical thermodynamic engine achieves during the conversion of heat into work, or on the contrary a temperature that creates a difference by the application of work to the system.
Working of Heat Engine
A heat engine contains basically a heat reservoir, engine and a cold sink. The heat that we produce as internal combustion or external combustion is given to the engine where the movement of the piston takes place. The power generated is given to the machine that is connected to the engine and hence the work is done. Excess heat is given to the sink where the temperature will remain the same at both reservoir and sink.
Heat engines operate similar to the automobile engines in a cyclic manner, the energy in the form of heat is added to one part of the cycle and is used to do work in the other part of the cycle.
Heat Engine PV Diagram
Heat engines can be typically illustrated on a PV diagram,
Isothermal
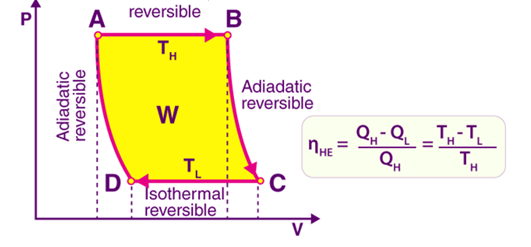
Fig 1: Heat Engine PV diagram
Pressure-Volume (PV) diagrams are the basic tool for the study of heat engines that use gas as the working substance diagram will be a closed-loop for a cyclic heat engine. The area of the loop is the representation of the amount of work done during the cycle.
The idea of the efficiency of an engine cycle can be obtained by comparing the PV diagram with the Carnot cycle, which is the most efficient type of heat engine.
Explanation of PV diagram:
- The fluid changes from liquid to vapour isothermally if the source is at a high temperature. This vaporization process occurs at constant pressure and increasing volume.
- At the turbine end, the gas expands reversibly and adiabatically and it follows the equation of state for an adiabatic and reversible process.
- The fluid changes from a gas to liquid isothermally if the source is at a low temperature. This condensation process occurs at constant pressure and decreasing volume.
- At the compressor end, the liquid is compressed reversibly and adiabatically by increasing its pressure to the original point.
Heat Engine Efficiency
The efficiency is the fraction of heat input at high-temperature changes to work. In the second law of thermodynamics, it says that no engine is 100% efficient.
Efficiency, η = Work done / Heat input
We know that,
Work done, W = Q1 – Q2
Heat input = Q1
Then,
Efficiency, η = W / Q1
= (Q1 – Q2) / Q1
=1 – (Q2 / Q1)
Carnot Engine
A Carnot engine is an ideal engine that can operate in a reversible closed thermodynamic cycle where the working substance goes through four successive operations such as isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression. It is the basis of other thermodynamic cycles that have vast applications in industries. Two common applications are the Carnot heat engine and refrigerators.
Although the Carnot engine is the ideal engine, in reality, no engine achieves Carnot’s theoretical maximum efficiency since friction plays an important role. The efficiency of a Carnot engine uniquely depends on the temperature of the hot and cold reservoir.
Carnot engine basically draws heat (Q1) from the source and rejects heat (Q2) to the sink while performing an amount of work, W = Q1 – Q2.
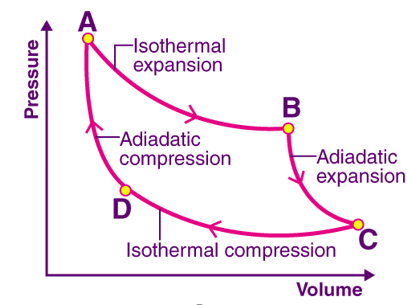
Fig 2: The Carnot Cycle
The complete cycle incorporates:
- Isothermal Expansion: During the isothermal expansion of an ideal gas we use the temperature of source T1 which will draw Q1 amount of heat. Since the expansion is isothermal the total change in internal energy is zero and the heat absorbed by the gas will be equal to the work done by the gas on the environment.
- Adiabatic Expansion: During the adiabatic expansion of an ideal gas, the temperature of an ideal gas falls from source temperature T1 to sink temperature T2. Here, the pressure falls and volume increases because no heat energy is being supplied to gas as it expands. The work is less and the pressure must be lower.
- Isothermal Compression: During the process of isothermal compression of an ideal gas sink temperature T2 further goes down as it rejects heat Q2 to the sink.
- Adiabatic Compression: During adiabatic compression of an ideal gas temperature naturally raises from T2 to T1 and hence working substance returns to its original state by completing one cycle.
The efficiency of the Carnot engine is given as,
η =Work done / Heat input
We know that,
Work done, W = Q1 -Q2
Heat input =Q1
Then,
Efficiency, η =W / Q1
=(Q1-Q2) /Q1
=1-(Q2 /Q1), which is the efficiency of the heat engine.
If Q2 = 0, then efficiency = 100%. This is known as the Carnot engine.
It is an ideal case where the efficiency is 100%. However, there will be some loss of energy in the system and hence, for every engine, there will be a limit of efficiency.
Meanwhile, it is also known that,
Thermodynamically, (Q2/Q1) = (T2/T1)
Therefore,
η = 1 – (T2/T1)
Work done in each step:
Isothermal expansion:
Wa → b = Q1= n R T 1 ln(v2 / v1)
Adiabatic expansion:
Wb → c = ( nR /( γ -1))(T1-T2)
Isothermal compression:
Wc → d = nRT2ln(v3/v4)
Adiabatic compression:
Wd → a = ( nR /( γ -1))(T1-T2)
Hence, the total work done by the gas on the environment in one complete cycle is given by, W= Wa → b+Wb → c+Wc → d +Wd → a
Net efficiency = (net work done by the gas) / (heat absorbed by the gas)
=W / Q1
=(Q1-Q2) / Q1
=1-(Q2 / Q1
Carnot’s theorem states that:
- Heat engines that are working between two heat reservoirs are less efficient than the Carnot heat engine that is operating between the same reservoirs.
- Irrespective of the operation details, every Carnot engine is efficient between two heat reservoirs.
- Maximum efficiency is given as:
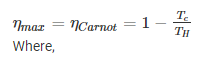
TC: absolute temperature of the cold reservoir
TH: absolute temperature of the hot reservoir
𝜼: the ratio of work done by the engine to heat drawn out of the hot reservoir
Concept of Entropy
It was Introduced by the German Physicist Rudolf Clausius in 1850, and is a highlight of 19th century Physics. The word “entropy” is derived from the Greek word, which means “turning”.
The second law of thermodynamics states the total entropy of a closed system cannot decrease. However, within a system, entropy of one system can decrease by raising entropy of another system. Some scientists predict the entropy of the universe will increase to the point where the randomness creates a system incapable of useful work.
It was derived to provide a quantitative measure for the spontaneous changes and Clausius introduced the concept of entropy as a precise way of expressing the Second Law of Thermodynamics, Clausius form of the second law states that spontaneous change for an irreversible process in an isolated system is a measure of randomness or irregularity or disorder of the system, the more or the randomness, higher is the entropy.
Solid state has the lowest or least entropy, the gaseous state has the highest entropy and the liquid state has the entropy that lies between the two.
Entropy is a state function. The changes in its value during any process, is called the entropy change.
ΔS = S2 -S1 = ∑S products – ∑S reactants
1) When a system absorbs heat, the molecules begin to move faster because the kinetic energy increases. Therefore, disorder increases. Greater the heat absorbed, greater will be the disorder.
2) For equal amount of heat absorbed at low temperature, the disorder will be more than at high temperature. This proves that entropy change is inversely proportional
To temperature.
ΔS = eve / T
Entropy change during a process is defined as the quantity of heat (q) absorbed isothermally and reversibly divided by the absolute Temperature (T) at which the heat is absorbed.
Thermodynamic scale of temperature
A temperature scale in which the temperature, T, is a function of the energy possessed by matter. Thermodynamic temperature is therefore a physical quantity that can be expressed in units, termed kelvin. The zero of the scale is absolute zero. The temperature of the ice point (0 °C) is 273.15 kelvin. Thermodynamic temperature can be converted to Celsius temperature by subtracting 273.15 from the thermodynamic temperature.
Any temperature scale in which the ratio of the temperatures of two reservoirs is equal to the ratio of the amount of heat absorbed from one of them by a heat engine operating in a Carnot cycle to the amount of heat rejected by this engine to the other reservoir, the Kelvin scale and the Rankine scale are examples of this type.
The second Carnot principles state that the thermal efficiencies of all reversible heat engines operating between the same two reservoirs are the same.
A temperature scale is independent of the properties of the substance, and are used to measure temperature are called, thermodynamic temperature scale
The temperatures present on the Kelvin scale are called the Absolute temperatures.
For reversible cycles
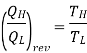
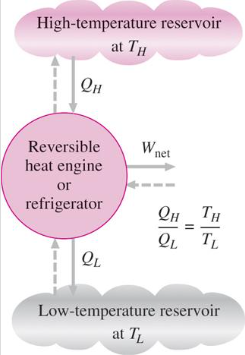
Statement of Second law of thermodynamics
The second law of thermodynamics states that any spontaneously occurring process will always lead to an escalation in the entropy (S) of the universe. In simple words, the law explains that an isolated system’s entropy will never decrease over time.
Nonetheless, in some cases where the system is in thermodynamic equilibrium or going through a reversible process, the total entropy of a system and its surroundings remains constant. The second law is also known as the Law of Increased Entropy.
While the first law of thermodynamics gives information about the quantity of energy transfer is a process, it fails to provide any insights about the direction of energy transfer and the quality of the energy. The first law cannot indicate whether a metallic bar of uniform temperature can spontaneously become warmer at one end and cooler at others. All that the law can state is that there will always be energy balance if the process occurs.
It is the second law of thermodynamics that provides the criterion for the feasibility of any process. A process cannot occur unless it satisfies both the first and second laws of thermodynamics.
The Second Law of Thermodynamics states that the state of entropy of the entire universe, as an isolated system, will always increase over time. The second law also states that the changes in the entropy in the universe can never be negative.
Molecular and Statistical interpretation of Entropy
The second law of thermodynamics specifies that all the processes should increase the total entropy of the universe, however when the universe is separated into system and surroundings the changes in entropy is differed from the system level prospective, Many processes results in an increase in a system's entropy ΔS>0ΔS>0:
- Increasing the volume that a gas can occupy will increase the disorder of a gas
- Dissolving a solute into a solution will increase the entropy of the solute - typically resulting in an increase in the entropy of the system. (Note: the solvation of a solute can sometimes result in a significant decrease in the solvent entropy, leading to a net decrease in entropy of the system)
- Phase changes from solid to liquid, or liquid to gas, lead to an increase in the entropy of the system
Some processes result in a decrease in the entropy of a system ΔS<0ΔS<0:
- When a gas molecule is dissolved in a liquid, it is much more confined by the neighbouring molecules than in its gaseous state., therefore the entropy of gas will decrease when a gas is dissolved in a liquid.
- When a liquid changes its phase to a solid (freezing) of when a gas changes to a liquid (condensation), there occurs a decrease in the disorder of the substance thereby the entropy also decreases.
- A chemical reaction between gas molecules that results in a net decrease in the overall number of gas molecules will decrease the disorder of the system, and result in a decrease in the entropy
2NO(g)+O2(g)→2NO2(g)ΔS<0
(2NO(g)+O2(g)→2NO2(g)ΔS<0
What is the molecular basis for the above observations for the change in entropy? Let's first consider the last example, the decrease in entropy associated with a decrease in the number of gas molecules for a chemical reaction
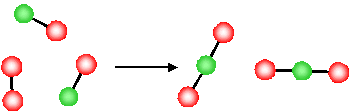
2NO(g)+O2(g)→2NO2(g)2NO(g)+O2(g)→2NO2(g)
The product of this reaction (NO2NO2) involves the formation of a new N-O bond and the O atoms, originally in a separate O2O2 molecule, are now connected to the NONO molecule via a new N−ON−O bond.
- Since they are now physically bonded to the other molecule (forming a new, larger, single molecule) the O atoms have less freedom to move around
- The reaction has resulted in a loss of freedom of the atoms (O atoms)
- There is a reduction in the disorder of the system (i.e., due to the reduction in the degrees of freedom, the system is more ordered after the reaction). ΔS<0.
Molecular Degrees of Freedom
The atoms, molecules, or ions that compose a chemical system can undergo several types of molecular motion, including translation, rotation, and vibration
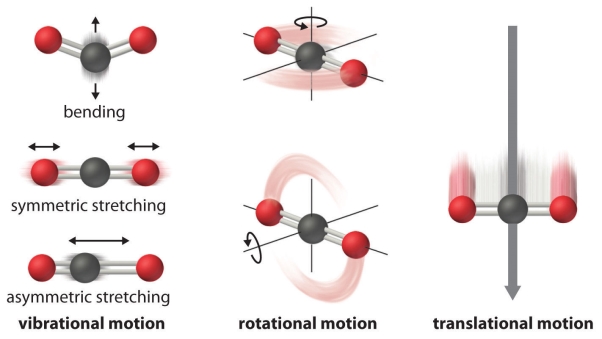
Fig 3: Molecular motions
Molecular Motions. Here the carbon dioxide molecule is considered, and the different motions are depicted here, Vibrational, rotational, and translational motions. No molecular motion would be observed only in a perfect crystalline substance at absolute zero a zero entropy. Practically this is not possible.
- Translational motion. The whole molecule moves in some direction three dimensionally.
- Rotational motion. The whole molecule rotates around any axis, (though its position is not changed transitionally)
- Vibrational motion. The atoms that are present within the molecule have some amount of freedom movement that is relative to each other, this displacement can be periodic motion like the vibration of a tuning fork.
These forms of motion form the ways in which molecules store energy, the greater the molecular motion of a system, greater will be the possible microstates and higher the Entropy.
Statistical Interpretation
The entropy is state function and its importance is often sought for its meaning at the microscope level.
Entropy is defined as the measure of “disorder.” According to this concept, on a microscopic scale, in a closed system, the disorderness is more therefore the entropy increases. However, this concept is misleading as it does not explain the increase in entropy by reversible heating at constant volume or pressure, also why there is an increase during the reversible isothermal expansion of an ideal gas. Nor does it seem to agree with the freezing of a supercooled liquid or the formation of crystalline solute in a supersaturated solution; however, in an isolated system such processes can take place spontaneously, but are also accompanied by an apparent decrease of disorder.
Therefore, Entropy should not be interpreted as a measure of disorder, a more satisfactory explanation of entropy at the microscopic level is required.
A rigorous interpretation is provided by the discipline of statistical mechanics, based on the behaviour of macroscopic amounts of microscopic particles a precise expression of entropy is derived. Suppose we focus our attention on a particular macroscopic equilibrium state. Over a period of time, while the system is in this equilibrium state, the system at each instant is in a microstate, or stationary quantum state, with a definite energy. The microstate is accessible to the system, meaning its wavefunction is compatible with the system’s volume and any other conditions and terms imposed by the system. The system, while in the equilibrium state, continually jumps from one accessible microstate to another, and the macroscopic state functions described by classical thermodynamics are time averages of these microstates.
The fundamental concept shows that accessible microstates of equal energy are probable equally, is the assumption of the statistical mechanics, therefore when the system is in equilibrium an equal fraction of its time is spent in each microstate, at this equilibrium state the statistical entropy is given by the equation.
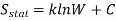
Where kk is the Boltzmann constant k = R/NA, W is the number of accessible microstates, and CC is a constant.
In the case of an equilibrium state of a perfectly-isolated system of constant internal energy UU, the accessible microstates are the ones that are compatible with the constraints and whose energies all have the same value, equal to the value of UU.
It is more realistic to treat an equilibrium state with the assumption the system is in thermal equilibrium with an external constant-temperature heat reservoir. The internal energy then fluctuates over time with extremely small deviations from the average value UU, and the accessible microstates are the ones with energies close to this average value. Microcanonical ensemble is used for the derivation of the results in an isolated system, according to the statistical language, and also for a system of constant temperature the canonical ensemble is applied.
Calculation of entropy change for reversible and irreversible processes.
Entropy is a state function. The entropy change is determined by its initial and final states only.
In analyzing irreversible process, it is not necessary to make a direct analysis of actual reversible process.
Substitute actual process by an imaginary reversible process. The entropy change for imaginary reversible process is same as that of an irreversible process between given final and initial states.
Because H and U are state functions, the amount of heat entering the surroundings is independent of the path; q is the same whether the transfer occurs reversibly or irreversibly.
In order to understand the entropy, change in reversible and irreversible process, we need to understand the concept of entropy first. For a Carnot heat engine working at T1 and T2 it has been observed that the heat absorbed (q) and heat returned (q1) are related as given below 
Therefore we can for a particular system, the ratio of heat absorbed or lost isothermally and reversibily to the absolute temperature at which tjis takes place is a constant parameter, if we consider q1 as the heat absorbed at T1 the equation becomes
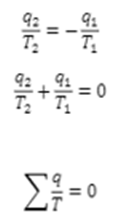
Entropy changes in reversible process
Suppose that the heat absorbed by the system and heat lost by the surroundings are under completely reversible conditions, in other words qrev is the heat absorbed and lost by the surroundings at temperature T, then we can say that the entropy change in the system will be given by the following relation
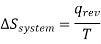
Similarly , the entropy change in the surrounding will be
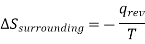
Therefore the total Entropy will be

Hence , we can conclude that the entropy change in an isolated system is always zero i.e the sum of entropy change in system and entropy change in te surrounding is zero under reversible conditions.
Entropy changes in Irreversible process
Every reversible process becomes irreversible even if only one part of it becomes irreversible, To understand this, let us suppose that qrev heat lost by the surrounding, although this heat would be absorbed by the system depends upon the heat absorbed reversibily. Therefore , entropy change of the system at an absolute temperature T will be
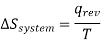
Similarly , the entropy change in the surrounding will be
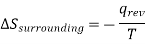
Therefore the total Entropy of the isolated system ( system + surrounding) will be

Furthermore , as we know that the Wrev > W irrev and internal energy is a state function that is independent of whether the process is reversible or irreversible mathematically it is
ΔE =qrev-Wrev = qirrev -Wirrev
We can conclude that
qrev >qirrev
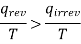
Or
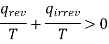
Therefore from the above equations we get
ΔS system + ΔS surrounding > 0
The physical interpretation of the above equation lies in the fact that all irreversible processes occur via a net increase in entropy , in other words, the total entropy change of an isolated system in any irrversible process is always greater than zero, the results equation can therefore be genrealised as
ΔS system + ΔS surrounding > 0
Where the sign = stands for reversible and > for irreversible phenomena respectively.
The Third Law states, “The entropy of a perfect crystal is zero when the temperature of the crystal is equal to absolute zero (0 K).”
The third law of thermodynamics also refers to a state known as “absolute zero”. This is the lowest point on the Kelvin scale. So, 0 Kelvin becomes the lowest temperature in the universe. It is -273.15oC or -459.7oF. But reality works differently; actually, no object or system can attain zero Kelvin, as per the second law of thermodynamics.
To get too absolute zero it requires an infinite number of steps. Getting absolute zero will violate the second law of thermodynamics. According to the second law of thermodynamics, the heat cannot spontaneously move from a colder body to a hotter body. This implies that when a system approaches absolute zero it will tend to draw heat or energy from something nearby, and if this happens, it will never actually become zero.
We started with the first law of thermodynamics which talks about the conservation of energy and the fact that it can neither be created or destroyed and then moved on to the second law of thermodynamics which spoke about entropy and disorder. Finally, we moved on to the third law of thermodynamics which brought the concept of absolute zero.
Concept of Residual entropy
Residual entropy is the entropy of a substance that refers to the difference in the entropy non-equilibrium state and the crystal state of the substance that is close to absolute zero.
In other words,
The entropy obtained by a substance also at absolute zero is called as residual entropy.
Example: -
Consider a crystal made up of AB molecule where A and B are similar atoms which has very small dipole moment. These molecules can adopt different orientations such as -ABABAB- or -ABBAAAB- at random. These kinds of arrangements, show very little difference in energy, thus they exhibit some disorder even at absolute zero, this is called as residual entropy. This type of entropy is commonly seen in carbon dioxide.
Calculation of absolute entropy of molecules
The entropy is made an absolute quantity by setting S(O), It is tempting to set the S (0) to zero and make the entropy thus an absolute quantity. As seen in case of enthalpy it is impossible to set H(0), although if CpCp data are available we could construct an enthalpy function (albeit with a floating zero point) by integration of Cp (instead of Cp/TCp/T !).
Still for entropy SS the situation is a bit different than for H. Here we can actually put things on an absolute scale. Both Nernst and Planck have proposed to do so. Nernst postulated that for a pure and perfect crystal SS should indeed to go to zero as TT goes to zero. This postulate is known as the third law of thermodynamics.
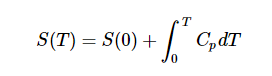
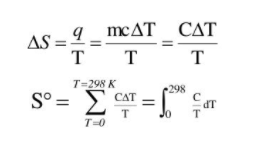
Both Helmholtz and Gibbs free energies are important thermodynamic functions known as Thermodynamic potentials.
The Helmholtz free energy is defined as,
A=U−TS
Where, U is the internal energy, T is the absolute temperature and S is the Entropy
The above definition may be obtained from the internal energy function by means of one Legendre transform.
The Helmholtz free energy has (T,V) as the natural pair of variables.
Differentiating the expression for A,
DA=dU−TdS−SdT
Using the combined mathematical form of first and second laws of thermodynamics,
TdS=dU+pdV,
⇒dA=−pdV−SdT
Thus, A=A(V,T)
That is why the Helmholtz free energy is known as thermodynamic potential at constant volume.
It stays constant during any isothermal-isochoric change.
For such a system, the Helmholtz free energy tends to minimize as the system tends to equilibrium.
Now coming to Gibbs free energy, the expression is,
G=U+pV−TS
Where symbols have their usual meaning.
The above relation may be derived from the internal energy function by means of Legendre's transformations to change variables.
It may also be cast in the form,
G=H−TS where, H=U+pV is the enthalpy
Now, Differentiating G,
DG=dU+ pdV + Vdp – SdT − TdS
Again using the combined mathematical form of the first and second law of thermodynamics (for reversible transformations),
DG=Vdp − SdT
Thus, G=G(T,p)
The Gibbs function is also called thermodynamic potential at constant pressure.
Variation of entropy (S) with Temperature, Pressure and Volume
Consider one mole of ideal gas filled with a weigh less and frictionless piston. If the system absorbs a very small amount of heat δqrev isothermally and reversibly at temperature T, the total entropy change in the system can be given by the following equation

The above equation may be written in the following form if the process is carried out under reversible conditions.

After putting the value of work of expansion (-PdV), the equation becomes
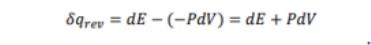
Using the first equation and the first equation
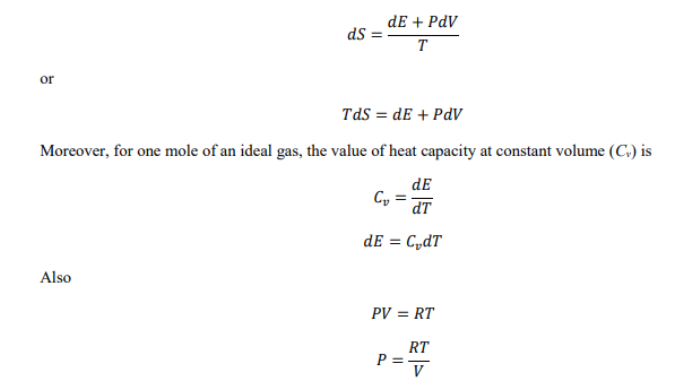
Where R is the gas constant, while P,T and v are the pressure , temperature and volume respectively, Now when the value of the above equation is put in the ideal gas equation we get.

Now consider the initial state ( T1, V1), is converted to the final state (T2,V2), the total Entropy will be calculated by the equation
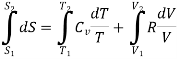
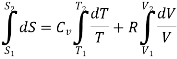
Since, from ideal gas equation , the following is also true for thr initial and final state of the system
P1V1 = R T1
P2V2 = R T2
Dividing the equation we get
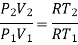
Or
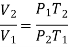
Therefore ΔS, can be written
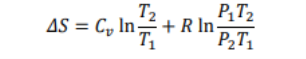
We know that Cp-Cv = R therefore, after putting Cv=Cp-R in the above equation, we get
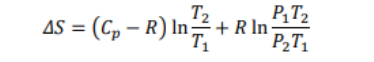

Variation of Gibbs free energy on temperature, pressure and Volume
Gibbs free energy is equal to the enthalpy of the system minus the product of the temperature and entropy. The equation is given as;
G = H – TS
Where,
G = Gibbs free energy
H = enthalpy
T = temperature
S = entropy
Gibbs free energy is a state function hence it doesn’t depend on the path. So, change in Gibbs free energy is equal to the change in enthalpy minus the product of temperature and entropy change of the system.
ΔG=ΔH-Δ(TS)
If the reaction is carried out under constant temperature{ΔT=O}
ΔG=ΔH-TΔS
This equation is called the Gibbs Helmholtz equation
ΔG>0; the reaction is non-spontaneous and endergonic
ΔG<0; the reaction is spontaneous and exergonic
ΔG=0; reaction is at equilibrium
Gibbs free energy, denoted G, combines enthalpy and entropy into a single value. The change in free energy, ΔGΔG, is equal to the sum of the enthalpy plus the product of the temperature and entropy of the system. ΔGΔG can predict the direction of the chemical reaction under two conditions:
- Constant temperature and
- Constant pressure.
Variation of Helmholtz free energy (A) with temperature, pressure and volume
Helmholtz free energy is a thermodynamics concept in which, thermodynamic potential is used to measure the work of a closed system with constant temperature and volume. It can be defined in the form of the following equation:
F=U−TS
Where,
- F is the Helmholtz free energy in Joules
- U is the internal energy of the system in Joules
- T is the absolute temperature of the surroundings in Kelvin
- S is the entropy of the system in joules per Kelvin
When a process occurs at constant temperature T and pressure P, e can rearrange the second law of thermodynamics and define a new quantity known as Gibbs free energy
Gibbs free energy G=H-TS
Where H is enthalpy, T temperature and S is the Entropy. Gibbs free energy is represented using the symbol G
When using Gibbs free energy to determine the spontaneity of a process, we are only concerned with changes in G, rather than its absolute value. The change in Gibbs free energy, for a process is written as ΔG,
Which is the difference between G final, the Gibbs free energy of the products, and G initial, the Gibbs free energy of the reactants.
ΔG System = ΔH system – TΔS system
This equation allows us to determine the change in Gibbs free energy using the enthalpy change ΔH, and the entropy change ΔS of the system, we use ΔG to find out if a reaction is spontaneous in the forward direction, backward direction or if the reaction is at equilibrium.
ΔG>0; the reaction is non-spontaneous and endergonic
ΔG<0; the reaction is spontaneous and exergonic
ΔG=0; reaction is at equilibrium
The Joule-Thomson effect also known as Kelvin–Joule effect or Joule-Kelvin effect is the change in fluid’s temperature as it flows from a higher-pressure region to lower pressure.

Fig 4: Gas packet, in Joule-Kelvin effect
According to the thermodynamic principle, the Joule-kelvin effect is well explained, when we consider a separate gas packet that is present in the opposite direction of flow. If the gas packet has to pass through, the upstream gas has to do some work to push through the packet. Therefore the work will equal the volume of the packet multiplied by the times of upstream pressure.
W 1 =V packet 1 ×P 1
As the packet goes through the restriction, some room has to be made by displacing a fixed amount of the down stream gas, which will include performing the work that will be equal to the product of packet volume and downstream pressure.
W 2 =V packet 2 ×P 2
Due to the different effects of compressibility, the work performed upstream is not equal to the amount of work done downstream for real gases. Since depressuring is viewed as an adiabatic process,the changes in the internal energy has to follow the first law of thermodynamics , and it is also seen that the gas does not exchange work of heat with its sorrounding’s
U 2 −U 1 =W 1 −W 2
Gas molecules are subjected to repulsive and attractive forces, (Van der Waals forces) as they are in random motion. When the gas pressure is lowered, i.e., the average distance between the molecules increases, the attractive forces become dominant for many gases at ambient temperature which results in an elevation in potential energy.
Most of the real gases need more work downstream at ambient temperature, due to the effects of compressibility.
P 1 ×V 1 <P 2 ×V 2
This indicates that the internal energy decreases when the gas passes through the restriction.
In general this is applicable for many gases, when there is a decrease in pressure the temperature also decreases., but not true for every gas and condition. Depressuring is an isenthalpic process which reveals that enthalpy doesn’t change. The temperature can either decrease or increase for any gas based on how the internal energy changes to maintain the enthalpy constant
When we consider a gas , it refers to the temperature where the gas does not show any cooling or heating effect i.e., Joule-Thomson coefficient µ = 1. Below this temperature, it shows cooling effect and above this temperature, it shows heating effect.
Any gas like H2, He etc, shows heating effect at room temperature, these gases show a low inversion temperature is low. However, if these gases are just cooled below inversion temperature and then subjected to Joule-Thomson effect, they will also undergo cooling.
The gaseous system obeys the Joule-Thomson effect only when the temperature is below a specifie value. The characteristic temperature below which a gas expands adiabatically into a region of low pressure through a porous plug with a fall in temperature is called as inversion temperature (Ti).
Ti is characteristic of a gas and it is related to the Vander Waal’s constant a' and b',
2a Ti = 2a / Rb
There occurs no increase or decrease in temperature ( Joule Thomson effect), which does not happen in inversion temperature. Only when the temperature of the gas is below the inversion temperature there is a fall in temperature during adiabatic expansion. If the temperature of the gas is above Ti there is a small rise in temperature. For gases like H2 and He, during joule’s experiment, instead of getting cooled they are warmed up, they however these gases have a whose Ti values are very low -80 o C and -240 o C respectively, These gases will obey Joule-Thomson effect only when they are cooled to a temperature below these Ti values
The Gibbs–Helmholtz equation is a thermodynamic equation used for calculating changes in the Gibbs energy of a system as a function of temperature. It is named after Josiah Willard Gibbs and Herman von Helmholtz.
The equation is:

Where H is the enthalpy, T the absolute temperature and G the Gibbs free energy of the system, all at constant pressure p. The equation states that the change in the G/T ratio at constant pressure as a result of an infinitesimally small change in temperature is a factor H/T2
These are the set of thermodynamics equations derived from a symmetry of secondary derivatives and from thermodynamic potentials. These relations are named after James Clerk Maxwell, who was a 19th-century physicist.
Derivation of Maxwell’s relations
Maxwell’s relations can be derived as:

Common forms of Maxwell’s relations

Where,
T is the temperature
S is the entropy
P is the pressure
V is the volume
U is the internal energy
H is the entropy
G is the Gibbs free energy
F is the Helmholtz free energy
With respect to pressure and particle number, enthalpy and Maxwell’s relation can be written as:
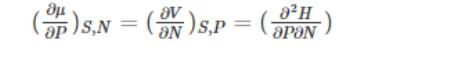
An equation of state (EOS) is a fundamental equation, which expresses the relationship between pressure, specific volume and temperature. The simplest equation of state is that for an incompressible substance (e.g., solids and liquids), which states that the specific volume is constant. The next simplest EOS is that for an ideal gas. Ideal (perfect) gas equation is a special equation of state, which is applicable to ideal gases. The molecular forces of attraction between gas molecules are small compared to those in liquids. In the limit when these forces are zero, a gas is called a perfect gas. In addition, the volume of the molecules should be negligible compared to total volume for a perfect gas. The perfect or ideal gas equation of state is given by

The ideal gas equation is satisfactory for low molecular mass, real gases at relatively high temperatures and low pressures. Ideal gas equation can be used for evaluating properties of moist air used in air conditioning applications without significant error. For ideal gases, the change in internal energy and enthalpy are sole functions of temperature. Assuming constant specific heats (p c, cv) in the temperature range T1 to T2, for ideal gases one can write the change in internal energy (u), enthalpy (h) and entropy (s) as:
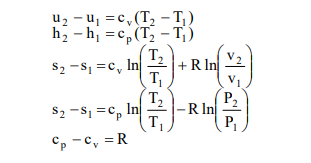
For gases with complex molecular structure or for real gases at high pressure and low temperatures or for gases approaching the saturated vapour region, the use of Ideal gas equation results in significant errors. Hence more complex but more realistic equations of states have to be applied. The accuracy of these EOS depends on the nature of the gas. Some of these EOSs are given below: van der Waals equation
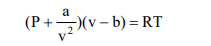
Where a and b are constants that account for the intermolecular forces and volume of the molecular gas respectively.
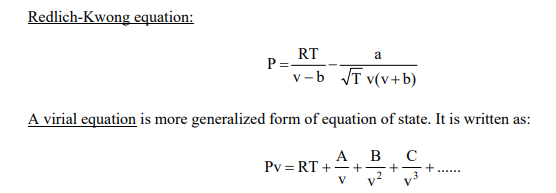
Where A, B, C, are all empirically determined functions of temperature and are called as virial coefficients
Key takeaway
The French physicist Carnot 1824 and was later expanded by others in the year 1830-1840, the cycle deals with the theoretical idea of thermodynamic cycle.it highlights the higher levels of efficiency that any classical thermodynamic engine achieves during the conversion of heat into work, or on the contrary a temperature that creates a difference by the application of work to the system.
The second law of thermodynamics states that any spontaneously occurring process will always lead to an escalation in the entropy (S) of the universe. In simple words, the law explains that an isolated system’s entropy will never decrease over time
The third law of thermodynamics states that the entropy of a system at absolute zero is a well-defined constant. This is because a system at zero temperature exists in its ground state, so that its entropy is determined only by the degeneracy of the ground state.
References:
1. Engel T. & Reid P., Physical Chemistry 3rd Ed. Pearson (2013).
2. McQuarrie, D. A. & Simon, J. D. Molecular Thermodynamics Viva Books Pvt. Ltd.: New Delhi (2004).
3. Kheterpal S.C., Pradeep’s Physical Chemistry, Vol. I & II, Pradeep Publications.