Unit – 4

Solutions and Colligative Properties

4.1 Dilute solutions

A dilute solution, refers to the solution in which the amount of the solute is less than the amount of the solvent. The behaviour of the dilute solutions is ideal as the changes in volume and heat occur, which is accompanied by mixing of solute and solvent and is negligible for all purposes. Dilute solutions obey Raoult’s law.

Dilution refers to the manner in which an additional solvent is added to a solution to decrease its concentration, however this keeps the amount of the solute constant, but increases the total amount of solution, thereby decreasing its final concentration.

4.2 Lowering of Vapour pressure

Vapour pressure is a property of liquid which related to evaporation. In other words, it is the pressure that is exerted by a vapour in equilibrium with its phases either as solid or liquid at a given temperature and in a closed system.

In simple terms, we can define vapour pressure as a measure of the tendency of a material to change its state to solid/liquid to gas or vapour when the temperature increases. It indicates the rate of evaporation of liquid. It is also closely related to the tendency of particles to escape from the liquid or solid-state.

Relation Between Vapour Pressure and Temperature

The substance with a high vapour pressure at room temperature is called a volatile substance. The temperature at which the vapour pressure at the surface of a liquid is equal to the pressure exerted by surrounding is denoted as the boiling point of that substance.

As the temperature of a liquid substance increases, the molecules’ kinetic energy also increases. Thus, the number of molecules transitioning into a vapour also increases and thereby increasing the vapour pressure of the liquid.

Simply say, with an increase in the temperature, the vapour pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form vapour bubbles inside the bulk of a substance. Volatile components such as gases and solvents are characterised by high vapour pressure can be transported with winds and components with low vapour pressure are transported with soil, sediment etc.

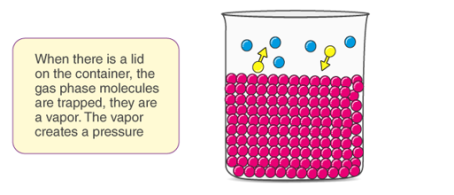
Fig: Pictorial Representation of Concept of Vapour Pressure

The vapour pressure of any substance increases nonlinearly with temperature. As moving to height, atmospheric pressure decreases because air is less dense at higher altitude. Because the atmospheric pressure is low then the vapour pressure of liquid needs to be lower to reach the boiling point. Therefore, low heat is required to make vapour pressure equal to atmospheric pressure.

The concept of vapour pressure can be understood by this example, when a closed container is taken and half filled with water. The container is then heated and evaporation takes place, the water in the container escapes in the form of vapour, some of the molecules will be converted to vapour during evaporation. As a result, the amount of liquid in the container decreases and the amount of vapour increases. The evaporated gas molecules will randomly move along the empty space in the container, as a result of this random movement, some of the molecules will come in contact with the uppermost layer of the container and begin to condense.

In the beginning the rate of evaporation will not be equal to the rate of condensation, after sometime this equilibrium will be reached. At that equilibrium, the rate of evaporation is equal to the rate of condensation.

As time changes the number of molecules in a gaseous state increase while the rate of condensation also increases. At last, it reaches a stage where the rate of evaporation becomes equal to the rate of condensation. This stage is known as the equilibrium stage. At this point, the pressure exerted by the molecules on the wall is known as the vapour pressure of the liquid.

The ratio of the lowering of vapour pressure of a solution and the vapour pressure of the pure component is known as relative lowering of vapour pressure.

The vapour pressure of a liquid is the pressure applied by its gaseous phase where condensation and vaporization are in equilibrium, when a non-volatile substance is dissolved in a volatile liquid it results in lowering of the liquid’s vapour pressure.

This concept can be explained by understanding the effect of non-volatile solute molecules on the liquid’s tendency of vaporisation., for vaporisation to take place the solvent molecules must be present at the surface of the solution, the rate of vaporisation is reduced by the presence of non-volatile solutes, as they decrease the surface area available to the solute molecules.

The net result is that the vaporisation condensation equilibrium is achieved with fewer solvent molecules in the vapour phase, the presence of non-volatile solutes lowers the vapour pressure of a solution by impeding the evaporation of solvent molecules.

Raoult’s law describes the relationship between the vapour pressures of solution components and the concentrations of the components.

The partial pressure exerted by any component of an ideal solution is equal to the vapour of the pure component multiplied by its mole fraction in the solution.

If A is the solvent and B is solute we can write

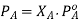
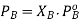
PA  is the partial pressure exerte by component A in the solution , POA  is the vapour pressure of Pure A and XA is the mole fraction in the solution.

B is a non volatile substance in one whose vapour pressure is negligible containing only non volatile solutes is due only to the solvent.

Since the solvent is the only volatile component of this solution, its vapour pressure may be computed as per Raoult’s law.

subtracting 1

From each side we get 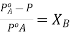. This is expression for RLVP

Since PB is zero

Hence we can say P is less than 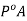and we can write the lowering of vapour pressure as

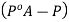
And the relative lowering can be written as

When a non-volatile solute (B) is dissolved in a liquid, the vapour pressure 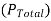of the solution becomes lower than the vapour of pure solvent.

From Raoult’s las: Vapour pressure of the solution is given by:

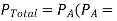Partial vapour pressure of the solvent in solution)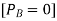

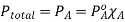
Where Vapour pressure of pure A and 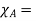mole fraction of A.

For Binary solution:

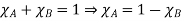
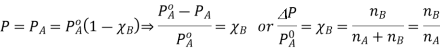
For dil. Solution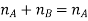

Relative lowering of vapour pressure=

Vapour pressure is the pressure exerted by the vapours over the liquid under the equilibrium conditions at a given temperature. Let us now take an example of a pure liquid, the surface of which is occupied by the molecules of the liquid. Suppose that a non-volatile solute is now added to this pure liquid. Since dissolved molecules are not volatile, the vapor above the solution consists only of solvent molecules (pure liquid). After adding the solute, the vapor pressure of the solution at a given temperature is lower than that of the pure liquid.

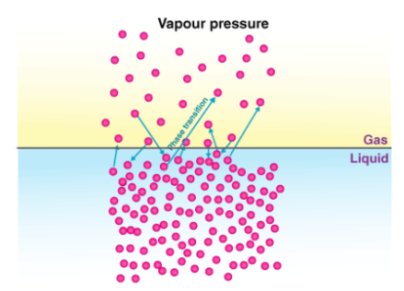
This decrease in vapor pressure is due to the fact that after the addition of the dissolved substance to the pure liquid (solvent), the liquid surface now had molecules of both the pure liquid and the dissolved substance. The phase is reduced and this also reduces the pressure exerted by the vapor phase. This is known as the relative decrease in vapor pressure. This decrease in vapor pressure, regardless of its nature, depends on the amount of non-volatile solute added to the solution and is therefore one of the colligative properties.

Experimental determination of relative lowering of vapour pressure and molecular weight determination

Relative lowering of vapour pressure (ΔP)

The vapor pressure of a non-volatile, non-electrolytic solution is always less than the vapor pressure of the pure solvent. When represents a closed system in which a pure solvent is in equilibrium with vapor, the molar Gibbs free energy of the solvent in the liquid and gaseous state (& Dgr; G = 0) is in equilibrium. When a solute is added to a solvent, dissociation occurs and the free energy (G) decreases, due to the increase in entropy. To maintain equilibrium, the free energy of the steam phase must also decrease. At a given temperature, the only way to reduce the free energy of the steam is to reduce its pressure. Therefore, the vapor pressure of the solution has to decrease in order to maintain equilibrium.

We know that from the Raoult's law the relative lowering of the vapour pressure is equal to the mole fraction of the solute

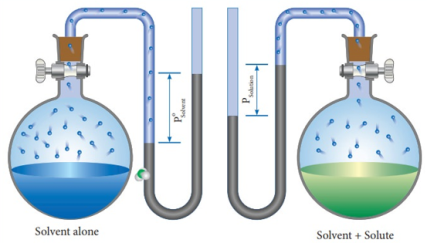
Fig: Measuring relative lowering of vapour pressure

From the diagram above it is clear that the relative decrease de the pressure only depends on the mole fraction of the solute (xB) and is independent of its nature. Hence the relative decrease in vapor pressure is a colligative property. 

4.3 Raoult’s and Henry’s Laws and their applications

Raoult's law is named after FrançoisMarie Raoult, a French chemist who discovered during an experiment that when substances were mixed in a solution, the vapor pressure of the solution decreased at the same time. Raoult's law was drawn up in 1887 and is also considered the law of thermodynamics.
Raoult's law states that the partial vapor pressure of a solvent in a solution (or mixture) is equal to or identical to the vapor pressure of the pure solvent multiplied by its mole fraction in the solution.

Mathematically, Raoult’s law equation is written as;

Psolution = ΧsolventP0solvent

Where,

Psolution = vapour pressure of the solution

Χsolvent  = mole fraction of the solvent

P0solvent = vapour pressure of the pure solvent

Henry’s law refers to a gas law that provides an explanation about the dissolution of a gas in a liquid medium. This law states that the quantity of gas dissolved in a liquid is directly proportional to the partial pressure of that gas that is in equilibrium with the liquid. This can be given in an equation as below.

[A(aq)] = kH.PA(g)

Where, [A(aq)] is the concentration of the gas A that is dissolved in the solution,

kH is Henry’s law constant

PA(g) is the partial pressure of A(g)

What is the Importance of Raoult’s law?

Assume that we have a closed container filled with a volatile liquid A. After a while, the vapor particles of A begin to form through evaporation. In the course of time, the vapor particles of A are in dynamic equilibrium with the liquid particles (on the surface). The pressure exerted by the vapor particles of A at a given temperature is called the vapor pressure of A at that temperature.

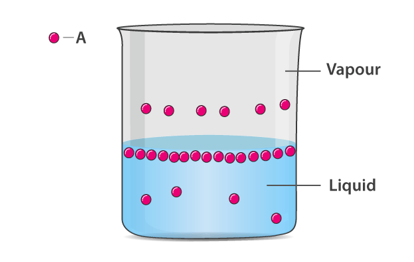
For every liquid there is a fraction of the molecules on the surface that have enough energy to escape into the vapor phase.

Now imagine that we add another liquid B (dissolved) to this container. This causes the B particles to occupy the space between the A particles on the surface of the solution.
For every liquid there is a fraction of the molecules on the surface that have enough energy to escape into the vapor phase.

Since we now have fewer A-particles on the surface, the number of A-vapor particles in the vapor phase will be less. This leads to a lower vapor pressure of A.
If we now assume that B is equally volatile, we have fewer B particles in the vapor phase than pure liquid B

This new pressure (partial pressure) of each (A and B) is given by Raoult's law and depends on the concentration of each component in the liquid phase.
Raoult's law shows that as the mole fraction of a component decreases, so does its partial pressure in the vapor phase.

Raoult's law is sufficient to describe ideal solutions. However, the ideal solutions are difficult to find and rare. The various chemical components must be chemically the same.

The graphs below show pressure is the mole fraction for A and B.

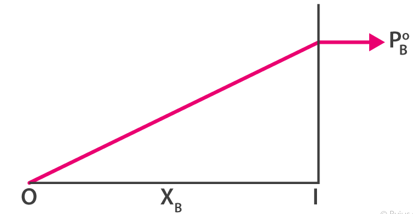
Combining both the graphs.

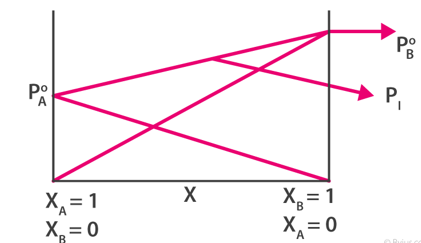
In the above diagram, we have also added the graph for the total vapour pressure of solution i.e. PA + PB.

As far as the application of the law goes, it is also useful in calculating the molecular mass of an unknown solute.

Limitations of Raoult’s Law

There are a few limitations to Raoult’s law.

Raoult's law is suitable for describing ideal solutions. However, ideal solutions are difficult to find and rare. The various chemical components must be chemically the same.
Because many of the liquids in the mixture do not have the same uniformity in terms of forces of attraction, these types of solutions tend to deviate from the law.

There is a negative or positive deviation. A negative deviation occurs when the vapor pressure is less than expected by Raoult's law. An example of a negative deviation is a mixture of chloroform and acetone or a solution of water and hydrochloric acid.

Alternatively, a positive reaction occurs when the cohesion between similar molecules is greater than the adhesion between different or different molecules. Both components of the mixture can easily escape from the solution. An example of a positive deviation is the mixtures of benzene and methanol or ethanol and chloroform.

Henry’s law constant is a proportionality constant and depends on the parameters like solvent, solute and temperature. Therefore, for a particular gas, the law varies at different temperatures Therefore, when calculating the solubility of a gas in water, one should obtain the value of Henry’s law constant at that particular temperature.

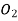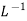is bubbled through water at 293 K. Assuming that exerts a partial pressure of 0.98 bar. Calculate the solubility of in . The value of Henry law constant (kH) for 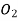is 34.84 k bar.

Solution

According to Henru’s law

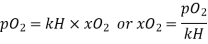
Mol of 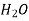in 1L=55.5

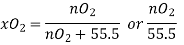
Difference Between Henry’s Law and Raoult’s Law

Definition

Henry’s Law: Henry’s law is a thermodynamic law that refers to the gas that is dissolved in a liquid medium.

Raoult’s Law: Raoult’s law is a thermodynamic law that gives an explanation about the relationship between the vapour pressure of a solution and the partial pressures of solutes in that solution.

Concept

Henry’s Law: Henry’s law states the quantity of gas dissolved in a liquid is directly proportional to the partial pressure of that particular gas and also is in equilibrium with that liquid.

Raoult’s Law: Raoult’s law refers to the vapour pressure of a solvent above a solution and is equal to the vapour pressure at that particular temperature, multiplied by the mole fraction of the solvent.

Proportionality Constant

Henry’s Law: The proportionality constant in Henry’s law is called Henry’s law constant.

Raoult’s Law: The Raoult’s law does not use a proportionality constant.

Following is the table explaining the difference between Henry’s law and Raoult’s law:

Conclusion

The chemical behaviour of solutions that are in contact with their vapour pressure is specified by Henry’s law and Raoult’s law, the difference between these two laws is that henrys law specifies the behaviour of solutes in solution, whereas the Raoults law explain the bahaviour of solvent in a solution.

Applications:

• Henry's Law in carbonated soft drinks: When the bottle with soft drinks is opened, part of the gas escapes and causes a certain shock. This is due to the lower pressure on the liquid and the carbon dioxide comes out in the form of bubbles.
• Henry's Law in Respiration: The amount of oxygen that dissolves in the bloodstream is directly proportional to the partial pressure of oxygen in the air in the alveoli.

Raoults law: Two applications in chemistry:

Calculating the Vapor Pressure of a Solvent;

Calculating the Molecular Mass (Formula Weight) of a Solute.

4.4 Thermodynamic derivation using chemical potential to derive relations between the four colligative properties:

Properties, is a property of a solution that depends on the ratio between the total number of solute particles present in the solution and the total number of solvent particles. The Colligative properties are not dependent on the chemical nature of the solution’s components. Thus, these properties are linked to several quantities that express the concentration of a solution, like molality, normality and molarity. The four properties that are colligative in nature that is exhibited by a solution are:

• The boiling point of elevation
• The freezing point of depression
• The relative lowering of vapour pressure
• The Osmotic pressure

The word “colligative” is taken from the Latin word has been adapted or taken from the Latin word “colligatus” which means to “bound together”. When a solution is defined, the colligative properties help to analyse how the properties of solution is linked to the concentration of solute in a solution.

What are Colligative Properties?

Non-volatile solute that are dilute exhibit some properties that depend only on the number of solute particles present in the solution and not on the solute present in the solution. These properties are called colligative properties. Such properties are seen mostly in dilute solutions.

(i) Elevation of boiling point of solution

Boiling point elevation refers to the increase in the boiling point of a solvent after the addition of a solute. When a non-volatile solute is added to a solvent, the resulting solution has a higher boiling point than the solvent pure. The boiling point of a solution of sodium chloride (salt) and water is higher than that of pure water.

The increase in the boiling point is a colligative property of matter, the amount of solute added. The concentration of the solute in the solution, the higher the increase in boiling point.

A graph detailing the elevation in the boiling point of water upon the addition of sucrose is provided above. At 1atm of pressure, pure water boils at 100oC. However, a 10 molal solution of sucrose in water boils at approximately 105oC.

Why Does Boiling Point Elevation Occur?

The boiling point of a liquid is the temperature at which its vapor pressure equals the pressure of its surroundings. Non-volatile substances do not evaporate easily and have a very low vapor pressure (assuming zero). When added to a solvent, the vapor pressure of the resulting solution is lower than that of the pure solvent.

Therefore, more heat has to be added to the solution to bring it to the boil. This increase in the boiling point of the solution is the increase in the boiling point. An increase in the concentration of the added solute is accompanied by a greater decrease in the vapor pressure of the solution and a greater increase in the boiling point of the solution.

A pressure v/s temperature graph detailing the boiling point elevation of a solution is provided below.

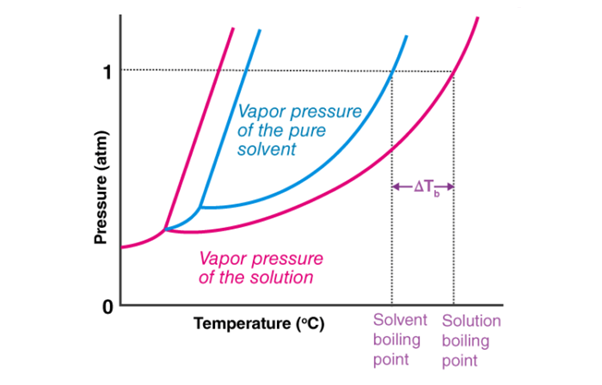
Here, ΔTb represents the increase in the boiling point of the solution. The graphic shows that –

1. The freezing point of the solution is lower than that of the pure solvent (lowering of the freezing point).

2. The boiling point of the solution is higher than that of the pure solvent.

Note: The boiling point of a liquid also depends on the pressure of its surroundings (this is why water boils at temperatures below 100 ° C at high altitudes, where the ambient pressure is low).

Note: The boiling point of a liquid is also dependent on the pressure of its surroundings (which is why water boils at temperatures lower than 100oC at high altitudes, where the surrounding pressure is low).

Boiling Point Elevation Formula

The boiling point of a solution containing a non-volatile solute can be expressed as follows:

Boiling point of solution = boiling point of pure solvent + boiling point elevation (ΔTb)

The elevation in boiling point (ΔTb) is proportional to the concentration of the solute in the solution. It can be calculated via the following equation.

ΔTb = i*Kb*m

Where,

• i is the Van’t Hoff factor
• Kb is the ebullioscopic constant
• m is the molality of the solute

It is important to note that this formula becomes less precise when the concentration of the solute is very high. Also, this formula doesn’t hold true for volatile solvents.

If a non-volatile solute is added resulting in the lowering of vapour pressure through Raoul’s law, then the temperature must be raised to restore the vapour pressure to a value that corresponds to the pure solvent. The temperature at which the vapor pressure is 1 atm is higher than normal boiling point by a known specific amount called boiling point elevation, and when the addition of a nonvolatile solute reduces the vapor pressure of the solution according to Raoult's law, it follows that the temperature has to be increased in order to bring the vapor pressure back to the value of the pure solvent. In particular, the temperature at which the vapor pressure is 1 atm is higher than the boiling point in an amount known as boiling point height. The exact relationship between the boiling point of the solution and the mole fraction of the solvent is very complicated, but with dilute solutions the increase in boiling point is directly proportional to the molar concentration of the solute:

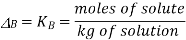
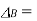Boiling point elevation (K)

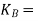molal boiling point elevation constant

Note that the constant of KB proportionality is a property of the solvent as it is the only component that contributes to vapor pressure.

The boiling point of a liquid is the temperature at which the vapour pressure is equal to atmospheric pressure. The addition of non-volatile liquid to a pure solvent, there is a decrease in the vapour pressure of the solution, to make this vapour pressure equal to atmospheric pressure, the temperature of the solution has to be increased. The difference in the boiling point of the solution and the boiling point of the pure solvent is termed as elevation in boiling point.

If T0b is the boiling point of the pure solvent and Tb is the boiling point of the solution then elevation in boiling point is given as

∆Tb =T0b-Tb

Experimental results show that there is a relation between elevation in boiling point and molality ‘m’ of the solute present in solution

∆Tb ∝ m

∆Tb = kb m

Where,

Kb = molal elevation constant

Substituting the value of ‘m’ in the above relation we get

∆Tb = 1000 x kb x m2 / M2 x m1

Where,

m2 = mass of solvent in g

M1 = mass of solvent in kg

M2 = molar mass of solute

Example 1

Calculate the boiling point of a 3.5% solution (by weight) of sodium chloride in water.

1 kg of the given solution contains 0.035kg of NaCl and 0.965kg of H2O. Since the molar mass of NaCl is 58.5, the number of moles of NaCl in 1 kg of the solution is:

(35g)/(58.5g.mol-1) = 0.598 moles

The molality of NaCl in 1kg of the solution can be calculated as:

m = (0.598mol)/(0.965 kg) = 0.619 molal

The boiling point elevation constant of water is 0.512 oC.kg/molal. Since NaCl dissociates into 2 ions, the Van’t Hoff factor for this compound is 2. Therefore, the boiling point elevation (ΔTb) can be calculated as follows:

ΔTb = 2*(0.52oC/molal)*(0.619 molal) = 0.643oC

Boiling point of the solution = boiling point of pure solvent + boiling point elevation

= 100oC + 0.643oC = 100.643oC

Therefore, the boiling point of the 3.5% NaCl solution is 100.643oC.

Example 2

10 grams of a non-volatile and non-dissociating solute is dissolved in 200 grams of benzene. The resulting solution boils at a temperature of 81.2oC. Find the molar mass of the solute.

Let x = number of moles of solute. The boiling point of pure benzene is 80.1oC and it’s ebullioscopic constant is 2.53oC/molal. From the boiling point elevation formula, the following relationship can be obtained:

(81.2oC – 80.1oC) = (1)*(2.53oC.kg.mol-1)(x/0.2 kg)

x = (1.1oC*0.2kg)/(2.53oC.kg.mol-1)

x = 0.0869 moles

Since 0.0869 moles of the solute has a mass of 10 grams, 1 mole of the solute will have a mass of 10/0.0869 grams, which is equal to 115.07 grams. Therefore, the molar mass of the solute is 115.07 grams per mole.

(ii) Freezing Point Depression

The freezing point of a substance is the temperature at which the solid and liquid forms can coexist indefinitely meaning they are in equilibrium that is, they are in equilibrium. In the presence of these conditions the molecules pass between the two phases at an equal rate, as their escaping tendencies from the two phases are similar.

For example, a liquid solvent and its solid like water and ice are at equilibrium given in (1 below), on addition of non-volatile solute (such as salt, sugar, or automotive antifreeze liquid) to the water. This leads to the fact that the mole fraction of the H2O molecules in the liquid phase is reduced and thus the tendency of these molecules to escape from it, not only into the vapor phase (as we saw before), but also into the solid phase (ice) This has no influence on the speed with which the H2O molecules escape from the ice into the aqueous phase, so that the system is no longer in equilibrium and the ice begins to melt 2.

If the solid is prevented from melting the tendency of the molecules to escape, from the solid should be reduced, and this can be only achieved by reducing the temperature., this helps to lower the tendency of molecules to escape from both the phases but it affects those in the solid more than those in the liquid, so we eventually reach the new, lower freezing point where the two quantities are again in exact balance and both phases can coexist 3.

If vapour pressure is taken into consideration, then the vapour pressure of the solid and liquid should have the same freezing point. Dilution of the liquid (the solvent) by the non-volatile solute results in the decrease of vapour pressure of the solvent by the Raoult’s law, therefore reducing the temperature of the vapour pressure of the liquid frozen forms of the solution will be equal. As with boiling point elevation, in dilute solutions there is a simple linear relation between the freezing point depression and the molality of the solute:

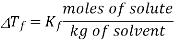
Note that Kf values are all negative!

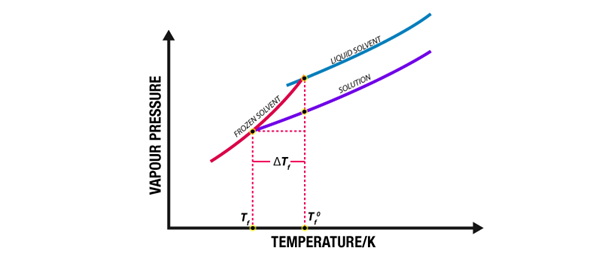
The freezing point of a substance is defined as the temperature at which the vapour pressure of its liquid is equal to the vapour of the corresponding solid. According to Raoult's law, when a non-volatile solid is added to the solvent, the vapor pressure decreases and would now be equal to that of the solid solvent at a lower temperature. The difference between the freezing point of the pure solvent and its solution is called the freezing point depression.

If T0f is the boiling point of the pure solvent and Tf is the boiling point of the solution then depression in freezing point is given as

∆Tf =T0f-Tf

Just like elevation in boiling point, depression in freezing point is also directly related to molality ‘m’.

∆Tf = 1000 x kf x m2 / M2 x m1

Where,

k f = molal depression constant

m2 = mass of solvent in g

M1 = mass of solvent in kg

M2 = molar mass of solute

Freezing point depression refers to the lowering of the freezing point of solvents upon the addition of solutes.

It is a colligative property of solutions that is generally proportional to the molality of the added solute. The depression in the freezing point of a solution can be described by the following formula.

ΔTf = i*Kf*m

Where

• ΔTf is the freezing point depression,
• i is the Van’t Hoff factor,
• Kf is the cryoscopic constant, and
• m is the molality.

Freezing Point Depression in Solutions

According to Raoult's law, "the vapor pressure of a pure solvent decreases with the addition of a solute." Since the vapor pressure of a non-volatile solvent is zero, the total vapor pressure of the solution is lower than that of the pure solvent.

Why does the Freezing Point Depression Occur?

The reason why the freezing point of a solvent is lowered when a solute is added is explained below.

• At the freezing point of a solvent there is an equilibrium between the liquid and solid state of the solvent.

• This implies that the vapor pressures of both the liquid and the solid phase are the same.

• After adding a non-volatile dissolved substance, the vapor pressure of the solution is lower than the vapor pressure of the pure solvent.

• This brings solid and solution into equilibrium at lower temperatures.
Below is a graph showing the depression of freezing point of water after adding sucrose.

A graph detailing the freezing point depression of water upon the addition of sucrose to it is provided below.

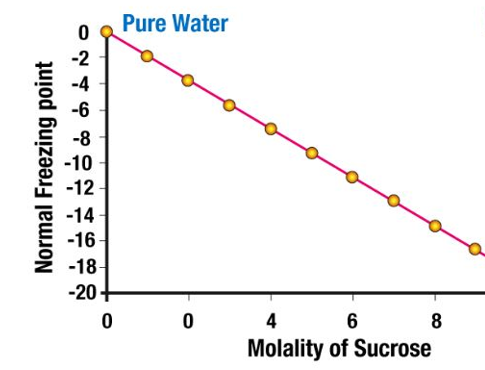
Freezing Point Depression Graph

From the graph, it can be observed that the increase in the molality of sucrose causes further depression in the freezing point of the solvent (water).

Freezing Point Examples

The freezing point of sea water is below 0 ° C; At temperatures below the freezing point of pure water, it remains liquid due to the salts dissolved in it.

• Another example of solvent freezing point depression is seen in vodka. It can be thought of as a solution of ethanol in water, and its freezing point is lower than that of water but higher than that of pure ethanol.

• Many organisms can survive in freezing climates because their bodies can produce compounds such as glycerin and sorbitol that help lower the freezing point of water in their bodies.

Some major applications of freezing point depression are listed below.

• In cold areas with temperatures between 0 ° C and 15 ° C, sodium chloride is distributed on roads to lower the freezing point of the water and prevent ice formation.

• At temperatures below 18oC, calcium chloride is used instead of NaCl to melt ice on the streets. This is because CaCl2 dissociates into 3 ions, which causes greater depression at the freezing point of water.

• Radiator fluids used in many automobiles generally consist of ethylene glycol and water. This prevents the radiator from freezing in the cold season.

• The molar mass of a certain dissolved substance can be determined from the formula for lowering the freezing point.

(iii)Measurement of Elevation of Boiling Point

The elevation of boiling point in a dilute solution is small and requires a very sensitive thermometer, the Beckmann thermometer is specifically used for this purpose.

Beckmann thermometer: Beckmann thermometer is a differential thermometer. The thermometer is designed in such a way that it records very minute changes temperature, but does not measure the actual temperature of the solvent or of the solution. The thermometer has several designs the most common one is described below.

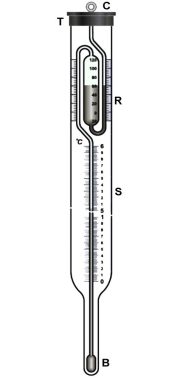
Figure: Beckmann thermometer

The thermometer consists of a large bulb B present at the bottom and a reservoir with mercury R present at the top, the thermometer is calibrated from 0to 6K and the wale S is subdivided into 0.01 K. The mercury in the two reservoirs can be accustomed by careful manipulation, depending on whether ebullioscopy or cryoscopy measurements are carried out.

Beckmann’s Method: This device is generally used to estimate the temperature rise. A known volume of a certain mass of the solvent is first added to the boiler tube to fill approximately two thirds of its capacity.

By definition, the boiling point is the temperature at which the vapor pressure of the liquid corresponds to the ambient pressure and the liquid also turns into vapor.

The boiler pipe is connected on one side to a reflux condenser and on the other side to a tube E for the addition of the dissolved substance. An insulated jacket surrounds the boiler tube and the Beckman thermometer is inserted into the boiler tube through a rubber stopper so that the lower bulb of the thermometer is in contact with the solvent. The boiling point of a liquid is the temperature at whose vapor pressure corresponds to the pressure of its surroundings.

Figure: Complete Beckmann apparatus

The boiler pipe is heated with the help of a Bunsen burner or an electrical supply. First, the thermometer reading is noted, which shows the boiling point of the pure solvent. The experiment is repeated after adding the dissolved substance of known mass. The difference in the Beckmann measurement in these two experiments gives a measure of the increase in the boiling point. Since the mass of the solute, the solvent, and K for the solvent are known, the relative molecular weight of the solute can be easily determined. When a non-volatile solute is added to a solvent, the vapor pressure of the resulting solution is lower than that of the pure solvent.

We know that pure water boils at 100 ° C at 1 atm pressure, but the boiling point changes when a small amount of salt is added due to the displacement of solvent molecules by the solute, it has been shown experimentally that the addition of any Form of non-volatile solutes in a liquid increases its boiling point. The vapor pressure is reduced. The amount by which the boiling point changes is directly proportional to the amount of solute added. In order for the vapor pressure to match atmospheric pressure, a higher temperature is required and a higher boiling point is observed.

Freezing Point Depression

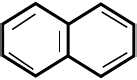
When a small amount of non-volatile solute is dissolved in a volatile solvent, the vapor pressure of the solvent over the solution will be less than the vapor pressure of the pure solvent at the same temperature. Therefore, the temperature at which the equilibrium vapor pressure reaches atmospheric pressure is higher for the solution than for the pure solvent. Similarly, because of the reduction in vapor pressure over the solution the freezing point of the solution, is lower than the freezing point of pure solvent. The amount by which the freezing point of the solution is decreased from that of the pure liquid, is called the freezing point depression. The solute in this is laboratory experiment is naphthalene, C10H8 which has the following structure and is non polar. The freezing point will be the temperature where the graph plateaus since the kinetic energy doesn’t change during the physical state change. For a solution on, the graph will look a little different. Instead of a long horizontal portion, the graph will start gradually curving downward shortly after levelling off. This occurs because as the solution freezes, the part of the solution that hasn’t frozen yet will become more concentrated since the solute remains in the solution.

Calculations:

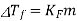
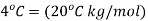
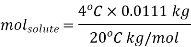
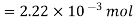
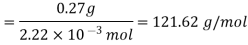
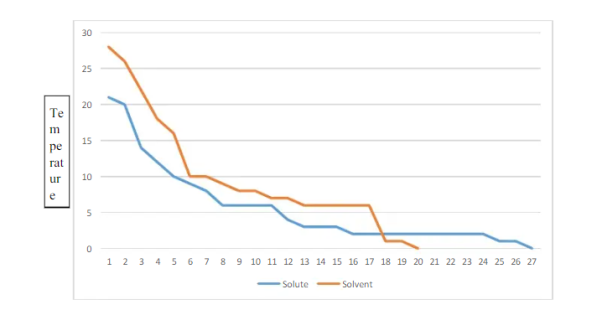
Figure. Plot of Temperature Vs Time

When a dilute solution begins to freeze, the solid crystals of solvent form at a lower temperature than they do when the pure liquid solvent is cooled. This phenomenon is called freezing point depression and is a colligative property that depends only on the concentration, and not the chemical properties, of the solute.

The quantitative expression of freezing point depression is:

ΔTf = Kf m, where m is the molality (moles solute per kg

Of solvent), Kf is the freezing point depression constant of the solvent

And ΔTf is the difference between the freezing point of the pure solvent and that of the solution. The constant Kf depends on the solvent but not on the solute. The solvent will be cyclohexane, which has

Kf  = 20. This method is clearly inadequate for opaque mixtures, and it is subject to errors from a phenomenon known as super cooling. A more accurate technique is to measure a cooling curve, which is a temperature vs. Time plot for a sample losing heat at an approximately constant rate.

Factors Affecting Vapour Pressure

There are four factors on which vapour pressure depends. They are:

Nature Of Liquid

Nature of liquid is explained on the basis of its intermolecular forces. That is, as the magnitude of the intermolecular forces increases vapour pressure will decrease.

Effect Of Temperature

As the temperature of the liquid increases the kinetic energy associated with the liquid also increases. And due to this increase in kinetic energy the escaping tendency of molecule increases and hence vapour pressure increases. So, we can conclude that vapour pressure is directly proportional to temperature.

Concentration Of Solute

The presence of solute in the liquid will decrease the vapour pressure. And this fall in vapour pressure also varies with the concentration of solute.

Vapour Pressure Is Independent of Humidity

Temperature

Temperature is the only property that affects the vapour pressure for a certain amount of water vapour in the air. Humidity will affect only if all the other variables are constant. So don’t be confused between the effect of temperature and humidity.

Volume

Vapour pressure will not be affected by the volume of the container. As we know that liquid in the container will be in equilibrium with the vapour. When the volume is changed say decreased, then some of the vapour in the container turns into a liquid state. And if the volume increases some of the liquid will change into its vapour state.

Surface Area

Normally vapour pressure is independent of surface area. Change in surface area will not affect the vapour pressure of a substance.

The vapour pressure of a liquid is the pressure applied by its gaseous phase where condensation and vaporization are in equilibrium, when a non-volatile substance is dissolved in a volatile liquid it results in lowering of the liquid’s vapour pressure.

This concept can be explained by understanding the effect of non-volatile solute molecules on the liquid’s tendency of vaporisation., for vaporisation to take place the solvent molecules must be present at the surface of the solution, the rate of vaporisation is reduced by the presence of non-volatile solutes, as they decrease the surface area available to the solute molecules.

The net result is that the vaporisation condensation equilibrium is achieved with fewer solvent molecules in the vapour phase, the presence of non-volatile solutes lowers the vapour pressure of a solution by impeding the evaporation of solvent molecules.

Raoult’s law describes the relationship between the vapour pressures of solution components and the concentrations of the components.

The partial pressure exerted by any component of an ideal solution is equal to the vapour of the pure component multiplied by its mole fraction in the solution.

If A is the solvent and B is solute we can write

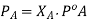
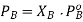
PA  is the partial pressure exerte by component A in the solution , POA  is the vapour pressure of Pure A and XA is the mole fraction in the solution.

B is a non volatile substance in one whose vapour pressure is negligible containing only non volatile solutes is due only to the solvent.

Since the solvent is the only volatile component of this solution, its vapour pressure may be computed as per Raoult’s law.

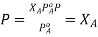subtracting 1

From each side we get .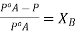

This is expression for RLVP

Since PB is zero

Hence we can say P is less than 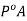and we can write the lowering of vapour pressure as

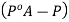
And the relative lowering can be written as

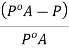
Relative lowering of vapour pressure (ΔP)

The vapor pressure of a non-volatile, non-electrolytic solution is always lower than the vapor pressure of the pure solvent. If one considers a closed system in which a pure solvent is in equilibrium with steam, then the molar Gibbs free energy of the solvent in the liquid and the gaseous state is in equilibrium (ΔG = 0). When a solute is added to a solvent, dissociation occurs and the free energy (G) decreases due to the increase in entropy. In order to maintain equilibrium, the free energy of the steam phase must also decrease. At a given temperature, the only way to decrease the free energy of the steam is to decrease its pressure. Therefore, the vapor pressure of the solution has to decrease in order to maintain equilibrium.
We know that from Raoul’s law the relative decrease in vapor pressure is equal to the mole fraction of the solute

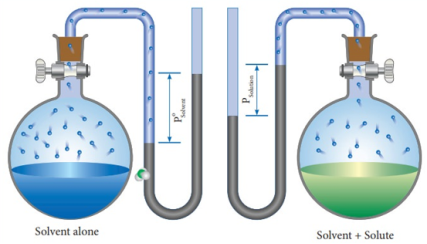
Fig: Measuring relative lowering of vapour pressure

From the above diagram, it is clear that the relative lowering of vapour pressure depends only on the mole fraction of the solute (xB) and is independent of its nature. Therefore, relative lowering of vapour pressure is a colligative property.

Osmotic pressure and the Solute

Osmosis Definition

“Osmosis is a process by which the molecules of a solvent pass from a solution of low concentration to a solution of high concentration through a semi-permeable membrane.”

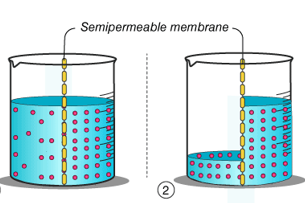
Fig: Osmosis through a semipermeable membrane

Osmosis is a process that is passive in nature and does not require any energy, in the process the molecules move from a region of higher concertation to a region of lower concentration until the concentration are the same eon both sides of the semipermeable membrane. Any solvent can undergo the process of osmosis including gases and supercritical liquids.

Osmotic Solutions

There are three different types of solutions:

• Isotonic Solution
• Hypertonic Solution
• Hypotonic Solution

An isotonic solution is a solution where the concentration of the solutes is the same both inside and outside the cell.

A hypertonic solution is a solution where the concentration of the solute is higher outside the cell than inside the cell.

A hypotonic solution the concentration of the solute is higher inside the cell than the outside.

Types of Osmosis

Osmosis is of two types:

1. Endosmosis: When a substance is placed in a hypotonic solution, the solvent molecules move within the cell and the cell becomes swollen or undergoes deplasmolysis. This is known as endosmosis.
2. Exosmosis: When a substance is placed in a hypertonic solution, the solvent molecules move out of the cell and the cell becomes flaccid or undergoes plasmolysis. This is known as exosmosis.

Effects of osmosis on cells

Osmosis affects cells differently. An animal cell is lysed in comparison to a plant cell when it is placed in a hypotonic solution. The plant cell has thick walls and needs more water. The cells do not explode when placed in a hypotonic solution. In fact, a hypotonic solution is ideal for a plant cell.

An animal cell can only survive in an isotonic solution. In an isotonic solution, the plant cells are no longer swollen and the plant leaves fall off.
The osmotic flow can be stopped or reversed, also called reverse osmosis, by applying external pressure on the sides of the solute. The minimum pressure required to stop solvent transfer is called the osmotic pressure.

Endosmosis: When a substance is placed in a hypotonic solution, the solvent molecules move within the cell and the cell becomes swollen or undergoes deplasmolysis. This is known as endosmosis.

Exosmosis: When a substance is placed in a hypertonic solution, the solvent molecules move out of the cell and the cell becomes flaccid or undergoes plasmolysis. This is known as exosmosis.

Effects of osmosis on cells

Osmosis affects cells differently. An animal cell is lysed in comparison to a plant cell when it is placed in a hypotonic solution. The plant cell has thick walls and needs more water. The cells do not explode when placed in a hypotonic solution. In fact, a hypotonic solution is ideal for a plant cell.
An animal cell can only survive in an isotonic solution. In an isotonic solution, the plant cells are no longer swollen and the plant leaves fall off.
The osmotic flow can be stopped or reversed, also called reverse osmosis, by applying external pressure on the sides of the solute. The minimum pressure required to stop solvent transfer is called the osmotic pressure.

Significance of Osmosis

• Osmosis influences the transport of nutrients and the release of metabolic waste products.
• It is responsible for the absorption of water from the soil and conducting it to the upper parts of the plant through the xylem.
• +the water and intercellular fluid cells.
• The turbidity of cells is maintained.
• It is a process by which plants maintain their water content despite the constant water loss due to transpiration.
• This process controls the cell-to-cell diffusion of water.
• Cell turgor is introduced by osmosis that regulates the movement of plants and the parts of the plant.
• Dehiscence of fruits and sporangia are also controlled by osmosis.
• Drought injury against plants can be protected by a high osmotic pressure.

(iv)Osmotic Pressure

It is the pressure that is required to prevent water from diffusing through a membrane by osmosis. Osmotic pressure is estimated by the concentration of the solute. Water diffuses to the area of higher concentration from the area of lower concentration, this continues until the concertation is uniform throughout (when concentrations of the substances in both areas are different)

Osmotic pressure can be calculated using the equation:

Π=MRT

Where Π denotes the osmotic pressure,

M is the molar concentration of the solute,

R is the gas constant,

T is the temperature

Examples and Applications

Plants keep their upright shape with the help of osmotic pressure. When enough water is supplied to the plant, its cells (which contain various salts) absorb water and expand. This expansion of the plant cells increases the pressure exerted on their walls. Making them stand up.

If the plant is given too little water, its cells become hypertonic (shrink due to water loss), causing them to wither and lose their firm, upright posture.
Another important application of osmotic pressure is the desalination and purification of seawater, which involves the process of reverse osmosis.

Exercise 1

One mole of table salt is dissolved in one litre of water. At a temperature of 27oC, what would be the osmotic temperature of this solution?

The molar concentration of table salt (sodium chloride) in the solution = 1mol/1litre = 1M

Since salt (NaCl) dissociates into two ions, the value of the van’t Hoff factor here is 2. Converting 27oC to the Kelvin scale, the required temperature becomes 300K.

Therefore, the osmotic pressure of the solution is:

π = (2) * (1 mol.L-1) * (0.0821 atm.L. Mol-1.K-1) (300 K)

π = 49.26 atm.

The osmotic pressure of the 1M salt solution is 49.26 atmospheres at a temperature of 27oC.

Exercise 2

The osmotic pressure of a potassium chloride solution (at 300K) is 50 atmospheres. What is the molar concentration of potassium chloride in this solution?

Rearranging the osmotic pressure equation, the following equation can be obtained:

π = iCRT ; C = π/(iRT)

Here, the value of i is 2 (since KCl dissociates into two ions). Therefore, the molarity of KCl is:

C = (50 atm)/(2)*(0.0821 atm.L.mol-1.K-1)*(300K)

C = 50/49.26 M = 1.015 M

Therefore, the molar concentration of potassium chloride in the solution is 1.015 M.

Determination of Osmotic Pressure by Pfeffer’s method

Abbe Nollet (1748) was the first person to notice the phenomenon of osmosis and made measurements of the osmotic pressure. He chose pigs bladder as the semi permeable membrane, however the membrane failed to meet the requirements as the results were semi quantitative and the pig’s bladder was not a very good semi-permeable membrane. It was the botanist Pfeffer, he was successful in making a good semi permeable membrane and succeeded in making measurements for osmotic pressure. The Pfeffer Cell Apparatus, invented by Wilhelm Pfeffer in 1877, the instrument measured the minimum pressure that was required to stop a pure solvent from passing into a solution across a semipermeable membrane that is called the osmotic pressure.

The osmotic pressure of a solution at a particular temperature is defined as the additional hydrostatic pressure that is required that builds up when the solution is separated from the solvent by a semipermeable membrane. It is denoted by p.

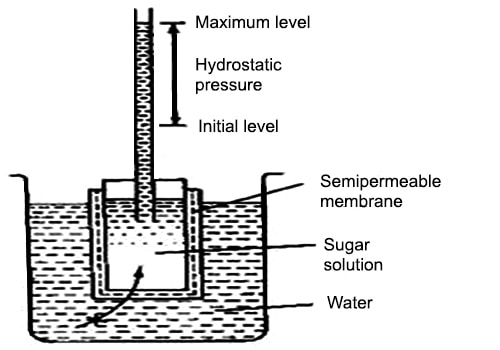
Fig: The Pfeffer’s apparatus for determination of osmotic pressure

Pfeffer’s method: he developed a technique by depositing gelatinous copper ferrocyanide in the pores of an earthen pot, this earthen pot was used as the semipermeable membrane. Osmosis is mainly a diffusion of a solution through a semipermeable membrane. His apparatus for the measurement of osmotic pressure is shown in Figure. The porous pot, that has deposits of copper ferrocyanide in its pores is connected to a manometer. The pot is filled with the solution to be examined and this is placed in a vessel that consists of the solvent. The entire set up is paled in a thermostat and maintained this way till equilibrium is reached. At equilibrium, the difference in the heights of mercury columns in the two tubes gave the osmotic pressure. Osmotic pressure is the excess pressure that should be applied to a given solution in order to increase its vapor pressure until it becomes equal to that of the solution. The osmotic pressure of a solution is the pressure difference needed to stop the flow of solvent across a semipermeable membrane.

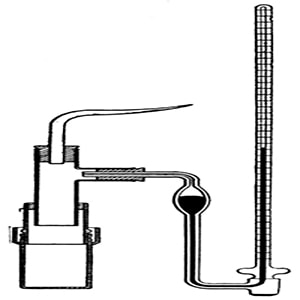
Fig: Pfeffer ‘s apparatus for measurement of osmotic pressure

The osmotic pressure of a particular solution is proportional to the molar concentration of the solute particles present in the solution. This method is slow as it may take few days for equilibrium to be reached, also if the pressure is too high the membrane may break and it cannot be used again. When a semipermeable membrane (animal bladders, skins of fruits and vegetables) separates a solution from a solvent, then only solvent molecules are competent to pass through the membrane. Pfeffer’s method was improved by Berkeley and Hartley.

Determination of molar mass weights from relative lowering of vapour pressure

The molar mass of a non-volatile solute can be determined by measuring the relative lowering of vapour pressure, for this a known mass of the solute is dissolved in a known solvent. The relative lowering of vapour pressure is measured experimentally.

According to Raoult’s law the relative lowering of vapor pressure is,

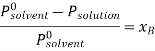
Let wAand wB be the weights of the solvent and solute respectively and their corresponding molar masses are MA and MB, then the mole fraction of the solute xB is

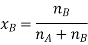
Here, nA & nB are the moles of the solvent and the solute respectively. For dilute solutions nA>>nB. Hence nA +nB ≈ nA. Now

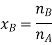
Number of moles of solvent and the solute are,

Therefore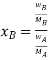

Thus Relative lowering of vapour pressure =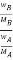

Relative lowering of vapour pressure

From the equation the molar mass of the solute (MB) can be calculated using the known the values of wA, wB, MA and the measured relative lowering of vapour pressure.

In order to account for extent of association or dissociation, Van’t Hoff introduced a factor 'i'.

4.5 Dissociated and associated solutes in solution

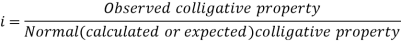
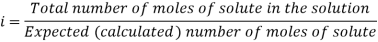
Degree of association is defined as the fraction of the total number of molecules which associate to form a bigger molecule.

Degree of Dissociation

Degree of dissociation is defined as the fraction of the total number of particles that dissociate, i.e., break into simpler ions.

The Van’t Hoff factor offers insight on the effect of solutes on the colligative properties of solutions. It is denoted by the symbol ‘i’. The Van’t Hoff factor is defined as the ratio of the particle’s concentration formed when a substance is dissolved to the substance concentration by mass.

The degree to which a substance dissociates or associates in a solution is described by the Van’t Hoff factor. For example, the value of i is generally 1 when the non-electrolytic substance is dissolved in water, however when an ionic compound is dissolved in water the value of i is equal to the total number of ions present in one formula unit of the substance.

For example, the Van’t Hoff factor of CaCl2 is ideally 3, as CaCl2 dissociated into one Ca2+ ion and two Cl– ions. Sometimes these ions associate with each other causing a decrease in the total number of particles in the solution.

This factor is named after the Dutch chemical physicist Jacobus Henricus Van't Hoff, who received the first Nobel Prize in Chemistry. It is important to note that the measured value of the Van't Hoff factor for electrolyte solutions is generally lower than the predicted value (due to ion pairing). The greater the charge on the ions, the greater the deflection.

Van't Hoff explained that when solutes dissolve in a solvent, they dissociate into ions. Since the colligative properties only depend on the number of dissolved particles, the dissociation of dissolved molecules into ions leads to an increase in the number of particles and thus influences the colligative properties.

Effects of Association/Dissociation

• Association is the union of two or more particles into one unit.
• An example of the association of two particles is the dimerization of carboxylic acids when they are dissolved in benzene.
• Dissociation refers to the division of a molecule into several ionic units.
• For example, sodium chloride (NaCl) dissociates into Na + and Cl– ions when it dissolves in water.

The effects of the association or dissociation of a solute on the solution, its colligative properties, and the Van’t Hoff factor are tabulated below.

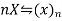
Let x be the degree of association.

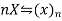
Initially  1 0

In solution  1-x x/n

Total moles (or molecules) in the solution =1-x+x/n

Total moles (or molecules ) in the solution=1-x+x/n

As osmotic effect is proportional to the number of moles (or molecules)

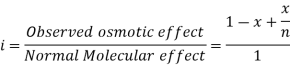
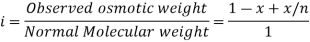
The previous example shows the dissociation of a molecule, reactions such as this can be easily described with respect to the fraction of reactant molecules that bring about equilibrium in a sample as the reactant molecules dissociate completely, this fraction is known as degree of dissociation. For the reaction in the previous example

A(g)⇌2B(g)

Mole fraction A and b can be expressed as

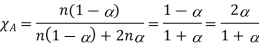
Based on mole fractions

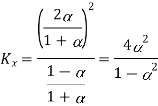
And Kp is expressed as

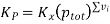
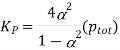
From the values given below, the equilibrium constant at 250C and the degree of dissociation for a system with a total pressure of 1.00 atm for the reaction

N2O4(g)⇌2NO2(g)N2O4(g)⇌2NO2(g)

Solution

First, the value of Kp can be determined from ΔGorxn via an application of Hess' Law.

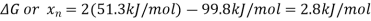
So, using the relationship between thermodynamics and equilibria

The degree of dissociation can then be calculated from the ICE tables at the top of the page for the dissociation of N2O4(g)N2O4(g):

Solving for αα,

α=0.273α=0.273

Note: since a represents the fraction of N2O4 molecules dissociated, it must be a positive number between 0 and 1

Relation between osmotic pressure and lowering of vapour pressure

Van’t Hoff equation for dilute solutions is

π=Vn​RT.....(i)

In case of a dilute solution, The volume of solution can be taken as equal to that of the solvent. If N is the number of moles of the solvent of molecular weight M and density ρ, the volume V is given by

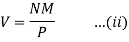
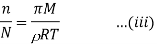
From Raoult’s law

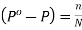   (iv)

Or [From (iii) and (iv)]

The factor 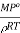is constant at constant temperature

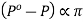
Or lowering of V.P∝ osmotic pressure

Abnormal Colligative Properties of solutions.

The colligative properties are dependent on the number of particles of the solute, in few cases when the solute dissociates or associates in the solution, abnormal results occur for molecular mass

As studied earlier the colligative properties of a solution depends solely on the number of particles of the solute and not on their nature. But sometimes while measuring colligative properties abnormal results are obtained due to the following reasons:

1. When the solution is very concentrated, the particles present in the solution of the solute begin to interact with each other, therefore the solution should not be highly concentrated.
2. In case of association of two or more molecules of solute associate together to form a bigger molecule, the number of effective molecules in the solution therefore decreases. As the colligative property is inversely proportional to molar mass, the molar mass of such particles when calculated on the basis of colligative property the value will be higher than the true molar mass of the solute.
3. In case of dissociation of two or more particles of the solute in the solution, the number of effective solute particles increases. In such cases the value of the observed colligative property will be greater than that calculated on the basis of undissociated solute particles. The molar mass of the solute calculated from the measurement of colligative property will be lower than the true molar mass of the solute.

Key takeaway

Colligative properties, is a property of a solution that depends on the ratio between the total number of solute particles present in the solution and the total number of solvent particles. The Colligative properties are not dependent on the chemical nature of the solution’s components 

We can observe the colligative properties of solutions by going through the following examples. If we add a pinch of salt to a glass full of water its freezing temperature is lowered considerably than the normal temperature. Alternatively, its boiling temperature is also increased and the solution will have a lower vapour pressure. There are changes in its osmotic pressure as well.

Similarly, if we add alcohol to water, the solution’s freezing point goes down below the normal temperature that is observed for either pure water or alcohol.

References:

1. Engel T. & Reid P., Physical Chemistry 3rd Ed. Pearson (2013).

2. McQuarrie, D. A. & Simon, J. D. Molecular Thermodynamics Viva Books Pvt. Ltd.: New Delhi (2004).

3. Kheterpal S.C., Pradeep’s Physical Chemistry, Vol. I & II, Pradeep Publications.