Unit – 1

Conductance-1

1.1 Arrhenius theory of electrolytic dissociation

1.1.1 The Main Points of the Theory are

When dissolved in water, an electrolyte separates into two types of charged particles, one with a positive charge and the other with a negative charge. Ions are charged particles with a positive charge. Cations are positively charged ions, while anions are negatively charged.

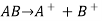
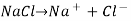
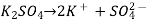
Electrolyte Ions

The contemporary version of the idea states that solid electrolytes are made up of ions kept together by electrostatic attraction. These forces are diminished when an electrolyte is dissolved in a solvent, and the electrolyte dissociates into ions. The ions have been solvated.

Ionization is the process of breaking down molecules into ions in an electrolyte. The degree of ionisation or degree of dissociation is the percentage of total molecules present in solution that are ions. It's indicated by

It has been discovered that not all electrolytes ionise to the same degree.

Some are nearly totally ionised, whereas others are only marginally ionised. A lot of things influence the degree of ionisation.

Ions in solution constantly re-unite to produce neutral molecules, resulting in a condition of dynamic equilibrium between the ionised and non-ionized molecules, i.e., AB A+ + B-.

Applying the law of mass action to situations that aren't in equilibrium =K [A+] [B-] /[AB]

The ionisation constant is K. Electrolytes with a high K value are known as strong electrolytes, whereas those with a low K value are known as weak electrolytes.

Electrolysis happens when an electric current is passed through an electrolytic solution and the positive ions (cations) travel towards the cathode and the negative ions (anions) travel towards the anode and are discharged.

Ions are always discharged in equal amounts, regardless of their relative speeds.

The total charge on one set of ions is always equal to the total charge on the other set of ions, making electrolytic solutions always neutral. However, the number of ions in two sets does not have to be equal all of the time.

AB    A+ + B-	NaCl    Na+ + Cl-	(Both ions are equal)
AB2    A2+ + 2B-	BaCl2    Ba2+ + 2Cl-	(Anions are double that of cations)
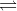A2B   2a+ + B2-	Na2SO4   2Na+ +	(Anions are double that of cations)

Electrolytes in solution have properties that are similar to those of ions in solution. For example, acidic solutions always contain H+ ions, whereas basic solutions contain OH- ions, and the characteristics of H- ions and OH- ions are the same in both cases.

The ions act as molecules to lower the freezing point, raise the boiling point, lower the vapour pressure, and establish the osmotic pressure. The conductiveness of an electrolytic solution is determined by the nature and number of ions because current is carried through the solution by ion movement.

1.1.2 Evidences in Favour of Ionic Theory

A large number of experimental observations are available which support Arrhenius theory. A few of them are given below:

Ions Present in Solid Electrolytes

Electrolytes are made up of ions, according to X-ray diffraction research. A crystal of NaCl, for example, does not contain NaCl units but rather Na+ and Cl- ions. Each Na+ ion has six Cl- ions surrounding it, and each Cl- ion has six Na+ and Cl- ions around it. In their fused state, ionic compounds act as good conductors. Only if ions are already present in ionic materials is this conceivable.

Ohm's Law Applicability

Electrolytic solutions, like metallic conductors, follow Ohm's law, which states that the current flowing conductor's strength is proportional to the potential difference (E) applied across the conductor and inversely proportional to the conductor's resistance. I = E/R is a mathematical formula.

Only if ions are already present in the solution and no part of the current has a direct influence on the ions is this possible.

Ionic Reaction

Well-known inorganic chemistry processes provide evidence for the presence of ions in aqueous electrolyte solutions. When Ag+ ions come into contact with chloride ions, a white precipitate of silver chloride forms.

When AgNO3 solution is introduced to CCl4, CHCl3, or C2H5Cl, however, no precipitation occurs because these compounds are non-electrolytes and do not provide Cl- ions in solution.

Because no ionisation of the acid happens in the common reaction, an acid that gives all tests of H+ ions in aqueous solution does not give the same tests when dissolved in any organic solvent.

Heat of Neutralization

The heat released when one gramme equivalent of a strong acid is neutralised by one gramme equivalent of a strong base is always the same, i.e., 13.7 kcal. This can be explained using the Arrhenius hypothesis, which states that when an acid is dissolved in water, it produces H+ ions and OH- ions, and the neutralisation process involves the common reaction.

13.7 kcal = H+ + OH- H2O

As a result, the heat of neutralisation is the heat of forming H2O from H+ and OH- ions.

Abnormal Colligative Properties

The anomalous behaviour of electrolytes toward colligative qualities can be described using ionic theory. The number of molecules actually dissolved when an electrolyte is dissolved in water is related to ionisation. The fact that you can't Hoff, is always greater than one, I = 1 + (n-1) where 'n' is the number of ions created by ionisation of one electrolyte molecule and' is the degree of ionisation.

Colour of Solution

The electrolytes in solution's colour. CuSO4 is blue in solution due to the presence of Cu2+ ions, if any is owing to their ions. Because of the presence of ions, potassium permanganate (KMnO4) appears purple in solution.

Explanation of Some Other Phenomena

Electrolysis, conductivity, salt hydrolysis, solubility product, and other phenomena are all explained satisfactorily by ionic theory. 

1.1.3 Limitations of Arrhenius Theory

Strong electrolytes do not obey Ostwald's dilution law, which is based on Arrhenius theory, because they conduct electricity in their infused condition, that is, in the absence of water. This is in contrast to Arrhenius theory, which states that ionisation requires the presence of a solvent. Arrhenius theory assumes independent existence of ions but fails to account for the factors that govern ion mobility. 

1.1.4 Factors Pertaining to Degree of Ionization

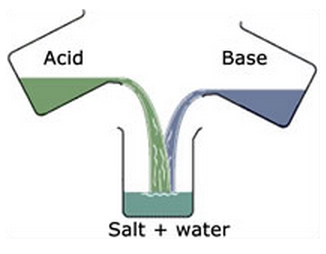
The degree of ionization of an electrolyte in solution depends upon the following factors:

Nature of Solute

Less ions are produced in solution when the ionisable sections of a substance's molecule are bound together by covalent bonding rather than electrovalent bonding. Weak electrolytes are the name given to such compounds. This group includes H2S, HCN, NH4OH, and CH3COOH. Strong electrolytes such as NaCl, Ba (NO3)2, KOH, and others, in which electron transport appears to be more or less complete, produce ions almost instantly when dissolved. In solution, strong electrolytes are practically totally ionised.

Nature of Solvent

The solvent's principal job is to break up the electrostatic interaction between the two ions and separate them. In any medium, the force of attraction that holds the ions together is expressed as

F= 1/ (K) (q1 q2)/r2

Where K is the dielectric constant of medium.

Any solvent with a high dielectric constant value has the ability to separate ions. Because it has the highest dielectric constant, water is thought to be the best solvent. At 250°C, the dielectric constants of some of the solvents are listed below.

Dilution

The concentration of an electrolyte's solution is inversely related to the level of ionisation. When a result, as the dilution of the solution grows, the degree of ionisation increases, implying that the concentration of the solution decreases.

Temperature

The degree of ionisation increases as the temperature rises. This is because when the temperature rises, the molecular speed increases, overcoming the forces of attraction between the ions.

Key takeaway:

• The Arrhenius theory states that acids are substances that dissociate in water to produce electrically charged atoms or molecules called ions, one of which is a hydrogen ion (H+), and that bases ionise in water to produce hydroxide ions (OH). It was proposed by the Swedish scientist Svante Arrhenius in 1887. Even though it had flaws, it was the first theory to offer comprehensive criteria for acids and bases. It was also the first theory on acids and bases to acknowledge the role of solvents in neutralisation and water generation during the reaction.
• As CuSO4, AlCl3, CO2, and SO2 cannot be represented by the formula HA, the theory is unable to explain their acidic qualities. Similarly, because the basic properties of Na2CO3, amines, pyridine, and NH3 cannot be described by the formula BOH, the theory is unable to explain them.

1.2 Conductivity, Equivalent and molar conductivity and their variation with dilution for weak and strong electrolytes.

1.2.1 Variation of molar conductivity with concentration:

1. The ability to conduct molar water

The conductance of volume V of a solution containing one mole of electrolyte retained between two electrodes with an area of cross-section A and a distance of unit length is the molar conductivity of a solution at a particular concentration.

K/c = m

In this case,

c = moles per volume concentration

a measure of a substance's ability to conduct electricity.

Molar conductivity is denoted by the letter m.

Because there is just one mole of electrolyte in the solution, the previous equation can be changed to:

V = m

As the total volume, V, of a solution containing one mole of electrolyte grows, molar conductivity increases with decreasing concentration. The concentration drops as a result of dilution. The molar conductivity of a solution is known as limiting molar conductivity, °m, when the concentration approaches zero. Strong and weak electrolytes have different molar conductivity variations with concentration.

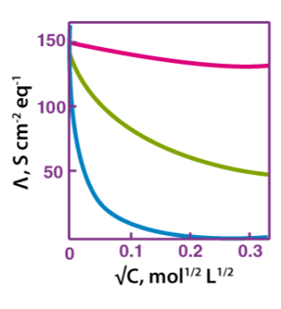
1. For strong electrolytes, molar conductivity varies with concentration:

The molar conductivity of strong electrolytes increases slowly with dilution. The plot of molar conductivity vs c1/2 is a straight line with a y-intercept of °m. The value of the limiting molar conductivity, °m, can be calculated using either the graph or the Kohlrausch law. The plot's general equation is as follows:

The molar conductivity of strong electrolytes increases slowly with dilution. The plot of molar conductivity vs c1/2 is a straight line with a y-intercept of °m. The value of the limiting molar conductivity, °m, can be calculated using either the graph or the Kohlrausch law. The plot's general equation is as follows:

m = °m -Ac1/2 m = °m -Ac1/2 m = °m -Ac1/2

Where -A is the slope of the line as a constant. The value of "A" for a given solvent is determined by the type of electrolyte present at a specific temperature.

With a poor electrolyte concentration:

The graph between molar conductivity and c1/2 (where c is the concentration) is not a straight line for weak electrolytes. At greater concentrations, weak electrolytes have lower molar conductivities and a lower degree of dissociation, which increases quickly at lower concentrations. As a result, by extrapolating molar conductivity to zero concentration, m° cannot be achieved as a limiting molar conductivity. As a result, we apply the Kohlrausch law of independent ion migration to determine the molar conductivity, m°, of weak electrolytes.

1.2.2 Weak and Strong Electrolytes:

The systematic research of electrolytic solutions began in the late 1800s, mostly in Germany, before the specifics of dissociation and ionisation were well understood. These experiments discovered that the equivalent conductivities of electrolytes all decrease with concentration (or, more precisely, with the square root of the concentration), but in different ways, as seen by their behaviour at very low concentrations. As a result, electrolytes were divided into three categories: weak, intermediate, and strong.

You'll note that conductivities vs. c graphs begin at c=0. Of course, measuring the conductance of an electrolyte at vanishingly small concentrations (let alone 0!) is impossible, but for strong and intermediate electrolytes, a sequence of observations can be extrapolated to zero. The resulting values, denoted by °, are known as limiting equivalent conductance’s or "equivalent conductance’s at infinite dilution."

• Strong electrolytes
• Intermediate electrolytes
• Weak electrolytes

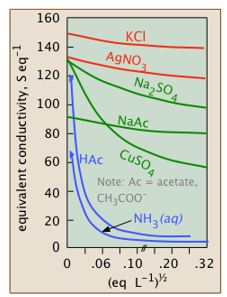
Conductivity diminishes as concentrations increase

We might expect the conductivity of a solution to be precisely proportional to the concentrations of ions in the solution because ions are charge carriers. If the electrolyte is completely dissociated, the conductivity should be proportional to the concentration of the electrolyte. However, this ideal behaviour is never observed; rather, the conductivity of all electrolytes decreases as concentration rises.

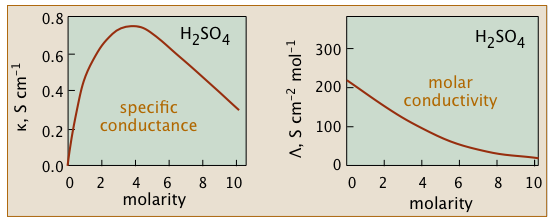
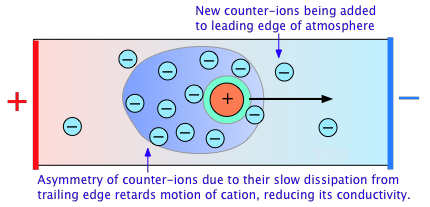
Electrolytic solutions' non-ideality is reflected in their colligative properties, particularly freezing-point depression and osmotic pressure. The presence of the ionic atmosphere, which was mentioned above, is the fundamental cause of this. We would expect their charges to partially cancel, limiting their inclination to migrate in response to an applied potential gradient, to the extent that ions with opposite charge signs are more likely to be closer together.

The fact that an ion's counter-ion cloud cannot keep up with it as it migrates through the solution has a secondary consequence. Instead, on the leading edge of the motion, new counter-ions are constantly obtained, while older ones are left behind on the opposite side. Because the lost counter-ions take some time to disperse, there are always more counter-ions on the trailing edge. The ensuing asymmetry of the counter-ion field retards the central ion, lowering its rate of migration and therefore its contribution to the solution's conductivity.

P. Debye and W. Huckel developed a quantitative treatment of these effects in the early 1920s, which was built upon by Ostwald a few years later. This work was one of the most important advances in physical chemistry in the first half of the twentieth century, and it established a solid theoretical foundation for the behaviour of electrolytic solutions. Even yet, for most ions, the Debye-Huckel theory fails at concentrations greater than 10–3 M L–1.

Not all Electrolytes Totally Dissociate in Solution

The effects stated just above explain a lot of the graphs for strong electrolytes. Many salts are not entirely ionised in water, as evidenced by the presence of intermediate electrolytes, which was shortly validated by measurements of their colligative properties.

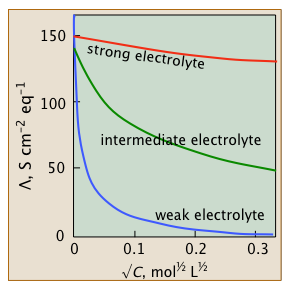
The Le Chatelier effect predicts that when the concentration of "free" ions increases, the equilibrium MX (aq)=M+(aq) +X–(aq) (8.10.9C.1) would move to the left, resulting in the curvature of the graphs for intermediate electrolytes. The actual concentrations of these ions are lower in more dilute solutions, but their fractional abundance in respect to the undissociated form is higher. As the concentration of the solution approaches 0, nearly all of the (MX (aq)) dissociates, and the conductivity reaches its limiting value.

Weak electrolytes are dissociated only at extremely high dilution

Of course, dissociation is a matter of degree. For the dissociation of an intermediate electrolyte salt MX, the equilibrium constants are typically in the range of 1-200. This is in contrast to the enormous number of weak acids (and weak bases) with dissociation constants ranging from 10–3 to less than 10–10.

These weak electrolytes, like intermediate electrolytes, will be completely dissociated at zero concentration; if the scale of the weak-electrolyte plot (blue) above were magnified by many orders of magnitude, the curve would resemble that of the intermediate electrolyte above it, and a value for ° could be extrapolated. However, at such a high dilution, the conductivity of water itself (that is, the H+ and OH– ions in equilibrium with the huge 55.6 M L–1 concentration of water) would cover it, making measurements of in this region almost unmeasurable.

Key takeaway:

• As the total volume, V, of a solution containing one mole of electrolyte grows, molar conductivity increases with decreasing concentration. The concentration drops as a result of dilution. The molar conductivity of a solution is known as limiting molar conductivity, °m, when the concentration approaches zero.
• Molar conductivity is the conductance property of a solution containing one mole of electrolyte or a function of a solution's ionic strength or salt concentration.
• The concentration of the electrolyte affects molar conductance. The amount of ions available per unit volume decreases as the solution becomes more dilute, lowering the conductivity.

1.3 Molar conductivity at infinite dilution.

Limiting molar conductivity is the molar conductivity of a solution at infinite dilution. In other words, the molar conductivity is known as limiting molar conductivity as the electrolyte concentration approaches zero.

Conductivity drops as the number of ions per unit volume that hold the current in a solution drops with dilution, whereas molar conductivity increases as the concentration of a solution falls. The increase in total volume containing one mole of the electrolyte causes the rise in molar conductivity.

1.4 Kohlrausch law of independent migration of ions.

1.4.1 Kohlrausch law states that:

The equivalent conductivity of an electrolyte at infinite dilution is equal to the sum of the conductances of the anions and cations, according to Kohlrausch's law.

The conductance of a volume of solution containing one mole of electrolyte retained between two electrodes with the unit area of cross-section and distance of unit length is the molar conductivity of a solution at a certain concentration. The molar conductivity of a solution increases as the concentration of the solution decreases. The increase in total volume containing one mole of the electrolyte causes the rise in molar conductivity. The molar conductivity is known as limiting molar conductivity, m°, as the electrolyte concentration approaches zero.

While comparing the values of limiting molar conductivities of different strong electrolytes, Kohlrausch noticed some patterns. Kohlrausch proposed that the “limiting molar conductivity of an electrolyte can be expressed as the total of the individual contributions of the electrolyte's anions and cations” based on his observations. This law is known as the Kohlrausch law of independent ion migration. For example, knowing the limiting molar conductivities of sodium ion and chloride ion can help estimate sodium chloride's limiting molar conductivity, m°. The following are some of the most important uses of Kohlrausch's law of independent ion migration: The Kohlrausch law can be used to calculate the limiting molar conductivities of any electrolyte. At increasing concentrations, weak electrolytes have lower molar conductivities and a lower degree of dissociation. For weak electrolytes, the graph between molar conductivity and c1/2 (where c represents the concentration) is not a straight line. At lower concentrations, the molar conductivity of a weak electrolyte increases dramatically. As a result, by extrapolating molar conductivity to zero concentration, m° cannot be achieved as a limiting molar conductivity. As a result, for weak electrolytes, we apply the Kohlrausch law of independent ion migration to determine the limiting molar conductivity, m°. The Kohlrausch law can also be used to calculate the value of the dissociation constant from the value of molar conductivity, as well as to limit molar conductivity for a weak electrolyte at a given concentration.

When dissociation is complete at infinite dilution, each ion contributes a definite amount to the electrolyte's equivalent conductance, regardless of the nature of the ion with which it is associated, and the value of equivalent conductance at infinite dilution for any electrolyte is the sum of contributions of its constituent ions," i.e., anions and cations. As a result

=

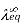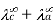
Where,

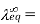Equivalence Conductivity at Infinite Dilution

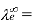Conductivity of Cation

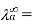Equivalence Conductivity of Anion

According to Kohlrausch’s law. “Conductivity of ions is constant at infinite dilution and it does not depend on nature of co-ions.”

For AxBy type electrolyte,

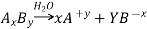
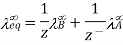
Here Z+and Z- are the charges present on cation and anion.

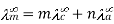
Here m and n are the number of moles of cations and anions.

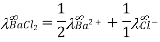
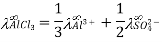
1.4.2 Uses of Kohlrausch’s law:

Calculation of Molar Conductivity at Infinite Dilution for Weak Electrolytes

As previously stated, the molar conductivity of weak electrolytes at infinite dilution cannot be established experimentally, for two reasons: first, the conductance of such a solution is low, and second, dissociation of such an electrolyte does not occur even at enormous dilutions.

Kohlrausch's law can be used to calculate the molar conductivity of such an electrolyte at infinite dilution.

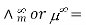Molar conductance at infinite dilution=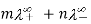

Where m and n are number of ions formed.

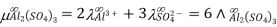
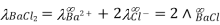
Calculation of Degree of Dissociation

According to the Arrhenius hypothesis of electrolytic dissociation, the increase in molar conductivity with dilution is entirely due to a rise in electrolyte dissociation, with the molar conductivity at infinite dilution being the highest since dissociation is nearly complete.

As a result, if is the molar conductivity of a solution at any concentration C and is the molar conductivity at infinite dilution (i.e., 0 concentration), we get

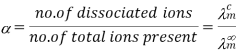
This link, however, is only observed to remain true for weak electrolytes. Kohlrausch's law, as mentioned in the first use, can be used to compute the value of for weak electrolytes.

Calculation of Dissociation Constant for a Weak Electrolyte

Using the formula, the dissociation constant (K) of the weak electrolyte at concentration C of the solution can be computed using the degree of dissociation (as computed above).

=
 

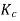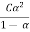
Calculation of Solubility of Sparingly Soluble Salt

Sparingly soluble salts are salts that dissolve just little in water, such as AgCl, BaSO4, and PbSO4.

Because they only dissolve a small amount of water, their solutions are called eternally dilute. Their concentration is also equivalent to their solubility because their solutions are saturated.

We can determine the specific conductivity (K) and molar conductivity of such solutions by determining their specific conductivity (K).

1.5 Debye-Huckel –Onsager equation, Wien effect.

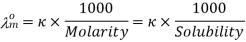
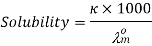
1.5.1 Debye-Huckel –Onsager equation:

Peter Debye and Erich Hückel proposed the Debye–Hückel hypothesis as a theoretical explanation for departures from ideality in electrolyte and plasma solutions. It's a linearized Poisson–Boltzmann model that uses a very simple electrolyte solution model but nevertheless gives accurate mean activity coefficient predictions for ions in dilute solution. The Debye–Hückel equation is a good place to start when dealing with non-ideality in electrolyte solutions.

An ideal solution in the chemistry of electrolyte solutions is one whose colligative qualities are proportionate to the solute concentration. Real-world solutions may deviate from this idealised state. The idea of activity was created to accommodate these effects in the thermodynamics of solutions: the properties are thus proportional to the activities of the ions. The activity factor, a, is proportional to the concentration factor, c. The activity coefficient, is the proportionality constant.

All of the ions' activity coefficients are equivalent in a perfect electrolyte solution. Electrolyte solution ideality can only be obtained in very dilute solutions. The non-ideality of more concentrated solutions is caused mostly (but not only) by electrostatic forces that attract ions of opposing charge while repelling ions of the same charge. As a result, unlike in a perfect solution, ions are not distributed evenly throughout the solution.

Because an electrolyte solution must contain both positively and negatively charged ions, single ion activity coefficients cannot be studied experimentally. A mean activity coefficient, on the other hand, is defined. For instance, the electrolyte NaCl

In general, a fully dissociated electrolyte with formula AnBm has a mean activity coefficient of

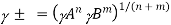
Because the quantity of inter-ionic interaction rises as the electrolyte concentration increases, activity coefficients are themselves functions of concentration. Debye and Hückel established a theory that could be used to compute single ion activity coefficients. The idea might be evaluated against experimental data by computing the mean activity coefficients from them. It was discovered that for "dilute" solutions, it provided great agreement.

A full examination of the assumptions and their limits, as well as the mathematical development and applications, is included in a description of Debye–Hückel theory.

The image is a snapshot of a 2-dimensional segment of an idealised electrolyte solution. Ions are depicted as spheres with a single electrical charge. The solvent (light blue) is depicted as a smooth, unstructured medium. On average, each ion is surrounded by ions with opposite charges rather than ions with similar charges. These ideas were turned into a quantitative theory including ions with charges of z1e+ and z2e, with z being any integer. The main assumption is that deviation from ideality is caused by electrostatic interactions between ions, which are mediated by Coulomb's law: in a medium of relative permittivity r, the force of interaction between two electric charges separated by a distance r is given by

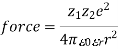
The solute is also considered to be totally dissociated; it is a strong electrolyte, with spherical ions that are not polarised by the electric field. Except insofar as it impacts the ions' effective sizes, ion solvation is ignored.

The solvent's only function is to provide a medium with a constant relative permittivity (dielectric constant).

There isn't any electrostriction here.

Individual ions in the vicinity of a "central" ion can be represented as a statistically averaged cloud of continuous charge density with a minimum closest approach distance.

Each cation is surrounded by a spherically symmetric cloud of other ions, according to the last assumption. There is a net negative charge in the cloud. Each anion is similarly enveloped by a cloud of net positive charge.

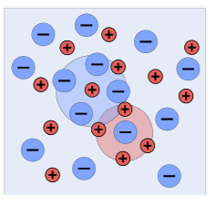
An idealized representation of a solution of a 1:1 electrolyte

1.6 Waldens rules.

1.6.1 The validity of Walden’s rule:

The Stokes-Einstein equation (1) ties the diffusion coefficient to the solution's viscosity, while the Nernst-Einstein equation (2) ties the diffusion coefficient to the equivalent conductivity. 1

D stands for diffusion coefficient, k for Boltsmann's constant, T for temperature, r for radius, v for viscosity, R for universal gas constant, F for Faraday constant, and z for ion charge. D is removed from the equation to get a relationship between the electrolyte's equivalent conductivity and viscosity. Walden's Rule is the name given to this statement. 1

According to Walden's Rule, the product of a particular electrolyte's limiting equivalent conductivity and viscosity at infinite dilution is a constant at a given temperature. This can be written as an equation, where 0 represents the limiting molar conductivity and 0 or/0 represents the viscosity. 1

To explain how big neutral molecules influence ion limiting mobilities in solution.

Sucrose and other large molecules were used. The sucrose solutions' viscosities were calculated as a percentage. Because viscosities change with temperature, the solutions were held at 20.0°C 0.9.8°F. Various masses of sucrose were dissolved in various quantities of distilled water to produce a spectrum of sucrose solutions with different viscosities: 5%, 10%, 20%, 30%, and 50%. For instance: 10 g sucrose was dissolved in 90 ml distilled water to make a 10% sucrose solution. The solutions were prepared as described before, with the exception that the sucrose and distilled water were used in a weight-to-weight ratio, and the density of water at 20°C is 0.9982g/cm 3. 2

Salts containing various cations and anions of varying concentrations could be added to sucrose solutions of various viscosities. In the initial experiment, tetramethylammonium iodide was employed as the additional salt. Tetramethylammonium iodide concentrations of 0.01, 0.03, 0.05, 0.07, and 0.09 moldm -3 were tested. 3 The salts were added to the sucrose solutions and stirred until they were completely dissolved. A Janeway conductivity metre can be used to determine the conductivity of the solutions (Table 3). This metre can also be used to monitor the temperature of the solutions. Various cations and anions have different trends, which can be seen. Different organisations investigated various salts at varied viscosities.

Because the salts utilised in the study are all strong electrolytes, they entirely breakdown into ions. The quantity of ions in a solution and their mobility determines its conductivity. Where m is the molar conductivity, is the conductivity, and c is the concentration, the molar conductivities 3

Kohlrausch's Law of Independent Migration asserts that cations can be assumed to travel independently of anions and vice versa at infinite dilution, i.e., 0 This Law can be used to calculate the limiting molar conductivity. At low concentrations, the molar conductivities of strong electrolytes vary linearly with the square root of the concentration, according to law.

The Walden's product is the product of 0 and 0. The Walden's Rule is no longer followed when the non-electrolyte lowers conductance much less than fluidity, i.e., it is no longer a constant. 2,5 of the Walden's goods vary between 97 and 235. The product increased considerably when the sucrose solution had a viscosity more than 30%, according to the NMe 4I a salt. The Walden's Rule is not followed at sucrose viscosities of around 30% or higher, according to this alteration. When using KCl as the additional salt, Stokes discovered that the rule was broken above 40% sucrose solution. 2 Because high viscosity solutions solvate the same ions to various degrees, the hydrodynamic radius changes.

m drops when c 1/2 increases in all strong electrolytes (Fig.). There is a linear relationship as a result of this. This is because of three factors: relaxation, electrophoretic effect, and ion pairing. 2 When one ion comes into close contact with another ion, the relaxation effect occurs, causing the ion atmosphere to be distorted. This distortion may obstruct ion mobility, resulting in a reduction in ion conductivity. 2 The relaxing effect becomes more pronounced as the ion concentration rises, as the likelihood of making intimate contact with other ions rises. The electrophoretic effect is the slowing of ion mobility due to viscous drag between ions as they travel in solution. The ionic strength of the solution has a direct relationship with this impact. As the ion concentration rises, this impact becomes more prominent, and conductivity falls. 3 Anions and cations in the solution could potentially join together to form a neutral molecule, which is also a worry. Neutral molecules do not conduct electricity. Because the quantity of ions in a solution is important, an increase in salt concentration could increase the likelihood of ion partnering, lowering conductivity.

The trend for NaCl and LiCl was fairly similar because they both had a linear connection and the only difference is the cations. The molar conductance of Na+ ions is higher than that of Li+ ions. Ions migrate without losing their hydration shells. Li+ ion is more structure-making and has a larger primary and secondary solvation shell than Na+ ion, which is less structure-making and more structure-breaking. The solvation shell of the Na+ ion is smaller. The size of the solvation shells decreases as the ion radius increases. Because the ions undergo increased relaxation and electrophoretic action as the solvation grows in size, the conductivity drops. The LiCl salt, on the other hand, produces some strange consequences (Fig. 4). Because the Li+ ion's tiny ionic radius has a significant polarising effect, the size of the solvation shell remains essentially constant throughout a wide range of water densities.

When comparing the salts NaCl, NBu 4Br, and NMe 4I, a similar pattern emerges. The solvation shells and the size of the anion differ. The size of the solvation shells increases as the anion radius decreases, as does the relaxation and electrophoretic effect. Ion mobility would be hampered, and conductivity would be reduced.

Alkyl ammonium ions, such as NBu 4+, have a unique behaviour since they are hydrophobic and scarcely hydrated. The result is an exponential curve. These ions' intrinsic ion sizes are very critical, making ion pairing crucial. As the extent of ion pairing grows, the limiting molar conductivity drops, for example, from methyl ammonium ions to butyl ammonium ions. At low concentrations, ion pairing is more important since the amount of ions in the solution is affected significantly, resulting in an exponential curve.

The varying viscosities of sucrose solution show a consistent tendency that can be explained by the Stokes' Law model. 3 The dependence of 0 on ion size can be explained using this model. The conductivity of a solution decreases as it becomes more viscous. Ions move with their solvation shells intact and are subject to two types of forces: viscous drag and electrostatic force. Ions effectively "swim" across the solution, therefore as the viscosity rises, ion mobility becomes more difficult, lowering the conductivity. When a solution gets viscous, the retarding force kicks in and the conductance drops. For salts like HCl, other transport mechanisms such as "hopping" exist. 2 The same approach was used to perform novel processes such as weak electrolytes, divalent ions, and salt combinations.

CaCl 2 and other divalent ions were studied. Because this is a powerful electrolyte, it should dissociate fully. The linear relationship was observed, however divalent ions had a larger limiting molar conductivity than monovalent ions (Fig 7). This is related to a rise in the valency of the currency. Because the Ca 2+ ion has a valence of 2, it can hold the primary and secondary solvation shells together more tightly. Overall, this results in a reduced ion size, which leads to increased ion mobility and conductance. Divalent ion trends should be similar to monovalent ion trends. Mg 2+ ions have a broad solvation shell and are strongly structure-forming. However, as the ionic radius grows to Ca 2+ and Sr 2+, the structure breaks down and the solvation shell shrinks, increasing conductivity.

Because a weak electrolyte like sodium oxalate is not fully ionised in solution, the process is reversible.

The effects of ion pairing and solvation on sodium oxalate can change conductivity.

The equilibrium changes to the right when the activity of disodium oxalate decreases, resulting in a change in the degree of ionisation. Because conductivity is proportional to the amount of ions, the degree of ionisation is critical. Because Kohlrausch's Law does not apply to weak electrolytes, a different equation is employed to find the limiting molar conductivity: Ostwald's Dilution Law (6), where K an is the association constant.

Extrapolating 1/0, the intercept, and 1/K a0 2; the gradient of the line can be done using a plot of 1/m versus mc (Fig).

9 The K a value at 5% viscosity is 0.036, indicating that the equilibrium is to the right. The K a value at 30% viscosity is 1.7289, indicating that the equilibrium is to the left. The molar conductance is determined by the quantity of ions dissociated.

Salt mixtures (Table) revealed that the alkyl ammonium ions dominate, with a pattern that is quite similar to the alkyl ammonium salt. Ion pairing of the big alkyl ammonium ions with any halides in the solution would drastically influence conductivity (Fig).

The validity of Walden's Rule can be determined by the fact that at around 30% sucrose concentration, the rule begins to break and is no longer followed. The conductance of ions is determined by a number of parameters, including salt content, viscosity, ion radius, transport mechanism, and solvation size. This has an impact on the relaxation effect, electrophoretic effect, ion pairing extent, viscous drag, retarding force, and electrostatic force. All of these variables can affect ion mobility, which is crucial for determining how conductive a solution is. This inquiry, however, has numerous inaccuracies. The sucrose solutions' viscosity and the amount of salt added were simply estimates. Some salts, such as NMe 4I, are not particularly soluble in high percent viscosities since the solutions are already saturated, which means that not all of the salts have been fully dissolved, which might lead to mistakes. The temperature of the solutions differed slightly, which could affect the sucrose solution's viscosity. Because the data was acquired by multiple parties using various equipment, there could be some calibration or human errors.

The study might be enhanced if each group used the same viscosities to make comparisons easier. The salts' solubility might be tested ahead of time to guarantee that the quantities of salts added would dissolve in solutions. By employing a water bath to keep the temperature of the solutions consistent, the viscosity errors can be reduced. Additional innovations, such as the influence of temperature, the non-electrolyte employed, other salts such as HCl, changes in conductance, and Walden's product between weak and strong electrolytes, could be pursued further.

References:

1. A 1:1 ratio of each salt was used as a salt mixture.
2. Bockris, J.O., Reddy, A. K. N. Modern Electrochemistry 1: Ionics. 2003. 2nd ed. Springer
3. Hamer, W. J. The Structure of Electrolytic Solutions. In: Stokes, R. H. Mobility of Ions in Relation to Viscosity. New York: John wiley & sons, Inc, 1959. Pp. 289-307
4. P.W. Atkins, Physical Chemistry. 1998, 6th ed. Oxford University Press
5. Misra, P. P., Das, N. C., Das, P.B., Cellular and Molecular Life Sciences., 1979, 35 (6): 724- 725
6. Mendolia, M.S. Farrington, G. C., Chem. Mater. 1993, 5, 174- 181
7. R. W. Impey, P. A. Madden, I. R. McDonald, J. Phys. Chem., 1983, 87, 5071-5083
8. S. H. Lee, P. T. Cummings, J. Chem. Phys., 2000, 112, 864- 869
9. D. R. Lide, Handbook of Physicas and Chemistry, 2000, 81st ed. CRC Press
10. R. Buchner, Priv- Doz, F. Samani, P. M. May, P, Sturm, G. Hefter, Chem. Phys. Chem., 2002, 4 (4), 373 - 378