Unit – 2
Conductance-II
2.1.1 What is Ionic Mobility?
The capacity of ions to flow through a medium under the influence of an electric field is known as ionic mobility or electrical mobility. Ions are electrically charged particles with either a negative or positive charge. As a result, the mobility of these ions can be affected by an electric field. The method of separating ions in the gas phase according to their mobility is known as "ion mobility spectrometry." Furthermore, we call this separation "electrophoresis" when it occurs in the liquid phase.
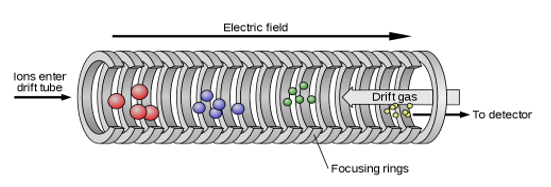
Figure: Ion Mobility Spectrometry
In addition, the ionic mobility can be defined mathematically as the ratio of the drift velocity to the magnitude of the electric field. It goes like this:
μ=vd/E
Vd denotes the ion's drift velocity, and E denotes the magnitude of the applied electric field. This equation holds true in both the gaseous and liquid phases. The electric field, on the other hand, should be consistent throughout the medium.
2.1.2 What is Ionic Velocity?
The speed of an ion travelling through a medium in a unit electric field is called ionic velocity. It's referred to as drift velocity, and it's a mean number. The electric field must be uniform and capable of exerting a force on the moving charged particle in this case. We can also express this ionic velocity as follows:
Vd = μE
Vd denotes the ionic velocity, whereas E denotes the magnitude of the external electric field. Ms-1 is the unit of measurement for this velocity.
2.1.3 What is the Difference Between Ionic Mobility and Ionic Velocity?
Ionic mobility and ionic velocity are two chemical principles that are closely connected. The main distinction between ionic mobility and ionic velocity is that ionic mobility refers to ions' capacity to move through a medium, whereas ionic velocity refers to how quickly they travel through it. Furthermore, another key distinction between ionic mobility and ionic velocity is that ionic mobility is measured in m2 V1 s1, whereas ionic velocity is measured in ms1.
| Ionic mobility | Ionic velocity |
Definition | Ionic mobility is the ability of ions to move through a medium upon the effect of an electric field | Ionic velocity is the speed obtained by an ion moving through a medium under a unit electric field |
Theory | Ability of ions to move through a medium | How fast the ions move through the medium |
Unit of Measurement |  |  |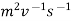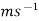
2.1.4 Summary – Ionic Mobility vs Ionic Velocity
Ions are electrically charged particles. Cations and anions are the two main types of ions. Both of these ions, however, can contribute to an electrolyte's conductance. Ionic mobility and ionic velocity, in short, are two chemical principles that describe how ions travel across a material. The main distinction between ionic mobility and ionic velocity is that ionic mobility refers to ions' capacity to move through a medium, whereas ionic velocity refers to how quickly they travel through it.
Ionic mobility is the average velocity with which a given ion wanders through a given gas under the influence of an electric field. Temperature, electrolyte nature, and ion size are all factors that influence ionic mobility. The following is the relationship between ionic mobility and transportation number: ta or tc = an or c Where a and c are ionic mobilities, respectively.
- Definition:
“The transport number, transference number, or Hittorf number of an ion is expressed by sets symbols like t+ and t– or tc and ta or nc and na.”
According to this definition,
Evidently,
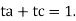
- Determination of transport number: Hittorf's approach, moving boundary method, emf method, and ionic mobility can all be used to calculate the transport number.
- Factors affecting transport number
As the temperature rises, the cation and anion transport numbers tend to approach 0.5.
- Transport number and Ionic mobility: The conductivity of a solution containing 1 g ion at infinite dilution when two appropriately big electrodes are put 1 cm apart is known as ionic mobility or ionic conductance.
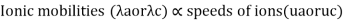
Unit of ionic mobility is Ohm–1 cm2 or V–1S-1cm2
Ionic mobility and transport number are related as,
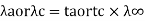
Absolute ionic mobility refers to how quickly an ion moves across a unit potential gradient. Its metric is
-1
Absolute ionic mobility =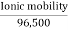
2.3.1 Measurement of Transference Number: Moving boundary method:
Different approaches, such as Hittorf's method, moving boundary method, and electromotive force of concentration cells, can be used to determine the Transference Number.
The Moving Boundary Method is briefly discussed here.
The direct observation of ion movement under the influence of an applied electric field is the basis for this method. Consider the following: The transport numbers of H+ and CI ions present in hydrochloric acid must be determined. The major or experimental electrolyte is hydrochloric acid. The indicator electrolyte is a different electrolyte that contains a common ion (Cl-). The speed of the indicator electrolyte's cation is chosen. The speed of the indicator electrolyte's cation should be slower than that of the experimental electrolyte's cation. Because the speed of Cd++ ions is slower than that of H+ ions, CdCl2 can be used as an indicator electrolyte. A concentrated CdCl2 solution is employed to allow the HCI solution to float on top of it. This is how the moving border method works. Figure depicts the configuration.
The electrolyte MA solution to be examined is sandwiched between the solutions of two additional salts MA' and MA, with MA' and MA sharing the anion A and MA' and MA sharing the cation M. The salts should be chosen in such a way that the densities decrease as you go down. Also, the ion M should have a lower speed than M, and the ion A' should have a lower speed than A ion.
Figure: Moving boundary method
This is necessary to maintain clear boundaries between the three electrolyte solutions. The horizontal line P depicts the initial sharp boundary between the solutions of MA and MA, whereas the horizontal line R depicts the initial sharp boundary between MA' and MA. Ionic migration begins when current is passed from the source B, and the border P moves lower, to P', while the border R moves to R'. PP' and RR are the distances travelled by the two borders in time t, which are proportional to the cationic and anionic velocities, respectively. As a result
t+ = u+ / (u– + u+) = PP’ / (PP’ + RRꞌ)
t– = u– / (u+ + u–) = RR’ / (RR’ + PPꞌ) … …. … (14.23)
As a result, the transportation numbers are calculated. It's worth noting that the electrolytes MA, MA', and M'A should have been chosen with caution if he wanted good outcomes. In practise, one boundary must be formed and the rate of its movement must be observed to determine the transference number of one ion; the transference number of the other ion may then be estimated as
t+ + t– = 1.
The transference number is determined as follows under this condition: Assume that the moving cation's boundary is swept through a distance of 'l' in a tube with a cross-section of 'a', resulting in a volume swept out by the passage of Q coulombs of electricity of 'a' (l x a). The equivalent mass of cation must pass through any given site if 1F of electricity passes through the solution t. If c is the equivalent mass of the solution, then the volume of the solution containing ‘l' equivalent man of electrolyte is 1000/c. As a result, the canon boundary will sweep across a volume of 1000/c t+ during the passage of 1 F of electricity. As a result, the identical boundary will sweep out a volume of – for the passage of Q coulombs.
(1000 x t+ x Q) / (c x F)
Hence, l x a = (1000 x t+ x Q) / (c x F)
Or, t+ = (l x a x c F) / 1000Q.
Key takeaway:
- The ratio of the electric current derived from the cation to the total electric current is known as the transference number. If the transference number is close to 1, it means that the cation is primarily responsible for ion conductivity in the polymer electrolyte.
- The transport number, denoted by the symbols t+ or t_, is the percent of current transported by a given species, such as Li+ or PF6-. Because the sum of the transport numbers is 1, every transport number for a particular species must fall between 0 and 1.
1) Degree of dissociation of weak electrolytes:
This can be explained in a variety of ways. In other words, as the electrolyte is diluted, the entropic gain associated with dissociation overwhelms any counterion attraction.
In terms of math, given a m: n electrolyte dissociating according to the reaction
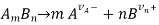
Define the degree of dissociation as cT if the initial concentration of the electrolyte AmBn is cT.
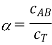
The concentration of dissociated AmBn is given by cAB. The equilibrium constant equation can be expressed as follows, assuming ideality and unit molarity as standard concentrations.
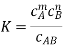
And the degree of dissociation is determined. In the case of a 1:1 electrolyte, this results in
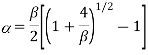
Where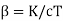 
. As cT→0 it follows from this last expression that α→1 #QED
PS The following equation.
Does not hold over the entire concentration range cT. It can be obtained from Eq. (1) by assuming K<<1 and therefore β<<1. For increasingly dilute solution Eq. (2) fails and α→1.
2) Ionic product of water:
Water self-ionization (the process by which water ionises into hydronium ions and hydroxide ions) occurs only in extremely small amounts. When two water molecules collide, a hydrogen ion can be transferred from one molecule to the other. A positively charged hydronium ion and a negatively charged hydroxide ion are the end products.
We often use the simplified form of the reaction:
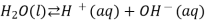
The equilibrium constant for the self-ionization of water is referred to as the ion-product for water and is given the symbol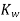 
.
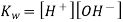
The mathematical product of the concentrations of hydrogen ions and hydroxide ions is the ion-product of water. Because H 2 O is a pure liquid, it is not included in the ion-product expression. According to a reaction that favours the reactants, the value of is relatively small. In pure water, the experimentally determined value is 1.0 10 -14 at 25°C.
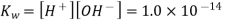
The concentrations of hydrogen and hydroxide ions in pure water are the same. The term "neutral" refers to pure water or any other aqueous solution in which this ratio holds. The square root of is used to calculate the molarity of each ion.
A solution that is acidic is one in which the concentration of hydrogen ions exceeds the concentration of hydroxide ions. When hydrogen chloride is dissolved in water, it ionises to create H + and Cl ions.
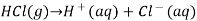
This increases the concentration of H + ions in the solution. According to LeChâtelier’s principle, the equilibrium represented by
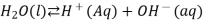
Is forced to the left, towards the reactant. As a result, the concentration of the hydroxide ion decreases.
A basic solution is one in which the hydroxide ion concentration is larger than the hydrogen ion concentration. In water, solid potassium hydroxide dissociates into potassium and hydroxide ions.
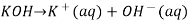
When the concentration of OH ions rise, the concentration of other ions decreases.
The ionic product of water is the product of water concentrations and ions at a particular temperature. It's referred to as. The value increases as the temperature rises, indicating that the concentration of H+ and OH- ions rises as well.
Because the amount of hydronium and hydroxide ions in water is so small at any given time, the concentration of undissociated water molecules remains virtually unchanged and can be regarded a constant due to this minute ionisation. The ionic product is a constant that is used to represent water.
3) Solubility and solubility product of sparingly soluble salts.
- The Solubility Product
When a somewhat soluble ionic substance is given to water, some of it dissolves to produce a solution, bringing the pure solid and its ions into equilibrium. The equilibrium can be stated as follows, with the solid salt on the left, for the dissolution of calcium phosphate, one of the two primary components of kidney stones:
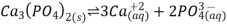
Basic anions, such as S2, PO43, and CO32, react with water to create OH and the appropriate protonated anion, as explained in Section 17.4 and in more advanced chemistry courses. As a result, their calculated molarities are merely approximate, assuming no protonation in aqueous solution.
The solubility product (Ksp) of a sparingly soluble salt is the equilibrium constant for dissolving. The concentration of a pure solid, such as Ca3(PO4)2, does not appear directly in the equilibrium constant equation because it is a constant. As a result, the equilibrium constant expression for calcium phosphate dissolution is
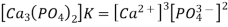
Ksp for calcium phosphate is 2.07 1033 at 25°C and pH 7.00, suggesting that the concentrations of Ca2+ and PO43 ions in solution that are in equilibrium with solid calcium phosphate are extremely low. Table 17.1.1 illustrates the magnitude of Ksp for various typical salts, which indicates that the magnitude of Ksp varies substantially for different substances. Although in Equations 17.1.2 and 17.1.3, Ksp is not a function of pH, changes in pH can impact a compound's solubility, as detailed below.
- As with any K, the concentration of a pure solid does not appear explicitly in Ksp.
Table: Solubility Products for Selected Ionic Substances at 25°C | ||||||
Solid | Color | KspKsp |
| Solid | Color | KspKsp |
*These contain the Hg22+ ion. | ||||||
Acetates |
| Iodides | ||||
Ca(O2CCH3)2·3H2O | White | 4 × 10−3 |
| Hg2I2* | Yellow | 5.2 × 10−29 |
Bromides |
| PbI2 | Yellow | 9.8 × 10−9 | ||
AgBr | Off-white | 5.35 × 10−13 |
| Oxalates | ||
Hg2Br2* | Yellow | 6.40 × 10−23 |
| Ag2C2O4 | White | 5.40 × 10−12 |
Carbonates |
| MgC2O4·2H2O | White | 4.83 × 10−6 | ||
CaCO3 | White | 3.36 × 10−9 |
| PbC2O4 | White | 4.8 × 10−10 |
PbCO3 | White | 7.40 × 10−14 |
| Phosphates | ||
Chlorides |
| Ag3PO4 | White | 8.89 × 10−17 | ||
AgCl | White | 1.77 × 10−10 |
| Sr3(PO4)2 | White | 4.0 × 10−28 |
Hg2Cl2* | White | 1.43 × 10−18 |
| FePO4·2H2O | Pink | 9.91 × 10−16 |
PbCl2 | White | 1.70 × 10−5 |
| Sulfates | ||
Chromates |
| Ag2SO4 | White | 1.20 × 10−5 | ||
CaCrO4 | Yellow | 7.1 × 10−4 |
| BaSO4 | White | 1.08 × 10−10 |
PbCrO4 | Yellow | 2.8 × 10−13 |
| PbSO4 | White | 2.53 × 10−8 |
Fluorides |
| Sulfides | ||||
BaF2 | White | 1.84 × 10−7 |
| Ag2S | Black | 6.3 × 10−50 |
PbF2 | White | 3.3 × 10−8 |
| CdS | Yellow | 8.0 × 10−27 |
Hydroxides |
| PbS | Black | 8.0 × 10−28 | ||
Ca (OH)2 | White | 5.02 × 10−6 |
| ZnS | White | 1.6 × 10−24 |
Cu (OH)2 | Pale blue | 1 × 10−14 |
|
|
|
|
Mn (OH)2 | Light pink | 1.9 × 10−13 |
|
|
|
|
Cr (OH)3 | Gray-green | 6.3 × 10−31 |
|
|
|
|
Fe (OH)3 | Rust red | 2.79 × 10−39 |
|
|
|
|
Solubility products are assessed empirically by directly measuring one of the component ions' concentration or the compound's solubility in a specific amount of water. Ksp, like KK, is described in terms of the molar concentrations of the component ions, whereas solubility is commonly represented in terms of mass of solute per 100 mL of solvent.
A color photograph of a kidney stone, 8 mm in length. Kidney stones form from sparingly soluble calcium salts and are largely composed of Ca(O2CCO2) ·H2O and Ca3(PO4)2.
4) Conductometric Titrations:
What is Conductometric Titration?
Conductometric titration is a quantitative laboratory method for determining the concentration of a particular analyte in a mixture. Conductometric titration is continuously adding a reactant to a reaction mixture and documenting the resulting change in the reaction mixture's electrolytic conductivity. The electrical conductivity of an electrolytic solution is determined by the amount of free ions in the solution as well as the charge assigned to each of these ions.
An abrupt change in conductivity after continual addition of the titrant (and continuous recording of the corresponding change in electrolytic conductivity) indicates that the stoichiometric point has been achieved in this method of titration. In the conductometric titration procedure, the change in the concentration of the hydroxyl and hydrogen ions is connected to an increase or reduction in electrolytic conductivity (which are the two most conducting ions).
Conductometric titration using a standard solution of a base can be used to assess an acid's strength. The graph below shows an example of a curve plotted for a titration process.
Conductometric titration is particularly useful for titration of homogeneous suspensions or coloured solutions, which cannot be done with conventional chemical indicators.
- Principle
The conductometric titration technique works on the following principle: one ion is replaced with another during the titration process, and the difference in the ionic conductivities of these ions directly affects the overall electrolytic conductivity of the solution.
It's also worth noting that the ionic conductance values of cations and anions differ. Finally, the conductivity of an electrolytic solution is affected by the presence of a chemical reaction.
- Theory
The principle behind this sort of titration is that conductivity measurement can be used to determine the end-point of the titration process. In a neutralisation reaction between an acid and a base, adding the base lowers the solution's conductivity at first. This is because the cationic component of the base would replace the H+ ions.
The concentration of ionic entities will increase after the equivalence point is achieved. As a result, the solution's conductance increases. When the conductance values are represented visually, two straight lines with opposite slopes will result. The equivalency point is where these two lines intersect.
- Process
The general procedure for conductometric titration of an acid with a base is as follows:
1. Dilute 10 mL of acid with roughly 100 mL of purified water (so that the changes in the conductance brought on by the addition of the base become small).
2. Fill a burette halfway with the base and take note of the initial volume.
3. A conductivity cell must be put into the diluted acid solution with both electrodes thoroughly immersed in this stage.
4. Now you may connect the conductivity cell to a digital conductometer to get an initial reading.
5. Now, drop by drop, add the base to the acid solution. The amount of base added, as well as the change in conductance, must be recorded.
6. A significant increase in the solution's conductance indicates that the endpoint has been reached. After the titration's endpoint, however, a few more readings are required.
7. The observed data must now be visually represented. The point of intersection between the two lines can be used to find the equivalence point.
The acid's strength may now be determined using the formula S2 = (V1S1)/10, where S2 is the acid's strength, V1 is the volume of base added (as per the conductometric titration graph's equivalence point), and S1 is the strength of the base (already known). The acid (V2) has a volume of 10 ml in this case.
- Advantages and Disadvantages of Conductometric Titration
The conductometric titration procedure has a number of advantages, which are stated below.
1. Titrations of very dilute solutions and weak acids benefit greatly from this method.
2. When compared to a few other titration methods, the end-point of this type of titration is particularly acute and exact.
3. This method of titration is used for colourful or turbid solutions where the endpoint of the titration using normal indications is difficult to see with the naked eye.
4. Acid-base titrations, redox titrations, precipitation titrations, and complicated titrations all use conductometric titration.
The following are the two significant drawbacks of this method of titration:
1. This procedure can only be used for a few specific redox titrations. Because of the large concentration of hydronium ions in the solution, the conductivity of the solution is obscured.
2. Conductometric titration has a low accuracy when the electrolyte concentrations are high, making the titration process unsatisfactory.
5) Hydrolysis constants of salts.
Salt is a chemical created when an acid and a base react to neutralise each other. They ionise in water and produce cations and anions. During the ionisation of salts, the cations or anions generated may exist as hydrated ions in aqueous solutions or interact with water to regenerate acids and bases. The interaction of cations or anions of salts with water is referred to as salt hydrolysis. Salts are classified into three groups based on their hydrolysis:
1. Salts that are acidic
2. Sodium bicarbonate
3. Salts with a neutral Ph
Let's look at how salts of the following sorts are hydrolyzed:
- Salts of strong acid and strong base: Because the bonds in the salt solution do not break apart, salts generated by neutralisation of strong acid and strong base are neutral in nature. They hydrate but do not hydrolyze in most cases. As a result, these salts are commonly referred to as neutral salts.
For example: NaCl
- Salts of weak acid and strong base: Salts formed by the neutralization of weak acid and strong base are basic in nature. For example: CH3COONa
CH3COONa (aq) → CH3COO− (aq) + Na+ (aq)
Acetate ion formed undergoes hydrolysis to form acetic acid and OH– ions.CH3COO−(aq) + H2O ⇋ Ch3COOH (aq) + OH−(aq)
Because acetic acid is a weak acid, it remains in solution unionised. As a result, the concentration of OH– ions rise, making the solution alkaline. The solution's pH is more than 7.
- Salts of strong acid and weak base: Salts formed by the neutralization of strong acid and weak base are acidic in nature. For example: NH4Cl
NH4Cl(aq) → Cl−(aq) + NH+4(aq)
Ammonium ion formed undergoes hydrolysis to form ammonium hydroxide and H+ ions.
NH+4(aq) + H2O ⇋ NH4OH (aq) + H+(aq)
As we know ammonium hydroxide is a weak base, it remains unionized in the solution. As a result, the concentration of H+ ions rise, making the solution acidic. Such solutions have a pH of less than 7.
- Salts of weak acid and weak base: Depending on the nature of the acids and bases involved, salts generated by neutralisation of weak acids and bases are acidic, basic, or neutral. Consider the following scenario: CH3COONH4 is a chemical compound with the formula CH3COONH. The hydrolysis of ions produced from these salts follows a general mechanism:
CH3COO− + NH+4 + H2O ⇋ CH3COOH + NH4OH
In such instances, the degree of hydrolysis is independent of the solution concentration, and the pH of such solutions is given by:
PH= 7 + 12 (pKa – pKb)
As a result, depending on the values of pKa and pKb, the pH of a solution can be less than 7 or larger than 7.
- Salt hydrolysis-
Hydrolysis of salt of weak acid and weak base-
In such salts, both the cation of weak base and anion of weak acid will undergo hydrolysis simultaneously.
Ex – CH3COONH4 (ammonium acetate), NH4F (ammonium fluoride)
NH4+ + CH3COO– + H2O ———> NH4OH + CH3COOH
According to law of mass action,
Hydrolysis constant ‘Kh ‘= [NH4OH] [CH3COOH] / [NH4+] [CH3COO–] [H2O]
Water is present in excess hence can be regarded as constant.
Kh = [NH4OH] [CH3COOH] / [NH4+] [CH3COO–] ————eq 1
CH3COOH ⇌ CH3COO– + H+
Ka = [CH3COO–] [H+] / [CH3COOH] ———– eq 2
NH4OH ⇌ NH4+ + OH–
Kb = [NH4+] [OH–] / [NH4OH] ———— eq 3
H2O ⇌ H+ + OH–
Kw = [H+] [OH–] ———– eq 4
By eq (2), (3) and (4)
Kw / Ka. Kb = [NH4OH] [CH3COOH] [H+] [OH–] / [NH4+] [OH–] [CH3COO–] [H+]
Kw / Ka. Kb = [NH4OH] [CH3COOH] / [NH4+] [CH3COO–] ——– eq 5
Comparing eq (1) and (5)
Kw / Ka. Kb = Kh
- Degree of hydrolysis and hydrolysis constant-
| 
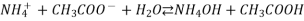
Weak ion Weak ion |
Before hydrolysis | C C 0 0 |
After hydrolysis | C(1-h) C(1-h) Ch Ch
|
Kh = [NH4OH] [CH3COOH] / [NH4+] [CH3COO–]
Water is present in excess hence can be regarded as constant.
Kh = Ch x Ch / C (1-h).C (1-h)
Kh = h2/(1-h)2
Because (1-h) is nearly equal to one therefore,
Kh = h2
h = √ Kh
h = degree of hydrolysis
Because,
Kh = Kw / Ka. Kb
h = √ (Kw / Ka. Kb)
” The degree of hydrolysis of salt of weak acid and weak base does not depend upon the concentration of salt”
- Expression for the pH of the salt solution –
CH3COOH ⇌ CH3COO– + H+
Ka = [CH3COO–] [H+] / [CH3COOH]
[H+] = Ka [CH3COOH] / [CH3COO–]
[H+] = Ka. Ch/ C(1-h)
[H+] = Ka. h / (1-h)
Because (1-h) is nearly equal to one therefore,
[H+] = Ka. h
Because,
h = √ (Kw / Ka. Kb)
[H+] = Ka√ (Kw / Ka. Kb)
[H+] = √ (Kw. Ka / Kb)
Taking log and reverting the sign throughout,
-log [H+] = – 1/2 log Kw -1/2 log Ka + 1/2 log Kb
-log [H+] = pH, – log Kw = pKw, – log Ka = pKa, – log Kb = pKb
PH = 1/2 pKw + 1/2 log pKa – 1/2 log pKb
PH = 7 + 1/2 log pKa – 1/2 log pKb
” The pH of salt of weak acid and weak base is independent of concentration of salt.
When pKa > pKb, then solution will be alkaline and pH value will be more than 7. In case pKb > pKa, then e solution will be acidic and pH value will be less than 7.
Key takeaway:
- Salt hydrolysis is a reaction in which one of a salt's ions interacts with water to generate an acidic or basic solution.
- Salts are ionic substances that form when an acid and a base react to neutralise each other in acid–base chemistry. Because basic salts include the conjugate base of a weak acid, they react with water to produce a solution with a pH greater than 7.0 when dissolved in water.
- Sodium sulphate is a salt made up of a strong base (sodium hydroxide) and a strong acid (sulphuric acid) (sulphuric acid). Hydrolysis does not occur in these salts. Their aqueous solutions have a pH of 7 and are neutral.
References:
- A 1:1 ratio of each salt was used as a salt mixture.
- Bockris, J.O., Reddy, A. K. N. Modern Electrochemistry 1: Ionics. 2003. 2nd ed. Springer
- Hamer, W. J. The Structure of Electrolytic Solutions. In: Stokes, R. H. Mobility of Ions in Relation to Viscosity. New York: John wiley & sons, Inc, 1959. Pp. 289-307
- P.W. Atkins, Physical Chemistry. 1998, 6th ed. Oxford University Press
- Misra, P. P., Das, N. C., Das, P.B., Cellular and Molecular Life Sciences., 1979, 35 (6): 724- 725
- Mendolia, M.S. Farrington, G. C., Chem. Mater. 1993, 5, 174- 181
- R. W. Impey, P. A. Madden, I. R. McDonald, J. Phys. Chem., 1983, 87, 5071-5083
- S. H. Lee, P. T. Cummings, J. Chem. Phys., 2000, 112, 864- 869
- D. R. Lide, Handbook of Physicas and Chemistry, 2000, 81st ed. CRC Press
- R. Buchner, Priv- Doz, F. Samani, P. M. May, P, Sturm, G. Hefter, Chem. Phys. Chem., 2002, 4 (4), 373 - 378
