Unit - 3

Electrochemistry-I

3.1 Quantitative aspects of Faradays laws of electrolysis

3.3.1 Faraday’s law of electrolysis:

What is an Electrolytic Cell?

An electrolytic cell is an electrochemical cell that promotes a chemical reaction through the induction of electrical energy.

Electrolysis is the process of carrying out non-spontaneous reactions under the influence of electric energy.

An electrolytic cell is an electrochemical cell that promotes a chemical reaction through the induction of electrical energy.

Electrolysis is the process of carrying out non-spontaneous reactions under the influence of electric energy.

Michael Faraday conducted substantial research on electrolysis of electrolyte solutions and melts. He was the first scientist to describe the Laws of Electrolysis in quantitative terms. He developed two laws to explain the quantitative characteristics of electrolysis, which are today known as Faraday's laws of electrolysis, namely the first and second laws of electrolysis.

“The amount of power transferred through the solution is directly proportional to the mass of any substance deposited or dissolved at any electrode during electrolysis.”

“The amount of any substance participating in a reaction at an electrode is directly proportional to the quantity of electricity transmitted through the solution,” according to another definition.

If Wg of any material is deposited or dissolved when Q coulombs of electricity are transmitted, then WQ is the result.

However, Q=It

As a result, WI it

Or W=Z I t

Where Z is the substance's electrochemical equivalent.

If I equal 1 unit (for example, 1 ampere) and t equals 1 unit (say, 1 second). When a current of one ampere is passed for one second, Z=W, i.e., the electrochemical equivalent of a substance equals the mass of the substance deposited or dissolved.

Electrolysis's main product.

The principal product of electrolysis is the substance generated directly by the current at the electrode surface during electrolysis. For instance, consider the electrode response.

Cu2+ + 2e– → Cu,

Copper (Cu) is the primary product.

Faraday’s – First Law of Electrolysis

It's one of the fundamental principles of electrolysis. It asserts that the amount of chemical reaction that takes place at any electrode under the influence of electrical energy is proportionate to the amount of electricity that passes through the electrolyte during electrolysis.

Faraday’s – Second Law of Electrolysis

When the same amount of power is passed through the electrolytic solution during electrolysis, a number of distinct compounds are freed in proportion to their chemical equivalent weights (Equivalent weight is defined as the ratio of the atomic mass of metal and the number of electrons required for reducing the cation).

We can derive from these electrolysis equations that the quantity of electricity required for oxidation-reduction is dependent on the electrode reaction's stoichiometry.

As an example,

++e

One mole of electrons is required for the reduction of one mole of sodium ions, as can be seen. We know that the charge on a single electron is 1.6021 10-19 C. As a result, the charge on one mole of electrons is:

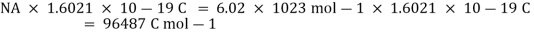
This quantity of electricity is indicated by F and is defined as the charge carried per unit mole of electrons.

The nature of the material being electrolyzed and the type of electrodes employed determine the outcome of an electrolytic reaction. An inert electrode, such as platinum or gold, does not participate in the chemical reaction and merely serves as a source or sink for electrons. A reactive electrode, on the other hand, is a participant in the reaction.

As a result, in the case of reactive and inert electrodes, various electrolytic products are formed. The products of electrolysis are affected by the oxidising and reducing species present in the electrolytic cell, as well as their standard electrode potential.

Key takeaway:

• Faraday's law ties the amplitude of the induced back EMF to the rate of change in the inducing magnetic field, while Lenz's law defines the direction of an induced current.
• There are two rules in Faraday's Laws of Electromagnetic Induction. The first law describes emf induction in a conductor, while the second law quantifies the emf produced. While Faraday's law specifies the amplitude of the EMF generated, Lenz's law specifies the direction in which the current will travel. This means that any magnetic field produced by an induced current will be the polar opposite of the original field change.

3.2 Rules of oxidation/reduction of ions based on half –cell potentials.

3.2.1 Standard electrode potential:

Standard Electrode Potential Definition

In an electrochemical cell, the standard electrode potential occurs when the temperature is 298K, the pressure is 1atm, and the concentration is 1M. The symbol Eocell denotes a cell's standard electrode potential.

Significance of Standard Electrode Potential

1. Redox reactions, which are made up of two half-reactions, constitute the foundation of all electrochemical cells.

2. The anode undergoes the oxidation half-reaction, which results in the loss of electrons.

3. At the cathode, a reduction reaction occurs, resulting in an electron gain. Electrons move from the anode to the cathode in this way.

4. The difference in the unique potentials of each electrode causes the electric potential to arise between the anode and the cathode (which are dipped in their respective electrolytes).

5. A voltmeter can be used to determine the cell potential of an electrochemical cell. A half-individual cell's potential, on the other hand, cannot be reliably quantified on its own.

6. It's also worth noting that this potential can alter as pressure, temperature, or concentration changes.

7. Standard electrode potential is required to achieve the individual reduction potential of a half-cell.

8. It is measured with the use of a conventional hydrogen electrode as a reference electrode (abbreviated to SHE). SHE has a 0-volt electrode potential.

9. By connecting an electrode to the SHE and measuring the cell potential of the resulting galvanic cell, the standard electrode potential of an electrode can be determined.

10. An electrode's oxidation potential is the inverse of its reduction potential. As a result, an electrode's standard electrode potential is characterised by its standard reduction potential.

11. Good oxidising agents have high standard reduction potentials, whereas good reducing agents have low.

Ca+ has a standard electrode potential of -3.8V, while F2 has a standard electrode potential of +2.87V. This means that F2 is an excellent oxidizer, whereas Ca is a reducing agent.

Standard Electrode Potential Example

The standard electrode potential of a zinc electrode can be calculated using the standard hydrogen electrode as shown below.

It should be emphasised that this potential is measured under normal conditions, which include a temperature of 298K, a pressure of 1 atm, and an electrolyte concentration of 1M.

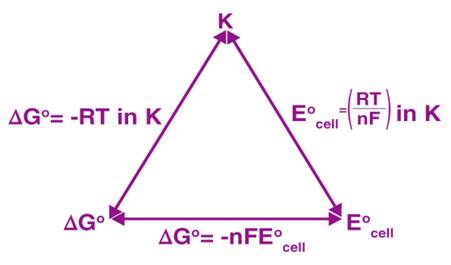
Spontaneity of Redox Reactions

The Go (Gibbs free energy) must be negative if a redox reaction is spontaneous. The following equation describes it:

ΔGocell = -nFE0cell

F is Faraday's constant, and n is the total number of moles of electrons for every mole of product created (approximately 96485 C.mol-1).

The E0cell can be calculated using the following formula:

E0cell = E0cathode – E0anode

As a result, the E0cell may be calculated by subtracting the anode's standard electrode potential from the cathodes. The E0cell must have a positive value for a redox reaction to be spontaneous (since both n and F have positive values, and the Go value must be negative).

This means that in a natural process,

E0cell > 0; which in turn implies that E0cathode > E0anode

Thus, the cathode and anode standard electrode potentials aid in forecasting the spontaneity of the cell reaction. It should be noted that in galvanic cells, the cell's Go is negative, whereas in electrolytic cells, it is positive.

3.2.2 Reduction potential:

What is Reduction Potential?

If oxidation occurs at the electrode, the electrode potential is oxidation potential, and the reduction potential is oxidation potential. Because reduction entails electron gain, an electrode's tendency to gain electrons is referred to as its reduction potential.

The electrode potential is the difference in potential between the metal electrode and the solution around it at equilibrium. It's also known as an electrode's tendency to lose or absorb electrons.

Reduction Potential Explanation

When a piece of metal is immersed in a solution containing its own ions, a potential difference between the metal and the solution is formed. The size of the potential difference is a measure of the electrodes' proclivity for oxidation or reduction, as well as their proclivity for losing or gaining electrons.

The half-cell is represented by the metal and ion, and the reaction is half reaction. The immersed metal acts as an electrode, and the potential created by reaction at the electrode-solution interface is referred to as the electrode potential. As a result, electrode potential refers to an electrode's tendency to lose or gain electrons. The reduction potential occurs when the reduction occurs at the electrode.

If the oxidation takes place at the electrode, it is called the oxidation potential

M ⇢ M2+ + 2e–

As metal ions begin to accumulate on the metal surface, the metal rod obtains a positive charge. Because oxidation is simply the reversal of reduction, the reduction potential can be derived by just changing the sign of the oxidation potential.

For an electrode, in general

Oxidation potential = – Reduction potential

For example, in a zinc electrode the standard oxidation potential is represented as

Eo (Zn/Zn2+) = 0.76V

And standard reduction potential as

Eo (Zn2+/Zn) = -0.76V

All of the electrode potentials are usually expressed as reduction potentials.

The International Union of Pure and Applied Chemistry (IUPAC) has recently adopted the reduction potential for the designation of electrode potential.

The electrode potential is known as the standard electrode potential and is represented by Eo when the half-cell reaction is carried out at 298K and the electrode is suspended in a solution of one molar concentration. The thermodynamic activity of various chemical compounds can be assessed using the Standard electrode potential Eo. However, there are no methods available to determine its absolute value. An electrode's electrode potential is assessed in comparison to a reference hydrogen electrode.

An electrode's electrode potential is determined by the concentration of ions in solution in contact with metal. Simply put, an electrode's oxidation potential is inversely proportional to ion concentration, while its reduction potential is directly proportional to ion concentration.

Half cells

A battery is made up of two half cells separated by an electrolyte. The electrodes are required to link the half cells to a circuit outside of the cell. Each electrode can be a part of a redox couple, although it isn't required.

The hydrogen half-cell’s standard conditions are hydrogen concentration [H+(AQ)], hydrogen gas pressure 105Pa, and temperature 298K.

All other half-cells are assessed against the standard hydrogen half-cell as a reference half-cell. In relation to the standard hydrogen half-cell, a list of electrode potentials has been developed. In this half-cell, the half reaction is

2H+(aq) + 2e– ⇌ H2(g)

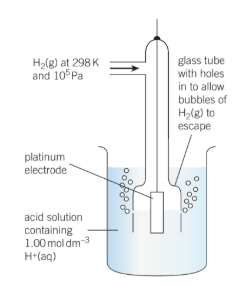
Because the potentials of the electrodes change with temperature, a standard temperature is established. This is 298 kilobytes. The voltages are affected by changing the concentration of any ions appearing in the half reactions, hence a standard concentration of 1.00 mol dm-3 is used. 105 psi is the standard pressure.

The potential of a conventional hydrogen half-cell is 0.0V, which is a convenient figure.

The potential difference between the half cell and a conventional hydrogen half-cell is defined as the standard electrode potential of a half-cell Eo.

Depending on whether the half-cell is at a greater or lower positive potential than the typical hydrogen half-cell, Eo Values have a sign. At 298K, measurements are taken with the metal dipped in a 1.00 mol dm-3 solution of a metal salt. Some of the values are

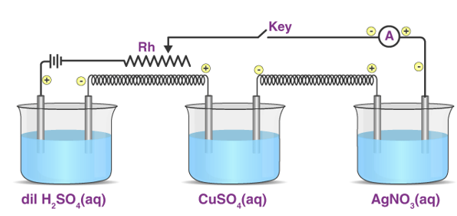
3.3.3 Electrochemical cell notation:

Cell Notation

Remember that for both oxidation and reduction reactions, standard cell potentials may be calculated using potentials E0cell. A positive cell potential implies that the reaction is proceeding spontaneously in the direction specified. A reaction with a negative cell potential, on the other hand, continues in the opposite direction spontaneously.

E0 reduction + E0 oxidation = Eo cell

Voltaic or galvanic (spontaneous) cells are described using cell notations. This unique shorthand describes the reaction circumstances (pressure, temperature, concentration, and so on), as well as the anode, cathode, and electrode components.

Remember that oxidation occurs at the anode and reduction occurs at the cathode. Electrons move from the anode to the cathode when the anode and cathode are connected by a wire.

A typical galvanic cell

A typical arrangement of half-cells linked to form a galvanic cell.

Using the arrangement of components, let’s put a cell together.

One beaker contains 0.15 M Cd (NO3)2 and a Cd metal electrode. The other beaker contains 0.20 M AgNO3 and an Ag metal electrode. The net ionic equation for the reaction is written:

2Ag+ (aq) + Cd (s) Cd {2+} (aq) + 2Ag (s)

In the reaction, the silver ion is reduced by gaining an electron, and solid Ag is the cathode. The cadmium is oxidized by losing electrons, and solid Cd is the anode.

The anode reaction is:

Cd (s) Cd {2+} (aq) + 2e-

The cathode reaction is:

2Ag+ (aq) + 2e- 2Ag (s)

Cell Notation Rules

1. The anode half-cell is discussed first, followed by the cathode half-cell. The reactants are mentioned first and the products are mentioned last within a half-cell. The oxidation reaction is described first, followed by the reduction reaction; as you read, your eyes will move in the direction of electron flow. Spectator ions are not included in this calculation.

2. A single vertical line (|) is drawn between two chemical species in distinct phases but physical contact (e.g., solid electrode | liquid with electrolyte). A salt bridge or porous membrane between the different half-cells is shown by a double vertical line (||).

3. Each chemical's phase (s, l, g, aq) is indicated in parenthesis. The electrolytes in the cells are indicated in parentheses with the phase notation if they are not at standard conditions, concentrations, or pressure. The electrolytes in the cells are presumed to be at standard conditions if no concentration or pressure is detected.  (1.00 M or 1.00 atm and 298 K).

Using these rules, the notation for the cell we put together is:

Cd (s) | Cd2+ (aq, 0.15 M) || Ag+ (aq, 0.20 M) | Ag (s)

The difference in electrical potentials for each electrode causes the cell potential to be (+0.46 V). While determining the electrical potential of a single electrode is impossible, we can give one a value of zero and use it as a reference. Figure 1 shows the standard hydrogen electrode, which was chosen as the zero electrode (SHE). The SHE is made up of 1 atm hydrogen gas bubbling through a 1 M HCl solution at ambient temperature. The electrode is made of platinum, which is chemically inert. The reference half-reaction is a reduction half-reaction.

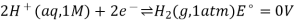
The standard reduction potential is E°. Standard circumstances are indicated by the superscript “°” on the E. (1 bar or 1 atm for gases, 1 M for solutes). For all temperatures, the voltage is defined as zero.

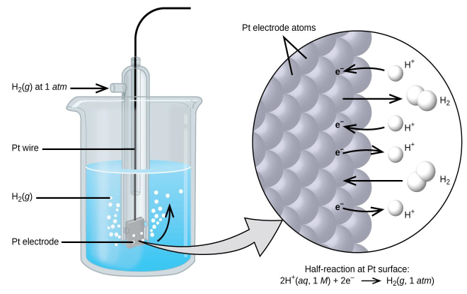
A 1 atm hydrogen gas is bubbled through a 1 M HCl solution. The electrode is made of platinum, which is resistant to the effects of 1 M HCl. Hydrogen gas is produced when electrons on the electrode's surface mix with H+ in solution.

To estimate the standard reduction potential for Cu2+, a galvanic cell with a SHE and a Cu2+/Cu half-cell can be utilised (Figure 2). Pt(s)H 2 (g,1atm) H+ (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+ (s)

From the anode to the cathode, electrons flow. The reversible reactions are as follows:

A 1 atm hydrogen gas is bubbled through a 1 M HCl solution. The electrode is made of platinum, which is resistant to the effects of 1 M HCl. Hydrogen gas is produced when electrons on the electrode's surface mix with H+ in solution.

To estimate the standard reduction potential for Cu2+, a galvanic cell with a SHE and a Cu2+/Cu half-cell can be utilised (Figure 2). Pt(s)H 2 (g,1atm) H+ (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+) (aq,1M) Cu (2+ (s)

From the anode to the cathode, electrons flow. The reversible reactions are as follows:

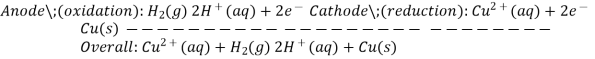
Subtracting the standard reduction potential for the reaction occurring at the anode from the standard reduction potential for the reaction occurring at the cathode yields the standard reduction potential. Because oxidation is the inverse of reduction, the minus sign is required.

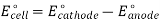
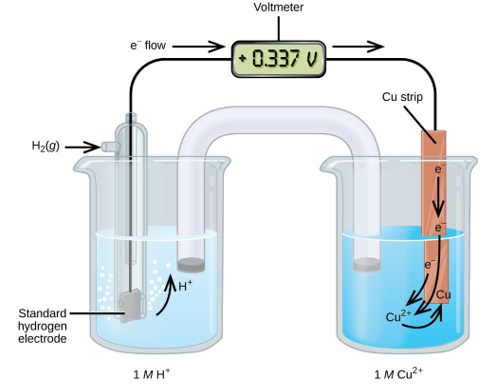
Figure. A galvanic cell can be used to determine the standard reduction potential of Cu2+.

Using the SHE as a reference, other standard reduction potentials can be determined. Consider the cell shown in Figure 3, where

Electrons flow from left to right, and the reactions are

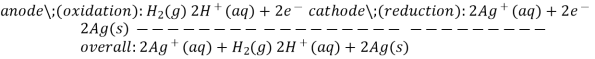
Subtracting the standard reduction potential for the reaction occurring at the anode from the standard reduction potential for the reaction occurring at the cathode yields the standard reduction potential. Because oxidation is the inverse of reduction, the minus sign is required.

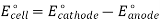
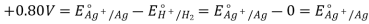
It's vital to note that the cathode reaction's potential isn't doubled.

The SHE is a hazardous substance that is only utilised in laboratories on rare occasions. It is most notable for establishing the zero for standard reduction potentials. Standard reduction potentials can be used to determine the standard cell potential, Ecell, for each cell once they've been determined.

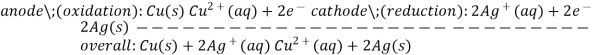
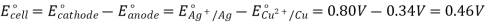
Note that even when a half-reaction is amplified by a factor, typical reduction potentials stay the same when calculating Ecell. Table 2 shows standard reduction potentials for a variety of reduction reactions.

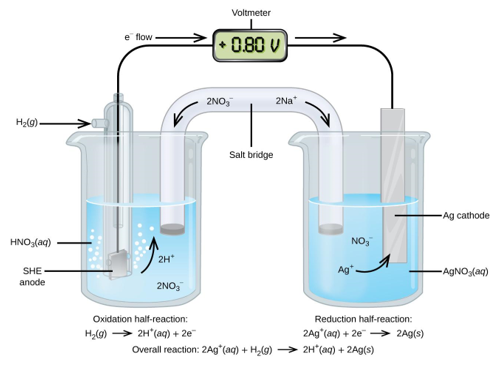
The standard reduction potential of Ag+ can be determined using a galvanic cell. The anode is the SHE on the left, which has a typical reduction potential of zero.

3.3 Applications of electrolysis in metallurgy and industry.

3.3.1 Electrolysis Applications

As previously stated, electrolysis is the process of changing the ions of a liquid chemical into a reduced or oxidised state by passing an electric current through it. As a result, electrolysis has a wide range of uses in both experimental and industrial products. The following are a few of the most important:

1) The equivalent eight of substances must be determined.

2) Alkali and alkaline earth metal metallurgy.

3) Metal’s purification.

4) Production of clean gases

5) Synthesis of chemicals such as sodium hydroxide, sodium carbonate, and potassium chlorate, among others.

6) Corrosion resistance, decorations, and other electroplating

Below, we'll go over the many electrolysis uses in depth.

3.3.2 Determination of Equivalent Eight of Substances

The mass of substances deposited is proportionate to their equivalent weight, according to Faraday's Second Law. The mass of any deposited substance can be calculated as follows:

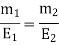
By running a known current through the solutions and identifying the mass of substances (M1 and M2) deposited in their corresponding cells, the equivalent mass of an unknown metal or substance can be computed. The equivalent mass of an unknown substance can be computed using the following equation if the equivalent mass of one material is known.

Electrolysis of Molten Salts

Alkali and alkaline earth metallurgy, as well as third-group metals Metal ores are concentrated and primarily transformed to oxides. Reducing agents such as charcoal, aluminium, and other metals are used to reduce oxides. Because alkali and alkali earth metals have the highest reduction potentials, no other metals or their compounds can reduce them.

Alkali and alkali earth metals can only be isolated by electrolyzing their molten chlorides directly. The melting point of pure halides is lowered when they are mixed with other halides, such as calcium chlorides.

Electrorefining – Purification of Metals

The purity of metals produced following concentration and reduction of ores ranges from 90 to 99 percent. An aqueous solution of the metal salt is electrolyzed with an impure metal as anode and a pure metal as cathode. Impurities are gathered at the bottom as mud, while pure metal of greater than 99 percent purity deposits on the cathode. Electrorefining is used to purify metals such as copper and nickel.

Electroplating

Electrolysis can be used to coat an object to the desired thickness with a certain metal. The cathode coating is applied to the object to be coated. The electrolyte is an aqueous solution of the metal salt to be coated. The anode can be the same metal or any inert metal. Metal ions from the electrolyte accumulate on the item during electrolysis. If the anode is constructed of the same metal as the cathode, the loss of metal ions in the solution will be compensated.

Deposition can be used to protect metals from corrosion and to create ornamentation, among other things. The corrosion resistance of iron is improved by coating it with metals such as zinc, lead, chromium, and nickel. Ornaments are made with gold and silver coatings on cheaper metals.

Electro-forming

Electroforming is the process of utilising electricity to create a duplicate of an object. To form a mould, the thing to be duplicated is crushed in wax. To make graphite powder conduct, it is uniformly coated. This is used as a cathode, with the electrolyte being the salt of the metal to be deposited. Wax and graphite are melted away after electrolysis provides the appropriate covering.

Manufacture of Pure Gases

Depending on the relative quantities of salt and water, aqueous salts hydrolyze to produce distinct compounds. Pure hydrogen and chlorine gases are produced by electrolysis of concentrated brine (sodium chloride). In the chlor-alkali industry, pure chlorine gas is collected via electrolysis of brine aqueous solution.

Hydrolysis of water in the presence of acid or base, or inert salts of alkali and alkaline earth metals, yields pure hydrogen and oxygen. Worldwide, the electrolysis of water produces a certain percentage of hydrogen for commercial usage.

Water electrolysis removes all of the conventional hydrogen isotopes, leaving just deuterium ions. Heavy water is the deuterium oxide that remains after regular water has been electrolyzed. In nuclear reactors, heavy water is utilised as a moderator to produce electrical energy from nuclear processes.

Manufacture of Compounds

Electrolysis produces compounds such as sodium hydroxide, sodium hydrosulphite, potassium permanganate, potassium chlorate, ammonium per-sulphate, heavy water, and others. Sodium hydroxide is a by product of the chloralkali industry's electrolysis of brine to produce chlorine gas.

Electrolysis of potassium manganite solution yields potassium permanganate. Electrolysis converts ammonium sulphate or ammonium bisulphate to ammonium persulphate.

Extraction Of Reactive Metals

The metals at the top of the electrochemical series are known as reactive metals. Electrolysis is used to extract metals that are higher in the electrochemical series than zinc. Other metals, such as carbon reduction, cannot remove these highly reactive metals. Electrolysis of a molten ionic compound of metal yields reactive metals.

Case Study: Extraction of Aluminium

Aluminium is extracted from aluminium oxide (Al2O3Al2O3) or known as bauxite.

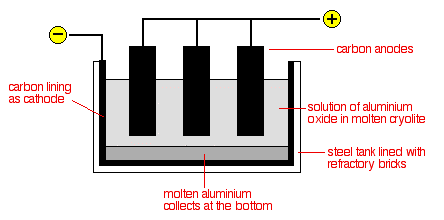
The electrolytic cell is a carbon-lined iron tank that serves as the cathode. Carbon blocks soaked in electrolyte serve as anodes. A solution of molten aluminium oxide in molten cryolite serves as the electrolyte. Cryolite serves as both a solvent for dissolving aluminium oxide and an impurity for lowering the melting point of the metal. The electrolytic cell is kept at a temperature of roughly 900°C.

Electrodes: Carbon

Ions present in electrolyte: Al3+, O-2

Reaction at cathode: Al3+(l) +3e−→Al(l)

Reaction at anode: 2O2−(l) →O2(g)+4e−

At the cathode, aluminium ions are discharged, resulting in a pool of molten aluminium at the tank's bottom.

When oxygen combines with the carbon anode at a high temperature, carbon dioxide gas is produced. As a result, the anodes steadily degrade into carbon dioxide gas and must be replaced on a regular basis.

3.4 Chemical cells

3.4.1 Galvanic cell:

What is Galvanic Cell?

A galvanic cell or voltaic cell is an electrochemical cell that converts the chemical energy of spontaneous redox reactions into electrical energy.

Galvanic cell is a type of electrochemical cell. A voltaic cell is an electrochemical cell that generates electricity through chemical processes.

Let's have a look at how a voltaic or galvanic cell is made.

Electrons are transferred from one species to another in oxidation-reduction processes. If a reaction occurs spontaneously, energy is released. As a result, the liberated energy is put to good use. To deal with this energy, the reaction must be divided into two half-reactions: oxidation and reduction. The reactions are put into two distinct containers with wire in order to move the electrons from one end to the other. This results in the formation of a voltaic cell.

Principle of Galvanic (Voltaic) Cell

The Gibbs energy of spontaneous redox reaction in the voltaic cell is primarily responsible for the electric work done by a galvanic cell. It consists of two half cells and a salt bridge in most cases. A metallic electrode immersed in an electrolyte is also included in each half cell. With the help of metallic wires, these two half-cells are externally connected to a voltmeter and a switch. A salt bridge is not always necessary when both electrodes are submerged in the same electrolyte.

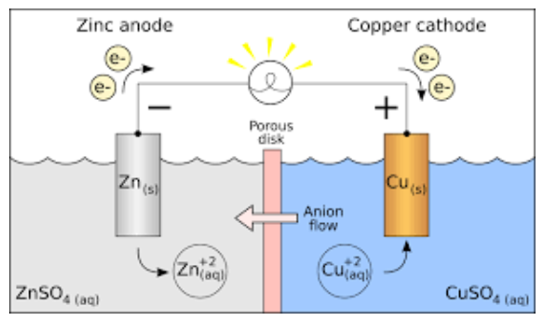
Galvanic Cell (Voltaic Cell) Diagram

Parts of Galvanic Cell

1. Anode - This electrode is where oxidation takes place.

2. Cathode - This electrode is where reduction takes place.

3. Salt bridge - A salt bridge contains the electrolytes needed to complete the circuit in a galvanic cell.

4. Half-cells – the reduction and oxidation reactions are compartmentalised.

5. External circuit - Allows electrons to travel freely between electrodes.

6. Load - A component of the circuit that relies on the flow of electrons to complete its function.

Working of Galvanic Cell

1. When an electrode is exposed to the electrolyte at the electrode-electrolyte interface in a galvanic cell, the atoms of the metal electrode tend to create ions in the electrolyte solution, leaving the electrons at the electrode behind. As a result, the metal electrode becomes negatively charged.

2. Metal ions in the electrolyte solution, on the other hand, have a tendency to settle on a metal electrode. As a result, the electrode becomes positively charged.

3. Charge separation is observable under equilibrium conditions, and the electrode can be positively or negatively charged depending on the inclinations of two opposing reactions. As a result, a potential difference between the electrode and the electrolyte develops.

4. The electrode potential is the difference in potential between the two electrodes.

5. The electrode that undergoes oxidation is known as the anode, while the electrode that undergoes reduction is known as the cathode.

6. The cathode has a positive potential in relation to the solution, whereas the anode has a negative potential in relation to the solution.

7. As a result, a potential difference occurs between the galvanic cell's two electrodes. The differential in potential is referred to as cell potential.

Cell potential is defined as the electromotive force of the galvanic cell when no current is extracted from it.

9. When the switch is turned on, electrons flow from the negative electrode to the positive electrode due to the potential difference.

Example of Galvanic Cell

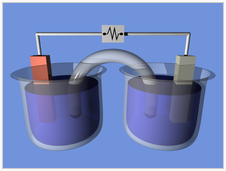
More than a century ago, electrochemical or galvanic cells were introduced as a technique for researching the thermodynamic features of fused salts. A galvanic cell, such as Daniel's cell, turns chemical energy into electrical energy. Copper ions are reduced at the cathode in Daniel's cell, while zinc is oxidised at the anode.

Daniel cell reactions at the cathode and anode are as follows:

At cathode: Cu 2+ + 2e– → Cu

At anode: Zn → Zn2+ + 2e–

3.4.2 What is an Electrochemical Cell?

An electrochemical cell is a device that may either create electrical energy from chemical processes taking place inside it or use electrical energy supplied to it to aid chemical reactions taking place inside it. Chemical energy can be converted to electrical energy or vice versa using these devices. A conventional 1.5-volt cell, which is used to power numerous electrical items such as TV remotes and clocks, is an example of an electrochemical cell.

Galvanic cells or Voltaic cells are cells that can generate an electric current from chemical reactions that occur within them. Electrolytic cells, on the other hand, are cells that undergo chemical reactions when an electric current is delivered through them.

Below is a diagram that shows the many components of an electrochemical cell.

Cell Electrochemical

A cathode and an anode are the most common components of electrochemical cells. The essential characteristics of the cathode and anode are listed below.

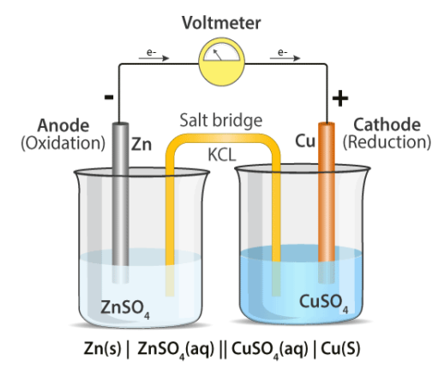
When signifying an electrochemical cell, the cathode must be depicted on the right-hand side, whilst the anode must be represented on the left-hand side.

3.4.3 Half-Cells and Cell Potential

1. The electrochemical process A cell is made up of two half-cells, each of which has an electrode dipped in an electrolyte. Both halves of the cell can use the same electrolyte.

2. These half cells are joined by a salt bridge, which offers a platform for ionic communication between them while preventing them from mixing. A filter paper soaked in a potassium nitrate or sodium chloride solution is an example of a salt bridge.

3. One of the electrochemical cell's half cells loses electrons due to oxidation, while the other obtains electrons through reduction. It should be observed that in both half cells, an equilibrium reaction occurs, and once the equilibrium is reached, the net voltage becomes 0 and the cell ceases to produce electricity.

4. The electrode potential describes the tendency of an electrode in contact with an electrolyte to lose or gain electrons. These potentials' values can be utilised to forecast the cell's overall potential. The electrode potentials are usually measured using a conventional hydrogen electrode as a reference electrode (an electrode of known potential).

Primary and Secondary Cells

1. Primary cells are essentially galvanic use-and-throw cells. In nature, the electrochemical events that occur in these cells are irreversible. As a result, the reactants are used up in the production of electrical energy, and the cell stops producing current once the reactants are depleted.

2. Secondary cells (also known as rechargeable batteries) are electrochemical cells with a reversible reaction, meaning they can work as both a Galvanic and an Electrolytic cell.

3. The majority of primary batteries (many cells connected in series, parallel, or a mix of the two) are wasteful and damaging to the environment. This is due to the fact that their manufacturing process consumes roughly 50 times the energy they contain. They also contain a high level of harmful metals and are classified as hazardous trash.

Types of Electrochemical Cells

The two primary types of electrochemical cells are

1.  Galvanic cells (also known as Voltaic cells)

2. Electrolytic cells

The key differences between Galvanic cells and electrolytic cells are tabulated below.

Applications of Electrochemical Cells

1. Many non-ferrous metals are electro refined using electrolytic cells. These metals are also electrowinning with them.

2. Electrolytic cells are used in the manufacturing of high-purity lead, zinc, aluminium, and copper.

3. Metallic sodium can be recovered from molten sodium chloride by sending an electric current across it in an electrolytic cell.

4. Galvanic cells are used in many commercially important batteries (such as lead-acid batteries).

5. Fuel cells are a type of electrochemical cell that may be used to generate renewable energy in a variety of remote settings.

The cell that undergoes the following reactions:

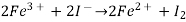
Has Eøcell = 0.236 V at 298 K. Calculate the standard Gibbs energy and the equilibrium constant of the cell reaction.

Solution:

By using the formula, 

ΔrG = -nFEcell

= -2 X 96487 X 0.236

= - 45541.864 J mol-1

= - 45.54 KJ mol-1

Now,

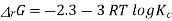
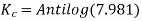
Key takeaway:

Two bars or slashes, which symbolise a salt bridge, separate the cell anode and cathode (half-cells). The anode goes on the left, whereas the cathode goes on the right. Within each half-cell, a single bar separates the individual solid, liquid, or aqueous phases.

3.5 Reversible and irreversible cells with examples.

3.5.1 Reversible process:

Every day, we witness several changes such as water boiling, iron rusting, ice melting, paper burning, and so on. In all of these processes, we notice that the system in question transitions from an initial state to a final state in which the system absorbs some heat from the environment and performs some work W on the environment. Now, how many of these systems can the system and its environment be restored to their original state? With popular instances like rusting and fermentation, we may conclude that it is not possible in the vast majority of circumstances. We will study about reversible and irreversible processes in this part.

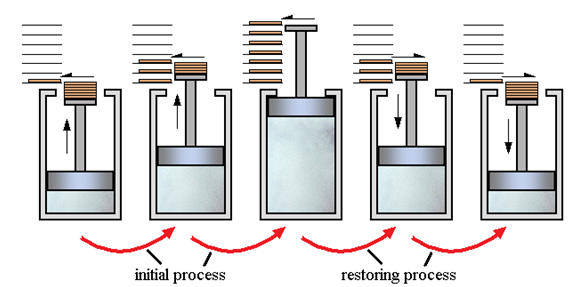
Reversible and Irreversible Processes

What are Reversible Processes?

A thermodynamic process (state I state f) is considered to be reversible if it can be reversed so that the system and its surroundings return to their original states with no further changes in the universe. As we all know, there are no such things as reversible processes in reality. Reversible processes can thus be simply characterised as idealizations or models of real processes, based on which the system or device's boundaries have to be specified. They assist us in determining the maximum efficiency a system can deliver under ideal operating conditions, as well as the target design that can be established.

Examples of Reversible Process

We've included a few instances of reversible processes below:

1. Springs' extension

2. Adiabatic compression or expansion of gases at a slow rate

3. The process of electrolysis (with no resistance in the electrolyte)

4. The motion of solids without friction

5. Gases are compressed or expanded at a slow, isothermal rate.

Reversible Changes

Reversible modifications are any alterations that can be reversed or are a temporary conversion. Reversible reactions are those that are reversible in nature. A material is transformed into a different form in this reaction, but no new chemical is produced. Melting, boiling, evaporation, freezing, condensation, and disintegration are examples of reversible transformations. Melting wax, freezing ice, and boiling water that evaporates as steam and condenses back to water are a few examples.

Reactions are the result of the interaction of two or more reactants to form a product (s). A two-way arrow () connects the reactants and products created in a reversible process. This indicates that reactants can be recovered from products.

Consider the following reaction:

A +B ⇌ C + D

A and B are two reactants that combine to form C and D. The reaction is reversible, as indicated by the two-headed arrow, and the reactants A and B can be recovered from C and D.

3.5.2 Irreversible cell and process:

What are Irreversible Processes?

An irreversible process is one in which the system and its surroundings do not revert to their original state after the process has been started. Consider the case of an automotive engine that has travelled a certain distance using a certain amount of fuel. The fuel burns to generate energy to the engine, converting itself to smoke and heat energy in the process. We will never be able to recover the energy lost by the fuel, nor will we ever be able to return to its original state. The irreversibility of a process is caused by a number of reasons, including:

1. Friction that turns the fuel's energy into heat energy.

2. The unregulated expansion of the fluid, which prevents the fuel from returning to its previous state. The reversal of heat transfer through a finite temperature is not feasible because the forward process is spontaneous in this scenario.

3. Intermixing of two different substances that cannot be separated since the process is spontaneous in nature, and the opposite is not possible.

As a result, depending on their ability to return to their original form from their final state, certain processes are reversible and others are irreversible.

Examples of Irreversible Processes

Irreversible Processes include the following:

1. Frictional relative motion

2. Suffocation

3. The transport of heat

4. Dissemination

5. Flow of electricity through a resistance

Irreversible changes

Irreversible alterations, in contrast to reversible changes, are permanent. Reactants combine to generate a completely new compound that cannot be undone. Heating, burning, combining, and powdering are only a few examples of procedures that result in irreversible alterations. Cooking a raw egg that cannot be transformed back to its original form is a common observed example. Another example is ash produced by the combustion of paper or other materials.

Irreversible reactions occur when a reaction occurs in just one direction. In such reactions, reactants entirely react to generate a product over a period of time. A one-way arrow () is used to represent reaction.

As an example,

A → B +C

Here, A is the reactant which is completely converted into products B and C which do not react to form A.

3.6 Electromotive force of a cell and its measurement:

3.6.1 Electromotive cell:

What is Electromotive Force?

The electric potential generated by an electrochemical cell or by changing the magnetic field is known as electromotive force. Electromotive force is frequently abbreviated as EMF.

Energy is converted from one form to another using a generator or a battery. One terminal becomes positively charged, while the other becomes negatively charged in these devices. As a result, an electromotive force is work performed on a single unit of electric charge.

The electromagnetic flowmeter, which is based on Faraday's law, employs electromotive force.

Symbol for Electromotive Force

The electromotive force symbol is ε.

What is Electromotive Force Formula?

Following is the formula for electromotive force:

ε = V + Ir

Where I. V is the cell's voltage and II. I is the circuit's current.

3. r is the cell's internal resistance.

The electromotive force (EVF) is the fourth force.

What is the unit of EMF?

Volt is the unit of electromotive force.

EMF is calculated by dividing the amount of Joules of energy provided by the source by each Coulomb required to transfer a unit electric charge across the circuit.

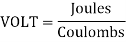
Dimension of Electromotive Force

EMF is given as the ratio of work done on a unit charge which is represented as follows:

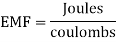
Therefore, EMF dimension is given as M1L2T-3I-1

Difference between Electromotive Force and Potential Difference

Can electromotive force be negative?

Yes, there is a possibility that the electromotive force is negative. Consider the case of an inductor that generates an EMF that is in opposition to the incoming power. The resulting EMF is thus interpreted as negative because the flow direction is opposite that of the true power. As a result, the electromotive force is possible to be negative.

What is the difference between terminal voltage and EMF?

The differences between terminal voltage and EMF are as follows:

I. The potential difference across the terminals of a load when the circuit is on is known as terminal voltage. EMF, on the other hand, is defined as the highest potential difference delivered by the battery while no current is flowing.

II. The terminal voltage is measured with a voltmeter, while the EMF is measured with a potentiometer.

Problem: - The storage battery of a car has an Emf of 12 V. If the internal resistance of the battery is 0.4Ω, what is the maximum current that can be drawn from the battery?

Answer: -

Emf of the battery, E = 12 V

Internal resistance of the battery, r = 0.4 Ω

Maximum current drawn from the battery = I

According to Ohm’s law, E=IR

I=(E/R) = (12/0.4) =30A

The maximum current drawn from the given battery is 30 A.

3.6.2 Calculation of emf of Daniell Cell

In Daniell cell, the electrode potentials of the half cells are written as:

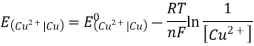
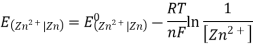
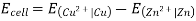
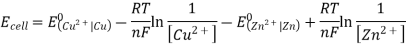
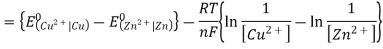
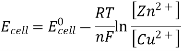
At ,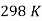

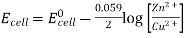
So, Nernst equation is generally represented as:

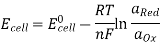Where,  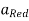is the activity (Concentration) of reduced species, and  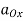is the activity (Concentration) of oxidised species.

The standard electrode potential, temperature, the number of electrons engaged in the chemical reaction, and the concentration of the reacting species all influence the electrode potential of an electrochemical.

3.7 Nernst equation; Standard electrode (reduction) potential and its application to different kinds of half-cells.

3.7.1 Nernst equation:

What is Nernst Equation?

The Nernst equation connects an electrochemical cell's cell potential, the standard cell potential, temperature, and the reaction quotient. The Nernst equation can be used to determine the cell potentials of electrochemical cells even under non-standard situations.

The Nernst equation is frequently used to compute an electrochemical cell's cell potential at any temperature, pressure, or reactant concentration. Walther Hermann Nernst, a German scientist, first proposed the equation.

Expression of Nernst Equation

The Nernst equation is a formula that compares an atom's or ion's capability to take up one or more electrons (reduction potential) under any conditions to that measured under standard conditions (standard reduction potentials) of 298K and one molar or atmospheric pressure.

Nernst Equation for Single Electrode Potential

Ecell = E0 – [RT/nF] ln Q

Where,

1. Ecell = cell potential of the cell
2. E0 = cell potential under standard conditions
3. R = universal gas constant
4. T = temperature
5. n = number of electrons transferred in the redox reaction
6. F = Faraday constant
7. Q = reaction quotient

The Nernst equation is used to calculate the single electrode reduction potential (Ered) for an atom/ion from the standard single electrode reduction potential (E°red).

⇒ Also Read: Redox Reactions

For a reduction reaction, Nernst equation for a single electrode reduction potential for a reduction reaction

Mn+ + ne– → nM is;

Ered = EMn+/M = EoMn+/M – [2.303RT/nF] log [1/[Mn+]]

Where,

1. R is the gas constant = 8.314 J/K Mole
2. T = absolute temperature,
3. n = number of moles of electron involved,
4. F = 96487 (≈96500) coulomb/mole = charged carried by one mole of electrons.
5. [Mn+] = active mass of the ions. For simplicity, it may be taken as equal to the molar concentration of the salt.

Nernst Equation at 25oC

For measurements carried out 298K, the Nernst equation can be expressed as follows.

E = E0 – 0.0592/n log10 Q

As a result of the Nernst equation, an electrochemical cell's overall potential is determined by the reaction quotient.

Derivation of Nernst Equation

Consider a metal that has come into contact with its own aqueous salt solution. Reactions in which a metal loses an electron to become an ion and an ion gains an electron to return to the atomic state are both possible and in equilibrium.

Mn+ + ne– → nM

In the reduction reaction, ‘n’ moles of an electron is taken up by the ion against a reduction potential of Ered.

1. The work done in the movement of electron

Wred = nFEred

Where,

F is Faraday = 96487 coulomb = electrical charge carried by one mole of electrons

2. The change in Gibbs free energy is a measure of spontaneity, as well as the greatest beneficial work (other than volume expansion) performed in a process.

Work completed and Gibbs free energy change:

Wred = nFEred = – ∆G or ∆G = – nFEred

3. G° is the change in free energy at standard circumstances of 298K and one molar / one atmospheric pressure. It can be deduced from the above relationship that

∆G° = – nFE°red

Where,

E°red is the reduction potential measured at standard conditions.

4. The concentration changes during the reaction, and the potential decreases as the process progresses.

The concentrations must be kept constant in order to get the maximal work or free energy change. This is only possible if the reaction is carried out in a reversible equilibrium state.

The vant Hoff isotherm states for a reversible equilibrium reaction:

∆G = ∆G° + RT ln K

Where,

1. K is the equilibrium constant
2. K = Product/Reactant = [M]n/[M]n+
3. R is the Gas constant =8 .314J/K mole
4. T is the temperature in Kelvin scale.

Determining Equilibrium Constant with Nernst Equation

The value of G becomes 0 when the reactants and products of the electrochemical cell reaches equilibrium. The reaction quotient and the equilibrium constant (Kc) are the same at this point. The cell potential at equilibrium is also 0 since G = -nFE.

The following equation is generated by substituting the values of Q and E into the Nernst equation.

0 = E0cell – (RT/nF) ln Kc

The relationship between the Nernst equation, the equilibrium constant, and Gibb’s energy change is illustrated below.

Nernst equation vs Equilibrium constant vs Gibb’s energy change

The equation is changed as follows by converting the natural logarithm into base-10 logarithm and substituting T=298K (standard temperature).

E0cell = (0.0592V/n) log Kc

Rearranging this equation, the following equation can be obtained.

Log Kc = (nE0cell)/0.0592V

As a result, the equilibrium constant and the standard cell potential are found to be related. E0cell will be greater than 0 when Kc is greater than 1, meaning that the equilibrium favours the forward reaction. E0cell will also have a negative value when Kc is less than 1, indicating that the opposite reaction will be preferred.

Nernst Equation Applications

The Nernst equation can be used to calculate:

I. The reduction or oxidation potential of a single electrode under any conditions

II. Electrode potentials that are commonly used

III. Assessing a substance's reductive or oxidative potential.

IV. Determining the viability of combining such single electrodes to generate an electric potential.

V. An electrochemical cell's emf

Ionic concentrations that are unknown

The Nernst equation can be used to determine the pH of solutions and the solubility of sparingly soluble salts.

Limitations of Nernst Equation

In an extremely dilute solution, an ion's activity is close to infinity, hence it can be represented in terms of ion concentration. The ion concentration, on the other hand, is not equivalent to the ion activity in solutions with very high concentrations. In order to employ the Nernst equation in these situations, experimental measurements must be taken to determine the ion's true activity.

Another flaw in this equation is that it cannot be utilised to determine cell potential while the electrode is conducting current. This is because the current flow changes the activity of the ions on the electrode's surface. When there is a current flowing through the electrode, extra considerations such as resistive loss and overpotential must be taken into account.

NERNST Equation Solved Examples

1. The standard electrode potential of zinc ions is 0.76V. What will be the potential of a 2M solution at 300K?

Solution:

The Nernst equation for the given conditions can be written as follows;

EMn+/M = Eo – [(2.303RT)/nF] × log 1/[Mn+]

Here,

1. E° = 0.76V
2. n = 2
3. F = 96500 C/mole
4. [Mn+] = 2 M
5. R =8.314 J/K mole
6. T =300 K

Substituting the given values in Nernst equation we get,

EZn2+/Zn = 0.76 – [(2.303×8.314×300)/ (2×96500)] × log 1/2 = 0.76 – [0.0298 × (-0.301)]

= 0.76 + 0.009 = 0.769V

Therefore, the potential of a 2M solution at 300K is 0.769V.

2. From the following standard potentials, arrange the metals in the order of their increasing reducing power.

1. Zn2+(aq) + 2e– → Zn(s): E° = -0.76 V
2. Ca2+(aq) + 2e– → Ca(s): E° = -2.87 V
3. Mg2+(aq) + 2e– → Mg(s): E° = -2.36 V
4. Ni2+(aq) + 2e– → Ni(s): E° = -0.25 V
5. Ni(s) → Ni2+(aq) + 2e–: E° = +0.25 V

The ability of a metal to give up electrons, i.e., lower standard potentials, enhances its reducing power. The rising order of reducing power of metals is obtained by arranging the reduction potentials in decreasing order.

Increasing order of reduction potentials is Ni (-0.25V) < Zn (-0.76V) < Mg(-2.36V) < Ca (-2.87).

3. What is the Cell Potential of the electrochemical cell in Which the cell reaction is: Pb2+ + Cd → Pb + Cd2+; Given that Eocell = 0.277 volts, temperature = 25oC, [Cd2+] = 0.02M, and [Pb2+] = 0.2M.

Solution

Since the temperature is equal to 25oC, the Nernst equation can be written as follows;

Ecell = E0cell – (0.0592/n) log10Q

Here, two moles of electrons are transferred in the reaction. Therefore, n = 2. The reaction quotient (Q) is given by [Cd2+]/[Pb2+] = (0.02M)/ (0.2M) = 0.1.

The equation can now be rewritten as:

Ecell = 0.277 – (0.0592/2) × log10(0.1) = 0.277 – (0.0296) (-1) = 0.3066 Volts

Thus, the cell potential of this electrochemical cell at a temperature of 25oC is 0.3066 volts.

3.7.2 Standard electrode potential:

Definition of a Standard Electrode Potential

In an electrochemical cell, the standard electrode potential occurs when the temperature is 298K, the pressure is 1atm, and the concentration is 1M. The symbol Eocell denotes a cell's standard electrode potential.

Standard Electrode Potential's Importance

1. Redox reactions, which are made up of two half-reactions, constitute the foundation of all electrochemical cells.

2. The anode undergoes the oxidation half-reaction, which results in the loss of electrons.

3. At the cathode, a reduction reaction occurs, resulting in an electron gain. Electrons move from the anode to the cathode in this way.

4. The difference in the unique potentials of each electrode causes the electric potential to arise between the anode and the cathode (which are dipped in their respective electrolytes).

5. A voltmeter can be used to determine the cell potential of an electrochemical cell. A half-individual cell's potential, on the other hand, cannot be reliably quantified on its own.

6. It's also worth noting that this potential can alter as pressure, temperature, or concentration changes.

7. Standard electrode potential is required to achieve the individual reduction potential of a half-cell.

8. It is measured with the use of a conventional hydrogen electrode as a reference electrode (abbreviated to SHE). SHE has a 0-volt electrode potential.

9. By connecting an electrode to the SHE and measuring the cell potential of the resulting galvanic cell, the standard electrode potential of an electrode can be determined.

10. An electrode's oxidation potential is the inverse of its reduction potential. As a result, an electrode's standard electrode potential is characterised by its standard reduction potential.

11. Good oxidising agents have high standard reduction potentials, whereas good reducing agents have low.

Ca+ has a standard electrode potential of -3.8V, while F2 has a standard electrode potential of +2.87V. This means that F2 is an excellent oxidizer, whereas Ca is a reducing agent.

Standard Electrode Potential Example

The calculation of the standard electrode potential of a zinc electrode with the help of the standard hydrogen electrode is illustrated below.

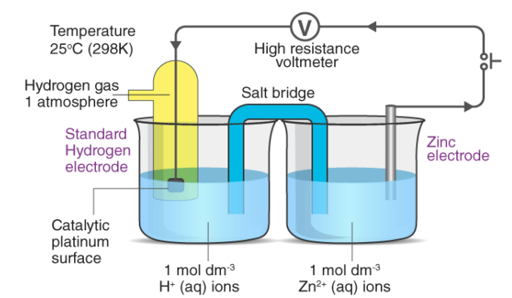
It should be emphasised that this potential is measured under normal conditions, which include a temperature of 298K, a pressure of 1 atm, and an electrolyte concentration of 1M.

Redox Reactions' Spontaneity

The Go (Gibbs free energy) must be negative if a redox reaction is spontaneous. The following equation describes it:

ΔGocell = -nFE0cell

F is Faraday's constant, and n is the total number of moles of electrons for every mole of product created (approximately 96485 C.mol-1).

The E0cell can be calculated using the following formula:

E0cell = E0cathode – E0anode

As a result, the E0cell may be calculated by subtracting the anode's standard electrode potential from the cathodes. The E0cell must have a positive value for a redox reaction to be spontaneous (since both n and F have positive values, and the Go value must be negative).

This means that in a natural process,

E0cell > 0; which in turn implies that E0cathode > E0anode

Thus, the cathode and anode standard electrode potentials aid in forecasting the spontaneity of the cell reaction. It should be noted that in galvanic cells, the cell's Go is negative, whereas in electrolytic cells, it is positive.

3.8 Application of EMF measurements in determining free energy.

3.8.1 EMF of cells:

The maximum potential difference between two electrodes of a cell is known as the electromotive force of a cell, or EMF of a cell. It's also known as the net voltage between the half-reactions of oxidation and reduction. An electrochemical cell's EMF is primarily used to identify whether it is galvanic or not.

In this session, we'll study more about this topic, including key formulas and how to compute the EMF of an electrochemical cell.

What is an Electrochemical Cell?

An electrochemical cell is a device that uses a chemical reaction to generate electricity. It is essentially a gadget that transforms chemical energy to electrical energy. An electrochemical cell cannot function without a chemical reaction that involves the exchange of electrons. Redox reactions are the name for these types of reactions.

The voltage of a cell is what distinguishes it. Regardless of cell size, a certain type of cell generates the same voltage. The chemical composition of the cell is the sole factor that affects the cell voltage when it is operated under perfect conditions.

Several factors, such as temperature differences, changes in concentration, and so on, might cause the cell voltage to diverge from this optimum value. The EMF value of a cell can be calculated using the Nernst equation, which was developed by Walther Nernst, if the cell's standard cell potential is known.

3.8.2 Types of Electrochemical Cell

Galvanic Cell

Galvanic Cell is named after Italian scientist Luigi Galvani. A galvanic cell is a type of electrochemical cell that serves as the foundation for many others, including the Daniell cell. It is made up of two separate metallic conductors known as electrodes, each of which is immersed in its own ionic solution. Each of these configurations is half of a cell. A half-cell cannot generate a potential difference by itself. However, when they are combined, they can make a significant difference. A salt bridge is utilised to chemically connect the two cells. It transfers electrons from the electron-rich half-cell to the electron-deficient half-cell in the needed amount.

Let's look at the Daniell cell theory and develop the Nernst equation for it to make things clearer.

Daniell Cell

The galvanic cell has been adapted into the Daniell cell. It's made up of zinc and copper electrodes that have been immersed in zinc and copper sulphate solutions, respectively. A salt bridge is used to connect two half cells together. The zinc electrode serves as the anode, while copper serves as the cathode.

When compared to the copper metal, the zinc metal comes out on top in the electrochemical series due to its larger oxidation potential. As a result of the oxidation of zinc, two electrons and a zinc ion are produced. When compared to the other electrode, this electrode gets a negative potential due to the release of electrons. It's referred to as an anode.

Copper, on the other hand, is reduced due to its higher reduction potential. The copper ion in the copper half-cell solution absorbs two electrons from the electrode and transforms into copper metal, which is then deposited in the electrode. Because this electrode consumes electrons, we refer to it as a positive electrode, and we refer to it as a cathode.

The following is a diagram of the anode reaction:

Zn(s) → Zn2+ (aq) + 2e–

The cathode reaction is represented as follows:

Cu2+ (aq) +2e– → Cu(s)

The combined cell reaction or overall cell reaction is as follows:

Zn(s) + Cu2+(aq) → Zn2+ (aq) + Cu(s)

Amount of Discount on Issue of Debenture

3.8.3 Electrode Potential

A potential difference is established across the contact when a metal electrode is immersed in a solution containing its own ions. The electrode potential is the difference in potential between two electrodes.

Consider the zinc electrode submerged in a zinc sulphate solution. By releasing two electrons, the zinc metal becomes oxidised and dissipated in the solution. A potential difference is created by the presence of electrons in the electrode and ions in the solution. Copper develops a positive potential in the same way. Due to the cell potential, the combination of these two cells.

In actuality, we can't tell the potential of a single half-cell by itself. We always need a standard half-cell whose potential value is already known to determine the potential of a single half-cell. To measure the overall potential, this standard half-cell is connected to the unknown half-cell.

The difference between the potentials of the two half cells is the overall potential. One example of a standard half-cell is the standard hydrogen electrode (SHE). SHE's potential value is set to zero volts by default. The potential difference between the standard hydrogen electrode and an unknown half-cell is measured. The measured result will be the potential difference of the unknown half-cell because SHE has zero volts.

The procedure for determining the standard electrode potential of zinc is depicted in the diagram below.

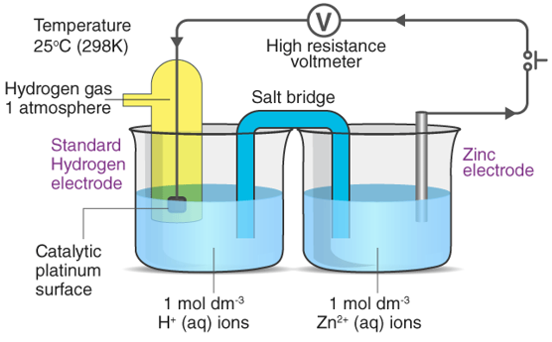
Electrochemical Series

Similarly, we calculate the standard potential values of various metals and arrange them in increasing order of potential to get the electrochemical series.

For the determination of cell potential, electrochemical series are required. It also aids in the selection of electrode metals for cell building.

The electrochemical series table demonstrates how a few elements are arranged in increasing order of their reduction potential. Fluorine has the highest reduction potential, while lithium has the lowest. Hydrogen has no possibility for reduction. Because all other elements are compared to hydrogen to get their standard electrode potential, this is the case.

Representation of an Electrochemical Cell

An electrochemical cell can be represented using special notations. This is useful in understanding the composition as well as it’s quantity in the cell.

The above-given Daniell cell can be represented as follows;

Zn | Zn2+ (1M) || Cu2+ (1M) | Cu

Let us break down this and understand its components:

1. The left side of the notation represents the anode. At the anode, Zn is converted to by releasing a set of two electrons per zinc atom. As the solution used is of 1M concentration, we include that too in the representation
2. Zn | Zn2+ (1M)
3. On the right side, we have the cathode. Here from the electrolyte absorbs a pair of electrons from the electrode and gets converted to Cu metal. Same as before, we are using a 1M copper sulfate solution.
4. Cu2+ (1M) | Cu
5. These two half-cells are combined using a salt bridge. The salt bridge is represented using the two vertical bars.

Zn | Zn2+ (1M) || Cu2+ (1M) | Cu

Finding the Cell Potential of an Electrochemical Cell

The electrochemical cell's cell potential or EMF can be computed by adding the electrode potentials of the two half-cells. The calculation is usually done using one of three methods:

1. By considering the anode's oxidation potential and the cathode's reduction potential.

2. By taking both electrodes' reduction potentials into account.

3. By calculating both electrodes' oxidation potentials.

A galvanic cell's standard cell potential (Eo) can be computed by adding the standard reduction potentials of the two half cells. Eo.

Eocell = Eored + Eoox

Or

Eocell = EoCathode + EoAnode

The cell potential of a galvanic cell = Potential of the half-cell on the right side (cathode) – Potential of the half-cell on the left (anode).

In the case of Daniell cell;

The cell potential of Daniell cell = Ecell = Ecu2+ | Cu – Ezn | Zn2+

The Nernst equation connects the half-equilibrium cell's state potential to its standard electrode potential, temperature, reaction coefficients, and reacting species activity.

For an electrode reaction Mn+ + n e– → M(s);

The equilibrium state EMF is given by;

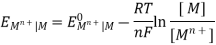
Where EMn+| M is the half-cell potential, EOMn+| M is the standard electrode potential of the half-cell, [ M] is the molar concentration of the metal, [ Mn+] is the molar concentration of the metal ion, R is the universal gas constant (8.314 J/K/mole), T is the temperature in kelvin, n is the number of electrons involved in the reaction and F is the Faraday’s constant (96500 C/mole).

The molar concentration of metallic solid is conventionally taken as one. Hence;

[ M] = 1

Now, substitute the values of R, F, T = 298K (room temperature) to the above equation and we obtain a new equation;

EMn+| M =, EOMn+| M – 0.059 / n X log 1 / [ Mn+]

Consider the case of a cell with two metals, M and N. Assume that M has a higher reduction potential than N. As a result, M is the cathode and N is the anode.

Hence, Anode reaction;

N → Nn+ + ne–

Cathode reaction;

Mn+ + ne– → M

We know;

The cell potential of a galvanic cell = Potential of the half-cell on the right side (cathode) – Potential of the half-cell on the left(anode).

EMF of cathode half-cell;

EMn+| M =, EOMn+| M – 0.059 / n X log 1 / [ Mn+]

EMF of anode half-cell;

ENn+| N =, EONn+| N – 0.059 / n X log 1 / [ Nn+]

Hence, the cell potential of the Galvanic cell is;

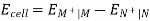
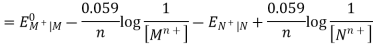
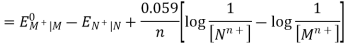
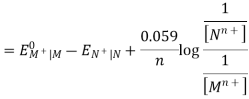
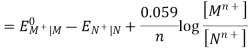
We have;

EOMn+| M – EONn+| N = EOcell

This is the standard cell potential of a galvanic cell at STP conditions.

Hence, we rewrite this as;

Ecell = EOcell + 0.059 / n X log [ Mn+] / [ Nn+]

For the Daniell cell:

The number of electrons involved in the process is 2, hence n = 2.

Ecell = EOcell + 0.059 / 2 X log [ Cu2+] / [ Zn2+]

From the electrochemical series;

EOcell = EOcathode – EOanode = ECu2+| Cu =, EOZn2+| Zn = 0.34 – (-0.76) = 1.1 V

Substitute this value and we get;

Ecell = 1.1 + 0.059 / 2 X log [ Cu2+] / [ Zn2+]

3.8.4 Evaluating Standard Cell Potential E° of Galvanic Cells

Two half-cells make up a galvanic cell. The (reduction) cathode is placed on the right-hand side of the cell, while the (oxidation) anode is placed on the left-hand side. For instance, the cell

Pt|H2|H+||Zn2+|Zn

Consists of the oxidation and reduction reactions:

• H2→2e−+2H+anode (oxidation) reactionH2→2e−+2H+anode (oxidation) reaction
• Zn2++2e−→Zncathode (reduction) reactionZn2++2e−→Zn cathode (reduction) reaction

The voltage difference between the two electrodes would be -0.763 V if the concentrations of H+H+ and Zn2+Zn2+ ions are 1.0 M and the pressure of H2H2 is 1.0 atm (the Zn electrode being the negative electrode). The foregoing parameters are known as the standard conditions, and the EMF achieved is known as the standard reduction potential.

Because the Zn half-cell is a reduction half-cell, the above cell is in reverse order compared to that given in many textbooks. However, because the Zn half-cell is a reduction half-cell, this arrangement offers the conventional reduction potentials directly. The negative voltage denotes the spontaneous nature of the reverse chemical reaction. This is because when Zn metal combines with an acid, it produces H2 gas.

The cell, for instance, is a good illustration.

Pt|H2|H+||Cu+|Cu

Consists of an oxidation and a reduction reaction:

• H2→2e−+2H+anode reactionH2→2e−+2H+anode reaction
• Cu2++2e−→Cu cathode reaction and the standard cell potential is 0.337 V. The positive potential indicates a spontaneous reaction,

Cu2++H2→Cu+2H+

But the potential is so small that the reaction is too slow to be observed.

Gibbs Free Energy and Cell Potential

Standard conditions for all of the reactants are required for an electrochemical cell's standard potential. The cell potential will depart from the standard potential when reactant concentrations range from the standard. Josiah Willard Gibbs developed a theory based on free energy to predict whether a chemical reaction would be spontaneous in the late 1800s:

ΔG=ΔGo+RT×lnQ

G stands for Gibbs free energy change, T for absolute temperature, R for gas constant, and Q for reaction quotient. A reaction quotient in chemistry is a function of the activity or concentrations of the chemical species participating in a reaction. Gibbs made a significant contribution by formalising the effect of reactant concentration on spontaneity.

Walther Nernst, a German chemist in the twentieth century, expanded Gibbs' theory to incorporate the effect of electric potential on charged species. The cell potential can be attributed to the change in Gibbs free energy for an electrochemical cell. As a result, Gibbs' theory is:

NFΔE=nFΔEo−RT×lnQ

Here, n is the number of moles of electrons, F is the Faraday constant (Coulomb’s mole), and ΔE is the cell potential.

The Nernst Equation

Finally, Nernst divided by the amount of charge transferred to arrive at a new equation that now bears his name. The Nernst equation is:

ΔE=ΔEo−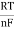×ln Q

The Nernst equation can be used to calculate the output voltage changes in a pair of half-cells under non-standard conditions.

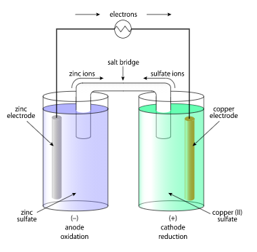
A typical galvanic electrochemical cell: The output of this pair of half-cells is well known under typical conditions. The output voltage changes when the concentration or activity of reactants changes, or when the temperature or pressure varies. The Nernst equation is used to compute it.

Cell Potential and Free Energy

The change in Gibbs free energy in a galvanic cell, where a spontaneous redox reaction drives the cell to produce an electric potential, must be negative.

An electrochemical cell, such as the galvanic cell, is always based on a redox reaction that can be divided into two half-reactions: oxidation at the anode, where electrons are lost, and reduction at the cathode, where electrons are gained. The electric potential difference between two electrodes generates electricity. This has to do with how quickly the oxidised species gives up electrons and how desperately the reduced species wants to get them back.

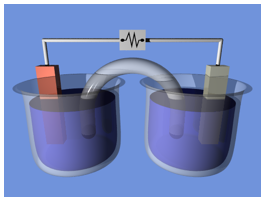
Electrochemical cell: A Daniell cell-like electrochemical cell setup for demonstration. A salt bridge connects the two half-cells, carrying ions between them. In the external circuit, electrons flow.

The individual potential of a reversible electrode in standard state, which is with solutes at an effective concentration of 1 M and gases at a pressure of 1 atm, is known as the standard electrode potential, abbreviated E° in electrochemistry. The most common temperature for tabulating values is 25 degrees Celsius (298 K).

Is It Oxidized or Reduced?

The larger the normal reduction potentials, the easier they are to reduce; in other words, they are just better oxidising agents. F2 has a potential of 2.87 V and Li+ has a potential of -3.05 V, for example. F2 is a good oxidising agent since it reduces easily. Li(s), on the other hand, prefers to be oxidised, making it an excellent reducing agent.

Zn2+, which has a standard reduction potential of -0.76 V, can be oxidised by any electrode with a standard reduction potential larger than -0.76 V and reduced by any electrode with a standard reduction potential less than -0.76 V.

The Sign of the change in Gibbs Free Energy

The change in Gibbs free energy in a galvanic cell, where a spontaneous redox reaction drives the cell to produce an electric potential, must be negative. The cell potential, which is positive when electrons flow freely through the electrochemical cell, is the polar opposite of this. The following equation describes the link between GoGo and EoEo:

ΔGo=−nFE0

Here, n is the number of moles of electrons and F is the Faraday constant (96,485CoulombsmoleCoulombsmole). As such, the following rules apply:

1. If E°cell > 0, then the process is spontaneous (galvanic cell)
2. If E°cell < 0, then the process is non-spontaneous (the voltage must be supplied, as in an electrolytic cell)

3.9 Enthalpy and entropy of a cell reaction.

3.9.1 Entropy of electrochemical cell:

The Gibbs function is related to entropy through its temperature dependence

A similar relationship can be derived for the temperature variance of Eo.

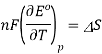
Consider the following data for the Daniel cell (Buckbeei, Surdzial, & Metz, 1969) which is defined by the following reaction

Zn(s)+Cu2+(aq) ⇌Zn2+(aq) +Cu(s) (10.4.3) (10.4.3) Zn(s)+Cu2+(aq) ⇌Zn2+(aq)+Cu(s)

From a fit of the data to a quadratic function, the temperature dependence of

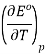
Is easily established.

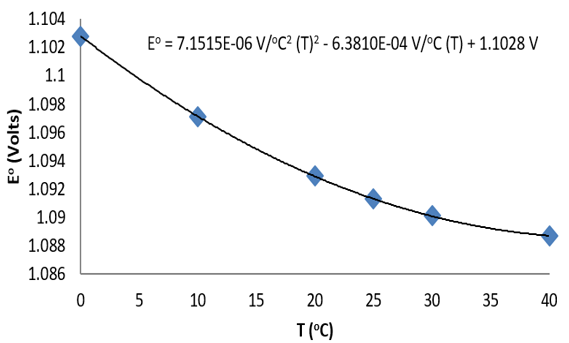
Figure: Temperature dependence of the cell potential for a Daniel cell.

The quadratic fit to the data results in

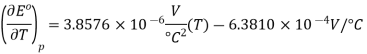
So, at 25 °C,

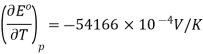
Noting that KK can be substituted for °C°C since in difference they have the same magnitude. So the entropy change is calculated (Equation 10.4.2) is

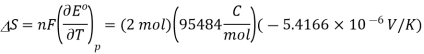
Because

The standard entropy change for the Daniel cell reaction at 25 °C is

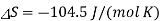
It is the negative entropy change that leads to an increase in standard cell potential at lower temperatures. For a reaction such as

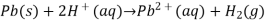
The standard cell potential drops with decreasing temperature due to a considerable increase in entropy (due to the generation of a gas-phase product). Because this is the reaction that most automobile batteries use, it explains why starting a car on a chilly winter morning can be difficult. Bratsch reports and discusses the temperature dependence of numerous typical cell potentials (Bratsch, 1989).

Connecting Free Energy (∆G) and Equilibrium (K)

Free Energy and Equilibrium have a straightforward link. All you need to know is that when G equals 0, G transforms into K since it is in equilibrium. This relationship is depicted by the main equation:

∆G= -RT ln K

T is temperature in K, ln is natural log, and K is the equilibrium constant, where R is the gas constant (8.3145 J/mol*K), T is temperature in K, ln is natural log, and K is the equilibrium constant. In most circumstances, you can use this equation to solve for either G or K if you are given any of these facts.

Sample Problem

Overall reaction for the corrosion or rusting of iron by oxygen:

4Fe (s) + 3O2 (g) <--> 2Fe2O3 (s)

Using the following data, calculate the equilibrium constant for this reaction at 25°C. 

Substance                 ∆H (kJ/mol)                     S° (J/K* mol)

Fe2O3                            -826                                    90

Fe (s)                                   0                                    27

O2 (g)                                  0                                    205

To calculate K, you will need to use this equation: ∆G= -RT ln K

First, you need to calculate ∆G using ∆G= ∆H- T∆S.

To skip a few steps, ∆H should be -1652 kJ or -1.652 X 106 J and ∆S should be -543 J/K. After plugging it into the equation, ∆G should equal to 

-1.490 X 106 J.  

Then, in the equation G= -RT ln K, plug in what you obtained for G. After converting 25°C to Kelvin, R is equal to 8.3145 J/K* mol, and T is equivalent to 298 K.

∆G= -RT ln K

-1.490 X 106 J= - (8.3145) (298) ln K

Ln K= 1.490x106/ 2.48x 103= 601

Take the inverse of the natural log (ln) of 601 and you should end up with K equalling to e601.

(Note: This number was too big in the calculator so we couldn't get an actual numerical answer.)

Final Answer: K= e601 

Connecting Free Energy (∆G) and Cell Potential (Ecell°)

Apart from enthalpy (∆H) and entropy (∆S), you can also relate free energy (∆G) with cell potential, E°. This relationship can be shown in

∆G= -nFEcell°

 In this equation, n is the number of moles of electrons being transferred, F stands for the constant Faraday which is 96,485 C/mol e-, and Ecell° is the cell potential of the reaction.

A galvanic cell will go in the direction that produces a positive cell potential (Ecell°) because reactions will mostly occur in nature if they are spontaneous. This equation confirms this because when the cell potential is positive, the ∆G will be negative which signifies the reaction is spontaneous.

Sample Problem

Chlorine dioxide (ClO2), which is produced by the reaction

2NaClO2 (aq) + Cl2 (g) → 2ClO2 (g) + 2NaCl (aq)

For municipal water treatment, it has been evaluated as a disinfectant. Calculate Ecell° and G at 25°C for the generation of ClO2 using data from the standard reduction potential chart, which lists the cell potentials of some reduction reactions.

Breaking up the equation into half-reactions is the first step. Because the Na ion is a spectator ion in this equation, ignore it.

ClO2- → ClO2

Cl2 → 2Cl-

Then balance the charges of each half-reaction using electrons.

ClO2- → ClO2 + e-

2e- + Cl2 → 2Cl-

Determine each half-cell reaction's potential. The standard reduction potential chart is used to determine the cell potential.

2e- + Cl2 → 2Cl-     Ecell°= 1.36

However, because one is an anode since it is losing an electron, we must convert it to a reduction half-reaction by flipping it backwards in order to determine the cell potential. Remember that we must also flip the cell potential when we flip the half-reaction.

Before: ClO2- → ClO2 + e-       Ecell°= 0.954

After: ClO2- → ClO2 + e-           Ecell°= -0.954

Then to find the cell potential, add the cell potential of each half-reaction together.

ClO2- → ClO2 + e-           Ecell°= -0.954

2e- + Cl2 → 2Cl-           Ecell°= 1.36

Ecell°= 0.406

Plug in the cell potential determined previously, the Faraday constant, and if we balance the total number of electrons transported between the two reactions, the moles of electrons exchanged are 2 mol e-.

∆G= -nFE°

∆G= -(2 mol e-) (96,485 C/mol e-) (0.406 J/C) = -78345.82 J

∆G= -78345.82 J (1 kJ/1000 J) = -78 kJ

3.9.2 Thermodynamic Data from Electromotive Force Measurements:

1 A. Maximum work

Recall that the change in Helmholtz energy A equals the maximum work for the system

A = wmax

And that the change in Gibbs free energy G equals the maximum non-expansion work for the system

G = wnon-pV, max

To prove the second statement, recall that

G = H  TS                                            
= U + pV  TS                                 
dG = dq + dw + pdV + Vdp  TdS  SdT

At constant p and T, dp = 0 and dT = 0

DG = dq + dw + pdV +  TdS

Since the maximum amount of work is produced by a reversible process, dq = TdS, which implies

DG = dwmax + pdV

Recognizing that dw = dwnon-pV + dwpV = dwnon-pV  pdV yields

DG = dwnon-pV,max  pdV + pdV
= dwnon-pV,max                    

Which upon integration implies

G = wnon-pV,max

1 B. Electrical work

Electrical work is defined as

Work = charge  potential

Electrical work done by an electrochemical cell is therefore defined as

welec =  F  E

Where is the stoichiometric number of electrons passing through the cell circuit, a unitless quantity calculated from cell half-reactions; F is Faraday's constant, which is the charge of a mole of electrons and equals 96,490 Coulombmol1; and E is the cell's electromotive force, usually measured in volts. Since then,

J = Coulomb·volt

The units of welec are J·mol1.

The work done on an electrochemical cell is therefore

welec = F E

1 C. Thermodynamic quantities

Identifying the non-expansion work for the system as the work done on a reversible electrochemical cell

wnon-pV = welec

Gives an expression for G in terms of electromotive force of an electrochemical cell

G = F E

To obtain expressions for S and H, recall that

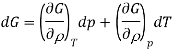
And

DG = Vdp  SdT

Equating coefficients implies that

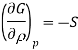
Or

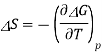
Recalling the expression for G yields

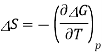
Thus, S depends on the temperature dependence of the electromotive force of an electrochemical cell.

Finally, H = G + TS at constant T and the previous results imply

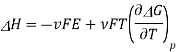
Chemical System

The reaction under study is

Zn (Hg) + PbSO4 (s) = ZnSO4 (0.02 m) + Pb (Hg)

Where the symbol s refers to the solid state and 0.02 m refers to the molality (moles per kg of solvent) of ZnSO4. Zn (Hg) and Pb (Hg) are mercury amalgams of zinc and lead, respectively.

The half-reactions for this reaction are

Zn (s) = Zn2+(aq) + 2e

2e + PbSO4 (s) = Pb (s) + SO42 (aq)

Thus, , the stoichiometric number of electrons passing through the cell, equals 2.

3. A. Heat release

The reaction would progress irreversibly to products if the reactants were mixed together directly. WpV=0 since no gases are involved in the reaction, and wnon-pV=0 because no electrical effort is required. As a result, the reaction would only emit heat, and the measured quantity at constant p would be qirreverible = H.

The oxidation and reduction reactions, on the other hand, can be separated into electrochemical half-cells. The electrons move via a circuit that allows them to perform electrical work. If the cell is operated in a reversible manner, that is, if the current flow is "infinitely slow,"

qreversible = TS

And as shown above

wnon-pV, reversible = G

3. B. Electrochemical cell

The oxidation (loss of electrons by Zn) and reduction (gain of electrons by PbSO4) half-cells in the following electrochemical cell are separated.

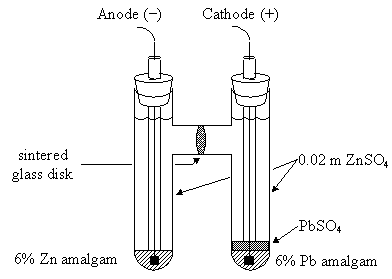
Observe that oxidation (loss of electrons) occurs at the anode and reduction (gain of electrons) occurs at the cathode.

3. C. Experimental details

Because the cell uses the same electrolyte throughout, there is no junction potential to impact the observed E value.

The frit allows ions to move between half-cells but prevents reactants from mixing directly.

The amalgam's aim is to improve electrical contact between the electrode and metals (while avoiding strain-induced potentials) and to act as a source and sink of metal atoms.

Because oxygen is a good oxidising agent and can reduce water at the cathode, it should be kept out of the cell.

1/2 O2 (g) + H2O (l) + 2 e  2 OH (aq)

Data Analysis

Traditionally, electrochemical measurements were done using a potentiometer or "bridge circuit," which applied an opposite voltage to impede current passage. Today, a high impedance voltmeter is used to make measurements.

The electromotive force of the cell is calculated as a function of temperature.

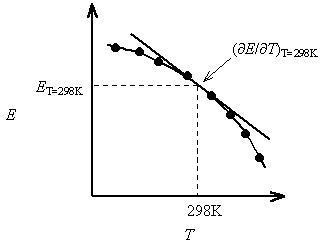
The data is fitted with a polynomial (which could be a straight line if necessary), and the values of ET=298K and (E/ T) T=298K are calculated. As previously stated, these values are related to G, S, and H.

Even though the process leads in the conversion of solid into aqueous ions, the above negative slope suggests that DS is negative, implying that entropy decreases. This may sound counterintuitive, but ions prefer to "organise" the water around them, resulting in a decrease in net entropy.

Relation to Standard Thermodynamic Quantities

The most common goal is to determine standard thermodynamic quantities. These numbers correspond to reactants and products in their standard states, i.e., with activity of one (or concentrations of 1 M for ideal solutions). Because the concentration of ZnSO4 in the current experiment is 0.02 m, the species involved are not in their typical states.

The dependency of electromotive force on concentration is described by the Nernst Equation.

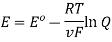
Where Eº is the electromotive force at the standard state and Q is the reaction quotient (or equilibrium constant K for ideal solutions)

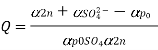
The Nernst Equation has a form that is consistent with Le Chatelier's Principle. Q is less than one, lnQ is negative, E is more positive, G is more negative, and the reaction proceeds spontaneously to make products if the reactant activities (concentrations) are substantial relative to the products. Excess reactants, according to Le Chatlier's Principle, push the reaction to produce more products.

The solid phases' activities are believed to be identical. The activity of a solution is defined as the product of its activity coefficient and its concentration, ai = I mi.

Where I denote the activity coefficient and mi denotes the molality of the species in question. The activity coefficient equals unity for perfect solutions. Unlike neutral species, which interact over short distances (with repulsive potential proportional to r12 and attractive potential proportional to r6), ionic species interact over very long distances (with Coulomb potential proportional to r1!). As a result, even dilute ionic species are frequently far from optimal.

The Debye-Huckel equation can be used to compute the activity coefficient for dilute ionic solutions (which assumes that all interactions between ions are based on Coulombic attraction or repulsion effects)

I1/2 | log= 0.509 | z+ z | log= 0.509

Where z+ is the positive ion's charge, z is the negative ion's charge, and I is the solution's ionic strength

Where zi is the charge for ion i.

Thus, measured values of E can be related to standard values of Eº by

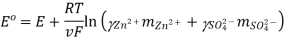
From which values for Gº, Sº, and Hº may be calculated.

3.10 Equilibrium constants:

It relates the amounts of reactants and products at equilibrium for a chemical reaction. For a general chemical reaction occurring in solution,

AA + bB ⇄ cC + dD

The equilibrium constant, also known as Keq, is defined by the following expression:

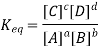
Where [A] is the equilibrium molar concentration of species A, and so on. In the expression for Keq, the coefficients a, b, c, and d in the chemical equation become exponents. The Keq is a numerical value that represents a distinctive numerical value for a specific reaction at a certain temperature; each chemical reaction has its unique Keq. In an equilibrium chemical reaction, the concentrations of each reactant and product are connected; the concentrations cannot be arbitrary numbers, but they do depend on each other. The concentrations of every product (whatever many products there are) are in the numerator of the expression for Keq, while the concentrations of every reactant are in the denominator, resulting in the common products over reactants definition for Keq.

Consider the following scenario. Assume we've reached this point of equilibrium:

A ⇄ B

There is one reactant, one product, and the coefficients on each are just 1 (assumed, not written). The Keq expression for this equilibrium is

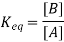
(On each concentration, the exponents of one are understood.) Assume that the Keq value for this chemical reaction is 2.0. If [B] = 4.0 M, then [A] must equal 2.0 M for the fraction's value to be 2.0:

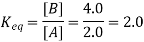
The units are assumed to be M and are omitted from the Keq statement by convention. Assume [B] is 6.0 M. [A] would have to be 3.0 M at equilibrium for the Keq value to remain constant (it is, after all, named the equilibrium constant):

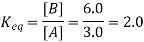
The reaction would not be at equilibrium if [A] was not equal to 3.0 M, and a net reaction would proceed until the ratio reached 2.0. The reaction will be at equilibrium at that point, and any net change will stop. (Remember, however, that chemical equilibrium is dynamic, thus forward and reverse reactions do not halt.)

With more sophisticated formulas for the Keq, the problem remains the same; only the mathematics becomes more difficult. In general, the missing concentration may be determined given a value for the Keq and all but one concentration at equilibrium.

To find a final answer in some sorts of equilibrium issues, square roots, cube roots, or even higher roots must be investigated. Check that you understand how to conduct these operations on your calculator; if you don't, ask your instructor for help. Earlier, the Keq was described in terms of concentrations. The Keq can also be described in terms of the partial pressures of the reactants and products, Pi, for gas-phase processes. In the case of a gas-phase reaction,

AA(g) + bB(g) ⇄ cC(g) + dD(g)

The pressure-based equilibrium constant, KP, is defined as follows:

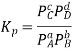
PA denotes the partial pressure of material A at equilibrium in different atmospheres, and so on. When substituting into the expression for KP, the units are ignored, just as they are when substituting into the expression for the concentration-based equilibrium constant.

Keq (based on concentration units) and KP (based on pressure units) have a straightforward relationship:

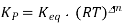
T is the absolute temperature, and n is the change in the number of moles of gas in the balanced chemical equation, defined as ngas, prods ngas, rcts. This equation states that if the number of moles of gas in reactants and products is the same, Keq = KP.

Finally, we must acknowledge that many chemical reactions include solid or liquid components. A chemical reaction, for example, is expressed as follows:

2 NaHCO3(s) ⇄ Na2CO3(s) + CO2(g) + H2O(ℓ) 

All three phases of matter are included in this chemical equation. Because there are multiple phases present, this type of equilibrium is called a heterogeneous equilibrium.

The following is the rule for heterogeneous equilibria: In Keq expressions, leave exclude the concentrations of pure solids and pure liquids. In the formulas of equilibrium constants, only partial pressures for gas-phase chemicals or concentrations in solutions are considered. As a result, the equilibrium constant equation for this reaction is as follows:

KP = PCO2

Because the expression would be incomplete without the two solids and one liquid, the Equilibrium Constant, Reaction Quotient, and Gibbs Free Energy

At equilibrium, K is the ratio of the relative number of products to reactants, whereas Q represents the ratio at any point in time during the reaction. The direction of the reaction can be determined by comparing the Q value to the K value. The free energy change is linked to the process' spontaneity. K (Gibbs Free Energy), G (Gibbs Free Energy), G (Gibbs Free Energy), G (G

(Equilibrium Constant), and Q (Reaction Quotient) are related as follows:

1. △G < 0 and Qc ˂ Kc or Kp at the start of the reaction: The reaction will proceed to form products.

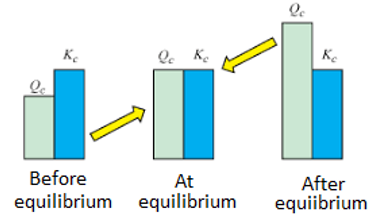
Equilibrium Constant vs Reaction Quotient

• Kc = Equilibrium constant measured in moles per liter.
• Kp = Equilibrium constant calculated from the partial pressures

Relationship between kc and kp

Consider the following reversible reaction: cC + dD ⇒ aA + bB

The equilibrium constant for the reaction expressed in terms of the concentration (mole/litre):

⇒ Kc​​=[A]a[B]b[C]c[D]d​

If the equilibrium involves gaseous species, then the concentrations are replaced by partial pressures of the gaseous substances. The equilibrium constant in terms of partial pressures is:

⇒ Kc​​=[pA]a[pB]b[pC]c[pD]d​

Where pA, pB, pC and pD represents the partial pressures of the substance A, B, C and D respectively. If gases are assumed to be ideal, then according to ideal gas equation:

PV = nRT or p = nRT/V

Where,

1. p is the pressure in Pa,
2. n is the number of moles of gas,
3. V is the volume in m3,
4. T is the temperature in Kelvin,
5. n/V = molar concentration = [C]

If C is in mol dm3 and p is in bar, then R = 0.0831 bar dm3 mol-1 K-1 or p = CRT

Substituting for pressure, in terms of concentration:

PA = [A] RT; pB = [B] RT; pC = [C] RT and pD = [D] RT

Substituting these values in expression for Kp:

⇒Kp​=[(A)RTa] [(B)RTb] [(C)RTc] [(D)RTd]​

⇒Kp​=[(A)] a(RT)a[(B)] b(RT)b[(C)]c(RT)c[(D)] d(RT)d​

⇒ Kp​=[(A)] a[(B)] b(RT)a(RT)b[(C)]c[(D)] d(RT)c(RT)d​

⇒ KP​=[(A)] a[(B)] b(RT)(a+b) [(C)]c[(D)] d(RT)(c+d)​

⇒ Kp​=[(A)] a[(B)] b[(C)]c[(D)] d(RT)(c+d) −(a+b)​

⇒ Kp​=Kc​ (RT)(c+d) −(a+b)

Where, △n = (c+d) – (a+b) i.e., number of moles of gaseous products – number of moles of gaseous reactants in the balanced chemical reaction.

Characteristics of Equilibrium Constant

1. It's reaction-specific, and it's fixed at a constant temperature.
2. To keep the value of the equilibrium constant, a catalyst changes the rate of forward and backward reactions in the same way.
3. Changes in concentration, pressure, temperature, and inert gases may influence the equilibrium, favouring one of the two reactions but not the equilibrium constant.

Is related to the standard free energy as, △G0 = -RT ln Kequ.

Equilibrium Constant for Predicting the Extent of Reaction

The equilibrium constant (Kc) can be used to forecast the magnitude of a reaction, or how quickly the reactants depart. The value of the equilibrium constant indicates the amount of reactants and products present.

Case 1: The bigger value of the equilibrium constant (>103) indicates that forward reaction is preferred, indicating that the concentration of products is substantially higher than the concentration of reactants at equilibrium.

For Example:

1. H2(g) + Br2(g)⇌ 2HBr(g) ⇒ Kc = 5.4×1018
2. H2(g) + Cl2(g)⇌ 2HCl(g) ⇒ Kc = 4×1031
3. H2(g) + 12O2(g) ⇌ H2O(g) ⇒ Kc = 2.4×1047

This shows that at equilibrium, concentration of the products is very high, i.e., reaction go almost to completion.

Case 2: Intermediate value of equilibrium constant (10-3 to 103) show that the concentration of the reactants and products are comparable.

For Example:

1. Fe3 (aq) + SCN (aq) ⇌ [Fe (SCN)]2 (aq) ⇒ Kc = 138 at 298 K
2. H2 (g) + I2 (g) ⇌ 2HI (g) ⇒ Kc = 57 at 700 K.

Case 3: Low value of equilibrium constant (<10-3) shows that backward reaction is favored i.e., concentration of reactants is much larger than that of products i.e., the reaction proceeds to a very small extent in the forward direction.

For Example:

1. N2 (g) + O2 (g) ⇌ 2NO (g) ⇒ Kc =4.8 × 10-31 at 298K
2. H2O (g) ⇌ H2 (g) + (1/2) O2 (g) ⇒ Kc = 4.1 × 10-48

Key takeaway:

• Every chemical equilibrium can be characterized by an equilibrium constant, known as Keq.
• The Keq and KP expressions are formulated as amounts of products divided by amounts of reactants; each amount (either a concentration or a pressure) is raised to the power of its coefficient in the balanced chemical equation.
• Solids and liquids do not appear in the expression for the equilibrium constant.

3.11 pH values, using hydrogen, Quinone-hydroquinone, glass electrodes.

3.11.1 Hydrogen potential and pH-value

The hydrogen potential is directly proportional to the activity or rather the concentration of hydronium ions in the solution, and hence to the pH value. The negative decadic logarithm of the hydrogen ions activity is used to get the pH value. The product of concentration and activity coefficient is activity. In diluted solutions, the latter can only be approximated. As a result, measuring the pH-value according to its definition can only be done roughly.

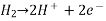
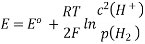
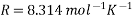
Saturated vapour pressure [bar]

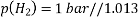
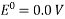
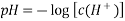
Hydrogen potential and hydrogen ions concentration and thereby the pH-value are directly depending on each other.

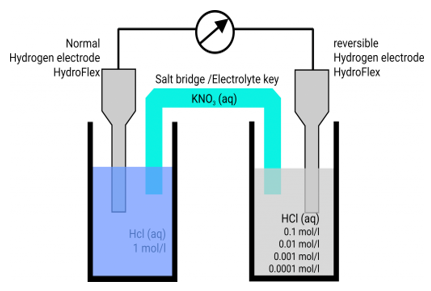
In hydrochloric acid, a concentration chain of two platinum hydrogen half cells

A concentration chain or rather a concentration cell is formed when two platinum hydrogen electrodes, one immersed in an acid with a proton’s concentration of 1 mol/l, pH = 0, (normal hydrogen electrode, NHE) and the other in a solution with an unknown proton’s concentration (reversible hydrogen electrode, RHE), are connected by a salt bridge.

The potential of the spontaneous occurring reaction sets as soon as two half cells are touched and the circuit is closed. The hydrogen ions are converted to hydrogen due to the increased proton concentration in the left half-cell. As a result of the removal of electrons from the electrode, it now has a higher positive potential than the electrode in the right half-cell. As a result, the decrease occurs in the left half-cell. The positive pole of the galvanic cell is that cell, which is comparable to the cathode. Hydrogen is oxidised to hydrogen ions in the right half-cell. The electrode on the right has a lower voltage than the electrode on the left (negative pole). The oxidation takes occurs in the right half-cell, making the right half-cell equivalent to the anode. The electrons freely flow from the negative pole to the positive pole, or from the anode to the cathode in this case (galvanic cell). From the diluted to the concentrated cell, electrons travel from the right to the left.

E = E (right) – E (left) – E (right) – E (left) – E (right) – E (right (left). According to the IUPAC, the standard hydrogen electrode must be the left cell.

Calculation of potential according to convention

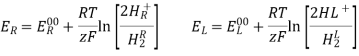
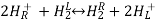
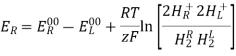
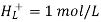
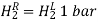
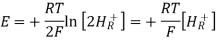
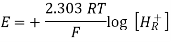
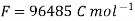
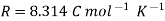
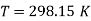
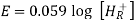
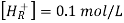
Calculation of the potential according to the convention E = E (right) – E (left)

Depending on the proton concentration, the potential changes technically with a positive sign.

However, the protons function has a logarithmic function. Negative potentials are obtained for concentrations less than 1 mol/l; for a concentration of 0.1 mol/l, the potential is -0.059 V. Calculating potentials is easier if the protons concentration is converted to a pH value.

PH = 0.059 (25°C) E = 0.059

Because E 0 Volt, the reaction proceeds from right to left, as we would expect given the various concentrations. In such a concentration chain, you must connect the standard hydrogen electrode to the negative pole to monitor negative potentials (COM-port).

The platinum hydrogen pH-electrode pHydrunio is such a measuring chain. The outer hydrogen electrode measures the hydrogen potential in the measuring solution. Against a normal hydrogen electrode (per definition: reference potential of 0 mV) the blue straight in the diagram arises, according to the calculation E = -0.059 pH (25°C).

But, the inner reference electrode of our pH-electrode is placed in buffer pH 7. That has to be considered in the calculation of the potential.

Hence, an offset of 0.414 V arises at 25°C and the measuring voltages are equivalent to the orange straight.

Depending on the proton concentration, the potential changes technically with a positive sign.

However, the protons function has a logarithmic function. Negative potentials are obtained for concentrations less than 1 mol/l; for a concentration of 0.1 mol/l, the potential is -0.059 V. Calculating potentials is easier if the protons concentration is converted to a pH value.

PH = 0.059 (25°C) E = 0.059

Because E 0 Volt, the reaction proceeds from right to left, as we would expect given the various concentrations. In such a concentration chain, you must connect the standard hydrogen electrode to the negative pole to monitor negative potentials (COM-port).

3.11.2 Quinones:

Quinones are conjugated cyclic diketones, not aromatic chemicals. However, because quinones and related aromatic arenols are easily interconverted and their chemistry is mainly interconnected, it is convenient to study their chemistry now.

There have been a variety of quinone like structures created, the most frequent of which are the 1,2 and 1,4-quinones, which are typified by 1,2- and 1,4-benzenediones. 1,2-quinones are often more difficult to manufacture and more reactive than 1,4-quinones. A few 1,6- and 1,8-quinones have also been discovered.

No 1,3-quinones are known, possibly because they would have non-planar, highly strained structures and therefore would be unstable:

A number of quinones are known in which the quinone arrangement extends over more than one ring. Examples are:

Reduction of Quinones

A characteristic and important reaction of quinones is reduction to the corresponding arenediols. The reduction products of 1,4-quinones are called hydroquinone’s:

Electrochemical reduction and a number of reducing chemicals can be used to produce reduction (metals in aqueous acid, catalytic hydrogenation). These reductions are rare among organic reactions in that they are fast and reversible enough to provide easily repeatable electrode potentials in an electrolytic cell. The square of the hydrogen-ion concentration determines the position of the 1,4-benzenediol-1,4-benzenedione equilibrium (Equation 26-2). As a result, the electrode potential is pH sensitive; a change of one unit of pH in water affects the electrode potential by 0.059V0.059V. The half-cell potential created by this equilibrium was commonly employed to calculate pH values of aqueous solutions before the invention of the glass-electrode pH metre. Because the quinone interacts permanently with alkali over pH 9, the procedure isn't particularly useful above that point.

The link between half-cell reduction potentials and quinone structures has been studied extensively. The potentials are greatest when the resonance stabilisation associated with the creation of the aromatic ring is greatest, as one might predict.

When hydroquinone and quinone alcohol solutions are combined, a brown-red hue appears and a green-black 1:1 complex known as quinhydrone crystallises. The diol acts as an electron donor, and the dione acts as an electron acceptor in this charge-transfer complex (Section 24-6C). Quinhydrone is a water-insoluble compound that readily dissociates into its constituents in solution.

Two electrons are required for the reduction of a quinone, and these electrons can be transmitted simultaneously or one at a time. A single-electron transfer produces a semiquinone, which has both a negative charge and an odd electron (a radical anion):

A variety of approaches have been used to demonstrate that electrolytic reduction of quinones produces rather stable semiquinone radicals. Reversible dimerization processes create peroxides from certain semiquinone radicals.

Mild oxidation of NN, NN, N′N′, N′N′-tetramethyl-1,4-benzenediamine produces a semiquinone cation-radical that is highly stable. "Wurster's Blue" is the name given to the cation, which can be isolated as a brilliant-blue perchlorate salt:

Quinones of Biological Importance

Many reactions analogous to the arenediol-arenediol pair occur during oxidation and reduction in biological systems. (Section 20-9), and (Section 15-6C).

The relationship between the reduction of oxygen (12O2+2H+2eH2O) and the oxidation of NADH (NADHNAD+H+2e) is a key question in metabolic oxidation. The path for electron transfer from NADH to oxygen (oxidation plus phosphorylation; Section 20-10) is indirect and convoluted, and it begins with the oxidation of NADH by flavin mononucleotide (FMN) via the reaction FMN+NADH+HFMNH2+NAD. However, the reduced form of FMN, FMNH2, does not react with oxygen directly. Instead, it converts a coenzyme Q (CoQ) quinone to the equivalent arenediol:

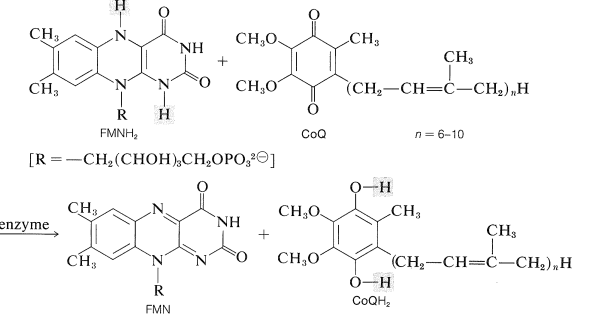
This process allows the reduced material to infiltrate into a less polar part of the oxidative apparatus by forming a somewhat polar reductant (CoQH2) from a strongly polar reductant (FMNH2). The reduced CoQ is involved in a series of oxidation-reduction events involving electron transfer between a variety of iron-containing proteins known as cytochromes, rather than directly reacting with oxygen. The reduced form of a copper-containing cytochrome combines with oxygen at the end of this series of reactions. The electron-carrier sequence can be summarised as follows:

Photosynthesis involves a similar process (Section 20-9). You may recall that the transport of electrons from the photosystem that oxidises water (H2O1/2O2+2H+2e) to the photosystem that lowers NADP (NADP+2H+2eNADPH+H) is an important aspect of photosynthesis. The electron-transfer pathway is complicated, just like in oxidative phosphorylation. However, plastoquinone, a quinone that closely resembles mammalian coenzyme Q, is one of the electron carriers. Plastoquinone is reduced to the hydroquinone form, which is part of an electron-transport chain including iron- and copper-containing proteins, similar to coenzyme

One of the most important naturally occurring chemicals with quinone-type structures is the blood antihemorrhagic factor, vitamin K11, which is a substituted 1,4-naphthalenedione found in green plants:

Degradation and synthesis have both been used to determine the structure of vitamin K1. Surprisingly, vitamin K1's lengthy alkyl side chain isn't required for its blood clotting activity because 2-methyl-1,4-naphthoquinone is nearly as active on a molar basis.

Quinones are found widely as natural colours in plants, fungus, lichens, marine organisms, and insects, in addition to having an important part in the oxidation-reduction processes of living things (see alizarin, Section 28-4A, as representative of a natural anthraquinone-type dye).

Photographic Developers

The arenediol-arenediol oxidation-reduction system is used extensively in photography. When minute grains of silver bromide in a photographic emulsion are exposed to blue light (or any visible light in the presence of properly sensitising dyes), a stable activated form of silver bromide is produced, with the activation including the creation of some sort of crystal defect. When the emulsion is exposed to a developer, such as an alkaline aqueous solution of 1,4-benzenediol (hydroquinone) and sodium sulfite, the activated silver bromide particles are converted to silver metal significantly faster than conventional silver bromide particles. When the unreduced silver bromide is removed with sodium thiosulfate ("fixing"), the emulsion is left with a suspension of finely divided silver in the shape of the familiar photographic negative.

Photographic developing agents come in a variety of forms. Arenediols aren't all the same. In fact, the majority are aromatic amino alcohols or diamines, but they all have the ability to perform redox reactions similar to those outlined for 1,4-benzenediol, regardless of structural changes. Several significant innovators' structural formulas and commercial names are listed.

1,4-Benzenediamine is also a good developer, however it can induce dermatitis in people who are sensitive to it. In colour photography, NN, NN-Diethyl-1,4-benzenediamine is used as a developer. Benzenediamine derivatives are formed when these chemicals combine with silver bromide:

Addition Reactions of Quinones

Quinones, like their open-chain analogues, have the ability to create 1,4-addition products since they are, -unsaturated ketones (Section 17-5B). Such additions are rather easy to achieve with 1,4-benzenedione. Because the products are unstable, they must be enolized to produce substituted 1,4-benzenediols. The addition of hydrogen chloride and the acid-catalyzed addition of ethanoic anhydride are two examples. The anhydride acylates the hydroxyl groups of the adduct in the latter process. When the product is hydrolyzed, 1,2,4-benzenetriol is produced:

Quinones are often easy to Diels-Alder, as long as they have at least one double bond that isn't part of an aromatic ring. The mono- or diadduct can be made from 1,4-benzenedione and 1,3-butadiene. Under the influence of acid or base, the monoadduct enolizes to a 1,4-benzenediol derivative:

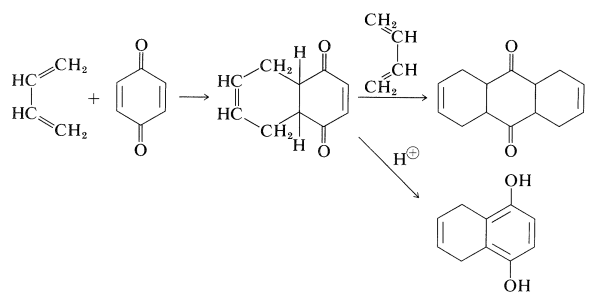
Quinones of Cyclobutadiene

The ease with which benzoquinones can be converted to stable aromatic systems accounts for their peculiar features as, -unsaturated ketones. What if the quinone was made from nonaromatic compounds like cyclobutadiene, cyclooctatetraene, or pentalene? How would these attributes change? There is no definitive answer to this topic because few such chemicals have been created, with the mono- and diphenylcyclobutenediones being the most well-known so far:

For example, 3 can be made by hydrolyzing the cycloaddition product of ethynylbenzene and trifluorochloroethene with sulfuric acid (Section 13-3D):

The dione, 3, is a yellow crystalline solid that is substantially less reactive than 1,2-benzenedione, despite its stretched four-membered ring (ortho-benzoquinone). It cannot be converted to cyclobutenediol, does not perform Diels-Alder reactions, and produces a substitution product rather than an addition product when combined with bromine. The bromo molecule thus generated rapidly hydrolyzes to a hydroxy compound, 4, a very powerful acid with an ionisation constant 109 times that of benzenol:

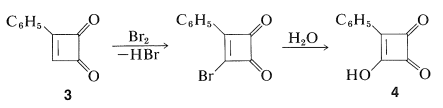
A similar molecule, 3,4-dihydroxy-1,2-cyclobutenedione, 5, has also been synthesised, and it is a powerful dibasic acid. It's also known as "squaric acid":

According to the evidence so far, the quinones that correlate to cyclobutadiene have a higher aromatic character than the cyclobutadienes themselves.

3.11.3 Principles of the Glass-Electrode Method:

The known pH of a reference solution is calculated using the glass-electrode method, which involves utilising two electrodes, a glass electrode and a reference electrode, and measuring the voltage (difference in potential) generated between the two electrodes. The electromotive force is proportional to the difference in pH between the liquids inside and outside the thin glass barrier. The electrode membrane is the name given to this thin membrane. When the temperature of the solution is 30 °C and the pH within is 1 higher than the pH outside, roughly 60 mV of electromotive force is generated.

The pH of the liquid inside the glass electrode is usually about 7. When the electromotive force generated at the electrode membrane is measured, the pH of the sample can be calculated.

When measuring the electromotive force generated at the electrode membrane of a glass electrode, a second electrode is required. The reference electrode is the other electrode that is used in conjunction with the glass electrode. The potential of the reference electrode must be exceedingly steady. As a result, the liquid connection is equipped with a pinhole or a ceramic substance.

To put it another way, a glass electrode is used to generate precise electromotive force as a result of a pH difference. And a reference electrode is designed to prevent electromotive force from being caused by a pH variation.

On the market, there are a variety of pH glass electrodes. Because each pH glass electrode has its own set of characteristics, it's important to pick the right one for the job.

What different kinds of pH glass electrodes are available?  What are the main characteristics of pH glass electrodes and which membrane glass is recommended for which measurement application?

Due to the process of taking pH measurements, the glass membrane of a pH glass electrode changes over time. Alkali ions dissolve from the glass surface when exposed to water, and the oxide groups of the silicate become OH groups, forming a source layer. To hydrogen ions, this source layer seems to be an ion exchanger. There is a consistent balance between the sample solution and the glass surface using a unique pH glass electrode membrane, which is only reliant on the hydrogen ion concentration in the solution and the source layer.

Because pH glass electrodes have a wide range of capabilities, a variety of membrane glasses are required to get precise and consistent pH measurements in all applications. L-, H-, S-, A-, and N- are the five various varieties of pH glass electrodes offered by SI Analytics. The following are the key characteristics of these pH glass electrodes:

1. L type pH glass electrode: Wide application range, low impedance, accurate and quick response times over a wide temperature range.

2. H type pH glass electrode: Designed for greater temperatures (up to 135°F) and severe pH values, with exceptional accuracy in the stronger alkaline range (Na+).

3. S type pH glass electrode: Tolerates rapid temperature changes and gives consistent measurement values in hot alkali solutions with a quick response time.

4. A pH glass electrode of the following type: Drinking water, surface water, sewage, and general applications all benefit from quick response times.

5. N type pH glass electrode: Useful for the entire pH range and practically all types of samples at normal temperatures.

The following examples illustrate the use of different pH glass electrodes:

1. The so-called "alkaline measurement mistake" develops when using a strong alkaline media. This error occurs when sodium ions are confused with hydrogen ions (cross sensitivity), resulting in measurement inaccuracy starting at a pH of 12 in the presence of sodium ions. Under extreme circumstances, this mistake could result in a pH unit discrepancy. In these instances, a pH glass electrode of type H should be utilised.

2. Applications involving hot alkaline treatments or sterilisation with superheated steam place high demands on the pH glass electrode's membrane glass consistency. A pH glass electrode corrodes and matures faster in these conditions. In this scenario, a S type pH glass electrode would be the best option.

3. The range of uses and low conductivity of the pH glass electrodes present a barrier in common applications such as drinking water measurements. This could result in delayed reaction times and data that is unstable or untrustworthy. The A type pH glass electrodes were created to meet these needs. These pH glass electrodes have a quick response time and can be used for a long time.

What different kinds of pH Glass Electrode Membrane Shapes are available?

Glass pH electrodes come in a variety of membrane designs. Each pH glass electrode is made to fit a specific pH measurement application.

1. Sphere pH glass electrode membrane: Excellent consistency, low resistance due to high surface area, and suitable for most applications.

2. Dome pH glass electrode membrane: They have a higher resistance, are shock-proof, and are easy to clean, making them ideal for automated cleaning systems.

3. Flat pH glass electrode membrane: High resistance, shock-proof, easy to clean, and suitable for surface pH measurements.

4. Cylinder pH glass electrode membrane: Medium resistance, shock-proof, and suitable for a wide range of applications, including fermentation.

5. Spear pH glass electrode membrane: High resistance, ideal for penetrating semi-solid media and measuring systems with automated ultrasonic cleaning.

6. Cone pH glass electrode membrane: Sturdy, smooth, simple to clean, and generally applicable.

The type and shape of the pH glass electrode membrane glass are critical to making reliable pH measurements. The pH glass electrodes' findings and features are influenced by the glass composition, manufacturing methods, and shape. Only the greatest pH glass electrode will give you with the highest level of accuracy and dependability.

.

References:

1. A 1:1 ratio of each salt was used as a salt mixture.
2. Bockris, J.O., Reddy, A. K. N. Modern Electrochemistry 1: Ionics. 2003. 2nd ed. Springer
3. Hamer, W. J. The Structure of Electrolytic Solutions. In: Stokes, R. H. Mobility of Ions in Relation to Viscosity. New York: John wiley & sons, Inc, 1959. Pp. 289-307
4. P.W. Atkins, Physical Chemistry. 1998, 6th ed. Oxford University Press
5. Misra, P. P., Das, N. C., Das, P.B., Cellular and Molecular Life Sciences., 1979, 35 (6): 724- 725
6. Mendolia, M.S. Farrington, G. C., Chem. Mater. 1993, 5, 174- 181
7. R. W. Impey, P. A. Madden, I. R. McDonald, J. Phys. Chem., 1983, 87, 5071-5083
8. S. H. Lee, P. T. Cummings, J. Chem. Phys., 2000, 112, 864- 869
9. D. R. Lide, Handbook of Physicas and Chemistry, 2000, 81st ed. CRC Press
10. R. Buchner, Priv- Doz, F. Samani, P. M. May, P, Sturm, G. Hefter, Chem. Phys. Chem., 2002, 4 (4), 373 - 378