Unit - 4
Thermodynamic & kinetic aspects and reaction mechanism of metal complexes
4.1.1 Stability of Metal Complexes
The ability of a metal complex to persist in favourable conditions and have a long shelf life is referred to as "stability." The term "stability of metal complex" cannot be applied universally because the complex may be stable to one reagent/condition but decompose in the presence of another reagent/condition. Metal complexes can be explained in terms of their thermodynamic and kinetic stability. A metal complex, on the other hand, is said to be stable if it does not react with water, causing the system's free energy to decrease, or thermodynamic stability. If the complex reacts with water to form a stable product and there is a known mechanism for the reaction, it is said to have kinetic stability. For example, the system might not have enough energy to break a strong bond, but once it is broken, a new bond that is stronger than the old one can be formed. The bond dissociation energy, Gibbs free energy, standard electrode potential, pH of the solution, and rate constant or activation energy for substitution reactions are used to determine the stability of a complex compound in aqueous solution.
Thermodynamic Properties
• Thermodynamic properties are characteristics of a system that can be used to specify its state. Thermodynamic properties can be either extensive or intensive.
• The properties of an intensive system are those that are independent of the amount of matter in the system. Temperature and pressure are two properties that necessitate a great deal of thought.
• The system's mass determines the value of extensive properties. Volume, energy, and enthalpy are all important properties to consider.
Thermodynamic stability
The term "thermodynamic stability" refers to a complex's tendency to exist in equilibrium conditions. It determines how much of the complex will form or be converted into another complex at the point of equilibrium. To put it another way, thermodynamic stability of complexes is proportional to the metal-ligand bond energies and measures a metal ion's proclivity to form a specific metal complex. Complexes' thermodynamic stability is represented by the formation constant. The formation constant, also known as the stability constant, is the equilibrium constant for determining the formation metal composition.
Metal complexes are usually made in aqueous solution rather than in gaseous form from their respective starting materials. When a metal cation is hydrated in an aqueous solution, an aqua complex of the type forms. [M(H2O)x]n+ is a compound of [M(H2O) and [M(H2O) When a ligand replaces the water molecule in the aqua complex ion, a new metal complex forms and equilibrium is established, as shown in the diagram.
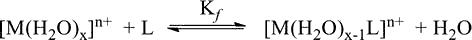
E1
Where x is the number of water molecules, n is the oxidation number of the metal cation, and L is the neutral and monodentate ligand. For ease of understanding, the above reaction can be written in a generalised form as follows:
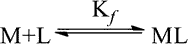
E2
The equilibrium constant Kf of the reaction is given by:
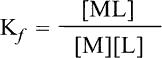
E3
In the equation above, the concentration of water is not considered. Because the solution is dilute, the effect of water molecules entering the bulk solution on the equilibrium constant is minimal. According to Eq. 1, the higher the value of Kf, the more stable the resulting complex will be (3). The equilibrium constant (Kf > 1.0) has a large value. Furthermore, the activity of complex ML is greater than the product of M and L's activities when they are in equilibrium. As a result of the high value of Kf, the ligand L binds to the metal ion more strongly than H2O, implying that L is a stronger ligand than H2O. Lignand L is weaker than H2O if Kf is less than 1.0. As a result, the stability constant is used to assess the complex's thermodynamic stability. With the exception of K1 to Kn, which is K1 > K2 > K3 >... > Kn1 > Kn, the value of successive stability constants decreases on a regular basis. Using [Cd(NH3)4]2+ as an example [3, 4], this trend can be seen:
The steady decrease in the value of stepwise formation constants from K1 to Kn is due to:
• The number of H2O molecules that need to be replaced decreases as the number of ligands in the coordination sphere grows, as does the likelihood of water molecule replacement.
• The influence of electrostatics
• Steric hindrance is caused by having too many ligands.
• Statistical Parameters (number of replaceable positions)
In some cases, Kn+1 > Kn is observed due to unusual structural changes and changes in the metal ion's electronic configuration. Because of changes in the metal ion's electronic structure, the crystal field stabilisation energy varies (CFSE). The complex with a higher CFSE value will be more stable, with a high equilibrium constant. The formation of the [CdBr4]2 complex in aqueous solution is a good example of this. In aqueous solution, the [CdBr4]2 complex forms. In the reaction of aqua complex [Cd(H2O)6]2+ with Br ligand, the stepwise equilibrium or stepwise formation constants K1, K2, K3, and K4 are found. The order of stepwise formation constants is K1 > K2 > K3 > K4, which differs from the common trend of K1 > K2 > K3 > K4. Cd2+ halo complexes have tetrahedral halo complexes, whereas most M2+ ions, including Cd2+, have octahedral aqua complexes. The reaction sequence for making [CdBr4]2 is as follows:
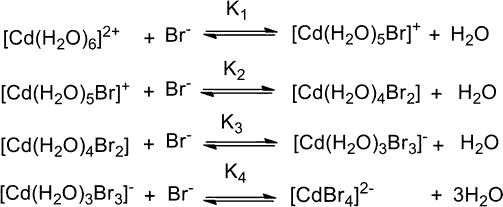
The structure transforms from a six-coordinated octahedral [Cd(H2O)3Br3] complex to a four-coordinated tetrahedral [CdBr4] complex in the final step. In addition to the electronic configuration change that results in K4 > K3, there are two more complex factors to consider.
According to the following equations, the formation constant (Kf) is proportional to the standard Gibbs free energy change (G°) and the standard electrode potential (E°):
ΔG°=−RTlnKfE4
ΔG°=−nFE°E5
Hence RTlnKf=nFE°E6
Because G° is a thermodynamic property, the formation constant is used to determine thermodynamic stability. The formation constant, Gibbs free energy change, and standard electrode potential are used in Eqs. (4) to (6) to determine the thermodynamic stability of a complex (6). A large negative G° value indicates that the equilibrium position favours the product (complex), making the complex formed more stable.
Stepwise formation of complex and stepwise formation constants
The formation constant explains how metal cations and ligands come together to form a complex. Bjerrum (1941) defined the formation of a metal complex in aqueous solution as the substitution of a ligand (L) for a water molecule [5, 6]. It is assumed that this reaction occurs in several steps, each with its own equilibrium constant, known as the stepwise formation constant (K). Take a look at the reactions that result in a complex [MLn]:
The equilibrium constant K1 for the complex (ML) with one ligand (L) can be calculated by assuming the value of activity coefficients to be unity.
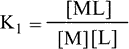
When the metal complex ML reacts with a second ligand L, a new metal complex ML is formed.,
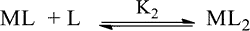
And the equilibrium constant K2 will be
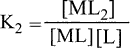
The equilibrium constant is also represented as follows for the formation of the complex MLn from MLn1 and L,
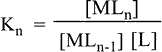
Stepwise formation constants are the equilibrium constants K1, K2,..., Kn. On the other hand, the overall reaction's equilibrium constant can be calculated as
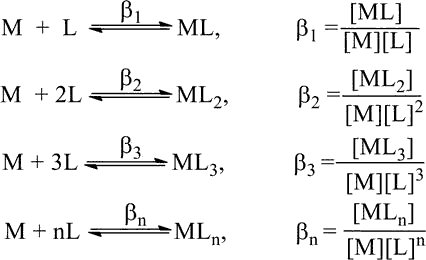
K1, K2, K3,..., Kn are stepwise stability or formation constants, and 1, 2, 3,..., n are overall formation constants. Ks and s are related stepwise constants' products. Consider the product of K1, K2, K3,..., Kn stepwise formation constants.
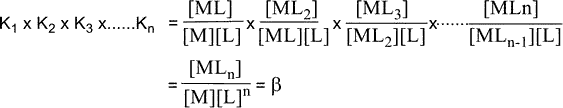
The overall formation constant () equals the product of the stepwise formation constants K1, K2, K3,..., Kn, as shown in the equation above.
Kinetic stability
The rate of reaction, activation energy, and other properties of metal complexes in solution are all addressed by kinetic stability. The stability of a compound is less important than how quickly it reacts. By determining the rate at which the reaction occurs, it aids in the establishment of equilibrium.
Based on reaction rates, Taube classifies complexes as labile or inert. If the rate of ligand substitution is high, the complex is called labile. A labile copper complex is Cu(NH3)4(H2O)2+.
When concentrated hydrochloric acid is added to the solution, the complex turns green, giving rise to the complex [CuCl4]2+. Inert complexes, on the other hand, have a very slow rate of ligand exchange, and the ligands are difficult to exchange. At room temperature, for example, the cobalt complex [Co(NH3)6]3+ has a slow reaction and no reaction. HCL was added to the aqueous solution. However, only one NH3 ligand was found to be substituted by Cl ligand when the aqueous solution of the complex was heated with 6M hydrochloric acid.
4.1.2 Relation between thermodynamic and kinetic stabilities
The thermodynamic and kinetic descriptions of metal complexes' stability and reactivity, respectively, are used. Stable and unstable are thermodynamic terms, whereas labile and inert are kinetic terms. A metal complex is considered labile if it reacts in 1 minute at 25°C, and inert if it takes longer.
The energy change that occurs while starting materials are converted to products, referred to as G for the reaction, is referred to as thermodynamic stability.
The equation G = HTS = RTlnK gives the change in free energy, where S is entropy, H is enthalpy, and K is the reaction's equilibrium constant. The ability of a metal complex to undergo ligand substitution reactions is referred to as kinetic stability. Labile complexes are those that undergo a fast ligand substitution reaction, while inert complexes are those that take a long time. Complexes' thermodynamic and kinetic stabilities are often parallel, but they are not always. Because it undergoes ligand substitution reaction very quickly, [Ni(CN)4]2 is a good example of a thermodynamically stable and kinetically inert complex. The cobalt complex [Co(NH3)6]3+, on the other hand, is kinetically inert but thermodynamically unstable. In acidic solution, the complex [Co(NH3)6]3+ was found to decompose at a rate of 1025, indicating that it is thermodynamically unstable. When the complex is kept in acidic solution for several days, however, no ligand substitution reaction occurs, indicating that it is kinetically inert. The stability of a complex is largely determined by the conditions, as shown in the preceding two examples, and it is always advisable to mention the conditions, such as pH, temperature, and so on, when discussing the complex's stability. To summarise, a stable complex does not have to be inert, and an unstable complex does not have to be labile.
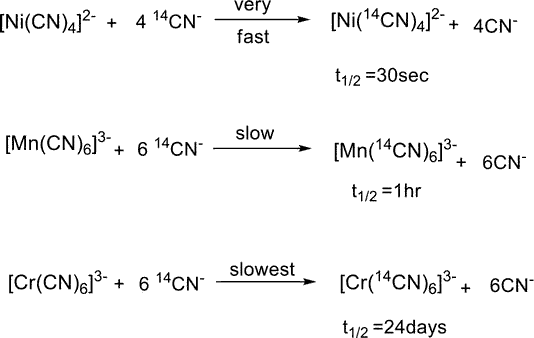
Take a look at the [Ni(CN)4]2, [Mn(CN)6]3, and [Cr(CN)6]3 complexes. Although all of the complexes are thermodynamically stable, they behave differently kinetically. When carbon-14-labeled cyanide ions react in solution with metal complexes, the rate of exchange can be measured. It proves that not all stable complexes are inert and vice versa by showing that [Ni(CN)4]2 is labile, [Mn(CN)6]3 is less labile, and [Cr(CN)6]3 is inert.
4.2.1 Difference between thermodynamic and kinetic stability
To comprehend the distinction between kinetic and thermodynamic stability, you must first comprehend potential energy surfaces and how they relate to a system's state.
A potential energy surface depicts a system's potential energy as a function of one or more of the system's other dimensions. The other dimensions, in most cases, are spatial in nature. Chemical systems' potential energy surfaces are typically complex and difficult to depict. Fortunately, we can simplify things by beginning with simple 2-d models and then expanding our knowledge to the generalised N-d case.
So let's begin with the most basic type of potential energy: gravitational potential energy. This is simple for us because we live on the planet and are constantly influenced by it. If given the chance, things tend to move from higher to lower places, which we have developed an intuitive sense of. If I showed you this image, for example:
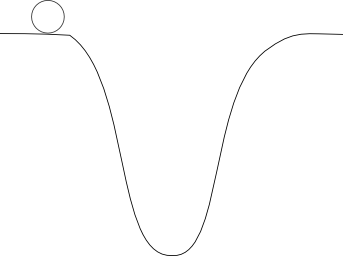
You can probably guess that the rock will eventually roll downhill and come to rest at the valley's bottom.
However, you intuitively understand that it will not move unless something causes it to do so. To put it another way, it requires some kinetic energy to get started.
By slightly altering the surface, I could make it even more difficult for the rock to move:
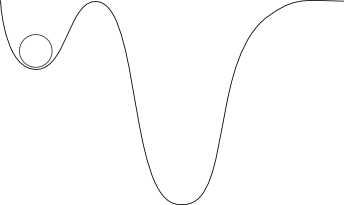
The rock will not move until it gains enough kinetic energy to overcome the small hill that separates the valley it is in from the deeper valley to the right.
The potential energy surface's first valley is known as a local minimum. This means that the first derivative of potential energy with respect to position is zero in mathematical terms:
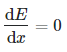
And the second derivative is positive:
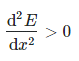
To put it another way, the slope is 0 and the shape is concave upward (or convex).
The global minimum is in the deep valley to the right (at least as far as we can tell). The mathematical properties are the same, but the energy magnitude is lower – the valley is deeper.
If you combine all of this (and are willing to accept a little anthropomorphization), you could say that the rock wishes to reach the global minimum, but its ability to do so is limited by the amount of kinetic energy it possesses.
It requires at least enough kinetic energy to overcome all of the local maxima that lie between its current local minimum and the global minimum.
We call it kinetically stable or kinetically trapped if it doesn't have enough kinetic energy to move away from its current position. We call it thermodynamically stable if it has reached the global minimum.
To apply this concept to chemical systems, we must modify the potential energy used to describe the system. At the molecular level, gravitational potential energy is far too weak to be useful. Instead, we examine one of several thermodynamic potential energies for large systems of reacting molecules.
Which one we pick is determined by the state variables that are constant. We use the Gibbs Free Energy (GG for NPT systems) or the Helmholtz Free Energy (HFT for NVT systems) for macroscopic chemical reactions when there are a constant number of particles, constant temperature, and either constant pressure or volume (NPT or NVT) (AA for NVT systems).
Under the right circumstances, each of these is a thermodynamic potential, which means it does the same thing as gravitational potential energy: it lets us predict where the system will go if given the chance.
We don't have to do much with kinetic energy; the only difference between the kinetic energy of a rock on a hill and the kinetic energy of a large group of molecules is how we measure it. We can measure velocity for single particles, but we must measure temperature for large groups of molecules. Increasing the temperature, in other words, raises the kinetic energy of all molecules in a system.
We can determine whether a transition between two states is thermodynamically favourable if we can describe the thermodynamic potential energy of the system in different states – we can calculate whether the potential energy would increase, decrease, or remain the same.
We are in a thermodynamically stable state if we examine all available states and decide that the one we are in has the lowest thermodynamic potential energy.
In your example of methane gas, we can use Gibbs free energy to determine that the products are more thermodynamically stable than the reactants, and thus methane gas in the presence of oxygen at 1 atm and 298 K is thermodynamically unstable.
However, without outside assistance, methane would take an extremely long time to react. Because the transition states along the lowest-energy reaction path have a much higher thermodynamic potential energy than the reactants' average kinetic energy, this is the case. Because they are stuck in a local minimum, the reactants are kinetically trapped and thus stable. The activation energy is the minimum amount of energy required to overcome a barrier in the form of heat (a lit match).
This concept can be applied to a wide range of systems. Glasses are one of the most well-known and studied examples.
Glasses are interesting because they are physical phase examples of kinetic stability. Thermodynamic stability is usually what governs phase changes. Although the molecules in glassy solids would have a lower potential energy if they were arranged in a crystalline structure, they are "stuck" with a liquid-like disordered structure because they lack the energy to break out of the local minimum.
Thermodynamically favorable but kinetically unfavorable
Take a look at how much easier it is to understand. This means that the products have a lower free energy than the reactants and are therefore more stable. The reactants "wish" to be converted into the products as a result of this. Graphite and diamond, for example, are both carbon compounds, but graphite has a lower free energy than diamond. As a result, diamond desires to become graphite. When your skin is washed, it wants to dissolve in the soap. The dissolution reaction's products (your skin dissolved in soap) are more stable in this case than the reactants (your undissolved skin and the soap separately).
The examples above were chosen because, despite the fact that the reaction should work (the products are more stable than the reactants, and nature always tries to make things as stable as possible), it doesn't. When you wash your hands, the diamond on your ring finger is safe. The reaction is slow, even though it is thermodynamically favourable. It's simply too difficult to break all of the diamond's bonds and re-form them in a new, more stable graphite configuration. To understand why this is, return to the first reaction diagram, which shows the hump between reactants and products. That hump represents how difficult it is to get a reaction to happen in a reasonable amount of time. The hump for graphite conversion in diamond is quite high. The reaction does not proceed thermodynamically because it is kinetically unfavourable.
4.2.2 Stability
It is important to distinguish between thermodynamic and kinetic stability when discussing the concept of stability.
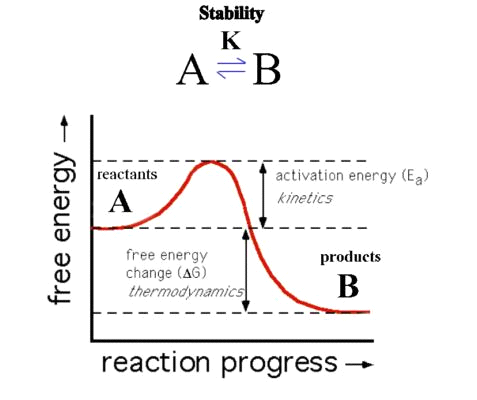
G is negative because B is at a lower energy than A. As a result, the reaction should occur spontaneously, with B being the thermodynamically more stable species.
However, the reaction as shown has an Activation Barrier (Ea) that prevents it from progressing, so it may take a long time to complete. Thermodynamics only describes the reaction's beginning and end points, not its intermediate or transition states. A is described as inert if the kinetics is slow, and as labile if it moves quickly.
The conditions that distinguish them are: if the reaction takes longer than 1 minute at 0.1 M and 25°C, it is INERT; if the reaction takes less than 1 minute at the same temperature, it is LABILE.
We rely on the samples being kinetically stable, or inert, in the lecture on isomerism.
We look at the changes in free energy, enthalpy, and entropy during the reaction in the lecture on Chelation and Stability.
We need to know two formulas when it comes to thermodynamic stability:
ΔG⦵ = - RT ln(K) or alternatively ΔG⦵ = - 2.303RT log10(K) ---(1)
ΔG⦵ = ΔH⦵ - TΔS⦵ ---(2)
The first shows how the free energy is related to the stability constant, while the second shows how the free energy is broken down into its component enthalpy and entropy terms.
4.3.1 Difference Between Stepwise and Overall Stability Constants
What are Stepwise Stability Constants?
The equilibrium constants for each step of the ligand substitution process are known as stepwise stability constants. The ligand substitution occurs in a stepwise manner when water ligands surround a transition metal ion complex. The ligand that is involved in the substitution replaces only one water molecule in this case. To better understand this process, let's look at an example.
Example
Consider the case of ammonia ligand substitution.
[Cu(H2O)6]2+ is the chemical formula for hexaaquacopper(II) ion. Ammonia ligands can be used in place of the six water ligands (NH3). At a time, one water ligand is replaced by an ammonia ligand.
[Cu(H2O)6]2++NH3 ↔ [Cu(NH3)(H2O)5]2+ K1
[Cu(NH3)(H2O)5]2++ NH3 ↔ [Cu(NH3)2(H2O)4]2+ K2
[Cu(NH3)2(H2O)4]2++ NH3 ↔ [Cu(NH3)3(H2O)3]2+ K3
[Cu(NH3)3(H2O)3]2++ NH3 ↔ [Cu(NH3)4(H2O)2]2+ K4
[Cu(NH3)4(H2O)2]2++ NH3 ↔ [Cu(NH3)5(H2O)]2+ K5
[Cu(NH3)5(H2O)]2++ NH3↔ [Cu(NH3)6]2+ K6
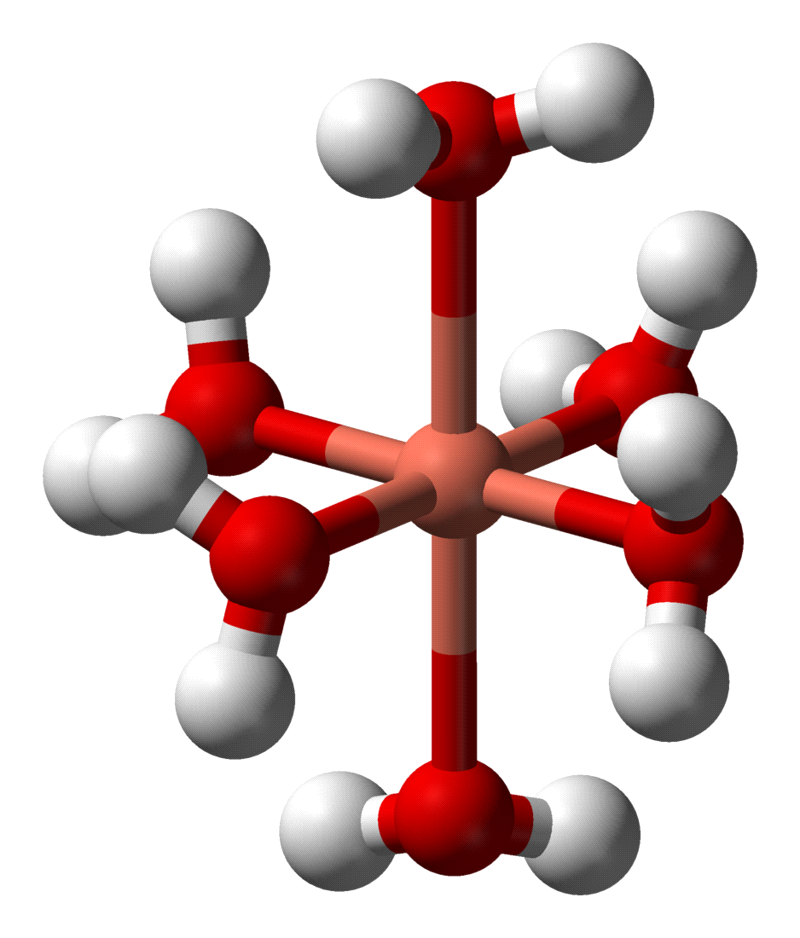
Figure: A 3D diagram of a hexaaquacopper(II) ion.
For the first substitution, K1 is the stability constant. It is k2 for the second substitution and vice versa for the third. Expressions can be found below for each of the above equilibriums.
K1 =[Cu(NH3)(H2O)5]2+ / [Cu(H2O)6]2+* NH3
Where the concentrations of each chemical species inside the brackets are [Cu(NH3)(H2O)5]2+, [Cu(H2O)6]2+, and NH3.
Other stepwise stability constants can also be expressed using the same expressions (K2, K3, K4, K5 and K6).
What are Overall Stability Constants?
The overall stability constant is the overall reaction's equilibrium constant. The overall stability constant for the above reaction is given below.
[Cu(H2O)6] Cu(H2O)6 Cu(H2O)6 Cu(
[Cu(NH3)6] Cu(NH3)6 Cu(NH3)6 Cu(NH3)6 Cu(NH3)6 Cu(NH3)6 Cu(NH2+)
As a result, the equilibrium constant for the equilibrium between a transition metal ion surrounded by water ligands and a transition metal ion surrounded by substituted ligands is the overall stability constant. The expression for the overall stability constant can then be calculated as shown below.
Kstab = [Cu(NH3)6]2+ / [Cu(H2O)6]2+ * NH3 overall
What is the Relationship Between Stepwise and Overall Stability Constants?
Multiplying all of the stepwise stability constants together yields the overall stability constant. As an illustration, consider the following:
Overall Kstab = K1 * K2 * K3 * K4 * K5 * K6
What is the Difference Between Stepwise and Overall Stability Constants?
Stepwise vs Overall Stability Constants | |
Stepwise stability constants are equilibrium constants given for each step of the process of ligand substitution. | The overall stability constant is the equilibrium constant of the overall reaction. |
Nature | |
The stepwise stability constants are given for steps of a substitution reaction that takes place in a transition metal ion complex. | The overall stability constant is given for the whole substitution reaction that takes place in a transition metal ion complex. |
Value | |
The values of stepwise stability constants are lower than the overall stability constant of the same reaction. | The overall stability constant always has a higher value than each stepwise stability constant. |
4.3.2 Stability constants part 1
We can think about the sequence of substitution reactions that will occur when we add another ligand L to an aqueous solution of a metal ion Mn+, which will contain the complex ion [M(OH2)6]n+, as we've seen. We can calculate an equilibrium constant K for each of the six steps.
To make things simpler, I've removed the water ligands, charges, and square brackets from the molecules in question, so M stands for [M(OH2)6]n+, ML stands for [ML(OH2)5]n+, and so on. As a result, the square brackets in the expressions for the equilibrium constants have the usual meaning of the concentration of that specific species. Because water is both a solvent and a reactant, its concentration can be assumed to be constant, so I've excluded it from these expressions.
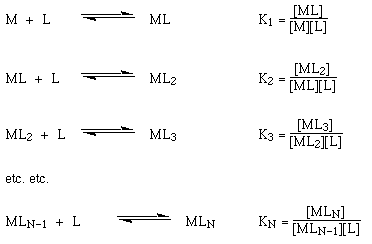
K1 to KN are called the STEPWISE STABILITY CONSTANTS or STEPWISE FORMATION CONSTANTS.
There is however a different way of looking at this reaction:
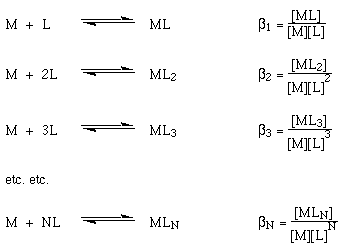
In this case β1 to βN are called the OVERALL STABILITY CONSTANTS.
We can easily see the relationship between these two types of stability constants:
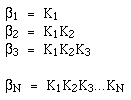
If you need proof of this, we just need to multiply one out:
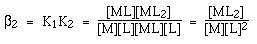
The stability of a coordination compound depends upon the following factors:
(1) Charge density of the central metal ion:
(i)I Charge density is defined as the ratio of charge magnitude to metal ion radius.
(ii) The charge density of a complex influences its stability.
(iii) For example the ionic radii of divalent ions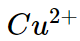 
and
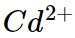are 69 pm and 97 pm respectively hence charge density of 
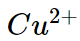ion is higher than that of 
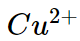. Therefore the complex 
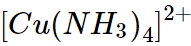is more ions is,
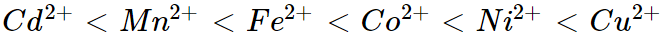
(2) Nature of ligands: The ligands are Lewis bases because they donate electron pairs to the complex's central metal ion, forming coordinate bonds. As a result, the greater the ligands' basic strength, the greater their tendency to donate electrons, and thus the complex's stability.
CN-, for instance, is more basic than NH3. As a result, cyano complexes of a metal ion are more stable than ammine complexes of the same metal ion.
4.5.1 Substitution Reaction
What is Substitution Reaction?
A substitution reaction occurs when one chemical compound's functional group is replaced by another group, or when one atom or molecule of a compound is replaced by another atom or molecule.
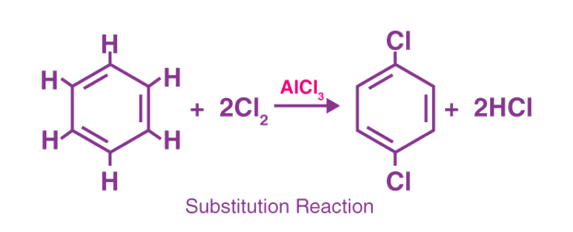
Substitution Reaction Example
In the field of organic chemistry, these types of reactions are said to be extremely important. When CH3Cl reacts with the hydroxyl ion (OH-), for example, it produces methanol, which is the original molecule. The following reaction is as shown below-
CH3Cl + (−OH) ————-CH3OH( methanol) + Cl-
Another example is when ethanol reacts with hydrogen iodide to produce iodoethane and water. The reaction is as shown-
CH3CH2OH + HI———— CH3CH2OI + H2O
Substitution Reaction Conditions
There are certain conditions that must be met in order for the substitution reaction to occur. They include: Keeping low temperatures, such as room temperature
A strong base like NaOH must be diluted. Dehydrohalogenation may occur if the base has a higher concentration.
An aqueous solution, such as water, is required.
Substitution Reactions – Types
Nucleophilic and electrophilic substitution reactions are the two kinds of substitution reactions. The type of atom attached to its original molecule differs greatly between these two types of reactions. The atom is said to be an electron-rich species in nucleophilic reactions, but an electron-deficient species in electrophilic reactions. The following is a quick rundown of the two types of reactions.
4.5.2 Nucleophilic Substitution Reaction:
(a) What are nucleophiles?
Nucleophiles are species that are strongly attached to the region of a positive charge, whether in the form of an ion or a molecule. The presence of negative ions on a molecule is said to be fully charged. Cyanide ions, water, hydroxide ions, and ammonia are common examples of nucleophiles.
(b) What is Nucleophilic substitution reaction?
In organic chemistry, a nucleophilic substitution reaction occurs when a nucleophile attaches to the other substance's positively charged atoms or molecules.
(c) Mechanism of Nucleophilic substitution reaction:
This paper discusses two mechanisms of nucleophilic substitution reactions. The SN1 reaction and the SN2 reaction, where S stands for chemical substitution, N for nucleophilic, and the number represents the reaction's kinetic order.
SN2 Reaction – Mechanism of SN2 Reaction
The leaving group is eliminated while the nucleophile is added simultaneously in this reaction. The nucleophile is easily accessible to the central carbon atom in SN2.
A number of factors influence the rate of SN2 reactions. Below, we'll go over them.:
• The numerical value 2 in SN2 indicates that the rate of reaction is affected by two concentrations of substances: nucleophile and substrate.
• Rate = k [Sub][Nuc] is the rate equation for the reaction mentioned above.
• Because aprotic solvents like acetone, DMSO, or DMF do not add H+ ions to the solution, they are best for the SN2 reaction.
• The complex turns green when concentrated hydrochloric acid is added to the solution, yielding the complex [CuCl4]2+. The ligand exchange rate in inert complexes is very slow, and the ligands are difficult to exchange. The cobalt complex [Co(NH3)6]3+, for example, has a slow reaction at room temperature and no reaction at all. The aqueous solution was infused with HCL. When the aqueous solution of the complex was heated with 6M hydrochloric acid, only one NH3 ligand was found to be replaced by Cl ligand.
Learn more about the SN2 reaction mechanism in detail.
SN1 Reaction – Mechanism of SN1 Reaction
There are certain factors that affect the SN1 reaction as well. A few are discussed below:
• Only one concentration, i.e. the substrate, affects the rate of reaction instead of two.
• Rate = k[Sub] is the rate equation for the reaction described above.
• The slowest step determines the reaction rate. As a result, the leaving group departs at a specific rate, which aids in determining reaction time.
• The leaving group is thought to be better with a weaker conjugate base.
• Bulky groups attached to the carbocations can be used to determine the SN1 reactions.
• The tertiary carbocation reaction is faster than the secondary carbocation reaction, which is faster than the primary carbocation reaction.
• In the rate-determining step, the nucleophile isn't required.
Learn more about the SN1 reaction mechanism in detail.
Example of Nucleophilic Substitution Reaction:
The hydrolysis of alkyl bromide (R-Br) under basic conditions, where the nucleophile is nothing but the base OH and the leaving group is the Br, is a good example of a nucleophilic substitution reaction. R-Br + OH ————– R-OH + Br
In the field of organic chemistry, nucleophilic reactions are equally important, and these reactions are broadly classified as occurring at the carbon atom of a saturated aliphatic carbon compound.
4.5.3 Electrophilic Substitution Reactions:
(a) What are electrophiles?
Electrophiles play a role in the electrophilic substitution reaction. Electrophiles are molecules that donate two electrons to form a covalent bond. Aromatic compounds are primarily involved in electrophilic reactions. The excess electrons in these compounds can be shared throughout the reaction system.
(b) What is Electrophilic substitution reaction?
Electrophilic substitution reactions are chemical reactions in which an electrophile replaces a functional group but not a hydrogen atom in a compound. Hydronium ion (H3O+), hydrogen halides like HCl, HBr, HI, sulphur trioxide (SO3), nitronium ion (NO2+), and others are examples of electrophiles.
(c) Types of Electrophilic substitution reaction:
Here, we'll look at two different types of electrophilic substitution reactions. Aromatic electrophilic substitution and aliphatic electrophilic substitution are two types of electrophilic substitution reactions.
Electrophilic Aromatic Substitution
An electrophile replaces an atom attached to the aromatic ring, which is mostly hydrogen, in this type of electrophilic substitution. Aromatic halogenation, alkylating Friedel-Crafts reactions, aromatic nitration, aromatic sulfonation, and aromatic acylation are some of the reactions that occur. It also includes acylation and alkylation.
Electrophilic Aliphatic Substitution
An electrophile dislocates one functional group in this kind of electrophilic substitution reaction. SE1, SE2, SE2, and SEi are the four electrophilic aliphatic substitution reactions that are analogous to the nucleophile SN1 and SN2 (Substitution Electrophilic). The substrate ionises to a carbanion, which quickly recombines with the electrophile during the SE1 reaction. The old and newly formed bonds are present in a single transition state during the SE2 reaction.
Radical reactions and organometallic substitution reactions are two other types of substitution reactions. Check out the Electrophilic substitution reaction mechanism for more information on aromatic and aliphatic electrophilic substitution.
4.5.4 Types of Inorganic Reactions
Combination Reactions
A synthesis reaction, also known as a combination reaction, occurs when two or more substances combine to form a single new substance. Synthesis reactions are another name for combination reactions. A combination reaction takes the following general form:
A+B→AB(11.3.1)
Two elements combining to form a compound is an example of a combination reaction. When solid sodium metal reacts with chlorine gas, solid sodium chloride is formed.
2Na(s)+Cl2(g)→2NaCl(s)(11.3.2)
This reaction can also be classified as a redox reaction because of the changes in oxidation states. The oxidation state of sodium changes from 0 to 1, while the oxidation state of chlorine changes from 0 to 1.
In order to write and balance the equation correctly, you must remember the seven elements that exist in nature as diatomic molecules (H2, N2, O2, F2, Cl2, Br2, and I2).
One type of combination reaction that occurs frequently is the reaction of an element with oxygen to form an oxide. Metals and nonmetals both readily react with oxygen in most situations. Magnesium reacts quickly and dramatically when ignited, combining with oxygen in the air to produce fine magnesium oxide powder.
2MgO(s)+O2(g)+2MgO(s)+2MgO(s)+2MgO(s)+2MgO(s)+2 (11.3.3)
Decomposition Reactions
When a complex substance is broken down into two or more simpler substances, it is called a decomposition reaction. The general form of a decomposition reaction is ABA+B. (11.3.4)
Most decomposition reactions require a source of energy, such as heat, light, or electricity.
Compounds with only two elements are known as binary compounds. The simplest type of decomposition reaction occurs when a binary compound decomposes into its constituent elements. Mercury (II) oxide, a red solid, decomposes into mercury and oxygen gas when heated.
2HgO(s)+2Hg(l)+O2(g) (11.3.5)
The reaction is classified as a decomposition reaction even if one or more of the products is still a compound. Metal carbonates decompose into metal oxide and CO2 when exposed to oxygen. When calcium carbonate is exposed to air, it decomposes into calcium oxide and carbon dioxide.
CaCO3(s)→CaO(s)+CO2(g)(11.3.6)
When heated, metal hydroxides decompose into metal oxides and water. Sodium hydroxide decomposes to produce sodium oxide and water.
2NaOH(s)→Na2O(s)+H2O(g)(11.3.7)
Single-Replacement Reactions
When one element in a compound replaces another similar element in a single-replacement reaction, also known as a single-displacement or substitution reaction. In its most basic form, a single-replacement reaction is written as A+BCAC+B. (11.3.8)
In this reaction, element AA is a metal that replaces element BB, which is also a metal. The general equation when a nonmetal replaces another nonmetal in a compound is:
Y+XZ→XY+Z(11.3.9)
Y is a nonmetal and replaces the nonmetal Z in the compound with X.
Magnesium, unlike copper, is a more reactive metal. In an aqueous solution of copper (II) nitrate, a strip of magnesium metal replaces the copper. Aqueous magnesium nitrate and solid copper metal are the products of the reaction.
Mg(s)+Cu(NO3)2(aq)→Mg(NO3)2(aq)+Cu(s)(11.3.10)
Many metals react readily with acids, producing hydrogen gas as one of the byproducts. Aqueous zinc chloride and hydrogen are created when zinc reacts with hydrochloric acid. (see figure below).
Zn(s)+2HCl(aq)→ZnCl2(aq)+H2(g)(11.3.11)
Figure: Zinc metal reacts with hydrochloric acid to give off hydrogen gas in a single-replacement reaction.
Figure: Pictured here is about 3 pounds of sodium metal reacting with water. When sodium metal is dropped into a container of water, it reacts quickly and produces hydrogen gas. A large piece of sodium will frequently generate enough heat to ignite hydrogen.
Double-Replacement Reactions
The positive and negative ions of two ionic compounds exchange places to form two new compounds in a double-replacement reaction, also called double-displacement. A double-replacement reaction takes the following general form:
AB+CD→AD+CB(11.3.12)
B and D are negatively charged anions, while A and C are positively charged cations in this reaction. Between substances in aqueous solution, double-replacement reactions are common. A solid precipitate, a gas, or a molecular compound such as water is usually one of the products of a reaction.
When the cations from one reactant combine with the anions from the other to form an insoluble ionic compound in a double-replacement reaction, the result is a precipitate. The following reaction occurs when aqueous potassium iodide and lead (II) nitrate solutions are mixed.
2KI(aq)+Pb(NO3)2(aq)→2KNO3(aq)+PbI2(s)(11.3.13)
Figure: When a few drops of lead (II) nitrate are added to a solution of potassium iodide, a yellow precipitate of lead (II) iodide immediately forms in a double-replacement reaction.
Combustion Reactions
When a substance reacts with oxygen gas, energy is released in the form of light and heat. The presence of O2 as a reactant in combustion reactions is required. Water vapour is produced by the combustion of hydrogen gas (see figure below).
2H2(g)+O2(g)+2H2O(g)(11.3.14)
Notice that this reaction also qualifies as a combination reaction.
Figure: The Hindenburg was a hydrogen-filled airship that crashed in 1937 while attempting to land in New Jersey. The hydrogen exploded in a massive fireball, completely destroying the airship and killing 36 people. The chemical reaction was straightforward: hydrogen reacted with oxygen to form water.
A hydrocarbon, a compound made entirely of carbon and hydrogen, is used in many combustion reactions. Carbon dioxide and water are always produced when hydrocarbons are burned. Many hydrocarbons are used as fuel because they produce a large amount of heat energy when burned. Propane (C3H8) is a gaseous hydrocarbon that is commonly used in gas grills as a fuel source.
C3H8(g)+5O2(g)→3CO2(g)+4H2O(g)(11.3.15)
4.6.1 Ligand Substitution Reactions
Transition metal complexes can swap ligands, which is important in their synthesis, stereochemistry, and catalytic chemistry. Reaction kinetics are inextricably linked to the mechanisms of chemical reactions. Transition metal reactions have mechanisms that are inferred from experiments that look at the concentration dependence of the incoming and outgoing ligands on the reaction rate, the detection of intermediates, and the stereochemistry of the reactants and products, similar to organic chemistry.
Kinetics vs. Thermodynamics. It's important to remember the difference between thermodynamics and kinetics when thinking about transition metal complex reactions. Take the formation of the square planar tetracyanonickelate complex as an example:
Ni2+(aq)+4CN−(aq)=[Ni(CN)4]2−(aq)K(eq)≈1030M−4(5.12.1)
The equilibrium of [Ni(CN)4]2- is very stable thermodynamically, implying that the equilibrium above is very far to the right. The complex, on the other hand, is labile kinetically, which means it can rapidly exchange its ligands. The exchange of a 13C labelled CN- ion with a bound CN- ligand, for example, occurs in tens of milliseconds.
[Ni(CN)4]2−(aq)+⋅CN−(aq)⟶[Ni(CN)3(⋅CN)]2−+CN−(aq)kexchange≈102M−1s−1
(5.12.2)
A compound can be thermodynamically unstable but kinetically inert, which means it takes a long time to react. The [Co(NH3)6]3+ ion, for example, is unstable in acid, but it takes about one week at room temperature to complete its hydrolysis reaction with concentrated HCl:
[Co(NH3)6]3+(aq)+6H3O+(aq)⟶[Co(H2O)6]3+(aq)+6NH+4(aq)Keq≈1030(5.12.3)
Transition metal complexes were classified as labile if their reaction half-life was one minute or less, and inert if they took longer to react, according to Henry Taube, who studied the mechanisms of ligand exchange reactions in simple test tubes. The dynamic range of ligand substitution rates spans at least 15 orders of magnitude. The Taube definition of lability is useful for classifying reactions with low and high activation energies on the timescale of most laboratory experiments. The crystal field stabilisation energy (CFSE) is important in determining the activation energy and thus the rate of ligand substitution, as we'll see.
For his work on the electron transfer and ligand exchange reactions of transition metal complexes, Henry Taube (Stanford University) won the Nobel Prize in Chemistry in 1983.
Crystal field stabilization energy and ligand exchange rates. Consider the substitution of one water molecule for another in an octahedral [M(H2O)6]n+ complex, which is a very common and straightforward ligand exchange reaction. We know that G° = 0 and Keq = 1 for this reaction because the products are identical to the reactants (except for the label). Using isotopically labelled water, NMR can be used to track the reaction's progress (typically containing 17O or 18O):
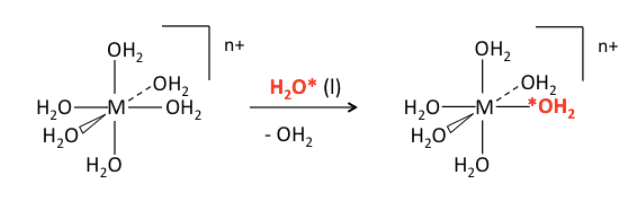
The vast difference in rate constants - roughly 14 orders of magnitude - for different metal ions and oxidation states is the most striking aspect of this (otherwise boring) reaction:
Mn+ | Log k (sec-1) |
Cr3+ | -6 |
V2+ | -2 |
Cr2+ | 8 |
Cu2+ | 8 |
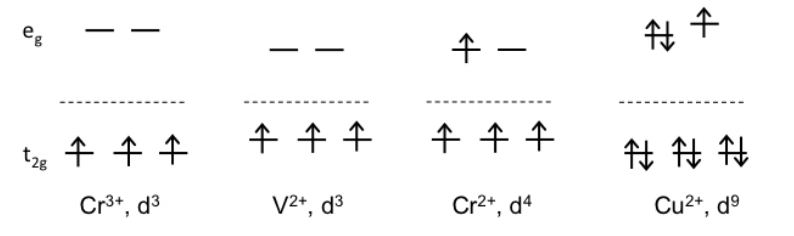
While it may appear strange that the same ion in two different oxidation states (Cr3+ vs. Cr2+) would be inert or labile, the difference can be explained by drawing d-orbital splitting diagrams for the complexes. We discovered that octahedral complexes with a high CFSE (Cr3+, V2+) are inert. On the other hand, ions with electrons in high-energy eg orbitals (such as Cr2+ and Cu2+) are more labile. The energy penalty for distorting the complex away from octahedral symmetry - to make, for example, a 5- or 7-coordinate intermediate - is particularly high in the case of Cr3+ and V2+. For Cr2+ and Cu2+, which already have electrons in antibonding eg orbitals, the activation energy for ligand substitution is lower.
We can now predict trends in ligand substitution rates using the rules we developed for calculating the CFSE of transition metal complexes:
• Because of their high CFSE, octahedral complexes with d3 and d6(low spin) configurations, like Cr3+ (d3), Co3+ (d6), Rh3+ (d6), Ru2+ (d6), and Os2+ (d6), are substitution-inert.
• Square planar d8 complexes are also substitution-inert, particularly those in the 4d and 5d series. Pd2+, Pt2+, and Au3+ complexes are all examples.
• Fe3+, V3+, V2+, Ni2+, and main group ions (Be2+, Al3+) that are hard Lewis acids are examples of intermediate cases. These complexes have water exchange rates in the range of 101-106 s-1 and form strong metal-oxygen bonds.
• On a nanosecond timescale (k 108-109 s-1), ions with zero CFSE exchange water molecules. Alkali metal (Li+, Na+, K+, Rb+, Cs+) and alkali earth (Mg2+, Ca2+, Sr2+, Ba2+) cations, as well as Zn2+, Cd2+, Hg2+, and Mn2+, have d0, d5 (high spin), and d10 electron counts. The CFSE is zero in these cases, and the energetic cost of breaking octahedral symmetry is low.
• Because Lewis acid strength decreases with increasing ion size, faster exchange occurs with larger ions (e.g., Ba2+ > Ca2+ and Ga3+ > Al3+) for p-block elements.
• As a Jahn-Teller ion, the Cu2+ ion (d9) is already distorted from octahedral symmetry and thus quite labile, exchanging water ligands at a rate of about 108 s-1.
Ligand Substitution Mechanisms. For an MLn complex undergoing ligand substitution, there are essentially three different reaction mechanisms:
A MLn complex loses a ligand to form an MLn-1 intermediate in the dissociative mechanism, and the incoming ligand Y reacts with the MLn-1 fragment: Ln1ML+L,k1L,k1Ln1M+Y,k2Ln1MY 5.12,4)
The mechanism for ligand substitution on an octahedral ML6 complex is shown below. In this example, the intermediate state includes a trigonal bipyramidal ML5 fragment as well as free L and Y ligands.
The concentration of Y has no effect on the rate of reaction if the rate-determining step is the dissociation of L from the complex, resulting in the first-order rate law:
Illustration of the dissociative ligand substitution mechanism for an ML6 complex. The reaction energy profile is shown at the right.
Rate=k1[MLn](5.12.5)
This reaction is first order in ML6 and zero order in Y in the case of an octahedral complex, but only if the highest energy transition state occurs before the formation of the ML5 intermediate. The rate law becomes more complicated when the two transition states have similar energy levels (as in the animation to the right). We can simplify the problem in this case by assuming that the MLn intermediate has a low steady-state concentration. The rate law that emerges as a result of this process is:
Rate=k1k2[Y][MLn]k−1[L]+k2[Y](5.12.6)
When k2[Y] >> k-1[L], the rate law is reduced to the simpler first-order rate law. Because dissociation of a ligand is required to form the transition state, the entropy of activation is always positive in the dissociative mechanism.
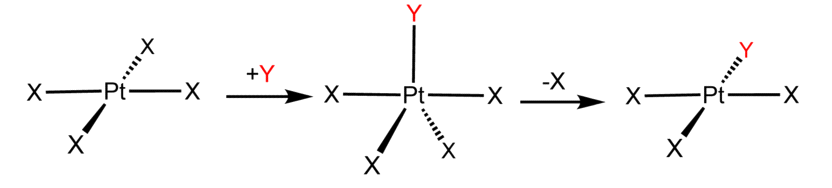
In the associative mechanism, the incoming ligand Y attacks the MLn complex, forming a transient MLnY intermediate, which then loses a ligand L, resulting in the MLn-1Y product.
Associatively substituted complexes are usually coordinatively unsaturated or contain a ligand that can change its bonding to the metal, such as a nitric oxide ligand that can bend or change its hapticity (NO). The associative pathway is preferred in homogeneous catalysis because the binding event, and thus the reaction selectivity, is dependent not only on the nature of the metal catalyst but also on the molecule involved in the catalytic cycle.
Berry pseudorotation mechanism
Vaska's complex (IrCl(CO)[P(C6H5)3]2) and tetrachloroplatinate are two examples of associative mechanisms found in the chemistry of d8 square planar metal complexes (II). These compounds (ML4) bind the incoming (substituting) ligand Y to form pentacoordinate intermediates ML4Y, which dissociate one of their ligands in a subsequent step. The Berry pseudorotation provides a low-energy pathway for all ligands to sample both the equatorial and axial sites, despite the fact that the incoming ligand is initially bound at an equatorial site. According to the principle of microscopic reversibility, ligand dissociation must start at an equatorial location. When Y is dissociated, no reaction occurs, but when L is dissociated, net substitution occurs, yielding the d8 complex ML3Y. Choosing a rate is usually the first step. As a result, the activation entropy is negative, indicating that the transition state has increased order. Second-order kinetics governs associative reactions: the rate at which product appears is determined by the concentrations of both ML4 and Y.
The Trans Effect, which is connected with the associative mechanism, controls the stereochemistry of certain ligand substitution reactions.
The labilization (increased reactivity) of ligands that are trans to other ligands, also known as trans-directing ligands, is referred to as the trans effect. Trans ligand labilization, which is most noticeable in square planar complexes but also seen in octahedral complexes, is thought to be caused by electronic effects. The cis effect is most commonly observed in octahedral complexes.
In addition to the kinetic trans effect, trans ligands have an impact on the molecule's ground state, the most notable of which are bond lengths and stability.. Some authors prefer the term trans influence to distinguish this from the kinetic effect, while others prefer more specific terms like structural trans effect or thermodynamic trans effect to differentiate this from the kinetic effect.
The discovery of the trans effect is credited to Ilya Ilich Chernyaev, who recognised and named it in 1926.
The intensity of the trans effect (as determined by the rate of substitution of the trans ligand) is determined by the following sequence:
Weak field ligands are not trans-directing, but strong field ligands are.
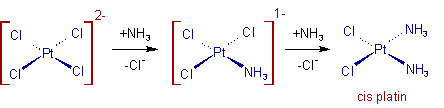
The synthesis of cisplatin and its trans isomer is a well-known example of the trans effect. The first NH3 ligand is randomly added to one of four equivalent positions starting with PtCl42. Due to the fact that Cl has a greater trans effect than NH3, the second NH3 is added trans to a Cl and thus cis to the first NH3.
If, on the other hand, one starts from Pt(NH3)42+, the trans product is obtained instead:
The trans effect in square complexes can be explained using the associative mechanism described above, which passes through a trigonal bipyramidal intermediate. In general, ligands with high acidity (as in phosphines) or low-ligand lone-pair–d repulsions (as in hydride) prefer the intermediate's more -basic equatorial sites, which prefer the intermediate's more -basic equatorial sites. The second equatorial position is taken by the incoming ligand. Because the departing trans ligand occupies the third and final equatorial site, the kinetically preferred product is the one in which the ligand trans to the one with the greatest trans effect is removed.
• The interchange mechanism is similar to the associative and dissociative pathways except that no distinct MLnY or MLn-1 intermediate is formed. Nucleophilic substitution via the SN2 pathway at a tetrahedral carbon atom is analogous to this coordinated mechanism in organic chemistry. The interchange mechanism is classified as either associative (Ia) or dissociative (Id) depending on how important M-Y and M-L bonding are in the transition state (Id). If a strong M-Y bond forms during the transition state, the mechanism is Ia. The mechanism is Id if the weakening of the M-L bond is more important in achieving the transition state.
• The exchange of bulk and coordinated water in [V(H2O)6]2+ is an example of the Ia mechanism. The slightly more compact ion [Ni(H2O)6]2+, on the other hand, uses the Id mechanism to exchange water.
Effects of ion pairing. When highly charged cationic complexes interact with anionic ligands, ion pairs form, and these ion pairs frequently go through the Ia pathway. A ligand in the first coordination sphere can swap positions with the nucleophilic incoming ligand, resulting in net substitution. The chromium(III) hexaaquo complex's "anation" (reaction with an anion) is a good example:
[Cr(H2O)6]3++SCN−⟷[Cr(H2O)6],NCS2+[Cr(H2O)6]3++SCN−⟷[Cr(H2O)6],NCS2+
[Cr(H2O)6],NCS2+⟷[Cr(H2O)5NCS]2++H2O
4.7.1 TRANS EFFECT
Some ligands preferentially direct the substitution trans to themselves during substitution reactions of square planar metal complexes. The nature of the ligand trans to it influences which leaving group is chosen.
The Trans effect is defined as a ligand's effect on the rate of substitution of another ligand positioned trans to it in square planar complexes.
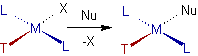
'T' stands for trans directing group, and 'Nu' stands for nucleophilic ligand that preferentially replaces the trans to ligand 'T' ligand 'X'. Ilya Ilich Chernyaev, a Russian chemist, discovered the Trans effect in square planar Platinum(II) complexes for the first time. The Trans effect, however, can also be seen in octahedral complexes.
A kinetic effect is the true Trans effect.
EXAMPLE:
Kinetic trans and cis effects are shown in the diagram below. In both cases, we can see that X1 has a bigger impact than X2. For each effect, the shown geometries are the most common. The metals and oxidation states shown are representative of what is available.
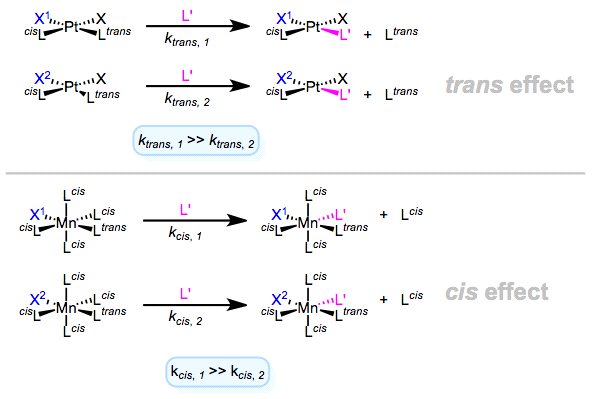
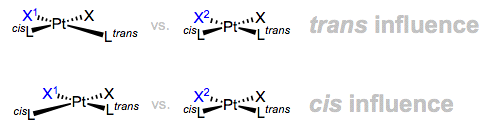
Figure: The interaction of trans and cis influences. The lengths of the bonds are noticeably longer.
The cis/trans thermodynamic and kinetic effects are now complete. It's worth noting that the kinetic trans effect occurs more frequently in d8 square planar complexes than in d6 octahedral complexes (particularly when the departing L is CO). However, the question of what makes a strong trans effect ligand remains unanswered.
4.7.2 DIFFERENCE BETWEEN TRANS INFLUENCE AND TRANS EFFECT
In general there are two factors contributing to trans direction of substitution as described below:
1) Trans influence: This is a thermodynamics factor. By weakening the M-L bond trans to them in the ground state, some ligands make substitution easier.
Strong - donors, like H-, I-, Me-, PR3, and others, destabilise the M-L bond trans to themselves, making it easier to replace the ligand.
2) Trans effect: Because it is a kinetic factor, this is a true trans effect. When the transition state stabilises, this occurs.
Strong -acceptors, such as NO+, C2H4, CO, CN-, and others, stabilise the transition state by accepting electron density donated to the metal via -interaction from the incoming nucleophilic ligand.
This is debatable because the -interaction has the potential to strengthen the M-L bond, especially in the trans position.
4.7.3 MECHANISM OF TRANS EFFECT
Kinetic studies:
Both S and V are negative, indicating the associative mechanism, A or Ia.
The activation entropy is denoted by S.
V = Change in volume due to the reactants forming a transition state.
When the V is negative, the transition state is compressed in relation to the reactants. The volume of the transition state is smaller than the combined volume of the reactants.
The experimentally observed rate law for a square planar substitution reaction is as follows: ML2TX + Nu ------> ML2TNu + X
Rate = k1[ML2TX] + k2[ML2TX][Nu] rate = k1[ML2TX] rate = k2[ML2TX] rate = k2[ML2T
T = trans directing ligand, R = reverse directing ligand, S = reverse directing lig
X = trans to T ligand
Nucleophile is a term that refers to someone who likes to eat
The associative mechanism is revealed by the rate's dependence on Nu concentration.
The stereo chemical maintains its configuration during substitution. Occasionally, the 5 or 6 coordinated species are isolated during the reaction. The presence of bulky groups on metal complexes slows the rate of substitution. The associative mechanism is once again revealed.
Mechanism:
The above kinetic data, combined with the preferential substitution of certain ligands at the trans position, suggest the formation of a 5-coordinate trigonal planar transition state (or intermediate).
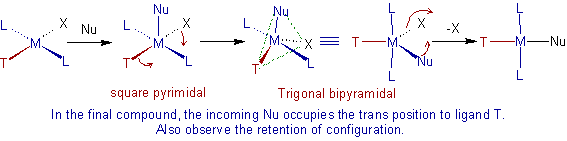
Why the trans substitution is favored?
The removal of electron density in the equatorial plane reduces electrostatic repulsion in the 5-coordinate Trigonal bipyramidal transition state. As shown below, the -interaction of the trans directing ligand, T, aids in the removal of electron density.
* Due to the loss of CFSE during the formation of a trigonal bipyramidal complex from a square planar one, square planar substitution reactions are slow. The loss of CFSE increases as the group progresses. As a result, the 4d and 5d series square planar substitutions are slower. This is why Pt(II) complexes are used in the majority of square planar substitution kinetic studies..
* The rough order of trans-directing effect of various ligands is:
NO+, CO, CN-, C2H4 > PR3, H- > Me- > Ph- > NO2-, I-, SCN- > Br- > Cl- > Py, NH3, OH-, H2O
4.7.4 ILLUSTRATIONS OF TRANS EFFECT
The Trans effect can affect the product formed in substitution reactions. The trans effect is well-known in the synthesis of cis-platin, cis-diamminedichloridoplatinum (II). It's made by substituting ammonia molecules for the two chloro groups in PtCl42.
Ammonia is substituted for any of the chloro groups at random in the first step. In the second step, however, the ammonia group preferentially substitutes the chloro group cis for the first ammonia. Because Cl- has a stronger trans effect than NH3, this is the case.
Pt(NH3)42+, on the other hand, is used to make the trans product. In this case, the second Cl group is preferred over the first at the trans position.
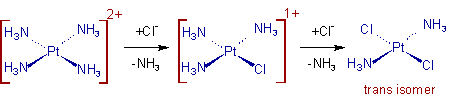
4.8.1 Theories of trans effect
The Trans effect is a kinetic phenomenon that affects the activation energy of a reaction. The kinetic Trans effect differs from the ground state and static trans effects. This has an impact on physical properties like vibrational frequency, band length, and chemical shift. One of two theories can explain the phenomenon of the trans effect.
The Polarization theory
The polarisation (effect of -bonding) of a ligand is proportional to its Trans effect, according to this theory. There is no trans effect because the overall dipole generated by the [Pt(X)4] type complex is zero. In the [PtL(X)3] type complex, the dipole across the opposite X cancels each other, so there is no trans effect. Because the dipoles of the two ligands X and L are opposite, they are not cancelled (trans). Due to its larger size, L has a higher polarisability than X. Pt (II) deforms due to L's induced dipole, resulting in more effective bonding and higher bond energy in L-Pt compared to Pt-X trans to it. As a result, the Pt-X bond has become weaker, while the Pt-L bond has become longer. The rate of X substitution increases as the Pt-X bond weakens and becomes Pt-L. Due to its greater polarisability, L has a greater trans effect than X..
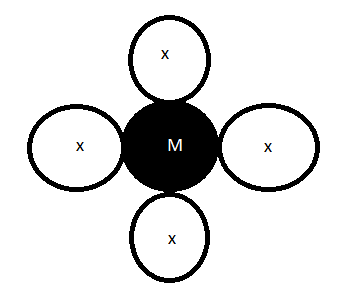
Figure: electrostatic polarization in Pt(II) complex
M-X bonds become weaker and longer as the Trans effect of L increases. With increasing polarisability, the Trans effect of ligands that are unable to form metal ligand-bonds increases, e.g.
Cl-< Br-< I-
Polarisability increases
Trans effect increases
B. The π- bonding Theory
Metal-ligand -bonds ( d-d or d-p bond) can be formed when ligands with vacant or* orbitals accept electrons from filled metal orbitals. CO, CN-, C2H4, PR3, and other ligands are examples of -bonding ligands. The ability of -bonding ligands to form metal–ligand–bonds increases as their Trans directing ability increases. The formation of the -bond, for example, increases the electron density on the Pt-L bond while decreasing Trans of L in the [PtLX3] type complex. As a result of these findings, the Pt-X bond is weaker than the Pt-L bond, and thus substitution occurs from X to L.
The -acceptor ligands increase the reaction intermediate's stability (i.e. trigonalbipyramidal). Because of the poor bonding of this bond with Pt, the incoming Y enters in the direction of the Pt-X bond, trans to L. (II). The d-p and d-d bond formations are depicted below.
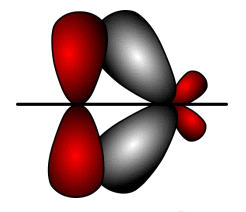
Figure: The d-p bond is formed. Overlapping between the ligand's vacant p orbitals and the metal ions' filled d orbitals.
Figure: Formation of dπ-dπ bond. Overlapping between vacant d orbitals of ligand and filled d orbitals of metals ions
Key takeaway:
The trans effect refers to a group's ability to direct substitution into its opposite position (i.e. trans) in the planner complex.
With increasing polarisability, the Trans effect of ligands that cannot form metal-ligand-bonds increases.
The ability of -bonding ligands to form metal–ligand -bonds increases as their Trans directing ability increases.
The ultrafast T-jump method was used to resolve the dynamics of ligand substitution in labile cobalt complexes.
In chemical and biological systems, ligand exchange of hydrated metal complexes is common. We investigated this process, specifically the transformation of aqua cobalt (II) complexes to their fully halogenated species, using the ultrafast T-jump. The findings reveal a stepwise mechanism with time scales ranging from hundreds to nanoseconds. When the structure is preserved, the dynamics are significantly faster, but when the octahedral-to-tetrahedral structural change bottlenecks the transformation, it becomes rate-limited. Bimolecular kinetics and energetics (enthalpic and entropic) evidence is presented for a reaction in which the ligand aids the displacement of water molecules while the entering ligand remains in the activated state. The reaction time scale differs from that of ionic diffusion by one to two orders of magnitude, implying the presence of a collisional barrier between the ion and the much larger complex.
Aside from being of fundamental interest in the chemical literature, coordinated metal ions are essential for biological catalysis and function, such as in metabolism (1, 2). Cobalt complexes are structurally prototypical systems that are biologically relevant in areas such as vitamin B12 function (3) and cancer therapy biomedical applications (4, 5). Ligand substitution reactions (6–8), in which the ligand coordinated to the metal ion is replaced by a free one(s) from solution, are multistep processes that occur in aqueous media and are part of the hydration mechanism. The temperature- or ligand-concentration-dependent exchange is frequently accompanied by dramatic colour changes.
Cobalt aquachloro complexes are the subject of the studies presented here (II). Steady-state, optical, and x-ray absorption studies (9, 10) revealed that the complex in aqueous halide solution Co(H2O)mXn)(2n)+ (X = Cl) exists with different numbers of coordinated chloride, namely, [Co(H2O)6]2+, [Co(H2O)5X]+, [Co(H2O)4X2], [Co(H2O)X3], and [ Because of the crystal field stabilisation energy, the first three species have an octahedron configuration, while the latter two have a tetrahedron configuration (9, 11).
When [Cl] or temperature are increased, the spectroscopic shift from pink to dark blue occurs as the equilibrium shifts from the octahedral to the tetrahedral structure, each with its own absorption. The equilibrium shifts when there is a sudden change in temperature (e.g., T-jump) or concentration, and coordinated water molecules are gradually replaced by free chloride ions. The structural interconversion from octahedral to tetrahedral configuration occurs simultaneously with this change:
The nature of the dynamics and the free energy surface must be clarified for this complicated reaction.
We investigated the substitution processes involved over a wide range of concentrations, temperatures, and time scales using the ultrafast T-jump (12, 13). It was possible to capture the elusive intermediates by carefully adjusting the reactant concentration and temperature at the start. The experimental results show that the formation of the final product, tetrachloro tetrahedral species, from the hydrated reactant, hexaaqua octahedral species, is a sequential substitution process with a rate-limiting configurational change from octahedral to tetrahedral coordination along the reaction coordinate. The significance of the measured rates in terms of the mechanism and collision-controlled entry into activated complexes is discussed.
Results and Discussion
The transition state must be properly defined in order to understand the mechanism of each individual reaction. As proposed by Lanford and Gray in 1965 (6), the mechanisms of reactions between positive metal ions and ligands in aqueous solution can be divided into three categories: associative, dissociative, and interchange. The substitution in octahedral aqua cobalt complexes is generally thought to favour a dissociative interchange activation (15–17), based on kinetic studies of activation volume (14); bond breakage is involved in the formation of the activated complex of decreased coordination number. The rates and activation energies reported here indicate that association is a critical process; as discussed below, the incoming ligand plays a significant role in bond formation and the activated complex.
Coordination Rates and the Activated State.
For various concentrations and initial temperatures, the steady-state and transient behaviours are shown in Figs. 1 and 2. At different wavelengths, distinct transient behaviour is observed. For a probing wavelength of 480 nm, a decay is observed (Fig. 2A), indicating the depletion of the initial population of hexaaqua complexes at concentration-dependent rates. Depending on the ligand concentration, a rise or decay is observed (Fig. 2B) for detection wavelengths between 550 and 630 nm.The accumulation or depletion of intermediate populations determines the behaviour in this region. The formation of the final chloro cobalt complexes causes a rise in absorption (Fig. 2C) at probing wavelengths of 630 nm.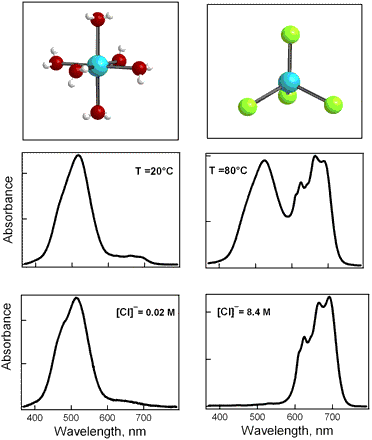
Octahedron and tetrahedron structures and the spectra of the cobalt complexes. Spectroscopic evidence of equilibrium shift at different sample temperatures (Middle) and ligand concentration (Bottom) are shown with the two structures (Top).
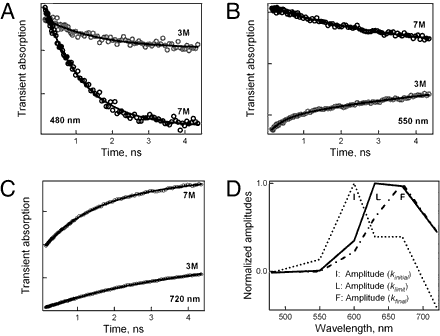
At various wavelengths, representative transients for cobalt complexes. (A) Decay curves, which show the rate of depletion of the initial reactants, the hexaaqua octahedral species, as a function of ligand concentration. (B) The formation or depletion of intermediate states as represented by rise or decay curves. (C) The final product, the tetrachloro tetrahedral species, is formed by rising curves. (D) The observed rates' amplitude has distinct peaks and a blue shift from kinital to kfinal behaviour.
To improve quantification, we used a multiphase exponential model to fit the datasets of all transients recorded under various conditions, and we were able to obtain consistent amplitudes and rate constants (shared as global parameters). The findings show that three distinct components exist: kinitial1 (200–1,000 ps), klimit1 (1–10 ns), and kfinal1 (200–1,000 ps); the components differ, as discussed below. Only samples with a low to medium [Cl]/[Co2+] ratio (5.0) show the first rate process, kinitial, which represents the relatively fast octahedron configuration substitution process (Eq. 2a and b). Following this initial process, a slower rate step with an amplitude that peaks between the kinitial and kfinal processes (Fig. 2D) indicates that the octahedral–tetrahedral structural change (Eq. 2c) is the sequential substitution's rate-limiting step, as discussed below. The study of this amplitude's concentration dependence (Fig. 3) reveals that the amplitude shifts significantly with concentration. Finally, at high [Cl]/[Co2+] ratios (>12), a relatively fast process with rate constant kfinal is recovered, which is assigned to the tetrahedral chlorocobaltic product substitution rate. (Eq. 2d):
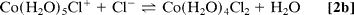
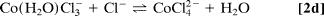
The concentration dependence of the reaction rates is plotted in Fig. 3, which follows a linear relationship with the chloride activity (aCl);k = kligand aCl + kwater. The rate constants of ligand (chloride) and water attack, respectively, are represented by the slope (kligand) and intercept (kwater). The average chloride activity, aCl, is given by aCl = [Cl]100.19[Cl]0.53 (10) and is significant for high concentration solutions (>5 M). The substitution in octahedral complexes was expected to follow a dissociative interchange pathway (15–17), in which the rate of leaving water molecule(s) becomes a deciding step. The observed linearity over a wide range and up to 13 M, on the other hand, suggests that the chloride anation is the bimolecular process' rate-limiting step. As a result, it's a mechanism of interchange in which the bond-forming association is crucial.
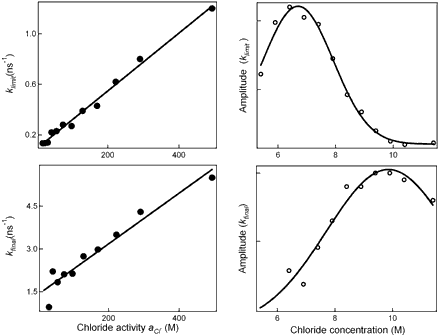
Rates and their amplitude dependencies on concentration. (Left) The rates (shown here: klimit and kfinal) follow a linear relationship with chloride activity al−. (Right) The amplitude of the observed rates dramatically shifts with concentration.
The temperature dependence and energetics of the activated state provide more evidence for this theory. The activation energy (Ea) and entropy (S) of observed rate constants vs. Temperature are calculated using the Eyring relationship (Eq. 3) ,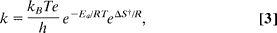
The activation energy is calculated using e rather than enthalpy (H = Ea RT). The Boltzmann constant, R, and absolute temperature are denoted by kB, R, and T, respectively. The activation energy Ea and entropy S are 15.6 0.6 kJ/mol and 43.7 2.0 J/molK, respectively, according to the data shown in Fig. 4. The negative entropy value indicates that the entering ligand and departing water are both rotated and translated confined in the activated complex. The activation energy of cobalt complexes (47 kJ/mol) is nearly three times smaller than the activation energy deduced from the Eyring relationship (approximately 16 kJ/mol) (14). The low activation energy can be explained as a result of the ligand-assisted labilization process, in which the activation energy is compensated by the energy of chloride in the coordinated position, which aids in the removal of water. Swift (18) observed the relaxation time of the structural conversion of cobalt aqua ions, Co(H2O)42+ + 2H2O Co(H2O)62+, to be 50–200 ms. The relaxation time for the above process and the chloride-assisted structural conversion (Eq. 2c) can be compared; chloride ion participation increases the rate by seven to eight orders of magnitude over the broad range of concentrations investigated here. The ligand's labilization effect is due to a significant decrease in the activation barrier (both enthalpic and entropic), as a result of an associative interchange process.
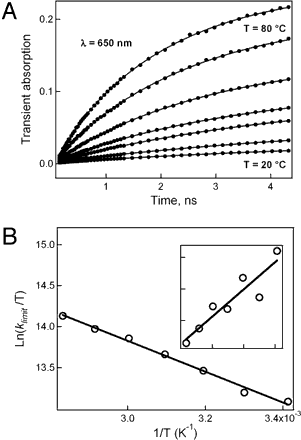
Temperature dependence of reaction rates. (A) The transients measured by absorption change at different temperatures in the range of 20°C–80°C. (B) The Eyring plot of ln(klimit T−1) vs. T−1 gives the activation energy of 16 kJ/M. (Inset) The temperature dependence in ln(kinitial T−1) vs. T−1 has a negative activation energy.
Ionic Diffusion and Collisions
Because the reactions involve bimolecular collisions in solution, the effect of diffusion should be considered. Debye's theory can be used to estimate the diffusion of two ions with charges Z1 and Z2 at low electrolyte concentrations.,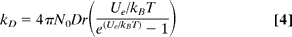
Where D = D1 + D2, D1 and D2 are the ions' diffusion coefficients, Ue = z1z2e2/4r is the electrostatic potential, N0 is Avogadro's number, and r is the distance between the two ions' closest approach (19). The diffusion coefficient for Cl in water is estimated to be 4.4 105 cm2s1 using the Stokes–Einstein equation [Do = kBT/6r]; the contribution of the complex to the diffusion rate can be ignored due to its size being much larger than the chloride ion. . In the range of 1–50 109 M1s1, the typical diffusion-controlled rate is estimated. It is faster by one to two orders of magnitude than observed reaction rates. As a result, the process must account for collision efficiency as well as the geometrical constraint that exists between the large complex and the small chloride ion (20).
Mechanism
The following picture of a two-step process can be drawn from the above results. By electrostatic interactions, the ligand diffuses into the second coordination sphere and forms an ion pair. This is a pre-association process based on the Eigen and Wilkins concept (21, 22). When successful collisions occur, the reaction occurs. Because the cobalt complexes become more negatively charged and less sterically crowded as the reaction progresses toward the product, we would expect the water attack kinetics to accelerate while the chloride attack kinetics to slow. Indeed, the rate constants' observed trend (Table 1) supports this simple picture. The rate-limiting step is structural conversion from octahedral to tetrahedral coordinate, where chloride is anated to the complex in a stepwise manner along the reaction coordinate. The large desolvation enthalpy (two extra water molecules are removed when the substitution is coupled with the structural change) as well as possible entropic penalty contributions from rearrangement of the activated complex configuration could all contribute to the dynamical bottleneck. Water exchange is orders of magnitude slower (or longer) without the help of ligands. 14 and 17.
Schematic of the free energy surface of the ligand substitution in labile cobalt complexes, with the rate-determining step being that of structural change.
Conclusion
The ultrafast T-jump study shows that the substitution of the Co(II) ion in aqueous solution occurs in multiple steps, with the octahedral-to-tetrahedral structural change being the rate-limiting step. The reaction has the characteristics of an associative interchange mechanism, in which the ion in the coordination shell is essential for water liberation and structural changes. In theoretical simulations using transition path sampling, the “simultaneous” interaction of the entering and departing groups with the metal centre has been elucidated for similar octahedral complexes of Cr (23). The activation energy of entering and departing ions is significantly reduced due to favourable interactions with the metal centre. Only one rate, kinitial, was observed along the reaction coordinate of the Co system, despite the fact that there are two initial steps along the reaction coordinate. This suggests that the kinitial process may be multifaceted. The “abnormal” negative activation enthalpy deduced from kinitial vs. T (Fig. 4 Inset) supports the hypothesis that this multistep process includes a fast preequilibrium step.
The study of the dynamics of metal complexes associated with biomolecules, such as those involving proteins or DNA, is a natural extension of our research using this ultrafast T-jump method.
Methods
Ultrafast T-Jump.
The ultrafast T-jump setup is described in detail in previous articles from this lab (12, 13). The laser system is made up of two optical parametric amplifiers (OPA) that are pumped by a femtosecond Ti/Sapphire amplifier. The pump pulses were set at 1.5 m (70 J per pulse), the OH stretching and bending frequency's overtone. The probe pulse can be tuned to arbitrary wavelengths, in this case, the absorption bands of the octahedral and tetrahedral species, ranging from 240 nm to 800 nm. This selectivity enables a global examination of all transients and, as a result, the significant components of transient relaxations. Within 5–10 ps, the T-jump raises the temperature by 5°C-10°C, reaching the water (medium) relaxation time scale. The relaxation toward the new equilibrium is probed using a delayed second optical pulse following the T-infrared jump's pulse. Using a temperature-controlled UV-Vis spectrometer, all steady-state measurements were taken (Cary 500).
Cobalt Complex Preparation.
Barnstead Nanopure water (18M) was used to make Co(II) chloride solutions, and the different [Cl]/[Co2+] ratios (from 2 to 6500) were tuned by adjusting the lithium chloride (from Aldrich, reagent grade) concentration in the solutions studied.
Substitution processes with DNA constituents and amino acids
In biological systems, Zn(II) and Cu(II) prefer O-carboxylate, carbonyl, and N-imidazole donor bioligand due to their square pyramidal structure. N1 and N7 allow inosine-5'-monophosphate (5'-IMP) and guanosine-5'-monophosphate (5'-GMP) to coordinate with metal ions. The N7 atom is deprotonated in our experiment (pH 7.38). The nucleotide's 5'-monophosphate residue (pK a 6) is also expected to be partially deprotonated at this pH. 1H and 31P NMR spectroscopy were used to confirm binding to Zn(II) through the N7 position of 5'-GMP in a neutral or weakly acidic medium. During the investigation of transition metal ions' hydrolytic cleavage ability, the possibility of Cu(II) complex interaction with oxygen from phosphate residue in DNA was confirmed, owing to steric hindrance..
According to a comparison of the reactivity of the two complexes, [CuCl2(terpy)] is at least 2-10 times more reactive than [ZnCl2(terpy)] (see Tables 1 and 2). Both complexes with 5'-IMP and 5'-GMP have second-order rate constants for the first reaction step that are of the same order of magnitude (Table 1 and 2). The similar reactivity of 5'-IMP towards [CuCl2(terpy)] for both reaction steps could be due to a decrease in the electronic density on the copper(II) centre caused by the tridentate chelate, 2,2′:6′,2”-terpyridine's -acceptor ability, resulting in both chloride being equal for parallel substitution routes. In comparison to cisplatin-based drugs, coordination's versatility may allow for the treatment of various cancer types with varying toxicity. According to the literature, there are few studies of ligand-substitution reactions between Zn(II) and Cu(II) complexes and biologically relevant nucleophiles, so bioligand reactivity was compared to kinetic data for substitution reactions of the [PtCl(terpy)]+ complex [17b). By comparing the order of reactivity of biomolecules in substitution reactions with Pt(II), it was discovered that the order of reactivity of biomolecules in substitution reactions with Pt(II) is the same, and platinum(II) complex react slightly faster with DNA constituent.
According to the hard-soft acid nature of metals, five-coordinate metal centres Zn(II) and Cu(II) prefer O-carboxylate bioligands. L-Met and DL-Asp are coordinated by O-carboxylate donor atoms, but the formation of chelate O-N-ammine has not been observed. It is well known that Cu/Zn-superoxide dismutase contains zinc(II) ion coordination to a L-aspartic acid via oxygen (O-Asp81) (SOD1). For the first step between complexes and DL-Asp, similar reactivity orders were obtained (for [ZnCl2(terpy)] k 1 = 79 ( 2 mol1 L s-1; for [CuCl2(terpy)] k 1 = 96 ( 3 mol1 L s-1). The rate constants show that the substitution of the first chloride in the Zn(II) complex by DL-Asp slows down the second substitution step by almost ten times. The substitution reactions between Zn(II) and Cu(II) complexes with L-methionine are the slowest, according to the data in Tables 1 and 2. At pH 7.38, reactions between the zwitterionic form of L-methionine and complexes occur (pK a1 = 2.65 and pK a2 = 9.08 are the dissociation constants for L-Met).
The similar kinetic behaviour of [ZnCl2(terpy)] and [CuCl2(terpy)] complexes suggests that the strong -acceptor ability of the tridentate chelate 2,2′:6′,2′′-terpyridine, as well as steric hindrance and electronic properties of the first coordinated nucleophiles, control the rates of nucleophilic substitution reactions. The extreme liability of [Zn(H2O)6]2+ and [Cu(H2O)6]2+ (k 298 > 107 s-1) with diffusion controlled rate constants is well known. Water exchange rates in complexes are reduced when bi-, tri-, and tetra-dentate ligands are present in the inner coordination sphere. The metal ion is forced into a different geometry by the strong ligand field. Furthermore, because of this, the rate constants of ligand-substitution reactions are reduced by a factor of 103. Based on the information in the literature, it can be concluded that the square pyramidal coordination geometry around Cu(II) has a greater impact on the rates of ligand-substitution reactions in the [CuCl2(terpy)] complex than the electronic properties and steric hindrance induced by the first coordinated biomolecules. This could explain why the rate constants for both reaction steps with 5'-IMP and DL-Asp were of similar order of magnitude (see Table 2).
For reactions involving L-methionine at pH 7.38, the activation parameters H and S were calculated using an Eyring equation (see, Supplementary Material, Fig. S5). For both reaction steps, every available activation parameter supports an associative mechanism A or Ia. (Tables 1 and 2). The significantly negative activation entropies indicate that bond formation appears to dominate the activation process in the studied systems. As a result, six-coordinate transition states are expected.The substitution reaction processes have an associative mechanism (A) that involves the formation of an intermediate with a higher coordination number, followed by the displacement of a weakly bound ligand. In many associative interchange reactions, there is no well-defined intermediate and bond formation between the central metal ion and the entering nucleophile takes precedence.
Parallel pathways involving water and nucleophile attacks can be observed if an associative mechanism is proposed, as is well known. Although the presence of 0.010 mol L1 NaCl was sufficient to suppress the parallel hydrolytic pathway in some experimental conditions (see Supplementary Material, Figs. S1 and S2), direct nucleophilic attacks are important and occur in the manner described in Scheme 1. In the presence of 0.002 mol L1 LiCl, the mechanistic study of complex-ligand substitution reactions between the five-coordinate [CuCl2(pytBuN3)] complex and TU, TMTU revealed an associative interchange (Ia) mechanism for both chloride displacement. On the five-coordinate [Cu(tren)H2O]2+ and substituted tren complexes, similar results were reported for water exchange and ligand-substitution reactions. Only one ligand can be replaced in this case, however.
Scheme 1 The reaction pathways for dichlorido Zn(II) and Cu(II) complexes with biologically relevant nucleophiles that have been proposed.
The negative activation entropies for displacement of both zinc ions from Zn2(ZP1) are consistent with an associative mechanism, in which the entering nucleophile attacks ZP1-bound metal (ZP1 = zinc fluorescent sensor of the Zinc pyr family), according to the literature data.. Alternative chelators for mobile zinc were tris(2-pyridylmethyl)-amine (TPA) and N,N,N′,N′-tetrakis(2-pyridylmethyl)ethylenediamine (TPEN) in this study. Theoretical calculations on the water-exchange pathway for [Zn(H2O)4L]2+ 2H2O (L = sp-hybridized N-donor ligands and sp2-, sp3-hybridized O-donor ligands) show that moving one water molecule from the second coordination sphere to a vacant coordination site on the divalent zinc ion forms a six-coordinate intermediate [Zn [20c,20d] 2+ H2O
Substitution processes with glutathione
Under pseudo-first-order conditions, the kinetics and mechanism of the substitution processes of [ZnCl2(terpy)] and [CuCl2(terpy)] complexes with tripeptide GSH with respect to the complex concentration were investigated. The absorbance always shows an exponential growth or downtrend versus time, indicating first-order kinetics with respect to the nucleophile (v= -d[Nu]/dt = k obsd[Nu]) regardless of the system. The kinetics traces revealed two reaction steps, but a different reaction mechanism for substitution reactions involving the [ZnCl2(terpy)] complex and glutathione (Fig. 5)
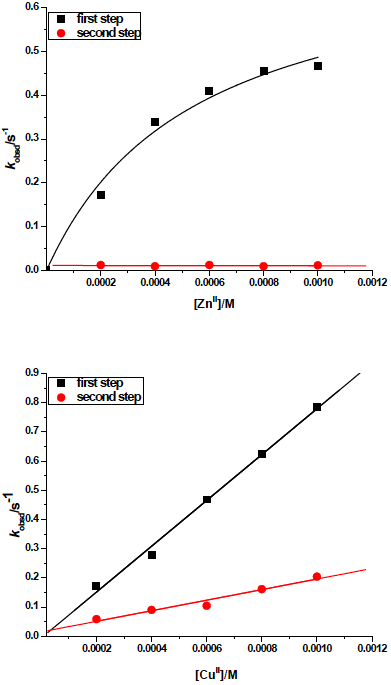
Fig. 5 Pseudo-first order rate constants for the first and second substitution reactions of the [ZnCl2(terpy)] and [CuCl2(terpy)] complexes with glutathione at pH 7.38 (0.005 mol L1 phosphate buffer) in the presence of 0.010 mol L1 NaCl at 22°C in the presence of 0.010 mol L1 NaCl.
At low concentrations, first-order linear dependence, k obsd1, on the complex concentration was observed for substitution reactions between [ZnCl2(terpy)] and glutathione. Saturation kinetics were observed at higher concentrations. These can be explained by thinking of the first step as a very fast pre-equilibrium formation of an intermediate (pseudo-octahedral complex), followed by rearrangement to the final complex, with GSH replacing one chloride (Scheme 1). Equation 3 could be used to determine the value of the rate second-order constant k 2 that described the substitution of one chloride and the pre-equilibrium constant K 1.
k obsd1=k 2k 1[ZnII ]1+ k 1 [ZnII ] (3)
The obtained results are summarized in Table.
Table. Second-order rate constants for the reactions of the [ZnCl2(terpy)] and [CuCl2(terpy)] complexes with glutathione in the presence of 0.010 mol L1 NaCl at 22°C at pH 7.38 (0.005 mol L1 phosphate buffer).
K 1= 1831 mol1 L was discovered to be the pre-equilibrium constant. The second substitution step, k obsd2= k 2', is unaffected by glutathione concentration, indicating that chelation is taking place. When GSH is deprotonated at pH 7.38, an O-carboxylate and N-ammine group from the (-glutamyl residue can be used to form a five-membered chelate ring. The rise and fall in absorbance at 281 nm as a function of time is typical of a reaction involving an intermediate in the overall process of reactant to product transformation.
The pre-equilibrium constant was discovered to be K 1= 1831 mol1 L. (Table 3). Glutathione concentration has no effect on the second substitution step, k obsd2= k 2', indicating that chelation is taking place. An O-carboxylate and N-ammine group from the (-glutamyl residue can be used to form a five-membered chelate ring when GSH is deprotonated at pH 7.38. The rise and fall in absorbance at 281 nm as a function of time is typical of a reaction involving an intermediate in the overall reaction to product transformation process. Table shows that glutathione is the best nucleophile and that the Cu(II) complex has a tenfold higher affinity for glutathione than the Zn complex (II). Furthermore, because copper and zinc balance is crucial for maintaining glutathione levels, this finding could be extremely significant. Glutathione may help remove excess copper from cells, but it has little or no impact on Zn(II) transport. Glutathione is used as a protective agent in cancer treatment and is given either before or after cisplatin. Platinum drugs may also be inactivated in the glutathione reaction because Pt(II) complexes have a high affinity for the S-thiol group. To understand why Zn(II) and Cu(II) complexes react with glutathione slower than Pt(II), several factors must be considered, including the hard-soft nature of the metals, the versatility of biomolecule coordination, and different geometrical structures of complexes..
4.10.1 Substitution reactions of octahedral complexes
The most extensively mechanistically studied organic reaction is the substitution of ligands in octahedral metal complexes. It is crucial, and a number of significant observations and results are discovered. Substitution in octahedral systems was first investigated in aqueous solutions for classical coordination complexes. Recently, some important discoveries have been made about the mechanism by which organometallic complexes react to ligand substitution. Following a discussion of the aqueous reaction mechanisms, we will look at these organometallic complexes.
The following three sections address the following topics:
Points that are unique to Co(III), owing to the fact that it is the metal/oxidation state that has received the most research. In general, octahedral complexes undergo substitution reactions. At the octahedral level, a little organometallic substitution chemistry.
4.10.2 In aqueous solutions, substitution reactions of classical octahedral complexes
The reaction of the aquo ions M(H2O)6n+ is the most fundamental reaction to investigate. Water substitution by water and water substitution by an anionic ligand, X-, are both possible reactions. All of the possible mechanisms A, I, and D can be seen in these seemingly simple reactions. In fact, in octahedral systems, Ia and Id mechanisms predominate, while D and A mechanisms are uncommon.
4.10.3. Eigen-Wilkins mechanism
Eigen shared the Nobel Prize in Chemistry with Norrish and Porter in 1967 for this and other work on reaction mechanisms. Interchange reactions start with a pre-equilibrium state, which leads to the formation of an encounter complex, which then rearranges to produce the products. All molecular reactions in solution that occur at rates less than the diffusion limit can be explained using the Eigen-Wilkins mechanism.
Unfortunately, under certain conditions, such as large concentrations of X, constant concentration of H2O (a very likely case), and small or large k-w, kx, etc., the rate expressions predicted by the Eigen-Wilkins mechanism can all reduce to the same expression.
As a result, the rate law is nearly useless for determining the nature of the substitution mechanism in octahedral complexes. The Id mechanism appears to be active in most octahedral complexes, according to the evidence. The evidence that supports this conclusion will be presented and discussed in the remainder of this section.
4.10.4 Substitution reactions of aquo ions: Substitution of water by water
The factors which we can examine here are the following:
(a) how the rate differs depending on the metal
b) Dimensional and charge considerations
(c) LFSE (Ligand Field Stabilization Energy) factors
(d) The procedure
Many different types of reactions can be used to investigate these factors, but the substitution of water by X (anation) and the substitution of X by H2O are the two most commonly studied. (Thermolysis)
Unfortunately, under the right conditions of large [X], constant [H2O], small or large k–w, kx, etc., all of these rate expressions reduce to the same expression, Rate = kf[complex][X].
When it comes to determining the nature of the substitution mechanism in octahedral complexes, the rate law is practically useless.
According to the evidence, the Id mechanism is active in the majority of octahedral complexes.
4.10.5 Substitution reactions of aquo ions: Substitution of water by water
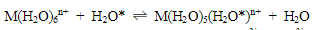
Most metals have a hydration number of 6 (exceptions include Be2+ and Ca2+, which have a hydration number of 4; lanthanides have a higher hydration number). The substitution of bound H2O by solvent water, as shown in the equation above, is the most basic ligand substitution process. Various techniques, such as relaxation methods and NMR, have been used to investigate the kinetics of this reaction. For the vast majority of metal aquo ions, kinetic data is available, and the measured rate range is enormous, spanning 18 orders of magnitude (figure). Most metals have fast substitution, but the slow ones can be more useful in kinetic studies.
Solvent interferes with nucleophilic substitution reactions by replacing the leaving group and forming a different complex before the nucleophile attacks, which not only affects the mechanism of the reaction but also provides incorrect information about the kinetics of the reaction. The substitution reaction of the octahedral complex has been studied kinetically in an aqueous medium. The presence of acid or base in the medium can affect the rate of substitution reactions in aqueous solution.
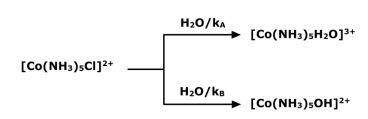
The nature of the product in hydrolysis reactions is determined by the pH of the solution; in acidic solution, the water-containing complex forms, while in basic solution, the hydroxo(HO-) complex forms. If you use the same formula for both SN1 and SN2 type reactions, the rate will be Rate of reaction =
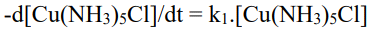in case of SN1 reaction and 
if the SN1 reaction occurs Because the concentration of water is sufficient, there will be virtually no change in water concentration. As a result, kinetic studies of acid or base hydrolysis will always lead to erroneous conclusions about the mechanism of the reaction. The hydrolysis rate constant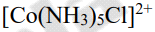 
is a million times faster than an acidic solution, i.e. kB is approximately 104 to 108 times higher than kA. The next module will cover acid and base hydrolysis.
Substitution of bound H
2O is dissolved in water as a solvent. A variety of techniques, including relaxation methods and NMR, have been used to investigate the kinetics of this reaction. The vast majority of metal aquo ions have kinetic data, and the measured range of rates is vast, covering 18 orders of magnitude (figure). Most metals have a quick substitution rate, but the slow ones can be more interesting in kinetic studies.
References:
1. Das Asim K., Fundamentals of Inorganic Chemistry, Vol. II, CBS Publications, 2nd Ed. 2010.
2. Selected Topic in Inorganic Chemistry, Mallick, Madan and Tuli, S. Chand Publisher. 17th Ed. 2010.
3. Mehrotra R.C. And Singh, A. Organometallic Chemistry, New Age International Publishers, 2nd Edn, 2000.
4. Gupta B. D. And Elias A. J., Basic Organometallic Chemistry, 2nd Edn., University Press (2013).
