Unit - 1
Sets
Introduction and significance of discrete mathematics
Computer science is all about the study of problems and solving problems by some process. The main goal is to develop an algorithm (a step by step list of some instructions in order to solve a certain problem).
According to K.H Rosen, discreet mathematics has more than one purpose but more importantly it equips computer science students with logical and mathematical skills.
By B.Miller and D. Ranum, A computing machine end is to develop an algorithm, a measure by step list of instructions in work outing a job. Algorithm are finite procedures that if followed will work out the job.
Discreet mathematics is the study of mathematics which deals on discreet structures like graphs, trees and networks.
It deals with discreet objects like integers and rational numbers which are separated from each other
Discreet mathematics is the language of computer science
The field of mathematics that are considered to be part of discrete mathematics include graph theory and the theory of computation. Topics in number theory such as congruence’s and recurrence relations are also considered part of discrete mathematics.
Theoretical computer science includes areas of Theoretical computer science includes areas of discrete mathematics relevant to computing. It draws heavily on graph theory and logic. Included within theoretical computer science is the study of algorithms for computing mathematical results.
Theoretical computer science also includes the study of various continuous computational topics.
We study about the following topics under discreet mathematics-
1. Information theory
2. Mathematical logic
3. Set theory
4. Graph theory
5. Discreet probability theory
6. Number theory
7. Trees
8. Topology
Review of sets, types and operations on sets
Sets- A set is a collection of well-defined objects which are called the elements or members of the set.
We generally use capital letters to denote sets and lowercase letters for elements.
If any element which exists in the set is to be denoted as-
Suppose an element ‘a’ is from a set X, then it is represented as- a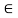 X
X
Which means the element ‘a’ belongs to the set X.
If the element is not form the group then we use ‘not belongs to’.
Representation of sets-
There are two ways to represent sets.
1. In first way, the elements of the set are separated by comma and contained in the bracket-{ }.
2. The second way is that we define the characteristic of the element.
For example-
Suppose we have a set ‘A’ of all odd integers which are greater than 3.
Then we can represent it two ways-
1. A = {5, 7, 9…….}
2. A = {x | x is an odd integer, x>3 }
Subsets-
Let every element of set X is also an element of a set Y, then X is said to be the subset of Y.
Symbolically it is written as-
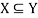
Which is read as- X is the subset of Y.
Note- If X = Y then 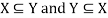
Proper sub-set-
A set X is called proper subset the set Y is-
1. X is subset of Y
2. Y is not subset of X
Note- every set is a subset to itself.
Equal sets-
If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.
We write it as X = Y and read as X and Y are identical.
Super set-
If X is a subset of Y, then Y is called a super set of X.
Null set-
A set which does not contain any element is known as null set.
We denote a null set by ∅
The null set is a subset of every set.
Singleton-
A set which has only one element is called singleton.
Example- A = {10} and B = {∅}
Theorem- if ∅ and ∅’ are empty sets then ∅=∅’
Proof: Let ∅≠ ∅’ then the following conditions must be true-
1. There is element x∈∅ such that x∉∅’
2. There is element x∈∅’ such that x∉∅.
But both these conditions are false since ∅’ and ∅’ has any elements if follows that ∅=∅’.
Operations on sets-
1. Union and intersection-
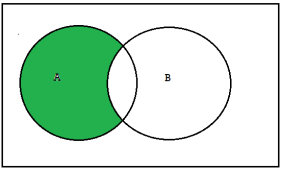
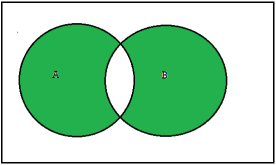
Union-We denote union of two sets as- A∪B, which is the set of all elements which belongs to A or to B.
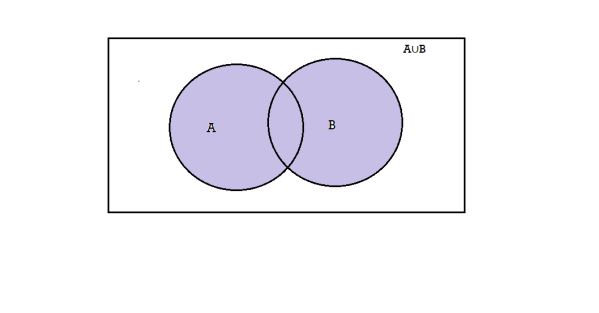
That is-
A∪B = {x |x∈∅A or x∈∅B}
Intersection- We denote intersection of two sets as- A∩B, which is the set of all elements which belongs to A and to B.
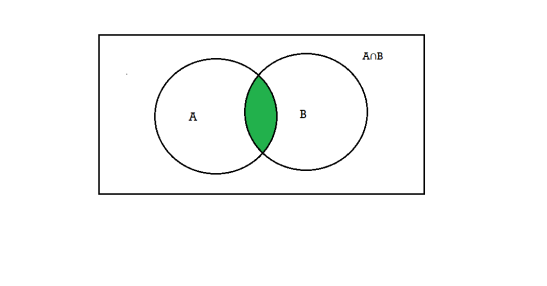
That is-
A∩B = {x |x∈∅A and x∈∅B }
Note- Two sets are said to be disjoint if they have no common elements in common.
Example: If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}
Then-
A∪B = {1, 2, 3, 4, 5, 6,7, 8, 9}
A∪C = {1, 2, 3, 4, 5, 6,7, 8, 9,10}
B∪C = {4, 5, 6,7, 8, 9, 10}
A∩B = {4, 5, 6}
A∩C = {5, 6}
B∩C = {5, 6, 7, 8, 9}
Property-1-
An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element
In A belongs to A ∪B, and every element in B belongs to A ∪B. That is,
A ⊆A ∪B and B ⊆A ∪B
Property-2-
An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element
In A belongs to A ∪B, and every element in B belongs to A ∪B. That is,
A ⊆A ∪B and B ⊆A ∪B
Complements, differences and symmetric differences-
Complement-
The complement of a set A, denoted by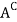 , is the set of elements which belong to U(universal set)but which do not belong to A. That is
, is the set of elements which belong to U(universal set)but which do not belong to A. That is
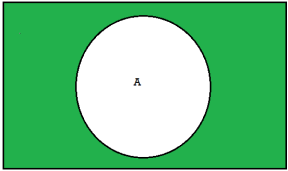
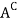 = {x | x ∈U, x /∈A}
= {x | x ∈U, x /∈A}
Difference-
The difference of A and B, denoted by A\B or A-B, is the set of elements which belong to A but which do not belong to B that is-
A-B = {x | x ∈A, x / ∈B}
The set A\B or A-Bis read “A minus B”.
Symmetric difference-
The symmetric difference of sets A and B, denoted by A⊕B, consists of those elements which belong to A or B but not to both. That is
A ⊕B = (A ∪B)-(A ∩B) or A ⊕B = (A-B) ∪(B-A)
Cardinality of sets-
If A is finite set with n distinct elements, then n is called the cardinality of A. The cardinality of A is denoted by |A| [or by n (A)].
Example: Let A = {a, b, c, d}, then A is a finite set and |A| = 4
Cardinality of union of two sets-
Number of elements in A ∪B: (Cardinality of union) If A and B are any two finite sets then, the numbers of elements in A ∪B, denoted by | A ∪B | is given by | A ∪B | = | A | + | B | −| A ∩B |
Principal of inclusion and Exclusion-
Let we have A and B are finite sets. Then A ∪B and A ∩B are
Finite and n(A ∪B) = n(A) + n(B) −n(A ∩B)
That is, we find the number of elements in A or B (or both) by first adding n(A) and n(B) (inclusion) and then
Subtracting n(A ∩B) (exclusion) since its elements were counted twice
For three sets-
n(A ∪B ∪C) = n(A) + n(B) + n(C) −n(A ∩B) −n(A ∩C) −n(B ∩C) + n(A ∩B ∩C)
Finite set-
If a set has finite number of elements then the set said to be a finite set.
Examples:
1. {2, 5, 9, 8, 11, 15, 19, 85}
2. The set of all vowels in English alphabets
3. The set of students in of high school in a particular school.
Infinite set-
If a set has infinite number of elements then the set said to be a infinite set.
Examples:
1. The set of all natural numbers.
2. The set of total points on a line.
Multi-set-
A multi-set is a generalization of a set where repetition of elements matters.
Like {4, 5, 6} and {5, 4, 6} are the same multi-set but the set {5, 5, 4, 6} is the different multi-set as there is repetition of the elements.
So that, “A multi-set is a set-like, unordered collection where multiplicity(repetition) of the elements matters.
Here multiplicity means how many times an element occurs in the set.
Notation-
If an element ‘a’ occurs ‘n’ times in a multi-set A then it can be represented as - 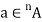 .
.
For example-
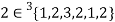 ,
, 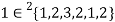 ,
, 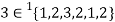
Ordered pair-
An ordered pair of element a and b, where a is designated as the first element and b as the second element, it is denoted by (a, b).
In particular
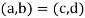
If and only if a = c and b = d. Thus
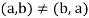
Unless a = b.
n-tuple-
A finite sequence over a set A is a function from {1, 2,….,n} into A, and it is usually denoted by
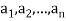
Such a sequence which is finite is called an n-tuple.
Here ‘n’ is a non-negative integer.
Tuples are written by listing the elements with parentheses ().
Cartesian product
Suppose we have two sets A and B, then we can form the set-
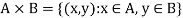
To be the set of all ordered pairs (x,y) where x is an element of A and y is an element of B.
Here we call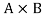 the Cartesian product of A and B.
the Cartesian product of A and B.
Example: If A = {1, 2} and B = {3, 4, 5} then find  .
.
Sol.
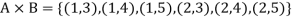
Example: Let A = {1, 2} and B = {a, b, c}, then-
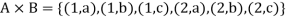
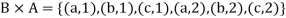
And
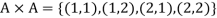
Note-
1. 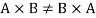
2. 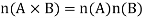
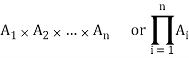
3. The Cartesian product of two sets of real numbers can be represented by tree diagrams.
Theorems-
If A, B, C are sets then-
1. 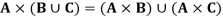
2. 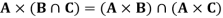
Proof-
1.
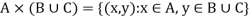
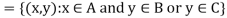
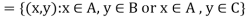
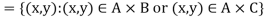
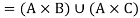
2.
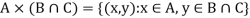
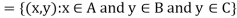
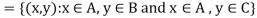
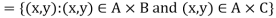
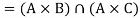
Theorem-
If A, B, and C are non-empty sets then A ⊆B ⇒A × C ⊆B × C
Proof: Let (a, b) be any element A × C, then
⇒a ∈ B and b ∈C (because A ⊆B)
⇒ (a, b)∈B × C
Hence A × C ⊆B × C
Cartesian product of n-sets-
Let 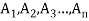 denote n sets where n ≥2 , then the Cartesian product
denote n sets where n ≥2 , then the Cartesian product 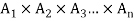 is the set ofall n-tuples of the form
is the set ofall n-tuples of the form 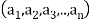 where
where 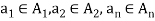
From the definition we have
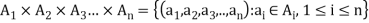
Application of sets and propositions
Set theory is a branch of mathematics that deals with the properties of well-defined collections of objects such as numbers and functions.
German mathematician George Cantor introduced a theory of abstract sets of entities.
Set theory is used in the following areas of computer science-
1. Data structure
2. Object-oriented systems
3. Databases
4. Machine learning
Many mathematical concepts can be defined precisely using set theory concepts.
Graphs, manifolds, rings and vector spaces can all be defined as sets.
Fuzzy set theory is a sweeping statement of set theory. Fuzzy sets deals with a particular kind of uncertainty.
In axiomatic set theory, axioms are set to be describe sets.
Propositions have many applications in computer science like designing of computing machines, AI, definition of data structures for programming languages etc.
Propositional logic concerned with statements to which the truth values “true” and “false” can be assigned.
A proposition is a collection of declarative statements that has either a truth value “true” or a truth value “false”
Applications of propositional logics are-
1. System specification
2. Boolean searching
3. Logic puzzles
4. Logic circuits
Relations:
We define a relation in terms of ordered pairs-
An ordered pair of elements of x and y, where x is the first element and y is the second element, it is denoted by (x, y),
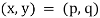
If and only if x = p and y = q
Thus (x, y)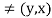 unless x = y
unless x = y
Product sets-
Suppose we have two sets X and Y. The set of all ordered pairs (x, y) where 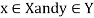 is called the Cartesian product of X and Y.
is called the Cartesian product of X and Y.
It is represented as follows-
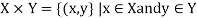
And it is read as X cross Y.
Relation-
Let X and Y are two sets, A relation from X to Y is a subset of  .
.
Now suppose R is a relation form X to Y, then R is a set of ordered pairs where each first element comes from X and each second element comes from Y.
For each pair 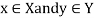 , one the following rule is true-
, one the following rule is true-
1. 
2.
The domain of a relation R is the set of all first elements of the ordered pairs which belongs to R, and range is the second element.
Pictorial representation of relations-
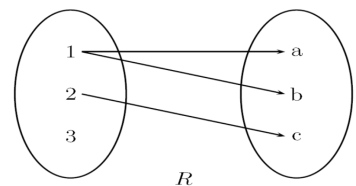
Let A = {1, 2, 3}, B = {a, b, c} and R ={(1, a), (1, b), (2, c)}
Then this relation can be represented as in picture format-
Inverse relation-
Let R be any relation from set X to set Y. The inverse of R is the relation form Y o X which consists of those ordered pairs which, when reversed, belong to R, such that-
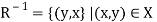
Example- If R = {(1, x),(1, y),(2, z)} then 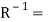 {(x, 1),(y, 1),(z, 2)}
{(x, 1),(y, 1),(z, 2)}
Composition of relations-
Let X, Y and Z are three sets and R be a relation from X to Y and S is a relation from Y to Z.
So that R is a subset of  and S is a subset of
and S is a subset of  .
.
Then R and S give a relation form X to Z which is denoted by RoS,
And can be defined as follows-
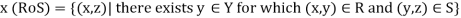
The relation RoS is called the composition of R and S.
Note- If R is a relation on a set A, that is, R is a relation from a set A to itself. Then the composition of R is RoR. Denoted by 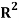 .
.
Types of relations-
1. Reflexive relations
A relation R on a set X is reflexive if xRx for every x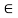 X. That is is (x, x)
X. That is is (x, x)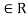 for every x
for every x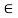 X. Thus R is not reflexive if there exists x
X. Thus R is not reflexive if there exists x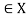 such that (x, x) does not belongs to R.
such that (x, x) does not belongs to R.
2. Symmetric and anti-symmetric relations-
A relation R on a set X is said to be symmetric if whenever xRy then yRx, that is if whenever (x, y)∈R then (y, x)∈R
R is said to be anti-symmetric if (x, y)∈X such that (x, y)∈R but (y, x)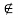 R
R
3. Transitive relation-
A relation R on a set X is said to be transitive if whenever xRy and yRzthen xRz, that is, if whenever (x, y), (y, z)∈R then (x, z)∈R
Equivalence relation-
A relation in a set R is said to be an equivalence relation in A, If R is reflexive, symmetric and transitive.
Irreflexive relation
A relation R on a set A is irreflexive if aRa for every a ∈A
Example-
Let A = {1, 2, 3} and
R = {(1, 2), (2, 3), (3, 1), (2, 1)}
Then the relation R is irreflexive on A.
Asymmetric relation-
A relation R defined on a set A is asymmetric if whenever aRb, then bRa.
Example:
Let A = {a, b, c} and R = {(a, b), (b, c)} be a relation on A. Then R is a symmetric.
Compatible relation-
A relation R in A is said to be a compatible relation if it is reflexive and symmetric.
If R is an equivalence relation on A, then R is compatible relation on A.
Universal relation-
A relation R in a set A is said to be universal relation if
R = A × A
Example:
Let A = {1, 2, 3}, then
R = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
Is a universal relation on A.
Complementary relation-
Let R be a relation from A to B, then the complement of R denoted by R′and is
Expressed in terms of R as follows;
ARb if a Rb
The inverse of a relation-
Let R be a relation from A to B. Then the relation 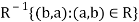 from B to A is called the inverse of R.
from B to A is called the inverse of R.
Example-1: A = {2, 3}, B = {3, 4, 5, 6} and R is a relation from A to B defined as follows-
(a, b) ∈R if “a divides b” write the solution set of R.
Sol: 2 divides 4 and 2 divides 6
⇒(2, 4) ∈R and (2, 6) ∈R
3 divides 3, 3 divides 6
⇒(3, 3) ∈R and (3, 6) ∈R
4 divides 4 ⇒(4, 4) ∈R
Thus R = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}
Example-2: Let Z denote the set of integers and the relation R in Z be defined by “aRb” iffa – b is an even integer”. Then show that R is an equivalence relation.
Sol.
1. R is reflexive; since
∅ = a −a is even, hence aRa for every a∈Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa
3. R is transitive: for if aRb and bRc then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴aRb and bRc⇒aR c
Thus, R is an equivalence relation.
Equivalence relations
Definition-
A relation R in a set A is said to be an equivalence relation in A, if R is reflexive, symmetric and transitive.
Example- Let A = {a, b, c}, and R = {(a, a), (a, b), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)} then R is an equivalence relation in A.
Transitive closure of relations
Let R be a relation on the set A. 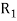 denote the transitive extension of R,
denote the transitive extension of R, 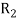 denote the transitive extension of
denote the transitive extension of 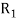 and in general
and in general 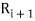 denote the transitive extension of
denote the transitive extension of 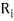 then the transitive closure of R is defined as the set union of R,
then the transitive closure of R is defined as the set union of R, 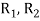 ,
,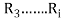 ,
,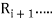 It is denoted by
It is denoted by 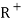
Thus
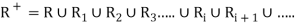
Example: Let A = {1, 2, 3, 4} and B = {a, b, c, d, e, f} consider the relation
R = {(1, a), (1, c), (1, e), (2, b), (2, d), (2, f), (3, c), (3, d), (4, a), (4, f)}
Let 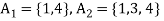 then
then 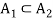
And
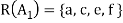
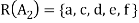
Clearly-

Thus,
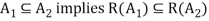
Partial ordering relations
Partial orderings-
A relation R on a set Sis called a partial order relation in Sif R is, Reflexive Anti-symmetric and transitive.
A set S together with a partial ordering R is called a partially ordered set.
We denote a partial order relation by the symbol ≤.
Comparability-
Suppose R be a partial order on Sand a, b ∈S whenever aRb or bRa, we say that a A a and b are comparable otherwise a And b are non-comparable.
Dual order-
If ≤is a partial order on a set S, then the converse of R is also a partial order on S. That means if ≤is a partial ordering on S, then ≥is also a partial ordering on S. (S, ≥) is called the dual of (S, ≤).
Partitions-
Let S be a set which is non-empty. Then the collection 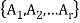 of subset of S is said to be a partition of S if-
of subset of S is said to be a partition of S if-
1. 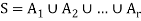
2. For any 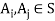
Either 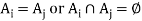
Cross partition-
If 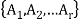 and
and 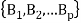 both are partition of set S which is non-empty, then
both are partition of set S which is non-empty, then 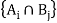 forms a partition of S
forms a partition of S
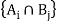 is called a cross partition of S.
is called a cross partition of S.
Ordered partition-
A partition a non-empty set is called an ordered partition of S if there is a specified order on the subsets of S.
An ordered t-tuple of sets 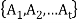 is called a t-part ordered partition if the sets
is called a t-part ordered partition if the sets 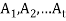 form a partition of S.
form a partition of S.
Theorem-
The number ‘m’ of ordered partitions of a set S with ‘n’ elements into r cells 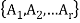 , where for each ‘i’, n(
, where for each ‘i’, n(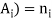 – follows-
– follows-
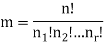
Example:
Find the number of ways to partition of 10 peoples into four groups 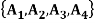
So that two teams contain 3 persons and two teams contain 2 persons.
Sol.
By using above theorem, we get-
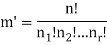
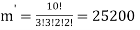 ordered partitions
ordered partitions
Here the group form an unordered partition so that we divide m’ by 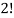 Because of the two cells with three elements each and
Because of the two cells with three elements each and 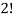 Because of the two cells with two elements each.
Because of the two cells with two elements each.
So that-
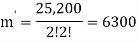
Example: There are 12 employees in a company. Find the number of ways that the 12 employees do three different tasks if four employees are to take each task.
Sol.
Here we find the number of ordered partitions of twelve employees into cells containing 4 employees each.
There are total - 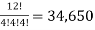 partitions
partitions
Hence the required number of ways, the employees can do the task is 34,650.
Axiom of choice and well ordering theorem:
There exists a choice functions for any non-empty collection of non-empty sets.
Let 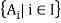 be a collection of nonempty disjoint sets. We assume every
be a collection of nonempty disjoint sets. We assume every 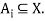
A function 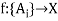 is called a choice function if
is called a choice function if 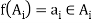 .
.
In other words, f “chooses” a point 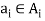 for each set Ai.
for each set Ai.
The axiom of choice lies at the foundations of mathematics and, in particular, the theory of sets. This “innocent looking” axiom, which follows, has as a consequence some of the most powerful and important results in mathematics.
Well ordering theorem:
Every set A can be well-ordered.
Zorn’s lemma:
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory. It states that a partially ordered set containing upper bounds for every chain necessarily contains at least one maximal element. The lemma was proved by Kazimierz Kuratowski in 1922 and independently by Max Zorn in 1935.
Zorn's lemma is equivalent to the well-ordering theorem and also to the axiom of choice, in the sense that within ZF (Zermelo–Fraenkel set theory without the axiom of choice) any one of the three is sufficient to prove the other two. An earlier formulation of Zorn's lemma is Hausdorff's maximum principle which states that every totally ordered subset of a given partially ordered set is contained in a maximal totally ordered subset of that partially ordered set.
Zorn's lemma can then be stated as:
Suppose a partially ordered set P has the property that every chain in P has an upper bound in P. Then the set P contains at least one maximal element.
Zorn's lemma (for non-empty sets) — Suppose a non-empty partially ordered set P has the property that every non-empty chain has an upper bound in P. Then the set P contains at least one maximal element.
Key takeaways-
- Suppose we have two sets X and Y. The set of all ordered pairs (x, y) where
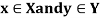 is called the Cartesian product of X and Y.
is called the Cartesian product of X and Y. - Let R be any relation from set X to set Y. The inverse of R is the relation form Y o X which consists of those ordered pairs which, when reversed, belong to R, such that-
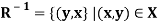
3. A relation R on a set X is reflexive if xRx for every x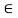 X. That is is (x, x)
X. That is is (x, x)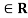 for every x
for every x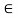 X. Thus R is not reflexive if there exists x
X. Thus R is not reflexive if there exists x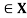 such that (x, x) does not belongs to R.
such that (x, x) does not belongs to R.
4. A relation R on a set X is said to be transitive if whenever xRy and yRz then xRz, that is, if whenever (x, y), (y, z)∈R then (x, z)∈R
5. A relation R defined on a set A is asymmetric if whenever aRb, then bRa.
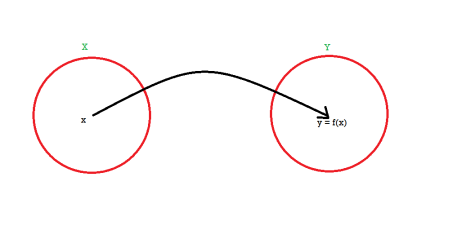
Let X and Y are two sets. A relation f from X to Y is said to be a function if for every x ∈ X there is a unique element y ∈ Y, such that (x, y) ∈ X
We denote it as f: X → Y, which means f is a function from X to Y.
We represent the function as-
Example: Let 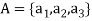 and
and 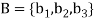
And 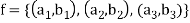
Hence the function can be represented as-
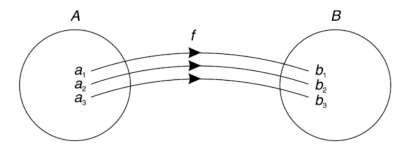
Here A is called the domain of f and B is called the co-domain of f
Surjective function (Onto-Mapping)-
A mapping 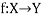 is said to be onto-mapping if the range set
is said to be onto-mapping if the range set 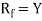
If 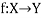 is onto then each element of B if f-image of at least one element of X.
is onto then each element of B if f-image of at least one element of X.
That means.
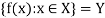
A mapping is said to be into if it is not onto.
Injective function (One-To-One Mapping)-
A mapping 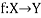 is said to be one-to-one mapping if distinct elements of X are mapped into distinct elements of Y.
is said to be one-to-one mapping if distinct elements of X are mapped into distinct elements of Y.
That means if f is a one-to-one mapping, then-
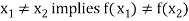
Or
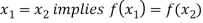
Bijective functions (One-To-One, Onto)-
A mapping 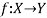 is said to be bijective mapping if it is both one-to-one and onto.
is said to be bijective mapping if it is both one-to-one and onto.
Identity function (Identity Mapping)-
If 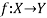 is a function such that every element of X is mapped onto itself then f is said to be an identity mapping.
is a function such that every element of X is mapped onto itself then f is said to be an identity mapping.
We denote identity mapping by 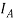 .
.
If 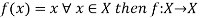 is an identity mapping.
is an identity mapping.
Partial functions-
Let X and Y be sets and A be a subset of X. A function f from A to Y is called a partial function from X to Y. The set A is a called the domain of f.
Constant function-
Let 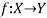 then f is said to be a constant function if every element of X is mapped onto the same element of Y.
then f is said to be a constant function if every element of X is mapped onto the same element of Y.
Inverse functions-
Let 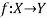 is a one-one and onto mapping, then
is a one-one and onto mapping, then 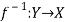 is called the inverse mapping of f.
is called the inverse mapping of f.
Inverse mapping can be defined as-
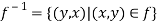
Example-1: Prove that 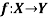 is both one-one and onto then
is both one-one and onto then 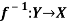 is both one-one and onto.
is both one-one and onto.
Sol.
Let f: X→Y be both one-one and onto.
Then there exist elements 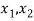 ∈X, and elements
∈X, and elements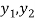 ∈Y
∈Y
Such that
f(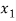 ) =
) = 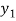 , and f (
, and f (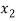 ) =
) =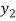
Or
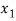 =
= 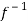 (
(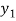 ) and
) and 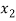 =
= 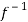 (
(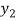 )
)
Now,
Let 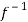 (
(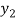 ) =
) =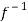 (
(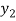 ), then
), then
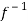 (
(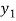 ) =
) =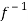 (
(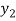 )
)
⇒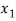 =
= 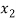
⇒f(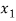 ) = f (
) = f (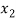 )
)
⇒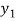 =
= 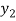
Thus 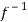 is one-one
is one-one
Since f is onto, for y∈Y, there is some element x∈X, such that f (x) = y.
Now
f(x) = y
⇒x= 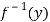
So that 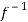 is onto.
is onto.
Hence 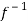 is both one-one and onto.
is both one-one and onto.
Composition of Functions
Let 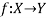 and
and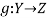 are two mappings, then the composition of these two mappings f and g is denoted by gof is the mapping from X into Z.
are two mappings, then the composition of these two mappings f and g is denoted by gof is the mapping from X into Z.
It is defined as-
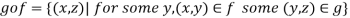
That means 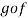 is a mapping defined as below-
is a mapping defined as below-
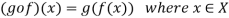
Example-1: Show that the inverse of an invertible mapping is unique.
Sol
Let 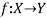
By any invertible mapping,
Let,
g: Y→X
h: Y→X
Are two different inverse mapping of f.
Let y ∈ Y and
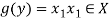
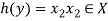
Now-
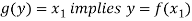
And
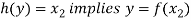
So that-
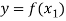 and
and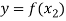
Now-
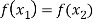
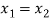
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Example-2: Prove that 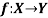 is both one-one and onto then
is both one-one and onto then 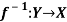 is both one-one and onto.
is both one-one and onto.
Sol.
Let f: X→Y be both one-one and onto.
Then there exist elements 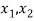 ∈X, and elements
∈X, and elements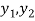 ∈Y
∈Y
Such that
f(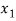 ) =
) = 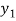 , and f (
, and f (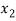 ) =
) =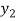
Or
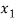 =
= 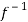 (
(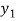 ) and
) and 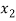 =
= 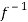 (
(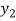 )
)
Now,
Let 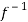 (
(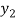 ) =
) =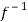 (
(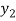 ), then
), then
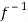 (
(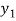 ) =
) =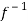 (
(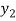 )
)
⇒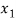 =
= 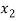
⇒f(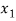 ) = f (
) = f (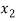 )
)
⇒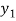 =
= 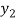
Thus 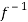 is one-one
is one-one
Since f is onto, for y∈Y, there is some element x∈X, such that f (x) = y.
Now
f(x) = y
⇒x= 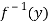
So that 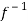 is onto.
is onto.
Hence 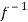 is both one-one and onto.
is both one-one and onto.
Invertible function-
A function f from a set X to a set Y is said to be a invertible function if there exists a function g from Y to X, such that-
f(g(y)) = y
And
g(f(x)) = x
For every x ∈ X and y∈ Y
Example-1: Show that the inverse of an invertible mapping is unique.
Sol
Let 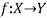
By any invertible mapping,
Let,
g: Y→X
h: Y→X
Are two different inverse mapping of f.
Let y ∈ Y and
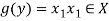
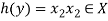
Now-
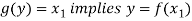
And
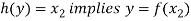
So that-
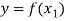 and
and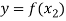
Now-
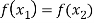
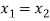
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Recursive Functions
Definition-
A function f is said to be Primitive recursive if it can be obtained from the initial functions by a finite number of operations of composition and recursion.
Example: Show that addition is primitive recursive.
Sol.
Addition is defined by a + 0 = a, a + (b + 1) = (a + b) + 1 for all natural numbers a a, b.
We define f (a, b) = a + b such that
f (a, b + 1) = a + b + 1 = (a + b) + 1
= f (a, b) + 1
= S (f (a, b))
Also f (a, 0) = a
We define f (a, b) as
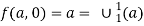
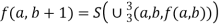
If follows that f comes from primitive recursion from 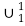 and
and 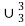 so that f is primitive recursive.
so that f is primitive recursive.
Characteristic function of a set:
Let U be a universal set and A be a subset of U. Then the function
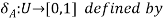
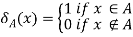
Is called a characteristic function of the set A.
Properties of characteristic function:
Let A and B be any two subsets of a universal set U. Then the following properties hold for all x 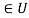 :
:
1. 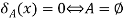
2. 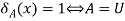
3. 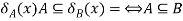
4. 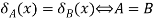
5. 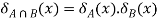
6. 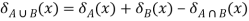
7. 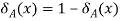
8. 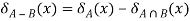
The operations I, =, +, . And –, used above are the usual arithmetical operations.
The values of characteristic functions are always either 1 or 0. The properties (1) to (8) can easily be
Proved using the definition of characteristic functions.
Set identities can also be proved by using the properties characteristic functions.
Example: Show that 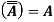
Sol:
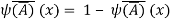
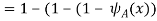
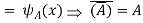
Example: f: R 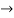 R is defined by f (x) = a x + b, where a, b, x
R is defined by f (x) = a x + b, where a, b, x 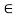 R and a
R and a 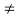 0.
0.
Show that f is invertible and find the inverse of f.
Sol:
Firstly, we shall show that f is one-to-one.
Let 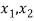
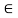 R such that f (
R such that f (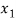 ) = f (
) = f (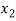 )
)
a x1 + b = ax2 + b
ax1 = ax2
x1 = x2
Thus f is one-one
To show that f is onto
Let y 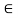 R such that y = f (x)
R such that y = f (x)
y = ax + b
ax = y - b
i.e., given y 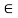 R , there exists an element
R , there exists an element
x = 1/a (y – b) ∈ R, such that f(x) = y
This proves that f is onto
Hence f is one-one and onto
Hence f is invertible and
f-1(y) = 1/a (y – b)
Example: Let U = {a, b, c, d, e, f } and A = {a, d, e} then find XA, where XA denotes the characteristic function of A.
Sol:
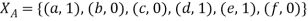
Since a 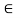 A
A 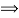
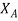 (a) = 1, d
(a) = 1, d 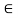 A
A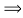 XA (d ) = 1, and e
XA (d ) = 1, and e 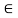 A
A 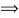
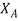 (e) = 1, b, c, f are not the
(e) = 1, b, c, f are not the
Members of A,
Thus
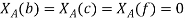
Cardinals and ordinals:
Cardinality:
Two sets A and B are said to be equipotent, or to have the same number of elements or the same cardinality, written A 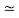 B, if there exists a one-to-one correspondence f : A → B. A set A is finite if A is empty or if A has the same cardinality as the set {1, 2, . . . , n} for some positive integer n. A set is infinite if it is not finite.
B, if there exists a one-to-one correspondence f : A → B. A set A is finite if A is empty or if A has the same cardinality as the set {1, 2, . . . , n} for some positive integer n. A set is infinite if it is not finite.
Familiar examples of infinite sets are the natural numbers N, the integers Z, the rational numbers Q, and the real numbers R.
Here you will be introduced to the idea of “cardinal numbers”. We will consider cardinal numbers simply as symbols assigned to sets in such a way that two sets are assigned the same symbol if and only if they have the same cardinality. The cardinal number of a set A is commonly denoted by |A|, n(A), or card (A). We will use |A|.
The obvious symbols are used for the cardinality of finite sets. That is, 0 is assigned to the empty set ∅, and n is assigned to the set {1, 2, . . . , n}. Thus |A| = n if and only if A has n elements. For example,
|{x, y, z}| = 3 and |{1, 3, 5, 7, 9}| = 5
The cardinal number of the infinite set N of positive integers is ℵ0 (“aleph-naught”). This symbol was introduced by Cantor. Thus |A| = ℵ0 if and only if A has the same cardinality as N.
Example: Let E = {2, 4, 6, . . .}, the set of even positive integers. The function f : N → E defined by f (n) = 2n is a one-to-one correspondence between the positive integers N and E. Thus E has the same cardinality as N and so we may write
|E| = ℵ0
A set with cardinality ℵ0 is said to be denumerable or countably infinite.
A set which is finite or denumerable is said to be countable. One can show that the set Q of rational numbers is countable.
Theorem: A countable union of countable sets is countable.
That is, if 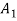
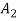 , . . . Are each countable sets, then the following union is countable:
, . . . Are each countable sets, then the following union is countable:
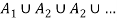
Theorem: The set I of all real numbers between 0 and 1 is uncountable.
Inequalities and Cardinal Numbers:
One also wants to compare the size of two sets. This is done by means of an inequality relation which is defined for cardinal numbers as follows. For any sets A and B, we define |A| ≤ |B| if there exists a function f: A → B which is one-to-one.We also write
|A| < |B| if |A| ≤ |B| but |A| 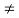 |B|
|B|
Cantor’s theorem: For any set A, we have |A| < |Power (A)| (where Power (A) is the power set of A, i.e., the collection of all subsets of A).
Countable and uncountable sets
A set S is said to be countable if it is either a finite set or countably infinite set.
A set is said to be uncountable otherwise.
Example-
Suppose we have a set of even natural numbers N = {2n: n∈N }. We can find a Bijection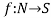 with the formula
with the formula 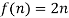 . So we can say that the set is Countably infinite and also countable.
. So we can say that the set is Countably infinite and also countable.
The set of odd natural numbers is also countably infinite.
Countably infinite and uncountably infinite sets-
Any set which can be put in a one-to-one correspondence with integers so that the prescription can be given for identifying its members one at a time is called a countably infinite set.
Any set which cannot be put in a one-to-one correspondence with integers is said to be uncountably infinite set.
Statements and compound statements:
A statement is a declarative statement which is true or false, but not both. Consider, for example, the following six sentences-
(i) Ice floats in water. (iii) 3 + 3 = 6 (v) Where are you going?
(ii) India is in Europe. (iv) 4 + 4 = 9 (vi) Do your homework.
The first four are propositions, the last two are not. Also, (i) and (iii) are true, but (ii) and (iv) are false.
In other words:
Statement-
When a declarative sentence which is true or false but not both is called statement
The truth values “true” and “false” of a statement are denoted by T ad F respectively. We can denote them by 0 and 1 as well.
Examples of statements are-
1. 2 + 11 = 12
2. Jaipur is in India
Compound statement (preposition):
Many propositions are composite, that is, composed of sub propositions and various connectives discussed subsequently. Such composite propositions are called compound propositions.
A proposition is said to be primitive if it cannot be broken down into simpler propositions, that is, if it is not composite.
For example, the above propositions (i) through (iv) are primitive propositions. On the other hand, the following two propositions are composite:
“Roses are red and violets are blue.” and “Vinay is smart or he studies every night.”
Statements can be connected by words like ‘not’, ‘and’, etc.
These words are known as logical connectives. The statements which do not contain any of the connectives are called atomic statements or simple statements.
The common connectives used are: negation (~) [or (¬)], and (∧) or (∨), if ... Then (→), if and only if (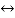 ), equivalence (≡) or (⇔). We will use these connectives along with symbols to combine various simple statements.
), equivalence (≡) or (⇔). We will use these connectives along with symbols to combine various simple statements.
Note- The fundamental property of a compound proposition is that its truth value is completely determined by the truth values of its sub-propositions together with the way in which they are connected to form the compound propositions.
Key takeaways
- Let X and Y are two sets. A relation f from X to Y is said to be a function if for every x ∈ X there is a unique element y ∈ Y, such that (x, y) ∈ X
- A mapping
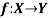 is said to be onto-mapping if the range set
is said to be onto-mapping if the range set 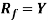
- A mapping
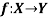 is said to be one-to-one mapping if distinct elements of X are mapped into distinct elements of Y.
is said to be one-to-one mapping if distinct elements of X are mapped into distinct elements of Y. - Let X and Y be sets and A be a subset of X. A function f from A to Y is called a partial function from X to Y. The set A is a called the domain of f.
Proofs in mathematics:
Here we will understand about the proof: So what is proof?
If we want a mathematical statement to be accepted as true, we would need to provide mathematically acceptable evidence to support it. This means that we would need to show that the statement is universally true. And this would be done in the form of a logically valid argument.
Definition: An argument (in mathematics or logic) is a finite sequence of statements 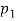 , · · · ,
, · · · , 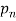 , p such that (p1 ∧ p2 ∧· · · ∧ p) → p.
, p such that (p1 ∧ p2 ∧· · · ∧ p) → p.
Each statement in the sequence, p1 , p2 , . . . , pn is called a premise (or an assumption, or a hypothesis). The final statement p is called the conclusion.
Other definitions:
We say that a proposition p follows logically from propositions p1 , p2 , · · ·, pn if p must be true whenever p1 , p2, · · · , pn are true, i.e., (p1 ∧ p2 ∧ · · · ∧pn ) ⇒ p.
[Here, note the use of the implication arrow ⇒'. For any two propositions r and s, r ⇒ s' denotes ‘s is true whenever r is true.’ Note that, using the contrapositive, this also denotes r is false whenever s is false'. Thus r → s' and r ⇒ s' are different except when both r and s are true or both are false.]
A proof of a proposition p is a mathematical argument consisting of a sequence of statements p1 , p2 , · · · , pn from which p logically follows. So, p is the conclusion of this argument.
The statement that is proved to be true is called a theorem.
Note- Sometimes, instead of showing that a statement p is true, we try to prove that it is false, i.e., that ∼ p is true. Such a proof is called a disproof of p.
Sometimes it happens that we feel a certain statement is true, but we don't succeed in proving it. It may also happen that we can't disprove it. Such statements are called conjectures. If and when a conjecture is proved, it would be called a theorem. If it is disproved, then its negative will be a theorem!
There’s a very famous conjecture which was made by a mathematician Goldbach in 1742. He stated that :
For every n ∈ N. If n is even and n > 2, then n is the sum of two primes.
To this day, no one has been able to prove it or disprove it. To disprove it several people have hunting for an example for which the statement is not true, i.e., an even number n>2 such that n cannot be written as the sum of two prime numbers.
A mathematical proof of a statement consists of one or more premises. These premises could be of four types:
i) A proposition that has been proved earlier (e.g., to prove that the complex roots of a polynomial in R[x] occur in pairs, we use the division algorithm); or
Ii) A proposition that follows logically from the earlier propositions or
Iii) A mathematical fact that has never been proved, but is universally accepted as true (e.g., two points determine a line). Such a fact is called an axiom (or a postulate);
Iv) The definition of a mathematical term (e.g., assuming the definition of ‘⊆’ in the proof of A ∩ B ⊆A).
Let’s do an example of a sequence of statements that will not form a valid argument. Consider the following sequence.
If Amit sees the movie, she won’t finish her homework.
Amit won’t finish her homework.
Therefore, Amit sees the movie.
Looking at the argument, can you say whether it is valid or not? Intuitively you may feel that the argument isn’t valid. But, is there a formal logical tool that you can apply check if your intuition is correct? What about truth tables? Let’s see.
The given argument is of the form
[(p → q) ∧ q] ⇒ p, where
p: Amit sees the movie, and
q: Amit won’t finish here homework.
Lets make the truth table-
p | q | p → q | (p → q) ∧ q |
T | T | T | T |
T | F | F | F |
F | T | T | T |
F | F | T | F |
This last column gives the truth values of the premises. The first column given corresponding truth values of the conclusion. Now, the argument will only be valid if whenever both the premises are true, the conclusion is true. This happens in the first row, but not in the third row. Therefore, the argument is not valid.
Different methods of proof:
Direct Proof:
A direct proof of p ⇒ q is a logically valid argument that begins with the assumptions that p is true and, in one or more applications of the law of detachment, concludes that q must be true.
So, to construct a direct proof of p ⇒ q, we start by assuming that p is true. Then, in one or more steps of the form p ⇒ q1, q1⇒ q2, ……., qn ⇒ q, we conclude that q is true.
Example: Give a direct proof of the statement ‘The product of two odd integers is odd’.
Sol:
Let us clearly analyse what our hypotheses are, and what we have to prove.
We start by considering any two odd integers x and y. So our hypothesis is p: x and y are odd.
The conclusion we want to reach is
q : xy is odd.
Let us first prove that p ⇒ q.
Since x is odd, x = 2m + 1 for some integer m.
Similarly, y = 2n + 1 for some integer n.
Then xy = (2m + 1) (2n + 1) = 2(2mn + m + n) +1
Therefore, xy is odd.
So we have shown that p ⇒ q.
Now we can apply modus ponens to p ∧ ( p ⇒ q) to get the required conclusion.
Note- the essence of this direct proof lies in showing p ⇒ q.
Example: Give a direct proof of the theorem ‘The square of an even integer is an even integer.’
Sol:
First of all, let us write the given statement symbolically, as
(∀ x ∈ Z)(p(x) ⇒ q(x))
Where p(x) : x is even, and
q(x) : x2 is even, i.e., q(x) is the same as p (x2 ).
The direct proof, then goes as follows.
Let x be an even number (i.e., we assume p(x) is true).
Then x = 2n, for some integer n (we apply the definition of an even number).
Then x2 = (2n)2 = 4n2 = 2(2n2).
x2 is even (i.e., q (x) is true).
Indirect Proofs:
Proof by contrapositive:
In the first method, we use the fact that the proposition p ⇒ q is logically equivalent to its contrapositive (~ q ⇒ ~ p),
i.e.,
(p ⇒ q) ≡ ( ~ q ⇒ ~ p).
For instance, ‘If Shreya does not agree with communalists, then she is not orthodox.’ is the same as ‘If Shreya is orthodox, then she agrees with communalists.’.
Because of this equivalence, to prove p ⇒ q, we can, instead, prove ~ q ⇒ ~ p. This means that we can assume that ~ q is true, and then try to prove that ~ p is true. In other words, what we do to prove p ⇒ q in this method is to assume that q is false and then show that p is false.
Example: Prove that ‘If x, y ∈ Z such that xy is odd, then both x and y are odd.’, by proving its contrapositive.
Sol:
Let us name the statements involved as below.
p : xy is odd
q : both x and y are odd.
So,
~ p : xy is even, and
~ q : x is even or y is even, or both are even.
We want to prove p ⇒ q, by proving that ~ q ⇒ ~ p. So we start by assuming that ~ q is true, i.e., we suppose that x is even.
The x = 2n for some n ∈ N.
Therefore, xy = 2ny.
Therefore xy is even, by definition.
That is, ~ p is true.
So, we have shown that ~ q ⇒ ~p. Therefore, p ⇒ q.
Proof by contradiction:
In this method, to prove q is true, we start by assuming that q is false (i.e., ~ q is true). Then, by a logical argument we arrive at a situation where a statement is true as well as false, i.e., we reach a contradiction r ∧ ~ r for some statement that is always false. This can only happen when ~ q is false also. Therefore, q must be true.
Example: Show that 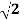 is an irrational number.
is an irrational number.
Sol:
Let us try and prove the given statement by contradiction. For this, we begin by assuming that 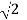 is rational. This means that there exist positive integers a and b such that
is rational. This means that there exist positive integers a and b such that 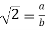 , where a and b have no common factors.
, where a and b have no common factors.
This implies:
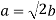
a2 = 2b2
⇒ a |2 2 ⇒ 2|a
Therefore, by definition, a = 5c for some c ∈ Z.
Therefore,
a2 = 4c2.
But a 2 = 2b2 also.
So 4c2 = 2b2 ⇒ 2c2 = b2 ⇒ 2| b2 ⇒2|b.
But now we find that 5 divides both a and b, which contradicts our earlier assumption that a and b have no common factor.
Therefore, we conclude that our assumption that 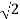 is rational is false, i.e,
is rational is false, i.e, 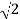 is irrational.
is irrational.
Truth table
The table showing the truth values of a statement formula is called ‘truth table’.
The truth table for a given statement form displays the truth values that correspond to all possible combinations of truth values for its component statement variables.
Laws of formal-
1. Law of contradiction- According to the law of contradiction the same predicate cannot be both affirmed and denied precisely of the same subject
For every preposition p is not the same that p is both true and false.
2. Law of excluded middle- If p is a statement, then either p is true or p is false and there cannot be middle ground.
Connectives-
Statements in mathematical logic are combinations of simpler statements joined by words and phrases like ‘and’. ‘or’, ‘if and only if’, etc. These words and phrases are called logical connectives.
Disjunction-
Definition: The disjunction of two propositions p and q is the compound statement 10 Elementary Logic p or q, denoted by p ∨ q.
For example, ‘Aman has a house or Amit has a house’ Is the disjunction of p and q, where-
p: Aman has a house, and
q: Amit has a house.
Example: Obtain the truth value of the disjunction of ‘The earth is flat’. And ‘3 + 5 = 2’.
Solution: Let p denote ‘The earth is flat,’ and q denote ‘3 + 5 = 2’. Then we know that the truth values of both p and q are F. Therefore, the truth value of p ∨ q is F.
Example-Let p: 5 + 2 = 7, q: 9 + 2 = 10 then p ∨q: 5 + 2 = 7 or 9 + 2 = 10
Truth table for disjunction-
p | q | p ∨ q |
T T F F | T F T F | T T T F |
Exclusive disjunction-
The exclusive disjunction of two propositions p and q is the statement ‘Either p is true or q is true, but both are not true. Either p is true or q is true, but both are not true’. We denote this by p ⊕q.
Conjunction-
Definition: We call the compound statement ‘p and q’ the conjunction of the
Statements p and q. We denote this by p ∧q.
Example- ‘3 + 1 ≠ 7 ∧ 2 > 0’ is the conjunction of ‘3 + 1 ≠ 7’ and ‘2 > 0’.
p | q | p ∧ q |
T T F F | T F T F | T F F f |
Example-
Obtain the truth value of the conjunction of ‘2 ÷5 = 1’ and ‘Ramesh is in Jaipur’.
Solution: Let p: 2 ÷5 = 1, and
q:Ramesh is in Jaipur.
Then the truth value of p is F. Therefore, from Table 3 you will find that the truth
Value of p ∧ q is F.
Negation-
The negation of a proposition p is ‘not p’, denoted by ~p.
Example-
If p is ‘Smriti is at the station.’, then ~ p is ‘Smriti is not at the station’.
Similarly, if p is ‘No person can live without food.’,~ p is ‘At least one person can live without food.’
Conditional connectives-
Given any two propositions p and q, we denote the statement ‘If p, then q’ by
p→ q. We also read this as ‘p implies q’. Or ‘p is sufficient for q’, or ‘p only if q’. We also call p the hypothesis and q the conclusion. Further, a statement of the form p → q is called a conditional statement.
Truth table for implication-
p | q | p q |
T T F F | T F T F | T F T T |
Definition for converse-
The converse of p → q is q → p. In this case we also say ‘p is necessary for q’, or ‘p if q’ when we combine an implication and its converse, then-
Let p and q be two propositions. The compound statement
(p→ q) ∧(q → p) is the bi-conditional of p and q. We denote it by p ↔ q, and
(Read) as ‘p if and only q’.
We use ‘if and only ‘if’ as iff
We also say that ‘p implies and is implied by q’. Or ‘p is necessary and sufficient for q’.
Example- Pradeep will get good marks if and only if he studies regularly means that Pradeep will get good marks if he studies regularly and Pradeep studies regularly if he gets good marks.
Truth table for two-way implication-
p | q | p q | qp | p↔q |
T T F F | T F T F | T F T T | T T F T | T F F T |
Algebra of propositions and logical arguments
A proposition (or statement) is a declarative statement which is true or false, but not both.
Example-
(i) Ice floats in water.
(ii) China is in Europe
(iii) 2 + 2 = 4
(iv) 2 + 2 = 5
Compound proposition-
Many propositions are composite, that is, composed of sub-propositions and various connectives discussed
Subsequently such composite propositions are called compound Propositions. A proposition is said to be primitive if it cannot be broken down into simpler propositions, that is, if it is not composite.
Following two propositions are composite:
“Roses are red and violets are blue.” and “John is smart or he studies every night.”
Basic logical operations-
1. Conjunction- p ⋀ q
Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,
p∧q
Read “p and q,” denotes the conjunction of p and q. Since p ∧q is a proposition it has a truth value, and this truth
Value depends only on the truth values of p and q.
Note- If p and q are true, then p ∧q is true; otherwise p ∧q is false.
2. Disjunction, p ∨q
Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,
p∨q
Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨q depends only on the truth values of p
And q as follows-
If p and q are false, then p ∨q is false; otherwise p ∨q is true
Negation-
Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by
¬p
The truth value of ¬p depends on the truth value of p as follows-
If p is true, then ¬p is false; and if p is false, then ¬p is true
Conditional and bi-conditional statement-
The statements are of the form “if p then q”. Such statements are called conditional statement and these are denoted by-
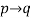
We read it as p implies q.
And another statement is of the form “p if and only if q”, such statement are called bi-conditional statement and it is denoted by-
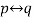
The truth value for conditional and bi-conditional value are given in the following tables-
p | q | p q |
T T F F | T F T F | T F T T |
p | q | p ↔ q |
T T F F | T F T F | T F F T |
Logical equivalences
Two propositions P(p, q, . . .)and Q(p, q, . . .) are said to be logically equivalent, or simply equivalent and denoted by
P(p, q, . . .) ≡Q(p, q, . . .)
Note- the prepositions are logically equivalent.
Prepositions and truth tables-
Suppose P(p, q, . . .) denote an expression constructed from logical variables p, q, . . ., which take on the value T or F which are true and false, and the logical connectives ∧, ∨, and ¬and others. Such an expression P(p, q, . . .) will be called a proposition.
The main property of a proposition P(p, q, . . .) is that its truth value depends exclusively upon the truth values of its variables, that is, the truth value of a proposition is known once the truth value of each of its variables
Is known. A simple concise way to show this relationship is through a truth table
A | B | A∨B |
True | True | True |
True | False | True |
False | True | True |
False | False | False |
A | B | A∧B |
True | True | True |
True | False | False |
False | True | False |
False | False | False |
A | ¬A |
True | False |
False | True |
Laws of prepositions-
The prepositions satisfy the following rules
Idempotent laws: | (1a) p ∨ p ≡ p | (1b) p ∧ p ≡ p |
Associative laws: | (2a) (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) | (2b) (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) |
Commutative laws: | (3a) p ∨ q ≡ q ∨ p | (3b) p ∧ q ≡ q ∧ p |
Distributive laws: | (4a) p ∨ (q ∧ r) ≡ q ∨ p | (4b) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) |
Identity laws: | (5a) p ∨ F ≡ p (6a) p ∨ T ≡ T | (5b) p ∧ T ≡ p (6b) p ∧ F ≡ F |
Involution laws: | (7) ¬¬ p ≡ p |
|
Complement laws: | (8a) p ∨ ¬p ≡ T (9a) ¬ T ≡ F | (8b) p ∧ ¬p ≡ T (9b) ¬F ≡ T |
DeMorgan’s laws: | (10a) ¬(p∨q) ≡ ¬p ∧ ¬q | (10b) ¬(p ∧ q) ≡ ¬ p ∨ ¬ q |
Tautologies-
A tautology is a formula which is always true for every value of its propositional variables-
Contradiction-
A Contradiction is a formula which is always false for every value of its propositional variables.
Contingency-
A Contingency is a formula which has both some true and some false values for every value of its propositional variables.
Validity of arguments by using truth tables
An argument is an assertion that is given set of prepositions 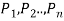 called premises, yields another preposition Q, called conclusion.
called premises, yields another preposition Q, called conclusion.
Such an argument is denoted by-
P1, P2, …, Pn ⊢ Q
The notion of a “logical argument” is defined as follows-
The argument P1, P2, …, Pn ⊢ Q is said to be valid if Q is true whenever all the premises 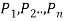 are true.
are true.
Note- An argument which is not valid is called fallacy.
Example: the following argument is valid-
p, p q ⊢ q
The proof of this rule follows from the truth table given below-
p | q | p q |
T T F F | T F T F | T F T T |
Consider an example-
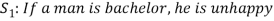
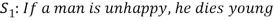
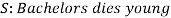
Here S denotes the conclusion of the argument and statements 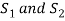 are the premises.
are the premises.
Here we claim the argument 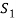 , S2 ⊢ S is valid
, S2 ⊢ S is valid
Well-ordering property of positive integers:
Theorem: Let S be a nonempty set of positive integers. Then S contains a least element.
Suppose S has no least element. Let M consist of those positive integers which are less than every element of S.
Then 1 ∈ M; otherwise, 1 ∈ S and 1 would be a least element of S. Suppose k ∈ M. Then k is less than every element of S. Therefore k + 1 ∈ M; otherwise k + 1 would be a least element of S.
By the Principle of Mathematical Induction, M contains every positive integer. Thus S is empty which contradicts the hypothesis that S is nonempty. Accordingly, the original assumption that S has no least element cannot be true.
Thus the theorem is true.
Division algorithm:
Let a and b be integers with b 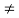 0. Then there exists integers q and r such that
0. Then there exists integers q and r such that
a = bq + r and 0 ≤ r < |b|
Also, the integers q and r are unique.
The number q in the above theorem is called the quotient, and r is called the remainder. We stress the fact that r must be non-negative. The theorem also states that r = a – bq
Division Algorithm using a Calculator:
Suppose a and b are both positive. Then one can find the quotient q and remainder r using a calculator as follows:
Step 1. Divide a by b using the calculator, that is, find a/b.
Step 2. Let q be the integer part of a/b, that is, let q = INT (a/b).
Step 3. Let r be the difference between a and bq, that is, let r = a − bq.
Example: Let a = 4461 and b = 16. We can find that the quotient q = 278 and the remainder r = 13 by long division,
Alternately, using a calculator, we obtain q and r as follows:
a/b = 278.8125 . . . , q = 278, r= 4461 − 16(278) = 13
As expected, a = bq + r, namely:
4461 = 16(278) + 13
Example: Let b = 2. Then any integer a can be written in the form
a = 2q + r where 0 ≤ r < 2
Thus r can only be 0 or 1. Thus every integer is of the form 2k or 2k + 1. The integers of the form 2k are called even integers, while those of the form 2k + 1 are called odd integers.
Divisibility:
Let a and b be integers with a 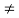 0. Suppose ac = b for some integer c. We then say that a divides b or b is divisible by a, and we denote this by writing
0. Suppose ac = b for some integer c. We then say that a divides b or b is divisible by a, and we denote this by writing
a | b
We also say that b is a multiple of a or that a is a factor or divisor of b. If a does not divide b, we will write a∤ b
Note-
Suppose a, b, c are integers.
(i) If a | b and b | c, then a | c.
(ii) If a | b then, for any integer x, a | bx.
(iii) If a | b and a | c, then a | (b + c) and a|(b − c).
(iv) If a | b and b 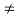 0, then a =
0, then a = 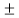 b or |a| < |b|.
b or |a| < |b|.
(v) If a | b and b | a, then |a| = |b|, i.e., a = 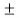 b.
b.
(vi) If a | 1 , then a = 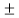 1
1
Note- Suppose a | b and a | c. Then, for any integers x and y, a | (bx +cy). The expression bx +cy will be called a linear combination of b and c.
Primes:
A positive integer p > 1 is called a prime number or a prime if its only divisors are 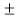 1 and
1 and 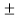 p, that is, if p only has trivial divisors. If n > 1 is not prime, then n is said to be composite.
p, that is, if p only has trivial divisors. If n > 1 is not prime, then n is said to be composite.
Examples:
(a) The integers 2 and 7 are primes, whereas 6 = 2 ・ 3 and 15 = 3 ・ 5 are composite.
(b) The primes less than 50 follow: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47
Note-
1. Every integer n > 1 can be written as a product of primes.
2. There is no largest prime, that is, there exists an infinite number of primes.
Greatest common divisor:
Suppose a and b are integers, not both 0. An integer d is called a common divisor of a and b if d divides both a and b, that is, if d | a and d | b. Note that 1 is a positive common divisor of a and b, and that any common divisor of a and b cannot be greater than |a| or |b|. Thus there exists a largest common divisor of a and b; it is denoted by
Gcd(a, b)
And it is called the greatest common divisor of a and b.
Example: For any prime p, we have gcd(p, a) = p or gcd(p, a) = 1 according as p does or does not divide a.
Example: For any integer a, we have gcd(1, a) = 1.
Note-
1. Let d be the smallest positive integer of the form ax + by. Then
d = gcd(a, b).
2. A positive integer d = gcd(a, b) if and only if d has the following two properties:
(1) d divides both a and b.
(2) If c divides both a and b, then c | d.
Simple properties of the greatest common divisor are:
(a) gcd(a, b) = gcd(b, a).
(b) If x > 0, then gcd(ax, bx) = x ・ gcd(a, b).
(c) If d = gcd(a, b), then gcd(a/d, b/d) = 1.
(d) For any integer x, gcd(a, b) = gcd(a, b + ax).
Euclidean algorithm:
Let a and b be integers, and let d = gcd(a, b). One can always find d by listing all the divisors of a and then all the divisors of b and then choosing the largest common divisor. The complexity of such an algorithm is f (n) = 0(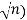 where n = |a| + |b|. Also, we have given no method to find the integers x and y such that
where n = |a| + |b|. Also, we have given no method to find the integers x and y such that
d = ax + by.
This subsection gives a very efficient algorithm, called the Euclidean algorithm, with complexity f (n) = O(log n), for finding d = gcd(a, b) by applying the division algorithm to a and b and then repeatedly applying it to each new quotient and remainder until obtaining a nonzero remainder. The last nonzero remainder is d = gcd(a, b).
Then we give an “unraveling” algorithm which reverses the steps in the Euclidean algorithm to find the integers x and y such that d = xa + yb.
Example: Let a = 540 and b = 168. We apply the Euclidean algorithm to a and b. These s eps, which repeatedly apply the division algorithm to each quotient and remainder until obtaining a zero remainder, are pictured in Fig. using long division and also in Fig. Where the arrows indicate the quotient and remainder in the next step. The last nonzero remainder is 12. Thus
12 = gcd(540, 168)
This follows from the fact that
Gcd(540, 168) = gcd(168, 36) = gcd(36, 24) = gcd(24, 12) = 12
Next we find x and y such that 12 = 540x+168y by “unraveling” the above steps in the Euclidean algorithm.
Specifically, the first three quotients in Fig. Yield the following equations:
(1) 36 = 540 − 3(168), (2) 24 = 168 − 4(36), (3) 12 = 36 − 1(24)
Equation (3) tells us that d = gcd(a, b) = 12 is a linear combination of 36 and 24. Now we use the preceding equations in reverse order to eliminate the other remainders. That is, first we use equation (2) to replace 24 in equation (3) so we can write 12 as a linear combination of 168 and 36 as follows:
(4) 12 = 36 − 1[168 − 4(36)] = 36 − 1(168) + 4(36) = 5(36) − 1(168)
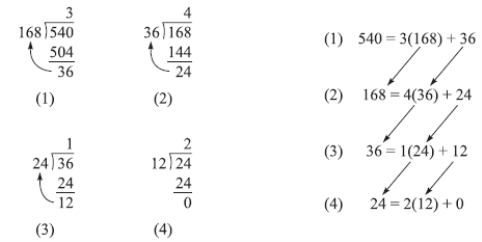
Next we use equation (1) to replace 36 in (4) so we can write 12 as a linear combination of 168 and 540 as follows:
12 = 5[540 − 3(168)] − 1(168) = 5(54) − 15(168) − 1(168) = 5(540) − 16(168)
This is our desired linear combination. In other words, x = 5 and y = −16.
LCM:
Suppose a and b are nonzero integers. Note that |ab| is a positive common multiple of a and b. Thus there exists a smallest positive common multiple of a and b; it is denoted by lcm(a, b) and it is called the least common multiple of a and b.
Examples:
(a) lcm(2, 3) = 6; lcm(4, 6) = 12; lcm(9, 10) = 90.
(b) For any positive integer a, we have lcm(1, a) = a.
(c) For any prime p and any positive integer a, lcm(p, a) = a or lcm(p, a) = ap according as p does or does not divide a.
Note- LCM(a, b) = |ab|/GCD(a, b)
Congruence relation between integers:
Let m be a positive integer. We say that a is congruent to b modulo m. Written
a ≡ b (modulo m) or simply a ≡ b (mod m) if m divides the difference a −b . The integer m is called the modulus. The negation of a ≡ b (mod m) is written
a _≡ b (mod m). For example:
(i) 87 ≡ 23 (mod 4) since 4 divides 87 − 23 = 64.
(ii) 67 ≡ 1 (mod 6) since 6 divides 67 − 1 = 66.
(iii) 72 ≡ −5 (mod 7) since 7 divides 72 − (−5) = 77.
(iv) 27 _≡ 8 (mod 9) since 9 does not divide 27 − 8 = 19.
Theorem:
Let m be a positive integer. Then:
(i) For any integer a, we have a ≡ a (mod m).
(ii) If a ≡ b (mod m), then b ≡ a (mod m).
(iii) If a ≡ b (mod m) and b ≡ c (mod m), then a ≡ c (mod m).
Remark: Suppose m is positive, and a is any integer. By the Division Algorithm, there exist integers q and r with 0 = r ≤ m such that a = mq + r. Hence
Mq = a − r or m| (a − r) or a ≡ r (mod m)
Accordingly:
(1) Any integer a is congruent modulo m to a unique integer in the set
{0, 1, 2, . . . , m − 1}
The uniqueness comes from the fact that m cannot divide the difference of two such integers.
(2) Any two integers a and b are congruent modulo m if and only if they have the same remainder when divided by m.
Residue Classes:
Since congruence modulo m is an equivalence relation, it partitions the set Z of integers into disjoint equivalence classes called the residue classes modulo m. By the above remarks, a residue class consists of all those integers with the same remainder when divided by m. Therefore, there are m such residue classes and each residue class contains exactly one of the integers in the set of possible remainders, that is,
{0, 1, 2, . . . , m − 1}
Generally speaking, a set of m integers {a1, a2, . . . , am} is said to be a complete residue system modulo m if each ai comes from a distinct residue class. (In such a case, each ai is called a representative of its equivalence class.)
Thus the integers from 0 to m−1 form a complete residue system. In fact, any m consecutive integers form a complete residue system modulo m.
The notation [x] m, or simply [x] is used to denote the residue class (modulo m) containing an integer x, that is, those integers which are congruent to x. In other words,
[x] = {a ∈ Z | a ≡ x (mod m)}
Accordingly, the residue classes can be denoted by
[0], [1], [2], . . . , [m − 1]
Or by using any other choice of integers in a complete residue system.
Example: The residue classes modulo m = 6 follow:
[0] = {. . . ,−18,−12,−6, 0, 6, 12, 18, . . .}, |3| = {. . . ,−15,−9,−3, 3, 9, 15, 21, . . .}
[1] = {. . . ,−17,−11,−5, 1, 7, 13, 19, . . .}, |4| = {. . . ,−14,−8,−2, 4, 10, 16, 22, . . .}
[2] = {. . . ,−16,−10,−4, 2, 8, 14, 20, . . .}, |5| = {. . . ,−13,−7,−1, 5, 11, 17, 23, . . .}
Note that {−2,−1, 0, 1, 2, 3} is also a complete residue system modulo m = 6, and these representatives have minimal absolute values.
Congruence Arithmetic:
Theorem:
Suppose a ≡ c (mod m) and b ≡ d (mod m). Then:
(i) a+ b ≡ c + d(mod m);
(ii) (ii) a・ b ≡ c ・ d(mod m)
Note- Suppose p(x) is a polynomial with integral coefficients. If s ≡ t (mod m), then using above Theorem repeatedly we can show that p(s) ≡ p(t) (mod m).
Example: Observe that 2 ≡ 8 (mod 6) and 5 ≡ 41 (mod 6). Then:
(a) 2 + 5 ≡ 8 + 41 (mod 6) or 7 ≡ 49 (mod 6)
(b) 2 ・ 5 ≡ 8 ・ 41 (mod 6) or 10 ≡ 328 (mod 6)
(c) Suppose p(x) = 3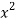 − 7x + 5. Then
− 7x + 5. Then
p(2) = 12 − 14 + 5 = 3 and p(8) = 192 − 56 + 5 = 141
Hence 3 ≡ 141 (mod 6)
Integers Modulo m:
The integers modulo m, denoted by 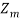 , refers to the set
, refers to the set
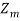 = {0, 1, 2, 3, . . . , m − 1}
= {0, 1, 2, 3, . . . , m − 1}
Where addition and multiplication are defined by the arithmetic modulo m or, in other words, the corresponding operations for the residue classes.
Cancellation Laws for Congruences:
Cancellation law: If ab = ac and a 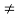 0, then b = c.
0, then b = c.
The critical difference between ordinary arithmetic and arithmetic modulo m is that the above cancellation law is not true for congruences. For example,
3 ・ 1 ≡ 3 ・ 5 (mod 6) but 1 _= 5 (mod 6)
That is, we cannot cancel the 3 even though 3 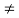 0 (mod 6). However, we do have the following Modified Cancellation Law for our congruence relations.
0 (mod 6). However, we do have the following Modified Cancellation Law for our congruence relations.
Modified Cancellation Law:
Suppose ab ≡ ac (mod m) and gcd(a, m) = 1.
Then b ≡ c(mod m).
Note- Suppose ab ≡ ac (mod m) and d = gcd(a, m).
Then b ≡ c (mod m/d)
Remainder Function and Modular Arithmetic:
Suppose k be any integer and let M be a positive integer. Then k (mod M) (We read it as: k modulo M) will denote the integer remainder when k is divided by M. More exactly, k (mod M) is the unique integer r such that
k = Mq + r where 0 ≤ r <M
When k is positive, simply divide k by M to obtain the remainder r. Thus
25 (mod 7) = 4, 25 (mod 5) = 0, 35 (mod 11) = 2, 3 (mod 8) = 3
If k is negative, divide |k| by M to obtain a remainder r
; then k (mod M) = M – r’
When r’ 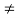 0. Thus
0. Thus
−26 (mod 7) = 7 − 5 = 2, −371 (mod 8) = 8 − 3 = 5, −39 (mod 3) = 0
The term “mod” is also used for the mathematical congruence relation, which is denoted and defined as follows:
a ≡ b (mod M) if any only if M divides b − a
M is called the modulus, and a ≡ b (mod M) is read “a is congruent to b modulo M”. The following aspects of the congruence relation are frequently useful:
0 ≡ M (mod M) and a }M ≡ a (mod M)
Arithmetic modulo M refers to the arithmetic operations of addition, multiplication, and subtraction where the arithmetic value is replaced by its equivalent value in the set
{0, 1, 2, . . . , M − 1} or in the set {1, 2, 3, . . . , M}
For example, in arithmetic modulo 12, sometimes called “clock” arithmetic,
6 + 9 ≡ 3, 7 × 5 ≡ 11, 1 − 5 ≡ 8, 2 + 10 ≡ 0 ≡ 12
Chinese remainder theorem:
Once a Chinese riddle asks the following question-
Is there a positive integer x such that when x is divided by 3 it yields a remainder 2, when x is divided by 5 it yields a remainder 4, and when x is divided by 7 it yields a remainder 6?
In other words, we seek a common solution of the following three congruence equations:
x ≡ 2 (mod 3), x ≡ 4 (mod 5), x ≡ 6 (mod 7)
Theorem (Chinese remainder theorem):
Consider the system
x ≡ r1 (mod 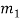 ), x ≡ r2 (mod
), x ≡ r2 (mod 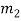 ), ・ ・ ・, x≡
), ・ ・ ・, x≡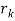 (mod
(mod 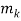 )
)
Where the mi are pairwise relatively prime. Then the system has a unique solution modulo M = 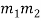 ・ ・
・ ・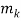
Proposition: Consider the system
x ≡ r1 (mod 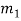 ), x ≡ r2 (mod
), x ≡ r2 (mod 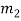 ), ・ ・ ・, x≡
), ・ ・ ・, x≡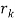 (mod
(mod 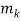 ) …….. (1)
) …….. (1)
Of congruence equations
Let M = 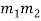 ・ ・
・ ・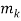 And
And
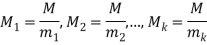
(Then each pair 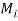 and
and 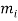 are co-prime.) Let
are co-prime.) Let 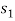 ,
, 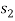 , . . . ,
, . . . , 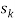 be the solutions respectively, of the congruence equations
be the solutions respectively, of the congruence equations
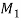 x ≡ 1 (mod
x ≡ 1 (mod 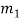 ),
), 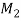 x ≡ 1 (mod
x ≡ 1 (mod 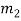 ), . . . ,
), . . . , 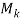 x ≡ 1 (mod
x ≡ 1 (mod 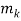 )
)
Then the following is a solution of the system (1)
x0 = M1 s1r1 + M2s2r2 + . . . +Mkskrk
Now we will solve the riddle asked by Chinese:
First method: (a) x ≡ 2 (mod 3) and (b) x ≡ 4 (mod 5)
Chinese remainder theorem tells us there is a unique solution modulo M = 3 ・ 5 = 15. Adding multiples of the modulus m = 5 to the given solution x = 4 of the second equation (b), we obtain the following three solutions of (b) which are less than 15:
4, 9, 14
Testing each of these solutions in equation (a), we find that 14 is the only solution of both equations. Now we apply the same process to the two equations
(c) x ≡ 14 (mod 15) and (d) x ≡ 6 (mod 7)
Chinese remainder theorem tells us there is a unique solution modulo M = 15 ・ 7 = 105 .
Adding multiples of the modulus m = 15 to the given solution x = 14 of the first equation (c), we obtain the following seven solutions of (b) which are less than 105:
14, 29, 44, 59, 74, 89, 104
Testing each of these solutions of (c) in the second equation (d) we find that 104 is the only solution of both equations. Thus the smallest positive integer satisfying all three equations is
x = 104
This is the solution of the riddle.
Second method:
Using the above notation, we obtain
M = 3 ・ 5 ・ 7 = 105, M1 = 105/3 = 35, M2 = 105/5 = 21, M3 = 105/7 = 15
We now seek solutions to the equations
35x ≡ 1 (mod 3), 21x ≡ 1 (mod 5), 15x ≡ 1 (mod 7)
Reducing 35 modulo 3, reducing 21 modulo 5, and reducing 15 modulo 7, yields the system
2x ≡ 1 (mod 3), x ≡ 1 (mod 5), x ≡ 1 (mod 7)
The solutions of these three equations are, respectively,
s1 = 2, s2 = 1, s3 = 1
We now substitute into the formula (1) to obtain the following solution of our original system:
x0 = 35 ・ 2 ・ 2 + 21 ・ 1 ・ 4 + 15 ・ 1 ・ 6 = 314
Dividing this solution by the modulus M = 105, we obtain the remainder
x = 104 which is the unique solution of the riddle between 0 and 105.
Fermat’s little theorem:
Let a 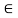 N and let p be a prime-
N and let p be a prime-
1. If p does not divide a then 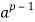 ≡ (mod p).
≡ (mod p).
2. In general,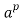 ≡ a (mod p).
≡ a (mod p).
Proof:
Suppose p is any prime number and a is any integer such that p ∤ a . Note that a _= 0 because otherwise p would divide a. Consider the set of integers
S = {a, 2a, 3a, . . . , (p − 1)a}.
We claim that no two elements of S are congruent modulo p. For suppose sa ≡ ra (mod p) for some integers s and r with 1 ≤ r < s ≤ p − 1. Then, by definition of congruence modulo p,
p | (sa − ra), or, equivalently, p | (s − r )a.
Now p ∤ a by hypothesis, and because p is prime, gcd(a, p) = 1. Thus, by Euclid’s lemma, p | (s − r ). But this is impossible because 0 < s − r < p.
Consider the function F from S to the set T = {1, 2, 3, . . . , (p − 1)} that sends each element of S to its residue modulo p. Then F is one-to-one because no two elements of S are congruent modulo p.
If a function from one finite set to another is one-to-one, then it is also onto. Hence F is onto, and so the p − 1 residues of the p − 1 elements of S are exactly the numbers
1, 2, 3, . . . , (p − 1).
It follows that
a ·2a ·3a · · · (p − 1)a ≡ [1·2·3 · · · (p − 1)] (mod p),
Or equivalently
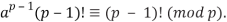
But because p is prime, p and (p − 1)! are relatively prime. Thus, by the cancellation theorem for modular congruence
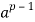 ≡ (mod p)
≡ (mod p)
References:
1. Edgar G. Goodaire and Michael M. Parmenter, Discrete Mathematics with Graph Theory, 3rd Ed., Pearson Education (Singapore) P. Ltd., Indian Reprint, 2005.
2. Kenneth Rosen Discrete mathematics and its applications Mc Graw Hill Education 7th edition.
3. V Krishna Murthy, V. P. Mainra, J. L. Arora, An Introduction to Linear Algebra, Affiliated East-West Press Pvt. Ltd.
4. J. L. Mott, A. Kendel and T.P. Baker: Discrete mathematics for Computer Scientists and
5. Mathematicians, Prentice Hall of India Pvt Ltd, 2008.
6. Schaum’s outlines discrete mathematics.
7. Discrete mathematics structures by G.Shanker rao.