Unit - 2
Principles of Mathematical Induction
Mathematical induction is a mathematical technique is used to prove a statement, a theorem or a formula is true for every natural number.
The technique has two steps to prove any statement-
1. Base step (it proves that a statement is true for the initial value)
2. Inductive step (it proves that is the statement is true for n’th iteration then it is also true for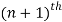 
iteration.
Example-1: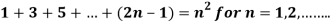 
Sol. Here for n = 1, 1 = 1²
Now let us assume that the statement is true for n = k
Hence we assume that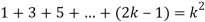 
is true.
Now we need to prove that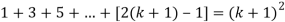
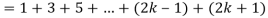
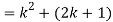
So that 
which satisfies the second step.
Hence-
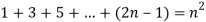
Example-2: Prove 1+2+...+n = n(n+1)/2 using a proof by induction.
Sol.
Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,
Step-1: Assume n=k holds: 1+2+...+k = k(k+1)/2
Show n=k+1 holds: 1+2+...+k+(k+1)=(k+1)((k+1)+1)/2
Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.
Step-2: Now start with the left side of the equation
1+2+...+(k+1)=1+2+...+k+(k+1)
=k(k+1)/2 + (k+1)
=(k(k+1)+2(k+1))/2 by 2/2=1 and distridution of division over addition
=(k+2)(k+1)/2 by distribution of multiplication over addition
=(k+1)(k+2)/2 by commutativity of multiplication
Example-3: Prove the following by using the principle of mathematical induction for all n ∈ N-
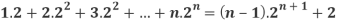
Sol. Here, n = 1,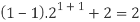 
, which is true
Step-1: Assume n = k holds-
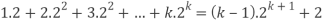
Now show n = k + 1 also holds-
Consider-
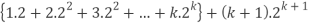
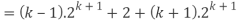
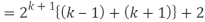
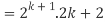
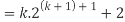
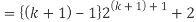
Which is also true for n = k + 1.
Hence proved.
Second form of mathematical induction:
Let P be a proposition defined on the integers n ≥ 1 such that:
(i) P(1) is true.
(ii) P(k) is true whenever P( j ) is true for all 1 ≤ j < k.
Then P is true for every integer n ≥ 1.
Pigeonhole principle (statement)-
If n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.
This principle can be applied to many problems where we want to show that a given situation can occur.
Example-1: Suppose a class contains 13 students, then two of the students (pigeons) were born in the same months (pigeonholes)
Example-2: Find the minimum number of elements that one needs to take from the set S = {1, 2, 3, . . . , 9} to be sure that two of the numbers add up to 10.
Here the pigeonholes are the five sets {1, 9}, {2, 8}, {3, 7}, {4, 6}, {5}. Thus any choice of six elements (pigeons) of S will guarantee that two of the numbers add up to ten.
Example-3: Show that if seven numbers from 1 to 12 are chosen, then two of them will add up to 13.
Sol.
First we will construct six different sets, each containing two numbers that add up to 13 as follows-
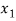= {1, 12}, 
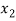= {2, 11}, 
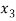= {3, 10}, 
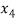= {4, 9}, 
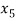= {5, 8}, 
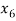= {6, 7}.
Each of the seven numbers belong to one of these six sets.
Since there are six sets, then according to the pigeonhole principle that two of the numbers chosen belong to the same set. These numbers add upto 13.
Generalized pigeonhole principle-
If n pigeonholes are occupied by kn+ 1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k + 1 or more pigeons.
Example- Find the minimum number of persons in a group that three of them are born in the same month.
Sol.
Here the n = 12 months are the pigeonholes, and k + 1 = 3 so k = 2. Hence among any kn+ 1 = 25 students (pigeons), three of them are born in the same month.
Example: Find the minimum number of students in a class to be sure that three of them are born in the same month.
Sol:
Here the n = 12 months are the pigeonholes, and k + 1 = 3 so k = 2. Hence among any kn + 1 = 25 students (pigeons), three of them are born in the same month.
Key takeaways
- If n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.
- If n pigeonholes are occupied by kn+ 1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k + 1 or more pigeons.
The principle of inclusion-exclusion is an important technique used in the theory of enumeration. When two tasks can be done at the same time, we can not use the sum rule to count the number of ways to do one of the two tasks. Adding the number of ways to do each tasks leads to an overcount, since the ways to do both tasks are counted twice. To correctly count the number of ways to do one of the two tasks, we add the number of ways to do each of the two tasks and then subtract in number of ways to do both tasks.
This technique is called the principle of inclusion-exclusion.
The Inclusion-Exclusion principle can be stated as below-
Let A and B any two finite sets, then-
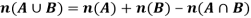
Meaning- Here if we have to find the number 
of elements in the union of A and B.
So then we add n(A) and n(B) which means we are including these two.
And then we exclude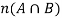 
.
Note- For three sets-
If we have three finite sets A, B and C then-
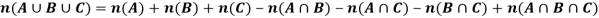
Example: Find the number of students at a college choosing at least one of the subject from mathematics, physics and statistics.
The data is given as-
65 study maths, 45 study physics, 42 study statistics
20 study maths and physics, 25 study maths and statistics, 15 study physics and statistics and 8 study all the three subjects.
Sol.
Here we need to find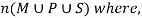 
Now by using Inclusion-Exclusion principle-
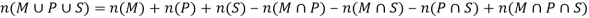
Which gives-
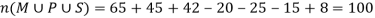
Therefore, we find that 100 students study at least one of the three subjects.
Example: A class contains 30 students majoring in computer science, 20 students majoring in mathematics and 8 joins in mathematics and computer science majors. How many students are in this class, if every student is majoring in mathematics, or computer science or both.
Sol:
Let A = The set of students majoring in computer science.
B = The set of students majoring in mathematics.
Then A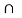 
B = the set of students who joins mathematics and compter science majors. and A
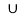B = the set of students majoring in mathematics or computer science or both
Then A = 30, B = 20 and A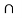 
B= 8 then
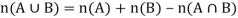
= 30 + 20 – 8 = 42
Therefore, there are 42 students in the class.
Example: In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T and 26 read newspaper I, 9 read both H and I, 11 read both H and T, 7 read both T and I, 3 read all three newspapers, Find the number of people who read at least one of the newspapers.
Sol:
Here we have,
H = 25, T = 26,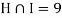 
, 
, 
, 
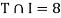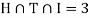
The number of people who read at least one of the newspapers
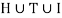
Hence, we know that-
If we have three finite sets A, B and C then-
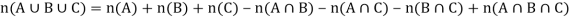
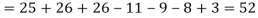
Do yourself:
In a class of 35 students, 15 study economics, 22 study physics and 14 study chemistry. If 11 students study both economics and physics, 8 study physics and chemistry and 5 study economics and chemistry and if 3 study all the three subjects. Find how many students of the class are not taking any of these subjects.
Here first we define relatively prime integers.
Relatively Prime Integers:
Two integers a and b are said to be relatively prime or coprime if gcd(a, b) = 1. Accordingly, if a and b are relatively prime, then there exist integers x and y such that ax + by = 1
Conversely, if ax + by = 1, then a and b are relatively prime.
Example:
(a) Observe that: gcd(12, 35) = 1, gcd(49, 18) = 1, gcd (21, 64) = 1, gcd (−28, 45) = 1
(b) If p and q are distinct primes, then gcd(p, q) = 1.
(c) For any integer a, we have gcd(a, a + 1) = 1, since any common factor of a and a + 1 must divide their difference (a + 1) − a = 1.
Note-
- Suppose gcd(a, b) = 1, and a and b both divide c. Then ab divides c.
- Suppose a | bc , and gcd(a, b) = 1. Then a | c
- Suppose a prime p divides the product ab. Then p | a or p | b.
Fundamental Theorem of Arithmetic:
Every integer n >1 can be expressed uniquely (except for order) as a product of primes.
The primes in the factorization of n need not be distinct. Frequently, it is useful to collect together all equal primes. Then n can be expressed uniquely in the form
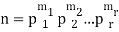
Where the mi are positive and p1 < p2 < ... < pr . This is called the canonical factorization of n.
Example:
Let F be the set of positive integers of the form 3x + 1. Thus F consists of the numbers:
1, 4, 7, 10, 13, 16, 19, 22, . . .
Note that the product of two numbers in F is again in F since:
(3x + 1)(3y + 1) = 9xy + 3x + 3y + 1 = 3(3xy + x + y) + 1
Our definition of primes makes perfectly good sense in F. Although 4 = 2 ・ 2 , the number 2 is not in F. Thus 4 is prime in F since 4 has no factors except 1 and 4. Similarly 10, 22, 25,… are primes in F. We list the first few primes in F:
4, 7, 10, 13, 19, 22, 25 , . . .
Note 100 = 3(33)+1 belongs to F. However, 100 has two essentially different factorizations into primes of F; namely,
100 = 4 ・ 25 and 100 = 10 ・ 10
Thus there is no unique factorization into primes in F.
Permutations-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are-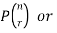 
Example: Consider the three letters x, y, z. The arrangements of the letter x, y, ztaken two at a time are-
Xy, yx, xz, zx, yz, zy
∴The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time
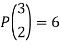
Note-A permutation of n objects taken r at a time is also called r-permutation
Factorial function-
The product of the positive integers from 1 to n is deoted by n!and we read it as “factorial “
Expressed as-
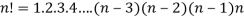
Note-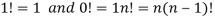 
Binomial coefficient-
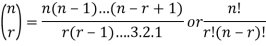
Example:
1. 
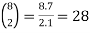
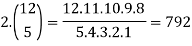
Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 
of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula-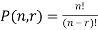 
Permutation with repetitions-
The number of permutations of n objects of which are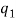 
are alike, 
are alike, 
Are alike is-
P(n, q, q2 , . . ., qr) = n!/ (q1! q2! . . . qr!)
Sampling with or without replacement-
Suppose we chose the samples with repetition, fro example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n =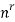 
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-
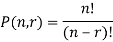
Example-
Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Example-
There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?
Solution: Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row =
Example- A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n=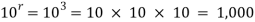 
(b) P (10, 3) = 10 × 9 × 8 = 720
Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.
Hence the number of circular permutations of n different objects = (n – 1)!
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
Note-
1. Property-1
C(n, r) = P(n, r)/r!
2. Property-2
C(n, n) = n!/n!(n – n)! = n!/n!0! = 1
3. Property-3
C(n, 0) = n!/0!(n – 0)! = n!/0!n! = 1
Generalized permutations and combinations
Generalized sum rule-
If we have tasks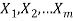 
that can be done in 
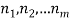ways respectively, and no two of these tasks can be done at the same time then there are 
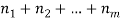ways to do one of these task.
Generalized product rule-
If we have sequential task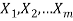 
that can be done in 
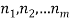, then there are 
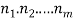to do the procedure.
Permutation and combination with unlimited repetitions-
Suppose U (n, r) denotes r-permutations of n-objects with unlimited repetitions and v (r, n) denotes the r-combination with unlimited repetitions, then-
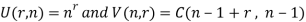
Let us consider a set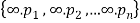 
where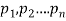 
are all distinct.
Any r-combination is of the form 
here each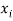 
is a non-negative integer and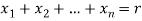 
The numbers 
are called repetition numbers. Conversely any sequence of non-negative integers-
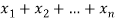
Corresponds to a r-combination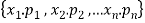 
.
The following observation we get-
The number of r-combination of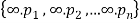 
= the number of non-negative integer solution of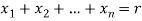 
= the number of ways of placing r indistinguishable balls in n numbered boxes.
= the number of binary numbers with n – 1 one’s and zeros.
= C (n – 1 + r, r)
= C (n – 1 + r, n - 1)
Example: Find the number of non-negative integral solutions to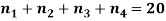 
Sol: We have n = 4, r = 20
The number of non-negative integral solutions
= C (4 – 1 + 20, 20)
= C (23, 20)
= 1,771
Example-Find the number of ways of placing 8 similar balls in 5 numbered boxes.
Solution:
The number of ways of placing similar balls in 5 numbered boxes is
= C (5 – 1 + 8, 8)
= C (12, 8) = 495
Example-How many outcomes are possible by costing a 6 faced die 10 times?
Solution:
This is same as placing 10 similar balls into 6 numbered boxes.
There are C (6 – 1 + 10, 10)
= C (15, 10) possible outcomes.
Combination of n things taking any number of them at a time when all the things are different:
Each one of the n different things may either be selected or not selected i.e., there are two ways of selecting for each one of the n things.
∴ The total number of combinations of n things taking any number of things is 2n.
But this includes the case in which all the things are rejected.
Hence the total number of ways in which one or more things are taken.
Corollary:
The total number of combinations of n things taken 1, 2, 3, …, n at a time i.e., C (n, 1) + C (n, l) + … +
C (n, n) =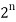 
– 1.
Example: In how many ways can a person invite one or more of his 5 friends to a party?
Solution: For every friend there are two possibilities i.e., he may be invited or he may not be invited to attend the party.
The number of ways in which we can invite his five friends at a party is 25.
But this includes the case when none of his friend is invited.
Hence, the number of ways in which he invites one or more of his five friends to a party is
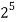– 1 = 32 – 1 = 31
Combination of n things taking any number of them at a time when all the things are not different:
Suppose that out of m + n + p + …, things m are alike, and of one kind, n are alike and of second kind and the rest are different, say they are k in number.
Out of m things we may take 0, 1, 2, … or m. Hence there (m + 1) ways of selecting the m things similarly, n things which are alike may be selected in (n + 1) ways and, P things which are alike may be selected in (P + 1) ways the remaing k different things may be selected in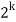 
ways. These include the case in which all are rejected.
∴ The total numbers of combinations
= (m + 1) (n + 1) (p 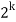+ 1) 
– 1
Basic identities:
Example: Prove that C (n, r) = C (n, n – r)
Sol:
C (n, r) denotes the number of selections of n objects when r-things are selected, and the remaining (n – r) objects are not selected. Therefore, selecting of r-things is the same as discarding (n – r) objects. For each selection of r things i.e., for each r-combination there is a discarding of n – r, remaining objects. The number of ways in which we discord (n – r) objects is C (n, n – r).
Since the set of r-combinations and the set of discarding of (n – r) objects are in one-one corresponding we get
C (n, r) = C (n, n – r)
Example: (Pascal’s Identity)
Show that C (n, r) = C (n – 1, r – 1) + C (n – 1, r)
C (n, r) is the number of r-combinations of n objects. Let n be any one of the n objects. Fix the object x the C (n, r) combinations can be grouped into:
(i) Those r-combinations that contain the objects x.
(ii) Those r-combinations that do not contain the object x.
Since the objects x is in all r-combinations of (i) we are to choose (r – 1) objects in each combinations of (i) from the remaining (n – 1) objects, this can be done in C (n – 1, r – 1) ways.
The number of combinations that contain x, is
C (n – 1, r – 1)
To count the number of r-combinations of (ii) i.e., the number of r-combinations which do not contain x, we omit the objects x from n objects and choose r objects from the remaining (n – 1) objects.
Therefore, the number r-combinations that do not contain x is C (n – 1, r).
Thus C (n, r) = C (n – 1, r – 1) + C (n – 1, r)
Example: (Pascals row sum identity)
Show that C (n, 0) + C (n, 1) + … + C (n, n) =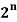 
Sol:
This is equivalent to finding the number of subsets of a set A with n elements. The number of subsets of A can be considered as follows:
The number of subsets having no elements (i.e., subsets with 0 elements is C (n, 0)
The number of subsets having 1 elements is C (n, 1) …
The number of subsets with n elements is C (n, n). Adding we get the number of elements in the power set of A.
i.e., | (A) | = C (n, 0) + C (n, 1) + … + C (n, n)
But the number of elements in the power set of A is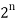 
.
Hence C (n, 0) + C (n, 1) + … + C (n, n) =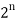 
Ordered partition:
A partition a non-empty set is called an ordered partition of S if there is a specified order on the subsets of S.
An ordered t-tuple of sets {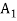
, 
, …, 
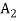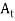} is called a t-part ordered partition if the sets 
, 
, …, 
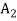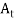form a partition of S.
Theorem:
Let S contain n distinct objects. Then the number of ways S can be partitioned in r
Subsets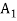 
, 
, …, 
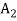with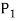 
objects in 
, 
objects in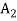 
…, and 
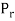objects in 
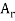is
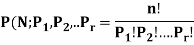
Example: A farmer buys 4 cows, 2 goats and 5 ducks from a person who has 7 cows, 5 goats and 8 ducks. How many choices the farmer have:
Sol:
The farmer can choose 4 cows from 7 cows in C (7, 4) ways, 2 goats from 5 goats in C (5,
2) ways and 5 ducks from 8 ducks in C (8, 5) ways.
∴ The farmer can choose 4 cows, 2 goats and 5 ducks in C (7, 4) C (5, 2) C (8, 5)
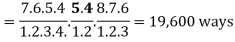
Example: There are twelve students in a class. Find the number of ways that the twelve students take three different tests if four students are to take each test.
Sol:
We find the number of ordered partitions of twelve students into cells containing four students each. There are
The required number of ways, the students can write the take the tests is 34,650.
Binomial theorem:
The numbers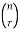
are called the binomial coefficients.
Binomial theorem gives a formula for the coefficients in the expansion of 
.
According to theorem-
Let n be a positive integer then for all a and b, then
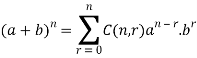
Example-1: Expand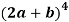 
Sol.
Here we have-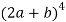
By using binomial theorem, we get
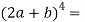
= C(4, 0)(2a)4 + C(4, 1)(2a)3b + C(4, 2) (2a)2b2 + C(4, 3) (2a) b3 + C (4, 4) b4
= 16 a4 + 32 a3b + 24 a2b2 + 8 ab3 + b4
Example-2: Find the term containing 
in the expansion of 
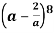
Sol.
The general term will be-
Tr+1 = C(8, r) a8-r (-2/a)r
= C (8, r) a8-r (-2 a-1)r
= C (8, r) a8-r (-2)r (a-1)r
= C (8, r) (-2)r a8-r a-r
= C(8, r) (-2)r a8-2r
Put 8 – 2r = 4 we get r = 2
Therefore the term contain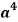s
is-
Tr+1 = T3 = C (8, r) (-r)r a4
= C (8, r) 4 a4
= 284 a4
= 112 a4
Note-
If we replace ‘a’ and ‘b’ by ‘x’ and ‘1’ then we get an another form of the binomial theorem-
(x+1)n =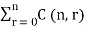 
xn – r = 
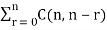xn - r
Example-3: In the expansion of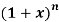 
, prove the following result-
C02 + C12 + C22 + . . . + Cn2 = 2n!/(n!)2
Sol. We have-
(1+x)n = C (n, 0) + C(n, 1)x + . . .+ C(n,n) xn
As we know that the coeff. Of the terms equivalent from the beginning and end are equal, so that-
(1+x)n = C (n, n) + C(n, n- 1) x + . . . + C (n, 0) xn
By multiplying the above two equations, we get-
(1+x)2n = [C (n, 0) + C(n, 1) x + . . . + C (n, n) xn ] x [C(n, n) + C(n, n- 1) x+ . . . + C (n, 0)]xn
From RHS, we see the coeff. Of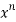
C(n, 0)2 + C(n, 1)2 + . . . + C(n, n)2
But the coeff. Of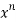
in 
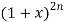is-
C(2n, n) = 2n!/n!n! = 2n!/(n!)2
C0 2 + C12 + Cn2 = 2n!/(n!)2
Example: If If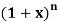 
= C (n, 0) + C (n, 1) x + C (n, 2) 
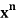+ … + C (n, n)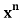
Prove that C (n, 1) + 2 C (n, 2) + 3 C (n, 3) + … + n C (n, n) = n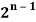 
.
Sol:
C (n, 1) x + 2 C (n, 2) x2 + … + n C (n, n)
= nx + 2 . 2(n – 1)/2! x2+ . . . + n xn
= nx + n(n – 1)x2 + . . . + nxn
= nx [ 1 + (n – 1) x + . . . + xn – 1]
= nx [ C(n – 1, 0) + C(n -1, 1)x + . . . + C(n -1, n – 1)xn – 1]
= nx (1+x)n – 1
Example: Prove that
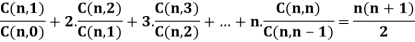
Sol:
We know that
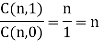
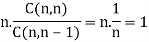
Adding, we get
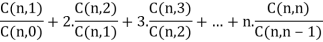
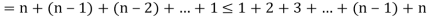
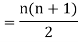
Note-
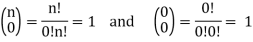
And
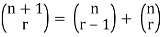
Multi-Nominal Theorems:
Let n be a positive integer, then for all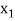 
+ 
+ … + 
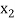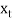
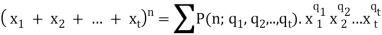
Where the summation extends over all sets of non-negative integers 
, 
, …, 
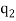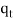
Where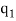 
+ 
+ … + 
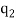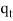= n.
Example: Find the coefficients of 
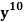
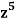
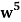in the expansion of 
.
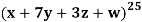Sol:
We have n = 25, x1 = x1, x2 = 74, x3 = 3 z, and x4 = w
∴ The coefficients of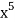 
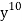
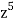
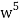in the expansion of 
.
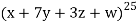Is
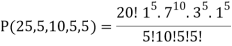
Recursion is a technique of defining a function, a set or an algorithm in terms of itself.
Suppose the set of natural numbers, we introduce the method of generating the set of natural numbers by recursion.
The natural numbers with zero are those objects which can be generated by starting with an initial object 0 and from any object “n” already generated passing to another uniquely determined object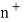 
, the successor of n. The objects differently generated are always distinct. Thus the natural numbers appear as a set of objects 0,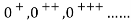
The transition to the usual notation is made upon introducing 1, 2, 3, 4, … to stand for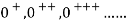 
and then employing the notation.
The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.
A recurrence relation is also called a difference equation.
The information accompanying a recursive formula about the beginning of the numeric function is called initial condition.
Example: Find a recurrence relation and initial conditions for 1, 5, 17, 53, 161, 485.
Sol.
Here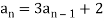 
is the recurrence relation and the initial condition is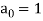 
Example: Check whether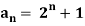 
is a solution to the recurrence relation 
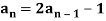with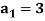 
.
Sol.
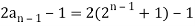
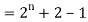
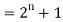
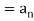
Key takeaways
- The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.
- A recurrence relation is also called a difference equation.
- The information accompanying a recursive formula about the beginning of the numeric function is called initial condition.
Linear recurrence relations with constant coefficients
Suppose r and k are non-negative integers. A recurrence relation of the form
c0(r) ar + c1(r) ar-1 + . . . + ck (r) ar-k = f(r) for r ≥ k
Here 
and f(r) are the functions of r is said to be a recurrence relation.
If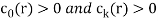 
then it said to be a linear recurrence relation of degree k..
Linear recurrence relation with constant coefficient-
If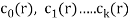 
are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.
A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form
an = C1 an-1 + C2 an – 2 + . . . + Ckan-k + f(n)
Where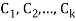 
are constant with 
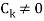and f(n) is a function of ’n’.
Example: Consider a following recurrence relation-
Sol.
It is a homogeneous linear second-order recurrence relation but it does not have constant coefficients because the coefficient of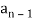 
is not a constant given initial conditions 
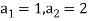, the next elements of the sequence follows-
a3 = 3(2) + 3(1) = 9, a4 = 4(9) + 3(2) = 42
Note-
If if f (r) = 0, then the recurrence relation is called a linear homogenous relation.
For example:
The following relations are linear recurrence relations with constant coefficients-
an – 6an-1 + 11 an-1 + 6an-3 = 2n
an – 9an-1 + 26 an-1 – 24 an-3 = 5n
Key takeaways
- If
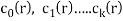are constants then the recurrence relation is called a linear recurrence relation with constant coefficients. - A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form
an = C1 an-1 + C2 an-2 + . . . + Ck an-k + f(n)
Where 
are constant with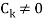 
and f(n) is a function of ’n’.
Solution of recurrence relations by the method of generating functions
Any numeric function that can be described by a recurrence relation together with an appropriate set of boundary conditions is called a solution of the recurrence relation.
If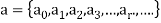 
Is a solution to a recurrence relation then it is said to satisfy the relation.
A given recurrence relation may or may not have a solution.
Method of generating functions-
Recurrence relations can also be solved by using generating functions. Some equivalent expressions used are given below-
Then
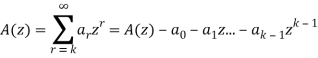
A(z) = 
A(z) =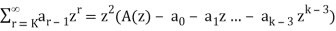 
A(z) =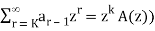 
Example: Solve the recurrence relation-
Sol.
Multiplying each term of the recurrence relation by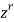 
, we find-
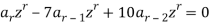
Now taking the sum to 2 to 
, we get
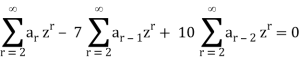
Replace each infinite sum by the corresponding equivalent expression given above,
We obtain-
[A(z) – a0 – a1z ] – 7 z [ A(z) – a0] – 10 z2 A(z) = 0
On simplifying, we obtain-
A(z) (1- 7z + 10 z2] = a0 + a1 z – 7 a0z
A(z) =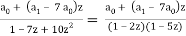 
Decomposing A (z) as a sum of partial fractions, we can write
A(z) = c1/(1 – 2z) + c2 /( 1 – 5z) = c,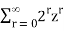 
+ c2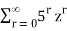 
The solution is-
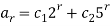
Generating functions, solution of recurrence relation using generating functions
For a numeric function-
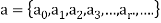
An infinite series is defined as-
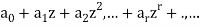which is called the generating function of a.
We denote it by A(Z).
The coefficient of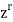 
is A (z) is the value of the numeric function a.
For example:
If the generating function is
Is
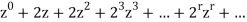
We can write the above series as below-
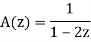
In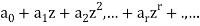 
the term 
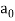is called the constant term.
Let
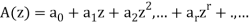
And
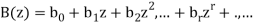
Are the generating functions.
A(z) and B(z) are equal if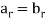 
, for each
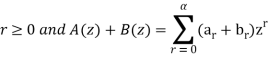
The product can be defined as-
A(z)B(z) = a0b0z0 + (a0b1 + a1b0) z + (a0b2 + a1b1 + a2b0) z2 + . . . + (a0br + a1br – 1 + . . . + ar b0) zr + . . .
Note-
- The ordinary generating function is the formal power series-
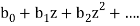
2. the exponential generating function (egf) is the formal power series
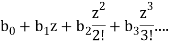
3. If the sequence has finitely many elements then the generating functions have finitely many terms.
References:
1. Edgar G. Goodaire and Michael M. Parmenter, Discrete Mathematics with Graph Theory, 3rd Ed., Pearson Education (Singapore) P. Ltd., Indian Reprint, 2005.
2. Kenneth Rosen Discrete mathematics and its applications Mc Graw Hill Education 7th edition.
3. V Krishna Murthy, V. P. Mainra, J. L. Arora, An Introduction to Linear Algebra, Affiliated East-West Press Pvt. Ltd.
4. J. L. Mott, A. Kendel and T.P. Baker: Discrete mathematics for Computer Scientists and
5. Mathematicians, Prentice Hall of India Pvt Ltd, 2008.
6. Schaum’s outlines discrete mathematics.
7. Discrete mathematics structures by G.Shanker rao.
