Unit - 1
Differential equations and mathematical models
Overview:
We study the solutions of differential equations which are: variables separable, homogeneous, nonhomogeneous, exact, non-exact using integrating factors, linear, Bernoulli, higher degree, Clairaut’s, Lagrange’s. We consider geometrical applications and physical problems of law of natural growth, natural decay, Newton’s law of cooling, velocity of escape from earth and simple electrical circuits.
Modeling is a technique of transforming a physical problem to a “mathematical model”.
Mathematical formulation of problems involving continuously or discretely changing quantities leads to ordinary or partial differential equations, linear or non-linear equations, integral equations or a combination of these.
Differential Equations – A differential equation is an equation involving an unknown function and its derivatives.
For example: y + 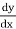 = 8x and
= 8x and 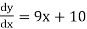
A differential equation with only single independent variable is known as ordinary differential equation.
Or in other words- A differential equation is an ordinary differential equation if the unknown function depends on only one independent variable
Notation: the expression y’, y’’, y’’’ …….yⁿ are used to represent derivatives.
Here, y’ =  , y’’ =
, y’’ = 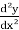 and so on.
and so on.
1st order linear differential equations-
A 1st order linear differential equations is linear when it is given in the form below-
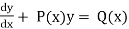 ,
,
Where P(x) and Q(x) are the functions of x
Here we will learn about degree and order of an ordinary differential equation:
Here we will learn about degree and order of an ordinary differential equation:
Order: The order is the highest derivative:
For example:
(1) 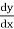 + y³ = 8x, here it has only first derivative so its ‘first order’.
+ y³ = 8x, here it has only first derivative so its ‘first order’.
(2) 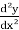 + y³ = 7x, here it has a second derivative so its ‘second order’ and so on.
+ y³ = 7x, here it has a second derivative so its ‘second order’ and so on.
Degree: Degree is known as the exponent of higher derivative.
For example: (1) 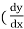 )² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
)² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
(2)  ) +
) +  y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
Formation of differential equations
We can form a differential equation by differentiating the ordinary equation and eliminating the arbitrary constant.
Example1: From the differential equation by eliminating arbitrary constant.
y = A cos x + B sin x
Sol:
Differentiate the given equation,
 -----------------(1)
-----------------(1)
Now, we will differentiate equation(1) again ,
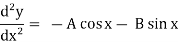
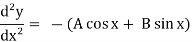
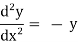
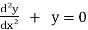 ans.
ans.
Example:2- From the differential equation by eliminating arbitrary constant.
y² = Ax² + Bx² + C
Sol:
We will differentiate the given function, we get

Again differentiate,
 + 2
+ 2
On differentiating again, we get
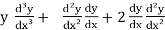 = 0 ans.
= 0 ans.
Key takeaways:
- Differential Equations – A differential equation is an equation involving an unknown function and its derivatives.
- Order: The order is the highest derivative
- Degree: Degree is known as the exponent of higher derivative.
General and particular solutions
A relation between the variables which satisfies the given DE, is called the solution of that DE.
General solution-
The general solution of a DE is that in which the number of arbitrary constants is equals to the order of DE. General solution is also called complete solution.
Particular solution-
A particular solution is that which can be obtained from the general solution by giving particular values to the arbitrary constants.
Or in other words, Particular solution is a solution obtained from the general solution by choosing particular values of the arbitrary constants. Integral curve of D.E. Is the graph of the general/particular solution of D.E.
Linear
An nth order O.D.E. In the dependent variable y is said to be linear in y if
i. y and all its derivatives are of degree one.
Ii. No product terms of y and/or any of it derivatives are present.
Iii. No transcendental functions of y and/or its derivatives occur.
Solution or integral or primitive
Solution or integral or primitive of a D.E. Is any function which satisfies the equation i.e., reduces it to an identity.
In Explicit solutions the dependent variable can be expressed explicitly in terms of the independent variable, like y = f (x). Otherwise the solution is said to be an implicit solution where F (x, y) = 0 where F (x, y) is an implicit function.
Let’s understand how to solve differential equations:
(1) The solution of equations of the form 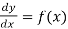
This type of equation can be solved by direction integration:
Y = 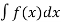
Example: Find the general solution of x 2 – 4x³
2 – 4x³
Solution: rearranging the given equation:
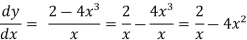
On integrating both sides,
y = 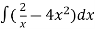 = 2 In x -
= 2 In x - 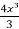 + c
+ c
This is the general solution.
Example: Find the particular solution of the differential equation 5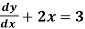 , given the boundary condition y = 1
, given the boundary condition y = 1 , when x = 2.
, when x = 2.
Solution:
Rearrange the diff. Equation,
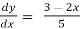 =
=  -
- 
y = 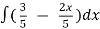 =
= 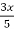 -
-  + c, which is the general solution.
+ c, which is the general solution.
Put the boundary conditions to find c,
1 -
- 
Which gives, c = 1
Hence the particular solution is,
y = 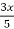 -
- 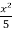 + 1.
+ 1.
(2) The solution of equation of the form  ,
,

Example: Find the general solution of 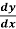 = 3 + 2y
= 3 + 2y
Solution: here,  = 3 + 2y gives,
= 3 + 2y gives,
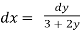 ,
,
Integrating both sides,
 ,
,
By substitution, u = (3 +2y),
X =  In(3 + 2y) + c.
In(3 + 2y) + c.
Example: Determine the particular solution of (y² - 1)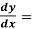 3y given that y =1 when x = 2
3y given that y =1 when x = 2 .
.
Solution: It gives,
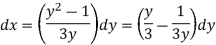

When putting the values, y =1 ,x = 2 ,
,
The particular solution will be,
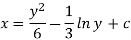
(3) The solution of equation of the form 
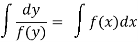
Example-1: Solve the equation 4xy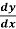 = y² - 1
= y² - 1
Solution: on separating variables, we get
(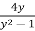 ) dy =
) dy = dx
dx
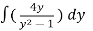 =
= 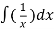
Using substitution, u = y² - 1
2In(y² - 1) = In x + c.
Example-2: Determine the particular solution of 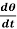 = 2
= 2 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
Solution:  = 2
= 2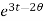 = 2
= 2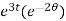 ,
,
 = 2
= 2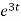 dt
dt
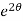 dθ =
dθ = 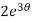 dt
dt
Now integrating both sides,
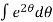 =
= 
The general solution is,
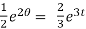 + c.
+ c.
When t = 0 and θ = 0, c =
 =
= 
Key takeaways:
- The general solution of a DE is that in which the number of arbitrary constants is equals to the order of DE. General solution is also called complete solution.
- A particular solution is that which can be obtained from the general solution by giving particular values to the arbitrary constants.
- In Explicit solutions the dependent variable can be expressed explicitly in terms of the independent variable, like y = f (x). Otherwise the solution is said to be an implicit solution where F (x, y) = 0 where F (x, y) is an implicit function.
Definition-
An exact differential equation is formed by differentiating its solution directly without any other process,
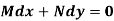
Is called an exact differential equation if it satisfies the following condition-

Here  is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 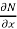 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Step by step method to solve an exact differential equation-
1. Integrate M w.r.t. x keeping y constant.
2. Integrate with respect to y, those terms of N which do not contain x.
3. Add the above two results as below-
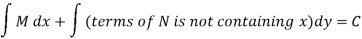
Example-1: Solve 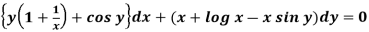
Sol.
Here M =  and N =
and N = 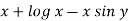

Then the equation is exact and its solution is-

Example-2: Solve-

Sol. We can write the equation as below-

Here M = 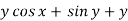 and N =
and N = 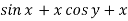
So that-
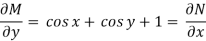
The equation is exact and its solution will be-

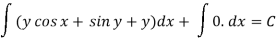
Or
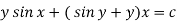
Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,
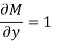
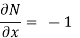
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Equation reducible to exact form-
1. If M dx + N dy = 0 be an homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor.
Example: Solve-
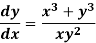
Sol.
We can write the given equation as-

Here,
M = 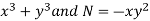
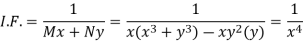
Multiply equation (1) by 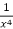 we get-
we get-
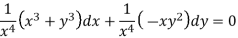

This is an exact differential equation-
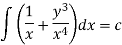

2. I.F. For an equation of the type 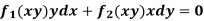
IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor.
Example: Solve-

Sol.
Here we have-
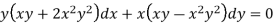
Now divide by xy, we get-
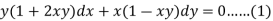
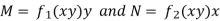
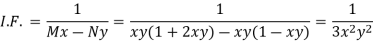
Multiply (1) by 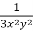 , we get-
, we get-
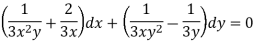
Which is an exact differential equation-

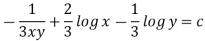
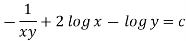
3. In the equation M dx + N dy = 0,
(i) If 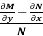 be a function of x only = f(x), then
be a function of x only = f(x), then 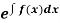 is an integrating factor.
is an integrating factor.
(ii) If  be a function of y only = F(x), then
be a function of y only = F(x), then 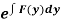 is an integrating factor.
is an integrating factor.
Example: Solve-
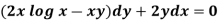
Sol.
Here given,

M = 2y and N = 2x log x - xy
Then-
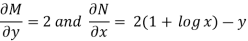
Here,

Then,
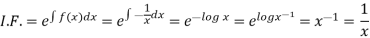
Now multiplying equation (1) by 1/x, we get-
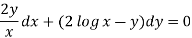
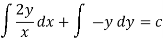
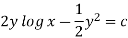
4. For the following type of equation-
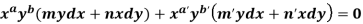
An I.F. Is 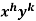
Where-
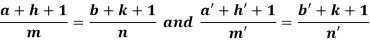
Example: Solve-

Sol.
We can write the equation as below-
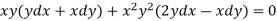
Now comparing with-
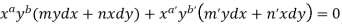
We get-
a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1
I.F. = 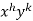
Where-


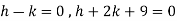
On solving we get-
h = k = -3

Multiply the equation by 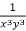 , we get-
, we get-

It is an exact equation.
So that the solution is-
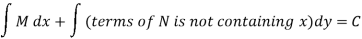
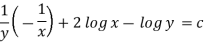
Variable separable-
Separation of variable is the method to solve the differential equations:
We will understand this method by some examples-
Example1: Solve 
Sol.
Separate the variables,
Ydy = dx
Integrate both sides,
 =
= 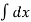

Now simplify,
y² = x(x + C)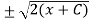
y = 
Example: Solve 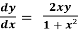
Sol. Separate the variables,
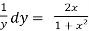 dx
dx
Integrate on both sides,
 =
= 
Let, u = 1 + x² , so , du = 2x dx,
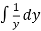 =
= 
In(y) = In(u) +C
Let, C = In(k) In(y) = In(u) +In(k)
y = uk
Put, u = 1 + x²
y = k(1 + x²)
Homogeneous equations: equations reducible to homogeneous form
A first order differential equation is homogeneous when it can be written in the form,
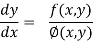
And each term of 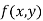 and
and 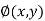 is of the same degree.
is of the same degree.
Working rules:
1. Put y = vx so, 
2. Separate the variable
3. Integrate on both sides
4. Now put y =  and solve.
and solve.
Example1: solve the equation:
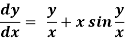
Sol. Here the function is,

We will put y =vx as mentioned above , so that 
v + 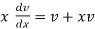

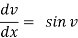
Separate the variables,
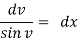
Cosec v dv = dx
On integrating,
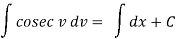
Log tan  = x +C
= x +C
Log tan  = x +C ans.
= x +C ans.
Example: Solve 
Sol.
On solving  , we get,
, we get, 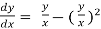
Let y = vx and 
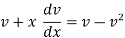

Separate the variable,

Integrate,
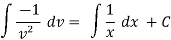

Or
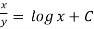 ans.
ans.
Equations reducible to homogeneous form
Case 1- The equation of the form,

Can be reduced to the homogeneous form by substitution if 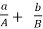
x = X + h and y = Y +k
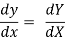
Given equation reduces to,

Choose h and k,

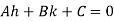
Then the equation becomes homogeneous,
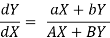
Case-2:
If 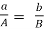 , then the values of h and k will not be finite,
, then the values of h and k will not be finite,
If 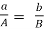 = if
= if  (say)
(say)
Then,
A =am, B = bm
Then the equation becomes,

Put, (ax+ by) = z then apply the method of variable separable.
Example: solve ( x+ 2y) ( dx – dy) = dx + dy
Solution:
On solving the given eq.
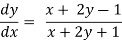
Now, here, we see that
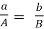 (case-2)
(case-2)
So we put, x +2y = z
1 +2 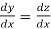
Here original eq. Becomes
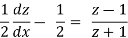
On solving it becomes,
(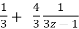 ) dz = dx
) dz = dx
Now integrate,
(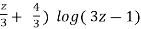 = x + C
= x + C
Put the value of z, it becomes,
3( x+2y) + 4log ( 3x +6y – 1) = 9x + 9C
A differential equation of the form

Is called linear differential equation.
It is also called Leibnitz’s linear equation.
Here P and Q are the function of x
Working rule
(1)Convert the equation to the standard form 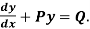
(2) Find the integrating factor.
(3) Then the solution will be y(I.F) = 
Example-1: Solve-
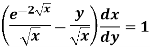
Sol. We can write the given equation as-

So that-
I.F. = 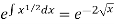
The solution of equation (1) will be-

Or
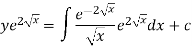
Or
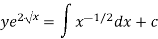
Or

Example-2: Solve-
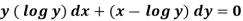
Sol.
We can write the equation as-

We see that it is a Leibnitz’s equation in x-
So that-

Therefore the solution of equation (1) will be-
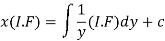
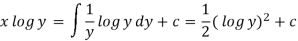
Or
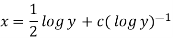
Example-3: Solve sin x 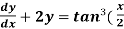 )
)
Solution: here we have,
Sin x 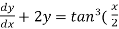 )
)
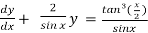 which is the linear form,
which is the linear form,
Now,
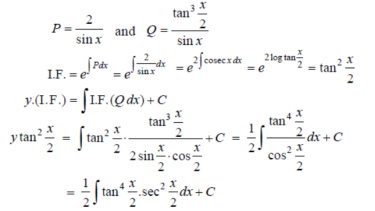
Put tan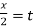 so that
so that  sec²
sec² dx = dt, we get
dx = dt, we get
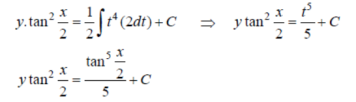
Which is the required solution.
Bernoulli’s equation-
The equation

Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
Working procedure to solve the Bernoulli’s linear equation-
Divide both sides of the equation –

By , so that
, so that

Put 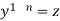 so that
so that 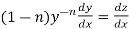
Then equation (1) becomes-
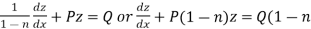 )
)
Here we see that it is a Leibnitz’s linear equations which can be solved easily.
Example: Solve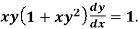
Sol.
We can write the equation as-

On dividing by 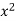 , we get-
, we get-

Put  so that
so that 
Equation (1) becomes,
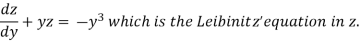
Here,

Therefore the solution is-
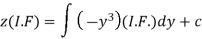
Or
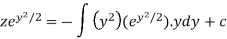
Now put 

Integrate by parts-

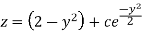
Or
Example: Solve 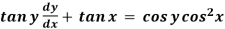
Sol. Here given,
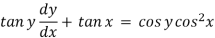
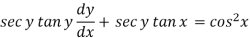
Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-

Here,
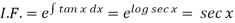
Then the solution will be-
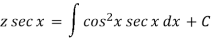
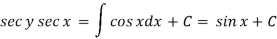
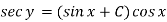
Example: Solve- 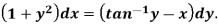
Sol. Here given-
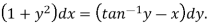
We can re-write this as-

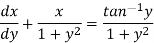
Which is a linear differential equation-
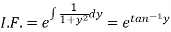
The solution will be-

Put 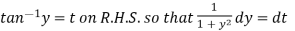
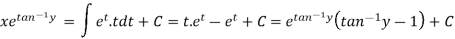
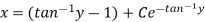
Key takeaways:
- The equation

Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
2. A differential equation of the form

Is called linear differential equation.
Generalizing Integrating Factors:
Let us consider the standard form of a linear first-order DE
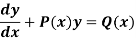
Rewriting in differential form through formal multiplication by dx, we get
[P(x)y - Q(x)]dx + dy = 0:
If this equation were exact, we would have P(x) = 0, which is not generally true. However, let us multiply the equation by the integrating factor 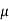 (x) =
(x) = 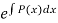
[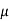 (x)P(x)y -
(x)P(x)y - 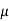 (x)Q(x)]dx +
(x)Q(x)]dx + 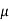 (x)dy = 0
(x)dy = 0
Now the exactness condition is 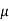 (x)P(x) =
(x)P(x) =  ‘(x), which you may recall is exactly how we derived the formula for the integrating fact or, which means that the new equation is exact!
‘(x), which you may recall is exactly how we derived the formula for the integrating fact or, which means that the new equation is exact!
Definition:
If the equation
M(x, y)dx + N(x, y)dy = 0 ……… (1)
Is exact, then  (x, y) is an integrating factor of equation (1).
(x, y) is an integrating factor of equation (1).
Example: Show that 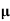 (x; y) =
(x; y) =  is an integrating factor for
is an integrating factor for
(2y - 6x)dx + (3x - 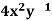 )dy = 0;
)dy = 0;
And use this integrating factor to solve the DE.
Sol:
Here we find  and
and  , so the original equation is not exact.
, so the original equation is not exact.
Multiplying through by  (x, y) gives
(x, y) gives
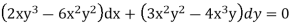
Re-checking the exactness condition, we have

So the new equation is exact, verifying that 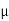 (x; y) is an integrating factor for the original equation. We now solve the DE:
(x; y) is an integrating factor for the original equation. We now solve the DE:


Therefore, an implicit solution is 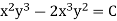
Note- it is possible to lose or gain solutions when multiplying by an integrating factor. In this case, y = 0 is a solution of the revised equation but not of the original equation. This extraneous solution appears because when multiplying by  = x
= x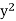 , we are actually multiplying by zero if y = 0. In general, you should always check whether any solutions to
, we are actually multiplying by zero if y = 0. In general, you should always check whether any solutions to  (x, y) = 0 are also solutions to the original DE.
(x, y) = 0 are also solutions to the original DE.
Finding Integrating Factors:
So if we can determine an integrating factor for a non-exact DE, we can convert it to an exact DE and easily solve it. The question which remains is: how can we find an integrating factor? Since we know that the equation
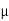 (x, y)M(x; y)dx +
(x, y)M(x; y)dx + 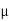 (x, y)N(x, y)dy = 0
(x, y)N(x, y)dy = 0
Is exact, the condition for exactness must be satisfied; that is,
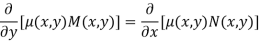
Applying the product rule and some algebra gives the partial differential equation
 …………(2)
…………(2)
Which usually is more difficult to solve than the equation we first started with. We say usually" because there are two exceptions which will help us out.
The exceptions are when the integrating factor is a function of just one variable, not
Two. Suppose first that 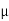 (x) depends only on x. Then the equation (2) reduces to
(x) depends only on x. Then the equation (2) reduces to
 …….. (3)
…….. (3)
Which is separable if 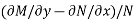 is a function of x alone. Similarly, if
is a function of x alone. Similarly, if  (y)
(y)
Depends only on y, then (2) reduces to
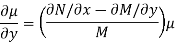
Which again is separable if 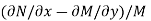 is a function of y alone.
is a function of y alone.
In these cases, we can solve these separable equations for 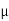 , if we solve equation (3) we obtain
, if we solve equation (3) we obtain
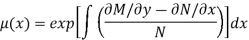
Example: Solve the DE (2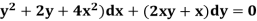
Sol:
Checking for exactness, we have 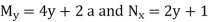 , therefore, the equation is not exact. However,
, therefore, the equation is not exact. However,
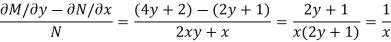
Is a function of x alone.
So we have the integrating factor

After multiplying the original DE by the IF, we have
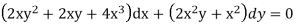
The new equation is exact since 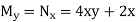 , Now integrate M and N:
, Now integrate M and N:

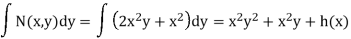
Therefore, an implicit solution is
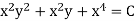
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
- J. Sinha Roy and S Padhy: A course of Ordinary and Partial differential equation Kalyani
- Martin Braun, Differential Equations and their Applications, Springer International, Student Ed. Publishers, New Delhi.
- Higher engineering mathematics, HK Dass