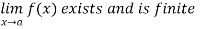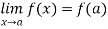Unit - 3
Limits of functions
The intuitive idea of limit was used both by Newton and Leibnitz in their independent invention of Differential Calculus around 1675. Later this notion of limit was also developed by D’Alembert.
“When the successive values attributed to a variable approach indefinitely a fixed value so as to end by differing from it by as little as one wishes, this last is called the limit of all the others.”
The intuitive idea of the function f having a limit L at the point c is that the values f (x) are close to L when x is close to (but different from) c. But it is necessary to have a technical way of working with the idea of ‘‘close to’’ and this is accomplished in the e-d definition given below.
Definition Let A 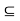 R. A point c
R. A point c 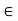 R is a cluster point of A if for every
R is a cluster point of A if for every 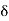 > 0 there exists at least one point x
> 0 there exists at least one point x 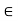 A; x
A; x 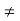 c such that |x - c| <
c such that |x - c| <  .
.
We can define this in the language of neighborhoods as-
A point c is a cluster point of the set A if every d-neighborhood  = (c-
= (c-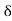 , c+
, c+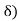 of c contains at least one point of A distinct from c.
of c contains at least one point of A distinct from c.
For example, if A := {1, 2}, then the point 1 is not a cluster point of A, since choosing 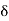 := 1 2 gives a neighborhood of 1 that contains no points of A distinct from 1. The same is true for the point 2, so we see that A has no cluster points
:= 1 2 gives a neighborhood of 1 that contains no points of A distinct from 1. The same is true for the point 2, so we see that A has no cluster points
Theorem A number c 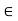 R is a cluster point of a subset A of R if and only if there exists a sequence (
R is a cluster point of a subset A of R if and only if there exists a sequence (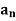 ) in A such that lim
) in A such that lim 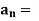 c and
c and 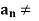 c for all n
c for all n 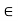 N.
N.
Proof:
If c is a cluster point of A, then for any n 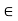 N the (1/n)-neighborhood
N the (1/n)-neighborhood 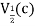 contains at least one point an in A distinct from c. Then
contains at least one point an in A distinct from c. Then 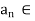 A;
A; 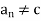 , and
, and 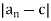 < 1/n implies lim
< 1/n implies lim  = c.
= c.
Conversely, if there exists a sequence (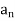 ) in A
) in A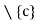 with
with  = c then for any
= c then for any 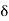 > 0 there exists K such that if n
> 0 there exists K such that if n 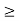 K, then
K, then 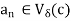 . Therefore the d-neighborhood
. Therefore the d-neighborhood 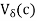 of c contains the points
of c contains the points 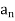 , for n
, for n 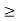 K, which belong to A and are distinct from c.
K, which belong to A and are distinct from c.
Definition of limit:
Let A 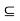 R, and let c be a cluster point of A. For a function f : A
R, and let c be a cluster point of A. For a function f : A 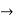 R, a real number L is said to be a limit of f at c if, given any
R, a real number L is said to be a limit of f at c if, given any 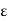 > 0, there exists a
> 0, there exists a 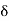 > 0 such that if x
> 0 such that if x 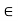 A and 0 < |x - c| <
A and 0 < |x - c| <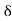 , then |f(x) – L| <
, then |f(x) – L| < 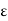
Note:
- Since the value of
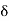 usually depends on
usually depends on 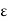 , we will sometimes write
, we will sometimes write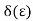 instead of
instead of 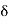 to emphasize this dependence.
to emphasize this dependence.
- The inequality 0 < |x - c| is equivalent to saying x
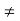 c.
c.
If L is a limit of f at c, then we also say that f converges to L at c. We often write
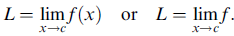
We also say that ‘‘f (x) approaches L as x approaches c.’’
If the limit of f at c does not exist, we say that f diverges at c.
Example: Let a function f: R 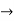 R be defined as
R be defined as
f(x) = 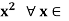 R.
R.
Find its limits when x 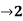
Sol: By intuition, it follows that

In other words, we have to show that for a given 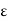 > 0, there exists a
> 0, there exists a 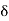 > 0 such that
> 0 such that
0 < |x – 2| < 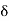 implies |f(x) – 4| <
implies |f(x) – 4| <  .
.
Suppose that an 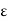 > 0 is fixed. Then consider the quantity |f(x) – 4|, which we can write as
> 0 is fixed. Then consider the quantity |f(x) – 4|, which we can write as
|f(x) – 4| = |x2 – 4| = |(x – 2)(x + 2)|.
Note that the term |x – 2| is exactly the same that appears in the 6–inequality in the definition.
Therefore, this term should be less than. In other words,
|x – 2| < 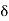
Implies 2 – 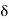 < x < 2 +
< x < 2 + 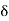
Implies x 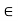 ] 2 –
] 2 – 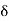 , 2 +
, 2 + 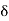 [.
[.
We restrict 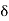 to a value 2 so that x lies in the interval ] 2 –
to a value 2 so that x lies in the interval ] 2 – 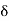 , 2 +
, 2 + 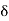 [
[ 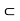 ] 0, 4[. Accordingly, then
] 0, 4[. Accordingly, then
|x + 2| < 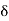 . Thus, if
. Thus, if 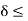 2, then
2, then
|x – 2| < 2 implies 0 < |x + 2| <  , and further that
, and further that
|x – 2| < 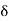 2
2 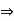 |x + 2| |x – 2| <
|x + 2| |x – 2| < 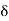 |x – 2| < 6
|x – 2| < 6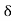 .
.
If 6 is small then so is 6 . In fact it can be made less than by choosing
. In fact it can be made less than by choosing 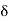 suitably. Let us, therefore, select 6 such that
suitably. Let us, therefore, select 6 such that 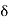 = min.(2,
= min.(2, 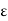 /6). Then
/6). Then
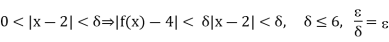
Theorem: if 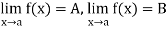 then A=B
then A=B
Proof: In short, we have to show that if 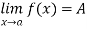 has two values say A and B, then A = B. Since
has two values say A and B, then A = B. Since
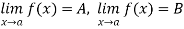 given a number E > 0, there exists numbers
given a number E > 0, there exists numbers 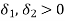 such that
such that
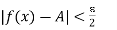 whenever
whenever 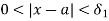
And
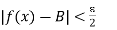 whenever
whenever 
If we take equal to minimum of 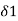 and
and 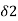 , then we have
, then we have
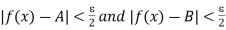 whenever
whenever 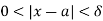
Choose an x0 such that 0 < |x0 – a| < 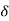 . Then
. Then
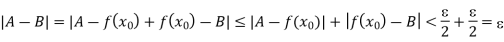
E is arbitrary while A and B are fixed. Hence |A – B| is less than every positive number 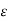 which implies that |A – B| = 0 and hence A = B.
which implies that |A – B| = 0 and hence A = B.
Right Hand Limits and Left Hand Limits
Let a function f be defined in a neighbourhood of a point ‘a’ except possibly at ‘a’. It is said to tend to a number A as x tends to a number ‘a’ from the right or through values greater than ‘a’ if given a number 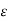 > 0, there exists a number
> 0, there exists a number 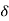 > 0 such that
> 0 such that
|f(x) –A| < 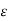 for a <x < a +
for a <x < a +  .
.
We write, it as
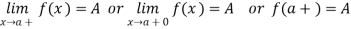
The function f is said to tend to a number A as x tends to ‘a’ from the left or through values smaller than ‘a’ if given a number E > 0, there exists a number 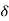 > 0 such that
> 0 such that
|f(x) – A| < 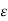 for a – 6 < x < a.
for a – 6 < x < a.
We write it as
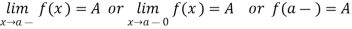
Example: Find the limit of the function f defined by
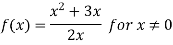
When x tends to zero.
Sol:
The given function is not defined at x = 0 since f(0) =0/0 which is not defined or indeterminate form.
If x tends to 0, then f(x) = 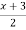 . Therefore
. Therefore
Right Hand Limit =
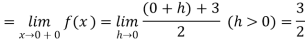
Left Hand Limit =

Since both the right hand and left hand limits exist and are equal,

Example: Consider the function I defined by
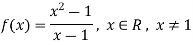
As limit tends to 1
Sol:
Note that f(x) is not defined at x = 1.
For any x 

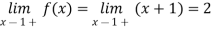
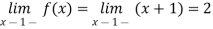
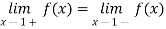
By theorem 2, 
 can be seen by
can be seen by  definition as follows:
definition as follows:
Corresponding to any number E > 0, we can choose 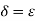 itself. Then, it is clear that
itself. Then, it is clear that
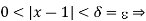
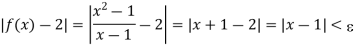
From Theorem 2, it follows that f(l+) and f(l–) also exist and are both equal to 2.
Key takeaways:
- When the successive values attributed to a variable approach indefinitely a fixed value so as to end by differing from it by as little as one wishes, this last is called the limit of all the others.
- Let A
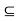 R. A point c
R. A point c 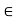 R is a cluster point of A if for every
R is a cluster point of A if for every 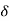 > 0 there exists at least one point x
> 0 there exists at least one point x 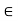 A; x
A; x 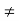 c such that |x - c| <
c such that |x - c| < 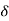 .
. - A number c
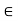 R is a cluster point of a subset A of R if and only if there exists a sequence (
R is a cluster point of a subset A of R if and only if there exists a sequence (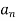 ) in A such that lim
) in A such that lim 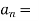 c and
c and 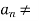 c for all n
c for all n 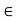 N.
N. - The inequality 0 < |x - c| is equivalent to saying x
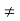 c.
c.
We know that a sequence is also a function but a special type of function.
In the case of a sequence, there are natural numbers only which exceed any choice of m. But for a function with a domain as an arbitrary set of real numbers, this is not necessary the case. Thus in a way, the notion of the limit of a function at infinity is a generalization of that of limit of a sequence.
Theorem: Let a function f be defined in a neighbourhood of a point ‘a’ except possibly at ‘a’. Then f(x) tends to a limit A as x tends to ‘a’ if and only if for every sequence (xn), xn 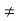 a for any natural number n, converging to ‘a’, f(xn) converges to A.
a for any natural number n, converging to ‘a’, f(xn) converges to A.
Proof:
Let, 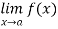 = A. Then for a number E > 0, there exists a 6 > 0 such that for 0 < |x – a| < 6 we
= A. Then for a number E > 0, there exists a 6 > 0 such that for 0 < |x – a| < 6 we
Have 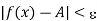
Let (x,) be a sequence (xn 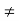 a for any n
a for any n 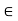 N) such that (xn) converges to a i.e. xn
N) such that (xn) converges to a i.e. xn  a.
a.
Then corresponding to 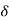 > 0, there exists a natural number m such that for all n
> 0, there exists a natural number m such that for all n 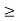 m
m
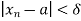
Consequently, we have
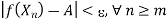
This implies that f(xn) converges to A.
Conversely, let f(xn) converge to A for every sequence xn which converges to a, xn 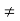 a for any n.
a for any n.
Suppose 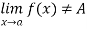
Then there exists at least one 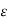 , say
, say 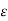 =
= 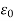 such that for any
such that for any  > 0 we have an
> 0 we have an  such that
such that
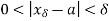
And 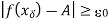
Let 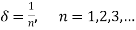
We get a sequence (x,) such that x, = 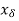 where 6 = 1/n and
where 6 = 1/n and
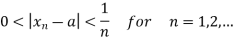
And 

Since
1/n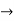 0 and |
0 and |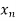 – a| <1/n , it follows that x,
– a| <1/n , it follows that x, 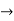 a.
a.
But 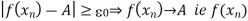
i.e. f(xn) does not tend to A.
Therefore xn 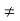 a " a and
a " a and 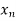 tends to a as n tends to
tends to a as n tends to  whereas f(
whereas f(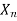 ) does not converge to A, contradicting our hypothesis. This completes the proof of the theorem.
) does not converge to A, contradicting our hypothesis. This completes the proof of the theorem.
Algebraic Operations on Functions
Let f and g be two functions with domain D 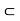 R. Then the sum, difference, product, quotient of f and g denoted by f + g, f – g, fg, f/g are functions with domain D defined by
R. Then the sum, difference, product, quotient of f and g denoted by f + g, f – g, fg, f/g are functions with domain D defined by
(f + g) (x) = f(x) + g(x)
(f – g) (x) = f(x) – g(x)
(fg) (x) = f(x). g(x)
(f/g) (x) = f(x)/g(x)
Provided in the last case g(x) 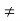 0 for all x in D.
0 for all x in D.
Now we prove the theorem.
Theorem:
- If
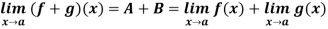
- If

- If
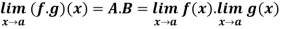
- If further
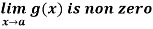 then
then 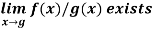 and
and 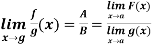
Proof:
Proof of part-1:
Since 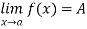 and
and 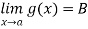 , corresponding to a number
, corresponding to a number 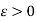 There exist numbers
There exist numbers
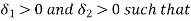
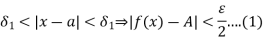

Let 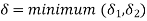 Then from (1) and (2) we have that
Then from (1) and (2) we have that

Which shows that 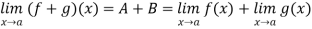
Proof of part-2: Similarly as above we can prove the part-2.
Proof of part-3:
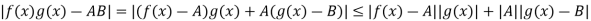
…………(3)
Since 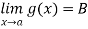 corresponding to 1, there exists a number
corresponding to 1, there exists a number 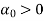
such that 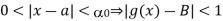
Which implies that |g(x) 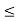 |g(x) – B| + |B|
|g(x) – B| + |B| 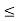 1 + |B| = K (say) ………..(4)
1 + |B| = K (say) ………..(4)
Since f(x) = A, corresponding to  < 0, there exists a number
< 0, there exists a number 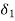 > 0 such that number
> 0 such that number 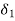 < 0 such that
< 0 such that
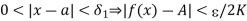 …………(5)
…………(5)
Since 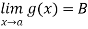 corresponding to
corresponding to 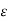 > 0, there exists a number
> 0, there exists a number 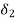 > 0 such that
> 0 such that
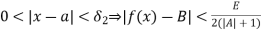 ……….(6)
……….(6)
Let 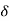 = min (
= min ( ,
, 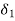 ,
, 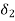 ). Then using (4), (5) and (6) in (3), we have for 0 < |x – a| <
). Then using (4), (5) and (6) in (3), we have for 0 < |x – a| < 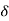 ,
,
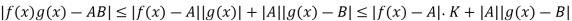
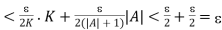 …………..(7)
…………..(7)
Therefore 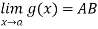 it means
it means 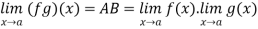
Proof of part-4:
First we show that g does not vanish in a neighbourhood of a.
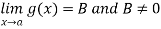 therefore |B|>0 Then corresponding to |B|/2 we have a number
therefore |B|>0 Then corresponding to |B|/2 we have a number 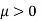 such
such
That for 0 < |x – a| < 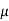 , |g(x) – B| < |B|/2
, |g(x) – B| < |B|/2
Now by triangle inequality, we have
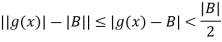
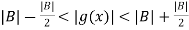 …………(8)
…………(8)
In other words. For 0 < |x – a| < 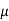 implies |g(x)| > |B|/2
implies |g(x)| > |B|/2
Again since  for a given number
for a given number 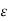 > 0, we have a number
> 0, we have a number 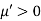 such that 0 < |x – a|
such that 0 < |x – a|
<  implies that
implies that

This proves that
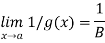
Now by part (iii) of this theorem, we get that

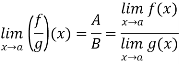
Note- if 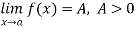 and
and  where A and B are finite real numbers then
where A and B are finite real numbers then
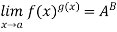
Example: Find the following limit
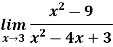
Sol:
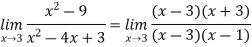
Hence
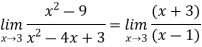
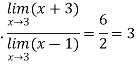
Example: Evaluate-
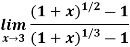
Sol:
To make the problem easier, we make a substitution which enables us to get rid of fractional powers 1/2 and 1/3. L.C.M. Of 2 and 3 is 6. So, we put 1 + x =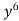
Then we have
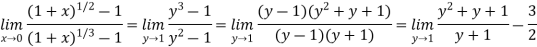
Key takeaways:
(f + g) (x) = f(x) + g(x)
(f – g) (x) = f(x) – g(x)
(fg) (x) = f(x). g(x)
(f/g) (x) = f(x)/g(x)
Continuous Functions:
We have seen that the limit of a function f as the variable x approaches a given point a in the domain of a function f does not depend at all on the value of the function at that point a but it depends only on the values of the function at the points near a. In fact, even if the function f is not defined at a then 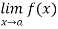 may exist.
may exist.
We have also seen that 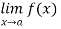 may exist, still it need not be the same as f(a) when it exists. Naturally, we would like to examine the special case when both
may exist, still it need not be the same as f(a) when it exists. Naturally, we would like to examine the special case when both 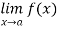 and f(a) exist and are equal. If a function has these properties, then it is called a continuous function at the point a.
and f(a) exist and are equal. If a function has these properties, then it is called a continuous function at the point a.
Definition: Continuity of a Function at a Point
A function f defined on a subset S of the set R is said to be continuous at a point a 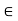 S, if
S, if
Note that in this definition, we assume that S contains some open interval containing the point a.
If we assume that there exists a half open (semi-open) interval [a, c[ contained in S for some c 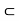 R, then in the above definition, we can replace
R, then in the above definition, we can replace 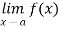 by
by 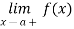 say that the function is continuous from the right of a or f is right continuous at a.
say that the function is continuous from the right of a or f is right continuous at a.
Similarly, you can define left continuity at a, replacing the role of  by
by 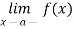
Thus, f is continuous from the right at a if and only if
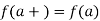
It is continuous from the left at a if and only if
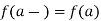
From the definition of continuity of a function f at a point a and properties of limits it follows that f(a+) = f(a–) = f(a) if and only if, f is continuous at a. If a function is both continuous from the right and continuous from the left at a point a, then it is continuous at a and conversely.
The definition X is popularly known as the Limit-Definition of Continuity.
Since 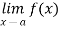 is also defined, in terms of and , we also have an equivalent formulation of the definition X. Note that whenever we talk of continuity of a function f at a in S, we always assume that S contains a neighbourhood containing a. Also remember that if there is one such neighbourhood there are infinitely many such neighbourhoods. An equivalent definition of continuity in terms of epsilon and delta is given as follows:
is also defined, in terms of and , we also have an equivalent formulation of the definition X. Note that whenever we talk of continuity of a function f at a in S, we always assume that S contains a neighbourhood containing a. Also remember that if there is one such neighbourhood there are infinitely many such neighbourhoods. An equivalent definition of continuity in terms of epsilon and delta is given as follows:
Definition: A function f is continuous at x = a if f is defined in a neighbourhood of a and corresponding to a given number E > 0, there exists some number 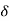 > 0 such that |x – a | <
> 0 such that |x – a | < 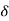 implies |f(x) – f(a)| < E.
implies |f(x) – f(a)| < E.
Example: Examine the continuity of signum function.
Sol:
The signum function, as we know a function f: R  R defined as
R defined as
f(x) = 1 if x > 0
= 0 if x = 0
= –1 if x < 0
This function is not continuous at the point x = 0. We have already seen that f(0+) = 1, f(0–) = –1.
Since f(0+) 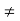 f(0–),
f(0–),  i does not exist and consequently the function is not continuous at
i does not exist and consequently the function is not continuous at
x = 0. For every point x 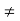 0 the function f is continuous. This is easily seen from the graph of
0 the function f is continuous. This is easily seen from the graph of
The function f. There is a jump at the point x = 0 in the values of f(x) defined in a neighbourhood
Of 0.
Note that if f: R 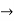 R is defined as,
R is defined as,
f(x) = 1 if x 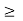 0.
0.
= –1 if x < 0.
Then, it is easy to see that this function is continuous from the right at x = 0 but not from the left.
It is continuous at every point x 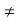 0.
0.
Similarly, if f is defined by f(x) = 1 if x > 0
= –1 if x 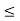 0
0
Then f is continuous from the left at x = 0 but not from the right.
Example: Discuss the continuity of the function sin x on the real line R.
Sol:
Let f(x) = Sin x for every x 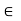 R
R
We show by the (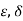 )-definition that f is continuous at every point of R.
)-definition that f is continuous at every point of R.
Consider an arbitrary point a 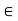 R. We have
R. We have
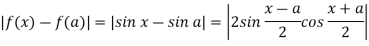
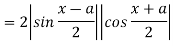
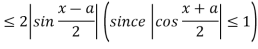
From Trigonometry, we know that
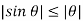
Therefore,
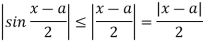
Consequently
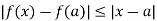 < if |x-a| < δ where δ=
< if |x-a| < δ where δ=
So f is continuous at the point a. But a is any point of R. Hence Sin x is continuous on the real line R.
Sequential continuity:
Definition: Sequential Continuity of a Function
Let f be a real-valued function whose domain is a subset of the set R. The function f is said to be continuous at a point a if, for every sequence (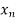 ) in the domain of f converging to a, we have,
) in the domain of f converging to a, we have,
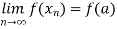
Example: Let f: R 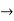 R be defined as
R be defined as

Prove that f is continuous on R by using the sequential definition of the continuity of a function.
Solution: Suppose (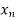 ) is a sequence which converges to a point ‘a’ of R. Then, we have
) is a sequence which converges to a point ‘a’ of R. Then, we have
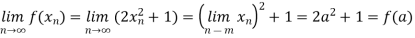
This shows that f is continuous at a point a belongs to R. Since a is an arbitrary element of R, therefore, f is continuous everywhere on R.
Key takeaways:
1. A function f defined on a subset S of the set R is said to be continuous at a point a  S, if
S, if
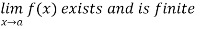
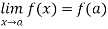
2. f is continuous from the right at a if and only if

It is continuous from the left at a if and only if
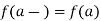
As we have proved limit theorems for sum, difference, product, etc. of two functions, we have similar results for continuous functions also. These algebra operations on the class of continuous functions can be deduced from the corresponding theorems on limits of functions, using the limit definition of continuity.
Theorem: Let f and g be any real functions both continuous at a point a 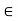 R. Then,
R. Then,
(i)  f defined by (
f defined by (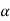 f) (x) =
f) (x) = 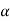 f(x), is continuous for any real number
f(x), is continuous for any real number 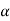 ,
,
(ii) f + g defined by (f + g) (x) = f(x) + g(x) is continuous at a,
(iii) f – g defined by (f – g) (x) = f(x) – g(x) is continuous at a,
(iv) fg defined by (fg) (x) = f(x) g(x) is continuous at a,
(v) f/g defined by (f/g) (x) = f(x)/g(x)
, is continuous at a provided g(a) 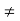 0.
0.
Proof:
Let 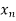 be an arbitrary sequence converging to a. Then the continuity of f and g imply that the sequences f(
be an arbitrary sequence converging to a. Then the continuity of f and g imply that the sequences f(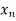 ) and g(
) and g(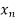 ) converge to f(a) and g(a) respectively. In other words, lim f(
) converge to f(a) and g(a) respectively. In other words, lim f(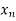 ) = f(a),
) = f(a),
Lim g(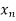 ) = g(a).
) = g(a).
Using the algebra of sequences, we can conclude that
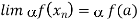

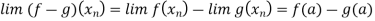
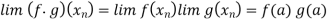
If infinite number of 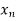 ’s are such that g(
’s are such that g(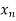 ) = 0, then g(
) = 0, then g( ) – g(a) implies that g(a) = 0, a contradiction.
) – g(a) implies that g(a) = 0, a contradiction.
This proves the parts (i), (ii), (iii) and (iv). To prove the part (v) we proceed as follows:
Since g(a) 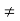 0, we can find a > 0 such that the interval ]g(a) –
0, we can find a > 0 such that the interval ]g(a) – 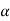 , g(a) +
, g(a) + 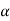 [ is either entirely to the right or to the left of zero depending on whether g(a) > 0 or g(a) < 0. Corresponding to a > 0, there exists a
[ is either entirely to the right or to the left of zero depending on whether g(a) > 0 or g(a) < 0. Corresponding to a > 0, there exists a  > 0 such that |x – a| <
> 0 such that |x – a| < 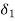 implies |g(x) – g(a)| <
implies |g(x) – g(a)| < 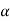 , i.e., g(a) –
, i.e., g(a) – 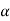 < g(x) < g(a) + at. Thus, for x such that |x – a| <
< g(x) < g(a) + at. Thus, for x such that |x – a| < 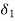 , g(x)
, g(x) 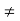 0. If (
0. If (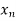 ) converges to a, omitting a finite number of terms of the sequence if necessary, then we can assume that g(
) converges to a, omitting a finite number of terms of the sequence if necessary, then we can assume that g(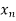 )
) 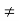 0, for all n. Hence,
0, for all n. Hence,
 converges to f(a)/ g(a) and so f/g is continuous at a. This completes the proof of the theorem.
converges to f(a)/ g(a) and so f/g is continuous at a. This completes the proof of the theorem.
In part (v) if we define f by f(x) = 1, then it follows that if g is continuous at ‘a’ and g(a) 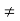 0, then its reciprocal function 1/g is continuous at ‘a’.
0, then its reciprocal function 1/g is continuous at ‘a’.
Theorem: Let f and g be two real functions such that the range of g is contained in, the domain of f. If g is continuous at x = a, f is continuous at b = g(a) and h(x) = f(g(x)), for x in the domain of g, then h is continuous at a.
Proof:
Given 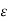 > 0, the continuity of f at b = g(a) implies the existence of an
> 0, the continuity of f at b = g(a) implies the existence of an 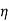 > 0 such that for
> 0 such that for
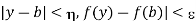 (1)
(1)
Corresponding to 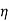 > 0, from the continuity of g at x = a, we get a
> 0, from the continuity of g at x = a, we get a 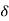 > 0 such that
> 0 such that

From (1) and (2) we get,
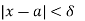 implies that
implies that
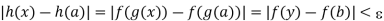
Where we have taken y = g(x). Hence h is continuous at a which proves the theorem.
Non-continuous Functions
A function f: S  R fails to be continuous on its domain S if it is not continuous at a particular point of S. This means that there exists a point a
R fails to be continuous on its domain S if it is not continuous at a particular point of S. This means that there exists a point a  S such that, either
S such that, either
(i)  does not exist, or
does not exist, or
(ii)  ) exists but is not equal to f(a).
) exists but is not equal to f(a).
But we know that a function f is continuous at a point a if and only if
f(a+) = f(a–) = f(a).
Thus, if f is not continuous at a, then one of the following will happen:
(i) Either f(a+) or f(a–) does not exist (this includes the case when both f(a+) and f(a) do not exist).
(ii) Both f(a+) and f(a–) exist but f(a+)  f(a–).
f(a–).
(iii) Both f(a+) and f(a–) exist and f(a+) = f(a–) but they are not equal to f(a).
If a function f: S 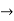 R is discontinuous for each b
R is discontinuous for each b 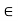 S, then we say that totally discontinuous an S.
S, then we say that totally discontinuous an S.
Example: Examine whether or not the function f: R 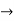 R defined as,
R defined as,
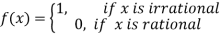
Is totally discontinuous.
Sol:
Let b be an arbitrary but fixed real number. Choose 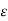 = 1/2. Let
= 1/2. Let 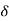 > 0 be fixed. Then the interval defined by
> 0 be fixed. Then the interval defined by 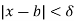
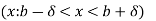
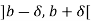
This interval contains both rational as well as irrational numbers.
If b is rational, then choose x in the interval to be irrational, If b is irrational then choose x in the interval to be rational. In either case,

And
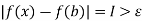
Thus, f is not continuous at b. Since b is an arbitrary element of S, f is not continuous at any point of S and hence is totally discontinuous.
There are certain discontinuities which can be removed. These are known as removable discontinuities. A discontinuity of a given function f: S  R is said to be removable if the limit of f(x) as x tends to a exits and that
R is said to be removable if the limit of f(x) as x tends to a exits and that
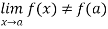
In other words, f has removable discontinuity at x = a if f(a+) = f(a–) but none is equal to f(a).
The removable discontinuities of a function can be removed simply by changing the value of the function at the point a of discontinuity. For this a function with removable discontinuities can be thought of as being almost continuous
We will now consider functions continuous on bounded closed intervals. They have properties which fail to be true when the intervals are not bounded or closed.
Theorem 1: A function f continuous on a bounded and closed interval [a, b] is necessarily a bounded function.
Proof: Let S be the collection of all real numbers c in the interval [a, b] such that f is bounded on the interval [a, c]. That is, a real number c in [a, b] belongs to S if and only if there exists a constant  such that |f(x)|
such that |f(x)| for all x in [a, c]. Clearly, S
for all x in [a, c]. Clearly, S 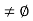 since a
since a  S and b is an upper bound for S.
S and b is an upper bound for S.
Hence, by completeness property of R, there exists a least upper bound for S. Let it be k (say).
Clearly, k  b. We prove that k
b. We prove that k 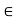 S and k = b which will complete the proof of the theorem.
S and k = b which will complete the proof of the theorem.
Corresponding to 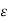 = 1, by the continuity of f at k(
= 1, by the continuity of f at k( b) there exists a d > 0 such tha
b) there exists a d > 0 such tha
|f(x) – f(k)| <  = 1 whenever |x – k| < d, x
= 1 whenever |x – k| < d, x  [a, b].
[a, b].
By the triangle inequality we have
|f(x)| – |f (k)| |f(x) – f(k)| < 1
Hence, for all x in [a. b] for which |x – k| < d, we have that
|f(x)| < |f(k)| + 1 ...(1)
Since k is the least upper bound of S, k – d is not an upper bound of S. Therefore, there is a number
c 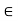 S such that
S such that
k – d < c 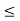 k
k
Consider any t such that k 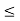 t < k + d. If x belongs to the interval [c, t] then |x – k| < d. For,
t < k + d. If x belongs to the interval [c, t] then |x – k| < d. For,
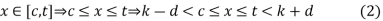
Now c  S implies that there exists
S implies that there exists 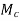 > 0 such that for all
> 0 such that for all
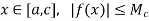
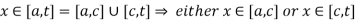
If x 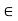 [a, c], by (3) we have
[a, c], by (3) we have
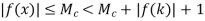
If, however, x 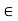 [c, t] then by (1) and (2) we have
[c, t] then by (1) and (2) we have

In any case we get that x 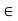 [a, t] implies that
[a, t] implies that
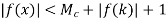
This shows that f is bounded in the interval [a, t] thus proving that t 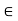 S whenever k t < k + d.
S whenever k t < k + d.
In particular k 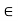 S. In such a case k = b. For otherwise we can choose a ‘t’ such that k < t < k + d and
S. In such a case k = b. For otherwise we can choose a ‘t’ such that k < t < k + d and
t 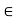 S which will contradict the fact that k is an upper bound. This completes the proof of the theorem.
S which will contradict the fact that k is an upper bound. This completes the proof of the theorem.
Example: Show that the function f defined by f(x) = 3 V x 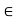 [0,
[0,  [ is continuous but not bounded.
[ is continuous but not bounded.
Sol:
The function f being a polynomial function is continuous in [0,  [. The domain of the function is an unbounded closed interval. The function is not bounded since the set of values of the function that is the range of the function is {
[. The domain of the function is an unbounded closed interval. The function is not bounded since the set of values of the function that is the range of the function is {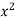 : x
: x 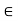 [0,
[0,  [ } = [0,
[ } = [0, 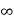 [ which is not bounded
[ which is not bounded
Example: Show that the function f such that f(x) = x for every x 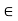 ]0, 1[ is continuous but does not attain its bounds.
]0, 1[ is continuous but does not attain its bounds.
Sol:
As mentioned the identity function f is continuous in ]0, 1[. Here the domain of f is
Bounded but is not a closed interval. The function f is bounded with least upper bound (1.u.b) =
1 and greatest lower bound (g.l.b) = 0 and both the bounds are not attained by the function, since range of f = ]0, 1[.
Example: Show that the function f such that
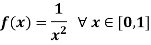
Is continuous but does not attain its g.l.b.
Solution: The function G given by G(x) = 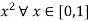 is continuous and G(x)
is continuous and G(x)  0
0  x
x 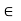 ]0, 1[ therefore its reciprocal function f(x) =
]0, 1[ therefore its reciprocal function f(x) = 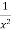 is continuous in ]0, 1[. Here the domain f is bounded but is not a closed interval.
is continuous in ]0, 1[. Here the domain f is bounded but is not a closed interval.
Further l.u.b. Of f does not exist whereas its g.l.b. Is 1 which is not attained by f.
Key takeaways:
A function f continuous on a bounded and closed interval [a, b] is necessarily a bounded function.
Bolzano’s Intermediate Value Theorem:
Statement:
Let f be a continuous function on an interval containing a and b. If K is any number between f(a) and f(b) then there is a number c, a 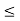 c S b such that f(c) = K.
c S b such that f(c) = K.
Proof:
Either f(a) = f(b) or f(a) < f(b) or f(b) < f(a). If f(a) = f(b) then K = f(a) = f(b) and so c can be taken to be either a or b. We will assume that f(a) < f(b). (The other case can be dealt with similarly.) We can, therefore, assume that f(a) < K < f(b).
Let S denote the collection of all real numbers x in [a, b] such that f(x) < K. Clearly S contains a, so S 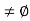 and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a
and b is an upper bound for S. Hence, by completeness property of R, S has least upper bound and let us denote this least upper bound by c. Then a  c
c 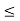 b. We want to show that f(c) = K.
b. We want to show that f(c) = K.
Since f is continuous on [a, b], f is continuous at c. Therefore, given 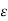 > 0, there exists a 6 > 0 such that whenever x is in [a, b] and |x – c| < 6, |f(x) – f(c) ( < G,
> 0, there exists a 6 > 0 such that whenever x is in [a, b] and |x – c| < 6, |f(x) – f(c) ( < G,
f(c) –  < f(x) < f(c) +
< f(x) < f(c) +  . ………..(1)
. ………..(1)
If c 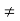 b, we can clearly assume that c + 6 < b. Now c is the least upper bound of S. So c –
b, we can clearly assume that c + 6 < b. Now c is the least upper bound of S. So c – 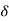 is not
is not
‘an upper bound’ of S. Hence, there exists a y in S such that c – 6 < y c. Clearly |y – c| < 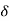 and so by (1) above, we have
and so by (1) above, we have
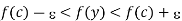
Since y is in S, therefore f(y) < K. Thus, we get
f(c) – S < K
If now c = b then K –  < K < f(b) = f(c), i.e., K < f(c) + E. If c
< K < f(b) = f(c), i.e., K < f(c) + E. If c 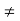 b, then c < b; then there exists an x such that c < x < c + 6, 6, x
b, then c < b; then there exists an x such that c < x < c + 6, 6, x 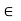 [a, b] and for this x, f(x) < f(c) +
[a, b] and for this x, f(x) < f(c) + 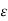 by (1) above. Since x > c, K
by (1) above. Since x > c, K  f(x), for otherwise x would be in S which will imply that c is not an upper bound of S. Thus, again we have K
f(x), for otherwise x would be in S which will imply that c is not an upper bound of S. Thus, again we have K 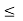 f(x) < f(c) + E.
f(x) < f(c) + E.
In any case,
K < f(c) + 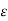 ……….(2)
……….(2)
We get for every 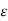 > 0
> 0
f (c) –  < K < f(c) +
< K < f(c) + 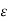
Which proves that K = f(c), since 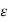 is arbitrary while K, f(c) are fixed. In fact, when f(a) < K < f(b) and f(c) = K, then a < c < b.
is arbitrary while K, f(c) are fixed. In fact, when f(a) < K < f(b) and f(c) = K, then a < c < b.
Location of roots theorem & preservation of intervals theorem
Theorem-1:
If f is a continuous function on the closed interval [a, b] and If f(a) and f(b) have opposite signs (i.e., f(a) f(b) < 0), then there is a point x0 in ]a, b[ at which f vanishes. (i.e., f(x0) = 0).
Theorem-2:
Let f be a continuous function defined on a bounded closed interval [a, b] with values in [a, b]. Then there exists a point c in [a, b] such that f(c) = c. (i.e., there exists a fixed point c for the function f on [a, b]).
Proof: If f(a) = a or f(b) = b then there is nothing to prove. Hence, we assume that f(a) 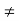 a and f(b)
a and f(b) 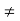 b.
b.
Consider the function g defined by g(x) = f(x) – x, x 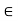 [a, b]. The function being the difference of two continuous functions, is continuous on [a, b]. Further, since f(a), f(b) are in [a, b], f(a) > a
[a, b]. The function being the difference of two continuous functions, is continuous on [a, b]. Further, since f(a), f(b) are in [a, b], f(a) > a
(since f(a) 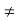 a, f(a)
a, f(a) 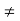 [a, b]) and f(b) < b. (Since f(b)
[a, b]) and f(b) < b. (Since f(b) 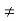 b, f(b)
b, f(b) 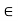 [a, b]). So, g(a) > 0 and g(b) < 0. Hence, by theorem-1, there exists a c in ]a, b[ such that g(c) = 0, i.e., f(c) = c. Hence, there exists ac in [a, b] such that f(c) = c.
[a, b]). So, g(a) > 0 and g(b) < 0. Hence, by theorem-1, there exists a c in ]a, b[ such that g(c) = 0, i.e., f(c) = c. Hence, there exists ac in [a, b] such that f(c) = c.
The above theorem-1 helps us sometimes to locate some of the roots of polynomials.
Example: The equation  + 2x – 11 = 0 has a real root lying between 1 and 2.
+ 2x – 11 = 0 has a real root lying between 1 and 2.
Sol:
The function f(x) = 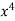 + 2x – 11 is a continuous function on the closed interval [1, 2], f(1) = –8 and f(2) = 9. Hence, by theorem-1, there exists an x0
+ 2x – 11 is a continuous function on the closed interval [1, 2], f(1) = –8 and f(2) = 9. Hence, by theorem-1, there exists an x0 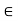 ]1, 2[ such that f(x0) = 0, i.e., x0 is a real root of the equation
]1, 2[ such that f(x0) = 0, i.e., x0 is a real root of the equation 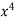 + 2x – 11 = 0 lying in the interval ]1, 2[.
+ 2x – 11 = 0 lying in the interval ]1, 2[.
Key takeaways:
- Let f be a continuous function on an interval containing a and b. If K is any number between f(a) and f(b) then there is a number c, a
 c S b such that f(c) = K.
c S b such that f(c) = K. - If f is a continuous function on the closed interval [a, b] and If f(a) and f(b) have opposite signs (i.e., f(a) f(b) < 0), then there is a point x0 in ]a, b[ at which f vanishes. (i.e., f(x0) = 0).
- Let f be a continuous function defined on a bounded closed interval [a, b] with values in [a, b]. Then there exists a point c in [a, b] such that f(c) = c. (i.e., there exists a fixed point c for the function f on [a, b]).
Here we will understand the concept of uniform continuity of a function.
The concept of uniform continuity is given in the whole domain of the function whereas the concept of continuity is pointwise that is it is given at a point of the domain of the function. If a function f is continuous at a point a in a set A, then corresponding to a number E > 0, there exists a positive number 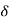 (a) to stress that
(a) to stress that 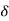 (a) in general depends an the point a chosen) such that |x – a| <
(a) in general depends an the point a chosen) such that |x – a| < 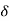 (a) implies that |f(x) – f(a)| <
(a) implies that |f(x) – f(a)| <  . The number
. The number 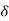 (a) also depends on E. When the point a varies
(a) also depends on E. When the point a varies 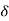 (a) also varies. We may or may not have a
(a) also varies. We may or may not have a 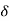 (a) which serves for all points a in A. If we have such a
(a) which serves for all points a in A. If we have such a 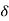 (a) common to all points a in A, then we say that f is uniformly continuous on A.
(a) common to all points a in A, then we say that f is uniformly continuous on A.
Definition-Uniform Continuity of a Function:
Let f be a function defined on a subset A contained in the set R of all reals. If corresponding to any number  > 0, there exists a number
> 0, there exists a number 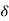 > 0 (depending only on G) such that
> 0 (depending only on G) such that
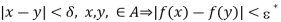
Then we say that f is uniformly continuous on the subset A.
An immediate consequence of the definition of uniform continuity is that uniform continuity in a set A implies pointwise continuity in A.
Theorem-1: If a function f is uniformly continuous in a set A, then it is continuous in A.
Proof: Since f is uniformly continuous in A, given a positive number E, there corresponds a positive number 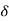 (a) such that
(a) such that
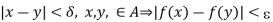 ……….(1)
……….(1)
Let a be any point of A. In the above result (1), take y = a. Then we get,
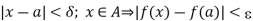
Which shows that f is continuous at ‘a’. Since ‘a’ is any point of A, it follows that f is continuous in A.
Example: Show that the function, f:R - R

Is uniformly continuous on R
Sol:
For a given 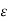 > 0,
> 0, 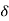 (a) can be chosen to be itself so that
(a) can be chosen to be itself so that
|x – y| <  (a) = G implies |f(x) – f(y)| = |x – y| <
(a) = G implies |f(x) – f(y)| = |x – y| <  .
.
Example: Show that the function, f:R - R
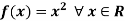
Is not uniformly continuous on R
Sol:
Let 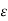 be any positive number. Let
be any positive number. Let 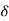 > 0 be any arbitrary positive number. Choose
> 0 be any arbitrary positive number. Choose
x > 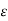 /
/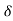 and y = x +
and y = x + 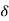 /2. Then
/2. Then

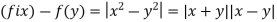
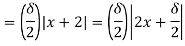
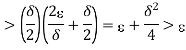
That is whatever 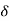 > 0 we choose, there exist real numbers x, y such that |x – y| <
> 0 we choose, there exist real numbers x, y such that |x – y| < 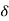 but |f(x) –
but |f(x) –
f(y)|> G which proves that f is not uniformly continuous.
Theorem: If f is a continuous function on a bounded and closed interval [a, b] then f is uniformly continuous on [a, b].
Proof: Let f be a continuous function defined on the bounded closed interval [a, b]. Let S be the set of all real numbers c in the interval [a, b] such that for a given 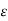 > 0, there exists positive number dc such that for points x1, x2 belonging to closed interval [a, c]
> 0, there exists positive number dc such that for points x1, x2 belonging to closed interval [a, c]
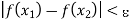 whenever
whenever 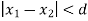
(In other words f is uniformly continuous on the interval [a, c]. Clearly a  S so that S is nonempty.
S so that S is nonempty.
Also b is an upper bound of S. Prom completeness property of the real line S has least upper bound which we denote by k. k 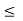 b.
b.
f is continuous at k. Hence given E > 0, there exists positive real number dk such that
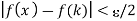 whenever
whenever 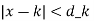 ………..(1)
………..(1)
Since k is the least upper bound of S, k – ½ is not an upper bound of S.
Therefore there exists a point c 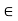 S such that
S such that
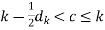 …………(2)
…………(2)
Since c 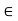 S; from the definition of S we see that there exists dc such that
S; from the definition of S we see that there exists dc such that
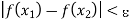 whenever
whenever 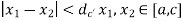 ……..(3)
……..(3)
Let d = min ((1/2) dk, dc) and b’ = min. (k + (1/2) dk, b).
Now let x1, x2 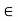 [a, b’] and |x1 – x2|. Then if x1, x2
[a, b’] and |x1 – x2|. Then if x1, x2 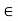 [a, c], |x1 – x2| < d
[a, c], |x1 – x2| < d  dc by the choice of d and dc, then |f(x1) – f(x2)| <
dc by the choice of d and dc, then |f(x1) – f(x2)| < 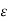 by (3). If one of x1 x2 is not in fa, cl, then both x1, x2 belong to the interval ]k – dk, k + dk[. For x1 does not belongs to {a, c], implies b’
by (3). If one of x1 x2 is not in fa, cl, then both x1, x2 belong to the interval ]k – dk, k + dk[. For x1 does not belongs to {a, c], implies b’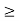 x1 > c > k – (1/2)dk > k – dk by (2) above. This means x1
x1 > c > k – (1/2)dk > k – dk by (2) above. This means x1  b’ implies x1
b’ implies x1  k + (1/2)dk < k – dk by the choice of b’. i.e.
k + (1/2)dk < k – dk by the choice of b’. i.e.
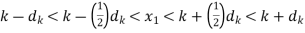 ………..(4)
………..(4)
|x1 – x2| < d implies that x1 – (1/2) dk < x2 < x1 + (1/2)dk since d 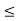 (1/2)dk by this choice of d. Thus we get from (4) above that
(1/2)dk by this choice of d. Thus we get from (4) above that
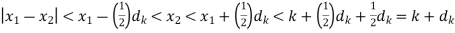 ………….. (5)
………….. (5)
Then (4) and (5) show that x1, x2 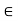 ]k – dk, k + dk[.
]k – dk, k + dk[.
Thus we get that |x1 – k| < dk and |x2 – k| < dy, which in turn implies, by (1) above, that
|f(x1) – (k)| < 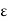 /2 and |f(x2) – f(k)| <
/2 and |f(x2) – f(k)| < 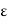 /2 .
/2 .
Thus |f(x1) – f(x2)| < |f(x1) – f(k)| + |f(k) – f(x2)| < 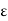 /2 +
/2 + 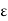 /2 = E. In other words, if |x1 – x2| < d and x1, x2 are in [a, b’] then |f(x1) – f(x2)| < E which proves that b’
/2 = E. In other words, if |x1 – x2| < d and x1, x2 are in [a, b’] then |f(x1) – f(x2)| < E which proves that b’ 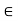 S i.e. b’
S i.e. b’ 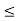 k. But k
k. But k  b’ by the choice of b’ since k
b’ by the choice of b’ since k 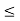 k + (1/2) dk and k a b. Thus we get that k = b’. This can happen only when k = b. For if k < b. i.e. k = b’ = min (k + (l/2) dk, b) < b, then it implies that min (k + (l/2) dk, b) = (k + (1/2) dk = b’, where b’
k + (1/2) dk and k a b. Thus we get that k = b’. This can happen only when k = b. For if k < b. i.e. k = b’ = min (k + (l/2) dk, b) < b, then it implies that min (k + (l/2) dk, b) = (k + (1/2) dk = b’, where b’ 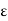 S i.e. k + (1/2) dk is in S and is greater than k which is a contradiction to the fact that k is the l.u.b of S. Thus we have shown that k = b
S i.e. k + (1/2) dk is in S and is greater than k which is a contradiction to the fact that k is the l.u.b of S. Thus we have shown that k = b 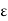 S. In other words there exists a positive number dk (corresponding to b) such that |x1– x2| < dk, x1, x2
S. In other words there exists a positive number dk (corresponding to b) such that |x1– x2| < dk, x1, x2 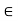 [a,
[a,
b] implies |f(x1) – f(x2)| < 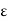 . Therefore f is uniformly continuous in [a, b].
. Therefore f is uniformly continuous in [a, b].
Non-uniform Continuity Criteria:
Let A 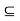 R and let f : A
R and let f : A 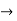 R. Then the following statements are equivalent:
R. Then the following statements are equivalent:
(i) f is not uniformly continuous on A.
(ii) There exists an 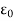 > 0 such that for every d > 0 there are points xd; ud in A such that |
> 0 such that for every d > 0 there are points xd; ud in A such that |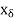 -
- 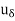 |<
|< 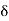 and |
and | - f(
- f(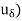 j
j 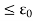
(iii) There exists an 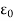 > 0 and two sequences (
> 0 and two sequences (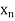 ) and (
) and (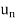 ) in A such that lim (
) in A such that lim (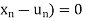 and |
and |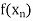 - f(
- f(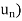 |
| 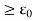
Uniform Continuity Theorem:
Let I be a closed bounded interval and let f : I 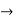 R be continuous on I. Then f is uniformly continuous on I.
R be continuous on I. Then f is uniformly continuous on I.
Proof:
If f is not uniformly continuous on I then, by the preceding result, there exists
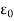 > 0 and two sequences (
> 0 and two sequences (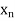 ) and (
) and (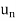 ) in I such that |
) in I such that |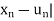 < 1/n and |
< 1/n and |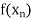 - f(
- f(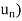 |
|  for all n
for all n 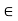 N. Since I is bounded, the sequence (
N. Since I is bounded, the sequence (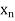 ) is bounded; by the Bolzano- Weierstrass Theorem, here is a subsequence
) is bounded; by the Bolzano- Weierstrass Theorem, here is a subsequence 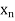 k of (
k of (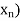 that converges to an element z. Since I is closed, the limit z belongs to I, by Theorem. It is clear that the corresponding subsequence
that converges to an element z. Since I is closed, the limit z belongs to I, by Theorem. It is clear that the corresponding subsequence  Þalso converges to z, since
Þalso converges to z, since

Now if f is continuous at the point z, then both of the sequences f(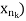 and f(
and f( must converge to f ðzÞ. But this is not possible since
must converge to f ðzÞ. But this is not possible since
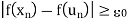
For all n  N. Thus the hypothesis that f is not uniformly continuous on the closed bounded interval I implies that f is not continuous at some point z
N. Thus the hypothesis that f is not uniformly continuous on the closed bounded interval I implies that f is not continuous at some point z 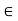 I. Consequently, if f is continuous at every point of I, then f is uniformly continuous on I.
I. Consequently, if f is continuous at every point of I, then f is uniformly continuous on I.
Key takeaways:
- If a function f is uniformly continuous in a set A, then it is continuous in A.
- If f is a continuous function on a bounded and closed interval [a, b] then f is uniformly continuous on [a, b].
- Let I be a closed bounded interval and let f : I
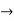 R be continuous on I. Then f is uniformly continuous on I.
R be continuous on I. Then f is uniformly continuous on I.
Monotone function:
A function f is monotone increasing on (a, b) if f(x) 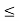 f(y) whenever x < y. A function f is monotone decreasing on (a, b) if f(x)
f(y) whenever x < y. A function f is monotone decreasing on (a, b) if f(x) 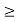 f(y) whenever x < y.
f(y) whenever x < y.
A function f is called monotone on (a, b) if it is either always monotone increasing or monotone decreasing. Basic applications and results
The following properties are true for a monotonic function f : R 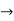 R:
R:
f has limits from the right and from the left at every point of its domain;
- f has a limit at infinity (either
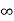 or –
or –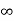 ) of either a real number,
) of either a real number, 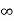 , or –
, or –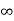 .
. - f can only have jump discontinuities;
- f can only have countably many discontinuities in its domain.
These properties are the reason why monotonic functions are useful in technical work in analysis.
Two facts about these functions are:
If f is a monotonic function defined on an interval I, then f is differentiable almost
Everywhere on I, i.e. the set of numbers x in I such that f is not differentiable in x has
Lebesgue measure zero.
4. if f is a monotonic function defined on an interval [a, b], then f is Riemann integrable.
An important application of monotonic functions is in probability theory. If X is a random
Variable, its cumulative distribution function
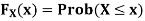
Is a monotonically increasing function.
A function is unimodal if it is monotonically increasing up to some point and then
Monotonically decreasing.
Note-
If f is increasing if -f is decreasing, and visa versa. Equivalently, f is increasing if
- f(x)/f(y)
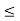 1 whenever x < y
1 whenever x < y - f(x) – f(y)
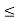 0 whenever x < y
0 whenever x < y
Inverse Function Theorem:
Let f : I 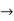 J be a function which is both one-one and onto. If f is continuous on I, then
J be a function which is both one-one and onto. If f is continuous on I, then 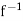 : J
: J 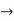 I is
I is
Continuous on J. For example the function.

f(x) = sin x
Is both one-one and onto. Besides f is continuous on , 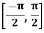 . Therefore, by Theorem above, the function
. Therefore, by Theorem above, the function
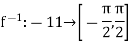
Defined by
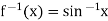
Is continuous on [–1, 1].
Key takeaways:
- A function f is called monotone on (a, b) if it is either always monotone increasing or monotone decreasing.
- If f is a monotonic function defined on an interval [a, b], then f is Riemann integrable.
- A function is unimodal if it is monotonically increasing up to some point and then monotonically decreasing.
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. Advanced engineering mathematics, by HK Dass
3. Mathematical analysis by Dr. Anju panwar
4. Real analysis by Dr. Sachin Kaushal
5. Real analysis by Ajit kumar & S.Kumaresan
6. Principles of real analysis by S.C Malik
7. A BASIC COURSE IN REAL ANALYSIS- AJIT KUMAR
8. Introduction to real analysis by robbert G. Bartle and Donald R. Sherbert